Introduction

As is known to all, the computational complexities of general T2 FLSs [1] are much higher than IT2 FLSs. Recently, as the alpha-planes representations of GT2 fuzzy sets (FSs [2,3,4,5,6]) were put forward by few study groups, the calculated amount of GT2 FLSs can be significantly decreased. As the secondary membership grades of interval T2 FSs are equal to one, they can only measure the uncertainty of membership function (MF) in a unified manner. For GT2 FSs, whose secondary membership grades lie between zero and one, therefore, they can measure the uncertainty of MF in a non-uniform way. In other words, GT2 FSs may be considered as more advanced uncertainty models than IT2 FSs. As the design degrees of freedom increase, general T2 FLSs [7,8,9,10,11] have the latent capacity to overmatch IT2 FLSs on dealing with more complex uncertainty environments.

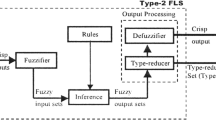
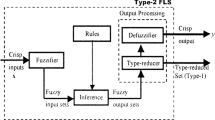
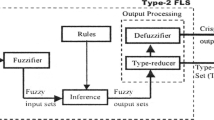
In general, T2 FLSs are made up of five blocks as: fuzzifier, fuzzy rules, fuzzy inference, TR and defuzzification. Among which, the type-reduction acts as translating the type-2 FS to the type-1 FS. Then, the module of defuzzification transforms the T1 FS to a output. The centroid type-reduction [12,13,14] is the most prevalent study method. In the early days, the iterative Karnik–Mendel (KM) algorithms [15] were opened up to perform the TR of interval T2 FLSs. Then, the continuous type of Karnik–Mendel (CKM) algorithms [16, 17] were put forward; moreover, the monotone property and super-convergence nature of them were also proved. Usually, it requires two to six iteration steps for each KM algorithm. For the sake of improving the computational cost, many other iterative algorithms are put forward gradually, they are enhanced Karnik–Mendel (EKM) algorithms [18], weighted based EKM algorithms [5, 19], enhanced opposite direction searching (EODS) algorithms [20,21,22] and so on. The other kinds of noniterative algorithms which achieve the output of systems directly were also put forward, they are Uncertainty Boundary (UB) algorithms [23], Coupland and John algorithms [24], Nagar and Bardini algorithms [13, 25], Nie and Tan algorithms [26, 27], Begian and Melek and Mendel algorithms [28, 29] and so forth. Interval T2 FLSs on account of NB algorithms have excellent shows over the impact of uncertainty [30,31,32]. Most recent theoretical researches about calculating the centroids of IT2 FSs show that the continuous type of NT algorithms are actually an accurate TR method. Furthermore, interval T2 FLSs on the basis of Begian–Melek–Mendel algorithms have advantages on both stability and robustness compared with the T1 FLSs. All these jobs have established foundations for investigating the noniterative algorithms for completing the centroid TR for general T2 FLSs.

The paper analyzes the sum and integral operations in the corresponding discrete and continuous algorithms. In addition, the Nagar and Bardini (NB) and Nie and Tan (NT) algorithms are demonstrated to be two specific circumstances of Begian–Melek–Mendel algorithms. For the GT2 FLSs on the basis of the alpha-planes expression of GT2 FSs, we provide the inference, type-reduction and defuzzification according to these three types of noniterative algorithms. Then, four simulation experiments are adopted to illustrate that while increasing the sampled number of primary variable, the computational results of discrete type of noniterative algorithms may accurately gain on the corresponding continuous type of noniterative algorithms.

The rest of the paper is arranged as the following. The next section provides the background knowledge of GT2 FLSs. Then, the third section gives the three kinds of noniterative NB, NT and BMM algorithms, and how to expand them three to complete the type-reduction of GT2 FLSs. According to the simulation instances, the fourth section illustrates and analyzes the computation results. Finally, the last section is the conclusion.

GT2 FLSs

From the viewpoint of inference [1, 33, 34], general T2 FLSs can be categorized into both the Mamdani type [9, 12, 35] and Takagi and Sugeno and Kang type [8, 36,37,38]. Take into account a Mamdani general T2 FLS which has m inputs \(x_{1} \in X_{1} ,x_{2} \in X_{2} , \cdots x_{m} \in X_{m}\), and a single output \(y \in Y\), and the system is described by M rules, in which the sth rule can be as

$$ \begin{aligned} & {\text{If}}\;x_{1} \;{\text{is}}\;\tilde{E}_{1}^{s} \;{\text{and}}\;x_{2} \;{\text{is}}\;\tilde{E}_{2}^{s} \ldots {\text{ and}}\;x_{m} \;{\text{is}}\;\tilde{E}_{m}^{s} ,\\ & \quad {\text{then}}\;y\;{\text{is}}\;\tilde{H}^{s} \;(s = 1,2, \ldots ,M) \end{aligned} $$
(1)

in which \(\tilde{E}_{i}^{s} (i = 1, \ldots ,n;\;s = 1,2, \ldots ,M)\) represents the antecedent GT2 fuzzy set, and \(\tilde{H}^{s} (s = 1,2, \ldots ,M)\) denotes the consequent GT2 fuzzy set.

For the sake of simplifying the expressions, singleton fuzzifier is used, i.e., when \(x_{i} = x^{\prime}_{i}\), let the vertical slice (secondary MF) \(\tilde{E}_{i}^{s} (x^{\prime}_{i} )\) of \(\tilde{E}_{i}^{s}\) be activated, then the \(\alpha\)-cut decomposition should be

$$ \tilde{E}_{i}^{s} (x^{\prime}_{i} ) = \mathop {\sup }\limits_{\forall \alpha \in [0,1]} \alpha /[a_{i,\alpha }^{s} (x^{\prime}_{i} ),b_{i,\alpha }^{s} (x^{\prime}_{i} )]. $$
(2)

For each rule, the firing interval for the relevant \(\alpha\)-level should be computed as

$$ E_{\alpha } :\left\{ \begin{gathered} E_{\alpha }^{s} (x^{\prime}) \equiv [\underline{e}_{\alpha }^{s} (x^{\prime}),\overline{e}_{\alpha }^{s} (x^{\prime})] \hfill \\ \underline{e}_{\alpha }^{s} (x^{\prime}) \equiv T_{i = 1}^{p} a_{i,\alpha }^{s} (x^{\prime}_{i} ) \hfill \\ \overline{e}_{\alpha }^{s} (x^{\prime}) \equiv T_{i = 1}^{p} b_{i,\alpha }^{s} (x^{\prime}_{i} ) \hfill \\ \end{gathered} \right. $$
(3)

in which T is the minimum or product t-norm.

Let the \(\alpha\)-plane of consequent \(\tilde{H}^{s}\) at the corresponding \(\alpha\)-level be \(\tilde{H}_{\alpha }^{s}\), then

$$ \tilde{H}_{\alpha }^{s} = \int\limits_{y \in Y} {[h_{L,\alpha }^{s} (y),h_{R,\alpha }^{s} (y)]/y} . $$
(4)

To get the firing rule \(\alpha\)-plane \(\tilde{A}_{\alpha }^{s}\), for each rule, combing the fired interval with its relevant consequent \(\alpha\)-plane, that is to say,

$$ \tilde{B}_{\alpha }^{s} :\left\{ \begin{gathered} {\text{FOU}}(\tilde{A}_{\alpha }^{s} ) = [\underline{u}_{{\tilde{A}_{\alpha }^{s} }} (y|x^{\prime}),\overline{u}_{{\tilde{A}_{\alpha }^{s} }} (y|x^{\prime})] \hfill \\ \underline{u}_{{\tilde{A}_{\alpha }^{s} }} (y|x^{\prime}) = \underline{e}_{\alpha }^{s} (x^{\prime}) * h_{L,\alpha }^{s} (y) \hfill \\ \overline{u}_{{\tilde{A}_{\alpha }^{s} }} (y|x^{\prime}) = \overline{e}_{\alpha }^{s} (x^{\prime}) * h_{R,\alpha }^{s} (y) \hfill \\ \end{gathered} \right.. $$
(5)

Aggregating all the \(\tilde{A}_{\alpha }^{s} (s = 1,2, \ldots ,M)\) to get the \(\alpha\)-plane \(\tilde{A}_{\alpha }\), that is to say,

$$ \tilde{A}_{\alpha } :\left\{ \begin{gathered} {\text{FOU}}(\tilde{A}_{\alpha } ) = [\underline{u}_{{\tilde{A}_{\alpha } }} (y|x^{\prime}),\overline{u}_{{\tilde{A}_{\alpha } }} (y|x^{\prime})] \hfill \\ \underline{u}_{{\tilde{A}_{\alpha } }} (y|x^{\prime}) = \underline{u}_{{\tilde{A}_{\alpha }^{1} }} (y|x^{\prime}) \vee \underline{u}_{{\tilde{A}_{\alpha }^{2} }} (y|x^{\prime}) \vee \cdots \vee \underline{u}_{{\tilde{A}_{\alpha }^{M} }} (y|x^{\prime}) \hfill \\ \overline{u}_{{\tilde{A}_{\alpha } }} (y|x^{\prime}) = \overline{u}_{{\tilde{A}_{\alpha }^{1} }} (y|x^{\prime}) \vee \overline{u}_{{\tilde{A}_{\alpha }^{2} }} (y|x^{\prime}) \vee \cdots \vee \overline{u}_{{\tilde{A}_{\alpha }^{M} }} (y|x^{\prime}) \hfill \\ \end{gathered} \right. $$
(6)

in which \(\vee\) represents the maximum operation.

Then, the \(Y_{C,\alpha } (x^{\prime})\) at the corresponding \(\alpha\)-level should be acquired by obtaining the centroid of \(\tilde{B}_{\alpha }\), that is to say,

$$ Y_{C,\alpha } (x^{\prime}) = \alpha /[l_{{\tilde{A}_{\alpha } }} (x^{\prime}),r_{{\tilde{A}_{\alpha } }} (x^{\prime})] $$
(7)

in which the \(l_{{\tilde{A}_{\alpha } }} (x^{\prime})\) and \(r_{{\tilde{A}_{\alpha } }} (x^{\prime})\) may be computed by different types of TR algorithms [5, 6, 12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] as

$$ l_{{\tilde{A}_{\alpha } }} (x^{\prime}) = \mathop {\min }\limits_{{u_{{\tilde{A}_{\alpha } }} (y_{i} ) \in [\underline{u}_{{\tilde{A}_{\alpha } }} (y_{i} ),\overline{u}_{{\tilde{A}_{\alpha } }} (y_{i} )]}} \left[ {\sum\limits_{i = 1}^{N} {y_{i} u_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} /\sum\limits_{i = 1}^{N} {u_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} } \right] $$
(8)

and

$$ r_{{\tilde{A}_{\alpha } }} (x^{\prime}) = \mathop {\max }\limits_{{u_{{\tilde{A}_{\alpha } }} (y_{i} ) \in [\underline{u}_{{\tilde{A}_{\alpha } }} (y_{i} ),\overline{u}_{{\tilde{A}_{\alpha } }} (y_{i} )]}} \left[ {\sum\limits_{i = 1}^{N} {y_{i} u_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} /\sum\limits_{i = 1}^{N} {u_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} } \right] $$
(9)

in which the special IT2 FS \(R_{{\tilde{A}_{\alpha } }} = \alpha /\tilde{A}_{\alpha }\), and N denotes the number of sampling.

Finally, aggregate every \(\alpha\)-planes \(Y_{C,\alpha }\) to construct the T1 FS \(Y_{C}\), i.e.,

$$ Y_{C} = \mathop {\sup }\limits_{\forall \alpha \in [0,1]} \alpha /Y_{C,\alpha } (x^{\prime}). $$
(10)

In practical computations, let the number of effective \(\alpha\)-planes be p, that is to say, the value of \(\alpha\) is usually equally decomposed into \(\alpha = \alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{p}\), thus, the crisp output of GT2 FLSs [39,40,41,42] should be

$$ y = \frac{{\sum\nolimits_{i = 1}^{p} {\alpha_{i} \left[ {\frac{1}{2}(l_{{\tilde{A}_{{\alpha_{i} }} }} (x^{\prime}) + r_{{\tilde{A}_{{\alpha_{i} }} }} (x^{\prime}))} \right]} }}{{\sum\nolimits_{i = 1}^{p} {\alpha_{i} } }}. $$
(11)

Three types of noniterative algorithms

Three types of discrete noniterative algorithms are provided here for investigating the centroid type-reduction for GT2 FLSs.

Nagar–Bardini noniterative algorithms

The closed form of NB algorithms [25] based IT2 FLSs were shown to own distinguish advantages to cope with far-ranging of uncertainty. According to the inference, let the output be the GT2 fuzzy set \(\tilde{A}\). Let the \(\tilde{A}\) be evenly discretized to \(n\) points, then the \(l_{{\tilde{A}_{\alpha } }}\) and \(r_{{\tilde{A}_{\alpha } }}\) can be calculated as

$$ l_{{\tilde{A}_{\alpha } }} = \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}, $$
(12)
$$ r_{{\tilde{A}_{\alpha } }} = \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}. $$
(13)

According to the continuous type of KM algorithms [14,15,16,17, 19], the continuous type of NB (CNB) algorithms should be provided as

$$ l_{{\tilde{A}_{\alpha } }} = \frac{{\int_{a}^{b} {y\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }}{{\int_{a}^{b} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }}, $$
(14)
$$ r_{{\tilde{B}_{\alpha } }} = \frac{{\int_{a}^{b} {y\overline{u}_{{R_{{\tilde{B}_{\alpha } }} }} (y){\text{d}}y} }}{{\int_{a}^{b} {\overline{u}_{{R_{{\tilde{B}_{\alpha } }} }} (y){\text{d}}y} }}. $$
(15)

Then, the type-reduced sets and defuzzified ouputs can be obtained in terms of Eqs. (10) and (11). Here, both the discrete NB algorithms and continuous NB algorithms calculate the output as the linear combination of 2 special type-1 FLSs: one relies the upper MFs, while the other depends on the lower MFs.

Nie–Tan noniterative algorithms

The discrete NT algorithms compute the defuzzified output of GT2 FS at the corresponding \(\alpha\)-level as

$$ y_{NT,\alpha } = \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} [\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }}{{\sum\nolimits_{i = 1}^{n} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }}. $$
(16)

Then, the continuous NT (CNT) algorithms solve it as

$$ y_{CNT,\alpha } = \frac{{\int_{a}^{b} {y[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y)]{\text{d}}y} }}{{\int_{a}^{b} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y)]{\text{d}}y} }}. $$
(17)

Most recent studies show that the CNT algorithms [26] are in reality an accurate TR approach. Here, the statements and explanations are provided as follows.

Theorem 1

[17]. The random sampling methods (algorithms) should obtain the precise centroid type-reduction of GT2 FLSs as the sampled number is infinity.

Proof.

According to the inference [43], suppose that \(R_{{\tilde{A}_{\alpha } }}\) be the output interval type-2 FS (under \(\alpha\)-level). Furthermore, along the y-axis, let the vertical slices number be m, and along the u-axis, l denotes the horizontal slices number, therefore, the embedded T1 fuzzy sets number is \(l^{m}\).

Let \(\overline{\mu }_{{R_{{\tilde{A}_{\alpha } }} }} (y)\), and \(\underline{\mu }_{{R_{{\tilde{A}_{\alpha } }} }} (y)\) be the upper bound and lower bound of FOU for \(R_{{\tilde{A}_{\alpha } }}\). Here, select M embedded type-1 fuzzy sets randomly for \(R_{{\tilde{A}_{\alpha } }}\), and suppose that \(\mu_{i} (y)\;(i = 1,2, \ldots ,M)\) be the ith embedded FS. Aggregating all M embedded fuzzy sets, therefore,

$$ \sum\limits_{i = 1}^{M} {u_{i} } (y) = \sum\limits_{j = 1}^{m} {\sum\limits_{i = 1}^{M} {u_{i} } } (y_{j} ). $$
(18)

So that,

$$ \mathop {\lim }\limits_{M \to \infty } \frac{1}{M}\sum\limits_{i = 1}^{M} {u_{i} } (y) = \mathop {\lim }\limits_{M \to \infty } \frac{1}{M}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{m} {u_{i} } } (y_{j} ). $$
(19)

As \(u_{i} (y_{j} )\) is a random number on \([\underline{u}_{i} (y_{j} ),\overline{u}_{i} (y_{j} )]\), therefore, the right side of Eq. (19) can be rewritten as

$$ \mathop {\lim }\limits_{M \to \infty } \frac{1}{M}\sum\limits_{i = 1}^{M} {\sum\limits_{j = 1}^{m} {u_{i} } } (y_{j} ) = \frac{1}{l}\sum\limits_{k = 1}^{l} {\sum\limits_{j = 1}^{m} {u_{k} (y_{j} )} } . $$
(20)

So that,

$$ \mathop {\lim }\limits_{M \to \infty } \frac{l}{M}\sum\limits_{i = 1}^{M} {u_{i} } (y) = \sum\limits_{k = 1}^{l} {\sum\limits_{j = 1}^{m} {u_{k} } } (y_{j} ). $$
(21)

For Eq. (20), it is sampled randomly as \(M \to \infty\) for the left, and the right is the aggregation. Attention that \(l/M\) is only a constant, therefore, it has nothing relations to the calculations of the centroid.

As for the continuous type interval type-2 FS \(R_{{\tilde{A}_{\alpha } }}\), just replace the \(\sum\nolimits_{j = 1}^{m} {}\) and \(\sum\nolimits_{k = 1}^{l} {}\) with the \(\int_{{y_{\min } }}^{{y_{\max } }} {}\) and \(\int_{{\underline{u} (y)}}^{{\overline{u}(y)}} {}\) will work. Therefore,

$$ \mathop {\lim }\limits_{M \to \infty } \frac{l}{M}\sum\limits_{i = 1}^{M} {u_{i} } (y) = \int\limits_{{y_{\min } }}^{{y_{\max } }} {\int\limits_{{\underline{u} (y)}}^{{\overline{u}(y)}} {u(y){\text{d}}\mu {\text{d}}y} } . $$
(22)

Theorem 2

[17]. For the \(R_{{\tilde{A}_{\alpha } }}\), let whose membership function of representative embedded FS be the form

$$ u^{ * } (y) = [\underline{u} (y) + \overline{u}(y)]/2. $$
(23)

Here, the centroid for IT2 fuzzy set \(R_{{\tilde{A}_{\alpha } }}\) should be calculated as

$$ C(\tilde{A}_{\alpha } ) = \frac{{\int_{{y_{\min } }}^{{y_{\max } }} {u^{ * } (y)y{\text{d}}y} }}{{\int_{{y_{\min } }}^{{y_{\max } }} {u^{ * } (y){\text{d}}y} }}. $$
(24)

Proof

For the interval type-2 FS \(R_{{\tilde{A}_{\alpha } }}\), choose M embedded FSs. Suppose that \(\mu_{i} (y)\) be the membership function for the ith embedded fuzzy set. Due to \(y_{j}\) is a vertical slice randomly selected, therefore, \(\mu_{i} (y)\) could be expressed as: \(u_{i} (y_{j} ) = \underline{u} (y_{j} ) + \varphi_{i} [\overline{u} (y_{j} ) - \underline{u} (y_{j} )]\), in which the random number \(\varphi_{i}\) is equally distributed on the interval [0, 1]. Therefore,

$$ \sum\limits_{i = 1}^{M} {u_{i} } (y_{j} ) = M\underline{u} (y_{j} ) + [\overline{u}(y_{j} ) - \underline{u} (y_{j} )]\sum\limits_{i = 1}^{M} {\varphi_{i} } . $$
(25)

Actually, \(\mathop {\lim }\limits_{M \to \infty } \sum\nolimits_{i = 1}^{M} {\varphi_{i} } = \frac{M}{2}\), so that,

$$ \mathop {\lim }\limits_{M \to \infty } \frac{1}{M}\sum\limits_{i = 1}^{M} {u_{i} } (y_{j} ) = \frac{1}{2}[\underline{u} (y_{j} ) + \overline{u}(y_{j} )]. $$
(26)

Computing the centroid a prevalent approach to defuzzify type-1 fuzzy set, i.e.,

$$ C(R_{{\tilde{A}_{\alpha } }} ) = \frac{{\int_{{y_{\min } }}^{{y_{\max } }} {\mu (y)y{\text{d}}y} }}{{\int_{{y_{\min } }}^{{y_{\max } }} {\mu (y){\text{d}}y} }}. $$
(27)

As \(y_{j}\) is just a random vertical slice of y, on the basis of Eq. (26), it can be obtained that

$$ \mathop {\lim }\limits_{M \to \infty } \frac{1}{M}\sum\limits_{i = 1}^{M} {u_{i} } (y) = \frac{1}{2}[\underline{u} (y) + \overline{u}(y)]. $$
(28)

According to Eq. (27) and theorem 1, \(u^{ * } (y) = [\underline{u} (y) + \overline{u}(y)]/2\) will be the membership function of representative embedded FS. Furthermore, this will be used to compute an accurate centroid of \(R_{{\tilde{A}_{\alpha } }}\). When \(R_{{\tilde{A}_{\alpha } }}\) is the continuous type, simply substitute the \(\sum\nolimits_{i = 1}^{M} {}\) by the \(\int_{{y_{\min } }}^{{y_{\max } }} {}\) for the proofs. Therefore, the continuous NT algorithms are actually equal to the exhaustive type-reduction algorithms, and this can be extended to perform the accurate type-reduction.

Begian–Melek–Mendel noniterative algorithms

The discrete BMM algorithms compute the output straightly, and the output of GT2 FS can be obtained as

$$ y_{BMM,\alpha } = a\frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }} + b\frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }} $$
(29)

in which the two adjustable coefficients are \(a\) and \(b\), respectively; here, the output is also a linear combination of 2 specific type-1 FLSs.

Then, the continuous BMM (CBMM) algorithms solve it as

$$ y_{CBMM,\alpha } = a\frac{{\int_{a}^{b} {y\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }}{{\int_{a}^{b} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }} + b\frac{{\int_{a}^{b} {y\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }}{{\int_{a}^{b} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y){\text{d}}y} }}. $$
(30)

In fact, the discrete BMM algorithms [14, 28, 29] can be considered as the more general form of discrete NB algorithms and NT algorithms. Then, the explanations are given as follows. Observe Eqs. (12), (13) and (29), it should be found that the NB algorithms and BMM algorithms are completely the same when \(a = a_{NB} = \frac{1}{2}\), and \(b = b_{NB} = \frac{1}{2}\). As for the NT algorithms, transforming Eq. (16) to

$$ \begin{gathered} y_{NT,\alpha } = \frac{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }} \times \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }} \\ \quad + \frac{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }} \times \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }} \hfill \\ \, = a_{NT} \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }} + b_{NT} \frac{{\sum\nolimits_{i = 1}^{n} {y_{i} \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}, \hfill \\ \end{gathered} $$
(31)

where \(a_{NT}\) and \(b_{NT}\) satisfy

$$ a_{NT} = \frac{{\sum\nolimits_{i = 1}^{n} {\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }} $$
(32)
$$ b_{NT} = \frac{{\sum\nolimits_{i = 1}^{n} {\overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )} }}{{\sum\nolimits_{i = 1}^{n} {[\underline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} ) + \overline{u}_{{R_{{\tilde{A}_{\alpha } }} }} (y_{i} )]} }}. $$
(33)

Observing Eqs. (29) and (31), as \(a = a_{NT}\) and \(b = b_{NT}\), we obtain that the NT algorithms and BMM algorithms will be the same.

Finally, the inner connections between the discrete and continuous algorithms for completing the centroid TR of GT2 FLSs should be as:

  1. (1)

    The discrete noniterative algorithms compute the centroids by means of the sum operation for the sampled points \(y_{i} (i = 1, \ldots ,n)\). In addition, the continuous noniterative algorithms compute in terms of the integral. In theory, the computational results of discrete noniterative algorithms can gain on the continuous noniterative algorithms while the number of samples approaches infinity.

  2. (2)

    For the discrete noniterative algorithms, the more precise calculation effects can be acquired by adding the number of samples.

  3. (3)

    Three discrete types of noniterative algorithms complete the numerical computations by means of the sum operation, while the continuous types of algorithms complete the calculations based on the integral.

Simulations

Four cases are given here. Suppose that the footprint of uncertainties (FOUs) and the related vertical slices (or secondary membership functions) of output GT2 FS be known according to the inference engine of GT2 FLSs. Here, four commonly used GT2 FSs are selected for studying. In case 1, the FOU is made up of the piecewise defined linear functions [2, 3, 5, 6, 19], while the related secondary MF is selected as the trapezoidal type membership function. In the second case, the FOU is made up of the linear functions and Gaussian functions [13,14,15,16, 26,27,28,29, 33], and the corresponding secondary membership functions is still selected as the trapezoidal type membership function. In case 3, the FOU is composed of the Gaussian type functions [2, 3, 5, 6, 19], while the corresponding secondary membership function is selected as the triangular type membership function. In the last case, the FOU is only a Gaussian primary membership function with uncertain standard deviations [13,14,15,16, 26,27,28,29, 33], and the corresponding secondary membership functions is the triangular type membership function. In experiments, the \(\alpha\) is equally divided into values as: \(\alpha = 0,1/\Delta , \cdots ,1\). Here, we let \(\Delta\) vary from one to a hundred with a step size of one. Figure 1 and Table 1 give the FOUs of all cases. In addition, Fig. 2 and Table 2 provide the related secondary membership functions.

Fig. 1
figure 1

Graphs for FOUs

Full size image
Table 1 Membership function expressions for FOUs
Full size table
Fig. 2
figure 2

Shape graphs for secondary membership functions

Full size image
Table 2 Second membership function expressions for four cases
Full size table

Consider the continuous noniterative algorithms as benchmark to calculate both the type-reduced sets for \(\Delta = 100\), and the defuzzified outputs for \(\Delta\)(Delta) ranging from one to a hundred with the step size of 1, and they are shown by Figs. 3 and 4, respectively. For the CBMM algorithms, here we choose the average of results of 20 random experiments for the adjustable coefficient a of CBMM algorithms, and another coefficient \(b = 1 - a\).

Fig. 3
figure 3

Type-reduced sets calculated by three kinds of continuous noniterative algorithms

Full size image
Fig. 4
figure 4

Defuzzified values calculated by the continuous noniterative algorithms

Full size image

Then, the computational accuracies between continuous noniterative algorithms and sampling-based noniterative algorithms in relation with the number of samples are studied. Here, the number of samples are chosen as 20, 50, 100, 200 and 2000 (only in last three examples).

Here, the absolute errors between three kinds of continuous noniterative algorithms and sampling-based discrete noniterative algorithms for calculating type-reduced sets and defuzzified outputs are provided in Figs. 5, 6, 7, 8, 9, 10.

Fig. 5
figure 5

The absolute errors of type-reduced sets between continuous NB algorithms and sampling-based discrete NB algorithms

Full size image
Fig. 6
figure 6

The absolute errors of defuzzified outputs between continuous NB algorithms and sampling-based discrete NB algorithms

Full size image
Fig. 7
figure 7

The absolute errors of type-reduced sets between continuous NT algorithms and sampling-based discrete NT algorithms

Full size image
Fig. 8
figure 8

The absolute errors of defuzzified outputs between continuous NT algorithms and sampling-based discrete NT algorithms

Full size image
Fig. 9
figure 9

The absolute errors of type-reduced sets between continuous BMM algorithms and sampling-based discrete BMM algorithms

Full size image
Fig. 10
figure 10

The absolute errors of defuzzified outputs between continuous BMM algorithms and sampling-based discrete BMM algorithms

Full size image

Next, the quantitative studies for the mean of absolute errors are performed. Then, Tables 3, 4, 5 provide the means of absolute errors for type-reduced sets between the continuous noniterative algorithms and sampling-based discrete noniterative algorithms. Furthermore, the means of absolute errors for centroid defuzzified values are given in Tables 6, 7, 8.

Table 3 Average of absolute errors of type-reduced sets between continuous NB algorithms and sampling-based NB algorithms
Full size table
Table 4 Average of absolute errors of type-reduced sets between continuous NT algorithms and sampling-based NT algorithms
Full size table
Table 5 Average of absolute errors of type-reduced sets between continuous BMM algorithms and sampling-based BMM algorithms
Full size table
Table 6 Average of absolute errors of defuzzified outputs between continuous NB algorithms and sampling-based NB algorithms
Full size table
Table 7 Average of absolute errors for defuzzified outputs between continuous NT algorithms and sampling-based NT algorithms
Full size table
Table 8 Average of absolute errors of defuzzified outputs between continuous BMM algorithms and sampling-based BMM algorithms
Full size table

Next, we investigate the unrepeatable calculation times for the continuous noniterative algorithms and their corresponding sampling-based discrete noniterative algorithms. Computer programs are completed with the software of Matlab 2013a. Here, we use the hardware platform as a double core CPU dell desktop.

Then, Tables 9, 10, 11, 12, 13, 14 provide the total computation times of noniterative algorithms for calculating the type-reduced sets and defuzzified values, respectively, where the time unit is the second(s). See from Figs. 5, 6, 7, 8, 9, 10 and Tables 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, the conclusions can be made as:

  1. (1)

    For calculating both the centroid type-reduced sets and defuzzified values, as the number of samples increases, the results of sampling-based noniterative algorithms will all be more and more close to their corresponding continuous type of noniterative algorithms.

  2. (2)

    In both examples 1 and 4, as the number of sampling is 100, the computational results of discrete type of noniterative algorithms will be the same as their related continuous type of noniterative algorithms (see Figs. 5a–10a, and Figs. 5d–10d); while for the middle two cases, the number of samples must be added to 19,000 to let the computational results of discrete type of noniterative algorithms be the same as their related continuous type of noniterative algorithms (see Figs. 5b–10b, and Figs. 5c–10c).

  3. (3)

    While calculating average of absolute errors for type-reduced sets and defuzzified values, the discrete type of noniterative algorithms could better gain on their related continuous type of noniterative algorithms as the samples is chosen as 19,000 (see Tables 3, 4, 5, 6, 7, 8).

  4. (4)

    For calculating the type-reduced sets and defuzzified values, the specific computational times of discrete noniterative algorithms are less than their corresponding continuous counterparts. Among them, the discrete type of noniterative algorithms which have the maximum number of samples take the longest computation times. Despite so, for the discrete type of noniterative algorithms which have the maximum number of samples, they only have about 0.6244%, 0.5208%, 0.7708%, and 0.6617%, 0.5635%, 0.6875% of their continuous counterparts, respectively (see Tables 9, 10, 11, 12, 13, 14).

  5. (5)

    According to the items (1)–(4), it is obviously that the proposed sampling-based noniterative algorithms could be outstanding approximation approaches for their related continuous counterparts. Furthermore, the efficiencies of formers are distinctly higher than the continuous counterparts.

Table 9 Calculational times comparisons of the continuous NB and sampling-based NB algorithms for calculating type-reduced sets
Full size table
Table 10 Calculational times comparisons of the continuous NT and sampling-based NT algorithms for computing type-reduced sets
Full size table
Table 11 Calculational times of the continuous BMM and sampling-based BMM algorithms for centroid type-reduced sets
Full size table
Table 12 Computational times comparisons of the CNB and sampling-based NB algorithms for computing defuzzified values
Full size table
Table 13 Computational times comparisons of the continuous NT and sampling-based NT algorithms for calculating defuzzified values
Full size table
Table 14 Computational times comparisons of the continuous BMM and sampling-based BMM algorithms for calculating defuzzified values
Full size table

Conclusions and expectations

The paper compares the sum operation and integral operations in discrete and continuous algorithms on the foundation of type-2 fuzzy logic theory. As for four types of general T2 fuzzy sets with different kinds of FOUs and secondary MFs, the continuous noniterative algorithms are selected as the criterion to calculate the type-reduced sets and centroid defuzzified outputs. Simulation instances are given to show the shows of proposed sampling-based discrete noniterative type of algorithms. As the number of samples is selected suitably, the proposed sampling-based noniterative type of algorithms can approach to the corresponding continuous counterparts exactly. In addition, the efficiencies of formers are significantly higher.

In the next, the author will investigate the initialization, searching space and stopping conditions of iterative algorithms for completing the center-of-sets (COS) type-reduction [2, 6, 13,14,15, 19,20,21,22,23,24,25,26,27,28,29, 33, 44,45,46] of T2 FLSs. Furthermore, design and application of IT2 FLSs and GT2 FLSs on the basis of swarm intelligence algorithms [8, 9, 11, 35, 37, 38, 47,48,49,50,51,52] will be investigated. Future studies will be focused on the theory [39,40,41,42, 53,54,55,56] of type-2 FLSs and their related algorithms.