Introduction

In this paper, we focus on constrained optimization problems over networks consisting of multiple agents, where the global objective function is a sum of local functions of all agents. These optimization problems have recently received great attentions and has arisen in many applications such as resource allocation [1,2,3], large-scale machine learning [4, 5], distributed spectrum sensing in cognitive radio networks [6], estimation in sensor networks [7, 8], coordination in multi-agent systems [9, 10], and power system control [11, 12]. Thus, the design of an optimization algorithm is necessary to solve such problems. Besides, we assume that each agent only knows its own objective function and can exchange information with its neighbors over networks. For this reason, efficient distributed optimization algorithms are necessitated using local communication and local computation over networks.

The seminal work concerning this problems was introduced in [13] (see also [14, 15]). Recently, Nedić et al. [16] proposed a distributed subgradient algorithm, which performs consensus step and descent step. Duchi et al. [17] proposed a distributed dual average method using a similar idea. Moreover, variants of the distributed subgradient algorithm can be also found in [18,19,20,21,22,23,24]. However, the projection step becomes prohibitive when dealing with massive data sets for solving the constrained optimization problem. To reduce the computational bottleneck of the projection step, the Frank–Wolfe algorithm (a.k.a. conditional gradient decent) was proposed in [25]. In the Frank–Wolfe algorithm, the projection step is eschewed by a more efficient linear optimization step. Recently, Frank–Wolfe algorithms have received much attention due to its versatility and simplicity [26]. Furthermore, variants of Frank–Wolfe methods can be found in [27,28,29,30]. In addition, a decentralized Frank–Wolfe algorithm over networks was presented in [31]. However, the full gradient vectors are employed at each iteration in the above methods.

Despite this progress, the computation of the full gradient vectors is a computational bottleneck for high-dimensional vectors. Therefore, the variants of Frank–Wolfe methods, which use the full gradient vectors to update the decision vectors, can be prohibitive for tackling high-dimensional data. Furthermore, the computation of the appropriate oracle can be prohibitive for high-dimensional data in each Frank–Wolfe iteration. For this reason, Lacoste-Julien et al. [32] presented a block-coordinate Frank–Wolfe method. Moreover, the variants of the work were prevailed in [33,34,35], which have been applied in many fields. Despite their success, nevertheless, the computation models of these algorithms belong to the centralized framework.

We have recently witnessed the rise of big data, which is high dimensional. Moreover, these data are sat over different networked machines. Therefore, distributed variants of block-coordinate Frank–Wolfe algorithms are desirable and necessary for tackling unprecedented dimensional optimization problems [36]. For this reason, we expect that the desired algorithm can greatly reduce the computational complexity by avoiding some expensive operations such as the computation of full gradient and projection operation at each iteration. Very recently, Zhang et al. [37] proposed a distributed algorithm for maximizing the submodular function by leveraging randomized block-coordinate and Frank–Wolfe methods, in which each local objective function needs to satisfy the diminishing returns property. Nonetheless, the objective function may not satisfy this property in some applications. For example, the loss function may be convex in multi-task learning and may be non-convex in deep learning. However, the distributed block-coordinate Frank–Wolfe variant over networks for convex or non-convex functions is barely known. Furthermore, the design and analysis of the variant remained hitherto an open problem.

To fill this gap, we propose a novel distributed randomized block-coordinate projection-free algorithm over networks. In the proposed algorithm, each agent randomly chooses a subset of the entries of gradient vector and moves along the gradient direction at each iteration, the projection step is replaced by the Frank–Wolfe step. Therefore, the computational burden is reduced for solving huge-scale constrained optimization problems. Furthermore, the proposed algorithm also suits the case that the structure of information is incomplete. For instance, the data are spread among the agents of the network. In addition, the convergence rate of our algorithm is theoretically analyzed for huge-scale constrained convex and non-convex optimization problems, respectively.

The main contributions of this paper are as follows:

  1. 1)

    We propose a distributed randomized block-coordinate projection-free algorithm over networks, where local communication and computation are adopted. The algorithm uses the block-coordinate descent and the Frank–Wolfe techniques to reduce the computational cost of the entire gradient vector and the projection step, respectively.

  2. 2)

    We theoretically analyze the convergence rate of our algorithm. The rate of \({\mathcal {O}}(1/t)\) and \({\mathcal {O}}(1/t^2)\) are derived under convexity and strong convexity, respectively.

  3. 3)

    We also derive the rate of \({\mathcal {O}}(1/\sqrt{t})\) under non-convexity, where t is the number of iterations.

  4. 4)

    We conduct simulation experiments on aloi and news20 datasets to evaluate the performance of our algorithm and confirm the theoretical results.

The remainder of the paper is organized as follows: in “Related work”, we review some related works. In “Problem formulation, algorithms design, and assumptions”, we first formulate the optimization problem; our algorithm is presented and the standard assumptions are also provided. In “Main results”, we describe the main results of the work. In “Convergence analysis”, we analyze the convergence properties of the proposed algorithm and prove the main results in detail. The performance of our designed algorithm is evaluated in “Experiments”. The conclusion of the paper is summarized in “Conclusion”.

Notation: We use boldface to denote the vector with suitable dimension. Scalars are denoted by normal font. We use \({\mathbb {R}}\) to denote the set of real numbers. Moreover, the symbol \({\mathbb {R}}^d\) denotes the set of real vectors with dimension d. The notation \({\mathbb {R}}^{d\times d}\) denotes the real matrix of size \(d\times d\). The notation \(\Vert \cdot \Vert \) denotes the standard Euclidean norm. The transpose operation of a vector \({\mathbf {x}}\) and a matrix A are designated as \({\mathbf {x}}^{\top }\) and \(A^{\top }\), respectively. The notation \(\langle {\mathbf {x}}, {\mathbf {y}}\rangle \) denotes the inner product of vectors \({\mathbf {x}}\) and \({\mathbf {y}}\). The identity matrix with suitable size is designated as I. The vector, in which all entries are 1, is designated as \(\mathbbm {1}\). Moreover, the expectation of a random variable X is designated as \({\mathbb {E}}[X]\). The main notations of this paper are summarized in Table 1.

Table 1 Summary of main notation
Full size table

Related work

Distributed optimization over networks is a challenging problem, where each agent only utilizes its local information. The framework of distributed computation models was developed in the seminal work [13], see also [14, 15]. In this framework, the goal is to minimize a common (smooth) function by communication. In contrast, a distributed subgradient descent method was presented in [16]. The objective is to minimize the sum of local functions by local communication and local computation. Its variants were developed in [17,18,19,20,21,22,23]. Furthermore, Chen et al. [24] developed distributed subgradient algorithm for weakly convex functions. To achieve fast convergence, accelerated distributed gradient descent algorithms were presented in [38,39,40,41,42]. Meanwhile, the distributed primal-dual algorithms were also developed in [43]. Moreover, Newton’s algorithms were developed in [44, 45], and quasi-Newton methods were provided in [46]. In addition, decentralized ADMM methods are considered in [47] and [48].

However, the projections is prohibitively expensive for massive data sets. Thus, the Frank–Wolfe method, which was presented in [25], is an efficient methods for solving large-scale optimization problems. In the Frank–Wolfe method, the projection step is replaced by a very efficient linear optimization step. The primal-dual convergence rate was analyzed in detail for Frank–Wolfe-type methods [26]. Furthermore, variants of Frank–Wolfe methods was found in [26,27,28,29,30]. In addition, Wai et al. [31] proposed a decentralized Frank–Wolfe algorithm over networks. Nevertheless, these methods need to compute the full gradient at each iteration.

Table 2 The comparison of different algorithms
Full size table

For high-dimensional data, however, the computations of the entire gradient are prohibitive. To reduce the computational burden, coordinate-descent methods were studied in [49], where a subset of the entries of the gradient vector is updated at each iteration. Thus, the main difference among coordinate descent algorithms is the criteria of choosing the coordinate of the gradient vector. In these methods, the maximal and the cyclic coordinate search was often used [49]. Nevertheless, the convergence is difficult to prove for the cyclic coordinate search [50], and the convergence rate is trivial for the maximal coordinate search [49]. In addition, Nesterov studied random coordinate descent method in [50], where the choice of the coordinate was random. In [51], the authors extended the method to composite functions. Furthermore, the parallel coordinate descent methods were also well studied in [52, 53]. In [54], the authors proposed a random block-coordinate gradient projection algorithms. Wang et al. [55] studied coordinate-descent diffusion learning over networks. Notarnicola et al. [56] proposed a blockwise gradient tracking method for distributed optimization. Besides, coordinate primal-dual variants for distributed optimization were also investigated in [57, 58].

Further, a block Frank–Wolfe method by combining the coordinate descent method and the Frank–Wolfe technique was proposed in [32] and extensions of the work were prevailed in [33,34,35, 37]. To the best of our knowledge, distributed block-coordinate Frank–Wolfe variants over networks for convex or non-convex functions have rarely been investigated. For this reason, this paper focuses on the design and analysis of these variants. The comparison of different algorithms is summarized in Table 2.

Problem formulation, algorithms design, and assumptions

Let \({\mathcal {G}}=\left( {\mathcal {V}},{\mathcal {E}}\right) \) denote a network, where \({\mathcal {V}}=\left\{ 1,2,\ldots ,n\right\} \) denotes the set of agents and \({\mathcal {E}}\subset {\mathcal {V}}\times {\mathcal {V}}\) designates the edge set. The notation \(\left( i,j\right) \in {\mathcal {E}}\) designates an edge, where agent i can send information to agent j, \(i,j=1,\ldots ,n\). We use the notation \({\mathcal {N}}_i\) to designate the neighborhood of agent i. The constrained optimization problem of this paper is formulated as follows:

$$\begin{aligned}&\text {minimize}~~ f\left( {\mathbf {x}}\right) :=\frac{1}{n}\sum \limits _{i=1}^n f_i\left( {\mathbf {x}}\right) \nonumber \\&\text {subject to} \quad {\mathbf {x}}\in {\mathcal {X}}, \end{aligned}$$
(1)

where \(f_i: {\mathcal {X}}\mapsto {\mathbb {R}}\) refers to the cost function of agent i for all \(i\in {\mathcal {V}}\), and \({\mathcal {X}}\subseteq {\mathbb {R}}^d\) denotes a constraint set.

Moreover, this paper assumes that the dimensionality d of the vector \({\mathbf {x}}\) is large. To solve the problem (1), distributed gradient descent (DGD) methods are proposed in recent years. For tackling the high-dimensional data, however, the computation of the full gradient is expensive and becomes a bottleneck. Furthermore, the projection step is also expensive and may become prohibitive in many computationally intensive applications. To alleviate this computational challenge, we propose a distributed randomized block-coordinate Frank–Wolfe algorithm to solve problem (1) for high-dimensional data.

In this paper, we assume that the communication pattern among agents is defined by a n-by-n weighted matrix, \(A:=\left[ a_{ij}\right] ^{n\times n}\). Moreover, suppose that

Assumption 1

For all \(i,j\in {\mathcal {V}}\), we have

  1. 1)

    When \(\left( i,j\right) \in {\mathcal {E}}\), then \(a_{ij}>0\); \(a_{ij}=0\) otherwise. Furthermore, \(a_{ii}>0\) for all \(i\in {\mathcal {V}}\).

  2. 2)

    The matrix A is doubly stochastic, i.e., \(\sum \nolimits _{i=1}^na_{ij}=1\) and \(\sum \nolimits _{j=1}^na_{ij}=1\) for all \(i,j\in {\mathcal {V}}\).

figure a

To reduce the computational bottleneck, each agent at each iteration randomly chooses a subset of the gradient vector. Therefore, the proposed algorithm is summarized in Algorithm 1. First, each agent i, \(i=1,\ldots ,n\), performs a consensus step, i.e.,

$$\begin{aligned} {\mathbf {z}}_i\left( t\right) =\sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {x}}_j\left( t\right) . \end{aligned}$$
(2)

Second, each agent i performs the following aggregating step:

$$\begin{aligned} {\mathbf {s}}_i\left( t\right)&=\sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {s}}_j\left( t-1\right) +Q_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) \nonumber \\&-Q_i\left( t-1\right) \nabla f_i\left( {\mathbf {z}}_i\left( t-1\right) \right) , \end{aligned}$$
(3)
$$\begin{aligned} {\mathbf {S}}_i\left( t\right) =\sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {s}}_j\left( t\right) , \end{aligned}$$
(4)

where \(Q_i\left( t\right) \in {\mathbb {R}}^{d\times d}\) denotes a diagonal matrix. Moreover, the definition of the diagonal matrix is presented as follows:

$$\begin{aligned} Q_i\left( t\right) :=\text {diag}\left\{ q_{i,t}\left( 1\right) ,q_{i,t}\left( 2\right) ,\ldots ,q_{i,t}\left( d\right) \right\} , \end{aligned}$$

where \(\left\{ q_{i,t}\left( k\right) \right\} \) is a Bernoulli random variable sequence, \(k=1,\ldots ,d\). Furthermore, \(\text {Prob}\left( q_{i,t}\left( k\right) =1\right) :=p_i\), \(\text {Prob}\left( q_{i,t}\left( k\right) =0\right) :=1-p_i\), where we assume \(0<p_i\le 1\).

Finally, each agent i performs the following Frank–Wolfe step, i.e.,

$$\begin{aligned} {\mathbf {v}}_i\left( t\right) :=\arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\langle {\mathbf {v}},{\mathbf {S}}_i\left( t\right) \rangle \end{aligned}$$
(5)

and

$$\begin{aligned} {\mathbf {x}}_i\left( t+1\right) :=\left( 1-\gamma _t\right) {\mathbf {z}}_i\left( t\right) +\gamma _t{\mathbf {v}}_i\left( t\right) , \end{aligned}$$
(6)

where \(\gamma _t\in \left( 0,1\right] \) denotes a step size. Furthermore, we have the initial conditions \({\mathbf {s}}_i\left( 0\right) =\nabla f_i\left( {\mathbf {z}}_i\left( 0\right) \right) \), \(Q_i\left( 0\right) =I_d\).

By the definition of \(q_{i,t}\left( k\right) \), we know that the k-th entry of the gradient vector is missing when \(q_{i,t}\left( k\right) =0\), thus the k-th entry of \({\mathbf {s}}_i\left( t\right) \) in Eq. (3) is updated without using the gradient information. Furthermore, the update can randomly vary over time and across agents. In addition, we use the more efficient linear optimization step to eschew projection.

In this paper, each agent sends information to its neighbors over network \({\mathcal {G}}\). To ensure the dissemination of the information from all agents, we formalize the following assumption, which is a standard assumption in [60].

Assumption 2

Suppose that the network \({\mathcal {G}}\) is strongly connected.

From Assumption 2, we have \(|\lambda _2 \left( A\right) |<1\), where \(\lambda _2\left( \cdot \right) \) denotes the second largest eigenvalue of a matrix. Furthermore, for any \(x\in {\mathbb {R}}^n\), from linear algebra, we obtain

$$\begin{aligned} \Vert Ax-\mathbbm {1}{\bar{x}}\Vert&=\left\| \left( A-\frac{1}{n}\mathbbm {1}\mathbbm {1}^{\top }\right) \left( x-\mathbbm {1}{\bar{x}}\right) \right\| \nonumber \\&\le \vert \lambda _2\left( A\right) \vert \Vert x-\mathbbm {1}{\bar{x}}\Vert , \end{aligned}$$
(7)

where \({\bar{x}}=\left( 1/n\right) \mathbbm {1}^{\top }x\). From Eq.  (7), we can see that the average \({\bar{x}}\) is computed at a linear rate by average consensus.

Next, we introduce the smallest integer \(t_{0,\theta }\) such that

$$\begin{aligned} \lambda _2\left( A\right) \le \frac{\left( t_{0,\theta }\right) ^{\theta }}{1+\left( t_{0,\theta }\right) ^{\theta }}\cdot \left( \frac{t_{0,\theta }}{1+t_{0,\theta }}\right) ^{\theta }. \end{aligned}$$
(8)

Therefore, following from Eq. (8), we obtain

$$\begin{aligned} t_{0,\theta }\ge \left\lceil \frac{1}{\left( \lambda _2\left( A\right) \right) ^{-1/\left( 1+\theta \right) }-1}\right\rceil . \end{aligned}$$
(9)

Besides, the following assumptions are also provided.

Assumption 3

The set \({\mathcal {X}}\) is bounded and convex. Moreover, the optimal set \({\mathcal {X}}^{*}\) is nonempty.

Moreover, we define the diameter of \({\mathcal {X}}\) as follows:

$$\begin{aligned} D:=\sup _{{\mathbf {x}},{\mathbf {x}}'\in {\mathcal {X}}}\left\| {\mathbf {x}}-{\mathbf {x}}'\right\| . \end{aligned}$$

Assumption 4

For any \({\mathbf {x}},{\mathbf {y}}\in {\mathcal {X}}\) and \(i\in {\mathcal {V}}\), there exist positive constants \(\beta \) and L such that

$$\begin{aligned} f_i\left( {\mathbf {y}}\right) \le f_i\left( {\mathbf {x}}\right) +\left\langle \nabla f_i\left( {\mathbf {x}}\right) ,{\mathbf {y}}-{\mathbf {x}}\right\rangle +\frac{\beta }{2}\left\| {\mathbf {y}}-{\mathbf {x}}\right\| \end{aligned}$$
(10)

and

$$\begin{aligned} \vert f_i\left( {\mathbf {x}}\right) -f_i\left( {\mathbf {y}}\right) \vert \le L\Vert {\mathbf {x}}-{\mathbf {y}}\Vert . \end{aligned}$$
(11)

Then, \(f_i\) is \(\beta \)-smooth and L-Lipschitz.

From the Lipschitz condition, we have \(\left\| \nabla f_i\left( {\mathbf {x}}\right) \right\| \le L\) for any \({\mathbf {x}}\in {\mathcal {X}}\). Furthermore, the relation (10) is equivalent to \(\left\| \nabla f_i\left( {\mathbf {y}}\right) -\nabla f_i\left( {\mathbf {x}}\right) \right\| \le \beta \left\| {\mathbf {y}}-{\mathbf {x}}\right\| \) for all \(i\in {\mathcal {V}}\).

In addition, a function \(f_i\) is \(\mu \)-strongly convex if the function \(f_i\) satisfies the following condition: for \(\mu >0\),

$$\begin{aligned} f_i\left( {\mathbf {y}}\right) \le f_i\left( {\mathbf {x}}\right) +\left\langle \nabla f_i\left( {\mathbf {x}}\right) , {\mathbf {y}}-{\mathbf {x}}\right\rangle +\frac{\mu }{2}\left\| {\mathbf {y}}-{\mathbf {x}}\right\| ^2 \end{aligned}$$

holds for any \({\mathbf {x}}, {\mathbf {y}}\in {\mathcal {X}}\). Moreover, by the definition of the function f, we also know that f is \(\mu \)-strongly convex. Besides, we also introduce the following parameter:

$$\begin{aligned} \alpha :=\min _{{\mathbf {u}}\in {\mathcal {B}}_{{\mathcal {X}}}}\left\| {\mathbf {u}}-{\mathbf {x}}^{*}\right\| , \end{aligned}$$
(12)

where \({\mathcal {B}}_{{\mathcal {X}}}\) designates the boundary set of \({\mathcal {X}}\). From Eq. (12), the solution \({\mathbf {x}}^{*}\) belongs to the interior of \({\mathcal {X}}\) if \(\alpha >0\).

Let \({\mathcal {F}}_t\) denote the filtration of \(\{{\mathbf {x}}_i(t)\}\) generated by our algorithm described in Eqs. (2)–(6) up to time t at all agents. Assumption 5 is adopted on the random variables \(q_{i,t}\left( k\right) \).

Assumption 5

The random variables \(q_{i,t}\left( k\right) \) and \(q_{j,t}\left( l\right) \) are mutually independent for all i, j, k, l. Furthermore, the random variables \(\left\{ q_{i,t}\left( k\right) \right\} \) are independent of \({\mathcal {F}}_{t-1}\) for all \(i\in {\mathcal {V}}\).

Main results

To find the optimal solution of the problem (1), the optimal set is defined as

$$\begin{aligned} {\mathcal {X}}^{*}=\left\{ {\mathbf {x}}\in {\mathcal {X}}\mid f\left( {\mathbf {x}}\right) =f^{*}\right\} , \end{aligned}$$

where \(f^{*}:=\min _{{\mathbf {x}}\in {\mathcal {X}}}f\left( {\mathbf {x}}\right) \). Besides, we introduce a variable, which is given by

$$\begin{aligned} \overline{{\mathbf {x}}}\left( t\right) :=\frac{1}{n}\sum \limits _{i=1}^n{\mathbf {x}}_i\left( t\right) . \end{aligned}$$

The first result shows the rate of convergence for convex cost functions.

Theorem 1

Let Assumptions 1–5 hold. For \(i\in \left\{ 1,\ldots ,n\right\} \), the function \(f_i\) is convex and let \(p_i=1/2\). Furthermore, \(\gamma _t=2/t\) for \(t\ge 1\). Then, we have

$$\begin{aligned} {\mathbb {E}}\left[ f\left( \overline{{\mathbf {x}}}\left( t\right) \right) \mid {\mathcal {F}}_{t-1}\right] -f^{*} \le \left( \beta D+2D\beta C_1+4DC'_2\right) \cdot \frac{2}{t}, \end{aligned}$$
(13)

where \(C_1:=t_{0,\theta }D\sqrt{n}\), \(C'_2:=\sqrt{2}n\beta \left( D+2C_1\right) \left( t_{0,\theta }\right) ^{\theta }\) with \(\theta \in \left( 0,1\right) \). Furthermore, assume that \(\alpha >0\) and all cost functions \(f_i\) are \(\mu \)-strongly convex. Then, for \(t\ge 2\), we have

$$\begin{aligned}&{\mathbb {E}}\left[ f\left( \overline{{\mathbf {x}}}\left( t\right) \right) \mid {\mathcal {F}}_{t-1}\right] -f^{*}\le \max \left\{ 2\beta D^2+4D\beta C_1+8DC'_2, \right. \nonumber \\&\quad \left. \zeta ^2\left( \beta D^2+2D\beta C_1+4DC'_2\right) ^2\big /2\mu \alpha ^2\right\} \cdot \frac{1}{t^2}, \end{aligned}$$
(14)

where \(\zeta \) is a constant and is greater than 1.

The detailed proof is provided in “Convergence analysis”. By Theorem 1, we can see that the rate of convergence is \({\mathcal {O}}(1/t)\) when the cost functions \(f_i\) are convex. Furthermore, the rate of convergence is \({\mathcal {O}}(1/t^2)\) under strong convexity.

When each function \(f_i\) is possibly non-convex, we will derive the convergence rate. To this end, we first introduce the “Frank-Wolfe” gap of f at \(\overline{{\mathbf {x}}}\left( t\right) \),

$$\begin{aligned} \Gamma \left( t\right) :=\max _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -{\mathbf {v}}\right\rangle . \end{aligned}$$
(15)

From Eq. (15), we have \(\Gamma \left( t\right) \ge 0\). Moreover, \(\overline{{\mathbf {x}}}(t)\) is a stationary point when \(\Gamma (t)=0\) to the problem (1). The second result shows the rate of convergence for non-convex cost functions.

Theorem 2

Let Assumptions 1–5 hold. Suppose that each function \(f_i\) is possibly non-convex and T is an even number. Moreover, \(\gamma _t=1/t^\theta \) with \(0<\theta <1\). Then, for all \(T\ge 6\) and \(t\ge t_{0,\theta }\), if \(\theta \in \left[ 1/2,1\right) \), we have

$$\begin{aligned} \min _{t\in \left[ T/2+1,T\right] }\Gamma \left( t\right)&\le \frac{1-\theta }{T^{1-\theta }}\left( 1-\left( 2/3\right) ^{1-\theta }\right) ^{-1}\Bigg (LD+ \nonumber \\&\times \left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \ln 2\Bigg ), \end{aligned}$$
(16)

where \(p_{\max }=\max _{i\in {\mathcal {V}}}p_i\), \(p_{\min }=\min _{i\in {\mathcal {V}}}p_i\), and \(C_2=\left( t_{0,\theta }\right) ^{\theta }2n\sqrt{p_{\max }}\beta \left( D+2C_1\right) \). If \(\theta \in \left( 0,1/2\right) \), we have

$$\begin{aligned} \min _{t\in \left[ T/2+1,T\right] }\Gamma \left( t\right)&\le \frac{1}{T^{\theta }}\cdot \frac{1-\theta }{1-\left( 2/3\right) ^{1-\theta }}\Bigg (LD+ \nonumber \\&\times \left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \nonumber \\&\times \frac{1-\left( 1/2\right) ^{1-2\theta }}{1-2\theta }\Bigg ). \end{aligned}$$
(17)

The detailed proof is provided in “Convergence analysis”. By Theorem  2, if the cost functions \(f_i\) are potentially non-convex, we can see that the quickest rate of convergence is \({\mathcal {O}}(1/\sqrt{T})\) when \(\theta =1/2\).

Convergence analysis

In this section, we will analyze the convergence rate. To this end, we define some variables as

$$\begin{aligned} \overline{{\mathbf {s}}}\left( t\right) :=\frac{1}{n}\sum \limits _{i=1}^n{\mathbf {s}}_i\left( t\right) , \end{aligned}$$
(18)
$$\begin{aligned} {\mathbf {g}}\left( t\right) :=\frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) , \end{aligned}$$
(19)
$$\begin{aligned} {\overline{\mathbf {v}}}\left( t\right) :=\frac{1}{n}\sum \limits _{i=1}^n{\mathbf {v}}_i\left( t\right) . \end{aligned}$$
(20)

Besides, we also obtain some equalities as follows:

Lemma 1

For any \(t\ge 0\), we have

  1. (a)

    \({\overline{\mathbf {s}}}\left( t+1\right) ={\mathbf {g}}\left( t+1\right) \);

  2. (b)

    \({\overline{\mathbf {x}}}\left( t+1\right) =\left( 1-\gamma _t\right) {\overline{\mathbf {x}}}\left( t\right) +\gamma _t{\overline{\mathbf {v}}}\left( t\right) .\)

Proof

(a) By Eq. (18), using Eq. (3) and the double stochasticity of A, we obtain

$$\begin{aligned} \overline{{\mathbf {s}}}\left( t+1\right)&=\frac{1}{n}\sum \limits _{i=1}^n{\mathbf {s}}_i\left( t+1\right) \nonumber \\&=\frac{1}{n}\sum \limits _{i=1}^n\sum \limits _{j=1}^na_{ij}{\mathbf {s}}_j\left( t\right) +\frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t+1\right) \nabla f_i \nonumber \\&\quad \times \left( {\mathbf {z}}_i\left( t+1\right) \right) -\frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) \nonumber \\&=\overline{{\mathbf {s}}}\left( t\right) +{\mathbf {g}}\left( t+1\right) -{\mathbf {g}}\left( t\right) . \end{aligned}$$
(21)

By recursively applying Eq. (21), we obtain

$$\begin{aligned} \overline{{\mathbf {s}}}\left( t+1\right) =\overline{{\mathbf {s}}}\left( 0\right) +{\mathbf {g}}\left( t+1\right) -{\mathbf {g}}\left( 0\right) . \end{aligned}$$

From the initial conditions \({\mathbf {s}}_i\left( 0\right) =\nabla f_i\left( {\mathbf {z}}_i\left( 0\right) \right) \) and \(Q_i\left( 0\right) =I_d\), we have

$$\begin{aligned} \overline{{\mathbf {s}}}\left( 0\right)&=\left( 1/n\right) \sum \limits _{i=1}^n{\mathbf {s}}_i\left( 0\right) \nonumber \\&=\left( 1/n\right) \sum \limits _{i=1}^nQ_i\left( 0\right) \nabla f_i\left( {\mathbf {z}}_i\left( 0\right) \right) \nonumber \\&={\mathbf {g}}\left( 0\right) . \end{aligned}$$

Therefore, part (a) is proved completely. (b) Using the double stochasticity of A, we obtain

$$\begin{aligned} \overline{{\mathbf {x}}}\left( t+1\right)&=\frac{1}{n}\sum \limits _{i=1}^n{\mathbf {x}}_i\left( t+1\right) \nonumber \\&=\frac{1}{n}\sum \limits _{i=1}^n\left[ \left( 1-\gamma _t\right) {\mathbf {z}}_i\left( t\right) +\gamma _t{\mathbf {v}}_i\left( t\right) \right] \nonumber \\&=\frac{1-\gamma _t}{n}\sum \limits _{i=1}^n\sum \limits _{j=1}^na_{ij}{\mathbf {x}}_j\left( t\right) +\frac{\gamma _t}{n}\sum \limits _{i=1}^n{\mathbf {v}}_i\left( t\right) \nonumber \\&=\left( 1-\gamma _t\right) \overline{{\mathbf {x}}}\left( t\right) +\gamma _t\overline{{\mathbf {v}}}\left( t\right) . \end{aligned}$$
(22)

Therefore, we finish the proof of part (b). \(\square \)

We now derive some important results, which are used in the convergence analysis.

Lemma 2

Let Assumption 1 hold. We assume that \(\gamma _t=1/t^{\theta }\) for \(\theta \in \left( 0,1\right] \). For \(i\in {\mathcal {V}}\) and \(t\ge t_{0,\theta }\), we get

$$\begin{aligned} \max _{i\in {\mathcal {V}}}\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \le C_1/t^{\theta }, \end{aligned}$$
(23)

where \(C_1=t_{0,\theta }D\sqrt{n}\).

Proof

We first have the following relation:

$$\begin{aligned} \max _{i\in {\mathcal {V}}}\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \le \sqrt{\sum \limits _{i=1}^n\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2}, \end{aligned}$$
(24)

where we have used the property of the Euclidean norm to obtain the last inequality. Moreover, if the following inequality holds:

$$\begin{aligned} \sqrt{\sum \limits _{i=1}^n\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2}\le \frac{C_1}{t^{\theta }}, \end{aligned}$$
(25)

where \(C_1=t_{0,\theta }D\sqrt{n}\), then the result is obtained by using Eq. (24). Therefore, we next prove that Eq.  (25) holds. To this end, we use induction to prove the above inequality. Because the constraint set \({\mathcal {X}}\) is convex, then \({\mathbf {z}}_i(t), \overline{{\mathbf {x}}}(t)\in {\mathcal {X}}\). Moreover, the set \({\mathcal {X}}\) is bounded by the diameter D, thus, Eq.  (25) holds for \(t=1\) to \(t=t_{0,\theta }\). Further, suppose Eq. (25) holds for \(t\ge t_{0,\theta }\). Since \({\mathbf {x}}_i\left( t+1\right) =(1-t^{-\theta }){\mathbf {z}}_i\left( t\right) +t^{-\theta }{\mathbf {v}}_i\left( t\right) \), we have

$$\begin{aligned}&\sum \limits _{i=1}^n\left\| {\mathbf {z}}_i\left( t+1\right) -\overline{{\mathbf {x}}}\left( t+1\right) \right\| ^2\nonumber \\&\quad =\sum \limits _{i=1}^n\left\| \sum \limits _{j\in {\mathcal {N}}_i}a_{ij}\left( 1-t^{-\theta }\right) {\mathbf {z}}_j\left( t\right) \right. \nonumber \\&\qquad \left. +\sum \limits _{j\in {\mathcal {N}}_i}a_{ij}t^{-\theta }{\mathbf {v}}_j\left( t\right) -\left( 1-t^{-\theta }\right) \overline{{\mathbf {x}}}\left( t\right) -t^{-\theta }\overline{{\mathbf {v}}}\left( t\right) \right\| ^2 \nonumber \\&\quad \le \vert \lambda _2\left( A\right) \vert ^2 \times \sum \limits _{j=1}^n\Bigg \Vert \left( 1-t^{-\theta }\right) \left( {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right) \nonumber \\&\qquad +t^{-\theta }\left( {\mathbf {v}}_j\left( t\right) -\overline{{\mathbf {v}}}\left( t\right) \right) \Bigg \Vert ^2, \end{aligned}$$
(26)

where we have used Eq. (7) to obtain the last inequality. Furthermore, using the Cauchy–Schwarz inequality, we also obtain

$$\begin{aligned}&\sum \limits _{j=1}^n\left\| \left( 1-t^{-\theta }\right) \left( {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right) +t^{-\theta }\left( {\mathbf {v}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right) \right\| ^2 \nonumber \\&\quad \le \sum \limits _{j=1}^n\left( \left( 1-t^{-\theta }\right) ^2\left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2+t^{-2\theta }\left\| {\mathbf {v}}_j\left( t\right) -\overline{{\mathbf {v}}}\left( t\right) \right\| ^2 \right. \nonumber \\&\qquad \left. +2t^{-\theta }\left( 1-t^{-\theta }\right) \left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \left\| {\mathbf {v}}_j\left( t\right) -\overline{{\mathbf {v}}}\left( t\right) \right\| \right) \nonumber \\&\quad \le \sum \limits _{j=1}^n\left( \left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2+t^{-2\theta }D^2 +2t^{-\theta }D\left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \right) \nonumber \\&\quad \le \sum \limits _{j=1}^n\left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2+nD^2t^{-2\theta } +2t^{-\theta }D\sqrt{n}\nonumber \\&\qquad \times \sqrt{\sum \limits _{j=1}^n\left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2} \nonumber \\&\quad \le t^{-2\theta }\left( C_1^2+nD^2\right) +2t^{-2\theta }DC_1\sqrt{n} \nonumber \\&\quad =t^{-2\theta }\left( C_1+D\sqrt{n}\right) ^2 \nonumber \\&\quad \le \left( \frac{C_1}{t^{\theta }}\cdot \frac{\left( t_{0,\theta }\right) ^{\theta }+1}{\left( t_{0,\theta }\right) ^{\theta }}\right) ^2, \end{aligned}$$
(27)

where the second inequality holds due to the boundedness of \({\mathcal {X}}\); the third inequality is from the inequality \(\sum \nolimits _{i=1}^n\vert x_i\vert \le \sqrt{n}\sqrt{\sum \nolimits _{i=1}^nx_i^2}\); in the fourth and last inequalities we have used the induction hypothesis. Besides, \(\phi \left( x\right) :=\left( x/\left( x+1\right) \right) ^\theta \) is a monotonically increasing function of x. Thus, combining Eqs.  (8), (26), and (27), we have

$$\begin{aligned} \vert \lambda _2\left( A\right) \vert \cdot \frac{1}{t^{\theta }}\cdot \frac{\left( t_{0,\theta }\right) ^{\theta }+1}{\left( t_{0,\theta }\right) ^{\theta }}&\le \left( \frac{t_{0,\theta }}{t_{0,\theta }+1}\right) ^{\theta }\cdot \frac{1}{t^{\theta }} \nonumber \\&\le \left( \frac{t}{t+1}\right) ^{\theta }\cdot \frac{1}{t^{\theta }} \nonumber \\&=\left( \frac{1}{t+1}\right) ^{\theta }. \end{aligned}$$
(28)

Using Eq. (28), we get

$$\begin{aligned} \sqrt{\sum \limits _{i=1}^n\left\| {\mathbf {z}}_i\left( t+1\right) -\overline{{\mathbf {x}}}\left( t+1\right) \right\| ^2}\le \frac{C_1}{\left( t+1\right) ^{\theta }}. \end{aligned}$$

Therefore, the induction step is finished. The result is proved completely. \(\square \)

By Lemma 2, we have \(\lim _{t\rightarrow \infty }\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| =0\).

Lemma 3

If Assumption 1 holds and \(\gamma _t=1/t^{\theta }\) for \(\theta \in \left( 0,1\right) \), then, we obtain for \(i\in {\mathcal {V}}\) and \(t\ge t_{0,\theta }\)

$$\begin{aligned} \max _{i\in {\mathcal {V}}}{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| \mid {\mathcal {F}}_{t-1}\right] \le \frac{C_2}{t^{\theta }}, \end{aligned}$$
(29)

where \(C_2=\left( t_{0,\theta }\right) ^{\theta }2n\sqrt{p_{\max }}\beta \left( D+2C_1\right) \).

Proof

From the property of the norm, we first have the following inequality:

$$\begin{aligned}&\max _{i\in {\mathcal {V}}}{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| \mid {\mathcal {F}}_{t-1}\right] \nonumber \\&\quad \le \max _{i\in {\mathcal {V}}}\sqrt{{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2\mid {\mathcal {F}}_{t-1}\right] } \nonumber \\&\quad \le \sqrt{\sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2\mid {\mathcal {F}}_{t-1}\right] }, \end{aligned}$$
(30)

where the first inequality is obtained using the inequality \({\mathbb {E}}\left[ \left\| {\mathbf {w}}\right\| \right] \le \sqrt{{\mathbb {E}}[\Vert {\mathbf {w}}\Vert ^2]}\) for any vector \({\mathbf {w}}\in {\mathbb {R}}^d\), we have also used the properties of the norm to obtain the last inequality. Therefore, if the following inequality holds:

$$\begin{aligned} \sqrt{\sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2\mid {\mathcal {F}}_{t-1}\right] }\le \frac{C_2}{t^{\theta }}, \end{aligned}$$
(31)

then the result of this lemma is obtained using Eq. (30). To prove Eq. (31), a variable is defined as

$$\begin{aligned} \Delta _i\left( t+1\right)&:=Q_i\left( t+1\right) \nabla f_i\left( {\mathbf {z}}_i\left( t+1\right) \right) \nonumber \\&\quad -Q_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) . \end{aligned}$$
(32)

Plugging Eq. (32) into Eq. (3) implies that

$$\begin{aligned} {\mathbf {s}}_i\left( t+1\right) =\sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {s}}_j\left( t\right) +\Delta _i\left( t+1\right) . \end{aligned}$$
(33)

In addition, we have employed induction to derive Eq. (31). Following from Lemma 2 and the boundedness of gradients, we can know that Eq. (31) holds for \(t=1\) to \(t=t_{0,\theta }\). Then, we assume that Eq. (31) holds up to \(t\ge t_{0,\theta }\). According to the definition of \({\mathbf {S}}_i\left( t\right) \) and Eq. (33), we have

$$\begin{aligned}&\sum \limits _{i=1}^n\left\| {\mathbf {S}}_i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2 \nonumber \\&=\sum \limits _{i=1}^n\left\| \sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {s}}_j\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2 \nonumber \\&\le \vert \lambda _2\left( A\right) \vert ^2\sum \limits _{i=1}^n\left\| {\mathbf {s}}_i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2 \nonumber \\&=\vert \lambda _2\left( A\right) \vert ^2\sum \limits _{i=1}^n\left\| \sum \limits _{j\in {\mathcal {N}}_i}a_{ij}{\mathbf {s}}_j\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2 \nonumber \\&=\vert \lambda _2\left( A\right) \vert ^2\sum \limits _{i=1}^n\left\| {\mathbf {S}}_i\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2, \end{aligned}$$
(34)

where in the first inequality we have used the conclusion of part (a) in Lemma 1 and Eq. (7). Furthermore, we introduce a variable, i.e.,

$$\begin{aligned} {\overline{\Delta }}\left( t+1\right) :={\mathbf {g}}\left( t+1\right) -{\mathbf {g}}\left( t\right) =\frac{1}{n}\sum \limits _{i=1}^n\Delta _i\left( t+1\right) . \end{aligned}$$

Therefore, the term \(\sum \nolimits _{i=1}^n\left\| {\mathbf {S}}_i\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\) can be bounded using the Cauchy–Schwarz inequality, i.e.,

$$\begin{aligned}&\sum \limits _{i=1}^n\left\| {\mathbf {S}}_i\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2 \nonumber \\&\qquad =\sum \limits _{i=1}^n\left\| \left( {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right) +\Delta _i\left( t+1\right) -\left( {\mathbf {g}}\left( t+1\right) -{\mathbf {g}}\left( t\right) \right) \right\| ^2 \nonumber \\&\qquad =\sum \limits _{i=1}^n\left\| \left( {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right) +\left( \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right) \right\| ^2 \nonumber \\&\qquad \le \sum \limits _{i=1}^n\left( \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2+\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2\right) \nonumber \\&\qquad +\sum \limits _{i=1}^n2\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| \cdot \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| , \end{aligned}$$
(35)

Further, the term \(\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| \) can be bounded as follows:

$$\begin{aligned} \left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2&=\left\| \left( 1-\frac{1}{n}\right) \Delta _i\left( t+1\right) \right. \nonumber \\&\quad \left. -\frac{1}{n}\sum \limits _{j\not =i}\Delta _j\left( t+1\right) \right\| ^2 \nonumber \\&\le 2\left( 1-\frac{1}{n}\right) \left\| \Delta _i\left( t+1\right) \right\| \nonumber \\&\quad +\frac{2}{n}\sum \limits _{j\not =i}\left\| \Delta _j\left( t+1\right) \right\| , \end{aligned}$$
(36)

where the last inequality is due to the inequality \((a-b)^2\le 2(a^2+b^2)\) for \(a,b\in {\mathbb {R}}^d\). In addition, by using the smoothness of \(f_i\) and Eq. (32), we also obtain

$$\begin{aligned}&{\mathbb {E}}\left[ \left\| \Delta _i\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\quad ={\mathbb {E}}\left[ \left\| Q_i\left( t+1\right) \nabla f_i\left( {\mathbf {z}}_i\left( t+1\right) \right) -Q_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\quad \le p_i\beta ^2\left\| {\mathbf {z}}_i\left( t+1\right) -{\mathbf {z}}_i\left( t\right) \right\| ^2 \nonumber \\&\quad =p_i\beta ^2\left\| \sum \limits _{j=1}^na_{ij}\left( \left( {\mathbf {x}}_j\left( t+1\right) -{\mathbf {z}}_j\left( t\right) \right) +\left( {\mathbf {z}}_j\left( t\right) -{\mathbf {z}}_i\left( t\right) \right) \right) \right\| ^2 \nonumber \\&\quad \le np_i\beta ^2\sum \limits _{j=1}^na_{ij}\left( \left\| {\mathbf {x}}_j\left( t+1\right) -{\mathbf {z}}_j\left( t\right) \right\| +\left\| {\mathbf {z}}_j\left( t\right) -{\mathbf {z}}_i\left( t\right) \right\| \right) ^2 \nonumber \\&\quad \le np_i\beta ^2\sum \limits _{j=1}^na_{ij}\left\| t^{-\theta }\left( {\mathbf {v}}_j\left( t\right) -{\mathbf {z}}_j\left( t\right) \right) \right\| ^2 \nonumber \\&\qquad +np_i\beta ^2\sum \limits _{j=1}^na_{ij}\left( \left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| +\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \right) ^2 \nonumber \\&\qquad +2np_i\beta ^2\sum \limits _{j=1}^na_{ij}\left\| t^{-\theta }\left( {\mathbf {v}}_j\left( t\right) -{\mathbf {z}}_j\left( t\right) \right) \right\| \nonumber \\&\qquad \times \left( \left\| {\mathbf {z}}_j\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| +\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \right) \nonumber \\&\quad \le np_i\beta ^2\sum \limits _{j=1}^na_{ij}\left( Dt^{-\theta }+2C_1t^{-\theta }\right) ^2 \nonumber \\&\quad =np_i\left( D+2C_1\right) ^2\beta ^2t^{-2\theta }, \end{aligned}$$
(37)

where the first inequality is derived by the definition of the matrix \(Q_i(t)\) and using the smoothness of \(f_i\); the second inequality is derived using the inequality \((\sum \nolimits _{i=1}^na_i)^2\le n\sum \nolimits _{i=1}^na_i^2\) and the fact that \(a_{ij}^2\le a_{ij}\) due to \(0\le a_{ij}\le 1\) for all \(i,j\in {\mathcal {V}}\); the third inequality is deduced using Eq. (6) and the triangle inequality; using Lemma 2 and the boundedness of \({\mathcal {X}}\) yields the fourth inequality; the last equality follows from Assumption 1.

Taking conditional expectation on both sides of Eq. (36), then applying Eq. (37), we obtain

$$\begin{aligned} P_1&:={\mathbb {E}}\left[ \left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\le 4np_i\left( 1-\frac{1}{n}\right) \left( D+2C_1\right) ^2\beta ^2 t^{-2\theta } \nonumber \\&\le 4np_i\left( D+2C_1\right) ^2\beta ^2 t^{-2\theta } \nonumber \\&\le 4np_{\max }\left( D+2C_1\right) ^2\beta ^2 t^{-2\theta }, \end{aligned}$$
(38)

where \(p_{\max }=\max _{i\in {\mathcal {V}}}p_i\). Taking conditional expectation on both sides of Eq. (35), and then using Eq.  (38), the Cauchy–Schwarz inequality, and the definition of \(C_2\), we have

$$\begin{aligned}&{\mathbb {E}}\left[ \sum \limits _{i=1}^n\left\| {\mathbf {S}}_i\left( t\right) +\Delta _i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\quad \le \sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2+\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\qquad +\sum \limits _{i=1}^n2{\mathbb {E}}\left[ \left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| \cdot \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| \mid {\mathcal {F}}_t\right] , \nonumber \\&\quad \le \sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2+\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\qquad +2\sum \limits _{i=1}^n\sqrt{P_1{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2\mid {\mathcal {F}}_t\right] } \nonumber \\&\quad \le \sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2+\left\| \Delta _i\left( t+1\right) -{\overline{\Delta }}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\qquad +2\sqrt{n}\sqrt{\sum \limits _{i=1}^nP_1{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| ^2\mid {\mathcal {F}}_t\right] } \nonumber \\&\quad \le C_2^2t^{-2\theta }+4np_{\max }\left( D+2C_1\right) ^2\beta ^2 t^{-2\theta }\nonumber \\&\qquad +4n\sqrt{p_{\max }}(D+2C_1)\beta C_2t^{-2\theta } \nonumber \\&\quad \le t^{-2\theta }\left( C_2+2n\left( D+2C_1\right) p_{\max }\beta \right) ^2 \nonumber \\&\quad \le \left( \frac{1+\left( t_{0,\theta }\right) ^{\theta }}{\left( t_{0,\theta }\right) ^{\theta }}\cdot \frac{C_2}{t^{\theta }}\right) ^2, \end{aligned}$$
(39)

where the following inequality:

$$\begin{aligned}&\sum \limits _{i=1}^n\sqrt{P_1{\mathbb {E}}[\Vert {\mathbf {S}}_i(t)-{\mathbf {g}}(t)\Vert ^2\mid {\mathcal {F}}_t]}\nonumber \\&\quad \le \sqrt{n}\sqrt{\sum \limits _{i=1}^nP_1{\mathbb {E}}[\Vert {\mathbf {S}}_i(t)-{\mathbf {g}}(t)\Vert ^2\mid {\mathcal {F}}_t]} \end{aligned}$$

is used to derive the third inequality. Taking conditional expectation on both sides of Eq. (34) and then using Eq.  (39), we deduce

$$\begin{aligned}&\sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \nonumber \\&\quad \le \left( \vert \lambda _2\left( A\right) \vert \cdot \frac{1+\left( t_{0,\theta }\right) ^{\theta }}{\left( t_{0,\theta }\right) ^{\theta }}\cdot \frac{C_2}{t^{\theta }}\right) ^2 . \end{aligned}$$
(40)

Furthermore, by Eq. (8), we have for \(t\ge t_{0,\theta }\)

$$\begin{aligned} \vert \lambda _2\left( A\right) \vert \cdot \frac{1+\left( t_{0,\theta }\right) ^{\theta }}{\left( t_{0,\theta }\right) ^{\theta }}&\le \left( \frac{t_{0,\theta }}{1+t_{0,\theta }}\right) ^{\theta }\le \left( \frac{t}{t+1}\right) ^{\theta }. \end{aligned}$$
(41)

Plugging Eq. (41) into Eq. (40), we obtain

$$\begin{aligned} \sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] \le \frac{C_2^2}{\left( t+1\right) ^{2\theta }}, \end{aligned}$$
(42)

which implies that

$$\begin{aligned} \sqrt{\sum \limits _{i=1}^n{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t+1\right) -{\mathbf {g}}\left( t+1\right) \right\| ^2\mid {\mathcal {F}}_t\right] }\le \frac{C_2}{\left( t+1\right) ^{\theta }}. \end{aligned}$$
(43)

Till now, we complete the induction step. Thus, Lemma 3 is proved completely. \(\square \)

Now, we start to prove Theorem 1 using Lemmata 1–3.

Proof of Theorem 1

Since each function \(f_i\) is \(\beta \)-smooth, the function f is also \(\beta \)-smooth. Thus, using Lemma 1 and the boundedness of \({\mathcal {X}}\), we have

$$\begin{aligned}&f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right) \le \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) ,\overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +f\left( \overline{{\mathbf {x}}}\left( t\right) \right) +\frac{\beta }{2}\left\| \overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2 \nonumber \\&\le \frac{\gamma _t}{n}\sum \limits _{i=1}^n\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) ,{\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle +f\left( \overline{{\mathbf {x}}}\left( t\right) \right) \nonumber \\&\quad +\frac{\beta }{2}\gamma _{t}^2\left\| \overline{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2 \nonumber \\&\le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) +\frac{\beta }{2}\gamma _t^2D^2+\frac{\gamma _t}{n}\sum \limits _{i=1}^n\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) ,{\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle . \end{aligned}$$
(44)

Furthermore, we also obtain that for \(i=1,\ldots ,n\) and \({\mathbf {v}}\in {\mathcal {X}}\)

$$\begin{aligned}&\left\langle \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&=\left\langle {\mathbf {S}}_i\left( t\right) ,{\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +\left\langle \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) -{\mathbf {S}}_i\left( t\right) , {\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\le \left\langle {\mathbf {S}}_i\left( t\right) ,{\mathbf {v}}-\overline{{\mathbf {x}}}\left( t\right) \right\rangle +D\cdot \left\| {\mathbf {S}}_i\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \nonumber \\&\le \left\langle \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}-\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +2D\cdot \left\| {\mathbf {S}}_i\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| , \end{aligned}$$
(45)

where the first equality holds by adding and subtracting \({\mathbf {S}}_i\left( t\right) \); using \({\mathbf {v}}_i\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle {\mathbf {v}},{\mathbf {S}}_i\left( t\right) \right\rangle \) implies that the first inequality holds; the last inequality is derived by adding and subtracting \( \frac{1}{n}\sum \nolimits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) )\) and using the fact that \({\mathcal {X}}\) is bounded. By taking expectation with respect to the random variables \(Q_i(t)\) on Eq. (45) and using Assumption 5, we obtain

$$\begin{aligned}&\left\langle \frac{1}{n}\sum \limits _{i=1}^np_i\nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\le \left\langle \frac{1}{n}\sum \limits _{i=1}^np_i\nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}-\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +2D\cdot {\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \right] . \end{aligned}$$
(46)

To estimate Eq. (46), we need to estimate the term

$$\begin{aligned} {\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) )\right\| \right] . \end{aligned}$$

By adding and subtracting \({\mathbf {g}}\left( t\right) \), using the triangle inequality, we get

$$\begin{aligned}&{\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \right] \le {\mathbb {E}}\left[ \left\| {\mathbf {S}}_i\left( t\right) -{\mathbf {g}}\left( t\right) \right\| \right] \nonumber \\&+{\mathbb {E}}\left[ \left\| {\mathbf {g}}\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \right] . \end{aligned}$$
(47)

Using Eq. (19) yields

$$\begin{aligned}&{\mathbb {E}}\left[ \left\| {\mathbf {g}}\left( t\right) - \frac{1}{n}\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \right] \nonumber \\&\qquad ={\mathbb {E}}\left[ \left\| \frac{\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) }{n} - \frac{\sum \limits _{i=1}^nQ_i\left( t\right) \nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) }{n}\right\| \right] \nonumber \\&\qquad \le \frac{1}{n}\sum \limits _{i=1}^np_i\left\| \nabla f_i\left( {\mathbf {z}}_i\left( t\right) \right) -\nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) \right\| \nonumber \\&\qquad \le \beta \cdot \frac{1}{n}\sum \limits _{i=1}^np_i\left\| {\mathbf {z}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| \nonumber \\&\qquad \le \beta p_{\max }\cdot \frac{C_1}{t}, \end{aligned}$$
(48)

where the second inequality is obtained since all functions \(f_i\) are \(\beta \)-smooth; the last inequality is due to Lemma 2. Combining Eqs. (29), (46), (47), and (48) yields

$$\begin{aligned}&\left\langle \frac{1}{n}\sum \limits _{i=1}^np_i\nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\le \left\langle \frac{1}{n}\sum \limits _{i=1}^np_i\nabla f_i\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}-\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +2D\cdot \frac{C_2}{t}+2\beta Dp_{\max }\cdot \frac{C_1}{t}. \end{aligned}$$
(49)

Moreover, letting \({\mathbf {v}}=\tilde{{\mathbf {v}}}\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}\right\rangle \) in Eq. (49) and using \(p_i=1/2\) for all \(i\in {\mathcal {V}}\), we further obtain

$$\begin{aligned} \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}_i\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle&\le \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&\quad +4D\cdot \frac{C_2}{t}+2\beta D\cdot \frac{C_1}{t}. \end{aligned}$$
(50)

Taking expectation conditional with respect to \({\mathcal {F}}_{t}\) and using Eq. (49), we deduce

$$\begin{aligned}&{\mathbb {E}}\left[ f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right) \mid {\mathcal {F}}_t\right] \le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) +\frac{\beta }{2}\gamma _t^2D^2+2\beta C_1D\frac{\gamma _t}{t} \nonumber \\&+4DC_2\cdot \frac{\gamma _t}{t}+\gamma _t\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle . \end{aligned}$$
(51)

Subtracting \(f\left( {\mathbf {x}}^*\right) \) from both sides of Eq.  (51) yields

$$\begin{aligned}&{\mathbb {E}}\left[ f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right) \mid {\mathcal {F}}_t\right] -f\left( {\mathbf {x}}^*\right) \le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( {\mathbf {x}}^*\right) \nonumber \\&+\frac{\beta }{2}\gamma _t^2D^2+2\beta C_1D\frac{\gamma _t}{t}+4DC_2\frac{\gamma _t}{t} \nonumber \\&+\gamma _t\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle , \end{aligned}$$
(52)

where the last inequality is derived using \(\Big \langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \Big \rangle \le 0\).

(a) Using \(\tilde{{\mathbf {v}}}\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}\right\rangle \) and the convexity of f, we deduce

$$\begin{aligned} f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( {\mathbf {x}}^*\right)&\le \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -{\mathbf {x}}^*\right\rangle \nonumber \\&\le \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -\tilde{{\mathbf {v}}}\left( t\right) \right\rangle . \end{aligned}$$
(53)

Letting \(h(t):=f(\overline{{\mathbf {x}}}(t))-f({\mathbf {x}}^{*})\), and then substituting Eq. (53) into Eq. (52), implies that

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right]&\le \left( 1-\gamma _t\right) h\left( t\right) +\frac{\beta }{2}\gamma _t^2D^2 \nonumber \\&\quad +2\beta C_1D\frac{\gamma _t}{t}+4DC'_2\frac{\gamma _t}{t}, \end{aligned}$$
(54)

where the last inequality is derived using \(f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( {\mathbf {x}}^*\right) \ge 0\). Assume that \({\mathbb {E}}\left[ h\left( t\right) \mid {\mathcal {F}}_{t-1}\right] \le \kappa /t\) for \(t\ge 2\). Since \(\gamma _t=2/t\) for \(t\ge 2\), from Eq. (54), we obtain

$$\begin{aligned}&{\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right] -\frac{\kappa }{t+1} \le \kappa \left( \frac{1}{t}-\frac{1}{t+1}\right) -\frac{2\kappa }{t^2}\nonumber \\&\qquad +\frac{2\beta D^2}{t^2} +\left( 2D\beta C_1+4DC'_2\right) \cdot \frac{2}{t^2} \nonumber \\&\quad \le \frac{2}{t^2}\left( \beta D^2+2D\beta C_1+4DC'_2-\frac{\kappa }{2}\right) \le 0, \end{aligned}$$
(55)

where using the relation \(1/t-1/\left( t+1\right) \le 1/t^2\) yields the second inequality; the last inequality is due to the definition of \(\kappa \), and specifically

$$\begin{aligned} \kappa =2\left( \beta D^2+2D\beta C_1+4DC'_2\right) . \end{aligned}$$

The induction step is completed and then the part (a) of Theorem 1 is proved.

(b) Because of the strong convexity of f and \(\alpha >0\), employing Lemma 6 in [59] yields

$$\begin{aligned} \left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -\tilde{{\mathbf {v}}}\left( t\right) \right\rangle \ge \sqrt{2\mu \alpha ^2h\left( t\right) }. \end{aligned}$$
(56)

Substituting Eq. (56) into Eq. (52) implies that

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right]&\le \sqrt{h\left( t\right) }\left( \sqrt{h\left( t\right) }-\gamma _t\sqrt{2\mu \alpha ^2}\right) \nonumber \\&+\frac{\beta }{2}\gamma _t^2D^2+\left( 2D\beta C_1+4DC_2\right) \cdot \frac{\gamma _t}{t}. \end{aligned}$$
(57)

When \(\sqrt{h\left( t\right) }-\gamma _t\sqrt{2\mu \alpha ^2}\le 0\), from Eq. (57), we obtain

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right]&\le \frac{\beta }{2}\gamma _t^2D^2+\left( 2D\beta C_1+4DC_2\right) \cdot \frac{\gamma _t}{t} \nonumber \\&=\left( 2\beta D^2+4D\beta C_1+8DC_2\right) \cdot \frac{1}{t^2} \nonumber \\&\le \left( 2\beta D^2+4D\beta C_1+8DC_2\right) \cdot \frac{4}{\left( t+1\right) ^2}, \end{aligned}$$
(58)

where the last inequality is derived using the relation

$$\begin{aligned} \frac{1}{M+t-1}\le \frac{M+1}{M}\cdot \frac{1}{M+t} \end{aligned}$$

for \(M\ge 1\). In addition, since

$$\begin{aligned} \eta&:=\max \left\{ 2\beta D^2+4D\beta C_1+8DC_2,\zeta ^2\left( \beta D^2\right. \right. \nonumber \\&\quad \left. \left. +2D\beta C_1+4DC_2\right) ^2\bigg /2\mu \alpha ^2\right\} , \end{aligned}$$
(59)

where \(\zeta \) is a constant such that \(\zeta > 1\). Thus, we obtain

$$\begin{aligned} 2\beta D^2+4D\beta C_1+8DC_2\le \eta . \end{aligned}$$

Therefore, we conclude

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right] \le \frac{\eta }{\left( t+1\right) ^2}. \end{aligned}$$
(60)

When \(\sqrt{h\left( t\right) }-\gamma _t\sqrt{2\mu \alpha ^2}>0\), by using Eqs. (57) and (59), we obtain

$$\begin{aligned}&{\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right] -\frac{\eta }{\left( t+1\right) ^2}\le \eta \left( \frac{1}{t^2}-\frac{1}{\left( t+1\right) ^2}\right) \nonumber \\&+\frac{2}{t^2}\left( \beta D^2+2D\beta C_1+4DC_2-\alpha \sqrt{2\mu \eta }\right) \nonumber \\&\le \frac{2}{t^2}\left( \frac{\eta }{t}+\beta D^2+2D\beta C_1+4DC_2-\alpha \sqrt{2\mu \eta }\right) \nonumber \\&\le \frac{2}{t^2}\left( \frac{\eta }{t}+\left( \beta D^2+2D\beta C_1+4DC_2\right) \left( 1-\zeta \right) \right) , \end{aligned}$$
(61)

where using \(1/t^2-1/\left( t+1\right) ^2\le 2/t^3\) yields the first inequality. Moreover, we define

$$\begin{aligned} t'=\inf _{t\ge 1}\left\{ \frac{\eta }{t}+\left( \beta D^2+2D\beta C_1+4DC_2\right) \left( 1-\zeta \right) \le 0\right\} . \end{aligned}$$

Because \(\varphi \left( t\right) =1/t\) is monotone decreasing and tends to 0 as \(t\rightarrow \infty \). Moreover, \(\zeta >1\) and thus, the parameter \(t'\) exists. For any \(t>t'\), Eq. (61) is less than or equal to 0. Therefore, we obtain

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t+1\right) \mid {\mathcal {F}}_t\right] \le \frac{\eta }{\left( t+1\right) ^2}. \end{aligned}$$
(62)

For \(t\le t'\), we have

$$\begin{aligned} \frac{\eta }{t}\ge \left( \beta D^2+2D\beta C_1+4DC_2\right) \left( \zeta -1\right) , \end{aligned}$$
(63)

namely,

$$\begin{aligned} \kappa \left( \zeta -1\right) \le \frac{\eta }{t}. \end{aligned}$$
(64)

Furthermore, let \(\zeta =2\) and using the result of part (a) in Theorem 1, we have

$$\begin{aligned} {\mathbb {E}}\left[ h\left( t\right) \mid {\mathcal {F}}_{t-1}\right] \le \frac{\kappa }{t}\le \frac{\eta }{t^2}. \end{aligned}$$
(65)

In addition, the inequality \({\mathbb {E}}\left[ h\left( t\right) \mid {\mathcal {F}}_{t-1}\right] \le \kappa /t\) holds for all \(t\ge 2\). Therefore, we obtain part (b). \(\square \)

We next prove Theorem 2.

Proof of Theorem 2

Using Eq. (15) and the fact

$$\begin{aligned} \tilde{{\mathbf {v}}}\left( t\right) \in \arg \min _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , {\mathbf {v}}\right\rangle , \end{aligned}$$

we deduce

$$\begin{aligned} \Gamma \left( t\right)&=\max _{{\mathbf {v}}\in {\mathcal {X}}}\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -{\mathbf {v}}\right\rangle \nonumber \\&=\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t\right) -\tilde{{\mathbf {v}}}\left( t\right) \right\rangle . \end{aligned}$$
(66)

Furthermore, \(\Gamma \left( t\right) \ge 0\). Because of the smoothness of f with \(\beta \), then

$$\begin{aligned} f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right)&\le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) +\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&+\frac{\beta }{2}\left\| \overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) \right\| ^2. \end{aligned}$$
(67)

Using Lemma  1 yields

$$\begin{aligned} \overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) =\gamma _t\left( \overline{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right) . \end{aligned}$$
(68)

Employing the triangle inequality implies that

$$\begin{aligned} \left\| \overline{{\mathbf {x}}}\left( t+1\right) -\overline{{\mathbf {x}}}\left( t\right) \right\|&=\frac{\gamma _t}{n}\left\| \sum \limits _{i=1}^n\left( {\mathbf {v}}_i\left( t\right) -{\mathbf {z}}_i\left( t\right) \right) \right\| \nonumber \\&\le \frac{\gamma _t}{n}\sum \limits _{i=1}^n\left\| {\mathbf {v}}_i\left( t\right) -{\mathbf {z}}_i\left( t\right) \right\| \nonumber \\&\le D\gamma _t, \end{aligned}$$
(69)

where the last inequality is derived since \({\mathbf {z}}_i\left( t\right) \), \({\mathbf {v}}_i\left( t\right) \in {\mathcal {X}}\). Thus, Eq. (67) is bounded, i.e.,

$$\begin{aligned} f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right)&\le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) +\gamma _t\left\langle \nabla f\left( \overline{{\mathbf {x}}}\left( t\right) \right) , \tilde{{\mathbf {v}}}\left( t\right) -\overline{{\mathbf {x}}}\left( t\right) \right\rangle \nonumber \\&+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\cdot \frac{\gamma _t}{t^\theta }+\frac{\beta }{2}\gamma _t^2D^2 \nonumber \\&=f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -\gamma _t\Gamma \left( t\right) \nonumber \\&\quad +\frac{\beta }{2}\gamma _t^2D^2+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\cdot \frac{\gamma _t}{t^\theta }. \end{aligned}$$
(70)

Using Eq. (70) implies that

$$\begin{aligned} \gamma _t\Gamma \left( t\right)&\le f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right) \nonumber \\&\quad +\frac{\beta }{2}\gamma _t^2D^2 +\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\cdot \frac{\gamma _t}{t^{\theta }}. \end{aligned}$$
(71)

By summing both sides of Eq. (71) over , we obtain

$$\begin{aligned}&\sum \limits _{t=T/2+1}^T\gamma _t\Gamma \left( t\right) \le \sum \limits _{t=T/2+1}^T\left( f\left( \overline{{\mathbf {x}}}\left( t\right) \right) -f\left( \overline{{\mathbf {x}}}\left( t+1\right) \right) \right) \nonumber \\&+\sum \limits _{t=T/2+1}^T\left( \frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\cdot \frac{\gamma _t}{t^{\theta }}+\frac{\beta }{2}\gamma _t^2D^2\right) \nonumber \\&=f\left( \overline{{\mathbf {x}}}\left( T/2+1\right) \right) -f\left( \overline{{\mathbf {x}}}\left( T+1\right) \right) \nonumber \\&+\sum \limits _{t=T/2+1}^T\left( \frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\cdot \frac{\gamma _t}{t^{\theta }}+\frac{\beta }{2}\gamma _t^2D^2\right) . \end{aligned}$$
(72)

In addition, since \(\gamma _t\ge 0\) and \(\Gamma \left( t\right) \ge 0\), then

$$\begin{aligned} \sum \limits _{t=T/2+1}^T\gamma _t\Gamma \left( t\right) \ge \left( \min _{t\in \left[ T/2+1,T\right] }\Gamma \left( t\right) \right) \left( \sum \limits _{t=T/2+1}^T\gamma _t\right) . \end{aligned}$$
(73)

Using the expression \(\gamma _t=t^{-\theta }\), for \(T\ge 6\) and \(\theta \in \left( 0,1\right) \), we get

$$\begin{aligned} \sum \limits _{t=T/2+1}^T\gamma _t&=\sum \limits _{t=T/2+1}^Tt^{-\theta }\ge \int _{T/2+1}^Tt^{-\theta }dt \nonumber \\&=\frac{1}{1-\theta }\left( T^{1-\theta }-\left( \frac{T}{2}+1\right) ^{1-\theta }\right) \nonumber \\&\ge \frac{T^{1-\theta }}{1-\theta }\left( 1-\left( \frac{2}{3}\right) ^{1-\theta }\right) . \end{aligned}$$
(74)

When \(\theta \ge 1/2\), we deduce that

$$\begin{aligned} \sum \limits _{t=T/2+1}^T\gamma _t^2=\sum \limits _{t=T/2+1}^Tt^{-2\theta }\le \sum \limits _{t=T/2+1}^Tt^{-1}\le \ln 2. \end{aligned}$$
(75)

Plugging Eq. (75) into Eq. (72) implies that

$$\begin{aligned} \sum \limits _{t=T/2+1}^T\gamma _t\Gamma \left( t\right) \le LD+\left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \ln 2, \end{aligned}$$
(76)

where the last inequality holds because f is L-Lipschitz. Combining Eqs. (73) and (76), we have

$$\begin{aligned} \min _{t\in \left[ T/2+1,T\right] }\Gamma \left( t\right) \le C_3\cdot \frac{1-\theta }{T^{1-\theta }}\left( 1-\left( 2/3\right) ^{1-\theta }\right) ^{-1}, \end{aligned}$$
(77)

where

$$\begin{aligned} C_3:=LD+\left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \ln 2. \end{aligned}$$

When \(\theta <1/2\), we also have

$$\begin{aligned} \sum \limits _{t=T/2+1}^T\frac{1}{t^{2\theta }}\le \int _{t=T/2}^T\frac{1}{t^{2\theta }}dt=T^{1-2\theta }\cdot \frac{1-\left( 1/2\right) ^{1-2\theta }}{1-2\theta }. \end{aligned}$$
(78)

Plugging Eq. (78) into Eq. (72) and using the Lipschitz condition of f, we deduce that

$$\begin{aligned}&\sum \limits _{t=T/2+1}^T\gamma _t\Gamma \left( t\right) \le LD+\left( \frac{\beta D^2}{2}\right. \nonumber \\&\quad \left. +\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \frac{1-\left( 1/2\right) ^{1-2\theta }}{1-2\theta }T^{1-2\theta } \nonumber \\&\le LDT^{1-2\theta }\nonumber \\&\quad +\left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \frac{1-\left( 1/2\right) ^{1-2\theta }}{1-2\theta }T^{1-2\theta }, \end{aligned}$$
(79)

where the last inequality is due to \(T^{1-2\theta }\le 1\) for all \(\theta <1/2\). Combining Eqs. (73), (74), and (79), we have

$$\begin{aligned} \min _{t\in \left[ T/2+1,T\right] }\Gamma \left( t\right) \le \frac{1-\theta }{1-\left( 2/3\right) ^{1-\theta }}\cdot \frac{C_4}{T^\theta }, \end{aligned}$$
(80)

where

$$\begin{aligned} C_4:=LD+\left( \frac{\beta D^2}{2}+\frac{2D\left( \beta C_1p_{\max }+C_2\right) }{p_{\min }}\right) \frac{1-\left( 1/2\right) ^{1-2\theta }}{1-2\theta }. \end{aligned}$$

Therefore, the results of Theorem 2 is obtained.

Fig. 1
figure 1

Comparison of the proposed algorithm, DeFW, EXTRA, and DGD for the convex problem on news20 and aloi datasets

Full size image
Fig. 2
figure 2

Comparison of the proposed algorithm with varying number of nodes on news20 and aloi datasets

Full size image

Experiments

The proposed algorithm is used to solve a multiclass classification problem with different loss functions and a structural SVM problem for evaluating the performance of our designed algorithm, respectively. In addition, the experiments are run in Windows 10 equipped with 1080Ti GPU and 64 GB memory. Moreover, we implement the experiment program in MATLAB 2018a.

Multiclass classification

We first introduce the multiclass classification problems: The notation \({\mathcal {S}}=\left\{ 1,\ldots ,\varrho \right\} \) designates the set of classes, each agent \(i\in \left\{ 1,\ldots ,n\right\} \) has access to a data example \({\mathbf {d}}_i\left( t\right) \in {\mathbb {R}}^d\), which denotes a class in \({\mathcal {S}}\), and needs to obtain a decision matrix \(X_i\left( t\right) =\left[ {\mathbf {x}}_1^{\top };\ldots ;{\mathbf {x}}_{\varrho }^{\top }\right] \in {\mathbb {R}}^{\varrho \times d}\). Furthermore, the class label is predicted by \(\arg \max _{h\in {\mathcal {S}}}{\mathbf {x}}_h^{\top }{\mathbf {d}}_i\left( t\right) \). The local loss function of each agent i is defined as follows:

$$\begin{aligned} f_i\left( X_i\left( t\right) \right) =\ln \left( 1+\sum \limits _{h\not =y_i\left( t\right) }\exp \left( {\mathbf {x}}_h^{\top }{\mathbf {d}}_i\left( t\right) \right) -{\mathbf {x}}_{y_i\left( t\right) }^{\top }{\mathbf {d}}_i\left( t\right) \right) , \end{aligned}$$

where \(y_i\left( t\right) \) designates the true class label. Moreover, the constraint set \({\mathcal {X}}=\{X\in {\mathbb {R}}^{\varrho \times d}\mid \left\| X\right\| _{*}\le \delta \}\), where \(\Vert \cdot \Vert _{*}\) is the Frobenius norm of a matrix and \(\delta \) is a positive constant.

Fig. 3
figure 3

Comparison of the proposed algorithm with different topologies on news20 and aloi datasets

Full size image

In our experiments, we employ some datasets to test the performance of the designed algorithm. For this reason, two relatively large multiclass datasets are chosen from the LIBSVM DataFootnote 1. Table 3 presents the summary of these datasets. Besides, the parameters are set by the theories suggest. For this reason, the step-size is set to be 2/t in these experiments.

Table 3 Summary of datasets
Full size table

Experimental results

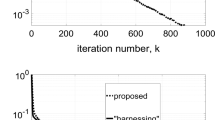
To demonstrate the performance advantage of our algorithm, we first compare the proposed algorithm with DeFW [31], EXTRA [39], and DGD [40] on different datasets with \(n=64\). As depicted in Fig. 1, the convergence speed of our algorithm is faster than DeFW, EXTRA, and DGD on two datasets news20 and aloi. At each iteration, the computational cost of the proposed algorithm is lower than DeFW, EXTRA, and DGD, the number of iterations in our designed algorithm is increased for a running time. Therefore, the convergence speed is accelerated correspondingly.

To investigate the impact of the number of nodes on the performance of our algorithm, we run the proposed algorithm on complete graphs with different nodes. As depicted in Fig. 2, the larger size of graph leads to the slower convergence rate. Furthermore, the convergence performance of our algorithm is comparable to the centralized gradient descent algorithm.

To evaluate the impact of network topologies on the performance of our algorithm, we run the proposed algorithm on a complete graph, a random graph (Watts–Strogatz), and a cycle graph, respectively. Moreover, the number of nodes in these graphs are set to be \(n=64\). The results are depicted in Fig. 3. We find that the complete graph can lead to slightly faster convergence than the random graph and the cycle graph. In other words, the better connectivity leads to the faster convergence rate in the proposed algorithm.

Conclusion

This paper has presented a distributed randomized block-coordinate Frank–Wolfe algorithm over networks for solving high-dimensional constrained optimization problems. Furthermore, detailed analyses of the convergence rate for our proposed algorithm are provided. Specifically, using a diminishing step-size, our algorithm converges at a rate of \({\mathcal {O}}(1/t)\) for convex objective functions; for the strongly convex objective functions, the convergence rate is \({\mathcal {O}}(1/t^2)\) when the optimal solution is an interior point of the constraint set. Moreover, our algorithm converges to a stationary point at a rate of \({\mathcal {O}}(1/\sqrt{t})\) under non-convexity by employing a diminishing step-size. Finally, the theoretical results have been confirmed by experiments. The results have shown that our algorithm is faster than the existing distributed algorithms. In the future work, we will devise and analyze of distributed adaptive block-coordinate Frank–Wolfe algorithms with momentum for training rapidly distributed deep neural networks.