Content-adaptive image compression and encryption via optimized compressive sensing with double random phase encoding driven by chaos

Abstract

With the advancement of multimedia technology and coming of big data era, the size of image data is significantly increased. However, the traditional image encryption methods cannot solve the emerging problems of efficient compression. To settle with this challenge, an effective content-adaptive image compression and encryption method based on compressive sensing and double random phase encoding (DRPE) is proposed in this paper. The original image is converted to one low-frequency part and three high-frequency parts by DWT and then permutated by sorting-based chaotic sequences. Afterward, a novel measurement matrix optimization algorithm based on adaptive step size is presented to measure the high-frequency components. To enhance the security of the scheme, the DRPE, quantization, and diffusion are successively performed on the complex matrix composed of the shuffled low-frequency component and three measurement value matrices to obtain the cipher image. Logistic-Sine chaotic system is utilized to produce the chaotic keystreams for the encryption process, and its system parameter and initial value are determined by the information entropy of the plain image and external key parameters, so that the proposed cipher can withstand known-plaintext and chosen-plaintext attacks effectively. Numerical experiments demonstrate the effectiveness of the proposed image compression and encryption algorithm.

Introduction

With the rapid development of multimedia technology and the arrival of big data era, more and more high-resolution images are sampled, transmitted, and stored over the Internet. Some of them may contain private information. Therefore, compressing and encrypting images before transmission are necessary [1]. Recently, many image encryption methods have been introduced based on chaotic systems [2,3,4], such as DNA sequence operations [5, 6], cellular automata [7], optical transform [8, 9], and others. However, these schemes cannot efficiently compress the images to save the transmission and storage pressures. Compressive sensing (CS) may compress, encrypt, and sample the plain image simultaneously [10,11,12], and some image encryption algorithms based on CS have been proposed accordingly.

In CS-based image encryption, measurement matrix (MM) is used as secret key [13], and it may be transmitted from the sender to the receiver for decryption. In the early age, the transmission of the whole measurement matrix may occupy huge amounts of storage space and transmission bandwidth [14, 15], which makes the secret key too large to be effectively distributed and stored. To settle this issue, chaotic systems are used to construct measurement matrix, and less parameters may get larger measurement matrix for CS. For instance, Zhou et al. [16] introduced a novel image compression–encryption hybrid algorithm based on key-controlled MM in CS, wherein the measurement matrices were generated by utilizing the circulant matrices and determining the original row vectors of the circulant matrices with one 1D logistic map. Huang et al. [17] proposed a compression–diffusion–permutation method for securing image, MM of CS was the Hadamard matrix generated by iterating a 2D Sine-Logistic modulation map, and using only a few keys of this chaos avoided the transmission and storage of the ordinary Gaussian matrix. In [18], a chaotic matrix was first produced by computing 1D logistic map with the initial value, and this matrix was quantified into − 1 or 1 to get the Bernoulli random matrix for CS. Recently, Wang et al. [19] provided an adjustable visual image cryptosystem based on 6D hyperchaotic system and compressive sensing, 3D Chen chaotic system was applied to provide the measurement matrix of CS, and only three initial values need to be transmitted. In this article, 1D Logistic-Sine chaotic system (LSS) is utilized to generate the MM for CS.

Besides, the performance of MM may affect the quality of the reconstructed images [20], and some scholars devote to present high-performance MMs. For example, Endra et al. [21] optimized the MM by use of the modified closed equiangular tight frame. Luo et al. [22] generated a chaos-combined asymptotic deterministic random measurement matrix (CADRMM) by use of the Logistic map and Lissajous map to generate more random chaotic sequences. In [23], an asymptotical deterministic random measurement matrix based on information entropy and counter (ADMMIC) was given to compress the plain image, 2D-LSCM chaotic system was utilized to generate the MM, and its parameters were controlled by information entropy of the plain image, so that random-like sequences may give more random MM and high-precision recovered images. In [24], 1D LSS was utilized to produce low-dimensional matrices, and then, they were extended with Kronecker product (KP) to get high-dimensional matrices, and the final measurement matrices were obtained by optimizing them with singular value decomposition (SVD). In this paper, a measurement matrix optimization algorithm based on adaptive step size is designed to improve the quality of the reconstructed image.

It is generally known that CS-based image encryption cannot attain perfect secrecy but computational secrecy [25]. Thus, some image encryption methods are combined with CS to enhance the security levels. Such as, a joint image compression–encryption scheme based on entropy coding and compressive sensing is given in [26], the higher bit planes of the plain image are manipulated entropy coding and the lower ones are performed CS compression. Sun et al. [27] provided an image encryption method based on CS and hyperchaotic map, row/column cyclic shift, and diffusion based on Galois field multiplication are utilized to upgrade the security level. Zhou et al. [28] proposed an image compression and encryption scheme by use of 2D CS and fractional Mellin transform, the plain image was measured from two directions to obtain the measurement value matrix, and then, nonlinear fractional Mellin transform was utilized to confuse it. An image encryption algorithm based on memristive chaotic system, elementary cellular automata (ECA), and CS was presented in [29], the original image was processed by DWT to obtain the sparse coefficient matrix, and then, zigzag shuffling and ECA were combined to confuse the coefficient matrix to upgrade the reconstruction quality. Huo et al. [30] combined DNA encoding with CS to give a novel image compression–encryption hybrid scheme, the plain image was processed by DNA encryption, and then, the resulting image was measured by CS to find the cipher image.

It is no denying that although there are so many CS-based image encryption algorithms, some of them still have the shortcomings in the compression and security. For example, the relation of the image encryption method and plain image is a bit less, so that it is vulnerable to withstand chosen-plaintext and known-plaintext attacks; the quality of the recovered image is lower especially in the high compression condition; besides, the randomness of the final cipher image gotten by some ciphers is unsatisfactory to make it resist entropy attack, et al.

Inspired by the above analyses, an effective content-adaptive image compression and encryption scheme based on compressive sensing and double random phase encoding (DRPE) is presented in this paper. Specifically, a measurement matrix optimization method for CS is designed, step size of gradient descent may be adjusted adaptively, and the stability of the algorithm is guaranteed. Besides, the integration of CS and DRPE may not only save hardware resources, but also improve the security of the proposed cipher. The contributions of our work can be summarized as follows:

• 1. We propose an effective image compression and encryption scheme by integrating CS and DRPE. CS is applied for compressing the plain image to narrow its size, and DRPE is used for diffusing the plain image to improve the security level of the proposed cipher.

• 2. We compress the plain image selectively by use of importance of the plain image, which can attain the balance of high-quality reconstruction image and high compression performance.

• 3. This paper designs a measurement matrix optimization algorithm based on adaptive step size, the threshold function is combined with Barzilai–Borwein method, Armijo criterion, and equiangular tight frame, so that the step size can be adjusted adaptively in the iteration, convergence speed of the algorithm is improved, and the stability of the algorithm is ensured.

• 4. The proposed cipher is highly sensitive to the plain image, and it is plain-image-content-adaptive. Logistic-Sine chaotic system is used to generate the chaotic keystreams for CS, DRPE, and diffusion, and its system parameter and initial value are calculated by the information entropy of the plain image and external key parameters, so that different keystreams are produced for different original image, and the proposed cipher can resist known-plaintext and chosen-plaintext attacks effectively.

The rest of this paper is organized as follows. “Preliminaries” give the preliminaries, such as double random phase encoding, gram matrix and cross-correlation coefficient, overall correlation coefficient, QR decomposition, and gradient descent method. The proposed measurement matrix optimization algorithm and image compression and encryption scheme are depicted in “The proposed measurement matrix optimization algorithm” and “The presented image compression and encryption scheme”. Performance analyses of measurement matrix optimization algorithm and image compression and encryption algorithm are demonstrated in “Performance analyses of measurement matrix optimization algorithm” and “Performance analyses of image compression and encryption algorithm”, respectively. Finally, this paper is concluded in “Conclusion”.

Preliminaries

Double random phase encoding

Since optical encryption has many merits, such as parallel computation, fast running speed, and processing data in various transform domains, it attracts wide attention from researchers. Among them, double random phase encoding (DRPE) is an effective method and applied for image encryption [31]. As shown in Fig. 1, optical encryption setup based on DRPE mostly consists of two phase plates and two optical lens. The plain image is encoded randomly by the first phase plate, and then, the obtained image is converted to frequency domain by use of the Fourier transform of the first optical lens; subsequently, the gotten frequency data are encoded randomly by the second phase plate, and then, the cipher image is found by performing inverse Fourier transform on it. The whole encryption process may be represented by

$$ \begin{aligned} \Psi (x,y) &= {\text{FT}}^{ - 1} \left \{ {\text{FT}}\{{f(x,y)\exp [i2 \pi n(x,y)]} \right.\\ & \quad \left. \cdot \exp [ i2\pi b(x,y)]\right\}, \end{aligned}$$

(1)

where FT denotes the Fourier transform, FT⁻¹ is its inverse operation, f (x, y) is the plain image, $\begin{aligned} \Psi (x,y) \end{aligned}$ is the cipher image, and n (x, y) and b (x, y) are two random phases.

Fig. 1

Optical encryption setup based on DRPE

Gram matrix and cross-correlation coefficient

The less the cross-correlation coefficient between the measurement matrix and sparse coefficient matrix is, the lower the correlation between them is, and the better the quality of the reconstructed image is. The cross-correlation coefficient may be computed by the following steps.

Let sparse coefficient matrix be $\Psi \in R^{N \times N}$, and measurement matrix be $\Phi \in R^{M \times N}$, and the multiplication between them is $D = \Phi \Psi$ . The new matrix $\tilde{D}$ is obtained by manipulating normalized operation on every column of D, the maximum cross-correlation coefficient μ (D) between arbitrary two column vectors of $\tilde{D}$ may be computed by [32]

$$ \mu (D) = \mathop {{\text{max}}}\limits_{i \ne j} \left\{ {\frac{{\left| {d_{i}^{{\text{T}}} d^{j} } \right|}}{{\left\| {d_{i} } \right\| \cdot \left\| {d_{j} } \right\|}}} \right\} = \mathop {\max }\limits_{i \ne j} \left\{ {\left| {\tilde{d}_{i}^{{\text{T}}} d_{j} } \right|} \right\}, $$

(2)

where d_i and $\tilde{d}_{i}$ denote the column vectors of D and $\tilde{D}$, respectively, and (·)^T means the matrix transpose.

The Gram matrix G may be obtained by $G = \tilde{D}^{{\text{T}}} \tilde{D}$, and the maximum cross-correlation coefficient may be gotten by [33]

$$ \mu = \mathop {\max }\limits_{i \ne j} \left| {g_{ij} } \right|, $$

(3)

where g_ij is the element at row i and column j of G. Accordingly, the average cross-correlation coefficient μ_av of G may be defined as [34]

$$ \mu_{av} = \frac{1}{n(n - 1)}\sum\limits_{i,j = 1,i \ne j}^{n} {\left| {g_{ij} } \right|} , $$

(4)

where n is the total number of matrix elements.

To recover the original signal in CS, the following condition should be met [35]:

$$ M > cK \cdot \mu^{2} (D) \cdot \log (N), $$

(5)

where N is the length of the signal, and parameter c > 0. From Eqs. (2–5), one may watch that when the cross-correlation coefficient μ(D) is less, the correlation of $\Phi$ and $\Psi$ is lower [35], and the uncorrelation between them is stronger. Therefore, to improve the effect of reconstruction algorithm, one may optimize the measurement matrix by reducing the cross-correlation coefficient.

To find the minimum cross-correlation, an optimization method of measurement matrix based on equiangular tight frame (ETF) was proposed in [36], and then, Welch boundary is obtained [37]. For a certain space R^M×N, the minimum value of cross-correlation coefficient μ is called as Welch boundary, that is, $\mu \ge \sqrt {(N - M)/(M(N - 1))}$. If and only if the column vector of matrix D satisfies ETF, the inner product of any two columns of D is equal to $\sqrt {(N - M)/(M(N - 1))}$, the equal sign in the above inequality holds, and here, M, N are the row and column of matrix $\Phi$, respectively. Let $\mu (D) = \sqrt {(N - M)/(M(N - 1))}$, and then, according to Eq. (6), the elements of Gram matrix G are contracted to make it approach to the ETF, and finally, the matrix H is obtained, and h_ij, g_ij are the elements located at the ith row and the jth column of H and G, respectively

$$ h_{ij} = \left\{ {\begin{array}{*{20}c} {\mu (D) \cdot {\text{sign}}(g_{ij} ),} & {\mu (D) \le \left| {\left. {g_{ij} } \right|} \right.} \\ {g_{ij} ,} & {\mu (D) > \left| {\left. {g_{ij} } \right|} \right.} \\ \end{array} } \right.. $$

(6)

Overall correlation coefficient

Reducing the square of non-zero eigenvalues of Gram matrix may effectively reduce the overall correlation coefficient between measurement matrix and sparse matrix. One finds that [38]

$$ \sum\limits_{s = 1}^{m} {\lambda_{s} } = n $$

(7)

$$ \sum\limits_{s = 1}^{m} {(\lambda_{s} } )^{2} = \sum\limits_{i,j}^{n} {\left[ {\left\langle {\tilde{d}_{i} ,\tilde{d}_{j} } \right\rangle } \right]}^{2} , $$

(8)

where λ_s (s = 1, 2,…,m) is the mth eigenvalue of Gram matrix, and $\tilde{d}_{i}$ is the ith column of $\tilde{D}$. From the definition of Gram matrix, it is evident that

$$ \left\langle {\tilde{d}_{i} ,\tilde{d}_{j} } \right\rangle = g_{ij} . $$

(9)

Normalize the column of $\tilde{D}$ to find that

$$ g_{ij} = \left\langle {\tilde{d}_{i} ,\tilde{d}_{j} } \right\rangle = 1. $$

(10)

Assuming that $\mu_{{{\text{all}}}} = \sum\nolimits_{i \ne j} {(g_{ij} )^{2} }$ is the overall correlation coefficient, and it may be expressed as

$$ \mu_{{{\text{all}}}} = \sum\limits_{i \ne j} {(g_{ij} )^{2} } = \sum\limits_{i,j = 1}^{n} {(g_{ij} )^{2} - } \sum\limits_{i = 1}^{n} {(g_{ii} )} = \sum\limits_{i,j = 1}^{n} {\left[ {\left\langle {\tilde{d}_{i} ,\tilde{d}_{j} } \right\rangle } \right]}^{2} - n = \sum\limits_{s = 1}^{n} {(\lambda_{s} )^{2} } - n. $$

(11)

Combining Eq. (7) with Eq. (11), the problem of minimizing overall correlation coefficient can be transformed into the following optimization problem:

$$ \min \mu_{{{\text{all}}}} = \sum\limits_{s = 1}^{m} {(\lambda_{s} )^{2} - n} \quad {\text{s.t.}}\sum\limits_{s = 1}^{m} {\lambda_{s} } = n. $$

(12)

From Eq. (12), one may see that when the square sum $\sum\nolimits_{s = 1}^{m} {(\lambda_{s} )^{2} }$ of the eigenvalues of the Gram matrix is minimum, the global correlation coefficient μ_all may get the minimum value. Since $\sum\nolimits_{s = 1}^{m} {\lambda_{s} = n}$, when $\lambda_{{1}} = \lambda_{{2}} = \cdots = \lambda_{n} = n/m$, μ_all may reach the minimum. Specifically, first, find the eigenvalues of Gram matrix, then set all the non-zero eigenvalues as the average value n/m, which not only makes the sum of the eigenvalues constant, but also renders the square sum of the eigenvalues the lowest [39].

QR decomposition

First, the measurement matrix $\Phi$ is decomposed by standard QR decomposition to obtain matrix Q and R. As for R, its principal diagonal elements are much larger than the non-diagonal elements [40], and then, one sets all non-diagonal elements to 0 to get matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R}$; thus, the new measurement matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi } = Q\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R}$ is obtained. The detailed steps are as follows.

Step 1: First, get a random measurement matrix $\Phi = R^{M \times N}$;

Step 2: Perform transpose operation on matrix $\Phi$ to get $\Phi^{{\text{T}}}$, and then manipulate QR decomposition on $\Phi^{{\text{T}}}$ to obtain $\Phi^{{\text{T}}} = QR$;

Step 3: Make all the non-diagonal elements of matrix R be zero to obtain the matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R}$;

Step 4: $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }$ is obtained by replacing R with $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R}$ in step 2, and then, its transpose $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }^{{\text{T}}}$ is the optimized result.

Through the above steps, the minimum singular value of the measurement matrix is increased by QR decomposition, so that the independence of the column vectors of the measurement matrix is improved, the purpose of optimizing the measurement matrix is achieved, and accordingly, the quality of reconstructed image is improved.

Gradient descent method

In this article, gradient descent method (GDM) is utilized to lessen the cross-correlation between the measurement matrix and sparse matrix. The optimization problem of measurement matrix may be derived to the following unconstrained optimization one:

$$ \mathop {\min }\limits_{G} \left\| {G - H_{2} } \right\|_{F}^{2} = \mathop {\min }\limits_{\Phi } \left\| {\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{2} } \right\|_{F}^{2} , $$

(13)

where $\left\| \cdot \right\|_{F}$ is the Frobenius norm, G is the Gram matrix, H₂ is gotten by contracting threshold function, $\Phi$ is the measurement matrix, and $\Psi$ is the sparse matrix. GDM is applied for renewing the measurement matrix, and the detailed steps are as follows.

First, to get the optimal measurement matrix, one function is defined as

$$ J(\Phi ) = \left\| {\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{2} } \right\|_{F}^{2} . $$

(14)

Next, the gradient of measurement matrix $\Phi$ is obtained by

$$ \frac{\partial J(\Phi )}{{\partial \Phi }} = \frac{\partial }{\partial \Phi }\{ {\text{tr}}(\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{2} )^{{\text{T}}} (\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{2} )\} = 4\Phi \Psi (\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{2} )\Psi^{{\text{T}}} , $$

(15)

where tr(·) is the trace of the matrix. Subsequently, regenerate the matrix $\Phi_{i + 1}$ by

$$ \Phi_{i + 1} = \Phi_{i} - \beta \frac{\partial J(\Phi )}{{\partial \Phi }} = \, \Phi_{i} - \eta \Phi_{i} \Psi (\Psi^{{\text{T}}} \Phi_{i}^{{\text{T}}} \Phi_{i} \Psi - H_{2} )\Psi^{{\text{T}}} , $$

(16)

where iteration step size η = 4β (β > 0).

Barzilai–Borwein strategy [41] is utilized to infer the iteration step η_i, and it may be computed by

$$ \begin{aligned} \eta_{i} &= \arg \mathop {\min }\limits_{i \in R} \left\| {\eta S_{i - 1} - Y_{i - 1} } \right\|^{2} \quad {\text{or}}\quad \\ \eta_{i} &= \arg \mathop {\min }\limits_{i \in R} \left\| {S_{i - 1} - \eta^{ - 1} Y_{i - 1} } \right\|^{2} , \end{aligned} $$

(17)

where $S_{{i - {1}}} = \Phi_{i} - \Phi_{i - 1}$, $Y_{{i - {1}}} = Q_{i} - Q_{i - 1}$, $Q_{i} = \Phi_{i} \Psi (\Psi^{{\text{T}}} \Phi_{i}^{{\text{T}}} \Phi_{i} \Psi - H_{2} )\Psi^{{\text{T}}}$. Through computing Eq. (17), two iteration steps are obtained and shown as

$$ \eta_{i} = \frac{{\left\langle {S_{i - 1} ,S_{i - 1} } \right\rangle }}{{\left\langle {Y_{i - 1} ,S_{i - 1} } \right\rangle }}\quad {\text{or}}\quad \eta_{i} = \frac{{\left\langle {S_{i - 1} ,Y_{i - 1} } \right\rangle }}{{\left\langle {Y_{i - 1} ,Y_{i - 1} } \right\rangle }}. $$

(18)

Specifically, one of them may be applied for achieving the adaptive adjustment of steps. To ensure the convergence of GDM, Armijo criterion [42] is adopted and the following inequality must hold:

$$ J(\Phi_{i} + \eta_{i} P_{i} ) \le J(\Phi_{i} P_{i} ) + \sigma \eta_{i} \left\langle {P_{i} ,\nabla J(\Phi_{i} )} \right\rangle , $$

(19)

where $P = - \nabla J(\Phi_{i} )$, $\nabla J(\Phi_{i} ) = \partial J/\partial \Phi = {4}\Phi \Psi (\Psi^{{\text{T}}} \Phi^{{\text{T}}} \Phi \Psi - H_{{2}} )\Psi^{{\text{T}}}$, 0 < σ < 1. If the relative change rate r of the objective function of two adjacent iterations satisfies Eq. (20), the iteration is terminated [42]

$$ r = \left| {\frac{{J(\Phi_{i} ) - J(\Phi_{i - 1} )}}{{J(\Phi_{i - 1} )}}} \right| < \varepsilon , $$

(20)

where $0 < \varepsilon < 1$.

To reduce the cross-correlation between the measurement matrix and sparse matrix, GDM is adopted. In the optimization process, the flexible iteration step is utilized; thus, the proposed method is more flexible and efficient compared with the fixed number of iterations.

The proposed measurement matrix optimization algorithm

To obtain better measurement matrix, we present an adaptive iteration step optimization method, as shown in Fig. 2. The detailed operation steps are as below.

Fig. 2

Flowchart of the proposed measurement matrix optimization method

Input: Sparse matrix $\Psi$, parameter η₀, σ, λ and threshold value μ;

Optimization objective: Minimizing μ_av(D) as small as possible, and $D = \Phi \Psi$, $\Phi$ is the measurement matrix, d_i, d_j are the ith column and jth column of matrix D, respectively;

Output: The optimized measurement matrix $\Phi = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }_{i}$.

Step 1: Initialize some parameters, including measurement matrix $\Phi_{0} \in R^{M \times N}$ and parameter η₀, σ, λ.

Step 2: Obtain the matrix D by $D = \Phi_{0} \Psi$, the Gram matrix G by use of $G = \tilde{D}^{{\text{T}}} \tilde{D}$, and then normalize the column of G.

Step 3: Perform eigenvalue decomposition on G to get $G^{\prime} = VH_{{1}} V^{{ - {1}}}$, fix the non-zero elements in the diagonal matrix H₁ as N/M to find matrix $\hat{H}_{{1}}$, and, finally, get matrix $G^{\prime\prime} = V\hat{H}_{{1}} V^{{ - {1}}}$, where M, N are the row and column of measurement matrix.

Step 4: Shrink the non-diagonal element of Gʺ according to Eq. (6) to get new matrix H₂.

Step 5: Regenerate $\Phi_{i}$ by use of GDM via

$$ \Phi_{i + 1} = \Phi_{i} - \eta_{i} \Phi_{i} \Psi (\Psi^{{\text{T}}} \Phi_{i}^{{\text{T}}} \Phi_{i} \Psi - H_{2} )\Psi^{{\text{T}}} , $$

(21)

where η_i > 0 denotes the ith iteration step size.

Step 6: Judge whether η_i satisfies Eq. (19), if so, perform step 7; otherwise, η_i = λη_i, and 0 < λ < 1, and then, go to step 6 to rejudge the condition again.

Step 7: Determine whether $\Phi_{i}$ satisfies Eq. (20), if so, manipulate step 8; otherwise i = i + 1, and then, go to step 4.

Step 8: Transpose $\Phi_{i}$ to $\Phi_{i}^{{\text{T}}}$, and then, perform QR decomposition on $\Phi_{i}^{{\text{T}}}$ to obtain $\Phi_{i}^{{\text{T}}}$ = QR.

Step 9: Set all the non-diagonal element of R as zero, and obtain a new matrix R̂.

Step 10: Obtain the matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }_{i}^{{\text{T}}} = Q\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{R}$, and the optimized measurement matrix $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }_{i}$ may be obtained by transposing $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Phi }_{i}^{{\text{T}}}$.

The presented image compression and encryption scheme

Generating the system parameter and initial value of chaotic system

In this paper, LSS is used to produce key sequences for image encryption, and it is derived by

$$ x(n + 1) = \bmod (ux(n)(1 - x(n)) + (4 - u)\sin (\pi x(n))/4,1), $$

(22)

where u is the system parameter, u ∈ (0, 4], and x is the state variable.

To improve the dependence of plain image and image encryption scheme, the plain image characteristic information is applied for generating the system parameter and initial value of the LSS chaotic system. First, compute the information entropy h of plain image P sized of M N; next, calculate the system parameters and initial value of LSS by

$$ \left\{ \begin{gathered} u = \bmod ((h \times t_{1} + t_{2} \times t_{3} + t_{4} ) \times 10^{6} ,1) \hfill \\ x(1) = \bmod ((h + t_{1} \times t_{2} \times t_{3} \times t_{4} ) \times 10^{6} ,4) \hfill \\ \end{gathered} \right., $$

(23)

where mod is the modular operation, and external key parameters t₁, t₂, t₃, t₄$\varepsilon$(0, + oo).

The adoption of information entropy of the plain image enhances the relationship between the algorithm and the plain image, so that the proposed method may resist chosen-plaintext and known-plaintext attacks effectively. For successful decryption, the information entropy should be sent to the receiver through a secure channel.

Producing the chaotic measurement matrix

In this section, two chaotic measurement matrices will be constructed and optimized according to “The proposed measurement matrix optimization algorithm”, and then, the optimized matrices are utilized to perceive the plain image. The generation process of the measurement matrix is as below.

Step 1: Iterate LSS system with the obtained u and x(1) for (n₀ + MN) times, remove the previous n₀ values (n₀ > 500) to avoid the harmful effect, and obtain the chaotic sequences X₁.

Step 2: Pick out the previous pq elements from X₁ to get the sequence X₂, and then obtain X₃ by preprocessing X₂ via

$$ X_{3} (n) = 1 - 2X_{1} (n), $$

(24)

where p = ceil(CR₁M/2), q = ceil(N/2), CR₁ = 0.5, ceil is a rounding up function, and n = 1,2,…, pq.

Step 3: Construct the measurement matrix $\Phi_{{1}}$ sized of p Xq by use of X₃

$$ \Phi_{1} = \sqrt{\frac{2}{p}} \left( {\begin{array}{*{20}c} {X_{3} (1)} & \cdots & {X_{3} (p(q - 1) + 1)} \\ \vdots & \vdots & \vdots \\ {X_{3} (p)} & \cdots & {X_{3} (pq)} \\ \end{array} } \right), $$

(25)

where $\sqrt {{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-\nulldelimiterspace} p}}$ is the normalized coefficient.

Step 4: First, pick out the previous p′q elements from X₁ to get the sequence $X^{\prime}_{2}$, next preprocess it according to Eq. (24) to find the sequence $X^{\prime}_{3}$, and finally generate another measurement matrix $\Phi_{2}$ sized of p′ Xq via

$$ \Phi_{2} = \sqrt {\frac{2}{{p^{\prime}}}} \left( {\begin{array}{*{20}c} {X^{\prime}_{3} (1)} & \cdots & {X^{\prime}_{3} (p^{\prime}(q - 1) + 1)} \\ \vdots & \vdots & \vdots \\ {X^{\prime}_{3} (p^{\prime})} & \cdots & {X^{\prime}_{3} (p^{\prime}q)} \\ \end{array} } \right), $$

(26)

where p′ = ceil(CR₂ M/2), CR₂ = 0.25 and $\sqrt {{2 \mathord{\left/ {\vphantom {2 {p^{\prime}}}} \right. \kern-\nulldelimiterspace} {p^{\prime}}}}$ is the normalized coefficient.

Generating the mask matrix for DRPE

In the proposed image encryption, DRPE is applied for confusing the measurement values of the plain image to upgrade the confusion effect, and its mask matrix is produced by the following steps.

Step 1: Collect the previous MN/16 elements from chaotic sequences X₁ to obtain X₄, and then sort X₄ in ascending order to get chaotic sequence X₅ and the corresponding index sequence D sized of 1X MN/16 according to

$$ [X_{5} ,D] = {\text{sort}}(X_{4} ). $$

(27)

Step 2: Pick out the previous MN/4 elements from chaotic sequence X₁ to get X₆, and then draw the last MN/4 elements from X₁ to find X₇; subsequently, process sequences X₆, X₇ according to Eq. (28) to get sequences X₈, X₉, and then resize them to obtain two mask matrices X₁₀, X₁₁ sized of M/2 XN/2

$$ \left\{ \begin{gathered} X_{8} = \bmod (((X_{6} + X_{7} ) \times 10^{6} ),1) \hfill \\ X_{9} = \bmod ((X_{6} \times 10^{3} + X_{7} \times 10^{3} ) \times 10^{6} ,1) \hfill \\ \end{gathered} \right.. $$

(28)

Step 3: Pick out the first MN/2 elements from chaotic sequence X₁ to get X₁₂, draw the last MN/2 elements from it to obtain X₁₃, and then modify them by use of Eq. (29) to get X₁₄ and X₁₅ with size of 1X MN/2

$$ \left\{ \begin{gathered} X_{14} = {\text{floor}}(\bmod (((X_{12} + X_{13} ) \times 10^{6} ),256)) \hfill \\ X_{15} = {\text{floor}}(\bmod ((X_{12} + X_{13} + X_{14} ) \times 10^{6} ,256)) \hfill \\ \end{gathered} \right.. $$

(29)

Step 4: Resize X₁₄ and X₁₅ to obtain the mask matrices X₁₆ and X₁₇ sized of M/2 XN for diffusion.

The complete image compression and encryption method

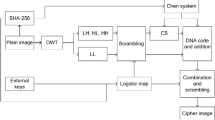
In this section, the proposed image compression and encryption method based on compressive sensing and DRPE is described in detail. First, the plain image is transformed to a low frequency and three high-frequency components by use of discrete wavelet transformation (DWT). Second, the four components are shuffled by index sequences, the obtained high-frequency components are compressed by CS, and a complex matrix is obtained by integrating them with the shuffled low-frequency component. Third, the complex matrix is processed by DRPE, quantization, and diffusion to get the cipher image. Since the low-frequency component contains important information of the plain image, it is not compressed. For the high-frequency components have less plain information, they are compressed to save storage room and transmission bandwidth. Compressing the plain image selectively based on importance of the plain image may not only ensure the quality of reconstructed images, but also reduce the data redundancy. Besides, the adoption of permutation and DRPE improves the security of the proposed cipher. The complete image encryption process is shown in Fig. 3, and the detailed steps are as below.

Fig. 3

The flowchart of the proposed image encryption

Step 1: Perform DWT on plain image P sized of MXN to get the low-frequency component LL and high-frequency components LH, HL, HH sized of M/2 XN/2.

Step 2: As described in “Generating the system parameter and initial value of chaotic system”, obtain the system parameter u and initial value x(1) of LSS system by use of information entropy h and keys t₁, t₂, t₃, t₄.

Step 3: Convert LL, LH, HL, and HH to sequences LL₁, LH₁, HL₁, and HH₁ sized of 1 XMN/4, respectively. Next, utilize index sequence D gotten in “Generating the mask matrix for DRPE” to shuffle them to obtain sequences LL₂, LH₂, HL₂, HH₂ via

$$ \left\{ \begin{gathered} LL_{2} (i) = LL_{1} (D(i)) \hfill \\ LH_{2} (i) = LH_{1} (D(i)) \hfill \\ HL_{2} (i) = HL_{1} (D(i)) \hfill \\ HH_{2} (i) = HH_{1} (D(i)) \hfill \\ \end{gathered} \right., $$

(30)

where i = 1, 2, …, MN/4.

Step 4: As demonstrated in “Producing the chaotic measurement matrix”, produce two measurement matrices: $\Phi_{1}$ sized of p q and $\Phi_{2}$ sized of p′ Xq, where p = ceil(CR₁ M/2), p′ = ceil(CR₂ M/2), q = ceil(N/2), CR₁ = 0.5 and CR₂ = 0.25.

Step 5: Resize sequences LL₂, LH₂, HL₂, HH₂ to matrices LL₃, LH₃, HL₃, HH₃ sized of M/2 XN/2, respectively. Subsequently, optimize $\Phi_{1}$ and $\Phi_{2}$ according to “The proposed measurement matrix optimization algorithm”, and then measure LH₃ by use of $\Phi_{1}$, perceive HL₃ and HH₃ using $\Phi_{2}$ to obtain the measurement value matrices LH₄ sized of p Xq, HL₄ and HH₄ sized of p′ Xq, and the detailed process may be represented as

$$ \left\{ \begin{gathered} LH_{4} = \Phi_{1} LH_{3} \hfill \\ HL_{4} = \Phi_{2} HL_{3} \hfill \\ HH_{4} = \Phi_{2} HH_{3} \hfill \\ \end{gathered} \right., $$

(31)

where p = 2q and q = ceil(N/2).

Step 6: Recombine LH₄, HL₄, HH₄ into one matrix L₁ sized of 2p Xq. Next, taking the matrix LL₃ as the real part and the matrix L₁ as the imaginary part, the complex matrix L₂ is constructed. Subsequently, obtain matrices X₁₁ and X₁₀ as described in “Generating the mask matrix for DRPE”, and perform DRPE on L₂ to get matrix L₃ sized of M/2 XN/2 via

$$ L_{{3}} = {\text{FT}}^{{ - {1}}} ({\text{FT}}\left( {L_{{2}} } \right) X_{{{1}0}} ) X_{{{11}}} , $$

(32)

where FT denotes the Fourier transform.

Step 7: Denote the real part of the matrix L₃ as L₄ and the imaginary part as LL₄, and then quantize L₄ to get the matrix L₅ according to

$$ L_{5} (i) = {\text{floor}}\left( {255 \times \frac{{L_{4} (i)}}{L\max - L\min }} \right), $$

(33)

where i = 1, 2, …, MN/4, Lmax, Lmin are the maximum and minimum values of matrix L₄, and LLmax, LLmin denote the maximum and minimum values of matrix LL₄. In the same manner, LL₄ is processed to obtain the matrix LL₅.

Step 8: As described in “Generating the mask matrix for DRPE”, obtain the matrices X₁₆ and X₁₇ with the size of M/2 XN by processing X₁. Subsequently, recombine L₅ and LL₅ to get the matrix L₆ sized of M/2 XN, perform diffusion operation on it to get cipher image C sized of M/2 XN according to

$$ C = L_{6} \oplus X_{16} \oplus X_{17} , $$

(34)

where is the XOR operation.

Figure 4 gives the flowchart of the proposed image decryption process, and it is the inverse operation of the image encryption. Before decryption, the keys h, t₁, t₂, t₃, t₄, Lmax, Lmin, LLmax, LLmin should be sent to the receiver. The cipher image C is operated by inverse diffusion, inverse quantization, inverse DRPE, reconstruction, inverse permutation, and inverse DWT to find the plain image P. Besides, the used key sequences in each stage are the same with those in the encryption.

Fig. 4

The flowchart of the image decryption process

Performance analyses of measurement matrix optimization algorithm

The proposed scheme is implemented with Matlab2016a on Intel (R) Core (TM) i5-4590 @ 3.30 GHz CPU, 4.00 GB RAM, and Windows 7 operating system. In the test, the initial measurement matrix is Gaussian random matrix, the CS reconstruction method is OMP, Lena sized of 256 × 256 is used as test image, and some parameters are arbitrarily chosen as η = 0.001, λ = 0.001, σ = 0.5.

Influence of measurement matrix optimization on reconstruction effect

To analyze the effect of measurement matrix optimization on reconstruction effect, compression rate CR of the plain image varies from 0.3, to 0.5, 0.7, and 0.9, the reconstructed Lena is obtained under the optimized and unoptimized conditions, and the results are shown in Fig. 5.

Fig. 5

The reconstructed Lena image with different CR for every row

As shown in Fig. 5 that first, after the measurement matrix is optimized, the recovered Lena image is clearer than that without optimization, just like the plain image, indicating the effectiveness of our optimization method; second, when CR = 0.3, the reconstructed Lena image gotten by our scheme has higher quality than that in [43, 44], especially around the eyes. Besides, the PSNR values between the reconstruction image and plain image are illustrated in Fig. 6 with CR changing from 0.1 to 0.9. From Fig. 6, one may conclude that PSNR gotten by our optimization method is the largest than [43, 44], and the proposed optimization algorithm can improve PSNR obviously when the compression ratio is small, especially from 0.2 to 0.4.

Fig. 6

PNSR vs CR

Influence of different chaotic systems on reconstruction effect

In the image encryption based on CS, measurement matrix is used as secret key, and it should be sent to the receiver for decryption. To reduce the transmission cost, chaotic systems are applied to generate measurement matrix, less parameters as secret key may produce larger measurement matrix. In this section, the effect of different chaotic system on reconstruction quality is analyzed. Chaotic systems are chosen as Tent map, Logistic map, and Logistic-Tent chaotic system (LTS), and they are described by

$$ X_{n + 1} = \left\{ \begin{gathered} rX_{n} /2,X_{n} < 0.5 \hfill \\ r(1 - X_{n} )/2,X_{n} \ge 0.5 \hfill \\ \end{gathered} \right. $$

(35)

$$ X_{n + 1} = rX_{n} (1 - X_{n} ) $$

(36)

$$ v_{n + 1} = {\text{LTS}}(r,v_{n} ) = \left\{ \begin{gathered} (rv_{n} (1 - v_{n} ) + (4 - r)v_{n} /2)mod1,v_{n} < 0.5 \hfill \\ (rv_{n} (1 - v_{n} ) + (4 - r)(1 - v_{n} )/2)mod1,v_{n} \ge 0.5 \hfill \\ \end{gathered} \right., $$

(37)

where system parameter r ∈ (0, 4] and state variables are X_n, v_n ∈ (0, 1).

The measurement matrix is produced by chaotic system, OMP is the reconstruction method, other parameters are set as in “Performance analyses of measurement matrix optimization algorithm”, and the PSNR between the recovered image and original image are listed in Table 1. From Table 1, one may conclude that when the measurement matrix is not optimized, the PSNR values gotten by different chaotic systems change a lot, and the maximum deviation is 6.61 dB for the same CR. Besides, after the measurement matrix is optimized, PSNR values obtained by different chaos are closer, and the maximum deviation decreases to 3.2 dB. Additionally, PSNR values are more than 30 dB with the optimized measurement matrix under the condition that CR = 0.6, and when the LSS is utilized, the largest PSNR is obtained. All in all, the reconstruction quality of the proposed image encryption is enhanced by optimizing the measurement matrix, and different chaotic systems may be used, broadening the selection range of chaotic system.

Table 1 PSNR gotten by different chaotic systems (unit: dB)

Performance stability analysis

A good optimization method should have stable performance after repeated use. When Gaussian random matrix is adopted, as for its randomness, the simulation results may be different for different test; thus, the PSNR of the same optimization algorithm is different under the same compression ratio. PSNR values gotten by 50-time manipulation are demonstrated in Fig. 7, with CR = 0.3.

Fig. 7

PSNR values vs experiment times

As is evident from Fig. 7 that PSNR values improve a lot after the measurement matrix is optimized, PSNR values change dramatically with the unoptimized measurement matrix, but when it is optimized, PSNR value varies very slow and is concentrated around 22 dB, which may indicate that the proposed measurement matrix optimization method makes the performance more stable.

Performance analyses of image compression and encryption algorithm

Encrypted images and decrypted images

In the experiment, the external keys are randomly set as t₁ = 0.2358, t₂ = 1.3545, t₃ = 10.8949, t₄ = 100.1564, parameters to optimize measurement matrix are fixed as η = 10^–6, λ = 10^–3, σ = 10^–2, and OMP is utilized for reconstruction. Lena, Peppers sized of 512 × 512, Lena sized of 1024 × 1024, Lena, Einstein, Peppers sized of 256 × 256, color Lena sized of 256 × 256 are used to test, and CR = 0.5. The encryption and decryption results are shown in Figs. 8 and 9. Wherein, in Fig. 8a–i are the plain image, encryption image, and decryption image of Lena512, Peppers512, and Lena1024, respectively.

Fig. 8

Encryption and decryption images sized of 512 × 512 and 1024 × 1024

Fig. 9

Encryption and decryption images sized of 256 × 256

In Fig. 9a–c are the plain image Lena256 and its encryption and decryption images, d–f are the plain image Einstein256 and its encryption and decryption images, g–i are the plain image Peppers256 and its encryption and decryption images, and j–l are the color plain image Lena and its encryption and decryption images. From Figs. 8 and 9, one may conclude that the encryption images have been compressed a half, their appearances are all noisy, nothing useful information may be derived from them, and thus, the plain image information is protected effectively; the decrypted images are just their corresponding plain images, indicating the effectiveness of the decryption method. Besides, the proposed image compression and encryption method may be applied for color image.

Comparison analyses of measurement matrix

In this section, the performance of our generated measurement matrix is compared with Toplitz, Gaussian, and Bernoulli measurement matrix. The plain images shown in Figs. 8 and 9 are used as test images, compression ratio is set as CR = 0.5, and the PSNR values gotten by different measurement matrices are computed and listed in Fig. 10. As is evident from Fig. 10 that among the five test images, the PSNR values gotten by our method are the largest than Toplitz, Gaussian, and Bernoulli measurement matrix, indicating the effectiveness of our measurement matrix generation method. Additionally, Lena512 (shown in Fig. 8a) is used as test image, the PSNR between the decrypted image and plain image is computed and listed in Table 2, and CR = 0.5. From Table 2, one may watch that PSNR value gotten by our method is more than Refs. [20, 45], verifying the satisfactory compression performance of the proposed scheme.

Fig. 10

PSNR values for different measurement matrices

Table 2 PSNR values between our algorithm and others

Key space analyses

The key space should be large enough to make the image encryption withstand any kinds of brute force attacks [24, 29]. The key used in our algorithm consists of (1) the information entropy h of plain image; (2) the external key t₁, t₂, t₃, t₄; (3) intermittent parameters Lmax, Lmin, LLmax, and LLmin. If the computation precision of the computer is 10^–14, our key space is about (10¹⁴)⁵ = 10⁷⁰ > 2²¹⁰, much larger than the general requirements of 2¹⁰⁰ to resist brute force attack [46]. Table 3 gives the comparison results of key space with other algorithms. As can be seen, our key space is larger than that in Refs. [47,48,49], indicating that our image encryption may withstand brute force attack effectively.

Table 3 Comparison results of key space

Histogram analyses

Histogram plots the distribution information of image pixels [50]. A good image encryption should generate cipher image with uniform histogram to prevent hackers from obtaining plain image information from them. The histograms of plain image Lena sized of 256 × 256 and its cipher image sized of 128 × 256 are shown in Fig. 11. It is evident from Fig. 11 that the histogram of plain image demonstrates very obvious statistical information; conversely, that of cipher image is evenly distributed and nothing useful information may be found, indicating that the proposed image encryption may resist the statistical attack effectively.

Fig. 11

Histogram of plain image and cipher image

Correlation of adjacent pixels

It is generally known that adjacent pixels of a meaningful plain image have strong correlations, and a cipher image gotten by a good encryption method is noise-like, and adjacent pixels have no correlations. To visually plot the correlation distribution of adjacent pixels, 7000 pairs of pixels are randomly chosen from the plain image Lena256 and its cipher image and their distribution are presented in Fig. 12. It may be seen that the distributions of plain image are concentrated in horizontal, vertical, and diagonal directions, indicating high correlation. While the distributions of cipher image are distributed evenly in these directions, indicating no-correlation.

Fig. 12

Correlation between adjacent pixels of plain image and cipher image: a horizontal correlation of plain image, b vertical correlation of plain image, c diagonal correlation of plain image, d horizontal correlation of cipher image, e vertical correlation of cipher image, and f diagonal correlation of cipher image

Additionally, to assess the correlation of two adjacent pixels in horizontal, vertical, and diagonal directions, the correlation coefficient CC of two adjacent pixels is defined by [45]

$$ {\text{CC}} = \frac{{L\sum\nolimits_{i = 1}^{L} {(x_{i} y_{i} ) - } \sum\nolimits_{i = 1}^{L} {x_{i} } \sum\nolimits_{i = 1}^{L} {y_{i} } }}{{\sqrt {\left( {L\sum\nolimits_{i = 1}^{L} {x_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{L} {x_{i} } } \right)^{2} } \right) \, \left( {L\sum\nolimits_{i = 1}^{L} {y_{i}^{2} } - \left( {\sum\nolimits_{i = 1}^{L} {y_{i} } } \right)^{2} } \right)} }}, $$

(38)

where x_i and y_i denote two different pixels in one image, and L is the total number of selected pixels.

Randomly choose 7000 pairs of pixels from plain images and their cipher images, calculate the CCs of adjacent pixels in horizontal, vertical, and diagonal directions, and list them in Table 4. As may be watched from Table 4 that the CCs of cipher images are very small, indicating that the correlation of adjacent pixels has been removed effectively, and the proposed image encryption may resist statistical attack well. Besides, Table 5 gives the comparison results with other studies for Lena256 image. It is evident that CCs gotten by our scheme are all less than those in Refs. [51,52,53].

Table 4 Correlation coefficients between adjacent pixels in the plain image and cipher image

Table 5 Comparison results on correlation coefficient with others

Information entropy

Shannon [54] introduced information entropy to describe the randomness and unpredictability of an information source in 1949. It may be computed by [55]

$$ H(m) = \sum\limits_{i = 0}^{{2^{n - 1} }} {v(m_{i} )\log \frac{1}{{v(m_{i} )}}} , $$

(39)

where v(m_i) is the probability of pixel v_i. For a truly random source composed of 2⁸ symbols, the entropy should ideally be 8. The information entropies of the plain images and cipher images are shown in Table 6. It is evident from Table 6 that the information entropy of the cipher image gotten by our image encryption is larger than 7.99, very close to 8, indicating that the plain image information is effectively concealed. Table 7 gives the comparison results with other methods. From Table 7, we may watch that the information entropy of our algorithm is larger than that in Refs. [14, 20, 45].

Table 6 Information entropy of plain image and cipher image

Table 7 Comparison with other algorithms for Lena512

Robustness analyses

Cropping attack analysis

Figure 13 displays the cipher images with different cropping attacks and their corresponding decrypted images. It may be seen from Fig. 13 that when the data loss varies from 16 × 16 to 4 × 256, to 256 × 4, to 256 × 4 × 2, the plain image information may still be recovered, indicating that the proposed method may resist cropping attacks to a certain extent.

Fig. 13

Cropping attack results

Noise attack analysis

In this section, Lena is used as plain image, its encrypted image is added different Gaussian noise (GN), Salt & Pepper noise (SPN), Speckle noise (SN), and then, the decrypted images are shown in Figs. 14, and 15 gives the PSNR values between the decrypted images and the original image. From Figs. 14 and 15, one may watch that first, as for SPN, PSNR values are higher than 30 dB, they are about stable when the noise intensity changes, which means that our algorithm has highly robustness to SPN; second, as for GN and SN, the PSNR values change dramatically; when noise intensity is 0.000007, the PSNR is lower than 20 dB, but one may find the plain image information from the recover images. Conclusively, the proposed image encryption may withstand noise attacks effectively.

Fig. 14

Noise attack results

Fig. 15

PSNR under different noise intensities

Conclusion

This paper introduced an effective image compression and encryption method based on CS and DRPE. First, the plain image is decomposed to one low-frequency component and three high-frequency components by use of DWT, and shuffled by index vectors generated from chaotic sequences. Next, shuffled high-frequency components are measured by optimized measurement matrix produced by a novel measurement matrix optimization algorithm based on adaptive step size. Subsequently, a new complex matrix is found by combining the shuffled low-frequency component and three measurement value matrices. Finally, the cipher image is obtained by performing DRPE, quantization, and diffusion on the complex matrix. The proposed cipher is content-adaptive, since the information entropy of the plain image is applied for generating initial value of the LSS chaotic system, and the iterated chaotic sequences are utilized in the complete encryption stage. Through the performance analyses and comparison of the proposed image encryption, our method has been proven to have large key space, highly sensitive key, resistance to statistical attacks, and it can be applied for image secure transmission and storage.