Introduction

Bayesian networks (BNs), a classical probabilistic graphical model, combine probability theory and graph theory to deal with uncertain problems, and are successfully applied to a wide range of domains such as prediction [5, 34], risk analysis [4, 14]. There are two components in this field: the BN structure and the BN parameter. In contrast with the BN parameter, the construction of the BN structure is more important [16, 27].

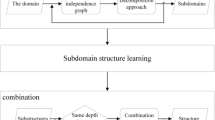
In the current era of big data, researchers pay more attention to learning BN structure from data. Existing algorithms for learning BN structures from data can generally be divided into three types: constraint-based (CB) [6, 24, 28, 29], score-based (SS) [10, 30, 33] and hybrid algorithms [3, 12, 15]. Among those algorithms, hybrid algorithms which combine merits of CB and SS algorithms show better performance. Despite hybrid algorithms have the advantage of scalability in some degree, they still suffer from the low accuracy and efficiency in the face of the task of learning BN structure in complex domains. To address this problem, researchers introduce the idea of divide and conquer into hybrid algorithms and propose decomposition hybrid algorithms (DHAs) [9, 18,19,20, 37]. Such structure learning algorithms improve the accuracy and efficiency of hybrid algorithms by decomposing the whole structural task into structural subtasks to reduce the computational complexity. In recent years, DHAs have been optimized from the no-recursive framework [18, 19] to the recursive framework [9, 20, 37]. DHAs with the recursive framework can achieve better partitioning effect by improving the efficiency of searching for separators [32]. We focus on DHAs with the recursive framework. Unless otherwise specified, DHAs refer to DHAs with the recursive framework for the latter. DHAs are composed of three steps: decomposition step, substructure learning step and combination step. Among three steps, combination step as an important step and is used to merge BN substructures into the whole BN structure.

In the combination step, combination methods [9, 20, 37] are adopted and fall into node determination, link determination and direction determination. Among three parts, the direction determination is the key and challenging part. The task of this part is to determine directions of edges in the combined structure according to substructures. The direction determination mainly deals with the orientation of contradictory edges in same node pairs between substructures and the restriction of directions of edges in the combined structure on the basis of properties. Merging rules proposed by [20] are widely adopted as the combination method and consist of three rules for determining nodes, links of edges and directions of edges. The direction determination rule in merging rules is designed according to the decomposition property and is expressed directions of edges are retained unchanged unless necessary redirections are made so that all v-structures are kept. The decomposition property [37] states that subdomains obtained in the decomposition step can ensure that each node and all its parent nodes are in one subdomain, and proves that the problem of learning the whole BN structure can be transformed into problems of learning BN substructures. The literature [20] holds that according to the decomposition property, if the whole structure and substructures are guaranteed to have same v-structures, they are equivalent. Therefore, the design principle of the direction determination rule is that it only needs to ensure that no new v-structure is generated after combination, and v-structures before combination are not destroyed.

However, there are problems with relying on keeping v-structures before and after combination to determine directions of edges in the whole structure by the direction determination rule. First, the direction determination rule assumes that structure learning algorithms can learn correct BN substructures to make all v-structures correct, but the reality is that structure learning algorithms cannot guarantee that substructures learned are completely correct. Once it happens, structure learning algorithms fail to make all learned v-structures correct and contradictory edges cannot be oriented in one case with this direction determination rule. The generation of a wrong edge makes both directions of an edge form a v-structure in two substructures, so the direction of this edge cannot be determined in the combination step because it is not possible to preserve two v-structures at the same time. Besides, the direction determination rule is not easy to operate in practice. When an edge is redirected to ensure that all v-structures are unchanged, it is likely to cause edges in its adjacent part to be redirected for keeping all v-structures unchanged, resulting in a cascade reaction. There are a large number of v-structures in a BN structure and the number of v-structures increases greatly with the size of the BN structure. Therefore, repeatedly detecting changes of v-structures and redirecting corresponding edges will produce huge complexity, resulting inaccurate orientation.

Therefore, this paper adopts a novel approach to determine directions of edges in combination step and proposes a two-stage combination method in a DHA. The aim in this paper is to improve the accuracy of edge orientations. For the first two steps of the DHA, the whole domain is recursively decomposed into several subdomains by finding minimal separators through a graph-partitioning algorithm [25] in the decomposition step, and an efficient hybrid algorithm proposed in [12] is employed to construct BN substructures in the substructure learning step. In combination step of the DHA, BN substructures are combined into the whole BN structure by the proposed two-stage combination method. In the first-stage combination method, we determine nodes, links of edges by node, link determination rules in merging rules and orient directions of contradictory edges with keeping directions of non-contradictory edges as follows. The task of direction determination in this stage is to orient contradictory edges. Determining the directions of contradictory edges are regarded as a permutation and combination problem. A heuristic algorithm searches the space of contradictory edges and the direction combination with the highest score is chosen. The heuristic algorithm adopts binary particle swarm optimization (BPSO) algorithm [12] and the score is evaluated by Bayesian information criterion (BIC) [26]. In the second-stage combination method, we modify directions of edges between nodes that do not satisfy the decomposition property (problematic nodes) and their parent nodes. The task of direction determination in this stage is to restrict directions of edges according to the decomposition property. We first determine the target domain where true parent nodes of a problematic node are located to classify all its parent nodes into candidate true parent nodes as well as false parent nodes, and then treat edges between different classes of parent nodes and the problematic node accordingly. We compare the proposed algorithm with four algorithms on two medium networks and two large networks, and experimental results indicate that the proposed algorithm can implement better performances. Finally, the proposed algorithm is applied to the thickening process of gold hydrometallurgy to solve the practical problem.

The organization of this paper is as follows. The related work is briefly introduced in the next section. The proposed algorithm is described in the third section. The fourth section shows detailed experimental results. The last section concludes the contributions of this paper.

Related work

Bayesian network

Bayesian network (BN) is a model for the expression and reasoning of uncertain knowledge based on probability theory and graph theory [11, 36]. It is used to express the dependency relationships between nodes and provide a concise expression for joint probability distribution. A BN can be represented by a tuple \(\left(G,P\right)\). \(G\) denotes a directed acyclic graph (DAG) and \(P\) stands for the joint probability distribution. \(G=(V,E)\) contains a set of nodes \(V=\left\{{x}_{1},{x}_{2},\dots {x}_{n}\right\}\) including \(n\) random variables or nodes \({x}_{i}\), and a set of edges \(E=\left\{<{x}_{1},{x}_{2}>...<{x}_{i},{x}_{j}>\right\}\) including links and directions. The link of the directed edge \(<{x}_{i},{x}_{j}>\) is an undirected edge between \({x}_{i}\) to \({x}_{j}\) and the direction of this edge is from \({x}_{i}\) to \({x}_{j}\). The node \({x}_{i}\) in \(<{x}_{i},{x}_{j}>\) is called the parent node of \({x}_{j}\) and the node \({x}_{j}\) in \(<{x}_{i},{x}_{j}>\) is called the child node of \({x}_{i}\). \(P=\left\{{\theta }_{1}\dots {\theta }_{n}\right\}\) is composed of the conditional probability table of each node \({\theta }_{i}\) and their correlation can be expressed as follows:

$$P\left({x}_{1},\dots ,{x}_{n}\right)=\prod_{i=1}^{n}P\left({x}_{i}|\pi \left({x}_{i}\right)\right)$$
(1)

where \(i=\mathrm{1,2},\dots ,n\) and \(\pi \left({x}_{i}\right)\) is a set of parent nodes of \({x}_{i}\).

For the sake of understanding the paper, related concepts are given.

Definition 1

[22] If the ordered node group \(\left(x,y,z\right)\) composed of three nodes in a DAG satisfies:

(1) there are directed edges \(x\to z\) and \(y\to z\) in the DAG and

(2) node \(x\) and node \(y\) are not adjacent in the DAG, then

(x, y, z) constitutes the v-structure \(x\to z\leftarrow y\).

Theorem 1

[13] Two DAGs with the same node set are said to Markov equivalent if they contain the same set of v-structures.

Decomposition hybrid algorithms

The divide-and-conquer strategy was introduced into hybrid algorithms to form decomposition hybrid algorithms (DHAs), which reduce the computational complexity and improve the learning accuracy by converting the whole structural task into structural subtasks. In the early work, DHAs are based on the no-recursive framework, which mean that decomposition and combination steps are both completed at one time. The literature [23] applied the idea of divide and conquer to MMHC algorithm to improve its performance. The skeleton acquired in the first step algorithm of MMHC algorithm is divided into subskeletons according to the local structure of each node “around” as a unit, then the substructures are recovered based on the subskeletons by the second step algorithm of MMHC algorithm, and finally, substructures are merged into the whole BN structure with the framework of fPDAG (feature partial directed graph). In the literature [35], nodes in the whole domain are partitioned into subdomains according to a cluster with high correlation among nodes with the help of a community detection algorithm, then substructures are learned through general structure learning algorithms, and finally substructures are merged into the whole structure by rules which solve conflicting structural and acyclic problems. In recent years, the no-recursive framework has been optimized for the recursive framework. The literature [32] proposes a recursive framework for CB learning, in which decomposition and combination steps are completed through several iterations. This algorithm can enhance the efficiency of finding separators to improve learning performances and the recursive framework has been applied to hybrid algorithms [9, 20, 37]. Figure 1 indicates the flowchart of DHAs with the recursive framework.

Fig. 1
figure 1

The flowchart of DHAs on the recursive framework

Full size image

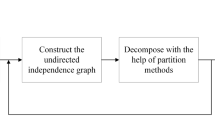
In the decomposition step, the task is to recursively split the whole node set into several small node sets. The whole node set at the beginning is decomposed into two small node subsets, each of which is recursively decomposed into two small node subsets until determination conditions are met at the end. In each iteration, decomposition is done by constructing the undirected independence graph on the current node sets. The processing can be depicted as a binary tree T [9, 20], whose root and non-leaf nodes represent undirected independence graphs as the basis for decomposition and leaf nodes represent node sets in subdomains that need not to be split any more. The undirected independence graph can be constructed by some undirected graphical model learning algorithms [20, 31] and Markov blanket discovery algorithms [9, 32]. In our proposed algorithm, we adopt a classic Markov blanket discovery algorithm called a forward–backward algorithm [32]. Decomposition approaches can be divided into three categories: maximal prime subgraph decomposition (MPD) methods [37], community detection algorithms [9] and graph-partitioning algorithms [20]. In our proposed algorithm, we adopt a graph-partitioning algorithm called general variable neighborhood search (GVNS) [25] to find minimal separators. For the determination condition, we use the usual judgment condition. If the undirected independence graph is complete, the split is terminated.

In substructure learning step, the literature [37] theoretically proves that data in subdomains after the division contain sufficient information about the relationships between nodes, so DAGs can be learned with the help of data in subdomains. Considering that sizes of subdomains obtained after decomposition are relatively small, SS algorithms and hybrid algorithms can perform better than CB algorithms in this circumstance. In our proposed algorithm, we adopt an efficient hybrid algorithm based on two heuristic searches proposed in [12] and this algorithm is called pMIC_BPSO_ADR.

In combination step, the whole BN structure is reunified by substructures based on combination methods. Merging rules proposed in [20] are used as the combination method to reunify BN substructures and the details are shown as follows.

Substructures \({\mathcal{G}}_{1}\) with nodes \(X\cup Z\) and \({\mathcal{G}}_{2}\) with nodes \(Y\cup Z\) combine the structure \({\mathcal{G}}_{12}\) according to merging rules as follow:

Rule 1 (node determination rule): the node set is \(X\cup Y\cup Z\), and

Rule 2 (link determination rule): the link set is \(({\mathbb{E}}\left({\mathcal{G}}_{1}\right)\cup {\mathbb{E}}\left({\mathcal{G}}_{2}\right))\backslash \big\{\left(i,j\right):{x}_{i}, {x}_{j}\in Z and \left(i,j\right)\notin \left({\mathbb{E}}\left({\mathcal{G}}_{1}\right)\cap {\mathbb{E}}\left({\mathcal{G}}_{2}\right)\right)\big\}\), and

Rule 3 (direction determination rule): the directions of all edges are kept unchanged except that a fraction of edges is necessarily reoriented so that all v-structures are kept, along with checking acyclicity.

Merging rules include the node determination rule for determining nodes in the combined structure, the link determination rule for determining links of edges in the combined structure, and the direction determination rule for determining directions of edges in the combined structure. In this step, determining directions of edges in the whole BN structure according to substructures is the challenging and key part. The principle of the direction determination rule in merging rules is to keep v-structures unchanged in the pre-merge and post-merge invariable according to the decomposition property. Although this rule works effectively to a certain extent, but there are still some problems. First, this rule only considers the case that structure learning algorithms can learn correct substructures to ensure that all v-structures are correct, but ignores the case that structure learning algorithms fail to learn correct substructures. Once structure learning algorithms cannot recover substructures well and produce wrong v-structures, this rule may not orient edges in one case. As shown in Fig. 2, Fig. 2a depicts the true structure of this network has one v-structure and a separator \(Z=\left\{u,v\right\}\) decomposes the whole domain into two subdomains \(X=\left\{w,u,v,z\right\}\) and \(Y=\left\{u,v,x,y\right\}\). Figure 2b shows actual substructures of two subdomains, while Fig. 2c shows substructures of two subdomains are separately learned. In Fig. 2c, because the edge between nodes \(x\) and \(v\) incorrectly learned, the wrong v-structure \(\left(u,x,v\right)\) is introduced. According to this rule, no matter which edge direction between \(u\) and \(v\) is selected, it will destroy the v-structure when merged. Therefore, the edge between \(u\) and \(v\) cannot be directed. Then, this rule will not be easy to operate in practice because of the cascade reaction produced by keeping v-structures invariable.

Fig. 2
figure 2

An example of a network with six nodes

Full size image

Binary particle swarm optimization

Particle swarm optimization (PSO) is a heuristic search algorithm derived from evolutionary theory. This algorithm first randomly initializes particles, and then find the optimal solution through iteration. In each iteration, each particle updates its state by tracking two extremes: personal best solution (pbest) and global best solution (gbest).

The state of the ith particle include position \({X}_{i}=\left({X}_{i1}\dots {X}_{iD}\right)\) and velocity \({V}_{i}=\left({V}_{i1}\dots {V}_{iD}\right)\). The particle velocity update formula and particle position update formula are as follows:

$$ V_{id}^{k + 1} = w \times V_{id}^{k} + c_{1} \times r_{1d}^{k} \times \left( {p_{{{\text{best}}}} \,_{id}^{k} - X_{id}^{k} } \right) + c_{2} \times r_{2d}^{k} \times \left( {g_{{{\text{best}}}} \,_{id}^{k} - X_{id}^{k} } \right), $$
(2)
$${X}_{id}^{k+1}={X}_{id}^{k}+{V}_{id}^{k+1},$$
(3)

where \({X}_{id}^{k}\) is the position of particle \(i\) in the dimension \(d\) at iteration \(k\), \({V}_{id}^{k}\) represents the velocity of particle \(i\) in the dimension \(d\) at iteration \(k\), \(w\) denotes the inertia weight, \({c}_{1}\) and \({c}_{2}\) are acceleration coefficients to adjust the maximum learning step size, and \({r}_{1d}^{k}\) and \({r}_{2d}^{k}\) are random numbers between 0 and 1.

PSO algorithms can only deal with continuous space. We adopt the following method to convert PSO for continuous space into BPSO for binary space. The particle velocity update formula is retained and the particle position update formula is modified to satisfy the binary space [12]. In this paper, the particle position update formula is modified as follows:

$${X}_{id}^{k+1}=\left\{\begin{array}{l}{\left({V}_{id}^{k}\right)}^{-1},\quad {\rm {rand}} <T\left({V}_{id}^{k+1}\right)\\ {V}_{id}^{k}, \quad{\rm {rand}} \ge T\left({V}_{id}^{k+1}\right)\end{array}\right.,$$
(4)

where \({\left({V}_{id}^{k}\right)}^{-1}\) is the complementary set of \({V}_{id}^{k}\) and the formula of T is as follows:

$$\mathrm{T}\left({V}_{id}^{k}\right)=\left|\frac{2}{\pi }\mathrm{arctan}({V}_{id}^{k})\right|.$$
(5)

The proposed algorithm

Overall design

In the combination step, the whole BN structure is reunified by a series of substructures through the proposed two-stage combination method. The high-level design of the proposed two-stage combination method is given in Algorithm 1.

figure a

From the bottom to the top of the binary tree T, the first-stage combination method is used to merge the substructures to obtain the structure \({\mathcal{G}}^{^{\prime}}\) (Line 1–7). In the first-stage combination method, we determine nodes, links of edges by merging rules and adopt the idea of permutation and combination to determine directions of contradictory edges with keeping directions of non-contradictory edges unchanged. In the second-stage combination method, directions of edges in the structure \({\mathcal{G}}^{^{\prime}}\) are restricted according to the decomposition property (Line 8). The \({\mathcal{G}}^{^{\prime}}\) obtained in the first-stage combination method may have the node that do not satisfy the decomposition property. This means that there are false parent nodes in its parent nodes to make that all of its parent nodes cannot be contained in one subdomain. To make the node in problem satisfy the decomposition property, false parent nodes are removed by modifying directions of edges between the node in problem and its false parent nodes. In addition, through analysis, nodes in problem belong to shared nodes which overlap between subdomains. Therefore, wrong directions of edges in \({\mathcal{G}}^{^{\prime}}\) exists in edges between shared nodes in problem and their false parent nodes, and needs to be revised.

The details of the first-stage combination method and the second-stage combination method are shown as follows.

The first-stage combination method

In the first-stage combination method, the structure \({\mathcal{G}}_{12}\) is composed of a pair of substructures \({\mathcal{G}}_{1}\) and \({\mathcal{G}}_{2}\) at height \(h\). Nodes and links of edges in \({\mathcal{G}}^{^{\prime}}\) are determined by Rule 1 and Rule 2 in merging rules. We determine directions of contradictory edges with keeping non-contradictory edges unchanged as follows. Under the premise of ensuring the acyclicity of the DAG \({\mathcal{G}}_{12}\), the problem of orienting contradictory edges is transformed into the problem of permutation and combination. We use BPSO to search the possible combination space and select the combination of contradictory edges with the highest BIC score. The flow diagram of direction determination for these edges is shown in Fig. 3. With the help of BPSO, the combination of contradictory edges with the optimal BIC score is found in the combination space by iterations. The termination condition of BPSO is to reach the maximum number of iterations, and the parameter value is determined according to experience. The relevant details of BPSO used in this method refer to [12]. The BIC scoring function [26] is applied to evaluate the candidate structure and is defined as follows:

Fig. 3
figure 3

The flow diagram of direction determination for contradictory edges

Full size image
$${\mathrm{Score}}_{\mathrm{BIC}}=\sum_{i=1}^{n}\left(\sum_{j=1}^{{q}_{i}}\sum_{k=1}^{{r}_{i}}{N}_{ijk}\mathrm{ln}\frac{{N}_{ijk}}{{N}_{ij}}-\frac{1}{2}\mathrm{ln}N\times {q}_{i}\left({r}_{i}-1\right)\right),$$
(6)

where \(n\) donates the number of BN nodes, \({q}_{i}\) denotes the number of all configurations of parent nodes for \(ith\) node, and \({r}_{i}\) represents the number of all states of \(i\mathrm{th}\) node. \({N}_{ijk}\) is the number of samples that \(i\mathrm{th}\) node in its \(k\mathrm{th}\) state and parents in \(j\mathrm{th}\) configuration. \({N}_{ij}\) denotes the number of samples that \(i\)th node in its parents in \(j\mathrm{th}\) configuration. \(N\) represents the number of samples in the dataset.

As shown in Fig. 3, the first processing box on the left and the two processing boxes on the right only require contradictory edges to be involved in, while the second, third processing boxes on the left and the output need all edges to participate.

Take the first and second processing boxes on the left as an example to explain how contradictory edges participate and the full structure is obtained. The schematic diagram is shown as follows.

As shown in Fig. 4, the BN structure is represented by the adjacency matrix. The adjacency matrix \({Z}_{0}\) is first obtained by initialization, and then is composed of the corresponding part of contradictory edges and the corresponding part of non-contradictory edges. Directions of contradictory edges are determined by the random orientation and then the corresponding part of contradictory edges is added to \({Z}_{0}\) according to the representation of the adjacency matrix to obtain the adjacency matrix \({Z}_{1}\). Directions of non-contradictory edges are obtained from the previous structure and then the corresponding part of non-contradiction edges is added to \({Z}_{1}\) according to the representation of the adjacency matrix to obtain the adjacency matrix \({Z}_{2}\). Through the above way, the full structure is acquired. The second processing box performs the acyclic processing for DAGs. Non-contradictory edges should be preserved as much as possible, so cycles are handled as follows. A cycle found by the depth-first search, is preferentially decyclized by trying to randomly reverse a contradictory edge in the cycle. If all attempts fail, a cycle is decyclized by trying to randomly reverse a non-contradictory edge in the cycle.

Fig. 4
figure 4

The schematic diagram describing first processing box to second processing box

Full size image

After the first-stage combination method, the DAG \({\mathcal{G}}^{^{\prime}}\) is finally obtained.

The second-stage combination method

In the second-stage combination method, we modify directions of edges between problematic nodes and their parent nodes in \({\mathcal{G}}^{\mathrm{^{\prime}}}\) to obtain the structure \({\mathcal{G}}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}\). The problematic node refers to the problematic shared node. The reason for the problematic share node is that its parent nodes contain false parent nodes to make that its parent node set is not in a subdomain, which is defined as the target domain. Therefore, we should find false parent nodes from its parent nodes and eliminate false parent nodes by reversing edges between the problematic shared node and false parent nodes.

The design of this method is shown in Algorithm 2. Considering that there may be several problematic shared nodes, we deal with them one by one. The current problematic shared node is processed, and then the next problematic shared node is processed. The processing of each shared node in problem \(X\) consists of two parts.

The first part is to ascertain the target domain to classify \(X\)’s parent nodes to candidate true parent nodes and false parent nodes through the BIC scoring function (Line 4–13). To avoid errors caused using the BIC scoring function in subdomains, we use the BIC scoring function in the whole domain rather than in subdomains. We test non-shared parent nodes in subdomains \(M\) involving \(X\) and its parent nodes in turn, and determine the target domain by identifying a true parent node with the BIC scoring function in the whole domain. According to the relationship between parent nodes and subdomains, we divide parent nodes of \(X\) into shared parent nodes and non-shared parent nodes.

Shared parent nodes of \(X\) are defined as its parent nodes that occurs more than once in \(M\).

Non-shared parent nodes of \(X\) are defined as its parent nodes except for shared parent nodes.

figure b

From the above definitions, non-shared parent nodes can correspond to subdomains one by one, while shared parent nodes cannot correspond to subdomains one by one. Fortunately, shared parent nodes are confirmed in the first-stage combination method. Shared parent Nodes belong to true parent nodes of \(X\), so we only need to consider non-shared parent nodes. Therefore, we can locate the target domain by confirming a true parent node in non-shared parent Nodes.

Th second part is to treat edges between different classes of parent nodes and \(X\) accordingly (Line 14–28). If the target domain \({M}_{T}\) is located. Parent nodes of \(X\) outside \({M}_{T}\) are confirmed as false parent nodes, and parent nodes inside \({M}_{T}\) are candidate true parent nodes. False parent nodes are directly eliminated by reversing edges, while candidate true parent nodes need to find out possible false parent nodes by BIC scoring function in the whole domain and then eliminate them by reversing edges. If the target domain is not located. This means that only shared parent nodes of \(X\) are real parent nodes, and all non-shared parent nodes are false parent nodes. Therefore, all non-shared parent nodes are directly eliminated by reversing edges. During the processing, acyclic treatments need to be performed to make the structure a DAG. To ensure the acyclicity of structures, we adopt ‘repair’ strategy [8] that uses the depth-first search to find cycles and randomly removes an edge within a cycle to ensure the acyclicity of substructures.

Illustration of the two-stage combination method

In this subsection, we illustrate the proposed method using a network with 9 nodes in Fig. 5a.

Fig. 5
figure 5

An example of a network with nine nodes

Full size image

Figure 5b shows two substructures that are decomposed according to a separator \(Z=\left\{\mathrm{1,2},3\right\}\) and learned by a structure learning algorithm.

We illustrate the first-stage combination method in Fig. 6. In Fig. 6a, contradictory edges include the edge between node 1 and node 2, the edge between node 1 and 3. These two edges need to be processed by the first-stage combination method. In Fig. 6b, we use the BPSO algorithm to search in the search space, and adopt BIC to score each candidate structure. In Fig. 6c, the structure with highest score is obtained.

Fig. 6
figure 6

An example of the first-stage combination method

Full size image

The second-stage combination method contains two parts. We illustrate the first part in the second-stage combination method in Fig. 7. In Fig. 7a, there is a problematic shared node, node 1 to be solved. The processing of node 1 is divided into three steps. In Fig. 7b, the step 1 is to determine non-shared parent nodes, node 5 and node 6. In Fig. 7c, the step 2 is to determine a true parent node of node 1, node 6. In Fig. 7d, the step is to determine the target domain, the domain in green box.

Fig. 7
figure 7

An example of the first part of the second-stage combination method

Full size image

We illustrate the second part in the second-stage combination method in Fig. 8. In Fig. 8a, the edge between node 6 and node 1 is redirected in the target domain. In Fig. 8b, the edge between node 5 and node 1 is reversed outside the target subdomain. In Fig. 8c, after the second part in the second-stage combination method, we obtain the structure. This structure obtained by the proposed method is compared with the true structure, and two structures are same.

Fig. 8
figure 8

An example of the second part in the second-stage combination method

Full size image

Experiments

All simulations are implemented based on a toolbox of FullBNT-1.0.7 in MATLAB. Our experimental platform adopts Intel 3.40 GHz CPU, Windows 10, and 8 G memory. The experiments are divided into two parts. In the first part, simulation experiments are carried out. We compare the proposed algorithm with other four algorithms with simulated data from four BN structures to verify the effectiveness of the proposed algorithm. In the second part, we use the proposed algorithm to construct a BN structure to solve practical problems in thickening process of gold hydrometallurgy.

Simulation experiments

We conduct all experiments on four benchmark networks including two medium networks (Insurance and Alarm networks) and two large networks (Hailfinder and Win95pts networks). The four benchmark networks cover many real-world domains including the medical diagnosis, the insurance assessment, the weather prediction, and the computer fault diagnosis. The details of four networks are summarized in Table 1. To take the influence of different sample sizes on algorithms into account and avoid the effect of randomness of algorithms, we carry out 10 repeated experiments using 5000, 10,000 and 20,000 cases for each network. The datasets are publicly available from the online BN repository at https://www.bnlearn.com/bnrepository/. To verify the effectiveness of the algorithm proposed in this paper, comparative experiments are carried out with four algorithms including AWMR (Algorithm With Merging Rules), a DHA which is different from the proposed algorithm using merging rules in combination stage; RLA [32], a CB algorithm based on the idea of divide and conquer; SAR [20], a hybrid algorithm based on the idea of divide and conquer; K2 [7], a classic SS algorithm. Codes of the proposed method are available at https://github.com/SophiaGhp/a-algorithm-based-on-two-stage-combination-method. AWMR is an algorithm used to compare performances of combination methods. RLA and SAR represent two classical decomposition algorithms. K2 algorithm is a classical traditional structure algorithm. The comparative studies focus on the effectiveness of structural learning algorithms. We evaluated performances of algorithms from aspects of the quality of the structure and the goodness of fit to data. The details of evaluation indicators are shown as follows.

  • Structure hamming distance (SHD) is used to describe differences between the constructed and the original structure. SHD between two DAGs is defined as the number of three operators demanded to make DAG match including deleted edges (D), added edges (A) and reversed edges (R).

  • BIC measures the fitting degree of learned structure and data.

Table 1 Description of the benchmark networks in the experiments
Full size table

Here, we need to explain that experiments do not include experiments under different orders, and the reasons are as follows. Existing structure learning algorithms according to search space can be divided into: ordering-based algorithms and graph-based algorithms. In ordering-based algorithms, the search for the network structure can be carried out in the space of orderings among the domain variables. K2 algorithm [7], order independent PC-based algorithm using quantile value (OIPCQ) [21], consensus network (CN) algorithm [2], and IPCA-CMI [1] belong to this type. In graph-based algorithms, the search for the network structure can be carried out in the space of DAGs. DHAs mentioned in this paper all belong to this type. Therefore, our proposed algorithm is a graph-based algorithm, and is not restricted by the node ordering.

Evaluation with structural difference

In this experiment, we compare our proposed algorithm with other four algorithms using structural difference in four benchmark networks and experimental results are shown in Tables 2, 3, 4 and 5. The optimal value in each case is indicated in bold in the tables. The structural difference contains SHD, A, D and R. The smaller value of SHD, A, D and R represents that the structure learned by the algorithm is better.

Table 2 Structural difference for the Insurance network
Full size table
Table 3 Structural difference for the alarm network
Full size table
Table 4 Structural difference for the Hailfinder network
Full size table
Table 5 Structural difference for the Win95pts network
Full size table

It is easy to find from Tables 2, 3, 4 and 5 that according to SHD, the proposed algorithm can find structure with higher accuracy in all cases compared against other four algorithms. From tables, we notice that K2 algorithm is inferior to other algorithms. It can be explained by the fact that unlike other algorithms, this algorithm always tries to directly find the optimal structure in the whole domain. In regard to RLA, although it has the advantage of the divide-and-conquer idea, its efficiency becomes worse in larger networks. As a CB structure learning algorithm, RLA only uses CI tests to learn the structure, instead of employing heuristic algorithms to find the optimal structure in search space. Therefore, it is very sensitive to CI tests, and poor CI tests will lead to low accuracy. Then, it is difficult to determine directions of some edges, and random orientation leads to low accuracy. As to AWMR and SAR, although they combine advantages of hybrid algorithms and the divide-and-conquer idea, merging rules used in combination step has problems stated in this paper, resulting in the low accuracy of the learned network. From tables, we can see that according to R value, the proposed algorithm can greatly reduce the error of reversed edges, and obtains the structure with higher accuracy.

Evaluation with BIC function

In this experiment, we calculate BIC scores with the learned network and the dataset to evaluate the performance of the algorithm. Experimental results on four benchmark networks are provided in Tables 6, 7, 8 and 9. The optimal value in each case is indicated in bold in the tables. The higher the BIC score is, the better the structure learned by the algorithm is.

Table 6 BIC scores for the Insurance network
Full size table
Table 7 BIC scores for the alarm network
Full size table
Table 8 BIC scores for the Hailfinder network
Full size table
Table 9 BIC scores for the Win95pts network
Full size table

As shown in Tables, we can easily find that the results of the proposed algorithm are better than other four algorithms in most cases, except for 5000 and 10,000 datasets in the Win95pts network. K2 algorithm is inferior to other four algorithms. Since a good node order is not obtained and the search space is huge, K2 algorithm is easy to fall into a local optimum, especially in large-scale networks. RLA achieves the best performance among all algorithms tested on 5000 and 10,000 datasets in the Win95pts network. It can be explained by the fact that this algorithm is completely based on CI tests and does not involve the participation of the scoring function. Therefore, in some cases, it can achieve better performance than algorithms used scoring functions using BIC score. Although the proposed algorithm does not obtain best performances using BIC score on 5000 and 10,000 datasets in the Win95pts network, it obtains best performances using structural difference on 5000 and 10,000 datasets in the Win95pts network. AWMR and SAR algorithms are both decomposition hybrid algorithms, and their performances are similar. Compared with these two structure learning algorithms used merging rules in combination step, the proposed algorithm used a two-stage combination method in combination step can achieve better performance.

Application in thickening process of gold hydrometallurgy

Hydrometallurgy is an important gold refining technology in industry. The gold hydrometallurgical process includes five main subprocesses: flotation, concentration, leaching, washing, and cementation. The effective operation of thickening subprocess is the key to ensure the efficiency of leaching subprocess. In the gold hydrometallurgical process, occurrence of abnormity is inevitable. Therefore, effective safe operation control is very important. The literature [17]constructs a model on safe operation control for thickening process of gold hydrometallurgy to make proper decisions to remove the abnormity smoothly. This model based on BN is proved accurate. The proposed algorithm is used to learn the BN structure for thickening process of gold hydrometallurgy, and is compared with the accurate BN structure in the literature [17]. The standard BN structure is a three-layer structure with 9 nodes. Three layers are the abnormal phenomenon layer, the abnormity layer and the corresponding decision layer. Each node is divided into two to three grades according to actual production needs. Refer to the literature [17] for the physical meanings and the grades of each node. The following is the process of applying the proposed algorithm to this background problem.

The structure learned by the proposed algorithm based on given data is compared with the standard structure, and the comparison results are shown in Fig. 9.

Fig. 9
figure 9

Comparison between learned structure and standard structure

Full size image

As can be seen from Fig. 9, compared with the standard network structure, the structure obtained by the proposed algorithm deletes one edge and has two reverse edges. By analyzing the abnormity in the thickening process of gold hydrometallurgy, the two inverted edges including the edge between node 2 and node 4, the edge between node 3 and node 5 can be revised by analyzing hierarchical properties of nodes. The missing edge between node 5 and node 8 can be added by analyzing the correlations between node 8 and other nodes. Therefore, after some modification steps, the structure learned by the proposed algorithm can be adopted to solve this practical problem.

Conclusion

In this paper, we propose a two-stage combination method in DHAs. The proposed combination method aims to advance a novel direction determination approach in the combination step. In the first-stage combination method, we determine directions of contradictory edges with keeping directions of non-contradictory edges unchanged by transforming the orientation problem into the permutation and combination problem. In the second-stage combination method, we modify edges between problematic nodes and their parent nodes by determining the target domain. The experimental results on four benchmark networks demonstrate that our proposed algorithm can get better performances using two evaluation indicators compared with other algorithms. Finally, the proposed algorithm is applied to the thickening process of gold hydrometallurgy to solve the practical problem. However, when dealing with the large network with high density, subnetworks divided with large sizes greatly increase the combination space of contradictory edges, which will limit the feasibility of our proposed algorithm. Therefore, in future work, we intend to introduce expert knowledge into the proposed two-stage combination algorithm, which can reduce the search space of contradictory edges and correct wrong edges at the same time.