An improved weighted optimization approach for large-scale global optimization

Abstract

It is a great challenge for ordinary evolutionary algorithms (EAs) to tackle large-scale global optimization (LSGO) problems which involve over hundreds or thousands of decision variables. In this paper, we propose an improved weighted optimization approach (LSWOA) for helping solve LSGO problems. Thanks to the dimensionality reduction of weighted optimization, LSWOA can optimize transformed problems quickly and share the optimal weights with the population, thereby accelerating the overall convergence. First, we concentrate on the theoretical investigation of weighted optimization. A series of theoretical analyses are provided to illustrate the search behavior of weighted optimization, and the equivalent form of the transformed problem is presented to show the relationship between the original problem and the transformed one. Then the factors that affect problem transformation and how they take affect are figured out. Finally, based on our theoretical investigation, we modify the way of utilizing weighted optimization in LSGO. A weight-sharing strategy and a candidate solution inheriting strategy are designed, along with a better allocation of computational resources. These modifications help take full advantage of weighted optimization and save computational resources. The extensive experimental results on CEC’2010 and CEC’2013 verify the effectiveness and scalability of the proposed LSWOA.

Introduction

In the field of optimization, large-scale global optimization (LSGO) refers to optimizing problems that usually involve more than hundreds or even thousands of decision variables [1,2,3]. LSGO problems are pretty common in real-world applications. For example, when solving large-scale control problems, the dimension of the system modeled by partial differential equations exceeds 10,000 [4]. Another example is a 2-h air traffic flow management problem [5]. It includes approximately 2400 paths, and the number of its state variables reaches 4 million. Furthermore, developments in machine learning and deep artificial neural networks have also heightened the need to deal with optimization problems that have billions of variables [6, 7].

With the increasing number of decision variables, LSGO problems become extremely difficult to handle, which is known as the “curse of dimension” [8]. In this case, the searching space [9], the problem complexity [10], and the computational cost [11] will become larger and larger. For solving LSGO problems, there is a consensus among the community, that is, the existing strategies can be divided into two categories, which are decomposition-based methods that are often under the cooperative co-evolution (CC) [12] framework and non-decomposition-based methods [13]. The former, decomposition-based methods, also known as the “divide and conquer” strategy, can effectively resolve a complex problem by splitting it into several simple ones. The latter, instead of explicitly decomposing the problem, deal with problems as a whole by an enhanced optimizer, e.g., multiple offspring sampling based hybrid algorithm (MOS) [14]. Furthermore, when it comes to large-scale multi-objective optimization problems, there are a few valuable approaches, e.g., decision variable clustering [15], problem transformation [16] and some specially designed offspring generation methods [17, 18].

In the above two categories, evolutionary algorithms (EAs) are mostly selected as the optimizer, which has shown competitive performance when solving LSGO problems. Compared with traditional optimization algorithms, EAs have unique advantages when dealing with complex problems and black-box problems—due to their loose requirements on the nature of the problem. EAs have been successfully used to solve some practical LSGO problems, such as parameter identification for building thermal models [19], large-scale capacitated arc routing problems [20], big electroencephalography (EEG) data optimization problems [21] and time-varying ratio error estimation (TREE) problems [22].

In the past decade, cooperative co-evolutionary algorithms (CCEAs) played a prominent role in LSGO. Based on certain decomposition strategies, the high-dimensional decision vector can be divided into several low-dimensional subcomponents. In each CC cycle, subcomponents are optimized by evolving their subpopulation separately in turn. For evaluation, the framework combines each subcomponent with the context vector to form a complete solution. A recent survey on CCEAs [23] provides a comprehensive review. In the survey, CCEAs are introduced in five parts: problem decomposition, subproblem optimizer, collaborator selection, individual fitness evaluation, and subproblem resource allocation. A key factor affecting the performance of CCEAs is the problem decomposition method because an inaccurate decomposition may lead to a pseudo-minimum [24]. One type of decomposition methods is manual grouping, e.g., $S_K$ grouping [24] and random grouping [25]. The other type is automatic grouping, which can detect variable interaction automatically, e.g., differential grouping (DG) [26], DG2 [27], and recursive differential grouping (RDG). Furthermore, several attempts have been made to deal with some special problems, e.g., fully separable problems [28] and non-separable problems [1, 2]. Nevertheless, automatic grouping methods will cost a lot of additional computational resources. For example, DG2 costs about 5,00,000 fitness evaluations (FEs) when detecting the interaction on 1000-D problems $f_1$–$f_{12}$ in CEC’2013 benchmark suite [29]. Meanwhile, it cannot decompose the fully non-separable problem $f_{15}$.

Non-decomposition-based methods are prevalent in early research. By strengthening the search ability of EAs or mixing multiple algorithms, this type of algorithm is more suitable for dealing with large-scale problems than before. Estimation of distribution algorithm (EDA) [30], multiple trajectory search (MTS) [31], competitive swarm optimizer (CSO) [32], and multiple offspring sampling based hybrid algorithm (MOS) [14] are some typical non-decomposition-based methods. The main drawback of non-decomposition-based methods lies in the poor scalability, that is, their performance deteriorates as the problem’s scale becomes larger and larger.

In recent years, weighted optimization has been introduced to solve LSGO problems. The main idea of the weighted optimization approaches is reducing the difficulty of the problem by optimizing the low dimensional weights that associated with subcomponents. These approaches do not rely too much on an accurate variable grouping, which overcomes the shortages of additional computational resources cost of decomposition-based methods and poor scalability of non-decomposition-based methods to some extent.

Adaptive weighting is the first weighted optimization method proposed along with DECC-G [25]. Adaptive weighting selects three selected solutions (the best, the worst, and the random one) at the end of each cooperative co-evolution (CC) cycle and improves them by the weighted optimization, respectively. The approach assigns weights to subcomponents of each candidate solution according to the variable grouping generated in CC stage and optimizes these weight variables by differential evolution. Besides, a novel adaptive weighting strategy is applied in cooperatively co-evolving particle swarms optimizer (CCPSO) [33]. However, adaptive weighting is claimed invalid according to the experiments by Omidvar et al. [34]. From their point of view, weighted optimization is not so efficient and it will cost some unnecessary computational resources.

In 2017, a weighted optimization framework (WOF) is successfully applied in tackling large-scale multi-objective optimization problems (LSMOPs) [16]. The proposed WOF is a universal framework that enables any embedded population-based meta-heuristic to tackle LSMOPs more efficiently. WOF integrates the weighted optimization and the original problem optimization. In the stage of the weighted optimization, the approach selects several candidate solutions according to crowding distance for problem transformation and optimization, and then the approach optimizes the original problem to balance the convergence and diversity. The framework is commendably applied to MMOPSO [35] with a random dynamic grouping [36] in recent work [37]. In addition, a large-scale multi-objective optimization framework (LSMOF) [38] is proposed to avoid the influence of the grouping methods and other settings. The problem reformulation method in LSMOF can be summarized as reconstructing decision space by a bi-direction weight association strategy and reducing objective space based on indicator function. By reformulation, a large-scale multi-objective optimization problem will be converted to a low-dimensional single-objective optimization problem. On account of these low-dimensional features, LSMOF can explore a set of quasi-optimal solutions efficiently to locate the Pareto optimal set.

It is noticed that WOF and LSMOF are just proposed for LSMOPs, while there is still a gap in the single-objective weighted optimization approaches. The previous single-objective approaches, e.g., adaptive weighting, do not take advantage of all beneficial information through the weighted optimization. It wastes the optimal weights and only helps improve several selected individuals, which cannot make a significant difference on the whole population. Meanwhile, what is unclear is the search behavior of weighted optimization although the concept of problem transformation has been proposed. Weighted optimization still needs a thorough theoretical analysis. Thus, in our work, we aim to theoretically investigate weighted optimization and verify its effectiveness in large-scale single-objective optimization.

Based on the above discussions, in this paper, we propose an improved large-scale weighted optimization approach (LSWOA) for helping tackle single-objective LSGO problems. First, we make a theoretical analysis on weighted optimization, which provides a detailed theoretical foundation of the proposed LSWOA. Second, based on our analysis, we design two improvement strategies and propose LSWOA afterward, which properly utilizes the weighted optimization and overcomes the shortcomings of previous approaches. Finally, the proposed approach is applied to several population-based LSGO algorithms. Experimental results show that the performance and the scalability of these LSGO algorithms have been improved significantly. The main contributions of our work are summarized as follows:

• 1. We make a specific theoretical analysis on weighted optimization. A vital proposition is proposed to show the relationship between the original problem and the transformed problem. The process of the weighted optimization is illustrated clearly by the proposition. Besides, we provide the factors that affect weighted optimization and illustrate how they affect the optimization.

• 2. According to our analysis, we propose an improved weighted optimization approach called LSWOA for LSGO. We design a weight-sharing strategy with the construction of candidate solutions and a candidate solution inheriting strategy. In addition, computational resources are efficiently allocated to weighted optimization and the original problem optimization. These improvements help make effective use of favorable information generated by the weighted optimization and save computational resources.

• 3. The proposed LSWOA can reformulate the original problems into representative low-dimensional transformed ones and share the optimal weights to the whole population. Through the application of the weighted optimization, LSWOA facilitates improving the performance of the algorithms for LSGO problems and helps tackle more complex problems better, e.g., non-separable problems and the problems with a larger scale.

The rest of the paper is arranged as follows. We first show the fundamental knowledge of weighted optimization in “Preliminary”. “Theoretical analysis” presents the theoretical analysis of weighted optimization. “The proposed LSWOA” introduces the proposed LSWOA. Then the experiments and results are shown in “Experimental studies” along with our discussions. Finally, conclusion and future work are given in “Conclusion”.

Preliminaries

In this section, the weighted optimization approach is reviewed. Then an essential concept, problem transformation, is presented to explain the transformation of optimization variable and the dimensionality reduction. At the same time, we introduce some terms of weighted optimization to pave the way for the theoretical analysis and algorithm improvement in the following sections.

Weighted optimization

Weighted optimization is an approach which can reduces the difficulty of the problem by optimizing the low-dimensional transformed problem. Here we present the detailed process of weighted optimization.

For a decision vector x, a specific grouping scheme is applied to divide the vector into m subcomponents which is denoted as ${\varvec{{x}}} = ({\varvec{{x}}}_{1}, {\varvec{{x}}}_{2},\ldots ,{\varvec{{x}}}_{m})$. Given a fixed candidate solution ${\varvec{{x}}}^{0}= ({\varvec{{x}}}_{1}^0, {\varvec{{x}}}_{2}^0,\ldots ,{\varvec{{x}}}_{m}^0)$, we assign a weight $w _{i}$ to tune the variables in a subcomponent integrally, i.e., the solution vector is transformed to ${\varvec{{x}}}' = (w _1{\varvec{{x}}}_{1}^0, w _2{\varvec{{x}}}_{2}^0,\ldots ,w _m{\varvec{{x}}}_{m}^0)$. In this way, we can optimize the low-dimensional weight vector ${\varvec{{w}}}=(w _1, w _2,\ldots ,w _m)$ by a certain EA while keeping ${\varvec{{x}}}_{0}$ fixed. This is the outline of weighted optimization.

In addition, the weight’s boundaries should be paid attention. Assume the lower and upper boundaries of x are lb and ub, we have:

$$\begin{aligned} \begin{aligned} {\varvec{{lb}}} \le w_i{\varvec{{x}}}_i^0\le {\varvec{{ub}}},\ \forall i\in \{1,2,\ldots ,m\}. \end{aligned} \end{aligned}$$

(1)

To ensure every element in sub-vector ${\varvec{{x}}}_i^0$ is not out of boundaries when applying a weight $w _i$, i.e., $lb \le w _ia _{i,j}\le ub$, $w _i$ has to hold the following constraint (supposed the dimension of sub-vector ${\varvec{{x}}}_i^0$ is s)

$$\begin{aligned} \begin{aligned} \frac{lb }{\max |x _{i,j}^0|}\le w _i\le \frac{ub }{\max |x _{i,j}^0|},\ \forall j\in \{1,2,\ldots ,s \}. \end{aligned} \end{aligned}$$

(2)

In other words, the boundaries of $w _i$ are determined by the largest absolute value of elements in ${\varvec{{x}}}_i^0$.

The main steps of weighted optimization can be generalized as follows:

• 1. Initialization: The algorithm determines a candidate solution ${\varvec{{x}}}^{0}= ({\varvec{{x}}}_{1}^0, {\varvec{{x}}}_{2}^0,\ldots ,{\varvec{{x}}}_{m}^0)$ which has been divided into m groups by a grouping scheme.

• 2. Problem Transformation: The original decision vector ${\varvec{{x}}}$ is reformulated to ${\varvec{{x}}}^{\prime }= (w _1{\varvec{{x}}}_{1}^0, w _2{\varvec{{x}}}_{2}^0,\ldots ,w _m{\varvec{{x}}}_{m}^0)$. Accordingly, The problem has been transformed from $\underset{{\varvec{{x}}}}{\min }f({\varvec{{x}}})$ to $\underset{{\varvec{{w}}}}{\min }f({\varvec{{x}}}')$.

• 3. Optimization: A weight population $P _w$ is generated randomly. The boundaries ${\varvec{{lb}}}_w$ and ${\varvec{{ub}}}_w$ are calculated by (2). Then, $P _w$ is evolved by a certain EA until the termination condition is reached. When evaluation is needed, P’ will be created by combining x and each weight vector in $P _w$.

Problem transformation

The concept of problem transformation is abstracted from weighted optimization, which is proposed in [16]. Problem transformation describes the change of objective function and decision variables. The objective function is transformed from the original problem to the low-dimension transformed problem with weight variables. Here, its mathematical expression is given.

Let Z be an optimization problem with n decision variables. Its feasible solution space is $\varOmega$. Then, the original problem is

$$\begin{aligned} \begin{aligned}&Z : \ \underset{{\varvec{{x}}}}{\min }\ \ \ f({\varvec{{x}}})\\&\text {s.t.} \ \ \ {\varvec{{x}}}\in \varOmega \subseteq \mathbb {R}^n. \end{aligned} \end{aligned}$$

(3)

A fixed candidate solution ${\varvec{{x}}}^0=(x _1^0,x _2^0,\ldots ,x _n^0)$ is selected as an initial point to generate a transformed problem cooperating with m weight variables ${\varvec{{w}}}=(w _1,w _2,\ldots ,w _m)$. We use transformation function $\psi = \psi ({\varvec{{w}}},{\varvec{{x}}}^0)$ to combine ${\varvec{{w}}}$ and ${\varvec{{x}}}^0$. Weight vector w is optimized by an optimizer to tune each sub-vector of ${\varvec{{x}}}^0$. The feasible space of the weight vector is $\varPhi$, which depends on the candidate solution and the boundaries. Then, the transformed problem can be formulated as

$$\begin{aligned} \begin{aligned}&Z _{{\varvec{{x}}}^0}:\ \underset{{\varvec{{w}}}}{\min } \ \ \ f_{{\varvec{{x}}}^0}({\varvec{{w}}})= f(\psi ({\varvec{{w}}},{\varvec{{x}}}^0))\\&\text {s.t.}\ \ \ {\varvec{{w}}}\in \varPhi \subseteq \mathbb {R}^m. \end{aligned} \end{aligned}$$

(4)

Compared with the original problem $Z$, the number of variables in the transformed problem $Z _{{\varvec{{x}}}^0}$ is reduced from n to m. As a result, the transformed problem is much easier to solve.

Transformation function refers to the combination of weights and the candidate solution. By means of transformation function, the decision variable changes from x to w. Here, interval-intersection transformation is used, which is a canonical transformation function used in [16] and [25]:

$$\begin{aligned} \begin{aligned}&\psi ({\varvec{{w}}},{\varvec{{x}}}^0)=(\underset{g(1)}{\underbrace{w _1x _1^0,\ldots ,w _1x _s^0}},\underset{g(2)}{\underbrace{w _{2}{} x _{s+1}^0,\ldots ,w _{2}{} x _{2s}^0}},\ldots ,\\&\qquad \qquad \qquad \quad \times \underset{g(m)}{\underbrace{w _mx _{n-s+1}^0,\ldots ,w _mx _n^0}})\\&\text {s.t.}\ \ \frac{lb }{\max \{|x _{g(i)}|\}}\le w _i\le \frac{ub }{\max \{|x _{g(i)}|\}}, \ \ \forall i=1,2,\ldots ,m . \end{aligned}\nonumber \\ \end{aligned}$$

(5)

Before problem transformation, a specific grouping strategy has divided the decision variables into m groups (assume that each group is the same size) which are denoted by $g(i),\ i=1,2,\ldots ,m$. $x _{g(i)}$ is the set of all elements in a variable group. Every sub-vector of the candidate is associated with a weight and tuned by the weight. Then we optimize the weight vector as a new decision vector. Interval-intersection transformation actually makes a product operation on w and ${\varvec{{x}}}^0$. When optimizing the weight variable $w_i$, a constraint limits the changes of $w_i$ to keep every weighted element within the boundaries lb and ub. Thus, the feasible space of the weight vector is obtained by all the constraints. In addition, there are other transformation functions, e.g., p value transformation [16] and its improved version [39].

Besides the transformation function, variable grouping is also an important factor affecting problem transformation. In LSGO, grouping strategy can be categorized into two types: grouping based on the variable interaction (e.g., ideal grouping) or without considering the interaction (e.g., random grouping). Variable interaction refers to the coupling between variables. For variables $x_1$ and $x_2$, if $\frac{\partial f}{\partial x_1\partial x_2}\ne 0$, there is some interaction between $x_1$ and $x_2$ [40], i.e., the two variables belong to the input variables of the same subfunction in its objective function. In general, variable grouping is related to how to assign weights to decision variables.

Here is an example to illustrate the problem transformation. For problem $Z:\underset{{\varvec{{x}}}}{\min }\ f({\varvec{{x}}})=(x_1+2)^2+(x_2-2)^2$, variables $x_1$ and $x_2$ are divided into a same group and controlled by a weight w. Given a candidate solution ${\varvec{{x}}}^0=(3,3)$, the problem is transformed to $Z_{{\varvec{{x}}}^0}:\underset{w}{\min }\ f_{{\varvec{{x}}}^0}(w)=(wx_1^0+2)^2+(wx_2^0-2)^2=(3w+2)^2+(3w-2)^2=18w^2+8$.

The above is all the details of the weighted optimization approach. Weighted optimization can reduce the dimension of the problem to reduce the difficulty of the problem effectively. However, existing studies highlight the dimension reducing feature of adaptive weighting, yet they may not clearly figure out the underlying mechanism which leads to the failure when optimizing some LSGO problems. In this paper, we conduct the theoretical analysis of weighted optimization, which is provided in the following section.

Theoretical analysis

In this section, we make a further analysis of weighted optimization first. Then, according to the analysis, we aim to determine what factors will affect the problem transformation and illustrate how they affect the problem transformation, which hence motivates the proposed algorithm LSWOA in this paper. The analysis would help answer the following questions:

• 1. How exactly is the search behavior of weighted optimization?

• 2. What is the mathematical relationship between the transformed problem and the original one?

• 3. What are the factors that affect the problem transformation? How do these factors change the mathematical form of transformed problems and then influence the optimization process?

Search behavior

To demonstrate the search behavior of weighted optimization better and explain the relationship between the transformed problem and the original one, we will show the convergence process of weighted optimization. The optimization of one-dimensional and multi-dimensional transformed problems will be analyzed as examples successively for better understanding. Here, the dimension of the transformed problem is the number of weights, which is also equal to the group number. Table 1 provides four examples for the following analysis. The original problems are provided in the second column. The third and fourth column provide the information about the candidate solutions and the variable grouping. The generated transformed problems are listed in the last column. Among these examples, Examples 1 and 2 show two 1-D transformed problems generated by the same original problem with two different candidate solutions while Examples 3 and 4 show two 2-D transformed problems generated by the same original problem with two different variable grouping.

Table 1 Four examples of problem transformation

The process of one-dimensional weighted optimization

One-dimensional weighted optimization is simple and easy to understand. Example 1 and Example 2 in Table 1 are two instances of one-dimensional weighted optimization.

We make a detailed explanation on Example 1. For problem $Z:\underset{{\varvec{{x}}}}{\min }\ f({\varvec{{x}}})=(x_1+2)^2+(x_2-2)^2$, given a candidate solution ${\varvec{{x}}}^0=(3,3)$, the problem is transformed to $Z_{{\varvec{{x}}}^0}:\underset{w}{\min }\ f_{{\varvec{{x}}}^0}(w)=(wx_1^0+2)^2+(wx_2^0-2)^2=18w^2+8$. We optimize $Z_{{\varvec{{x}}}^0}$ and then get the optimal $w^*=0$ and $f_{\min }=8$. The optimization process is illustrated in Fig. 1a. ${\varvec{{x}}}^*$ is the result solution produced by combining the best weights $w^*$ and the candidate solution ${\varvec{{x}}}^0$. The best weight $w^*$ indicates the best scaling factor from ${\varvec{{x}}}^0$ to ${\varvec{{x}}}^*$, i.e., $w=\Vert {\varvec{{x}}}^*\Vert$/$\Vert {\varvec{{x}}}^0\Vert$. It demonstrates that adjusting the weight is to scale down the candidate solution vector. The other example is illustrated in Fig. 1b. The problem transformation in Example 2 differs from Example 1 in the candidate solution, i.e., ${\varvec{{x}}}^1$, which leads to a different transformed problem: $\underset{w}{\min }\ f_{{\varvec{{x}}}^0}(w)=16w^2-16w+8$. Accordingly, the optimization path and the optimal solution are also different.

Fig. 1

The optimization process of two 1-D transformed problems with different candidate solutions (Examples 1 and 2 in Table 1). The candidate solutions $x^0$ and $x^1$ are optimized to the optimal solutions $x^*$ and $x^{1*}$ according to the red arrows. Here, the function is $f(x)=(x_1+2)^2+(x_2-2)^2$, and the grouping of variables is $(\underline{x_1,x_2})$

By reflecting on the convergence process, we can generalize the search behaviour of one-dimensional weighted optimization: the algorithm searches for better solutions on a straight line connecting the initial candidate solution and the origin O. This type of search is based on the original problem’s contour. So, the search sub-space has become a 1-D straight line of the original search space.

Fig. 2

The optimization process of the 2-D transformed problem (Example 3 in Table 1) generated with non-ideal grouping. Here, the function is $f(x)=x_1^2+(x_1+x_2)^2+x_3^2$, and the grouping of variables is $(\underline{x_1},\ \underline{x_2,x_3})$. Ellipsoids of different sizes are the contour of the 3-D function. The candidate solution $x^0$ is shown with yellow dots and the blue dots $x^*$ are the optimal solution. The original 3-D search space turns into a 2-D subspace (the dark plane in the sub-figure a), and the candidate solution is optimized according to the red arrow. The transformed problem is non-separable because of the non-ideal grouping

Fig. 3

The optimization process of the 2-D transformed problem (Example 4 in Table 1) generated with ideal grouping. Here, the function is $f(x)=x_1^2+(x_1+x_2)^2+x_3^2$, and the grouping of variables is $(\underline{x_1,x_2},\ \underline{x_3})$. Ellipsoids of different sizes are the contour of the 3-D function. The candidate solution $x^0$ is shown with yellow dots and the blue dots $x^*$ are the optimal solution. The original 3-D search space turns into a 2-D subspace (the dark plane in the sub-figure a), and the candidate solution is optimized according to the red arrow. The transformed problem is separable because of the ideal grouping

The process of multi-dimensional weighted optimization

Our work is based on multi-dimensional problem transformation. To illustrate multi-dimensional transformed problem, we take a 2-D transformed problem, Example 3, as an instance. In problem $Z:\underset{{\varvec{{x}}}}{\min }\ f({\varvec{{x}}})=x_1^2+(x_1+x_2)^2+x_3^2$, variables $x_1,x_2,x_3$ are divided into two groups, {$x_1$} and {$x_2,x_3$}. {$x_1$} is controlled by weight $w_1$ while {$x_2,x_3$} is controlled by weight $w_2$. Given a candidate solution ${\varvec{{x}}}^0=(1,1,1)$, the problem are transformed to $Z_{{\varvec{{x}}}^0}:\underset{w}{\min }\ f_{{\varvec{{x}}}^0}(w)=w_1^2+(w_1+w_2)^2+w_2^2$. We optimize $Z_{{\varvec{{x}}}^0}$ and get the optimal $w^*=0$ and $f_{\min }=0$. The process of weighted optimization is presented in Fig. 2a. The ellipsoids of different sizes in Fig. 2a is the contour of the 3-D problem Z, and it is sectioned by the plane $l_1Ol_2$. The subspace is illustrated in Fig. 2b, which has the contour cut from the original ellipsoid contour. The other 2-D transformed problem in Example 4 is illustrated in Fig. 3, where the generated transformed problem is non-separable on account of a non-ideal grouping. Without loss of generality, we give a proposition of the optimization of multi-dimensional transformed problems:

Proposition 1

For an n-dimensional problem Z, if the decision variables are divided into m groups, optimizing the transformed problem $Z_\mathbf{x ^0}$ is equivalent to searching for the best solution in a subspace of the original decision space. The subspace is constructed by m axes which formed by the straight lines connecting the origin O and the projection of $\mathbf{x} _i^0$.

Proof of Proposition 1

For problem $Z:\underset{{{\varvec{x}}}}{\min }f({\varvec{{x}}})=f(x_1,x_2, \ldots ,x_n)$, if $\{x_1,x_2,\ldots x_n\}$ are evenly divided as $\{x_1,\ldots ,x_s\},$ $\{x_{s+1},\ldots ,x_{2s}\}, \ldots ,\{x_n-s+1,\ldots ,x_n\}$ and $(x_1^0,x_2^0,\ldots x_n^0)$ is a candidate solution, the problem will be transformed as:

$$\begin{aligned} \begin{aligned}&Z _{{\varvec{{x}}}^0}:\ \underset{{\varvec{{w}}}}{\min }\ f_{{\varvec{{x}}}^0}({\varvec{{w}}})=f(x_1^0w_1,\ldots ,x_s^0w_1, \\&x_{s+1}^0w_2,\ldots ,x_{2s}^0w_2,\ldots ,x_{n-s+1}^0w_m,\ldots ,x_n^0w_m) \\&\text {s.t.}\ {\varvec{{w}}}\in \varPhi \subseteq \mathbb {R}^m. \end{aligned} \end{aligned}$$

(6)

From the perspective of variable transformation, each variable satisfies $x_i=x_i^0w,\ \forall i=1,2,\ldots ,n$. Then we have $\frac{x_1}{x_1^0}= \cdots =\frac{x_s}{x_s^0},\frac{x_{s+1}}{x_{s+1}^0}= \cdots =\frac{x_{2s}}{x_{2s}^0},\ldots ,\frac{x_{n-s+1}}{x_{n-s+1}^0}=\cdots =\frac{x_n}{x_n^0}$, which can be regarded as constraints for Z. Therefore, we obtain a constrained form

$$\begin{aligned} \begin{aligned}&Z_{c}:\ \underset{{\varvec{x}}}{\min }\ f(\varvec{{x}})=f(x_1,x_2,\ldots ,x_n)\\&\text {s.t.}\ \ \frac{x_1}{x_1^0}=\cdots =\frac{x_s}{x_s^0}, \\&\quad \frac{x_{s+1}}{x_{s+1}^0}=\cdots =\frac{x_{2s}}{x_{2s}^0},\ldots ,\frac{x_{n-s+1}}{x_{n-s+1}^0}=\cdots =\frac{x_n}{x_n^0}\\&{{\varvec{x}}}\in \varOmega \subseteq \mathbb {R}^n. \end{aligned} \end{aligned}$$

(7)

Besides the original range constraint on x (i.e., $\mathbf{x} \in \varOmega$), there are other m equality constraints and each constraint represents a straight line $l_i$. The subspace, denoted as $\varUpsilon$, is described by all the constraints. It is thus clear that $x^0$ is optimized in the search subspace $\varUpsilon$ according to the contour of Z. $\square$

The constrained form (7) illustrates the reduction of dimension clearly. In the constraints formed by each variable group, i.e., $\frac{x_1}{x_1^0}=\cdots =\frac{x_s}{x_s^0}$, the number of constraints is $s-1$. Therefore, the dimension of the transformed problem is equal to $n-m*(s-1)=m$.

Proposition 1 and the constrained form (7) are the key points of our theoretical analysis, which help us understand weighted optimization thoroughly. The essence of dimension reduction in weighted optimization is reducing the number of variables by equality constraints, i.e., searching for better solution in a potential subspace. According to Proposition 1 and the constrained form, we can figure out the influence factors and the limitation of weighted optimization.

With regard to the constrained form (7) and Proposition 1, we can obtain three enlightenments:

• 1. Weighted optimization has an excellent performance on the problem where the global optimum is located on the origin $(0,0,\ldots ,0)$, e.g., the problems in classic benchmark functions [41] and CEC’2005 benchmark suite [42]. The origin satisfies all the constraints, i.e., the origin must be in the search subspace. Therefore, the global optimum can be easily found by weighted optimization. This explains why weighted optimization usually works in the experiments using early benchmark problems that the global optima are at the origin. But there is no special effect for those problems where the global optima are shifted.

• 2. Some transformed problems are similar as long as their candidate solutions are close to each other and the variable grouping keeps unchanged. Thus, it is feasible to reuse the optimized weights of a transformed problem to similar ones. Following this idea, we can construct similar transformed problems and share weights to the similar ones for saving computational resources.

• 3. Weighted optimization has its limitations when searching for optimal solutions, i.e., it cannot obtain the global optimum of the original problem. Because weighted optimization provides a potential subspace, but the global optimum is often not in the subspace. Especially in the later stage of the original problem optimization, the candidate solution may be attracted by the local optimum, so the optimum of the transformed problem often becomes the local optimum of the original problem. Therefore, in the later stage of the whole optimization process, weighted optimization may not work.

Factors that influence problem transformation

For generating a transformed problem, candidate solution, grouping strategy, and transformation function are required. These three factors will affect problem transformation. By changing these factors, the search subspace will become different, which explains why problem transformation diversifies. The following analysis elaborates these three factors.

Candidate solution

The candidate solution ${\varvec{{x}}}^0$ determines the coefficients of the transformed problem. In (4), we observe that each element of ${\varvec{{x}}}^0$ affects each weight variable. When choosing different ${\varvec{{x}}}^0$, the transformed problem $Z_{{\varvec{{x}}}^0}$ differs in its inner coefficient but its form is still the same. However, if we investigate the question in terms of the constrained problem shown in (7) that the coefficient of constraints will change if the candidate solutions are different. It means the subspace $\varUpsilon$ will be created in a different position. Fig. 1a and b show the influence of different candidate solutions. Two candidate solutions ${\varvec{{x}}}^0$ and ${\varvec{{x}}}^1$ create two subspaces which are represented by dotted lines. Accordingly, the two transformed problems have different optima.

However, when the positions of candidate solutions are close, and the variable grouping is unchanged, their transformed problems can be regarded as similar because the coefficients of these transformed problems will not change much. Therefore, if we can find some specific candidate solutions close to each part of the population, the weights from optimizing these transformed problems can be reused to weigh the population. This analysis guides us to design a weight-sharing strategy in “Algorithm analysis”.

Variable grouping

Variable grouping is related to how decision variables are divided into groups and cooperate with weights. Two aspects (the grouping strategy and the grouping number) of variable grouping are taken into account.

The grouping strategy refers to the basis of grouping variables. In this part, the grouping strategy we study can be classified into ideal grouping and non-ideal grouping (e.g., random grouping). Ideal grouping divides all variables entirely based on interaction, which means that all variables in a group are interdependent while no interaction exists between each variable group. Non-ideal grouping does not exactly following the interaction. Here, we figure out the influence of these two types of grouping strategies on problem transformation, which is illustrated in Proposition 2.

Proposition 2

Given an additively separable problem Z, if the variables of Z are grouped ideally, the transformed problem $Z_{x^0}$ will be separable.

Proof of Proposition 2

If $f(x)=(x_1,x_2,\ldots ,x_n)$ is additively separable, $f(\mathbf{x} )$ can be expressed by the sum of sub-function $f(\mathbf{x} _i)$:

$$\begin{aligned} \begin{aligned} f({\varvec{{x}}})=\sum _{i=1}^{m}{f({\varvec{{x}}}_i)}. \end{aligned} \end{aligned}$$

(8)

Then, for a candidate solution $\mathbf{x} ^0$, if all variables are grouped ideally, the function of $Z_{x^0}$ will becomes

$$\begin{aligned} \begin{aligned} f_{{\varvec{{x}}}^0}({\varvec{{w}}})=\sum _{i = 1}^{m}f({\varvec{{x}}}_i^0\cdot w_i). \end{aligned} \end{aligned}$$

(9)

In (9), the decision variable has been transformed to w. The formula shows that $f_\mathbf{x ^0}(\mathbf{w} )$ can also be expressed by the sum of sub-functions $f(\mathbf{x} _i^0\cdot w_i)$. Therefore, $Z_{x^0}$ is a fully separable problem. $\square$

Correspondingly, a non-ideal grouping leads to a non-separable transformed problem. It is more challenging to solve non-separable problems than separable problems.

Figure 2 (Example 3 in Table 1) and Fig. 3 (Example 4 in Table 1) show the distinction between problem transformation with non-ideal grouping and that with ideal grouping. If variables are divided by ideal grouping, the subspace will section the original contour based on the separability of Z properly. Therefore, the sub-contour in Fig. 3b is a standard ellipse with a separability feature. However, in Fig. 2b, the variables are not grouped according to their interaction. So the sub-contour becomes a rotated ellipse with a non-separability feature. The performance of weighted optimization with the two different grouping strategies is tested in “Effect of grouping strategies”.

The grouping number determines the dimension of the transformed problem. It involves the fineness of weighted optimization, that is, the more variable groups are divided beforehand, the higher optimization accuracy we achieve. However, it means a lower convergence speed. Even when we divide each variable into a group, the transformed problem is equivalent to the original problem. This factor reminds us to adjust and balance the level of optimization between coarseness and fineness. Figure 4 shows the convergence characteristic of two transformed problems with different scales (40-D and 20-D). The two transformed problems are generated from the same original problem ($f_{10}$ in CEC’2010), but the former groups variables in a size of 25 while the latter’s grouping size is 50. The 40-D transformed problem can get better fitness, but it is harder to optimize than the 20-D one. The above analysis about grouping numbers enlightens us that it is necessary to allocate appropriate computational resources to a transformed problem according to its dimension.

Fig. 4

The convergence characteristic of two transformed problems with different grouping numbers (dimensions). The two transformed problems are generated from the same original problem (1000-D $f_{10}$ in CEC’2010). The candidate solution and the grouping strategy (random grouping) keep unchanged. The two transformed problems are optimized by DE with a population size of 50. The data in the figure are averaged after 25 independent tests

Transformation function

The transformation function can be considered as a combination operator applied to weights and the candidate solution. The transformation function we used in this work is the interval-intersection transformation, which is introduced in (5). In addition, an improvement transformation function is proposed in [39] aiming to uncouple the relationship between absolute variable values and the boundaries of the original variable:

$$\begin{aligned} \begin{aligned}&x _i= \left\{ \begin{array}{ll} x _i'+(w _j-1)\cdot (ub-x _{i}') &{} \ \ \text {if} \ w _j > 1 \\ lb+w _j\cdot (x _{i}'-lb) &{} \ \ \text {if} \ w _j \le 1 \end{array} \right. \\&w _j\in [0,2]. \end{aligned} \end{aligned}$$

(10)

Different transformation functions change the structure of constraints and make the search subspace vary. For example, every grouped variable using transformation function (5) leads to a line constraint connecting the origin to the candidate solution, while transformation function (10) lead to two lines connecting the candidate solution to the upper and lower bound points.

The proposed LSWOA

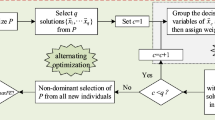
The pseudo-code of the proposed LSWOA is presented in Algorithm 1, which works with the cooperation of weighted optimization (Algorithm 2), weights sharing (Algorithm 3), and transformation function (Algorithm 4).

In LSWOA, the weighted optimization is utilized in two stages: population initialization and integrated optimization. The former refers to weighting the initial population at the beginning, and the latter refers to integrating the optimizations of the original problem and the transformed problem.

Algorithm description

The main framework of LSWOA is shown in Algorithm 1. Lines 1-8 demonstrate the stage of population initialization with weighting. First, the algorithm creates an initial population randomly (Line 2) and divides the decision variables into some groups stored in a cell g (Line 3). Then, q individuals are selected from the initial population, which can be seen as q reference candidate solutions preparing for weighted optimization (Line 4). There will be a sensitivity analysis of the parameter q in “Parameter sensitivity analysis”. By optimizing these candidate solutions using weighted optimization, the corresponding best weight vectors ${\varvec{{w}}}_i$ can be obtained (Line 6). These beneficial weight vectors are shared with the population (See Algorithm by an interval-intersection transformation function (Line 7). By repeating this process q times, an improved population is produced for the next optimization stage.

Lines 9–17 of Algorithm 1 demonstrate the integrated optimization stage. We allocate half of the total evaluation resources to the integrated optimization stage. In this stage, the optimizations of the original problem and the transformed problem are conducted in turn. First, the original problem is optimized by a practical algorithm A with $t_1$ FEs (Line 11). Then, a reference candidate solution ${\varvec{{x}}}_r$ is created synthetically for generating the transformed problem (Line 13). To make it more representative of the population, we use all individuals’ mean values to generate the reference candidate solution. After optimizing this unique transformed problem (Line 14), we share the best weight vector with the population in the same way (Line 15) and select the next generation’s population. Finally, the weighted optimization is banned after the integrated optimization stage if half of the computational resources are used to keep the diversity.

The process of the weighted optimization is provided in Algorithm 2. The systematic introduction of weighted optimization has been given in “Weighted optimization”. Line 2 demonstrates the initialization of the weight population. The weight population is randomly generated between the boundaries ${\varvec{{lb}}}_w$ and ${\varvec{{ub}}}_w$ which are calculated by Line 1. There is a candidate solution inheriting strategy in Line 3 aiming to keep the candidate solution’s fitness, which is setting a random weight individual as $(1,1,\ldots ,1)$ when initializing the weight population. Then, the weight population WP is optimized by a DE algorithm with $t_2$ FEs (Line 4). Note that the weight individual cannot be evaluated directly. For calculating its fitness, a transformed population is generated by combining the candidate solution ${\varvec{{x}}}$ and each weight individual ${\varvec{{w}}}_j$ using transformation function. Finally, the best weight vector is obtained according to the fitness of the weight population WP.

Algorithm 3 shows the weight-sharing strategy, which enables the population to be improved by a weight vector. In this algorithm, all the decision variables ${\varvec{{x}}}_j$ are picked out and combine with the same weight vector ${\varvec{{w}}}$ to produce a weighted population. Finally, a selection procedure is started to create an improved population.

Algorithm 4 presents the details of the transformation function. For an input solution x and a weight vector w, each variable group is multiplied by the corresponding weight. Then, we can obtain the weighted solution ${\varvec{{x}}}'$.

Algorithm analysis

In this subsection, we illustrate why LSWOA is effective. Three main improvements we make are presented, and the contributions that these improvements make are analyzed.

Compared with adaptive weighting, which only optimizes few selected individuals at the end of each CC cycle, LSWOA integrates the weighted optimization into the initialization and optimization stages of the algorithm. In these two stages, the weighted optimization helps to improve the quality of the whole population. For better utilizing the weights, a weight-sharing strategy with the construction of reference candidate solutions is proposed. The best weight vectors are obtained by the weighted optimization of some specific reference candidate solutions. Then these weight vectors can be shared with the whole population. Meanwhile, a candidate solution inheriting strategy is proposed to take the candidate solution as the initial information in each weighted optimization, which ensures a better performance of each weighted optimization. Furthermore, we design a computational resources allocation scheme for striking a balance between the weighted optimization and the original optimization.

Weight-sharing with the construction of reference candidate solutions

Weight-sharing refers to reusing the best weight vector of a transformed problem to other transformed problems. This strategy is based on the discussion of similar transformed problems when analysing the effect of the candidate solution in “Candidate solution”. It will cost too many computational resources if we want to solve transformed problems generated by all individuals in population. Thus, in the proposed LSWOA, we designed a weight-sharing method to evolve the population approximately. The condition of weight-sharing is that the two transformed problems are similar. In the process of problem transformation, similar transformed problems can be generated as long as the candidate solutions with similar positions are selected when the variable grouping is unchanged. According to the constraint form (7) of weighted optimization in “Search behavior”, similar candidate solutions will only make the constraint coefficients of the two problems slightly different. After sharing weights with all solution in the population, the next population is selected from the weighted population and the original population. In general, weight-sharing can be summarized as optimizing reference transformed problems, then directly improving the whole population through the experience information (the optimized weight vectors) generated in the weighted optimization process.

We select or construct reference solutions which can represent the population to some extent. In the initialization stage, we select q random individuals as the reference candidate solutions; and in the integrated stage, we create a representative solution by averaging all individuals in the population. It is designed because we simply treat the population as a cluster in the decision space along with the optimization. As the optimization runs, individuals distribute widely in the beginning and gather gradually afterwards. Thus, we select q random individuals to simulate the widely distributed population initially and use a mean vector to approximate the gathered population later.

Candidate solution inheriting

At the beginning of the weighted optimization, a weighted population is randomly generated but a weight individual is set as $(1,1,\ldots ,1)$. This strategy is called candidate solution inheriting.

In fact, the transformed problem is still with a medium scale and it is not easy to deal with by an ordinary EA. The candidate solution can provide a prior information, which greatly accelerates the convergence of the weighted optimization. A weight vector $(1,1,\ldots ,1)$ ensures that the candidate solution can be inherited. According to Proposition 1 in “The process of multi-dimensional weighted optimization”, the weight individuals will be randomly generated in the subspace when initializing. The weight individual $(1,1,\ldots ,1)$ can ensure that the candidate solution will not be lost in the subspace. In the early stage of the algorithm, the quality of candidate solutions is poor, which may not provide good initial information to guide the weighted optimization. But when the algorithm runs for a period of time, the fitness values of the initial candidate solutions are often better than that of the candidate solutions with random weights. Therefore, it is particularly important to apply this strategy in the integrated optimization stage.

Computational resource allocation

In previous study on adaptive weighting, weighted optimization is considered a waste of computational resources through their experiment [34]. So, it is necessary to allocate appropriate computational resources to weighted optimization and ordinary optimization.

According to the third enlightenment proposed in “The process of multi-dimensional weighted optimization”, we just apply the weighted optimization in the first half stage of the whole optimization. Weighting optimization have a high convergence speed, but the trade-off is reducing the optimization accuracy. Its optimization limitation is related to the search subspace (refers to “Search behavior”). The solution after the weighted optimization hardly reaches the global optimum of the original problem. To begin with, the weighted optimization and weight-sharing are implemented after population initialization. When entering the integrated optimization, we still use these two strategies in the first half of the whole optimization process, so that weighted optimization can speed up convergence and the applied EA helps to keep diversity. However, weighting optimization is banned in the later stage because it is hard to find a better solution than the candidate solution by optimizing its weights. Thus, some fitness evaluations are saved for optimizing the original problem.

Furthermore, the fitness evaluations of the weighted optimization should be assigned depends on the number of groups. On the basis of grouping analysis in “Factors that influence problem transformation”, we set $10*D*N/|g|$ evaluations for the weighted optimization every time to ensure a balance on the convergence accuracy and the cost of computational resources.

Experimental studies

In this section, we integrate LSWOA into two typical LSGO algorithms, DECC-G and SaNSDE, to verify its effectiveness first. In particular, we pay attention to the performance of the algorithms on non-separable and multi-modal problems. Then, we test the scalability of the proposed LSWOA. The number of variables is scaled to 5000 to investigate whether LSWOA is more helpful than 1000-D problems. Finally, we explore the impact of grouping strategy on the performance of weighted optimization.

Experimental settings

The algorithms we used to cooperate with LSWOA are introduced as follows:

• 1. DECC-G [25]: It is a cooperative co-evolution differential evolution with a random grouping that belongs to the decomposition approach. It is one of the most classic CCEAs. Although it is simple and easy to operate, it works well for separable problems. We compare the LSWOA-enhanced version, the adaptive-weighting-enhanced version, and the non-weighting version, denoted DECC-G-LSWOA, DECC-G-AW, and DECC-G-NW, respectively. Note that the widely used DECC-G refers to the adaptive weighting enhanced version (DECC-G-AW) in other literature.

• 2. SaNSDE [43]: It is a self-adaptive differential evolution with neighborhood search, which belongs to the non-decomposition approach. SaNSDE plays as a subcomponent optimizer in many DECC algorithms, e.g., DECC-DG [26] and DECC-RDG [44]. SaNSDE-LSWOA stands for the LSWOA-enhanced version of SaNSDE.

Our evaluation is implemented on three widely used LSGO test suites: benchmark functions for the CEC’2008, CEC’2010, and CEC’2013 special session and competition on large scale global optimization [45,46,47]. CEC’2010 and CEC’2013 benchmark suites are used to test the overall performance of LSWOA, and the CEC’2008 benchmark suite is used to test its scalability.

CEC’2008 benchmark suite has seven test problems. It only contains fully separable or non-separable problems. They are made up of some basic functions through rotated transformation. The dimension of problems in the benchmark suite is capable of being tuned.

CEC’2010 benchmark suite has 20 test problems, which are composed of six basic problems. By rotating some separable low-dimensional subproblems and combining them, the suite creates a series of partially separable problems. The suite consists of three fully separable problems ($f_1$ and $f_3$), 15 partially separable problems ($f_4$–$f_{18}$), and two fully nonseparable problems ($f_{19}$ and $f_{20}$). The modality of these problems is related to the basic functions that constitute them.

CEC’2013 benchmark suite is an advanced test suite with an extraordinary degree of difficulty. The benchmark suite has 15 test problems. It creates separability by the same mean with CEC’2010. The authors add more complex properties to it, e.g., different group sizes, conforming/conflicting overlap, and imbalance. In addition, for resembling real-world problems better, some no-linear transformations are added to break symmetry and make the landscape more irregular.

In our experiment, the population size is 50, while the dimension of benchmark problems is set to 1000. We allocate $3*10^6$ fitness evaluations for each algorithm to test their overall performance. All the algorithms are ran 25 times independently.

The settings of the weighted optimization are independent of the original problem optimization. For generating a transformed problem, random grouping is used as the decomposition strategy based on its simplicity and applicability (the influence of grouping strategy will be tested and discussed in “Effect of grouping strategies”). In the population initialization stage, we select q individuals from the population as reference candidate solutions where q is set to 5 here. Every time we apply the weighted optimization, the decision variables will be regrouped with a size of 25, i.e., the number of groups is 400. Note that the variable groups are only used in the weighted optimization yet do not preserve for problem decomposition in CC. The size of the weight population is the same as the original population. The fitness evaluations of the weighted optimization ($t_2$) is set to $10*D*N/|g|$ while the original optimization evaluations ($t_1$) is set to $5*t_2$. That means 20,000 FEs will be allocated to the weighted optimization with 400 groups in a 1000-D problem. The weight population size is 50, which is consistent with the setting of the original population.

For the specific parameters of the enhanced algorithms, the settings follow the related literature [25, 43]. The group size of DECC-G is 100 and the evaluation times of optimizing each subcomponent are $200*N$. Adaptive weighting in DECC-G costs $200*N$ FEs for each transformed problem. It is applied after every CC optimization cycle and adopts the same variable groups in the CC stage. The group size of DECC-i is dependent on benchmark problems. Meanwhile, SaNSDE is parameter-free.

For the experimental results, the best values are marked in bold. We make a Wilcoxon’s rank-sum test at a 0.05 significance level on each pair of algorithms. “+”, “−”, and “=” denote the LSWOA-enhanced version is significantly better than, significantly worse than, and statistically similar to the other, respectively.

Performance on benchmarks

The target of our experiment is to verify the effectiveness of the proposed LSWOA and confirm the difference we make on the previous weighted optimization approaches.

We record the performance of DECC-G, SaNSDE, and their weighted versions (DECC-G-LSWOA, DECC-G-AW, and SaNSDE-LSWOA) on the benchmark suites of CEC’2010 and CEC’2013. The results are shown in Tables 2 and 3. To present that our improvement is efficacious based on adaptive weighting, we discuss the differences in the performance between DECC-G-LSWOA and DECC-G-AW. Then, to show that our approach is helpful to enhance the original algorithm’s performance, we discuss the differences in the performance between DECC-G-LSWOA and DECC-G-NW as well as SaNSDE-LSWOA and SaNSDE. Finally, we analyze the applicability of LSWOA based on the performance of various test problems. Our comparison and discussion are carried out on the two benchmark suites together.

Table 2 The performance of each version on CEC’2010 benchmark suite with 1000 decision variables

The first set of comparison is showed in the first two columns of Tables 2 and 3. What we wonder is, compared with adaptive weighting, whether the improvement of applying weighted optimization on LSWOA is effective and whether the application of LSWOA can improve the original algorithm’s performance. DECC-G-LSWOA performs better than DECC-G-AW on 26 of 35 test problems in these two benchmark suites but slightly worse on only 2 problems. The results show that our application of weighted optimization is much better than that of adaptive weighting. We also make a Wilcoxon’s rank-sum test between DECC-G-AW and DECC-G-NW results (it was not marked in the tables). DECC-G-AW, by contrast, performs worse on 20 test problems than the no-weighted version (The total comparison results are 7 wins, 8 ties, and 20 losses). The results also confirms the viewpoint in [34]. Regarding the reason for the results, we believe that this is not because weighted optimization is useless or it wastes computational resources, but that adaptive weighting does not correctly apply weighted optimization.

Table 3 The performance of each version on CEC’2013 benchmark suite with 1000 decision variables

Table 4 The performance of SaNSDE-LSWOA and SaNSDE on CEC’2008 benchmark suite with 1000 and 5000 decision variables

The second set of comparisons are shown in the first and third columns, fourth and fifth columns of Tables 2 and 3, respectively. The LSWOA-enhanced versions of DECC-G and SaNSDE will be compared with their no-weighting versions. Regarding the decomposition algorithm, DECC-G-LSWOA performs better than DECC-G-NW in 20 out of 35 problems. The two algorithms get ties in nine problems, and DECC-G-LSWOA loses on six problems. Meanwhile, SaNSDE-LSWOA obtains a 14/2/4 comparison result on CEC’2010 and a 6/5/4 result on CEC’2013. LSWOA works excellently on CEC’2010 and still has an acceptable performance on CEC’2013. In general, compared with the algorithm without LSWOA, the performance of LSWOA versions gets enhanced. Our experiment fully proves that weighted optimization is effective if it is applied appropriately. LSWOA and adaptive weighting strategy both utilize weighted optimization method, but adaptive weighting does not fully use the information generated by weighted optimization, and it is arbitrary to choose candidate solutions. Furthermore, it does not apply weighted optimization at the right stage.

According to the experimental results, we can analyze the application characteristic of weighted optimization. Specifically, for fully separable problems $f_1$–$f_3$ of the two suites, DECC-G-LSWOA performs poorly on 5 problems. We can speculate the reason for its poor performance. DECC-G applies random grouping, so fully separable problems can be divided into perfect subproblems even if grouped randomly. Accordingly, the CC algorithm is so efficient that weighted optimization’s performance is far inferior. However, real-world problems are often non-separable. LSWOA has its advantages on these non-separable problems instead. For partially separable problems $f_4$–$f_{18}$ in CEC’2010 and $f_4$–$f_{11}$ in CEC’2013, DECC-G-LSWOA obtains 15 wins, 7 ties, and 1 lose. The separability of these problems decreases from $f_4$ to $f_{18}$. DECC with random grouping can hardly optimize these functions to the ideal level. The addition of LSWOA improves the performance of the algorithms to some extent. For fully nonseparable problems $f_{19}$ and $f_{20}$ in CEC’2010 and $f_{12}$–$f_{15}$ in CEC’2013, DECC-G-LSWOA plays better on 4 of 6 problems and shows invalid on 2 problems. Considering these problems that have not been improved, fully separable problems and multi-modal function are dominating. Especially for the Rosenbrock’s function and its variants ($f_8$, $f_{13}$, $f_{18}$, and $f_{20}$ in CEC’2010 and $f_{12}$ in CEC’2013), LSWOA scarcely improves the performance of the applied algorithms.

In addition, SaNSDE is not a decomposition-based algorithm, so there is no need to consider the separability of problems. What we should focus on is the problem difficulty. Among those problems in which SaNSDE-LSWOA performs poorly, Rastrigin function and Ackley function are in the majority (12 of 15). The two types of problems have a strong multi-modal property, which leads to bad performance for many algorithms used on them. In terms of our proposed LSWOA, it aims to reduce the dimension of the problem at the cost of precision. Therefore, when facing these multi-modal problems, weighted optimization will also be easily disturbed by these large numbers of local optima.

To sum up, the LSWOA-enhanced version performs better than the adaptive-weighting-enhanced version and no-weighting version. As long as weighted optimization is used reasonably, such as our proposed LSWOA, it will effectively improve the comprehensive performance of the applied algorithm. According to the studies of the experiment, we can generalize the positive impact of LSWOA. LSWOA ensures a promising performance for the applied algorithm even if facing complex problems. For instance, LSWOA helps to tackle fully nonseparable problems that CCEAs show lousy performance.

Scalability test

In this subsection, we investigate whether weighted optimization can work on higher dimensional problems. To investigate the scalability of LSWOA, we compared the performance of SaNSDE-LSWOA and SaNSDE for 1000-D and 5000-D problems. SaNEDE is parameter-free. It is not affected by the precision of variable grouping as a decomposition method, so it is more suitable for testing the performance of LSWOA. The benchmark we used is the CEC’2008 test suite as it can expand dimensions up to 5000-D. According to the technical report of the benchmark, the maximum number of FEs is set to 5000*D. Another parameter is set as previous.

The results are provided in Table 4. When the dimension is 1000, SaNSDE-LSWOA performs better than SaNSDE on 5 problems while worse on 2 problems. On $f_1$ and $f_3$, the application of LSWOA has a great effect. When the scale comes to 5000-D, the advantage of LSWOA is amplified. There are 6 problems that SaNSDE-LSWOA has better performance, and only on $f_6$ LSWOA lost its effectiveness. SaNSDE is largely enhanced by LSWOA on problems $f_1$, $f_3$, and $f_5$. The only counterexample is $f_7$, but there is no significant degradation.

The experiment shows that LSWOA can significantly improve the performance of LSGO algorithms in higher dimensions, i.e., the scalability of LSWOA is excellent. The reason why it is suitable for higher dimensions is its dimension reduction property, which could evolve the solution and the population with less computational resources.

Effect of grouping strategies

In this subsection, we will investigate how much the grouping strategy influences the performance of weighted optimization. The comparison objects are weighted optimization with random grouping and ideal grouping. According to Proposition 2, the transformed problem generated with ideal grouping is fully separable. This is the main reason for the effect. Also, the influence of grouping on weighted optimization has experimented on multi-objective problems [16]. Their results show that no grouping strategy has significant advantages on LSMOP.

To show the difference in performance more clearly, we compare the performance of weighted optimization directly. The test problems we used are all partially separable problems. They are divided into two parts, which are $f_{14}$ to $f_{18}$ of CEC’2010 benchmark suite and $f_8$ to $f_{11}$ of CEC’2013 benchmark suite. The problems in the first part are with a uniform 20(groups) * 50(D) separability, and the problems in the latter part are uneven separability with different group sizes, including 25, 50, and 100. In each test problem, five fixed candidate solutions are used for problem transformation. Using random grouping and ideal grouping, each candidate solution generates ten transformed problems. Thus, there are a total of 45 transformed problems for testing the effect of grouping strategy. Each transformed problem is also optimized 25 times independently for the significance test.

The results are shown in Table 5. In this table, the initial fitness values of the 45 candidate solutions are recorded. By contrasting the fitness of the solutions before and after the weighted optimization, we obtain the fitness improvement led by the weighted optimization. A larger improvement indicates a lower difficulty of the transformed problem, which means the grouping strategy is more effective. In this table, the transformed problem is denoted as TP. Random grouping and ideal grouping are denoted as RG and IG.

Table 5 The performance of weighted optimization with different grouping strategy on various transformed problems

According to Table 5, the performance varies when applying different grouping strategies. On the CEC’2010 benchmark, the weighted optimization with RG performs better than that with IG on 14 transformed problems, while on the other 11 transformed problems, the RG version has advantages. So there is not much difference between these two versions of optimizations on the CEC’2010 benchmark problems. Nevertheless, out of a total of 20 transformed problems in CEC’2013, the weighted optimization with RG performed better on 16. Ideal grouping is not suitable for the weighted optimization on the CEC’2010 benchmark problems.

The different sizes of non-separable groups may cause this difference. In theory, the transformed problem generated with ideal grouping is separable, which results in a lower difficulty than the non-separable transformed problem. However, the weighted optimization with IG does not work better. The reason may be that in these small-scale transformed problems, the impact of separability is not significant. The results in our experiment are consistent with that on LSMOP.

On the contrary, it has a poor performance on the transformed problems in the CEC’2013 benchmark. In fact, because of the uneven separability of $f_8$ to $f_{11}$ in the CEC’2013 benchmark, each weight will be associated with a different number of decision variables. That leads to an unbalanced transformed problem that is hard to solve.

In view of this experiment, the random grouping would be more suitable for weighted optimization. On the one hand, it is not easy to get accurate variable groups. On the other hand, the grouping method based on precise variable analysis cannot effectively improve the performance of weighted optimization.

Effect of optimization stages

In this subsection, we take a closer look at the effect and contributions of the population initialization stage (the first stage) and the integrated optimization stage (the second stage).

An experiment is designed to show the effect of the two stages on CEC’2013 in Table 6. Test problems are classified into three categories, that is, C1: fully separable problems, C2: partially separable problems, and C3 non-separable problems. Two variants, the version only adopting the first stage (DECCG-LSWOA_Ini) and only adopting the second stage (DECCG-LSWOA_Integ), are tested to compare with standard DECCG-LSWOA, which has both two stages. The comparison is about the times of wins, ties, and losses (by significance tests) from the perspective of standard LSWOA.

The results show that the standard version is more effective than the two variants adopting a single strategy, which indicates that each stage of LSWOA is helpful to the algorithm’s overall performance. In other words, every stage is indispensable. In addition, the integrated optimization stage seems to contribute more to the performance because the standard version beats DECCG-LSWOA_Integ fewer times than DECCG-LSWOA_Ini. The convergence characteristics are also shown in Fig. 5 on six problems of CEC’2013 along with two compared algorithms (DECCG-AW and DECCG-NW). It can be seen that the two variants are slightly worse than the standard algorithm, but they are still better than algorithms with adaptive weighting (AW) and no-weighting (NW). To summarize, When weighted optimization is applied to both population initialization and optimization, the algorithm’s performance can be improved to some extent.

Table 6 Comparison with two variants on CEC’2013

Fig. 5

The convergence characteristics of five algorithms on six problems of CEC’2013. The data in the figure are averaged after 25 independent tests

Parameter sensitivity analysis

In this section, we will examine the effect of different parameters q. The parameter q involves the number of selected individuals of the population in the population initialization stage, which indicates the degree of sampling the population. If the parameter q is set too large, more transformed problems will be created, which will result in a high cost of computational resources. By contrast, a small q can lead to low-quality weight vectors, which are not so beneficial to the population.

An experiment has been done to test the impact of q, which is shown in Table 7. The standard setting of q is 5, which is about the 10% of the population size. Now, the performance with a standard q will be compared to that with different settings, which are q = 2, q = 10, q = 18, and q = 25. Similar to the previous experiment, we also count the wins, ties, and losses between the standard and other settings. The test suite is CEC’2013 benchmark, which is classified into fully separable (C1: $f_1$–$f_3$), partially separable (C2: $f_4$–$f_{11}$), and non-separable (C3: $f_{12}$–$f_{15}$) here.

According to the experiment results, the standard setting q = 5 shows a better performance than q = 10, q = 18, and q = 25. Compared with q = 2, the standard setting does not seem to have some advantages. To sum up, it is better to set the parameter q to be relatively small as computational resources will not be over-expended. The reasonable range of parameter q would be 4–20% of the population size. Therefore, setting the parameter q to 5 in our standard version is proper.

Table 7 Comparison results of the parameter q with standard setting (q* = 5) and other settings on CEC’2013

Conclusion

In this paper, we focus on weighted optimization in LSGO. To begin with, we make further theoretical analyses on the weight optimization based on previous studies. We investigate the search behavior of weighted optimization and obtain an equivalent form of transformed problem, which can deduce a proposition about the relationship between the original problem and the transformed problem. According to our theoretical investigation, three factors (the candidate solution, the variable grouping, and the transformation function) that affect problem transformation are figured out.

Then, based on our analysis, we make some modifications on previous weighted optimization approaches and propose an improved approach to combine the weighted optimization with LSGO algorithms, which is termed LSWOA. LSWOA applies the weighted optimization in population initialization and the integrated optimization stage. By optimizing the low-dimensional transformed problems, the optimal weights are shared with the original population. Therefore, the population can be improved quickly to accelerate the overall convergence. The improvements we make can be summarized in three aspects. First, we design a weight-sharing strategy with the construction of reference candidate solutions. By weighing specific reference solutions and sharing these optimal weights, the population gets evolved. Second, we design a candidate solution inheriting strategy to retain the candidate solution, which improves the performance of weighted optimization. Finally, the computational resources are allocated to the weighted optimization and the original problem optimization in a better way, which helps improve the efficiency of the algorithm and achieve the balance of convergence and diversity.

At last, we conduct a series of experiments to verify the effectiveness of LSWOA. The performance of two enhanced algorithms, DECC-G-LSWOA and SaNSDE-LSWOA, are tested on CEC’2010 and CEC’2013 benchmark suites. Compared with the original algorithms and the adaptive-weighting-enhanced versions, the LSWOA-enhanced algorithms perform better on most problems, and they are more promising when tackling complex problems, e.g., non-separable problems and the larger scale problems.

In future work, we target to further strengthen the search ability of weighted optimization and find a better way to combine the weighted optimization and the original optimization. The promising works include applying self-adaptive grouping methods to tune the grouping size and designing novel transformation function to find a more potential search subspace.