Nonlinear pentagonal intuitionistic fuzzy number and its application in EPQ model under learning and forgetting

Abstract

In this current era, the concept of nonlinearity plays an important and essential role in intuitionistic fuzzy arena. This article portrays an impression of different representation of nonlinear pentagonal intuitionistic fuzzy number (PIFN) and its classification under different scenarios. A new de-intuitification technique of non-linear PIFN is addressed in this article along with its various graphical representations. Additionally, in this paper, we have observed this by applying it in an economic production quantity model where the production is not perfect and defective items are produced which are reworked. The model is considered under learning and forgetting, where learning is considered as linear, nonlinear PIFN and crisps arena. It is observed from the numerical study that high learning effects in rework lead to decrease in production of defective item, which, besides an economic advantage, may have a positive effect on the environment. Even though forgetting has an adverse effect, the average total cost is much less than that of the basic model which ignores worker learning and forgetting. Finally, comparative and sensitivity analysis result shows the utility of this noble work.

Introduction

The theory of impreciseness plays a leading role in various fields of modern science and technology due to natural presence of ambiguity, uncertainty in human minds. In the recent past, researchers from distinctive domains like environment and ecology, science and technology, financial mathematics, social media, medical experimental etc. have integrated the impression of vagueness in their relevant domains. In the year 1965, Professor Zadeh [1] put forth an incredible observation regarding the fuzzy set supposition. Few years later, in the year 1972, Chang and Zadeh [2] gave sketch the formative outline of fuzzy development and since then, quite a lot of works have been recognized in this research arena [3,4,5,6] along with the countless progression and upgrading postulations of fuzzy logic. Notably, fuzzy set doesn’t mull over the degree of uncertainty, which indicates the degree of non-belongingness. In the year 1986, Professor Atanassov [7] extended and expanded the concept of fuzzy set into intuitionistic fuzzy set (IFS) by incorporating the concept of both membership and non-membership functions of a fuzzy number. Subsequently, as an annex of intuitionistic fuzzy set, Zhang et al. [8] exhibited the concept of interval-valued intuitionistic fuzzy number and discussed its relevance in details. Later on, researchers developed triangular [9], trapezoidal [10] and pentagonal [11] intuitionistic fuzzy numbers to capture, handle and explore various complex features of many real life problems in a nice and meaningful way. Also, researchers developed the application of arithmetic operation [12], assignment difficulty [13], similarity measure and score function [14] in interval-valued intuitionistic fuzzy set. Moreover, multiple attribute decision making problems have been solved in intuitionistic sphere by using constructive operators like aggregation operator [15] and exponential operator [16]. Also, multi criteria decision making (MCDM) methods are developed on the ground of similarity measures [17, 18], inclusion measure [19], entropy measure [20, 21], cross-entropy measure [22] and distance measures [23]. Researchers applied the intuitionistic fuzzy number in various field of inventory management; for example Chakraborty et al. [24] applied intuitionistic fuzzy optimization technique for Pareto optimal solution of manufacturing inventory models with shortages, De and Sana [25] applied it into multi-period production based model. Furthermore, De et al. [26] introduced time sensitivity backlogging EOQ model, Banerjee and Roy [27] manifested multi-objective stochastic inventory model, Das et al. [28] focused time dependent backlogging EOQ model, Garai et al. [29] proposed generalized intuitionistic fuzzy inventory model, De and Sana [30] ignited intuitionistic fuzzy based backlogging EOQ model, Ali et al. [31] proposed multi objective fractional inventory model and Kaur and Deb [32] established an intuitionistic approach to an inventory model without shortages.

Classical EPQ model (Silver et al. [33]) assumes that the manufacturing process is failure free and all the items produced are of perfect quality. However, in real production environment, it is observed that the defective items are produced due to imperfect production processes. So the defective items must be rejected, repaired and reworked, and the corresponding substantial costs are incurred in the integrated total costing of the inventory system. Recently, numerous researchers are working on EPQ/EOQ models with imperfect quality items. Investment in inventory is essential to upgrade the machinery which will reduce the production of defective items. Dey and Giri [34] investigated a model with investment to reduce the production of defective items. Giri and Glock [35] has addressed on closed loop supply chain model with learning and forgetting during manufacturing and remanufacturing of the returned items. Jaber and Bonney [36] studied the effect of learning and forgetting on the EPQ model with both finite and infinite horizons. Jaber and Guiffrida [37, 38] integrated process quality into the learning curve when an imperfect process produces defects that need to be reworked. Glock and Jaber [39] had discussed multi-stage production-inventory model with learning and forgetting effects, rework and scrap of twice defective items. Several other interesting works [40,41,42,43,44,45,46,47, 54,55,56,57,58,59,60] had been published in learning based inventory model. Here, an attempt is made to discuss an EPQ model in a more realistic scenario incorporating few new features like system learning and forgetting as nonlinear PIFN and effect of new investment to improve the production quality and reduce the number of defective items.

Motivation and novelties of the work

From the literature survey, we noticed that the researchers had mainly focused on linear intuitionistic fuzzy number; they did not consider the non-linearity in case of intuitionistic fuzzy number. But we need non-linear membership functions in many cases especially if it contains any geometrical convexity or concavity. In reality, there are several cases, we need to consider non-linear intuitionistic fuzzy number to capture and handle the underlying uncertainties in a better way. In this research article, we have introduced a generalized nonlinear PIFN to give more flexibility on decision maker’s choice. We have introduced nonlinear pentagonal intuitionistic fuzzy number with symmetric and asymmetric representations and it has been successfully applied to an EPQ model where it is assumed that production process follows constant demand and imperfect items undergoes for rework. The paper incorporates the human behavior of learning due to repeated practice and experience along with forgetting due to the gap in the production from one cycle to the next cycle. Here, the workers experience due to learning is considered as symmetric nonlinear PIFN. The details of consideration of uncertain parameter are shown in the Flow Diagram 1. Also in practice, the total production time and produce quantity can’t be treated as a constant. Moreover, the numbers of defective items reduce when there is new investment on the machinery items involved in the production process. Thus, we have accounted all these factors in our proposed EPQ model to optimize the total cost (Fig. 1).

Fig. 1

Flow diagram of consideration non-linear membership function of uncertain parameter

Mathematical preliminaries

Definition 2.1

Intuitionistic fuzzy set: [7] Let a set X be fixed. An IFS $\tilde{A}^{i}$ in X is an object having the form $\tilde{A}^{i} = \left\{ {\left\langle {x,\mu_{{\tilde{A}^{i} }} \left( x \right), \vartheta_{{\tilde{A}^{i} }} \left( x \right)} \right\rangle :x \in X} \right\}$, where the $\mu_{{\tilde{A}^{i} }} \left( x \right):X \to \left[ {0,1} \right]$ and $\vartheta_{{\tilde{A}^{i} }} \left( x \right):X \to \left[ {0,1} \right]$ define the degree of membership and degree of non-membership respectively, of the element $x \in X$ to the set $\tilde{A}^{i}$, which is a subset of X, for every element of $x \in X$, $0 \le \mu_{{\tilde{A}^{i} }} \left( x \right) + \vartheta_{{\tilde{A}^{i} }} \left( x \right) \le 1$.

Definition 2.2

Pentagonal fuzzy number: [3] A pentagonal fuzzy number $\tilde{A} = \left( {a_{1} ,a_{2} ,a_{3} ,a_{4} ,a_{5} ;\mu_{{\tilde{A}}} } \right)$ should satisfy the following condition.

• 1. $\mu_{{\tilde{A}}} \left( x \right)$ is a continuous function in the interval [0,1].

• 2. $\mu_{{\tilde{A}}} \left( x \right)$ is strictly increasing and continuous function on $\left[ {a_{1} ,a_{2} } \right]$ and $\left[ {a_{2} ,a_{3} } \right]$.

• 3. $\mu_{{\tilde{A}}} \left( x \right)$ is strictly decreasing and continuous function on $\left[ {a_{3} ,a_{4} } \right]$ and $\left[ {a_{4} ,a_{5} } \right]$.

Definition 2.3

Pentagonal Intuitionistic number: [11] A linear Pentagonal Intuitionistic fuzzy number $\left( {\widetilde{{N_{Pen} }}} \right)$ is defined as $\widetilde{{N_{PenIn} }} = \left[ {\left( {s_{1} ,s_{2} ,s_{3} ,s_{4} ,s_{5} |t} \right);\pi } \right],\left[ {\left( {h_{1} ,h_{2} ,h_{3} ,h_{4} ,h_{5} |c} \right);\sigma } \right]$, where $\pi ,\sigma \in \left[ {0,1} \right]$. The accuracy membership function $\left( {\tau_{{\tilde{S}}} } \right):{\mathbb{R}} \to \left[ {0,\pi } \right]$ and the falsity membership function $\left( {\varepsilon_{{\tilde{S}}} } \right):{\mathbb{R}} \to \left[ {\sigma ,1} \right]$ are defined by:

$$ \pi _{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {t\frac{{x - s_{1} }}{{s_{2} - s_{1} }}} \hfill & {\quad {\text{if}}\;s_{1} \le x \le s_{2} } \hfill \\ {1 - \left( {1 - t} \right)\frac{{x - s_{2} }}{{s_{3} - s_{2} }}} \hfill & {\quad {\text{if}}\;s_{2} \le x < s_{3} } \hfill \\ 1 \hfill & {\quad {\text{if}}\;x = s_{3} } \hfill \\ {1 - \left( {1 - t} \right)\frac{{s_{4} - x}}{{s_{4} - s_{3} }}} \hfill & {\quad {\text{if}}\;s_{3} < x \le s_{4} } \hfill \\ {t\frac{{s_{5} - x}}{{s_{5} - s_{4} }}} \hfill & {\quad {\text{if}}\;s_{4} \le x \le s_{5} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;x > s_{5} } \hfill \\ \end{array} ,\;\;\sigma _{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {1 - \left( {1 - c} \right)\left( {\frac{{x - h_{1} }}{{h_{2} - h_{1} }}} \right)^{{n_{1} }} } \hfill & {\quad {\text{if}}\;h_{1} \le x \le h_{2} } \hfill \\ {c\left( {\frac{{h_{3} - x}}{{h_{3} - h_{2} }}} \right)^{{n_{2} }} } \hfill & {\quad {\text{if}}\;h_{2} \le x < h_{3} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;x = ~h_{3} } \hfill \\ {c\left( {\frac{{h_{4} - x}}{{h_{4} - h_{3} }}} \right)^{{m_{1} }} } \hfill & {\quad {\text{if}}\;h_{3} < x \le h_{4} } \hfill \\ {1 - (1 - c)\left( {\frac{{h_{5} - x}}{{h_{5} - h_{4} }}} \right)^{{m_{2} }} } \hfill & {\quad {\text{if}}\;h_{4} \le x \le h_{5} } \hfill \\ 1 \hfill & {\quad {\text{if}}\;x > h_{5} .} \hfill \\ \end{array} } \right.} \right. $$

Nonlinear Pentagonal Intuitionistic fuzzy number with asymmetry

Definition 3.1:

A non-linear Pentagonal Intuitionistic fuzzy number (NLPIFN) with asymmetry can be written as, $\widetilde{ A}_{{{\text{NLPEN}}}} = {[}\{ ( g_{1} ,g_{2} ,g_{3} ,g_{4} ,g_{5} ;s,t )_{{\left( {n_{1} ,n_{2} ;m_{1} ,m_{2} } \right)}} ;\pi_{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right){\text{\} }},\{ \left( {h_{1} ,h_{2} ,h_{3} ,h_{4} ,h_{5} ;c,d} \right)_{{\left( {n_{1} ,n_{2} ;m_{1} ,m_{2} } \right)}} ;\sigma_{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right)\} ]$ where membership and non-membership function can be explained as,

$$ \pi _{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {s\left( {\frac{{x - g_{1} }}{{g_{2} - g_{1} }}} \right)^{{n_{1} }} } \hfill & {\quad {\text{if}}\;g_{1} \le x \le g_{2} } \hfill \\ {1 - \left( {1 - s} \right)\left( {\frac{{x - g_{2} }}{{g_{3} - g_{2} }}} \right)^{{n_{2} }} } \hfill & {\quad {\text{if}}\;g_{2} \le x < g_{3} } \hfill \\ 1 \hfill & {\quad {\text{if}}\;x = ~g_{3} } \hfill \\ {1 - \left( {1 - t} \right)\left( {\frac{{g_{4} - x}}{{g_{4} - g_{3} }}} \right)^{{m_{1} }} } \hfill & {\quad {\text{if}}\;g_{3} < x \le g_{4} } \hfill \\ {t\left( {\frac{{g_{5} - x}}{{g_{5} - g_{4} }}} \right)^{{m_{2} }} } \hfill & {\quad {\text{if}}\;g_{4} \le x \le g_{5} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;x > g_{5} } \hfill \\ \end{array} ,\;\;\sigma _{{\tilde{A}_{{{\text{NLPEN}}}} }} \left( x \right) = \left\{ {\begin{array}{*{20}l} {1 - \left( {1 - c} \right)\left( {\frac{{x - h_{1} }}{{h_{2} - h_{1} }}} \right)^{{n_{1} }} } \hfill & {\quad {\text{if}}\;h_{1} \le x \le h_{2} } \hfill \\ {c\left( {\frac{{h_{3} - x}}{{h_{3} - h_{2} }}} \right)^{{n_{2} }} } \hfill & {\quad {\text{if}}\;h_{2} \le x < h_{3} } \hfill \\ 0 \hfill & {\quad {\text{if}}\;x = ~h_{3} } \hfill \\ {d\left( {\frac{{h_{4} - x}}{{h_{4} - h_{3} }}} \right)^{{m_{1} }} } \hfill & {\quad {\text{if}}\;h_{3} < x \le h_{4} } \hfill \\ {1 - (1 - d)\left( {\frac{{h_{5} - x}}{{h_{5} - h_{4} }}} \right)^{{m_{2} }} } \hfill & {\quad {\text{if}}\;h_{4} \le x \le h_{5} } \hfill \\ 1 \hfill & {\quad {\text{if}}\;x > h_{5} .} \hfill \\ \end{array} } \right.} \right. $$

Definition 3.2

${\varvec{\alpha}},{\varvec{\beta}}$-cut form of NLPIFNAS: The $\alpha ,\beta$-cut form of NLPIFNAS is classified as follows

$$ \begin{aligned} A_{\alpha ,\beta } & = \left\{ {x \in X|\pi_{{\tilde{A}_{NLPEN} }} \left( x \right) \ge \alpha , \sigma_{{\tilde{A}_{NLPEN} }} \left( x \right) \ge \beta } \right\} \\ & \quad = \left\{ {\begin{array}{*{20}l} {A_{1L} \left( \alpha \right) = g_{1} + \left( {\frac{\alpha }{s}} \right)^{{1/n_{1} }} \left( {g_{2} - g_{1} } \right)} \hfill & {\quad {\text{for}}\;\alpha \in \left[ {0,s} \right]} \hfill \\ {A_{2L} \left( \alpha \right) = g_{2} + \left( {\frac{1 - \alpha }{{1 - s}}} \right)^{{1/n_{2} }} \left( {g_{3} - g_{2} } \right)} \hfill & {\quad {\text{for}}\;\alpha \in \left[ {s,1} \right]} \hfill \\ {A_{2R} \left( \alpha \right) = g_{4} - \left( {\frac{1 - \alpha }{{1 - t}}} \right)^{{1/m_{1} }} \left( {g_{4} - g_{3} } \right)} \hfill & {\quad {\text{for}}\;\alpha \in \left[ {t,1} \right]} \hfill \\ {A_{1R} \left( \alpha \right) = g_{5} - \left( {\frac{\alpha }{t}} \right)^{{1/m_{2} }} \left( {g_{5} - g_{4} } \right)} \hfill & {\quad {\text{for}}\;\alpha \in \left[ {0,t} \right]} \hfill \\ \end{array} } \right.,\;\;\begin{array}{*{20}l} {A_{1L} \left( \beta \right) = h_{1} + \left( {\frac{1 - \beta }{{1 - c}}} \right)^{{1/n_{1} }} \left( {h_{2} - h_{1} } \right)} \hfill & {\quad {\text{for}}\;\beta \in \left[ {0,c} \right]} \hfill \\ {A_{2L} \left( \beta \right) = h_{2} + \left( {\frac{\beta }{c}} \right)^{{1/n_{2} }} \left( {h_{3} - h_{2} } \right)} \hfill & {\quad {\text{for}}\;\beta \in \left[ {c,1} \right]} \hfill \\ {A_{2R} \left( \beta \right) = h_{4} - \left( {\frac{\beta }{d}} \right)^{{1/m_{1} }} \left( {h_{4} - h_{3} } \right)} \hfill & {\quad {\text{for}}\;\beta \in \left[ {d,1} \right]} \hfill \\ {A_{1R} \left( \beta \right) = h_{5} - \left( {\frac{1 - \beta }{{1 - d}}} \right)^{{1/m_{2} }} \left( {h_{5} - h_{4} } \right)} \hfill & {\quad {\text{for}}\;\beta \in \left[ {0,d} \right]} \hfill \\ \end{array} , \\ \end{aligned} $$

where, $A_{1L} \left( \alpha \right)$, $A_{2L} \left( \alpha \right)$ is the increasing function based on $\alpha ,\beta$ and $A_{2R} \left( \alpha \right)$, $A_{1R} \left( \alpha \right)$ is the decreasing function corresponding to $\alpha ,\beta$.

Note: 3.1: If $g_{3} = h_{3} , n_{1} = n_{2} = m_{1} = m_{2} = 1$, as a result of non-linear Pentagonal Intuitionistic fuzzy number is converted into linear asymmetrical Pentagonal Intuitionistic fuzzy number.

Note: 3.2: If $g_{3} = h_{3} , c = d,s = t,$ then non-linear Pentagonal Intuitionistic fuzzy number is converted into non-linear partial symmetrical Pentagonal Intuitionistic fuzzy number.

Note: 3.3: If $g_{3} = h_{3} , c = d = s = t,$ then non-linear Pentagonal Intuitionistic fuzzy number is converted into non-linear symmetrical Pentagonal Intuitionistic fuzzy number.

Note: 3.4: If $g_{3} = h_{3} , c = d,s = t, n_{1} = n_{2} = m_{1} = m_{2} = 1$ then non-linear Pentagonal Intuitionistic fuzzy number is converted into linear Pentagonal Intuitionistic partial symmetrical fuzzy number.

Note: 3.5: If $g_{3} = h_{3} , c = d = s = t, n_{1} = n_{2} = m_{1} = m_{2} = 1$ then non-linear Pentagonal Intuitionistic fuzzy number is converted into linear symmetrical Pentagonal Intuitionistic fuzzy number.

The geometrical representation of different form of pentagonal intuitionistic fuzzy number is shown as follows (Figs. 2, 3, 4, 5, 6, 7).

Fig. 2

Non-linear pentagonal intuitionistic fuzzy number having asymmetry

Fig. 3

Linear pentagonal intuitionistic fuzzy number having asymmetry

Fig. 4

Non-linear pentagonal intuitionistic fuzzy number having partial symmetry

Fig. 5

Linear pentagonal intuitionistic fuzzy number having partial symmetry

Fig. 6

Non-linear Pentagonal Intuitionistic fuzzy number having symmetry

Fig. 7

Linear Pentagonal Intuitionistic fuzzy number having symmetry

De-intuitification of non-linear symmetric pentagonal intuitionistic fuzzy number

Defuzzification methods

Defuzzification is a process of where fuzzy numbers are transformed in crisp number. In other words, defuzzification is a technique to assign appropriate crisp value to a fuzzy number. There are several popular and standard methods of defuzzification which includes Centre of Area method [48], Bisector of Area method [53], Largest of Maxima method [50], Smallest of Maxima Method [52], Mean of Maxima method [51], etc. Defuzzification process is important for the following two major reasons:

• 1. Anyone can understand the relationship between fuzzy number and the crisp number.

• 2. Finding the crispified value of the fuzzy solutions.

De-intuitification of non-linear symmetric pentagonal intuitionistic fuzzy number based on alpha–beta (α, β)-cut method

The left and right α-cut of a non-linear fuzzy number are,

$$ \begin{aligned} {\varvec{L}}^{ - 1} \left( {\varvec{\alpha}} \right) & = g_{1} + \left( {\frac{\alpha }{s}} \right)^{{p_{1} }} \left( {g_{2} - g_{1} } \right)\quad {\text{for}}\;\alpha \in \left[ {0,s} \right],\;\;{\varvec{R}}^{ - 1} \left( {\varvec{\alpha}} \right) = g_{4} - \left( {\frac{1 - \alpha }{{1 - s}}} \right)^{{q_{1} }} \left( {g_{4} - g_{3} } \right)\;\;{\text{for}}\;\alpha \in \left[ {s,1} \right] \\ {\varvec{L}}^{ - 1} \left( {\varvec{\alpha}} \right) & = g_{2} + \left( {\frac{1 - \alpha }{{1 - s}}} \right)^{{p_{2} }} \left( {g_{3} - g_{2} } \right)\quad {\text{for}}\;\alpha \in \left[ {s,1} \right],\;\;{\varvec{R}}^{ - 1} \left( {\varvec{\alpha}} \right) = g_{5} - \left( {\frac{\alpha }{s}} \right)^{{q_{2} }} \left( {g_{5} - g_{4} } \right)\;\;{\text{for}}\;\alpha \in \left[ {0,s} \right] \\ {\varvec{L}}^{ - 1} \left( {\varvec{\beta}} \right) & = h_{1} + \left( {\frac{1 - \beta }{{1 - c}}} \right)^{{p_{1} }} \left( {h_{2} - h_{1} } \right)\quad {\text{for}}\;\alpha \in \left[ {0,c} \right],\;\;{\varvec{R}}^{ - 1} \left( {\varvec{\beta}} \right) = h_{4} - \left( {\frac{\beta }{c}} \right)^{{q_{1} }} \left( {h_{4} - h_{3} } \right)\;\;{\text{for}}\;\alpha \in \left[ {c,1} \right] \\ {\varvec{L}}^{ - 1} \left( {\varvec{\beta}} \right) & = h_{2} + \left( {\frac{\beta }{c}} \right)^{{p_{2} }} \left( {h_{3} - h_{2} } \right)\quad {\text{for}}\;\alpha \in \left[ {c,1} \right],\;\;{\varvec{R}}^{ - 1} \left( {\varvec{\beta}} \right) = h_{5} - \left( {\frac{1 - \beta }{{1 - c}}} \right)^{{q_{2} }} \left( {h_{5} - h_{4} } \right)\;\;{\text{for}}\;\alpha \in \left[ {0,c} \right]. \\ \end{aligned} $$

We proposed mean of interval method for de-intuitification as follows:

$$\begin{aligned} \check{A} & = \frac{{\mathop \int \nolimits_{\alpha = 0}^{1} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\alpha}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\alpha}} \right)} \right){\text{d}}\alpha }}{2} + \mathop \int \nolimits_{\alpha = 0}^{1} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\beta}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\beta}} \right)} \right){\text{d}}\beta }}{2}}}{2} \\ & = \frac{{\mathop \int \nolimits_{\alpha = 0}^{s} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\alpha}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\alpha}} \right)} \right){\text{d}}\alpha }}{2} + \mathop \int \nolimits_{\alpha = s}^{1} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\alpha}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\alpha}} \right)} \right){\text{d}}\alpha }}{2} + \mathop \int \nolimits_{\beta = 0}^{c} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\beta}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\beta}} \right)} \right){\text{d}}\beta }}{2} + \mathop \int \nolimits_{\beta = c}^{1} \frac{{\left( {{\varvec{L}}^{ - 1} \left( {\varvec{\beta}} \right) + {\varvec{R}}^{ - 1} \left( {\varvec{\beta}} \right)} \right){\text{d}}\beta }}{2}}}{2} \\ & = \left\{ {\mathop \int \limits_{\alpha = 0}^{s} \frac{{\left( {\left\{ {g_{1} + \left( {\frac{\alpha }{s}} \right)^{{p_{1} }} \left( {g_{2} - g_{1} } \right)} \right\} + \left\{\vphantom{\left. { + \mathop \int \limits_{\beta = c}^{1} \frac{{\left( {\left\{ {h_{2} + \left( {\frac{\beta }{c}} \right)^{{p_{2} }} \left( {h_{3} - h_{2} } \right)} \right\} + \left\{ {h_{4} - \left( {\frac{\beta }{c}} \right)^{{q_{1} }} \left( {h_{4} - h_{3} } \right)} \right\}} \right){\text{d}}\beta }}{2}} \right\}} {g_{5} - \left( {\frac{\alpha }{s}} \right)^{{q_{2} }} \left( {g_{5} - g_{4} } \right)} \right\}} \right){\text{d}}\alpha }}{2}}+ \mathop \int \limits_{\alpha = s}^{1} \frac{{\left( {\left\{ {g_{2} + \left( {\frac{1 - \alpha }{{1 - s}}} \right)^{{p_{2} }} \left( {g_{3} - g_{2} } \right)} \right\} + \left\{ {g_{4} - \left( {\frac{1 - \alpha }{{1 - s}}} \right)^{{q_{1} }} \left( {g_{4} - g_{3} } \right)} \right\}} \right){\text{d}}\alpha }}{2} \right.\\ & \quad \left.+ \mathop \int \limits_{\beta = 0}^{c} \frac{{\left( {\left\{ {h_{1} + \left( {\frac{1 - \beta }{{1 - c}}} \right)^{{p_{1} }} \left( {h_{2} - h_{1} } \right)} \right\} + \left\{ {h_{5} - \left( {\frac{1 - \beta }{{1 - c}}} \right)^{{q_{2} }} \left( {h_{5} - h_{4} } \right)} \right\}} \right){\text{d}}\beta }}{2} { + \mathop \int \limits_{\beta = c}^{1} \frac{{\left( {\left\{ {h_{2} + \left( {\frac{\beta }{c}} \right)^{{p_{2} }} \left( {h_{3} - h_{2} } \right)} \right\} + \left\{ {h_{4} - \left( {\frac{\beta }{c}} \right)^{{q_{1} }} \left( {h_{4} - h_{3} } \right)} \right\}} \right){\text{d}}\beta }}{2}} \right\}/2 \\ & = \left\{\vphantom{\left. { + \frac{{h_{2} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{{p_{2} + 1}} } \right\}\left( {h_{3} - h_{2} } \right)}}{{(p_{2} + 1)\left( c \right)^{{p_{2} }} }} + h_{4} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{{q_{1} + 1}} } \right\}\left( {h_{4} - h_{3} } \right)}}{{(q_{1} + 1)\left( c \right)^{{q_{1} }} }}}}{2}} \right\}} {\frac{{g_{1} s + \frac{{s\left( {g_{2} - g_{1} } \right)}}{{p_{1} + 1}} + g_{5} s - \frac{{s\left( {g_{5} - g_{4} } \right)}}{{q_{2} + 1}}}}{2}} + \frac{{g_{2} \left( {1 - s} \right) - \frac{{\left( {1 - s} \right)\left( {g_{4} - g_{3} } \right)}}{{q_{1} + 1}} + g_{4} \left( {1 - s} \right) + \frac{{\left( {1 - s} \right)\left( {g_{3} - g_{2} } \right)}}{{p_{2} + 1}}}}{2} \right. \\ & \quad \left.+ \frac{{h_{1} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{{p_{1} + 1}} } \right\}\left( {h_{2} - h_{1} } \right)}}{{(p_{1} + 1)\left( {\left( {1 - c} \right)^{{p_{1} }} } \right)}} + h_{5} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{{q_{2} + 1}} } \right\}\left( {h_{5} - h_{4} } \right)}}{{(q_{2} + 1)\left( {\left( {1 - c} \right)^{{q_{2} }} } \right)}}}}{2} { + \frac{{h_{2} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{{p_{2} + 1}} } \right\}\left( {h_{3} - h_{2} } \right)}}{{(p_{2} + 1)\left( c \right)^{{p_{2} }} }} + h_{4} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{{q_{1} + 1}} } \right\}\left( {h_{4} - h_{3} } \right)}}{{(q_{1} + 1)\left( c \right)^{{q_{1} }} }}}}{2}} \right\}/2. \\ \end{aligned} $$

For linear pentagonal intuitionistic fuzzy number we have $p_{1} = 1, p_{2} = 1,q_{1} = 1,q_{2} = 1$.

Thus,

$$ \begin{aligned} \check{A} &= \left\{\vphantom{\left. { + \frac{{h_{2} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{2} } \right\}\left( {h_{3} - h_{2} } \right)}}{2c} + h_{4} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{2} } \right\}\left( {h_{4} - h_{3} } \right)}}{2c}}}{2}} \right\}} {\frac{{g_{1} s + \frac{{s\left( {g_{2} - g_{1} } \right)}}{2} + g_{5} s {-} \frac{{s\left( {g_{5} - g_{4} } \right)}}{2}}}{2}} + \frac{{g_{2} \left( {1 - s} \right) - \frac{{\left( {1 - s} \right)\left( {g_{4} - g_{3} } \right)}}{2} + g_{4} \left( {1 - s} \right) + \frac{{\left( {1 - s} \right)\left( {g_{3} - g_{2} } \right)}}{2}}}{2} \right. \\ & \quad \left.+ \frac{{h_{1} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{2} } \right\}\left( {h_{2} - h_{1} } \right)}}{{2\left( {1 - c} \right)^{.} }} + h_{5} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{2} } \right\}\left( {h_{5} - h_{4} } \right)}}{{2\left( {1 - c} \right)^{.} }}}}{2} { + \frac{{h_{2} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{2} } \right\}\left( {h_{3} - h_{2} } \right)}}{2c} + h_{4} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{2} } \right\}\left( {h_{4} - h_{3} } \right)}}{2c}}}{2}} \right\}/2. \\ \end{aligned} $$

Application of NIPIFN in EPQ model

To produce superior quality product with minimum cost, the study of effects of learning and forgetting on production processes has gained much attention in the competitive market. Where learning enhances the procedures or patterns in production systems which optimizes the inventory and increase the throughput, the Forgetting counteracts learning, which may occur as a result of frequent or long interruptions in production. In this paper, we have considered a closed loop EPQ model where the production process is not perfect and all the defective items are sent back to the system for the rework/ correction. During regular production and rework, we have studied the effect of learning which in general uncertain and nonlinear in nature. So we have considered learning curves as NLPIFN. In addition to the facts stated above, we have also assumed the following:

• All items are screened while producing during T₁ and the inspection cost is included in the labour production cost.

• A fixed setup cost is charged for each cycle.

• The demand of the items is dependent on the retail price p. Thus we assume that the demand rate of item as $D\left( p \right) = a - bp\;\;{\text{where}}\;\;a,b > 0\;{\text{and}}\;p < a/b$. The use of symbol D and D(p) is interchangeably throughout the paper.

• The production rate (P) of perfect quality items must always be greater than or equal to the demand rate i.e., $Q\left( {1 - \beta } \right)$ ≥ DT₁ where β is the percentage of the defective items. Moreover, the rework rate (x) must always be greater than the demand rate and production of perfect items (i.e., x > P).

• Learning occurs during the production of finished items (regular and reworked items) which increases the rate of production. Again forgetting occurs during the break in production which reduces the production rate. Thus learning and forgetting depends upon the duration of production and break period.

• As learning is uncertain in nature so we consider it as linear, nonlinear PIFN.

• The manufacturer invests money to improve the production process quality by buying new machineries, improving old machine through maintenance and repair, worker training, etc. We consider Porteus [47] logarithmic investment function as $I\left( \beta \right) = \frac{1}{\tau }\ln \left( {\frac{{\beta_{0} }}{\beta }} \right),$ where $\tau$ is the percentage decrease in β, per unit of currency increase in investment and β₀ is the original percentage of defective items produced before investment (Figs. 8, 9).

Fig. 8

Inventory of non-defective item

Fig. 9

Inventory of defective item

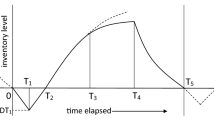
In this model we have observed that Q quantities of the item are produced in each cycle. The production process is not perfect and hence β% of defective items is produced. Thus Q(1-β) are perfect quality items which are produced and are separated by screening process during regular production time T₁. The βQ quantity of defective items are reworked after the regular production processes finishes and the rework process is perfect so no defective items remains in the inventory after T₂. The production time is not fixed and it depends on the learning and forgetting effect of the worker. As the time goes on the worker become more experienced and hence requires less time to produce. Also when there is no production the worker forgets the experience they have achieved. Since the tendency of human behavior to simultaneously learn and forget is uncertain so we have considered it in the production process of regular and defective items as trapezoidal dense Fuzzy number. Also manufacturer invests money to reduce the imperfect production.

The following notations are used throughout the paper:

Q:

Production lot size for each cycle (decision variable)

D:

Demand rate per unit time

P:

Production rate of perfect item by the manufacturer in the absence of learning

x:

Production rate of rework item by the manufacturer in the absence of learning

T₁:

Regular production time

T₂:

Rework time

T₃:

Depletion time

T:

Cycle time $\left( {T = T_{1} + T_{2} + T_{3} } \right)$

$a_{1}$:

Time to produce first unit of perfect item in the absence of learning (= 1/P)

$a_{2}$:

Time to produce first unit of rework item in the absence of learning (= 1/x)

$l_{1}$:

Learning coefficient associated with regular production, $l_{1} = \frac{{\ln c_{1} }}{\ln 2}$, where C₁ is learning rate in regular production (0 < l₁ < 1)

$l_{2}$:

Learning coefficient associated with reworking production, $l_{2} = \frac{{\ln c_{2} }}{\ln 2}$, where C₂ is learning rate in reworking production

$f_{1}$:

Forgetting coefficient associated with regular production

$f_{2}$:

Forgetting coefficient associated with reworking production

$\gamma$:

Percentage decrease in defective items per unit currency increase in investment

S:

Setup cost for each production run

$c_{1}$:

Labour production cost per unit item per unit time (inspection cost is included)

$c_{2}$:

Repair cost of per unit imperfect quality items per unit time

$h_{1}$:

Holding cost for each perfect item (i.e., serviceable item) per unit time

$h_{2}$:

Holding cost for each imperfect quality item being reworked per unit time

β:

Fraction of defective item

$\vartheta$:

Factional opportunity cost

TC:

Total cost for each cycle

T_i:

Total time elapsed for ith cycle $\left( {T_{i} = T_{1i} + T_{2i} + T_{3i} } \right)$

Model development and analysis

Researchers have worked on EPQ model under learning and forgetting along with various constrains. Here, we have tabulated a comparison Table 1 to show the novelty of our work.

Table 1 Literature survey of different EPQ models along with the underlying features

Learning and forgetting in regular production

We use Wright's [46] formulation of the learning effect is used to characterize the learning phenomenon of human. He proposes the relation between man hour required to produce unit item and cumulative production which is written as,

$$ \tau_{1j} = a_{1} j^{{ - l_{1} }} , $$

(1)

where $\tau_{1j}$ denotes time to produce jth unit during regular production and $a_{1} = \frac{1}{P}$. After the end of the production, forgetting occurs until the next production cycle begins. Let E_1i denote the experience (the amount learnt in equivalent unit) acquired in the beginning of ith production cycle which is transmitted from $\left( {i - 1} \right)$ th cycle. Then E_1i is given by Jaber and Bonney [36]

$$ E_{1i} = \left( {E_{{1\left( {i - `1} \right)}} + Q} \right)^{{1 + \frac{{f_{1} }}{{l_{1} }}}} \;\;\;S_{{1\left( {i - 1} \right)}}^{{ - \frac{{f_{1} }}{{l_{1} }}}} ,\;\;i = 1,2,3 \ldots ;\;E_{11} = 0, $$

(2)

where f₁ is the forgetting exponent during regular production run and S_1(i−1) is the total number of units that could have been produced in the $\left( {i - 1} \right) {\text{th}}$ cycle if there had been no disruption in the regular production process. If there is no forgetting i.e. f₁ = 0 then $E_{1i} = \left( {i - 1} \right)Q$. For partial transfer of learning or partial forgetting during regular production we have $0 < E_{1i} < \left( {i - 1} \right)Q,\quad i = 2,3, \ldots$. Then by Jaber and Bonney [36] S_1i is given as,

$$ S_{1i} = \left[ {\frac{{1 - l_{1} }}{{a_{1} }}\left( {T_{i} - T_{1i} } \right) + \left( {E_{1i} + Q} \right)^{{\left( {1 - l_{1} } \right)}} } \right]^{{\frac{1}{{1 - l_{1} }}}} ,\;\;\;i = 1,2,3, \ldots , $$

(3)

where T_1i is the regular production time and T_i is the total time of the given ith cycle and T_1i is given by,

$$ \begin{aligned} T_{1i} & = \mathop \int \limits_{{E_{1i} }}^{{E_{1i} + Q}} a_{1} j^{{ - l_{1} }} {\text{d}}j \\ & = \frac{{a_{1} }}{{1 - l_{1} }}\left( {\left( {E_{1i} + Q} \right)^{{1 - l_{1} }} - E_{1i}^{{1 - l_{1} }} } \right). \\ \end{aligned} $$

(4)

Now to evaluate the various inventory costs, we define a constant b_1i > 0 such that $E_{1i} = b_{1i} Q_{1i} ,\quad {\text{so}}\;0 \le b_{1i} \le i - 1,\quad i = 2,3, \ldots$. Thus Eq. (4) becomes

$$ T_{1i} = \frac{{a_{1} }}{{1 - l_{1} }}\left( {\left( {b_{1i} + 1} \right)^{{1 - l_{1} }} - b_{1i}^{{1 - l_{1} }} } \right)Q_{1i}^{{1 - l_{1} }} . $$

(5)

So,

$$ Q_{1i} = \left[ {\frac{{1 - l_{1} }}{{a_{1} }}T_{1i} \frac{1}{{\left( {\left( {b_{1i} + 1} \right)^{{1 - l_{1} }} - b_{1i}^{{1 - l_{1} }} } \right)}}} \right]^{{\frac{1}{{1 - l_{1} }}}} . $$

(6)

So for simplicity we use the symbol Q to represent $Q_{1i}$, which is interchangeable so, $Q = Q_{1i} = Q_{1i} \left( {T_{1i} } \right)$.

Thus for any time t the production quantity during the regular production run is

$$ Q\left( t \right) = Q_{1i} \left( t \right) = \left[ {\frac{{1 - l_{1} }}{{a_{1} }}t\frac{1}{{\left( {\left( {b_{1i} + 1} \right)^{{1 - l_{1} }} - b_{1i}^{{1 - l_{1} }} } \right)}}} \right]^{{\frac{1}{{1 - l_{1} }}}} . $$

(7)

Learning and forgetting during rework of defective items

As $\beta Q$ quantity of defective items has been reworked so similar to the regular production run, the rework is also subject to human behavior of learning and forgetting. If the rework rate is x (where x > P), then the time to rework the first item is 1/x. Thus time to inspect the jth unit is given by,

$$ \tau_{2j} = a_{2} j^{{ - l_{2} }} \;{\text{where}}\;a_{2} = \frac{1}{x}. $$

(8)

Thus $\tau_{21} \left\langle {\frac{1}{P}asx} \right\rangle P.$ If E_2i denotes the experience gathered during rework (equivalent number of items reworked) which is transferred from $\left( {i - 1} \right)$ th cycle to ith cycle is given as before,

$$ \begin{aligned} E_{2i} & = \left( {E_{{2\left( {i - `1} \right)}} + \beta Q} \right)^{{1 + \frac{{f_{2} }}{{l_{2} }}}} \quad S_{{2\left( {i - 1} \right)}}^{{ - \frac{{f_{2} }}{{l_{2} }}}} ,i = 1,2,3 \ldots ; \\ E_{21} & = 0, \\ \end{aligned} $$

(9)

where S_2i is the total number of items that could have been produced in the ith cycle if there were no disruption in the rework production process. If there is no forgetting i.e. f₂ = 0 then $E_{2i} = \left( {i - 1} \right)\beta Q.$ For partial transfer of learning or partial forgetting during rework of defective items we have $0 < E_{2i} < \left( {i - 1} \right)\beta Q,\quad i = 2,3, \ldots$. Then S_2i can be obtained as,

$$ S_{2i} = \left[ {\frac{{1 - l_{2} }}{{a_{2} }}\left( {T_{i} - T_{1i} - T_{2i} + T_{{1\left( {i + 1} \right)}} } \right) + \left( {E_{2i} + Q} \right)^{{\left( {1 - l_{2} } \right)}} } \right]^{{\frac{1}{{1 - l_{2} }}}} ,\quad i = 1,2,3, \ldots , $$

(10)

where T_1(i+1) is the regular production time of $\left( {i + 1} \right)$ th cycle where the defective items are produced and accumulated but is not reworked during that time since the rework of items are discontinued during $\left[ {T_{2i} , T_{{1\left( {i + 1} \right)}} } \right]$. So there is chance of forgetting till T_1(i+1).

Thus the rework time T_2i in the ith cycle,

$$ \begin{aligned} T_{2i} & = \mathop \int \limits_{{E_{2i} }}^{{E_{2i} + Q}} a_{2} j^{{ - l_{2} }} {\text{d}}j \\ & = \frac{{a_{2} }}{{1 - l_{2} }}\left( {\left( {E_{2i} + Q} \right)^{{1 - l_{2} }} - E_{2i}^{{1 - l_{2} }} } \right). \\ \end{aligned} $$

(11)

Now to evaluate the various inventory costs, we define a constant b_2i > 0 such that $E_{2i} = b_{2i} Q_{2i} ,\;\,{\text{so}}\;0 \le b_{2i} \le i - 1,\;i = 2,3, \ldots$. Thus Eq. (4) becomes

$$ T_{2i} = \frac{{a_{2} }}{{1 - l_{2} }}\left( {\left( {b_{2i} + 1} \right)^{{1 - l_{2} }} - b_{2i}^{{1 - l_{2} }} } \right)Q_{2i}^{{1 - l_{2} }} . $$

(12)

So,

$$ Q_{2i} \left( {T_{2i} } \right) = \left[ {\frac{{1 - l_{2} }}{{a_{2} }}T_{2i} \frac{1}{{\left( {\left( {b_{2i} + 1} \right)^{{1 - l_{2} }} - b_{2i}^{{1 - l_{2} }} } \right)}}} \right]^{{\frac{1}{{1 - l_{2} }}}} . $$

(13)

Thus for any time t the production quantity during the regular production run is

$$ Q_{2i} \left( t \right) = \left[ {\frac{{\left( {1 - l_{2} } \right)t}}{{a_{2} \left( {\left( {b_{2i} + 1} \right)^{{1 - l_{2} }} - b_{2i}^{{1 - l_{2} }} } \right)}}} \right]^{{\frac{1}{{1 - l_{2} }}}} . $$

(14)

Inventory level of the non-defective and defective items

There is always a demand of non-defective items in the entire replenishment cycle T. But during T_1i the manufacturer has to hold both defective and non-defective items. During T_2i the defective items are reworked and thus the inventory has only perfect items, partially reworked items and rest are originally perfectly produced items.

Inventory level of non-defective item

The inventory level of the non-defective items at any time t is given by

$$ I_{1i} \left( t \right) = \left( {1 - \beta } \right)Q_{1i} \left( t \right) - Dt,\quad 0 \le t \le T_{1i} , $$

(15)

$$ \begin{aligned} I_{2i} \left( t \right) & = Q_{2i} \left( t \right) - Dt + \left( {1 - \beta } \right)Q_{1i} \left( {T_{1i} } \right) \\ & \quad - DT_{1i} ,\quad 0 \le t \le T_{2i} , \\ \end{aligned} $$

(16)

$$ I_{3i} \left( t \right) = I_{max} - Dt, 0 \le t \le T_{3i} $$

(17)

where $Q_{1i} \left( {T_{1i} } \right)$ is the total quantity produced of which $\left( {1 - \beta } \right)Q_{1i} \left( {T_{1i} } \right)$ is perfect items and $\beta Q_{1i} \left( {T_{1i} } \right)$ is defective and thus $\beta Q_{1i} \left( {T_{1i} } \right) = Q_{2i} \left( {T_{2i} } \right)$. AlsoI_max is the maximum inventory of non-defective items after rework and it is given by $I_{\max } = Q_{1i} - D\left( {T_{1i} + T_{2i} } \right)$ and thus the depletion time T_3i where there is no production in the system but there is constant demand of item in the market is given by $T_{3i} = \frac{{I_{\max } }}{d}$.

Inventory level of defective item (yet to rework)

The inventory level of defective item which are not yet reworked is given for any time t is

$$ I_{4i} \left( t \right) = \beta Q_{1i} \left( t \right),\quad 0 \le t \le T_{1i} , $$

(18)

$$ I_{5i} \left( t \right) = \beta Q_{1i} \left( {T_{1i} } \right) - Q_{2i} \left( t \right),\quad 0 \le t \le T_{2i} . $$

(19)

Since during T_2i there are defective items which are yet to rework.

Various cost incurred in the inventory

To maintain an inventory the retailer has to abide certain costs which can’t be ignored. This cost includes holding cost of defective and non-defective items, cost to set machinery and labour (set up cost), cost to rework defective items (rework cost), and cost to reduce the production of defective items (investment cost).

Holding cost (HC)

The inventory has to hold both defective and non-defective items during both the duration T_1i and T_2i in the ith cycle. And only non-defective items during T_3i. Thus HC_i = (HC_ND)_i + (HC_D)_i.

Thus the holding cost for non-defective items in the ith cycle is HC_ND and it is given by

$$ \begin{aligned} \left( {{\text{HC}}_{{{\text{ND}}}} } \right)_{i} & = h_{1} \left[ {\mathop \int \limits_{0}^{{T_{1i} }} I_{1i} \left( t \right){\text{d}}t + \mathop \int \limits_{0}^{{T_{2i} }} I_{2i} \left( t \right){\text{d}}t + \mathop \int \limits_{0}^{{T_{3i} }} I_{3i} \left( t \right){\text{d}}t} \right] \\ & = h_{1} \left[ {\mathop \int \limits_{0}^{{T_{1i} }} \left( {\left( {1 - \beta } \right)\left( {\frac{t}{{\xi_{i} }}} \right)^{{\frac{1}{{1 - l_{1} }}}} - Dt} \right){\text{d}}t} \right. \\ & \quad + \mathop \int \limits_{0}^{{T_{2i} }} \left( {Q_{2i} \left( t \right) - Dt + \left( {1 - \beta } \right)Q_{1i} \left( {T_{1i} } \right) - DT_{1i} } \right){\text{d}}t \\ & \quad \left. { + \mathop \int \limits_{0}^{{T_{3i} }} \left( {Q_{1i} - D\left( {T_{1i} + T_{2i} } \right) - Dt} \right){\text{d}}t} \right] \\ & = h_{1} \left[ {\xi_{i} Q_{1i}^{{2\left( {1 - l_{1} } \right)}} \left[ {\left( {1 - \beta } \right)Q_{1i}^{{l_{1} }} - \frac{{D\xi_{i} }}{2}} \right] + \eta_{i} Q_{1i} \left( {\beta Q} \right)^{{1 - l_{2} }} } \right. \\ & \quad \left.\vphantom{\left[ {\mathop \int \limits_{0}^{{T_{1i} }} \left( {\left( {1 - \beta } \right)\left( {\frac{t}{{\xi_{i} }}} \right)^{{\frac{1}{{1 - l_{1} }}}} - Dt} \right){\text{d}}t} \right.} { - DT_{1i} T_{2i} - \frac{{DT_{2i}^{2} }}{2} + \frac{{\left( {Q_{1i} - D\left( {T_{1i} + T_{2i} } \right)} \right)^{2} }}{2D}} \right] \\ & = h_{1} \left[\vphantom{\left.+ \frac{{Q_{1i}^{2} }}{2D} - Q_{1i} \left( {T_{1i} + T_{2i} } \right) \right]} \left( {1 - \beta } \right)\xi_{i} Q_{1i}^{{2 - l_{1}}} + \eta_{i} Q\left( {\beta Q_{1i} } \right)^{{1 - l_{2} }}\right.\\ &\left.\quad + \frac{{Q_{1i}^{2} }}{2D} - Q_{1i} \left( {T_{1i}+ T_{2i} } \right) \right], \\ \end{aligned} $$

where $\xi_{i} = \frac{{a_{1} }}{{1 - l_{1} }}\left( {\left( {b_{1i} + 1} \right)^{{1 - l_{1} }} - b_{1i}^{{1 - l_{1} }} } \right),\;\,{\text{and}}\;\;\eta_{i} = \frac{{a_{2} }}{{1 - l_{2} }}\left( {\left( {b_{2i} + 1} \right)^{{1 - l_{2} }} - b_{2i}^{{1 - l_{2} }} } \right).$

Thus the holding cost for defective items in the i^th cycle is HC_D and it is given by

$$ \begin{aligned} \left( {{\text{HC}}_{D} } \right)_{i} & = h_{2} \left[ {\mathop \int \limits_{0}^{{T_{1i} }} I_{4i} \left( t \right){\text{d}}t + \mathop \int \limits_{0}^{{T_{2i} }} I_{5i} \left( t \right){\text{d}}t} \right] \\ & = h_{2} \left[ {\mathop \int \limits_{0 }^{{T_{1i} }} \beta \left( {\frac{t}{{\xi_{i} }}} \right)^{{\frac{1}{{1 - l_{1} }}}} {\text{d}}t + \mathop \int \limits_{0 }^{{T_{2i} }} \left( {\beta Q_{1i} - \left( {\frac{t}{{\eta_{i} }}} \right)^{{\frac{1}{{1 - l_{2} }}}} } \right){\text{d}}t} \right] \\ & = h_{2} \left[ {\frac{{1 - l_{1} }}{{2 - l_{1} }}\beta \xi_{i} Q_{1i}^{{2 - l_{1} }} + \frac{{\eta_{i} }}{{1 - l_{2} }}\left( {\beta Q_{1i} } \right)^{{2 - l_{2} }} } \right]. \\ \end{aligned} $$

$$ \begin{aligned} {\text{Thus}} \;\,{\text{HC}}_{i} & = \left( {{\text{HC}}_{{{\text{ND}}}} } \right)_{i} + \left( {{\text{HC}}_{D} } \right)_{i} \\ & = h_{1} \left[ {\left( {1 - \beta } \right)\xi_{i} Q_{1i}^{{2 - l_{1} }} + \eta_{i} Q\left( {\beta Q_{1i} } \right)^{{1 - l_{2} }} + \frac{{Q_{1i}^{2} }}{2D} - Q_{1i} \left( {T_{1i} + T_{2i} } \right)} \right] \\ & \quad + h_{2} \left[ {\frac{{1 - l_{1} }}{{2 - l_{1} }}\beta \xi_{i} Q_{1i}^{{2 - l_{1} }} + \frac{{\eta_{i} }}{{1 - l_{2} }}\left( {\beta Q_{1i} } \right)^{{2 - l_{2} }} } \right]. \\ \end{aligned} $$

Production cost (PC)

Since the production of all the items depends on work efficiency of the labour, i.e., it depends on the number of items produced per unit time considering learning capacity as well as forgetting behaviour of human nature, the production cost in the $i$th cycle is given by

$$ {\text{PC}}_{i} = c_{1} Q_{1i} T_{1i} = c_{1} \xi_{i} Q_{1i}^{{2 - l_{1} }} . $$

Rework cost (RC)

To amend each defective item per unit time, a cost incurred to rework in ith cycle is ${\text{RC}}_{i} = c_{2} \left( {\beta Q_{1i} } \right)T_{2i} = c_{2} \eta_{i} \left( {\beta Q_{1i} } \right)^{{2 - l_{2} }}$.

Investment cost (IC)

In this paper, our tendency is to produce better quality items and to reduce the production of defective items. To deal with such an important issue the decision maker has to make certain investments such as machine upgradation, purchase of better quality raw material, hiring of skilled labour, etc. which helps in reduction of defective items. Thus here a logarithmic investment function is used to interpret the investment cost incurred. Thus for $i$th cycle it is given IC_i

$$ {\text{IC}} = \frac{\vartheta }{\tau }\ln \left( {\frac{{\beta_{0} }}{\beta }} \right), $$

where $\vartheta$ is the factional opportunity cost.

Set up cost (SC)

To start an inventory the retailer has to invest some capital money to buy machinery, maintain the holding place of items, human labour, etc. This cost is considered as constant in each cycle, so for ith cycle SC_i = S_i.

Total cost (TC)

Thus the sum of all the above cost incurred for the ith cycle is

$$ \begin{aligned} {\text{TC}}_{i} & =\frac{1}{T}\left[ {{\text{HC}}_{i} + {\text{PC}}_{i} +{\text{RC}}_{i} + {\text{IC}}_{i} + {\text{SC}}_{i} } \right] \\& =\frac{1}{T}\left[ h_{1} \left[ \left( {1 - \beta } \right)\xi_{i}Q_{1i}^{{2 - l_{1} }} + \eta_{i} Q\left( {\beta Q_{1i} } \right)^{{1- l_{2} }} \right.\right.\\ &\quad\left.+ \frac{{Q_{1i}^{2} }}{2D} - Q_{1i} \left( {T_{1i} + T_{2i} }\right) \right] \\& \quad + h_{2} \left[ {\frac{{1 - l_{1} }}{{2 - l_{1} }}\beta\xi_{i} Q_{1i}^{{2 - l_{1} }} + \frac{{\eta_{i} }}{{1- l_{2} }}\left( {\beta Q_{1i} } \right)^{{2 - l_{2} }} } \right] \\& \quad \left. { + c_{1} \xi_{i} Q_{1i}^{{2 - l_{1} }} + c_{2}\eta_{i} \left( {\beta Q_{1i} } \right)^{{2 - l_{2} }} +\frac{\vartheta }{\tau }\ln \left( {\frac{{\beta_{0} }}{\beta }}\right) + S_{i} } \right] \\ & = \frac{{S_{i} D}}{{Q_{1i} }} +\frac{{Q_{1i} h_{1} }}{2} + \xi_{i} DQ_{1i}^{{1 - l_{1} }} \left({c_{1} - h_{1} \beta + h_{2} \beta \left( {\frac{{1 - l_{1} }}{{2 -l_{1} }}} \right)} \right) \\ & \quad + \eta_{i} D\beta^{{2 - l_{2}}} Q_{1i}^{{1 - l_{2} }} \left( {\frac{{h_{2} }}{{1 - l_{2} }} +c_{2} } \right) + \frac{D\vartheta }{{Q_{1i} \tau }}\ln \left({\frac{{\beta_{0} }}{\beta }} \right).\\ \end{aligned} $$

(20)

Thus the above total cost TC is function of Q and β.

For $i = 1$, we have $E_{11} = E_{21} = 0;\;\;{\text{and}}\;{\text{thus}}\;\xi_{i} = \frac{{a_{1} }}{{1 - l_{1} }}\;{\text{and}}\;\eta_{i} = \frac{{a_{2} }}{{1 - l_{2} }}$. The Eq. (20) takes the form

$$ \begin{aligned} {\text{TC}}\left( {p, Q,\beta } \right) & = \frac{{S_{i} D}}{Q} + \frac{{Qh_{1} }}{2} + \frac{{a_{1} DQ^{{1 - l_{1} }} }}{{1 - l_{1} }}\left( {c_{1} - h_{1} \beta + h_{2} \beta \left( {\frac{{1 - l_{1} }}{{2 - l_{1} }}} \right)} \right) \\ & \quad + \frac{{a_{2} D\beta^{{2 - l_{2} }} Q^{{1 - l_{2} }} }}{{1 - l_{2} }}\left( {\frac{{h_{2} }}{{1 - l_{2} }} + c_{2} } \right) + \frac{D\vartheta }{{Q\tau }}\ln \left( {\frac{{\beta_{0} }}{\beta }} \right). \\ \end{aligned} $$

(21)

Since Q is discrete and $\beta$ is continuous so it is not possible to prove analytically that the total cost ${\text{TC}}\left( {Q,\beta } \right)$ is jointly convex. Hence we check the optimality we have applied the following algorithm on the total cost.

Algorithm

Step 1: Set i = 1 and $\beta = \beta_{0} .$

Step 2: Solve for Q by $\frac{\partial TC}{{\partial Q}} = 0$ and obtain $Q = Q_{0} .$

Step 3: From the above value of $Q = Q_{0}$ obtain the value of β by using $\frac{\partial TC}{{\partial \beta }} = 0$ as $\beta = \beta^{*} .$

Step 4: Again substitute the value $\beta = \beta^{*}$ in step 2 and obtain the optimum value of Q as $Q = Q^{*} .$

Step 5: Evaluate the optimal average total cost $\widetilde{TC}^{*} \left( {Q^{*} ,\beta^{*} } \right)$ from (21) using $\beta = \beta^{*} \;\;and\;\;Q = Q^{*} .$

Step 6: Set i = i + 1 and considering $a_{{1\left( {i + 1} \right)}} = a_{1i} Q^{{ - l_{1} }} \;\;{\text{and}}\;\;a_{{2\left( {i + 1} \right)}} = a_{2i} Q^{{ - l_{2} }} .$

Step 7: If $\left| {Q_{i}^{*} - Q_{i - 1}^{*} } \right| > \varepsilon$ then go to step 2 else $i^{*} = i - 1$ and stop.

Thus i^* is the number of cycle till we have the maximum learning occurs.

Let us consider the learning during production and rework as non-linear Pentagonal Intuitionistic fuzzy number and then de-intuiting it by the above mentioned technique. Then,

$$ \begin{aligned} \widetilde{{l_{1} }} & = \left\{ {\frac{{g_{11} s + \frac{{s\left( {g_{12} - g_{11} } \right)}}{{p_{1} + 1}} + g_{15} s - \frac{{s\left( {g_{15} - g_{14} } \right)}}{{q_{2} + 1}}}}{2}} + \frac{{g_{12} \left( {1 - s} \right) - \frac{{\left( {1 - s} \right)\left( {g_{14} - g_{13} } \right)}}{{q_{1} + 1}} + g_{14} \left( {1 - s} \right) + \frac{{\left( {1 - s} \right)\left( {g_{13} - g_{12} } \right)}}{{p_{2} + 1}}}}{2}\vphantom{+ \frac{{h_{11} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{{p_{1} + 1}} } \right\}\left( {h_{12} - h_{11} } \right)}}{{(p_{1} + 1)\left( {\left( {1 - c} \right)^{{p_{1} }} } \right)}} + h_{15} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{{q_{2} + 1}} } \right\}\left( {h_{15} - h_{14} } \right)}}{{(q_{2} + 1)\left( {\left( {1 - c} \right)^{{q_{2} }} } \right)}}}}{2}} \right.\\ & \quad \left.+ \frac{{h_{11} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{{p_{1} + 1}} } \right\}\left( {h_{12} - h_{11} } \right)}}{{(p_{1} + 1)\left( {\left( {1 - c} \right)^{{p_{1} }} } \right)}} + h_{15} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{{q_{2} + 1}} } \right\}\left( {h_{15} - h_{14} } \right)}}{{(q_{2} + 1)\left( {\left( {1 - c} \right)^{{q_{2} }} } \right)}}}}{2} + {\frac{{h_{12} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{{p_{2} + 1}} } \right\}\left( {h_{13} - h_{12} } \right)}}{{(p_{2} + 1)\left( c \right)^{{p_{2} }} }} + h_{14} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{{q_{1} + 1}} } \right\}\left( {h_{14} - h_{13} } \right)}}{{(q_{1} + 1)\left( c \right)^{{q_{1} }} }}}}{2}} \right\}/2, \\ \end{aligned} $$

$$ \begin{aligned} \widetilde{{l_{2} }} & = \left\{ {\frac{{g_{21} s + \frac{{s\left( {g_{22} - g_{21} } \right)}}{{p_{1} + 1}} + g_{25} s - \frac{{s\left( {g_{25} - g_{24} } \right)}}{{q_{2} + 1}}}}{2}} + \frac{{g_{22} \left( {1 - s} \right) - \frac{{\left( {1 - s} \right)\left( {g_{24} - g_{23} } \right)}}{{q_{1} + 1}} + g_{24} \left( {1 - s} \right) + \frac{{\left( {1 - s} \right)\left( {g_{23} - g_{22} } \right)}}{{p_{2} + 1}}}}{2}\vphantom{+ \frac{{h_{11} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{{p_{1} + 1}} } \right\}\left( {h_{12} - h_{11} } \right)}}{{(p_{1} + 1)\left( {\left( {1 - c} \right)^{{p_{1} }} } \right)}} + h_{15} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{{q_{2} + 1}} } \right\}\left( {h_{15} - h_{14} } \right)}}{{(q_{2} + 1)\left( {\left( {1 - c} \right)^{{q_{2} }} } \right)}}}}{2}} \right.\\ & \quad \left.+ \frac{{h_{21} c + \frac{{\left\{ {1 - \left( {1 - c} \right)^{{p_{1} + 1}} } \right\}\left( {h_{22} - h_{21} } \right)}}{{(p_{1} + 1)\left( {\left( {1 - c} \right)^{{p_{1} }} } \right)}} + h_{25} c - \frac{{\left\{ {1 - \left( {1 - c} \right)^{{q_{2} + 1}} } \right\}\left( {h_{25} - h_{24} } \right)}}{{(q_{2} + 1)\left( {\left( {1 - c} \right)^{{q_{2} }} } \right)}}}}{2} + {\frac{{h_{22} \left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{{p_{2} + 1}} } \right\}\left( {h_{23} - h_{22} } \right)}}{{(p_{2} + 1)\left( c \right)^{{p_{2} }} }} + h_{24} \left( {1 - c} \right) - \frac{{\left\{ {1 - \left( c \right)^{{q_{1} + 1}} } \right\}\left( {h_{24} - h_{23} } \right)}}{{(q_{1} + 1)\left( c \right)^{{q_{1} }} }}}}{2}} \right\}/2. \\ \end{aligned} $$

Note 1: for linear pentagonal intuitionistic fuzzy number we have $p_{1} = 1, p_{2} = 1,q_{1} = 1,q_{2} = 1,$

Thus, $\begin{aligned}\check{l_{1}} & = \left\{ {\frac{{g_{11} s + \frac{{s\left( {g_{12}- g_{11} } \right)}}{2} + g_{15} s - \frac{{s\left( {g_{15} - g_{14}} \right)}}{2}}}{2}} \right.\\ &\left.+ \frac{{g_{12} \left( {1 - s} \right) -\frac{{\left( {1 - s} \right)\left( {g_{14} - g_{13} } \right)}}{2}+ g_{14} \left( {1 - s} \right) + \frac{{\left( {1 - s}\right)\left( {g_{13} - g_{12} } \right)}}{2}}}{2} \right.\\&\left. \quad + \frac{{h_{11} c + \frac{{\left\{ {1 - \left( {1 - c}\right)^{2} } \right\}\left( {h_{12} - h_{11} } \right)}}{{2\left({1 - c} \right)^{.} }} + h_{15} c - \frac{{\left\{ {1 - \left( {1 -c} \right)^{2} } \right\}\left( {h_{15} - h_{14} }\right)}}{{2\left( {1 - c} \right)^{.} }}}}{2}\right. \\ &\left.+ {\frac{{h_{12}\left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{2} }\right\}\left( {h_{13} - h_{12} } \right)}}{2c} + h_{14} \left( {1 -c} \right) - \frac{{\left\{ {1 - \left( c \right)^{2} }\right\}\left( {h_{14} - h_{13} } \right)}}{2c}}}{2}} \right\}/2, \\\end{aligned}$. $\begin{aligned}\check{l_{2}} & = \left\{ {\frac{{g_{21} s + \frac{{s\left( {g_{22}- g_{21} } \right)}}{2} + g_{25} s - \frac{{s\left( {g_{25} - g_{24}} \right)}}{2}}}{2}}\right.\\ &\quad\left. + \frac{{g_{22} \left( {1 - s} \right) -\frac{{\left( {1 - s} \right)\left( {g_{24} - g_{23} } \right)}}{2}+ g_{24} \left( {1 - s} \right) + \frac{{\left( {1 - s}\right)\left( {g_{23} - g_{22} } \right)}}{2}}}{2} \right.\\&\left. \quad + \frac{{h_{21} c + \frac{{\left\{ {1 - \left( {1 - c}\right)^{2} } \right\}\left( {h_{22} - h_{21} } \right)}}{{2\left({1 - c} \right)^{.} }} + h_{25} c - \frac{{\left\{ {1 - \left( {1 -c} \right)^{2} } \right\}\left( {h_{25} - h_{24} }\right)}}{{2\left( {1 - c} \right)^{.} }}}}{2} \right.\\&\left.+ {\frac{{h_{22}\left( {1 - c} \right) + \frac{{\left\{ {1 - \left( c \right)^{2} }\right\}\left( {h_{23} - h_{22} } \right)}}{2c} + h_{24} \left( {1 -c} \right) - \frac{{\left\{ {1 - \left( c \right)^{2} }\right\}\left( {h_{24} - h_{23} } \right)}}{2c}}}{2}} \right\} + /2.\\ \end{aligned}$

Then,

$$ \begin{aligned} \widetilde{{{\text{TC}}}}\left( {Q,\beta } \right) & = S\frac{D}{Q} + h_{1} \left( \frac{Q}{2} + a_{1} Q^{{\widetilde{{l_{1} }} + 1}} D\left( {\frac{1 - \beta }{{\widetilde{{l_{1} }} + 2}} -\frac{1}{{\widetilde{{l_{1} }} + 1}}} \right)\right. \\&\quad\left. -\frac{{a_{2} D\beta^{{\widetilde{{l_{2} }} + 2}}Q^{{\widetilde{{l_{2} }} + 1}} }}{\left( {\widetilde{{l_{2} }} + 2}\right)\left( {\widetilde{{l_{2} }} + 1} \right)} \right) + c_{1}\frac{{a_{1} Q^{{\widetilde{{l_{1} }}}} D}}{{\widetilde{{l_{1} }} +1}}+ c_{2} \frac{{a_{2} D\beta^{{\widetilde{{l_{2} }} + 1}}Q^{{\widetilde{{l_{2} }}}} }}{{\left( {\widetilde{{l_{2} }} + 1}\right)}} \\&\quad+ h_{2} D\left( {\frac{{a_{1} \beta Q^{{\widetilde{{l_{1}}} + 1}} }}{{\widetilde{{l_{1} }} + 2}} + \frac{{a_{2}\beta^{{\widetilde{{l_{2} }} + 2}} Q^{{\widetilde{{l_{2} }} + 1}}}}{{\left( {\widetilde{{l_{2} }} + 1} \right)\left({\widetilde{{l_{2} }} + 2} \right)}}} \right) \\ & \quad +\frac{\vartheta Q}{{\tau D}}\ln \left( {\frac{{\beta_{0} }}{\beta }}\right). \\ \end{aligned} $$

(22)

It is observed that the control parameters are not independent of each other. So to obtain the optimum solution let us acclimatize an iterative algorithm as below.

Numerical study

A numerical experiment with the following input parameter is conducted whose results are reported further. Also the learning during the normal production and rework time is 95% (which is equivalent to $l_{12} = 0.074$).

$$ \begin{aligned} S & = 4000;\;\;P = 150;\;\;a_{1} = \frac{1}{P};\;\;x = 650; \\ a_{2} & = \frac{1}{x};\;\;l_{1} = 0.074;\;\;l_{2} = 0.074;\;\;h_{1} = 2; \\ h_{2} & = 3;\;\;\beta_{0} = 0.2;\;\;c_{1} = 1;\;\;c_{2} = 10; \\ \vartheta & = 0.02;\;\;\tau = 0.002;\;\;{\text{TF}} = 1;\;\;d = 100. \\ \end{aligned} $$

To study the effect of forgetting, we assume that complete forgetting would occur if production and rework are interrupted for a period of one years (T_F = 1). Then, following Jaber and Bonney [36] we determine the forgetting slopes for production and inspection in the ith cycle as given below:

$$ f_{1i} = \frac{{l_{1} \left( {1 - l_{1} } \right)\log \left( {E_{1i} + Q} \right)}}{{\log \left( {R_{1} + 1} \right)}}, $$

$$ f_{2i} = \frac{{l_{2} \left( {1 - l_{2} } \right)\log \left( {E_{2i} + \beta Q} \right)}}{{\log \left( {R_{2} + 1} \right)}}, $$

where $r_{1} = \frac{{T_{F} }}{{T_{1i} }}\;{\text{and}}\;R_{2} = \frac{{T_{F} }}{{T_{2i} }},\;\;i = 1,2,3, \ldots$.

Thus keeping in mind the concept of learning and forgetting in our mind, let us observe how the model works under the crisps and Intuitionistic arena. In Table 2, we observe at which cycle the model will obtain the maximum learning under crisp arena.

Table 2 Optimal solution till learning occurs in crisps arena

From Table 2, we observe that the learning is maximum in 10^th cycle.

Since we have introduced a new concept of NLPIFN in the paper so we will observe at which cycle the model will obtain the maximum learning under NLPIFN arena. From this Table 3, we will understand the need to take learning as NLPIFN rather than crisp number.

Table 3 Optimal solution till learning occurs in nonlinear Pentagonal Intuitionistic FN arena $p_{1} = p_{2} = q_{1} = q_{2} = 2$

From Table 3, we can see that the learning occurs in 4th cycle only.

Let us also observe how this EPQ model works in linear PIFN arena rather than NLPIFN arena.

From Table4, we can observe that the maximum learning occurs in 8th cycle.

Table 4 Optimal solution till learning occurs in linear Pentagonal Intuitionistic FN arena $p_{1} = p_{2} = q_{1} = q_{2} = 1$

If we compare Tables 2, 3, and 4, we can see that it requires 10 cycles to obtain learning effect under crisps environment while in just 4 cycles to obtain the same in non-linear PIFN arena and 8 cycle in linear PIFA arena. Again more quantity of perfect quality items and less number of defective items are produced under non-linear PIFN arena than under crisps arena. It is also observed that it take less production time (T₁) in nonlinear Pentagonal Intuitionistic fuzzy number which means learning occurs faster in this arena.

Thus the detail comparative study of our crisps, linear and nonlinear PIFN is done below.

Thus, from Table 5 and Figs. 10 and 11, if we compare our nonlinear model with our linear or crisp model we can observe that, learning occurs fastest in nonlinear model thus the production of defective item get reduced. Investment of money for machine modernization or upgradation also reduces the production of defective items with increase in produced quantity. Also, it is observed that considering learning as NIPIFN, the total cost is minimum as compared with linear PIFN and crisps cases.

Table 5 Comparative result of the numerical example

Fig. 10

Behaviour of TC with respect to β

Fig. 11

Behaviour of TC with respect to Q

Figures 12, 13 and 14 give the 3D plot of total cost vs Q and β in three different environments.

Fig. 12

The 3D Plot of TC with respect to β and Q in crisp environment

Fig. 13

The 3D Plot of TC with respect to β and Q in linear PIFN environment

Fig. 14

The 3D Plot of TC with respect to β and Q in Nonlinear PIFN environment

Sensitivity analysis

As per the crisps value of Table 1, let us observe the sensitivity of the learning parameter as it is the crucial of all the parameters. With change in learning during regular and rework production, the quantity of the produced items changes a lot. So we have considered learning as uncertain parameter and have observed the sensitivity of learning in crisp arena.

It is observed from the above table that when there is more learning during rework there is less production of defective item. While during more learning in normal production, it takes less time to produce the optimum quantity of items.

Conclusion

In this article, we initiated the concept of non-linear pentagonal intuitionistic fuzzy number and their graphical classifications. Different forms of PIFN are addressed here along with its geometrical scenario based on symmetry and asymmetry. Also, a new de-intuitification method is developed in nonlinear PIFN arena using alpha/beta cut method. Here we have applied the concept of nonlinear PIFN in an EPQ model effectively where it is assumed that the production process produce imperfect items and it undergoes for rework. Moreover, this article incorporates the human behavior of learning due to repeated practice and experience along with forgetting due to the gap in the production from one cycle to the next cycle. In the existing literatures of EPQ model, we have considered learning and forgetting in the lot sizing model as crisps value. Since both learning and forgetting are human behaviour and it is imprecise, so considering it to be crisps (fixed) is not justified. Therefore, we have considered learning as nonlinear pentagonal intuitionistic fuzzy number. In this article, we also considered the effect of investment to produce better quality item under the effect of learning and forgetting of workers. Here, the workers experience due to learning is considered as symmetric nonlinear PIFN. Several managerial insights can be derived from the numerical analyses presented in this paper. First of all the model gives better result under nonlinear PIFN arena as learning occurs faster (in four cycle) as compared to linear PIFN or crisps arena. Secondly, the total cost incurred in the production process is very less in nonlinear PIFN arena as compared with other two situations. We also observe from Table 6, that good learning from the system helps the system to reduce the production of defective items. Furthermore, we have noticed that better system learning helps to cut down total production time. On the other hand unit production times increase during interruptions due to a loss of experience/knowledge.

Table 6 Sensitivity of learning parameter