Introduction

In recent years, dynamic optimization has caught the rising attention of researchers. Compared with static multi-objective optimization, dynamic multi-objective problems (DMOPs) are much closer to real-world application, like 5G ultra-dense networks [1], water quality anomaly detection [2], multi-crane-scheduling problem [3], and cycling energy systems [4]. However, it is worth mentioning that DMOPs contain dynamic characteristics, including changing Pareto front, Pareto set, the number of objectives or other parameters. Therefore, tracking the changing Pareto front quickly and accurately becomes particularly essential for DMOPs. Many researchers studied the field of dynamic optimization and various methods about solving DMOPs have been put forward. At the same time, new benchmarks, new problems, and new algorithms [5] are gradually emerging. How to design an effective algorithm for coping with DMOPs remains a great challenge for us.

Based on different dynamic characteristics, DMOPs can be divided into four categories [6]: (1) both Pareto front and Pareto set change, (2) Pareto front change but Pareto set doesn’t change, (3) Pareto set change but Pareto front doesn’t change, and (4) both Pareto front and Pareto set don’t change. An algorithm with superior performance should respond to these different changes timely. Also, convergence and diversity should be considered when measuring the performance of dynamic algorithms. In general, the dynamic nature of the environment may lead to moving Pareto front, and the right direction of next environmental change is unknown for us. This undoubtedly brings great challenges and difficulties to the optimization algorithms. Despite this, there are some unknown certain relationships between the current environment and the next change. Therefore, the past experience can be used as a powerful tool to predict the next change. Many researchers make full use of the information from the past environment and combine it with some static multi-objective algorithms (SMOAs). Of course, DMOPs can be solved through a single SMOA without any strategies as well. But obviously, after one iteration of a single SMOA, the initial population should be reset according to the basic idea. For multi-objective problems with dynamic characteristics, the reconfigured initial population is likely to evolve in the wrong direction, thus failing to obtain the optimal solution to the problem. To lower the probability of evolution in the wrong direction, some timely strategies to cope with change are essential.

These strategies for coping with change come from different perspectives, include predicting the next change direction, reusing the past environmental experience, or some self-adaptive methods. For the prediction method, some specific strategies are employed to predict the next environmental change, so that the population can be evolved towards the right direction, greatly reducing the possibility of reverse evolution. A novel knee point-based prediction approach was proposed by Zou et al. [7]. It maintained the non-dominated solutions around the knee regions and the burden of maintaining diversity and convergence at the same time was reduced for the most part. Memory-based schemes aim at storing the past experience about the non-dominated solutions, and recalling it when the next change occurs. A steady-state evolutionary algorithm for DMOPs was proposed by Jiang et al. [8]. The information from the previous environments was collected, and a part of outdated solutions were reused when facing the new environment.

What’s more, a combination of different types of techniques had been proposed. On the basis of prediction methods, the integration of evolutionary algorithms [9, 10] and machine learning becomes possible. Simões et al. [11] incorporated two prediction approaches into memory-based evolutionary algorithms. One used linear regression, and another combined nonlinear regression. The performance of algorithms can be greatly improved through these two methods. Jiang et al. [12] proposed a distribution algorithm based on domain adaptation and nonparametric estimation. Transfer learning, as a branch of machine learning, is considered to be promising for solving DMOPs. The past experience can be used for obtaining the high-quality individuals and the next initial population. Wang et al. [13] presented a novel effective model, which is called regression transfer learning prediction method. Some individuals with better predicted objective values are selected to form the initial population. Jiang et al. [14] successfully applied transfer learning to multi-task optimization and dynamic optimization. For DMOPs, transfer component analysis (TCA) [14] was adopted to construct the prediction model. Besides, various strategies to improve the performance of the algorithms were combined with transfer learning, including the knee point based [15], individual based [16], manifold based [17], or autoencoding evolutionary search [18]. It is visible that much great progress has been made in the application of transfer learning.

Transfer learning applies the knowledge from other fields or problems to a different but related domain. However, the training time is also one of the criteria to measure the quality of algorithms. Most of the existing methods require a long training time, which suggests that the performance of transfer learning approaches should be further improved. Accordingly, we propose an improved transfer learning method in this paper, which is the centroid distance strategy combined with transfer learning. The centroid distance strategy is employed before generating the initial population through the transfer learning. This strategy define some reference points according to different problems like NSGA-III [19], and then the distance between the population centroid and reference points is calculated as a basis of selecting individuals. Those with smaller distance will be selected for composing the population. In the next step, the population will be put into transfer learning method and the initial population for evolutionary iteration can be generated. The strategy we employed replace the random population with the smallest centroid distance population. This further improves the efficiency of looking for the optimal solutions and can locate the optimal solutions more quickly. Obviously, the training time can be saved a lot.

The approach proposed by this paper aims to improve the performance of NSGA-III in DMOPs. The knowledge about machine leaning is adopted for predicting the right direction. The direction of the next change can be predicted according to the environmental information in the last time. The motivation of this paper is mainly divided into two aspects, one is to improve the performance of NSGA-III algorithm in solving DMOPs, and the other is to map these individuals that obey different distributions into a latent space and generate an initial population for evolving.

The contributions of this paper are as follows: first, the integration of centroid distance and transfer learning is proposed. Besides, the centroid distance strategy and transfer learning both are combined with NSGA-III to verify the effectiveness, respectively. Second, the combination we propose is considered as a whole dynamic approach. Three evolutionary algorithms are incorporated with this approach and the percentage improvement of metrics is presented though experiments. Compared with the original algorithm, the algorithms incorporating the strategy have better diversity and convergence.

The rest of this paper is organized as follows: we introduce the preliminary studies and related work in Sect. The preliminary studies and related work. The concrete process of centroid distance and transfer learning is introduced in Sect. Proposed methods. Section Experiments shows some details of the experiments and results. At last, in Sect. Conclusions, the summary of this work will be drawn and the future direction will be given clearly.

The preliminary studies and related work

In this section, some established definitions about DMOPs are described. We next will introduce the basic knowledge of transfer learning. What’s more, the related work about our proposed approach is discussed at the end of this section.

Definitions of DMOPs

A formal DMOP can be expressed mathematically as:

$$\left\{ \begin{gathered} {\text{Minimize}} \, F\left( {{\mathbf{x}},t} \right) = \left( {f_{1} \left( {x,t} \right),f_{2} \left( {x,t} \right), \cdot \cdot \cdot ,f_{M} \left( {x,t} \right)} \right)^{T} \hfill \\ {\text{s.t.}} \,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathbf{x}} = (x_{1} ,x_{2} ,x_{3} ...,x_{n} ) \in \Omega \hfill \\ \end{gathered} \right.$$
(1)

where F(x, t) is the objective function, consisting of M objectives. x means the n-dimensional decision vector and Ω represents the decision space. The mapping of function variables is as follows: fi(x, t): Ωn × T → RM, Ω = [L1, U1] × [L2, U2] × … × [Ln, Un], i = 1, 2, 3, …, M. Li and Ui are the lower and upper boundaries of the i-th decision variable. Each function changes over time t. Here, a minimization problem is set in this paper, which is considered to be continuous for further research.

Definition 1

(Dynamic Pareto dominance): at time t, a decision variable x1 dynamically Pareto dominates another decision variable x2, denoted by x1 ≻ x2, if and only if

$$\left\{ \begin{gathered} \forall i = 1,...,M,f_{i} (x_{1} ,t) \le f_{i} (x_{2} ,t) \hfill \\ \exists i = 1,....,M,f_{i} (x_{1} ,t) < f_{i} (x_{2} ,t) \hfill \\ \end{gathered} \right.$$
(2)

Definition 2

(Dynamic Pareto-optimal Set (DPS)) : at time t, x and x* are decision variables from decision space Ω. If and only if there is no other decision variable x ∈ Ω satisfying x ≻ x*, the vector x* can be called as a non-dominated or Pareto-optimal solution. The Dynamic Pareto-optimal Set (DPS) is the set of all Pareto-optimal solutions at time t, which can be expressed as:

$${\text{DPS}}(t) = \{ x^{*} \in \Omega | \nexists x \in \Omega ,x \succ x^{*} \}$$
(3)

Definition 3

(Dynamic Pareto-optimal Front (DPF)): at time t, the set of all corresponding objective vectors of the DPS is defined as the Dynamic Pareto-optimal Front (DPF):

$${\text{DPF}}(t) = \{ F(x^{*} ,t)|x^{*} \in DPS\}$$
(4)

As can be seen from above definitions, DMOPs and static multi-objective problems are quite different. Dynamic features bring a lot of unknown changes to multi-objective problems. A higher standard for dynamic multi-objective evolutionary algorithms (DMOEAs) is put forward, which requires tracking the moving DPS and DPF. At the same time, the Pareto-optimal solutions to be found should be as diverse as possible.

Transfer learning

With the emergence of more and more machine learning application scenarios, transfer learning, as a branch of machine learning, has received more and more attention. In the field of machine learning, transfer learning is mainly to apply knowledge or patterns learned in a certain field or task to different but related fields or problems. Traditional machine learning is often based on the same distribution assumption and requiring a large amount of labeled data. Transfer learning learns from previously labeled data and applies it to unlabeled data to obtain results. Compared with traditional machine learning, transfer learning can not only meet the needs of universal models and individualization through adaptive learning, but also complete the requirements of specific applications through similar knowledge transfer. Besides, the process of transfer learning is not always successful, and negative transfer also occurs. Pan and Yang [20] defined negative transfer as the knowledge learned on the source domain, which has a negative effect on the learning. In practical applications, finding reasonable similarities and choosing or developing a reasonable transfer learning method can avoid the negative transfer.

Transfer learning can also be applied to DMOPs. When the environmental change occurs, transfer learning can be used as a prediction tool to apply the knowledge learned in the source domain to the target domain. The source domain refers to the past experience we get, and the target domain means the unknown changes we may meet. The core idea of transfer learning is to find the similarity between the source domain and the target domain, and use certain measurement criteria to measure the similarity. Through the similarity given by the measurement criteria, we can use certain methods to increase the similarity between the source domain and the target domain, thereby completing transfer learning more successfully. There are various measurement criteria, mainly to measure the difference between two data domains. The maximum mean difference (MMD) is the most frequently used metric in transfer learning.

Definition 4

(Maximum Mean Difference (MMD)): MMD measures the distance between two distributions in the regenerated Hilbert space, and it is a kernel learning method.

$${\text{MMD}}(X,Y) = \left\| {\frac{1}{{n_{1} }}\sum\limits_{i = 1}^{{n_{1} }} {\phi (\overrightarrow {{x_{i} }} )} - \frac{1}{{n_{2} }}\sum\limits_{j = 1}^{{n_{2} }} {\phi (\overrightarrow {{y_{j} }} )} } \right\|_{{\mathcal{H}}}^{2}$$
(5)

where \(\overrightarrow{{x}_{i}}\) and \(\overrightarrow{{y}_{j}}\) are two variables from source domain X and target domain Y, respectively. n1 and n2 are the number of X and Y, respectively. φ(•) maps the original variable to the Reproducing Kernel Hilbert Space (RKHS). The direct understanding of MMD is to obtain the distance of the mean value of the data of two domains in RKHS. The inner product in RKHS space can be converted into a kernel function, so the final MMD can be directly calculated by the kernel function. This will be discussed in Sect. Proposed methods.

Related works

To date, a great progress has been made in the field of DMOPs. Many DMOEAs and different strategies have emerged from various perspectives. The most DMOEAs can be divided into the following categories [21]: diversity-based approaches, prediction-based approaches, memory-based approaches, and parallel approaches.

The algorithms based on diversity aim at maintaining a good level of diversity during the search process. A modified NSGA-II for DMOPs was proposed by Deb et al. in 2006 [22]. Two versions of DNSGA-II were proposed. The first version of DNSGA-II (DNSGA-II-A) introduced a certain number of random individuals into the population to increase the diversity. Replacing some individuals with mutated solutions was employed for maintaining the diversity in the second version of NSGA-II (DNSGA-II-B). Grefenstette [23] studied the genetic algorithm on dealing with the dynamic environments. To respond to the environmental changes, a random immigrant genetic algorithm (RIGA) was put forward. In RIGA, some new genetic materials were put into the population and other individuals would be replaced randomly. Chen et al. [24] studied the use of additional objective in dynamic environments. The individual diversity was considered as an additional objective in the evolutionary process. A new diversity maintaining evaluation approach and a new diversity measurement were proposed and a useful selection pressure was added into the algorithm.

The core idea of prediction-based methods is easy to follow. Prediction-based approaches can be a complete model or framework, or it can be an effective strategy responding to the unknown changes. In fact, the previous information obtained from the past environment is employed for generating the new population to form a prediction model. When the environment changes, the generated population will be employed for predicting the moving DPF and DPS. A novel prediction-based reaction mechanism for DMOPs was proposed by Zhang et al. [25]. During the process, three subpopulations were generated according to different approaches, which were a linear prediction model, a sampling strategy, and a shrinking method. The whole population consists of these three subpopulations and was considered to be the initial population that responds to the next change. A multidirectional prediction approach and a multi-model prediction method were introduced by Gong et al. [26, 27] for DMOPs. In the multidirectional prediction, the moving DPF was predicted through the representative individuals generated by the clustering of optimized solutions, and finally the predicted solutions were created. According to the corresponding relations between the type of change and the response strategy, the prediction model corresponding to the type of problem change is selected to generate a predicted solution. Both prediction methods have proved to be superior to other algorithms in performance. In [6], Kalman filter was employed for predicting future changes. The Kalman filter (KF) prediction model made an estimation through feedback control. To avoid other problems caused by the system, a scoring scheme was introduced to obtain a proportion of KF and random re-initialization. The whole prediction process was combined with the structure of Multi-objective Evolutionary Algorithm with Decomposition Based on Differential Evolution (MOEA/D-DE).

When the environment changes slightly comparing with the past environment, storing the useful knowledge from past environments timely is of particular importance. An extra memory is employed to store information about non-dominated solutions, which can be recalled for dealing with new changes. Wang et al. [28] introduced some memory-based strategies, including explicit memory scheme, local search scheme, and hybrid memory scheme. The explicit memory scheme means to store the past solutions and reevaluate them, forming the next population by these solutions. The disadvantages of this mechanism are obvious. The loss of diversity and the vulnerability to local optimality are two major disadvantages. The local search scheme introduced a probability parameter which controls the proportion of local search and a local search operator. Obviously, the performance of local search is greatly affected by parameters, and different parameters may lead to completely opposite performance. The hybrid memory scheme combined explicit memory scheme and local search scheme; the number of memory solutions was controlled by a probability parameter.

The idea of “parallel” is also an important branch for solving DMOPs. Most parallel evolutionary algorithms divided a population into several subpopulations that evolve simultaneously with different processors. As in [29], M + 1 multiple subpopulations were divided from a whole population, where M is the number of objectives and a cellular genetic algorithm was employed for optimizing every subpopulation about each objective. The remaining last subpopulation was used for obtaining the best average of n objectives. Besides, aiming at the dynamic environmental changes, the hyper-mutation operator was utilized for DMOPs. A parallel evolutionary algorithm was proposed in [30], which applied the data decomposition into the algorithm. This parallel procedure was based on an island model and a master process. The master process divided the evolved population into some subpopulations and sent to every worker process. A multi-objective evolutionary algorithm was chosen to obtain the optimal solutions for each subpopulation. Then the found optimal solutions would be sent to the master and all the optimal solutions would form a new population by the master when the change occurs.

Dynamic multi-objective problems also have many practical applications. In addition to the above methods, many algorithms are applied to practical DMOPs, such as scheduling problems [31,32,33], routing problems [34, 35], and control problems [36]. In [31], the ant colony algorithm (ACO) was applied to the problem of railway junction rescheduling. The dynamic multi-objective railway junction rescheduling problem (DM-RJRP) was formulated in detail and the dynamic modification for a population-based ACO (DM-PACO) which adds an inbuilt memory was proposed. Through the simulated experiments, the performance of proposed algorithm can be verified on dealing with DM-RJRP. The other problems follow the similar process. There are many other practical application scenarios for DMOPs, including the resource management problems and mechanical problems. It can be seen that DMOPs are much closer to the real world, which requires more effective algorithms to deal with them.

In recent years, several researches combined with the machine learning techniques had been put forward in the area of computational intelligence. A novel approach based on transfer learning and genetic programming (GP) was proposed by Iqbal et al. [37] for image classification. The knowledge reconstruction ability of GP was employed to a large extent for obtaining useful information from two images in each class. The extracted knowledge through learning simple image classification problems would be reused to solve complex problems. A novel genetic transfer learning approach for bootstrap problems in evolutionary robotics was presented in [38], which was named as Family Bootstrapping (FB). FB divided the whole evolutionary process into two stages. In the first stage, the initial population was generated with the help of family ancestors which were the solutions evolved for a common source task. A task was selected from a set of related tasks. The evolutionary process started for employing evolution on the selected task in the second stage.

Although a lot of research has been carried out in the dynamic area, there are still problems to be considered. In the prediction-based approach, the data we employed in the experiments and the data to be predicted may not obey the same distribution. Some researches assume that the solutions predicted by the model and the individuals used for constructing the prediction model meet the condition of independent identical distribution (IID). However, from the point of real world, taking this IID assumption as a precondition does not correspond to the reality. Therefore, it is reasonable to believe that this assumption may cause the failure of some algorithms in solving DMOPs. According to the contents above, a centroid distance and transfer learning-based approach are proposed in this paper. Comparing with other existing dynamic algorithms, the IID assumption is not a precondition in this approach anymore, which is close to the dynamic problems in reality. As one of the efficient many-objective algorithms, NSGA-III can also be used to solve DMOPs, but in practical application, the algorithm performance has yet to be improved. So, the performance of the proposed method will be mainly reflected by the performance improvement of NSGA-III in this paper.

Proposed methods

In this section, the whole process of proposed TC_NSGAIII will be presented in detail. First, the centroid distance method is introduced to get a population closer to reference points. Second, transfer learning is adopted for obtaining a new initial population, and then the obtained population will be put into NSGA-III to get DPFs.

The centroid distance method

This approach is based on the centroid points of individuals. At the beginning of evolution, the initial population was made up of randomly generated individuals. For these randomly generated individuals, some processing on them should be conducted to make them closer to the true DPF. According to the changing characteristics of dynamic problems, it is reasonable to believe that although the environmental changes are different, they are related. The main idea of centroid distance method is to select some populations as the initial population of next evolution by calculating the distance between the centroid of random populations and reference points.

First of all, within the given range of decision variables, a corresponding population is randomly initialized. When an environmental change occurs, the objectives also change to some extent. For the changed objective functions, several reference points are defined corresponding to the objective functions. Then the centroid of the random population will be generated using the following formula:

$$C_{T} = \frac{1}{{\left| {P_{T} } \right|}}\sum\nolimits_{{x \in P_{T} }} x$$
(6)

where |PT| is the cardinality of PT, and x is a solution of decision space in PT. After getting the centroid of the random population, the distribution of population can be estimated roughly. Then the Euclidean distance between the centroid point and the reference point can be calculated by Eq. (7).

$${\text{distance}} = \sqrt {\sum {(C_{T} - Z_{{{\text{min}}}} )^{2} } }$$
(7)

where Zmin are the reference points defined by the changed objectives. The definition method is based on the reference points setting in NSGA-III. The minimum value of each changing objective is defined as a reference point and here Zmin is a set of reference points. The reason for defining reference points is that to measure the distance between the current population and the ideal points. We will set a distance threshold σ. When the distance is less than σ, that is, the centroid and the reference points are close to a certain degree, this random population can be used as the input population for next transfer learning. Otherwise, the population will be reinitialized until the distance is less than the threshold. In the evolution process, this method is used before the transfer learning strategy. The purpose of this method is to select the population closer to the DPF and put it into the transfer learning when the environment changes, which can improve the efficiency of transfer learning to solve DMOPs. The specific algorithm pseudo code is described in detail in Algorithm 1. Here a simple example is given to illustrate the concrete process of the centroid distance method. For example, when the number of objectives is 2, a random population RP containing 200 individuals is firstly obtained, which means RP is a 200 × 2 matrix. Then a set of reference points Zmin = {z1, z2}, where z1 and z2 represent the ideal optimal values of two objectives, respectively. When the number of iterations does not reach the maximum, the distance between the population centroid CT and Zmin will be calculated in a circular way. Suppose the obtained centroid CT = (c1, c2), where c1 and c2 mean the center in two objective directions, respectively. For random population RP, the distance can be calculated as:

$${\text{distance}} = \sqrt {(c_{1} - {\text{z}}_{1} )^{2} + (c_{2} - {\text{z}}_{2} )^{2} } ,$$
(8)

when the distance is less than our predefined threshold, the random population will be retained to the next stage as the initial population. Otherwise, the random population will be re-initialized.

To explore the influence of distance threshold σ on the generated initial population, a parameter sensitivity analysis is conducted. The different values of σ are set and different populations are retained. In this analysis, we set 50 different values for σ which are evenly distributed across the interval [0,10]. What’s more, every individual in the population has ten decision variables and the population size is set as 200. For each generation of the population, the average of each decision variable for the 200 individuals is calculated. Therefore, the tendency of decision variables changing with parameter σ can be obtained as Fig. 1. For easier observation and analysis, five decision variables are randomly selected form 10 decision variables. It can be seen that the overall trend of decision variables is greatly affected by the parameter σ. However, the affected range is small, and the values of the decision variables fluctuate from 0.45 to 0.57. In general, the individuals are not affected much, but the retained population has been filtered to a certain extent, which makes the initial population for evolution closer to the true DPF at the current time.

Fig. 1
figure 1

The parameter sensitivity analysis

Full size image
figure a

Transfer learning method

In transfer learning method, the transfer component analysis (TCA) [14] is mainly used for obtaining the initial population. Firstly proposed by Pan et al. [39], TCA is mainly applied to source and target domains that obey different distributions, and it assumes that there is a feature map φ making the mapped data obey similar distributions. The key is how to find the most suitable mapping to make the distribution the most similar. The TCA uses the MMD definition we introduced in Sect. The preliminary studies and related work. According to Eq. (5), MMD is the difference between the mean values of the source domain and the target domain after mapping. In the process of calculating MMD, TCA introduces kernel function and kernel matrix to find this distance. The kernel matrix used by TCA is:

$${\tilde{\mathbf{K}}} = \left[ \begin{gathered} K_{S,S} \;K_{S,T} \hfill \\ K_{T,S} \;K_{T,T} \hfill \\ \end{gathered} \right]$$
(9)

where KS,T is a kernel function and the value of KS,T is φ(Si)Tφ(Tj). φ represents a mapping function of feature. The meaning of KS,S, KT,S, and KT,T is similar to KS,T. What’s more, an MMD matrix L is also employed in TCA. Each element in the matrix L is evaluated as follows:

$$\begin{gathered} L_{ij} = \left\{ \begin{gathered} \frac{1}{{n_{1}^{2} }}\;\;\;\;\;\;\;\;x_{i} ,x_{j} \in D_{S} \hfill \\ \frac{1}{{n_{2}^{2} }}\;\;\;\;\;\;\;\;x_{i} ,x_{j} \in D_{T} \hfill \\ - \frac{1}{{n_{1} n_{2} }}\;\;\;\;\;{\text{otherwise}} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered}$$
(10)

Through a series of computational transformations, Eq. (5) can be reduced to:

$$MMD(X,Y) = tr({\tilde{\mathbf{K}}\mathbf{L}}) - \lambda tr({\mathbf{K}}),$$
(11)

where K is a symmetric matrix and KT = K. tr(K) means the trace of matrix K, which calculates the sum of the diagonal elements of a matrix. To simplify the calculation, Pan et al. [39] used the method of dimensionality reduction to construct the results. A lower dimensional matrix W is used in TCA.

$${\tilde{\mathbf{K}}} = ({\mathbf{KK}}^{{ - \frac{1}{2}}} {\mathbf{W}})({\mathbf{W}}^{T} {\mathbf{K}}^{{ - \frac{1}{2}}} {\mathbf{K}}) = {\mathbf{KWW}}^{T} {\mathbf{K}}.$$
(12)

According to the properties of the matrix trace, the final optimization goal of TCA is

$$\begin{gathered} \mathop {\min }\limits_{W} tr({\mathbf{W}}^{T} {\mathbf{KLKW}}) + \mu tr({\mathbf{W}}^{T} {\mathbf{W}}) \hfill \\ s.t.\;\;{\mathbf{W}}^{T} {\mathbf{KHKW}} = {\mathbf{I}}_{{n_{{1}} { + }n_{{2}} }} . \hfill \\ \end{gathered}$$
(13)

The following condition in Eq. (13) is to allow the source and target domains to maintain their respective data characteristics. And H is a center matrix, whose value is In1+n2 – [1/(n1 + n2)]11 T. In1+n2 is a (n1 + n2) × (n1 + n2) identity matrix. 1 means a (n1 + n2) × 1 matrix with all ones. Pan concluded by seeking the Lagrange duality: the solution to W is the leading m eigenvalues of (KLK + μI)−1KHK.

In summary, the general steps of the TCA method are as follows: Firstly, input the data matrix of the source and target domains. Then select some kernel functions to map and obtain the kernel matrix \({\tilde{\mathbf{K}}}\). The matrix H and L should be calculated according to Eqs. (10) and (13). At last, the lower dimensional matrix W can be generated through calculating the leading m eigenvalues. The process of TCA can be described in Algorithm 2.

figure b

TC_NSGAIII

The overall flow of TC_NSGAIII algorithm is described in this section. Combined with the methods in the previous two sections, we choose NSGA-III as the evolutionary algorithm. The main reason is that few studies focused on improving the performance of NSGA-III in addressing DMOPs. Adding environmental change strategies to the static NSGA-III can improve its ability to solve dynamic problems. The approach presented in this article is a good strategy for dealing with changes. The following describes the overall flow of the algorithm combined with NSGA-III.

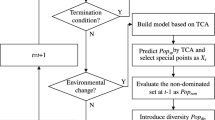
At the beginning of the TC_NSGAIII, the population is randomly initialized within the defined range. Then the centroid distance method is used for generating the input population of TCA. After that, according to the objective function before and after the change, two groups of solutions are randomly selected from the input population. The objective values of the two sets of solutions before and after the change are calculated and preserved as the source and target domain of TCA. The matrix W can be obtained from TCA and the mapping to the latent space can be obtained. For each particle mapped to the latent space, we look for the particle closest to it in the target domain, and use it as an individual in the initial population. The key steps of TC_NSGAIII can be represented by Fig. 2. The Fig. 2 describes the whole mapping process of TC_NSGAIII at time t. The centroid distance method is shown in Fig. 2a. By comparing the distance between the population centroid and the reference points, the population with the minimum distance is retained. The decision space can be mapped into the objective space at time t as depicted in Fig. 2b. Please note that we can get a matrix W when the input of TCA are the solutions from time t and t + 1. The latent space LS can be constructed using the matrix W and the mapping function φ(•) also can be obtained. Then the mapping particle j in the latent space can be shown clearly in Fig. 2. (d). The final goal is to find a decision variable x in time t + 1 such that φ(Ft+1(x)) is closet to j, which means the decision variable x should be an individual of predicted population.

Fig. 2
figure 2

The key steps of TC_NSGAIII

Full size image

Through above explanations about TC_NSGAIII, the whole process can be clarified clearly. Then the computing complexity analysis will be given. For centroid distance method, the major time is spent on the calculation of Euclidean distance. Since the population centroid and distance should be obtained in each cycle, it takes O(N × c) time where N and c represent the population size and the number of cycles, respectively. At the stage of transfer learning, the eigenvalue decomposition operation is the most time-consuming, whose time cost is O(d(m1 + m2)2). Here d means the number of nonzero eigenvectors. m1 and m2 show the number of solutions selected from source domain and target domain for constructing the latent space. According to [16], the overall complexity of one generation of NSGA-III is O(N2M), where M is the dimension of objective vectors. Therefore, the whole complexity of TC_NSGAIII can be expressed as O(Nc + d(m1 + m2)2 + 2N2M).

figure c

Experiments

Our experiments are mainly divided into two parts: the first part shows the effectiveness of TC_NSGAIII through strategies comparisons, and the performance improvement can be observed through the comparisons with original algorithms in the second part. The whole experiments are based on MATLAB R2018a, and the running environment is Intel(R) Core (TM) i3-8100 CPU @ 3.60 GHz.

Experimental settings

The proposed strategy is mainly used in the initialization phase of the algorithm. Through a series of selection and mapping methods, an initial population that is more consistent with the current environment can be obtained, and then the optimal solutions after the change can be obtained through evolution. Theoretically, the improved initial population through centroid distance and transfer learning is more adaptable to the changing environment, and then the solutions closer to the real DPF can be obtained. To verify the effectiveness of the proposed method, 12 test functions and eight different sets of dynamic parameters are employed, and three related metrics to measure the convergence and diversity of the algorithm.

The 12 test functions we use come from CEC 2015 [40]. The CEC 2015 test set contains a total of 12 dynamic questions, including various types of changes. These benchmarks come from some classic dynamic problems and with some variants added. Among them, FDA4, FDA5, and their variants are three-objective problems, and the rest are two-objective. There are mainly three types of changes, namely, DPS and DPF change at the same time, DPF changes but DPS does not change, and DPS changes but DPF does not change. The change characteristics of specific problems are shown in Table 1. According to [40], the properties of these benchmarks are different. For example, the DPF changes from convex to concave for dMOP2, HE2, and HE9. The discontinuous DPF can be seen in HE2. For DIMP2, the changing rate of every decision variable is fixed. All in all, these 12 benchmark functions contain different types of dynamic DPF changes, including continuous, discontinuous, concave, convex, and isolated. The CEC 2015 benchmark set is a good standard of measuring whether dynamic algorithms can adapt to various environmental changes well.

Table 1 Parameters of test functions
Full size table

In the 12 test benchmarks, we use the time parameter t and define it as t = (1/nt)⌊τT/τt⌋, where nt, τT, and τt mean the change severity, the maximum number of iterations, and change frequency, respectively. As described in Table 2, eight different dynamic parameters are set for conducting experiments. We set different change severity, change frequency and number of iterations to ensure that each function can be changed 20 times. The whole population size is set to 200, which means 200 solutions can be generated within the evolution process. Besides, the parameter σ of centroid distance method is set to 3.6. For transfer learning phase, the Gaussian kernel function is employed. The specific true DPFs of 12 test functions under eight different dynamic parameters can be observed through Fig. 3. Among these DPFs in Fig. 3, the red line depicts the DPF at the initial time step (t = 0), and the blue describes the general trend at the time step t = 1. It is obvious that the true DPFs of twelve functions are not identical as the time step changes.

Table 2 The dynamic parameters
Full size table
Fig. 3
figure 3

The true DPFs of 12 benchmarks. The red and blue lines represent the true DPFs at time 0 and 1, respectively

Full size image

Three metrics are mainly used to measure the performance of the dynamic algorithms. These three metrics are based on variants of the classic multi-objective metric inverted generational distance (IGD), which is a comprehensive evaluation metric. The overall performance can be measured by calculating the sum of the minimum distances between the real DPF and the set of individuals obtained by the selected algorithms. An algorithm with excellent comprehensive performance not only converges quickly but also has a good distribution. The specific formula of IGD is as follows:

$${\text{IGD}}(S,P^{*} ) = \frac{{\sum\nolimits_{{x \in P^{*} }} {{\text{min}}_{y \in S} {\text{dis}}(x,y)} }}{{\left| {P^{*} } \right|}}$$
(14)

where P* is a set of points evenly distributed on the real DPF, and S is the optimal Pareto optimal solution set obtained by the algorithm. What’s more, |P*| shows the number of solutions distributed on the real DPF, while dis(x, y) calculates the minimum Euclidean distance between the real DPF and obtained solutions. The overall meaning of the formula is to find the average value of the minimum distance from the point set on the real DPF to the obtained population. From the above equation, it can be seen that a smaller value of dis(x, y) means a better convergence, and then the convergence performance of the algorithm can be displayed concretely. However, a poor distribution represents that most individuals in the population are concentrated in a small area, and then the calculated dis(x, y) of many individuals will be large. Therefore, the smaller dis(x, y) obtained, the better the overall performance is. What’s more, to measure dynamic algorithms’ performance accurately, a variant of IGD was proposed [41]. Based on the definitions of IGD, some concepts about time steps had been added into the metric IGD. The metric MIGD gets the average value of IGD in some time steps over a single run, which is given by:

$${\text{MIGD}} = \frac{1}{\left| T \right|}\sum\nolimits_{t \in T} {{\text{IGD}}(S,P^{*} )} .$$
(15)

In Eq. (15), T represents some discrete time steps within a run. |T| is the cardinality of T. Obviously, it is worth noting that MIGD considers different dynamics in one environment, and the comprehensive performance can be evaluated through observing the final result of MIGD.

In addition, for a more in-depth study of DMOEAs, another metric was adopted. What can be seen obviously from Eq. (15) is that MIGD just takes only one environment into consideration when measuring DMOEAs. However, there is no doubt that more than one environmental change would occur in real-world applications. Therefore, a novel metric DMIGD used for measuring the overall performance under different environments was defined [14], which can be described as follows:

$${\text{DMIGD}} = \frac{1}{\left| E \right|}\sum\nolimits_{e \in E} {{\text{MIGD}}(S,P^{*} ,T)} ,$$
(16)

where E represents the number of environments in the experiments. According to Table 2, there are eight different configurations (S1–S8) in experiments, which means the value of |E| is 8.

The overall performance of an algorithm can be evaluated through above three metrics. Besides, comparing with the original algorithm, another variant about MIGD is adopted for measuring the performance improvement. Therefore, another metric is proposed in this paper for measuring the degree of improvement. The specific metric IR (Improvement Ratio) is based on the values of MIGD. By comparing with original values of MIGD, the degree of improvement can be expressed as a more intuitive percentage. The metric IR can be formulated as:

$${\text{IR}} = \frac{{{\text{MIGD}}_{ori} (S,P^{*} ,T) - {\text{MIGD}}_{imp} (S,P^{*} ,T)}}{{\left| {{\text{MIGD}}_{ori} (S,P^{*} ,T)} \right|}} \times 100\% .$$
(17)

The metric IR shows the difference between the original algorithm and the improved algorithm. The bigger the value of IR is, the more performance increases.

The overall experiments are mainly divided into two parts: the first part verifies the performance of TC_NSGAIII through comparing with six dynamic algorithms, and the improvement ratio is calculated through the second experiment, showing the efficiency of our proposed strategy. In addition, the other two algorithms are also combined with our proposed strategy, and the improvement is also obvious.

Our entire experiments are implemented with MATLAB R2018a. In the experiments, we use 12 test functions, which come from CEC 2015 [40]. The specific characteristics of 12 test functions can be shown in Table 1.

Performance comparisons with other algorithms

In this section, the experiments about the performance comparisons are conducted. The metrics MIGD and DMIGD mentioned above are employed, and some algorithms are compared with our proposed algorithm. At first, the MIGD values of four algorithms are compared, which proves the effectiveness of proposed algorithm. These four algorithms include NSGA-III combined both the transfer learning and centroid distance strategies (TC_NSGAIII), NSGA-III incorporated with the transfer learning method only (Tr_NSGAIII), NSGA-III combined the single centroid distance strategy (Ce_NSGAIII), and the original NSGA-III algorithm [19]. In addition to above four algorithms, other three dynamic algorithms are also adopted for comparison, which are Kalman prediction-based MOEA (MOEA/D-KF) [6], multi-objective particle swarm optimization with multidirectional prediction (MDP_MOPSO) [26], and NSGA-II combined with transfer learning (Tr_NSGAII) [14]. The main framework of compared algorithms will be described in detail next.

Because the individual in population is ten-dimensional, it is difficult to describe the individual accurately in a figure. To observe the performance of our proposed algorithm, the DPFs obtained by TC_NSGAIII at time 20 are shown in Fig. 4. On the whole, the DPFs of 12 benchmarks have certain regularity, especially for two-objective functions. Comparing with Fig. 3, the general trend is the same. Obviously, some differences exist between the obtained DPFs and true DPFs, which ensures the diversity of solutions. The convergence of DPFs can also be depicted clearly in Fig. 4. However, it is not accurate to depict the diversity and convergence of solutions on figures alone. Some metrics should be used for measuring the performance of an algorithm more precisely, such as MIGD and its variants.

Fig. 4
figure 4

The DPFs of 12 benchmarks obtained by TC_NSGAIII at time 20

Full size image

The MIGD values of four algorithms under eight different dynamic configurations are shown in Table 3. It is pretty obvious that the best results of TC_NSGAIII achieves 74 among 96 total results. The ratio of best results can be up to 78%. In the all results of twelve different benchmarks, TC_NSGAIII performs better than other three algorithms generally. The specific data in Table 3 suggest that the performance of TC_NSGAIII achieves best in dMOP2 and FDA5_iso. Even with eight different sets of dynamic parameters, the ratio of the optimal results in the two test functions mentioned reaches 100%. Combined with the dynamic characteristics and DPFs depicted in Table 1 and Fig. 3, our proposed algorithm is suitable for solving DMOPs with changing DPS or DPF. TC_NSGAIII performs equally on the other ten benchmark functions. For each of these 12 test functions, TC_NSGAIII can ensure more than five best results in eight experimental settings. We can see that the performance of TC_NSGAIII is significantly better than Tr_NSGAIII and Ce_NSGAIII. The last column in Table 3 represents the “winner” in this comparison. By comparative analysis, the combination of transfer learning and centroid distance can deal with varying degrees of changes, which is suitable for both two-dimensional and three-dimensional functions. From the perspective of different dynamic parameters, TC_NSGAIII reaches the 11 best results in 12 total functions when the experiments setting is “S4”. “S4” means that the change severity is set to 10 and the change frequency is set to 50. It implies that comparing other change types, TC_NSGAIII performs well when facing relatively severe and infrequent changes. In summary, the data in Table 3 fully reflect the effectiveness and necessity of combining the transfer learning and centroid distance strategy.

Table 3 The MIGD values of four comparative algorithms
Full size table

The specific experimental data in Table 4 show the DMIGD values of eight different algorithms. Except for the compared algorithms in Table 3, other three dynamic algorithms are employed for comparison. MOEAD-KF proposed by Arrchana et al. [6] used Kalman filter prediction to deal with DMOPs. Kalman filter can be an excellent prediction tool to estimate the process state. In this Kalman filter prediction model, a feedback control was employed for estimation. The Kalman filter was mainly divided into two groups: time update equations which predict the next state and measurement update equations used for information feedback. MDP_MOPSO combined multidirectional prediction with multi-objective particle swarm optimization algorithm, which was proposed by Rong et al. [26]. In multi-objective prediction model, the optimal solution of the problem was clustered into representative individuals. The representative individuals were used for predicting the moving DPF, and then the predicted solutions were generated. Tr_NSGAII incorporated transfer learning into NSGAII for solving DMOPs, which is put forward by Jiang et al. [14]. MOEA/D-SVR, proposed by Cao et al. [42], presented a support vector regression predictor with MOEA/D to generate the initial population in the new environment. A nonlinear mapping was used for mapping the historical solutions into a high-dimensional feature space.

Table 4 The DMIGD values of eight different algorithms
Full size table

The DMIGD values of eight compared algorithms can be shown in Table 4. It is obvious that the best results of TC_NSGAIII reaches 9 in 12 test functions. The metric DMIGD represents the overall performance of dynamic algorithms when facing unknown changes. Among the seven compared algorithms, TC_NSGAIII has better performance than other dynamic algorithms over different types of change. Comparing with NSGA-III and Tr_NSGAIII, the DMIGD values of TC_NSGAIII are smaller under 12 functions, which implies that TC_NSGAIII has better stability in tracking moving DPF.

Synthesizing the experimental data in Tables 3 and 4, the effectiveness and stability of TC_NSGAIII can be fully demonstrated. What’s more, TC_NSGAIII is competitive through comparing with some chosen dynamic algorithms. It shows good ability to respond to changes in both MIGD and DMIGD metrics, and more accurately tracks the true DPF of the next time step through the predicted population. There is no doubt that TC_NSGAIII is an outstanding dynamic multi-objective algorithm in dealing with different types of DMOPs.

Performance improvement experiments

The experiments about performance improvement are implemented in this section. Three classical evolutionary algorithms are chosen for combining with transfer learning and centroid distance strategies. These evolutionary algorithms are NSGA-III, MOPSO, and NSGA-II, respectively. It is worth mentioning that these three algorithms are not suitable for dynamic optimization. However, some dynamic strategies can be added to these algorithms to solve dynamic problems. It is not difficult to find that MOPSO and NSGA belong to different classes, which can prove the capability of strategies on different algorithms. The reasons why both NSGA-III and NSGA-II are chosen are as follows: first of all, the dynamic version of NSGA-II has been proposed by Deb et al. [22]. However, NSGA-III has not been employed for dynamic optimization. One of the innovations of this paper is to apply the strategies to NSGA-III to solve DMOPs. Second, applying the same dynamic strategy to NSGA-II and NSGA-III and comparing them, a conclusion can be drawn that which algorithm this strategy is more suitable for. It is very helpful to promote the follow-up research of NSGA-III in dynamic optimization.

The experimental data in Tables 5, 6, 7 represent the performance difference between original chosen algorithms and improved algorithms. The IR values in bold mean the positive performance improvements. The observation we can get from Tables 5, 6, 7 is that the overall effective ratio of TC_NSGAIII, TC_MOPSO, and TC_NSGAII is 92.71% (89 cases of total 96 tests), 78.13% (75 cases of total 96 tests), and 67.71% (65 cases of total 96 tests), respectively. By carefully analyzing the data in Tables 5, 6, 7, more precise information can be obtained. For TC_NSGAIII, there are 8 cases whose IR values exceed 100%, and the IR values of 33 tests are between 50 and 100%. For TC_MOPSO, there are no cases whose IR exceeds 100%, and the IR of 50 cases are greater than 50% and less than 100%. For TC_NSGAII, there are also no IR values exceeding 100%, and only 18 IR values are between 50 and 100%. The results we get from experiments show that the transfer learning and centroid distance strategy can indeed improve the performance of an algorithm when dealing with DMOPs. Through the comparison of the distribution of IR values, it is obvious that the IR values of TC_NSGAIII reach the highest, which means that TC_NSGAIII is more adaptable to changes in the dynamic environments. Although NSGA-II is often used for static multi-objective problems, the experiments demonstrate that our proposed strategy is more suitable for NSGA-III to solve DMOPs. The improved TC_NSGAIII is proved to be competitive through a series of experiments.

Table 5 The IR values of TC_NSGAIII under 12 test functions
Full size table
Table 6 The IR values of TC_MOPSO under 12 test functions
Full size table
Table 7 The IR values of TC_NSGAII under 12 test functions
Full size table

Conclusions

A new idea combining transfer learning and centroid distance strategy was proposed in this paper. Our approach was incorporated into the framework of NSGA-III to solve DMOPs. A given DMOP changes with different time steps, and the optimal solutions at different times obey different distributions. Therefore, some classical methods could not be used for dealing with these Non-IID problems. In addition, few studies applied NSGA-III to dynamic optimization, which makes the dynamic version of NSGA-III more valuable for research.

As an outstanding dynamic algorithm, it must be able to track the moving DPF quickly and accurately. In our proposed approach, the centroid distance was first used to find the solutions closer to the reference points in the initial population. And then, the found solutions were put into the transfer learning process. Transfer learning is mainly to map the source data before the change and the target data after the change to the same latent space, and then looks for the individuals closest to the real DPF in the mapped space to form a new initial population. To verify the feasibility and effectiveness of our method, two parts of experiments were conducted in this paper. Through the comparison with some original algorithms and other dynamic algorithms, it is obvious that TC_NSGAIII performs best on 12 CEC 2015 benchmarks, and the proposed technique can improve the performance of NSGA-III to a great extent.

More techniques should be further studied on DMOPs. For future works, we will focus on improving the efficacy of the proposed algorithms and try to propose more techniques on solving DMOPs. Besides, our proposed approach is expected to be integrated into more classical algorithms and applied to solve more DMOPs in real world.