Probabilistic screening and behavior of solar cells under Gaussian parametric uncertainty using polynomial chaos representation model

Abstract

The paper presents a hierarchical polynomial chaos expansion-based probabilistic approach to analyze the single diode solar cell model under Gaussian parametric uncertainty. It is important to analyze single diode solar cell model response under random events or factors due to uncertainty propagation. The optimal values of five electrical parameters associated with the single diode model are estimated using six deterministic optimization techniques through the root-mean-square minimization approach. Values corresponding to the best objective function response are further utilized to describe the probabilistic design space of each random electrical parameter under uncertainty. Adequate samples of each parameter corresponding Gaussian uncertain distribution are generated using Latin hypercube sampling. Furthermore, a multistage probabilistic approach is adopted to evaluate the model response using low-cost polynomial chaos series expansion and perform global sensitivity analysis under specified Gaussian distribution. Coefficients of polynomial basis functions are calculated using least square and least angle regression techniques. Unlike the highly non-linear and complex single diode representation of solar cells, the polynomial chaos expansion model provides a low computational burden and reduced complexity. To ensure reproducibility, probabilistic output response computed using proposed polynomial chaos expansion model is compared with the true model response. Finally, a multidimensional sensitivity analysis is performed through Sobol decomposition of polynomial chaos series representation to quantify the contribution of each parameter to the variance of the probabilistic response. The validation and assessment result shows that the output probabilistic response of the solar cell under Gaussian parametric uncertainty correlates to a Rayleigh probability distribution function. Output response is characterized by a mean value of 0.0060 and 0.0760 for RTC France and Solarex MSX83 solar cells, respectively. The standard deviation of $\pm$ 0.0034 and $\pm$ 0.0052 was observed in the probabilistic response for RTC France and Solarex MSX83 solar cells, respectively.

Introduction

The conventional power infrastructure widely employing fossil fuels for a centralized generation has seen a shift toward renewable-based technologies. Solar energy is quite popular among renewable due to its easy availability and potential. The role of the solar photovoltaic cell will be crucial in reshaping future energy systems through cost-effective innovations in solar cell material and manufacturing technology, advancement in power electronics, intelligent control, and forecasting models [1]. Thus, a photovoltaic engineer related to power generation and control needs to understand the electrical performance and behavior of different solar cell technologies under standard conditions. Consequently, accurate modeling of PV cell electrical performance is essential in planning, designing, and analyzing the technical or economical performance of photovoltaic based systems.

Modeling electrical characteristics is considered the most important diagnostic method for the characterization of solar cells. The current–voltage characteristic equation contains several electrical parameters. These parameters signify certain physical phenomena occurring in solar cells. Various equivalent circuit models based on physical phenomena and electrical properties have been developed to analyze the electrical characteristics of a PV cell. The most commonly adopted models are the single diode model and double diode model. Another advanced model includes an electrical equivalent representation of solar cells using three diodes [2].

Various techniques and methodologies have been adopted by researchers to estimate the electrical parameters of a solar photovoltaic cell. To improve the accuracy of the model, different analytical, numerical, graphical [3] and meta-heuristic approaches were proposed. In recent years, analytical methods such as Newton–Raphson method [4], Lambert W functions [5], piece-wise curve fitting [6], Levenberg–Marquardt method [7], and optimization techniques such as Differential evolution algorithm [8], Bacterial foraging optimization [9], Particle swarm optimization [10], Firefly algorithm [11, 12], and Genetic algorithm [13] were employed. The selection and identification of criteria for assessing the accuracy of optimization techniques is also an important research aspect. Standard statistical parameters such as the sum of squares error (SSE), root-mean-square error (RMSE), mean bias error (MBE), individual absolute error (IAE), etc. are commonly used by researchers to frame the objective or cost function which decides the accuracy and reliability of the model.

Easwarakhanthan et al. [7] proposed a modified Newton–Raphson with Levenberg parameter to extract five solar cell parameters from the experimental data. It requires the initialization of only two parameters instead of five using a reduced non-linear least-squares technique. Ishaque et al. [8] proposed a model for parameter extraction using differential evolution (DE) algorithm to minimize the derivative of power with respect to the voltage at maximum power point condition. Louzazni et al. [11] adopted the Firefly algorithm to minimize the sum of all individual absolute current error using experimental data-points. Beigi et al. [12] proposed a method by combining a pattern search algorithm as the local optimization problem with the Firefly algorithm to minimize the root-mean-square error (RMSE) in current values. Toledo et al. [14] proposed an analytic and quasi explicit method using four arbitrary points and their slopes on the I–V curve. The optimal solution of the five parameters of a solar cell is obtained by solving a fifth-degree polynomial. Cubas et al. [5] proposed a technique to modify the implicit Shockley current equation into an explicit expression using Lambert W function which can be solved to find the optimal values of solar cell electrical parameters. Liao et al. [15] proposed a teaching–learning-based optimization for estimating five and seven electrical parameters associated with a single diode and double diode model of a solar cell. It involves iterative improvement in mean score of the whole candidate population through previous learning.

It is to be noted that the scope of the articles reviewed in the literature survey is limited only to parameterization problem through objective function minimization or maximization techniques. These approaches are deterministic in nature. Under practical operating conditions, these electrical parameters may be subjected to uncertainties related to charge-carrier recombination, electrical losses, surface, and bulk defects, partial shading, optical hindrance, etc. [16]. These uncertainties in the electrical parameters of a solar cell are represented as random noise. Hence, a hierarchical probabilistic model is proposed for analyzing the single diode computational model response under random parametric uncertainties. Initially, a deterministic approach is adopted, as shown in Fig. 1, to minimize the user-defined objective function using six different optimization techniques. Out of six optimization methods, two classical and global optimization techniques, viz., the Multi-Variate Newton–Raphson (MV-NR) method and the Particle swarm optimization (PSO), are adopted for validation purposes. Firefly algorithm (FA), Black Widow Optimization (BWO), Wind-driven Optimisation (WDO), and its adaptive version, i.e., AWDO, are four recent meta-heuristic optimization techniques chosen for the optimal parameter extraction problem.

Fig. 1

Deterministic analysis for single diode model of a solar cell

The optimal values obtained using the most accurate algorithm technique are employed for further analysis. Eventually, a preliminary distribution of each electrical parameter is defined using known probability function as a result of randomization due to parametric uncertainty. Adequate numbers of samples are generated to test, validate, and examine the probabilistic response of solar cells through a multistage approach shown in Fig. 2. In this approach, the true model response is represented as a series of univariate and multivariate polynomials to form a polynomial chaos expansion model. Formulation of polynomial basis functions and calculation of coefficients are the two prerequisites for a polynomial chaos series representation. Least square regression (LSR) and least angle regression (LAR) techniques are employed for computing the coefficient of each polynomial basis function. Based on polynomial chaos expansion model, a multidimensional sensitivity analysis is also presented in Fig. 3. It is done to compute the impact of parametric uncertainty propagation on the model response due to first-order effects of each parameter and second-order interactions between two parameters. A diagnostic analysis based on Sobol indices is carried out to classify a set of electrical parameters into three segments: Sensitive, Interactive, and Insignificant.

Fig. 2

Multistage probabilistic analysis to define single diode model under uncertainties

Fig. 3

Multidimensional sensitivity analysis methodology for single diode model under random parametric uncertainty

To summarize, the main objectives of this research work are:

• 1. The deterministic parameterization problem requires the formulation of an objective function. In this research work, an improved objective function is formulated based on the division of the solar PV characteristic curve into two zones. Mathematically, it can be defined as the sum of root-mean-square error (RMSE) in each zone identified on the PV curve.

• 2. Probabilistic analysis through polynomial chaos series expansion using least square regression provides a significant advantage in terms of computation cost and complexity compared to the traditional Monte Carlo approach.

• 3. A reduced-degree polynomial chaos series expansion is achieved using least angle regression with a fewer number of coefficients compared to least square regression.

The work is segregated into following sections. Section 2 describes the equivalent single diode electrical model of a solar photovoltaic cell. Section 3 deals with the formulation of an objective function for the deterministic parameterization problem. Section 4 explains a hierarchical approach to examine the effect of probabilistic parametric uncertainty on the model response. The development of polynomial chaos expansion model based on two regression techniques is also explained in this section. Finally, a multidimensional sensitivity analysis is presented in the section based on Sobol decomposition of polynomial chaos expansion model using LSR, LAR, and true computation model using Monte Carlo approach. Deterministic response, probabilistic response, and global sensitivity results for the two solar PV cell test cases are presented in section 5.

Solar photovoltaic cell

Solar cells are the basic unit of any photovoltaic-based system. Solar photovoltaic cells derive their energy from the sun and convert it into electrical energy based on the photovoltaic effect. The electrical performance of the PV cells can be demonstrated using equivalent electrical models. To understand the electrical behavior of a solar cell shown in Fig. 4, we need to understand the physics behind it. Conversion of solar energy into electrical energy involves various mechanisms which include absorption of photons, generation of charge carriers, charge separation, transportations, and collection [17].

Fig. 4

Schematic diagram of an efficient silicon-based solar cell

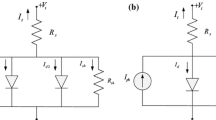
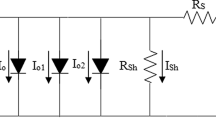
A solar cell performs two basic functions from an electrical point of view: photocurrent generation and photo-voltage generation. There are certain dissipative electrical losses associated with a solar cell. These can be mainly due to improper doping, manufacturing and designing defects, leakage paths, metal contacts, etc. These electrical losses can be represented using parasitic resistances. Series resistance $R_\mathrm{Se}$ is mainly due to internal losses due to charge recombination at the metal surface/contact. Shunt resistance $R_\mathrm{Sh}$ represents the effect of leakage current due to recombination at the junction and leakage current at the cell edges [18]. An ideal solar cell can be considered as a current source in parallel to a diode. Considering the effects of parasitic resistances, a solar photovoltaic cell can be represented using an equivalent electrical model, as shown in Fig. 5 [19]. The equation governing the electrical characteristics is defined by

$$\begin{aligned}&\;{I_{\mathrm{{PV}}}} = {I_{\mathrm{{Ph}}}} - {I_\mathrm{{O}}}\left( {{e^{\left( {\frac{{q\left( {{V_{\mathrm{{PV}}}} + {I_{\mathrm{{PV}}}}{R_{\mathrm{{Se}}}}} \right) }}{{nk{T_\mathrm{{c}}}}}} \right) }} - 1} \right) \nonumber \\&\qquad \qquad - \left( {\frac{{{V_{\mathrm{{PV}}}} + {I_{\mathrm{{PV}}}}{R_{\mathrm{{Se}}}}}}{{{R_{\mathrm{{Sh}}}}}}} \right) . \end{aligned}$$

(1)

Fig. 5

Single diode equivalent electrical model of a solar cell

The term n inside the exponential function is the diode ideality factor, and normally ranges between 1 and 2 for a practical diode. The term $I_\mathrm{O}$ represents reverse bias current in the dark or the reverse saturation current.

Equation (1) suggests that five parameters are required to be predicted for the accurate modeling of PV cells. These are photon current ($I_\mathrm{Ph}$), reverse saturation current ($I_\mathrm{O}$), diode ideality factor (n), series resistance ($R_\mathrm{Se}$), and shunt resistance ($R_\mathrm{Sh}$).

Objective function formulation

The solar photovoltaic cell can be modeled using a single diode model using Eq. (1) where five electrical parameters are unknown. The objective function is defined as the root-mean-square error (RMSE) between a specified number of measured and experimental values. In this paper, two different zones are identified on the power–voltage curve of the PV cell and the objective is to minimize the sum of RMSE for the two zones, as shown in Fig. 6. Zone 1 is selected where the error is based on measured and actual current values. Zone 2 is selected where the error is based on the measured and actual power values. The unknown parameters can be defined by vector S representing an optimal solution of five electrical parameters

$$\begin{aligned} S = {\left[ {{I_{\mathrm{{Ph}}}}\;\;{I_\mathrm{{O}}}\;\;n\;\;{R_{\mathrm{{Se}}}}\;\;{R_{\mathrm{{Sh}}}}} \right] ^\mathrm{{T}}}. \end{aligned}$$

(2)

Fig. 6

Typical V–I and P–V characteristics of a PV cell divided into two zones for framing the objective function

Equation (1) can be modified to frame the objective function for the parameterization problem as follows:

$$\begin{aligned}&I\left( {{I_{\mathrm{{PV}}}},{V_{\mathrm{{PV}}}},S} \right) \nonumber \\&\qquad = {I_{\mathrm{{Ph}}}} - {I_\mathrm{{O}}}\left( {{e^{\left( {{{q\left( {{V_{\mathrm{{PV}}}} + {I_{\mathrm{{PV}}}}{R_{\mathrm{{Se}}}}} \right) } \over {nk{T_\mathrm{{c}}}}}} \right) }} - 1} \right) - \left( {{{{V_{\mathrm{{PV}}}} + {I_{\mathrm{{PV}}}}{R_{\mathrm{{Se}}}}} \over {{R_{\mathrm{{Sh}}}}}}} \right) \end{aligned}$$

(3)

$$\begin{aligned}&\qquad P\left( {{I_{\mathrm{{PV}}}},{V_{\mathrm{{PV}}}},S} \right) = {I_{\mathrm{{Ph}}}}{V_{\mathrm{{PV}}}} - {I_\mathrm{{O}}}\left( {{e^{\left( {\frac{{q\left( {{V_{\mathrm{{PV}}}} + {I_{\mathrm{{PV}}}}\;{R_{\mathrm{{Se}}}}} \right) }}{{n\;k\;{T_\mathrm{{c}}}}}} \right) }} - \mathrm{{1}}} \right) \;{V_{\mathrm{{PV}}}}\nonumber \\&\quad - \;\left( {\frac{{{V_{\mathrm{{PV}}}}^\mathrm{{2}} + {V_{\mathrm{{PV}}}}\;{I_{\mathrm{{PV}}}}\;{R_{\mathrm{{Se}}}}}}{{{R_{\mathrm{{Sh}}}}}}} \right) .\;\; \nonumber \\ \end{aligned}$$

(4)

The root-mean-square error in the Zone 1 and Zone 2 can be defined as

$$\begin{aligned} {\xi _\mathrm{{1}}} = \sqrt{{1 \over {{n_\mathrm{{1}}}}}\sum \limits _{i = 1}^{{n_1}} {{{\left( {I\left( {{I_{\mathrm{{PV}}}}_\mathrm{{i}},{V_{\mathrm{{PV}}}}_\mathrm{{i}},S} \right) - {I_{\mathrm{{PV}}}}_\mathrm{{i}}} \right) }^2}} } \end{aligned}$$

(5)

$$\begin{aligned} {\xi _\mathrm{{2}}} = \mathrm{{ }}\sqrt{{1 \over {{n_\mathrm{{2}}}}}\sum \limits _{\mathrm{{j = 1}}}^{{\mathrm{{n}}_\mathrm{{2}}}} {{{\left( {P\left( {{I_{\mathrm{{Pv}}}}_\mathrm{{j}},{V_{\mathrm{{Pv}}}}_\mathrm{{j}},S} \right) - {I_{\mathrm{{Pv}}}}_\mathrm{{j}}} \right) }^\mathrm{{2}}}} }, \end{aligned}$$

(6)

where ‘$n_\mathrm{1}$’ and ‘$n_\mathrm{2}$’ are the number of experimental data-points in Zone 1 and Zone 2, (${I_{\mathrm{{P}}{\mathrm{{V}}_\mathrm{{i}}}}}$ , ${V_{\mathrm{{P}}{\mathrm{{V}}_\mathrm{{i}}}}}$) is the experimental value of current and voltage for ith sample, and S is the solution of the five unknown parameters.

Hence, the cost function (O.f.) can be defined as

$$\begin{aligned} O.f. = \xi = {\xi _1} + {\xi _2}. \end{aligned}$$

(7)

The objective is to minimize the cost function defined by Eq. (7) to find a unique solution of S within its defined range.

Probabilistic analysis for single diode model of a solar cell

Uncertainty quantification through probabilistic assessment is a statistical tool to understand a complex engineering process under extrinsic or intrinsic variations [20, 21]. It is important a decision-maker to quantify uncertainties for making a sensible judgement about the model response [22, 23]. However, modeling uncertainties becomes challenging in case of a non-linear, complex, and highly dimensional computational system. Hence, a probabilistic framework is essential to characterize a highly dimensional system under parametric uncertainty.

In a real-world scenario, these electrical parameters are often subjected to uncertainty under practical conditions or due to random events such as partial shading, undersirable recombination, electrical or optical losses, etc. within a solar cell. Hence, a probabilistic model is proposed to observe the model response pertaining to uncertainty in five electrical parameters through a multistage approach as follows.

Defining probability distribution for each uncertain electrical parameter

Each electrical parameter is assumed as a random variable ${{{{\tilde{X}}}_\mathrm{{i}}}}$ whose shape is defined by a probability distribution function ${f_{{{{{{\tilde{\mathrm{X}}}}}}_\mathrm{{i}}}}}({x_\mathrm{{i}}})$. Across a wide range applications, statisticians have employed Uniform, Gaussian, Beta, Log-Normal, and Weibull as probability distribution functions for real-world engineering problems [24, 25]. A Gaussian distribution is assumed for randomization of each electrical parameter. Gaussian distribution is typically employed to address uncertainties related to random noise in a parameter or signal. Each random parameter defined using Gaussian distribution is characterized by its mean ${{\mu _\mathrm{{i}}}}$ and standard deviation ${{\sigma _\mathrm{{i}}}}$. Gaussian distribution for each random variable can be mathematically written as

$$\begin{aligned} {f_{{{{{{\tilde{\mathrm{X}}}}}}_\mathrm{{i}}}}}({x_\mathrm{{i}}}) = \Pr \left[ {{{{\tilde{X}}}_\mathrm{{i}}} = {x_\mathrm{{i}}}} \right] = {1 \over {{\sigma _\mathrm{{i}}}\sqrt{2\pi } }}{e^{\left( { - {{{{({x_\mathrm{{i}}} - {\mu _\mathrm{{i}}})}^2}} \over {2{\sigma _\mathrm{{i}}}^2}}} \right) }}. \end{aligned}$$

(8)

Generating adequate samples for each random variable

The generation of an adequate number of samples from the known PDF is essential for randomization to simulate parametric uncertainty in five electrical parameters. Monte Carlo sampling is the most commonly used sampling strategy for analyzing and computing the probabilistic response of a dynamic model. However, sampling through conventional Monte Carlo approach becomes challenging in case of complex and multidimensional engineering problems. It requires a relatively large sample space (in the order of $10^\mathrm{6}$) for an accurate prediction of non-linear system response. Alternatively, Latin hypercube sampling is employed to recreate the input distribution through reduced sample space [26]. Unlike conventional MCS, LHS is a co-ordinated sampling strategy that relies on stratification of pre-specified input probability distribution. In the LHS technique, cumulative distribution curve is equally divided into $n_\mathrm{s}$ sections and a sample is randomly drawn from each stratified section [27]. Hence, $n_\mathrm{s}$ number of samples are generated using LHS.

Formulating a low-cost polynomial chaos expansion model

Consider the objective function in Eq. (7) as the uncertain true computational single diode model C representing the electrical characteristic of a solar cell. The non-linear computational model C involves five input random electrical parameters represented by $C({{\tilde{X}}_\mathrm{{i}}})$. The Gaussian distribution function is used to define the stochastic response of random electrical parameters due to system uncertainty

$$\begin{aligned}&C({\tilde{X}_\mathrm{{i}}}) = {\begin{array}{c} \left\langle {O.f.} \right\rangle _{\mathrm{under}}\\ {\mathrm{uncertainty}} \end{array}} \end{aligned}$$

(9)

$$\begin{aligned}&{{\tilde{X}}_\mathrm{{i}}} = {[{{\tilde{I}}_{\mathrm{{Ph}}}},{{\tilde{I}}_\mathrm{{O}}},{\tilde{n}},{{\tilde{R}}_{\mathrm{{Se}}}},{{\tilde{R}}_{\mathrm{{Sh}}}}]^\mathrm{{T}}}. \end{aligned}$$

(10)

${\sigma _\mathrm{{i}}}$ and ${\mu _\mathrm{{i}}}$ are the standard deviation and mean for each random electrical parameters. If the computational model defined by $C({{\tilde{X}}_\mathrm{{i}}})$ has a finite variance in the design space as defined in Eq. (11), then $C({{\tilde{X}}_\mathrm{{i}}})$ can be expressed as a polynomial function of order n through polynomial chaos expansion technique. Polynomial chaos expansion of uncertain single diode computational model $C({{\tilde{X}}_\mathrm{{i}}})$ is generally expressed as defined in Eq. (12)

$$\begin{aligned}&\mathrm{E}\left[ {{{\left( {O.f.} \right) }^2}} \right] = \int \limits _{{\mathrm{{D}}_{{{{{{\tilde{X}}}}}_\mathrm{{i}}}}}} {{C^2}(} {{\tilde{X}}_\mathrm{{i}}}) \cdot {f_{{{{{{\tilde{X}}}}}_\mathrm{{i}}}}}({x_\mathrm{{i}}}) \cdot \mathrm{{d}}{x_\mathrm{{i}}} < \infty \end{aligned}$$

(11)

$$\begin{aligned}&\quad O.f. = C({{\tilde{X}}_\mathrm{{i}}}) = \sum \limits _{\mathrm{{j = 1}}}^\mathrm{{T}} {{c_\mathrm{{j}}} \cdot {\psi _{\overrightarrow{{{\lambda }_\mathrm{{i}}}} }}({{{\tilde{X}}}_\mathrm{{i}}})}. \end{aligned}$$

(12)

${{\psi _{\overrightarrow{{{\lambda }_\mathrm{{i}}}} }}}$ are polynomial basis functions represented as multivariate polynomials which are orthonormal to the user-defined probability distribution function and ${{c_\mathrm{{j}}}}$ are the weights of each polynomial basis function.

Table 1 Example of univariate Hermite polynomials and associated polynomial basis functions up to fifth degree

Various researchers have investigated and discovered the correlation between different orthonormal polynomials and classical distributions [28]. For a standard Gaussian probability distribution function, orthonormal polynomials were discovered by C. Hermite represented by $H_\mathrm{p}$, a univariate polynomial basis function of degree ‘p’ can be written as [29]

$$\begin{aligned} \psi ({{\tilde{X}}_\mathrm{{i}}}) = \frac{{{H_\mathrm{{p}}}({{{\tilde{X}}}_\mathrm{{i}}})}}{{\sqrt{\mathrm{{p!}}}, }} \end{aligned}$$

(13)

where ${H_\mathrm{{p}}}({{\tilde{X}}_\mathrm{{i}}})$ can be computed using a recursive equation (14) provided initial conditions given by Eq. (15)

$$\begin{aligned}&{H_{\mathrm{{p + 1}}}}({{\tilde{X}}_\mathrm{{i}}}) = {{\tilde{X}}_\mathrm{{i}}} \cdot {H_\mathrm{{p}}}({{\tilde{X}}_\mathrm{{i}}}) - \mathrm{{p}} \cdot {H_{\mathrm{{p - 1}}}}({{\tilde{X}}_\mathrm{{i}}}) \end{aligned}$$

(14)

$$\begin{aligned}&\quad {H_\mathrm{{0}}}({{\tilde{X}}_\mathrm{{i}}}) = 1\mathrm{{\quad and \quad }}{H_\mathrm{{0}}}({{\tilde{X}}_\mathrm{{i}}}) = {{\tilde{X}}_\mathrm{{i}}}. \end{aligned}$$

(15)

For instance, univariate polynomials related to our problem are listed in Table 1 up to fifth degree.

A multivariate polynomial basis function is considered as the tensor product of univariate polynomials where the degree of each univariate polynomial is chosen as a subset of ${{\lambda }_\mathrm{{i}}}$ $\in$ (${{\lambda }_\mathrm{{1}}}$, ${{\lambda }_\mathrm{{2}}}$, ${{\lambda }_\mathrm{{3}}}$, ${{\lambda }_\mathrm{{4}}}$, ${{\lambda }_\mathrm{{5}}}$). To ensure less computational burden, a truncation scheme is adopted to limit the maximum degree of multivariate polynomials. A truncated series of multivariate polynomials of maximum degree ‘p’ can be defined using (16)

$$\begin{aligned}&{\psi _{\overrightarrow{{{\lambda }_\mathrm{{j}}}} }}({{\tilde{X}}_\mathrm{{i}}}) = \prod \limits _{\mathrm{{i = 1}}}^5 {\psi _{\overrightarrow{{{\lambda }_\mathrm{{j}}}} }^{\mathrm{{(i)}}}({{{\tilde{X}}}_\mathrm{{i}}})} ;\;\mathrm{{where}}\;\nonumber \\&0\le {{\lambda }_\mathrm{{i}}}'\mathrm{{s}} \le \,\mathrm{{p\,\, and }}\left| {\sum \limits _{\mathrm{{i = 1}}}^5 {{{\lambda }_\mathrm{{i}}}} } \right| \le \mathrm{{p}}. \end{aligned}$$

(16)

For better understanding, a few multivariate polynomial basis functions are derived for our polynomial chaos expansion-based model and are listed in Table 2 up to a maximum degree of p = 3.

Table 2 Example of a few multivariate Hermite polynomial and associated basis functions up to third degree

For a chosen maximal degree of ‘p’ and the dimension of input random parameters ($N_{d}$), the number of terms (T) present in the truncated polynomial chaos expansion series can be calculated using Eq. (17)

$$\begin{aligned} \mathrm{{T = }}\frac{{({N_\mathrm{{d}}} + \mathrm{{p)!}}}}{{{N_\mathrm{{d}}}!\mathrm{{ }} \cdot \mathrm{{ }}p!}}. \end{aligned}$$

(17)

The weights or coefficients of each multivariate or univariate polynomial basis function can be computed using the traditional least square minimization technique. The polynomial chaos computational model can be transformed into a linear square regression problem as

$$\begin{aligned} O.f. = C({{\tilde{X}}_\mathrm{{i}}}) + {\varepsilon _r} = \sum \limits _{\mathrm{{j = 1}}}^{{\mathrm{{T}}_{\mathrm{{LSR}}}}} {{c_\mathrm{{j}}} \cdot {\psi _{{{{{\uplambda }}}_\mathrm{{i}}}}}({{{\tilde{X}}}_\mathrm{{i}}})} + {\varepsilon _r}. \end{aligned}$$

(18)

Considering $n_\mathrm{s}$ as the number of samples of each random electrical parameter, the model response O.f. can be written in matrix form as

$$\begin{aligned} {\left[ {O.f.}\right] _{{\mathrm{{n}}_s}\mathrm{{x1}}}} = {\left[ {{\psi _\mathrm{{t}}}({{{\tilde{X}}}_\mathrm{{i}}})} \right] _{{\mathrm{{n}}_s}\mathrm{{x}}{\mathrm{{T}}_{\mathrm{{LSR}}}}}}{\left[ {{c_\mathrm{{T}}}} \right] _{{\mathrm{{T}}_{\mathrm{{LSR}}}}\mathrm{{x1}}}} + {\left[ {{\varepsilon _r}} \right] _{{\mathrm{{n}}_s}\mathrm{{x1}}}}. \end{aligned}$$

(19)

LSR-based polynomial chaos model response estimate can be written as

$$\begin{aligned} {\widehat{O.f.}_{\mathrm{{LSR}}}} = \widehat{C({{{\tilde{X}}}_\mathrm{{i}}})} = \widehat{{c_{{\mathrm{{T}}_{\mathrm{{LSR}}}}}}}{\psi _\mathrm{{T}}}({{\tilde{X}}_\mathrm{{i}}}). \end{aligned}$$

(20)

The objective is to find the values of coefficient = [$c_\mathrm{1}$, $c_\mathrm{2}$, $c_\mathrm{3}$, $c_\mathrm{4}$,....,$c_\mathrm{T}$]T by minimizing the mean square error optimization problem defined in the Eq. (21)

$$\begin{aligned} \widehat{{c_\mathrm{{T}}}} = \mathop {\arg \min }\limits _{{c_1},{c_2},{c_3}....{c_\mathrm{{n}}}} {1 \over {{\mathrm{{n}}_s}}}\sum \limits _{\mathrm{{i}} = 1}^{{\mathrm{{n}}_s}} {{{[{{(O.f.)}_\mathrm{{i}}} - \widehat{{{(O.f.)}_\mathrm{{i}}}}]}^2}}. \end{aligned}$$

(21)

The above equation can be analytically solved using matrix transformation to find the coefficients of each polynomial basis function ${\psi _\mathrm{{T}}}({{\tilde{X}}_\mathrm{{i}}})$

$$\begin{aligned} \widehat{[{c_\mathrm{{T}}}]} = {\left( {{{[{\psi _\mathrm{{T}}}({{{\tilde{X}}}_\mathrm{{i}}})]}^\mathrm{{T}}}[{\psi _\mathrm{{T}}}({{{\tilde{X}}}_\mathrm{{i}}})]} \right) ^{ - 1}}{[{\psi _\mathrm{{T}}}({{\tilde{X}}_\mathrm{{i}}})]^\mathrm{{T}}}[O.f.]. \end{aligned}$$

(22)

The values of coefficients $c_\mathrm{1}$, $c_\mathrm{2}$, $c_\mathrm{3}$, $c_\mathrm{4}$,....,$c_\mathrm{T}$ are substituted in the Eq. (22) to form a polynomial chaos expansion model using least square regression technique which can be represented as [30]

$$\begin{aligned} {(O.f.)_{\mathrm{{LSR}}}} = C{({{\tilde{X}}_\mathrm{{i}}})_{\mathrm{{LSR}}}} = \sum \limits _{\mathrm{{j = 1}}}^{{\mathrm{{T}}_{\mathrm{{LSR}}}}} {{c_\mathrm{{j}}} \cdot {\psi _{{{{{\uplambda }}}_\mathrm{{j}}}}}({{{\tilde{X}}}_\mathrm{{i}}})}, \end{aligned}$$

(23)

where $\lambda$ ranges from 0 to number of terms (T) specified by Eq. (17).

Since the solar cell single diode computation model is a highly non-linear and complex model which requires solving implicit Shockley diode equation, a large number of sample space (in order of $10^\mathrm{5}$) are required for polynomial chaos model fitting. For representing a polynomial chaos series expansion model up to $6\mathrm{th}$ degree, a total number of 462 coefficients and polynomial basis functions are required. This may result in more computation burden and higher complexity. To model a low-cost polynomial chaos expansion representation, a least angle regression (LAR) method is employed to limit the computation tasks [31].

The polynomial chaos computational model can be transformed into a least angle regression problem as

$$\begin{aligned} O.f{._{\mathrm{{True}}}} = C{({{\tilde{X}}_\mathrm{{i}}})_{\mathrm{{LAR}}}} + {\varepsilon _r} = \sum \limits _{\mathrm{{j = 1}}}^{{\mathrm{{T}}_{\mathrm{{LAR}}}}} {{c_\mathrm{{j}}} \cdot {\psi _{{{{{\uplambda }}}_\mathrm{{i}}}}}({{{\tilde{X}}}_\mathrm{{i}}})} + {\varepsilon _r}. \end{aligned}$$

(24)

The regression problem defined using LSR in (21) can be transformed by including a $L_\mathrm{1}$ penalty term to the mean square error

$$\begin{aligned} \widehat{{c_\mathrm{{T}}}} = \mathop {\arg \min }\limits _{{c_1},{c_2},{c_3}....{c_\mathrm{{n}}}} {1 \over {{\mathrm{{n}}_s}}}\sum \limits _{\mathrm{{i}} = 1}^{{\mathrm{{n}}_s}} {{{[{{(O.f.)}_\mathrm{{i}}} - \widehat{{{(O.f.)}_\mathrm{{i}}}}]}^2}} + \alpha \left\| {{c_\mathrm{{j}}}} \right\| , \nonumber \\ \end{aligned}$$

(25)

where $\alpha \left\| {{c_\mathrm{{j}}}} \right\|$ is the $L_\mathrm{1}$ norm penalty term. It is mathematically defined as the sum of the absolute values of each coefficient. The idea is to eliminate the higher order polynomial basis functions whose coefficients are closer to zero.

The coefficients of LAR-based polynomial chaos series expansion can be iteratively computed through the following steps:

• Step I: Initialize $\widehat{{c_{{\mathrm{{T}}_{\mathrm{{LAR}}}}}}} = 0$, i.e., each coefficient $c_\mathrm{j}$ are set to zero.

• Step II: Based on true model $(O.f.)_\mathrm{True}$, compute the residual matrix ${\varepsilon _r} = {(O.f.)_{\mathrm{{True}}}} - {\widehat{(O.f.)}_{\mathrm{{LAR}}}}$ and determine which polynomial basis function ${\psi _\mathrm{{j}}}({{\tilde{X}}_\mathrm{{i}}})$ has highest correlation with the current residual.

• Step III: Compute the coefficient of jth polynomial function by solving minimization problem (25) and update $\widehat{{c_{{\mathrm{{T}}_{\mathrm{{LAR}}}}}}}$ and ${\widehat{(O.f.)}_{\mathrm{{LAR}}}}$.

• Step IV: If ${1 \over {{\mathrm{{n}}_s}}}\sum \limits _{\mathrm{{i}} = 1}^{{\mathrm{{n}}_s}} {{{[{{(O.f.)}_\mathrm{{i}}} - \widehat{{{(O.f.)}_\mathrm{{i}}}}]}^2}}$ is below the user-specified convergence condition, then final LAR-based low-order polynomial chaos expansion model can be specified by (26) unless repeat steps II, III, IV to include influential polynomial basis functions

  $$\begin{aligned}&{(O.f.)_{\mathrm{{LAR}}}} = C{({{\tilde{X}}_\mathrm{{i}}})_{\mathrm{{LAR}}}}\nonumber \\&\qquad \quad = \sum \limits _{\mathrm{{j = 1}}}^{{\mathrm{{T}}_{\mathrm{{LAR}}}}} {{c_\mathrm{{j}}} \cdot {\psi _{{{{{\uplambda }}}_\mathrm{{j}}}}}({{{\tilde{X}}}_\mathrm{{i}}})} \;;\;{\mathrm{{T}}_{\mathrm{{LAR}}}}\; < \;{\mathrm{{T}}_{\mathrm{{LSR}}}}. \end{aligned}$$

  (26)

For cross-validation purposes, out of $n_\mathrm{s}$ samples, ($n_\mathrm{s}$/10) samples are employed for testing and others are employed for training the models.

Table 3 Deterministic results estimated using six different optimization techniques for two different solar cells

Performing multidimensional sensitivity analysis based on Sobol indices

It is important to understand which parameters cause significant deviation in model response, i.e., objective function value under random uncertainties. A multidimensional global sensitivity analysis is proposed which provides information about model-sensitive parameters. The analysis is based on Sobol decomposition which requires knowledge of statistical variances and means. To achieve computational benefits, the polynomial chaos expansion-based computational model is utilized to evaluate first-order, second-order, and total Sobol indices. Sobol indices are a measure of model sensitivity under global parametric variations. First-order indices quantify the amount of expected covariance in model response due to each random variable (${{\tilde{X}}_i}$’s) alone. Second-order indices quantify amount of expected covariance due to interactions between two input parameters (${{\tilde{X}}_i}$’s and ${{\tilde{X}}_i}$’s) at a time. The total Sobol indices quantify the impact of each random variable including interactions with other parameters, as well.

According to Sobol decomposition

$$\begin{aligned}&C({{\tilde{X}}_\mathrm{{i}}}) = {C_0} + \sum \limits _{\mathrm{{i}} = 1}^5 {{C_\mathrm{{i}}}({{{\tilde{X}}}_\mathrm{{i}}}} ) + \sum \limits _{\mathrm{{1}} \le \mathrm{{i}} \le \mathrm{{j}} \le \mathrm{{5}}} {C_{\mathrm{{ij}}}}({{{\tilde{X}}}_\mathrm{{i}}},{{{\tilde{X}}}_\mathrm{{j}}})\nonumber \\&\qquad \quad + \mathrm{{higher}}\;\mathrm{{order}}\;\mathrm{{terms}}. \end{aligned}$$

(27)

Fig. 7

Comparison of V–I and P–V characteristics for commercial RTC France (57 mm) solar cell using AWDO with experimental result

Fig. 8

Comparison of V–I and P–V characteristics for Solarex MSX83 (36 cells) solar cell using BWO with experimental result

The coefficients of polynomial chaos expansion models defined in Eqs. (20) and (23) can be arranged to find the coefficients $C_\mathrm{0}$, $C_\mathrm{i}$‘s and $C_\mathrm{ij}$’s in the Eq. (27). Unlike Monte Carlo-based approach, the first-order, second-order, and total Sobol sensitivity indices can be easily computed using Eqs. (28), (29) and (30), respectively

$$\begin{aligned}&S_{\mathrm{i}}^1 = {{{\mathrm{Partial}}\;{\mathrm{variance}}\;{\mathrm{due}}\;{\mathrm{to}}\;{{\mathrm{i}}^{{\mathrm{th}}}}{\mathrm{parameter}}} \over {{\mathrm{Total}}\;{\mathrm{variance}}}} = {{{D_{\mathrm{i}}}} \over D} \end{aligned}$$

(28)

$$\begin{aligned}&S_{{\mathrm{ij}}}^2 = {{{\mathrm{Partial}}\;{\mathrm{variance}}\;{\mathrm{due}}\;{\mathrm{to}}\;{\mathrm{interaction }} \, {\mathrm{between}}\;{{\mathrm{i}}^{{\mathrm{th}}}}\;{\mathrm{and}}\;{{\mathrm{j}}^{{\mathrm{th}}}}\;{\mathrm{parameter}}} \over {{\mathrm{Total}}\;{\mathrm{variance}}}}\nonumber \\&= {{{D_{{\mathrm{ij}}}}} \over D} \end{aligned}$$

(29)

$$\begin{aligned}&S_{\mathrm{i}}^T = {S_{\mathrm{i}}} + {S_{{\mathrm{ij}}}} + \;{\mathrm{higher}}\;{\mathrm{order}}\;{S_{\mathrm{i}}}'{\mathrm{s}} \end{aligned}$$

(30)

$$\begin{aligned}&{\mathrm{Where}}\;{D_i} = \sum \limits _{{\mathrm{j = }}1}^{{\mathrm{j < T}}} {C_{\mathrm{j}}^2} \;{\mathrm{,}}\;D = \sum \limits _{{\mathrm{j = }}1}^{{\mathrm{j = T}}} {C_{\mathrm{j}}^2}. \end{aligned}$$

(31)

Table 4 Single diode model electrical parameter estimation using different computational techniques

Fig. 9

Randomization of electrical parameters of a solar cell through Gaussian probability distribution

It is to be noted that in (28), those $C_\mathrm{i}$’s are chosen whose polynomial functions are defined only using ith parameter, whereas in (29), those $C_\mathrm{j}$’s are chosen whose polynomial functions is defined using both ith and jth parameter.

Multidimensional sensitivity analysis explained in this section can be considered as the screening test to determine the parameter that explains the variability in the model response under parametric uncertainty. Variability in the model response can be quantified using first-order effects, second-order interactions, and the total contribution of each random parameter.

Results and discussion

This section aims to assess the application of six different meta-heuristic algorithms: Firefly algorithm, Particle Swarm optimization, Multi-Variate Newton Raphson (MV-NR), Wind-Driven optimization (WDO), Adaptive Wind-Driven optimization (AWDO), and Black Widow optimization (BWO) for parameterization of a single diode model of a solar cell through an MATLAB code. An experimental database for a commercial (RTC France) 57 mm silicon solar cell under $1 \mathrm{kW/m}^\mathrm{2}$ at 308K is selected as a benchmark test case, while another experimental database for Solarex MSX83 (36 cells) solar panel under $1 \mathrm{kW/m}^\mathrm{2}$ at 298K is selected as a practical test case for solving the deterministic parameterization problem of a solar cell.

Table 3 lists the electrical parameters estimated using six different meta-heuristic techniques for two different solar PV cell test cases. Figure 7 shows the V–I and P–V characteristic curve for commercial (RTC France) 57 mm silicon solar cell estimated using AWDO, whereas Fig. 8 shows the VI and PV characteristic curve for Solarex MSX83 silicon solar cell estimated using BWO. For Case1, RMSE is minimum for Adaptive Wind-Driven optimization. Hence, the AWDO technique can be regarded as the most accurate technique for Case1 commercial RTC France solar cell. Similarly, for Case2, minimum RMSE is obtained using the BWO algorithm which ensures better accuracy compared to other deterministic algorithm techniques. For Case1, MPP point estimated using AWDO was (0.4511,0.6893,0.31095) against experimental MPP point (0.4512,0.6893,0.3110). For Case2, MPP point estimated using BWO was (0.4753,4.8883,2.3234) against experimental MPP point (0.4754,4.8838,2.3215).

The deterministic results obtained using the AWDO algorithm for $Case\,1$ and the BWO algorithm for $Case\, 2$ are used to define the probabilistic sample space of each random or uncertain parameter. Each electrical parameter is represented using a Gaussian PDF whose known supports are listed in Table 4. For $Case\, 1$, each mean (${\mu _\mathrm{{i}}}$’s) is obtained from the deterministic results using AWDO (most accurate). For $Case\, 2$, each mean (${\mu _\mathrm{{i}}}$’s) is obtained from the deterministic results using BWO (most accurate). For both the cases, standard deviation (${\sigma _\mathrm{{i}}}$) is assumed, such that upper and lower bounds are limited to $\pm$ $10\%$ of individual mean (${\mu _\mathrm{{i}}}$’s). For better visualization of multidimensional Gaussian distribution, the probabilistic design space of each random variable considered for analyzing uncertainty propagation is graphically shown as a 5 $\times$ 5 plot matrix in Fig. 9. $10^\mathrm{5}$ random samples of each electrical parameter are generated to analyze the probabilistic response of solar cell under random events.

The true model response under Gaussian parametric uncertainty can be examined through the Monte Carlo approach. Under this approach, the true model response is evaluated on each random sample. However, it may result in high computational time as the single diode model is represented using a highly non-linear implicit function. To achieve low computational burden and model complexity, an intrinsic representation of true model under uncertainty is expressed as the series of many univariate and multivariate polynomials popularly known as polynomial chaos representation.

Coefficients of polynomial chaos expansion model are computed using LAR regression-based learning techniques. Figures 10 and 11 show the logarithmic mapping of each coefficient computed using least angle regression techniques for two different solar cells. Analytically, polynomial chaos model (up to 6th degree) using LSR requires 462 coefficients to represent a single diode model response under uncertainty. However, the number of coefficients can be limited to achieve a simpler design and low-cost computation through least angle regression-based learning. Figures 10 and 11 show that the coefficients of the polynomial chaos model are limited to 49 and 84 using LAR for Case1 and Case2, respectively. A reduction in maximum degree can also be seen for the polynomial chaos expansion model based on LAR approach in both cases. Consequently, the computational time is significantly reduced using LAR. Out of $10^\mathrm{5}$ samples, $10^\mathrm{5}$ samples were excluded from the regression-based learning process for testing and validation purpose.

Fig. 10

Coefficients of polynomial chaos series representation using least angle regression (LAR) for RTC France (57 mm) solar cell

Fig. 11

Coefficients of polynomial chaos series representation using least angle regression (LAR) for Solarex MSX83 solar cell

To assess the reproducibility and accuracy of the model, the output response using each polynomial chaos expansion model is validated against the true response. Relative error was computed to examine the accuracy of each model as shown in Figs. 12 and 13. In the case of RTC France (57 mm) solar cell, a relative error of 1.11$\times$ $10^{-2}$ was obtained using LAR approach against a relative error of 2.79$\times$ $10^{-2}$ using LSR approach. A significant $50\%$ reduction in relative error is observed using LAR approach for Solarex MSX83 solar cell. Thus, it can be concluded that LAR-based polynomial chaos expansion model showed improved accuracy, efficient reproducibility, and less complexity with reduced dimensionality (Figs. 12 and 13).

Fig. 12

Validation of polynomial chaos model response using LSR for Case 1 and Case 2

Fig. 13

Validation of polynomial chaos model response using LAR for Case 1 and Case 2

A multidimensional sensitivity analysis is explained through Sobol decomposition of polynomial chaos series representation. For both Case1 and Case2 solar cell, first-order sensitivities graphically represented in Figs. 14 and 15 suggest that model response is most sensitive to variation in ideality factor n. Collectively, n and $I_\mathrm{Ph}$ contribute more than $65\%$ to the variability (or) deviation in the output. First-order sensitivities quantify the amount of deviation in output response due to variation in individual parameter space.

Fig. 14

Comparison of first-order Sobol indices for RTC France (57 mm) solar cell computed using three different models

Fig. 15

Comparison of first-order Sobol indices for Solarex MSX83 solar cell computed using three different models

Figures 16 and 17 represent the second-order sensitivities due to cross-influence of two random electrical parameters. It can be concluded that the mutual interaction between $I_\mathrm{Ph}$ and n, $I_\mathrm{O}$ and n significantly affects the electrical response under uncertainty. Although small, but the interaction between $I_\mathrm{Ph}$ and $I_\mathrm{O}$ also has a marginal effect on the variance of the output response.

Fig. 16

Comparison of second-order Sobol indices for RTC France (57 mm) solar cell computed using three different models

Fig. 17

Comparison of second-order Sobol indices for Solarex MSX83 solar cell computed using three different models

The total contribution of each random parameter including first-order effects, second-order, and higher order interactions with other random parameters can be explained using total Sobol indices shown in Figs. 18 and 19. It suggests that the variations in ideality factor ‘n’, photocurrent ‘$I_\mathrm{Ph}$’, and diode saturation current ‘$I_\mathrm{O}$’ have a significant impact on the probabilistic distribution of the model response, and eventually impacts the output electrical characteristics of solar cells under random events.

Fig. 18

Comparison of total Sobol indices for RTC France (57 mm) solar cell computed using three different models

Fig. 19

Comparison of total Sobol indices for Solarex MSX83 solar cell computed using three different models

Based on multidimensional sensitivity analysis, a diagnostic screening is performed for classifying electrical parameters associated with the single diode model of a solar cell into three classes. Sobol indices representing the contribution of each parameter and their interaction to the output variance are chosen as the attribute for the classification. Random variation in ’n’ individually contributes around $50\%$ in the case of RTC France (57 mm) solar cell and 48–53$\%$ in the case of Solarex MSX83 solar cell. Hence, ideality factor ‘n’ is categorized as ”Sensitive parameter”. Apart from individual contribution, variance in the output can also be quantified using mutual interaction between two or more parameters. Based on second-order Sobol indices, ideality factor ‘n’, photocurrent ‘$I_\mathrm{Ph}$’, and diode saturation current ‘$I_\mathrm{O}$’ are chosen as ”Interactive parameters”. As no significant contribution of $R_{Se}$ and $R_{Sh}$ was observed in output variance, series resistance $R_{Se}$ and shunt resistance $R_{Sh}$ are considered as ”Insignificant parameters”.

To obtain the probabilistic response of solar cells, the model response is evaluated on $10^\mathrm{5}$ random samples using conventional Monte Carlo approach, polynomial chaos model using LAR, and LSR learning approaches. It can be seen from Figs. 20 and 21 that the single diode model shows a unimodal response under Gaussian parametric uncertainty. The empirical probability distribution drawn from the probabilistic output response is plotted for each solar cell test case. The estimated probability distribution function illustrated in Figs. 22 and 23 suggests that the model response closely follows a Rayleigh distribution function under random parametric variations. In the case of RTC France (57 mm) solar cell, the probabilistic output response is characterized by a mean value of 0.0060 and a standard deviation of $\pm$ 0.0034 (around $56\%$ of the mean). Similarly, for Solarex MSX83 solar cell, the probabilistic response is characterized by a mean of 0.0761 and a standard deviation of $\pm$ 0.0052 (around $67\%$ of the mean). Finally, the cumulative distribution function can be plotted, as shown in Figs. 24 and 25, for each solar cell test case. It has been observed that the model response has a $50\%$ probability to attain a value less than or equal to the mean value under Gaussian uncertainty.

Fig. 20

Probabilistic response generated using Monte Carlo, LAR, and LSR-based approach for RTC France (57 mm) solar cell under Gaussian parametric uncertainty

Fig. 21

Probabilistic response generated using Monte Carlo, LAR, and LSR-based approach for Solarex MSX83 solar cell under Gaussian parametric uncertainty

Fig. 22

Estimated probability distribution as a function of output response under Gaussian parametric variation for Case 1

Fig. 23

Estimated probability distribution as a function of output response under Gaussian parametric variation for Case 2

Fig. 24

Estimated cumulative probability distribution for Case 1

Fig. 25

Estimated cumulative probability distribution for Case 2

Conclusion

The advancement in solar photovoltaic industry will empower the future power system considering solar energy’s tremendous potential and lower environmental impact. However, high penetration of solar-based energy system may not be always technically or economically feasible due to the intermittent behavior of solar as a resource. It is important to study the electrical behavior of solar cell for planning and control of solar photovoltaic-based generation. However, extrinsic factors such as partial shading, local hotspots, dusting, aging, and intrinsic factors such as radiative or surface charge-carrier recombination, bulk defects, and improper metal contacts may lead to parametric uncertainty which may impact the electrical response of solar cells. Thus, a hierarchical approach is presented to analyze the deterministic response of two different solar cells under standard conditions and probabilistic response under parametric uncertainty. The salient features of the proposed probabilistic analysis includes:

• Estimation of deterministic response to define the probability distribution of each random electrical parameter.

• Stochastic representation of true model response as a weighted sum of polynomial basis functions popularly known as polynomial chaos expansion.

• Identification of sensitive solar cell model parameters.

The best deterministic response obtained using six different algorithms is used to characterize the probabilistic distribution of each random electrical parameter. To reduce the model complexity and computation burden, two polynomial chaos expansion models are discussed and proposed. It can be concluded that least angle regression-based polynomial chaos representation provides an accurate probabilistic response with low computational cost and reduced dimensionality. It can be identified from the sensitivity results that n is the most influential parameter and contributes more than about $85\%$ to the variance in the model response under random uncertainties. Out of $85\%$, around $20\%$ contribution is due to second-order or higher order interactions with other parameters. Overall, the sensitivities can be arranged in descending order as n > $I_\mathrm{Ph}$ > $I\mathrm{O}$ > $R_\mathrm{Se}$ > $R_\mathrm{Sh}$. The low-cost polynomial chaos expansion model could be beneficial for control, planning, and fabrication engineers into study the probabilistic behavior of solar cells under parametric disturbances. This concept can be strongly recommended in solar energy forecasting or prediction models to increase the efficiency, accuracy, and robustness of the computational system.