Introduction

Modern network science has progressed rapidly and has become an important research tool in sociology, computer science, biology, etc. [4, 7, 9, 13, 28, 44]. The key to understanding the network is in-depth mining its intrinsic topology and finding the most represent backbone from a great number of complex connections. As the real-world networks tends to be highly dense and large scale, how to extract the fundamental features and reduce redundant of dense networks efficiently become one of the most popular issues in network science [19, 39, 42, 55].

Extracting the so-called backbone of a network is a very challenging problem, which relies on the concept of minimizing large-scale networks while still preserves the essential information of the original network [14]. Intuitively, nodes with a higher centrality value will be prior preserved as the core structure. With this respect, numerous researches and excellent works have proposed to handle such problem [46, 51], which can be classified into three categories: coarse-graining model, filtering model and generalist model.

Coarse-graining methods reduce the network size by grouping similar nodes, and they consider these groups as a single node [18]. In this sense, communities can be replaced by a single node under a coarse view [16, 53]. Song et al. propose the box-counting techniques to reduce the sizes of networks[43]. Zeng et al. proposed the new path-based algorithm to coarse-grain the directed networks, which can effectively preserve the synchronizability of the directed networks [52]. The most typical work is the spectral coarse-graining (SCG) method, proposed by Gfeller et al., which is mainly based on the relationships between the eigenvalue spectrum of the Laplacian matrix of the network and the synchronizability of the network to merge similar nodes [16, 17]. One significant weakness of these methods is that the extraction results highly depend on the community defined, where proper communities findings is an NP-hard problem [6].

Filter-based methods prune the network by discarding nodes or edges based on a statistical property. Generalist model can be viewed as the special term of filter-based method but focus on the edge’s dimensionality cutting. Previous researches achieve the backbone’s extractions by applying a hard threshold according to the node attributes, such as the degree, betweenness, coreness centrality, etc. [6, 25, 29, 41]. Grady et al. have introduced the robust link salience method to extract network skeletons of generic statistical properties based on the shortest path tree [20]. Yuan et al. have proposed the TP\(_{ks}\) index to identify the important nodes in the network and achieved the success in the analysis of the bicycle sharing networks [30, 37]. Zhang and Zhu have proposed the new measure, i.e., the strong ties, as skeletons of weighted social networks [56]. While researchers have also found that social network structures are robust to removing strong relationships, yet gradually falling apart as removing the weak ties [21]. Besides the above methods, disparity filter (DF), locally adaptive network sparsification (LANS), and globally and locally adaptive network backbone (GLANB), commonly extract the significant edges, according to the null model-based weights in networks [39, 42, 55].

All above methods follows one same rule: nodes or edges with scores higher than the predetermined values are preserved as the final core structure. However, these measures are limited in their performances to describe non-linear, localized, and dynamic properties of the systems from the views of nodes and edges. To uncover structural, temporal, and functional insights of complex systems, network motifs have been used extensively in recent years as they provide a tractable approximation of the networks that can be measured and updated within given memory and compute constraints [38]. Network motifs are patterns of interactions occurring in the complex system at a rate higher than those in a randomized network. To the best of our knowledge, most backbone extraction methods have been obtained only at the level of nodes or edges. In contrast, few attempts have been made here to abstract functional backbone except for Cao [12]. New measure motifs are the fully represented subgraph with higher-order connectivity patterns in networks [11], which are the basic building blocks that manipulate the activity of most complex systems [3]. Cao et al. first proposed a motif-based disparity filter, i.e., Motif-DF, in which he uses normalized motif weight of edges to extract functional backbone. However, when most of the edge weights connected to a certain vertex are large, partially normalized weights in Motif-DF will lower the significant global advantage of these edges and miss very important skeletons in the final result. Moreover, Motif-DF highly relies on the external static parameter named significance level \(\alpha \), to determine the number of edges preserved and performance in the backbone detection.

Inspired by the recent works [12, 54, 58], we introduce a novel motif h-backbone (Motif-h) method for directed networks, which combines and h-index method and weak ties theory into the significant motif edges finding. The new method will be designed to establish an adaptive h-index for each network, free from the constraint of fixed parameters, e.g. \(\alpha \) in Motif-DF. Besides, the new global normalization strategy preserves the advantages of edges and facilitates the optimal global selection of edges. Considering weak ties, we adopt the h-bridge in the second selection stage, where the weak ties have been ignored by the existing method, i.e., Motif-DF. The newly proposed Motif-h method will provide a particular perspective to study the distribution of motif edge strength and networks’ functional structure. At the same time, the Motif-h method simplifies the networks and preserves the vital functional structures effectively.

The outline of this work is as follows: the next section introduces the definitions related to the motifs and the motif backbone problem. In the subsequent section, the motivation and details of our Motif-h method are presented; then the performance among three methods, i.e., Motif-h, Motif-DF, and Entropy in various real-world networks is presented. The last section summarizes our work and shows the future directions.

Problem formulation and methodology

Motifs are the fundamental functional structures which can give a better perspective to make it easy to understand and analyze large-scale complex networks. One breakthrough work shows [35] that network motifs can build the blocks of complex networks, and different types of networks have distinct in the motif preserving [34, 36]. That means the combinations of motifs represent certain essential features in the network compared to nodes and edges.

Comparing with traditional backbone methods with the nodes or edges, the functional backbones with the related motifs preserved will extend the ability to understand structural, nonlinear information inside the complex topology. In this section, we will introduce the functional backbone problem based on the motifs, and the key notations are listed in Table 1.

Table 1 Notations and definitions
Full size table
Fig. 1
figure 1

All 13 three-node connected motifs of directed networks [35]

Full size image

Salient motifs and functional backbone problem

To illustrate the characters of motifs, we list 13 three-node motifs in Fig. 1, which have been widely found in various networks. Typically, different motifs serve distinct functions in different networks [33]. For example, the triangular motifs (\({{M}_{1}}-{{M}_{7}}\)) that are statistically significant exist in social networks; the feedforward loops \({{M}_{5}}\) are fundamental to transcriptional regulation networks and neural networks [31, 57]; the two-hop paths \(({M}_{8}-{M}_{13})\) help us to understand the travel patterns of air traffics [22, 40]; the open bidirectional wedges (\({{M}_{13}}\)) are the most potent motif for the information flow in functional brain networks [32]. \({{M}_{5}}\) and \({{M}_{9}}\) are tri-trophic food chains and omnivory chains, respectively, which represent the relationships among predators, consumers and resources in ecological networks [8, 48].

One famous open-source software, i.e., mfindert [34], gives a way to detect the motifs in various types of networks. For directed networks, there are 13 three-node motifs and 199 four-node motifs [45]. To simplify the calculations, we focus our research area on the motifs with three nodes. Basically, not every motif is of the same significance in real-world networks. Salient motifs are those whose occurrence is no less than that of the ensemble of randomized networks with identical degree sequences [34]. Therefore, we use the significance profile (\(\mathcal {SP}\)) approach to analyze the motifs with a much higher occurrence frequency than the expected [34].

Given a directed network \(\mathcal {G:=(V,E,N)}\), with \(\mathcal {N}\) vertices (or nodes) and \(\left| \mathcal {E} \right| = {L}\) edges (or links). Denote the significance of a motif \({{M}_{k}}\) as Z score:

$$\begin{aligned} {\mathcal {Z}(k)}=\frac{N_{k}^\mathrm{{real}}-\left\langle N_{k}^\mathrm{{rand}} \right\rangle }{\sigma (N_{i}^\mathrm{{rand}})}, \end{aligned}$$
(1)

where \(N_{k}^\mathrm{{real}}\) is the occurrences of the motif \({{M}_{k}}\) in real networks, \(\left\langle N_{k}^\mathrm{{rand}} \right\rangle \) and \(\sigma (N_{i}^\mathrm{{rand}})\) are the mean and standard deviation of the appearances of the motif \({{M}_{k}}\) in its corresponding randomized network ensemble. Then, the \(\mathcal {SP}\) value of \({{M}_{k}}\) is defined as the normalized Z score:

$$\begin{aligned} {\mathcal {SP}(k)}=\frac{{\mathcal {Z}(k)}}{\sum _k{\mathcal {Z}(k)}}\,\,\qquad k = 1,2,\ldots , 13. \end{aligned}$$
(2)

As we want to fully explore the complex network \(\mathcal {G}\), it is necessary to carefully construct the network structures and functions using salient motifs. To determine every salient motif \({M}_{k}\) from the according motif, we generate a motif edge strength matrix (see as Definition 2) to measure the functional strength of each edge [11]. Clearly, higher motif edge strength means that some pairs of nodes have stronger functional interactions than others. Thus, the salient motif set is denoted as

$$\begin{aligned} {\mathbb {M}=\{{{M}_{k}} |~ \mathcal {SP}(k)>0,k=1,\ldots ,13\}}\,, \end{aligned}$$
(3)

in which motifs with the \(\mathcal {SP}\) values greater than 0 are referred to as salient motifs.

Definition 1

Motif edge occurrences: Given a specific salient motif \({M}_{k} \in \mathbb {M}\), there is a related \({M}_k = \big \{M_k^1, M_k^2, \ldots , M_k^l\big \}\) set include all motif \(M_k\) in the current network, the motif edge occurrences according to \(M_k\) is defined as

$$\begin{aligned} o_{ij}^k = \sum _{c=1}^{l}{P_{kc}(e_{ij})}\,; \end{aligned}$$
(4)

where

$$\begin{aligned} P_{kc}(e_{ij}) \, = \, \left\{ \begin{array}{ll}1\,,\quad \quad \, &{} e_{ij} \in M_k^c \\ \\ 0\,, \quad \quad \, &{} \mathrm{{otherwise}} \end{array} \right. \, . \end{aligned}$$
(5)

Definition 2

Motif edge strength matrix: Given a specific salient motif \({M}_{k}\), the edge strength matrix \(W =(w_{{ij}})\) is defined as the total occurrence count of edge \(e_{ij}\):

$$\begin{aligned} w_{ij} = \sum _{M_k \in \mathbb {M}} o_{ij}^k = \sum _{M_k \in \mathbb {M}}\sum _{M_k^c \in {M}_k}^{l}{P_{kc}(e_{ij})}\,. \end{aligned}$$
(6)

In this paper, we aim at solving the problem of extracting the functional backbone from a dense complex network. A functional backbone is informally defined as a subset of nodes and edges of the original network which contains the most significant motifs with certain nodes and edges reserved.

Problem Definition: Given a directed graph \(\mathcal {G = (V,E,N)}\), find a smallest sub-graph \(\mathcal {G^* = (V^*,E^*,N^*)}\) maintains the highest motif degree (Definition 5) or motif centrality (Definition 6), such that \(\mathcal {E^*}\subset \mathcal {E}\), \(\mathcal {V^*}\subset \mathcal {V}\) and follows:

  1. (a)

    \(\mathcal {|MN_{G^*}|} \le \mathcal {|MN_{G}|}\), where \(\mathcal {MN_G}\) is the number of Motifs. (non-increase)

  2. (b)

    \(\mathcal {SP_{G^*}}(k) \ge \mathcal {SP_{G}}(k)\), where \(M_k \in \mathbb {M}\). (strengths enhance)

  3. (c)

    \(\mathcal {Z_{G^*}}(k) \rightarrow -\frac{\left\langle N_{k}^\mathrm{{rand}} \right\rangle }{\sigma (N_{i}^\mathrm{{rand}})}\), where \(M_k \notin \mathbb {M}\). (noisy disparity)

The motif-based disparity filter (Motif-DF) method

To solve the motif-based backbone extraction problem, Cao [12] gives the first attempt and proposed the motif based disparity filter (Motif-DF) method, where the edges should be preserved as backbone by comparing their weights via the null model, and the probability of the edges’ normalized weight as follows:

$$\begin{aligned} \tau _{ij} = 1 - \int _{0}^{\hat{w}_{ij}} (k-1)(1-x)^{k-2}\mathrm{{d}}x\, , \end{aligned}$$
(7)

where k is the degree of the source node, x is the particular value, and here we use the normalized motifs weight instead. The normalized motifs weight \(\hat{w}_{ij}\) is defined as

$$\begin{aligned} \hat{w}_{ij} = \frac{w_{ij}+a_{ij}}{\sum _{j}(w_{ij}+a_{ij})}\,, \end{aligned}$$
(8)

where \(a_{ij}\) is the element of adjacency matrix \(\mathcal {A}\), and the Motif-DF method preserves the nodes when \(\tau _{ij} \le \alpha \).

figure a

Motif-h method

h-strength and h-bridge

To solve the functional backbone extraction problem, we introduce a novel motif-h method which derives from the filter-based method but fully focus on silent motifs by h-index methods, i.e., h-strength and h-bridge. Considering the partial normalization in Motif-DF fails in selecting edges (see Eq. 8), as the strength weights of most edges connect to specific nodes are very high. This paper constructs the new h-strength with the novel global normalization, which will retain the edges’ original advantage and map the weights domain ([0  1]) to the same domain as the nodes’ number (\([0 ~~\mathcal {N}]\)):

$$\begin{aligned} \widetilde{w}_{ij} = \frac{\mathcal {N} w_{ij}}{max({w_{ij}})}\,. \end{aligned}$$
(9)

With respect to the motifs in networks, we first define a metric to measure the backbone nodes in terms of edges’ strength and quantities, a.k.a motif h-strength:

Definition 3

Motif h-strength:Given a network \(\mathcal {G}\), the motif h-strength is equal to \({h}_{\mathbb {M}}\), if \({h}_{{\mathbb {M}}}\) is the largest natural number such that there are \({h}_{{\mathbb {M}}}\) edges each with motif edge strength larger than or equal to \({h}_{{\mathbb {M}}}\). For the fully descent strength order edges set \(\{e_1, e_2, \ldots , e_S\}~\)in all salient motifs \(\mathbb {M}\), we have its h-strength index form as

$$\begin{aligned} h_{\mathbb {M}} = \max \big \{h~|~h \ge s,\, h \ge \widetilde{w}_{e_s}, \, h\in \mathbb {N},\, s \in {1, 2, \ldots , S} \big \}\,.\nonumber \\ \end{aligned}$$
(10)

To make it more adaptive to various requirements, we extend the h-strength, as the fractional-h form:

$$\begin{aligned} h_{\mathbb {M}}^\beta = \max \big \{h~|~h \ge s, h \ge \widetilde{w}_{e_s}^\beta , h\in \mathbb {N}, s \in {1, 2, \ldots , S} \big \}\,.\nonumber \\ \end{aligned}$$
(11)

Most of the current methods require an additional parameter to guide the number of filters, and the setting of the parameter is often not related to the nature of the network itself. Different networks have differentiated network properties due to complex connectivity relationships, and obviously, it is not wise to pick the same parameter to guide. With this respect, we newly proposed the motif h-strength, which provides a particular measure to analyze edges with high strength and edge strength distributions corresponding to each salient motif. In the Motif-h method, we only need to calculate the h-index of each network corresponding to the preservation of all edges larger than \(h_\mathbb {M}\), and no longer need an additional parameter intervention.

h-strength indicates that motifs with higher occurrences are more likely to have higher motif edge strength than others. Actually, besides the high weighted edges, weak ties also play a vital role as bridges in a network and the edge betweenness measures the total amount of an edge functioning as a bridge in a network. Naturally, edges with higher edge betweenness value are more critical. However, motif edge strength cannot find out those edges with low motif-strength but high betweenness value. In keeping with the motif h-strength, here we use the h-bridge to measure those critical edges [54]. In the network \(\mathcal {G}\), the bridge strength of an edge \({e}_{ij}\) is defined as

$$\begin{aligned} \mathcal {B}({{e}_{ij}})=\sum \limits _{v_s\ne v_t\in V}{\frac{{{\delta }_{st}}({{e}_{ij}})}{{\mathcal {N}}{{\delta }_{st}}}}=\frac{\mathrm{{BCL}}({e}_{ij})}{\mathcal {N}}, \end{aligned}$$
(12)

where \(\mathcal {N}\) is the size of the network, \({\delta }_{st}\) is the number of all shortest paths from node s to node t, \({{{\delta }_{st}}({{e}_{ij}})}\) is the total number of shortest paths passing through the edge \({e}_{ij}\). BCL\(({{e}_{ij}})\) is the edge betweenness, which is defined as the total number of shortest paths that pass through \(e_{ij}\) [5] from all vertices to all the other vertices, such that

$$\begin{aligned} \mathrm{{BCL}}(e_{ij})\,=\,\sum \limits _{v_s\ne v_t\in V}{\frac{{{\delta }_{st}}(e_{ij})}{{{\delta }_{st}}}} \, . \end{aligned}$$
(13)

Since BCL\(({{e}_{ij}})~\) value ranges in \(~[0 \,\,\mathcal {N}^2]~\) in a network. In this work, we use Eq. (12), so as to map the range to \([0\,\,\mathcal {N}]\). Besides the Motif h-strength, we also adopt the the h-index approach to rank the bridges in the network, then we get the h-bridge [54], such that

Definition 4

h-bridge: The h-bridge of a network is equal to \({{h}_{b}}\), if \({{h}_{b}}\) is the largest natural number such that there are \({{h}_{b}}\) edges each with a bridge at least equal to \({{h}_{b}}\) in the given network. With the fully descent strength order edges set \(\{e_1, e_2, \ldots , e_P\}~\) in current network, and its related bridge strength \(\{\mathcal {B}_1, \mathcal {B}_2, \ldots ,\mathcal {B}_P\}\), we have its h-bridge index form as

$$\begin{aligned} h_b = \max \big \{h~|~h \ge p, \,h \ge \mathcal {B}_p, \, h\in \mathbb {N}, \, p \in {1, 2, \ldots , P} \big \}\,.\nonumber \\ \end{aligned}$$
(14)

Here, we also give the Fractional-h form for the bridge edges:

$$\begin{aligned} h_b^\beta = \max \big \{h~|~h \ge p, h \ge \mathcal {B}_p^\beta , h\in \mathbb {N}, p \in {1, 2, \ldots , P} \big \}\,.\nonumber \\ \end{aligned}$$
(15)

Apparently, the motif h-strength quantifies the functionally significant edges for different salient motifs. Relatively, h-bridge characterizes the structurally critical edges whose removal disconnects the network.

Considering the weak ties and difference among the motifs, in this paper, we propose the Motif-h method to extract the backbones from the directed network, which is composed of all edges with motif edge strength larger than or equal to the \({h}_{\mathbb {M}}\) and with bridges larger than or equal to \({h}_{b}\), and the nodes connected by these edges. The details for the algorithm of Motif-h are shown in Algorithm 2, which consists of two parts: strong motif-weight edge extraction and weak ties (strong bridging) edge extraction:

figure b
Fig. 2
figure 2

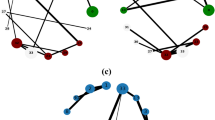
The process of extracting the motif h-backbone of the food web network. The subgraphs a–f in left side consist of edges with strength larger than or equal to the motif h-strength or h-bridge accordingly of the food web network; g a illustration of the original food web network. The nodes with darker color have larger degrees; h the connected motif h-backbone of the food web network

Full size image

Computational complexity

In this subsection, we will give the computational complexity of the two motif-based methods: one is the Motif-DF (Algorithm 1), the other one is our newly proposed Motif-h (Algorithm 2). The computational complexity of two filter-based methods are mainly determined by the two stages: (a) the edges’ weights computing and (b) extracting the backbone in the network \(\mathcal {G}\).

In Motif-DF method, the complexity of computing \(\hat{w}_{ij}\) is \(\mathcal {O}(|\mathcal {E}| \cdot \bar{k})\) and the computing \(\tau _{ij}\) is \(\mathcal {O}(|\mathcal {N}| \cdot \bar{k})\), where \(|\mathcal {E}|\) is the number of edges and \(\bar{k}\) is the average degree in network \(\mathcal {G}\). In our proposed Motif-h, the time of computing h-strength is \(\mathcal {O}(|\mathcal {E}|)\), and time of computing h-bridge is \(\mathcal {O}(|\mathcal {E}| \cdot \mathcal {N})\). Both complexity of extraction processes are \(\mathcal {O}(|\mathcal {E}|)\).

Evaluation metrics

Unlike the existing backbone problem, a functional backbone extraction issue aims to preserve as much as possible the salient motifs in the original network.

We choose the food web of Mangrove Estuary in dry seasons as an example. The network has 97 vertices and 1491 edges, where nodes represent species and edge represent energy flow among in the community [10]. In the food web network, the salient motifs are \({M}_{2},{M}_{3},({M}_{8}-{M}_{10}),\) in which \({M}_{2}\) is the most significant motif. As shown in Fig. 2, these salient motifs represent the natural properties of the network; when looking for the network skeleton, the final backbone should hold as many salient motifs as possible.

To evaluate the Motifs reserved in the functional backbone, we adopt the motif degree and motif centrality as two importance metrics in the experiments:

Definition 5

Motif Degree: Given a salient motif \({{M}_{k}}\), the motif degree \(d_{M_k}\) of \({{M}_{k}}\) is defined as the sum of nodes’ degree in \({M}_k\), and the total motif degree is defined as \( MD = \sum _{{M}_k \in \mathbb {M}} d_{M_k}\) in the current \(\mathcal {G}\).

Definition 6

Motif Centrality: Given a salient motif \({{M}_{k}}\), the motif centrality is defined as the average centrality of all its occurrences in the network. Suppose the total number of occurrence of \({M}_k\) in \(\mathcal {G}\) is n, the motif centrality of \({M}_k\) can be calculated as follows:

$$\begin{aligned} \mathrm{{MC}}({M}_k) = \frac{1}{(n-1)(n-2)}\sum _{i=1}^{l} \sum _{j=1}^{m} \mathrm{{BC}}(v_j)/m\,, \end{aligned}$$
(16)

where BC\((v_j)\) is the betweenness of some node \(v_j\), and m is the number of nodes in the motif, in this paper, we use \(m = 3\). The total motif centrality in \(\mathcal {G}\) is

$$\begin{aligned} \mathrm{{MC}}(\mathbb {M}) = \sum _{{M}_k \in \mathbb {M}} \mathrm{{MC}}(M_k)\,. \end{aligned}$$
(17)

Experiments and results

In this section, we conduct experiments to validate the effectiveness of our Motif-h compared with Motif-DF and Entropy methods under four real-world networks. The details of the data are as follows.

  • The Open flight network: The network we obtain is from the OpenFlights/Airline Route Mapper Route Database. It contains more than 60,000 routes between 3425 airports on 548 airlines around the world. We transform the data into a directed network with 3425 nodes and 37,595 edges after removing duplicated edges [24]. The data are available at https://openflights.org/data.html.

  • The WikiElec is a voting network in which users can support (trust) or oppose (distrust) other users in administer elections, which consists of 7194 nodes and 103,591 edges [50]. The data are available at https://github.com/WHU-SNA/STNE/tree/master/input.

  • The Transportation reachability network: It is a network of reachable cities in the United States and Canada, which includes 71,959 traffic paths between 456 cities [15, 27]. The data are available at http://snap.stanford.edu/data.

  • The Facebook (NIPS) is social networks belong to the conference, which includes 2888 people and 2981 connections. The data are available at http://www.konect.cc.

Before the backbone extraction procedures, we firstly calculate the SP values of each network to obtain the corresponding salient motifs set and the results are shown in Table 2. Obviously, there is variability in the kinds of salient motifs for different types of networks, which means that the frequency of occurrence of specific motif exposes the essential characteristics of the network.

Table 2 The salient ID in the real networks: an illustration of the \(\mathcal {SP}\) values for all 13 three-node motifs of four real-world networks
Full size table

In simulations, we compare our proposed Motif-h with two state-of-the-art, Motif-DF and Entropy methods, in terms of the motif degree and motif centrality preserving. For a fair comparison, we compare the backbone extraction of all nodes vs the two metrics. As the extraction of Motif-h is finished, we will extract the remaining nodes, randomly. Besides, Entropy method is a representative global threshold method, and the corresponding edge weights are computed as

$$\begin{aligned} {\hat{w}^E}_{ij} = \hat{w}_{ij} \log \hat{w}_{ij}\,. \end{aligned}$$
(18)

Moreover, trust networks are the special kind of directed networks [23], which is very common in social networks, and represents trust when the weight of the edge is greater than 0 [1], and vice versa for distrust. In this paper, we focus on the WikiElec network motif backbone problem,which is a common trust network [49]. Actually, the trust network extraction is not a simple task, often losing untrusted edges because of the comparison of edge real value. In the simulation comparisons, we split the trust network into two sub-networks \(\mathcal {G} = \mathcal {G}^{+} \cup \mathcal {G}^{-}\), containing the network’s positive and negative edges, respectively.

Fig. 3
figure 3

The changes of Motif degree after removing a proportion of backbone from the current networks. a The Open flight network; b the Facebook (NIPS) networks; c the Transportation reachability network; d the WikiElec network. The horizontal axis of the graph indicates the proportion of edges removed. The vertical axis of the graph represents the network degree after removing corresponding edges.

Full size image

With the initial selected salient motif set M according to Eq. (3), we calculate the bridging values and the motif edge strengths of all edges in each salient motif \({M}_{k}\). Then filter the candidate edges with \(\widetilde{w}_{ij} \ge {{h}_{{\mathbb {M}}}}\) and \(\mathcal {B}({e}_{ij})\ge {h}_{b}\), according to the motif edge strength values and bridging values, respectively.

By merging the edges qualified in the \({\Omega }_{b}\) and \({\widetilde{\Omega }}\), we achieve the final motif h-backbone set \(\Omega \). We show the procedures of extracting the motif h-backbone in Fig. 2. The left side of Fig. 2 shows the process of extracting the motif h-backbone of the food web network, panel (g) is the original food web network and the panel (h) is its motif h-backbone. Clearly, the original network is too dense to get useful information visually. Our Motif-h gives an abstract architecture by extracting the subgraphs from the dense network. The subgraphs on the left side of Fig. 2 are much more straightforward than the original network, which displays the edges coming from each salient motifs. The edges in the backbone that come from \({M}_{10}\) are in the majority, which describes respirations in the energy flow in the food web network. By combining the edges in the subgraphs, we obtain the functional backbone of the whole food web network.

Comparisons of motif degree and centrality

To verify the proposed method’s effectiveness in this paper, we have conducted comparative experiments on the three methods, i.e., Motif-h, Motif-DF, and Entropy, under four real-world networks. The network motif degree is an essential measure of the functional network backbone. For the detailed comparison, we recorded the remaining network after removing the important edges. The faster the network motif degree decreases, the more critical the extracted backbone is. As shown in Fig. 3 shows the whole process from the complete network to zero motif degree is recorded with an interval of 2%.

Fig. 4
figure 4

The changes of Motif centrality after removing a proportion of backbone from the current networks. a The Open flight network; b the Facebook(NIPS) networks; c the transportation reachability network; d the WikiElec network. The horizontal axis of the graph indicates the proportion of edges removed. The vertical axis of the graph represents the network centrality after removing corresponding edges

Full size image
Fig. 5
figure 5

The thresholds of different methods as the motif measures dropping to zeros. The gray bar represents the Entropy method, the orange bar represents the Motif-DF method and the blue bar represents our method.

Full size image

It is visible that our proposed algorithm decreases the motif degree the fastest among the four types of networks and requires the least number of skeletons to reduce the motif degree of all networks. These results indicate that our motif-h has a clear advantage in selecting the backbone and finding the more important network core structures with limited edges.

Note that three methods obtain similar results in the Facebook network, mainly because the number of edges in this network is not dense. As the network tends to be sparse, most exist edges in the networks tend to be necessary, and the sequence of edge selections in different methods becomes more consistent.

Figure 4 shows the comparisons in terms of motif centrality. Similar to the results on motif degree, we found that our proposed Motif-h method has a significant priority over Motif-DF and Entropy. Using motif-h to find the functional backbone, in four real-world networks, we only need 30% of extracted edges to reduce the motif centrality in the original networks significantly.

In addition to the two important indicators’ results, we also specifically analyze the minimum backbone ratios required when the two indicators’ values turn to almost zeros. Comparing with the two sub-graphs in Fig. 5, we found different algorithms have similar thresholds in both cases, Motif degree and Motif centrality. Comprehensively observing the three algorithms’ actual performance, we can notice that the thresholds of the motif proposed in this article are always in the lowest state, which validates our method’s effectiveness.

Conclusion

Unlike traditional backbone extraction methods, we motivate a new direction to find the challenging functional backbone to preserve the high-order structures, network motifs. In this work, we first introduce the Motif-h backbone extraction method based on the h-index and bridge nodes, to do such remarkable backbone findings. The new method utilizes the h-index measure to understand the individual network better and avoids certain global thresholds, which are two critical limitations often found in the most existing methods. Besides, this paper focuses on the vital role of weak connectivity in the network, and we first incorporate it into the backbone algorithm design, resulting in a unique two-stage selection mechanism. Simulation results show that our proposed Motif-h have much better performance in vital backbone finding and motifs preserving than two important methods, i.e., Motif-DF and Entropy.

Different types of networks often have typical high-order structures, and it is significant to use high-order structures to define the network skeleton. The research on module-based network backbone search has just begun, and many problems still need to be solved: how to efficiently find network motifs? [2, 47] How to forward the motifs results to the special network, e.g., temporal networks? [26, 36]