Introduction

Many optimization problems have several conflicting objectives that need to be optimized concurrently, which are known as multi-objective optimization [11], and many-objective optimization when the number of objectives is larger than three [28]. Over the past decades, a pile of successful multi-objective evolutionary algorithms (MOEAs) have been developed, which can largely be categorized into decomposition-based MOEAs, such as the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [53] and reference vector guided evolutionary algorithm (RVEA) [6]; Pareto-dominance based, e.g., the elitist non-dominated sorting genetic algorithm (NSGA-II) [12]; and performance indicator-based [14]. Note that many MOEAs combine decomposition or Pareto dominance with other criteria to address various challenges in multi-objective optimization [55].

It is well recognized, however, that most MOEAs require a large number of function evaluations before a set of diverse and well-converged non-dominated solutions can be found, which makes it hard for them to be directly applied to solve a class of data-driven optimization problems [24], whose objectives can be evaluated by means of conducting time-consuming computer simulations or costly physical experiments. Examples of real-world data-driven multi-objective optimization problems include blast furnace optimization [7], air intake ventilation system optimization [10], airfoil design optimization [29], bridge design optimization [34], design optimization for a stiffened cylindrical shell with variable ribs [57], optimization of operation of crude oil distillation units [19], resource allocation of trauma systems [47], and also neural architecture search [42, 58], among many others.

Data-driven surrogate-assisted evolutionary algorithms were first developed for single-objective optimization [23]. In recent years, more attention has been paid to data-driven surrogate-assisted multi-objective optimization [2, 9]. Similar to MOEAs, surrogate-assisted MOEAs can also be divided into four groups. The first group is based on decomposition, where surrogates are built to approximate the sub-problems formulated by the Tchebycheff function using random weights, known as ParEGO [27]. Alternatively, surrogates can also be constructed for each individual objective function to assist a decomposition-based MOEA, such as the Gaussian process assisted MOEA/D, called MOEA/D-EGO [54], K-RVEA [8], a Kriging-assisted RVEA, and surrogate-ensemble-assisted MOEA, called SAEMO [56]. The second group employs the non-dominance relation for environmental selection, and surrogates are adopted for approximating the objective functions [18, 46], or in local search [31]. In Ref. [32, 35], a surrogate is built for estimating the dominance relationship, and consequently only a single surrogate is required. The third category relies on a performance indicator-based MOEA, e.g., a Gaussian process-assisted hypervolume-based MOEA [15], and an enhanced inverted generational distance-based MOEA assisted by a dropout deep neural network (EDN-ARMOEA) [19]. Finally, surrogates have also been applied to assist other MOEAs, such as the surrogate-assisted two-archive evolutionary algorithm [40]. A good overview of data-driven evolutionary optimization can be found in a recently published book [25].

Despite its impressive success, data-driven evolutionary optimization is faced with several challenges. One is the lack of data, which is very expensive to collect. To address this issue, advanced learning techniques such as semi-supervised learning [17, 21, 41], knowledge transfer between different surrogates using transfer optimization [20, 52], and between different objectives using transfer learning [48, 49] have been adopted in surrogate-assisted optimization. Another solution is to reduce the computational cost of data collection by parallelizing expensive computer simulations [1, 5] in data-driven surrogate-assisted evolutionary optimization.

Little attention has been paid to data privacy concerns in data-driven optimization. One exception is our previous work reported in Ref. [51], which proposes a federated data-driven evolutionary algorithm (FDD-EA) for single-objective optimization based on federated learning [33, 60]. As its name suggests, federated learning aims to collaboratively train a global model using data distributed on multiple local devices without transmitting the local data to a central server. Instead, each client train a local model based on the local data and then the parameters (or the gradients) of the local models are transmitted to the server to generate the global model. Similarly, in FDD-EA, the central server averages the local models uploaded by the clients with a sorted averaging algorithm [51]. Then, the global and local models are made use of for approximating the objective function and estimating the uncertainty of the approximated fitness, based on which an infill criterion is designed for surrogate management in the federated optimization environment. Federated data-driven optimization has a wide range real-world applications, in such as the design of chemical reactors [36] and the optimization of engineering operation [39], where the entire system contains a large number of sub-systems and the collected data on each sub-system are not allowed to be sent to a central storage. By extending FDD-EA, this work proposes a federated data-driven evolutionary algorithm for multi-objective optimization. The main contributions of this paper are summarized as follows.

  • A federated data-driven multi-/many-objective evolutionary optimization algorithm (FDD-MOEA) is presented, in which multiple clients collaboratively train a global surrogate without uploading local data. To the best of our knowledge, this is the first work that enables federated data-driven multi-/many-objective optimization that does not require to store the local data on a central server, thereby preserving the privacy of the data.

  • An ensemble-based acquisition function is adopted for FDD-MOEA, in which the global surrogate is used to provide the approximated fitness and the local surrogates are used to provide an estimate of the uncertainty of the approximated fitness.

The remainder of this paper is arranged as follows. The next section presents the concepts of multi-objective optimization, federated learning and acquisition function. The main workflow and mechanisms of the proposed method, FDD-MOEA, are illustrated in in the subsequent section. Then, various empirical studies on test suites are given. The final section summarizes the contributions and future directions of this paper.

Background and motivations

In this part, we briefly illustrate the concept of multi-objective optimization, RBFN surrogate, federated learning and acquisition function.

Multi-objective optimization

Denote the minimization of vector of objectives by

$$\begin{aligned} \begin{aligned}&\min _x {\varvec{f}}({\varvec{x}}) = \left( f_1({\varvec{x}}), f_2({\varvec{x}}), f_3({\varvec{x}}), \ldots ,f_M({\varvec{x}})\right) ^T, \\&\text {subject to} \quad {\varvec{x}} \in R^d, \end{aligned} \end{aligned}$$
(1)

where \({\varvec{x}} \in R^d\) is the decision vector with dimension d, M is the number of objectives and \(M\ge 2\), and the profile formed by the projections of the aforementioned Pareto optimal solutions in the objective space is called Pareto front (PF). Note that this work focuses on the optimization of unconstrained MOPs.

Radial basis function networks

Radial basis function networks (RBFNs) [13] are widely adopted surrogate models due to their high computational efficiency and robustness on high-dimensional problems. The first hidden layer connected to the input of an RBFN is composed by a series of centers \(\{{\varvec{c}}_1,\ldots ,{\varvec{c}}_i,\ldots ,{\varvec{c}}_q\}\), where q is the number of centers, and \({\varvec{c}}_i \in R^d\) is the ith center. This layer calculates the distance between a sample point \({\varvec{x}} \in R^d\) and the ith center, \(\phi \left( ||{\varvec{x}}-{\varvec{c}}_i||\right) \), where \(\phi (\cdot )\) represents a radial basis function, and in this work we select the Gaussian function with a spread \(\delta _i\) as the basis function,

$$\begin{aligned} \phi \left( ||{\varvec{x}}-{\varvec{c}}_i||\right) =e^{-\frac{||{\varvec{x}}-{\varvec{c}}_i||}{2\delta _i^2}}. \end{aligned}$$
(2)

Suppose \(X\in R^{n_k\times d}\) and \(Y\in R^{n_k\times M}\) represent a dataset with \(n_k\) (indexing by j) sample pairs (\({\varvec{x}}_j\in R^d, {\varvec{y}}_j \in R^M\)), then the corresponding output of the RBFN can be calculated by

$$\begin{aligned}&\begin{bmatrix} {\hat{y}}_{1,1} &{} \ldots &{} {\hat{y}}_{1,M} \\ &{}&{} \ldots &{} \\ {\hat{y}}_{n_k,1} &{} \ldots &{}{\hat{y}}_{n_k,M} \\ \end{bmatrix} \nonumber \\&\qquad = \begin{bmatrix} \phi (||{\varvec{x}}_1-{\varvec{c}}_1||)&{} \ldots &{} \phi (||{\varvec{x}}_1-{\varvec{c}}_q||) \\ &{}&{} \ldots &{} \\ \phi (||{\varvec{x}}_{n_k}-{\varvec{c}}_1||)&{} \ldots &{} \phi (||{\varvec{x}}_{n_k}-{\varvec{c}}_q||) \\ \end{bmatrix}\nonumber \\&\qquad \begin{bmatrix} w_{1,1} &{} \ldots &{} w_{1,M} \\ &{}&{} \ldots &{}\\ w_{q,1} &{} \ldots &{} w_{q,M} \\ \end{bmatrix} + \begin{bmatrix} b_{1} &{} \ldots b_{M} \\ \end{bmatrix},\nonumber \\ \end{aligned}$$
(3)

which can further be simplified to be

$$\begin{aligned} \hat{{\varvec{y}}}_j = \varPhi _j {\varvec{w}} + {\varvec{b}}, \; \text {for}\; j=1,2, \ldots ,n_k, \end{aligned}$$
(4)

where \(\varPhi _j=[\phi (||{\varvec{x}}_j-{\varvec{c}}_1||), \ldots ,\phi (||{\varvec{x}}_j-{\varvec{c}}_q||)]\) denotes the distance between sample \(x_j\) and all centers, and \({\varvec{w}}=[w_{1}, \ldots ,w_{M}]\in R^{q\times M}\), in which \(w_{M}=[w_{1,M},w_{2,M}, \ldots ,w_{q,M}]^T\) are the weights of the connecting Mth attribute of \({\varvec{y}}_j\) and all centers, and \({\varvec{b}}=[b_1, \ldots ,b_M]\in R^{1\times M}\) is the bias, \({\varvec{\delta }}=\{\delta _1,\delta _2, \ldots ,\delta _q\}\in R^q\) stands for the spread vector of the RBFN. Hence, we can use \([{\varvec{w}},{\varvec{\delta }},{\varvec{c}},{\varvec{b}}]\) to represent the RBFN.

In terms of the training process, the centers of an RBFN is usually determined by random selection or K-means clustering. The least square method and backpropagation are two most popular methods [13] to train the weights \({\varvec{w}}\) and biases \({\varvec{b}}\). The least square method optimizes the weights and the biases through matrix inversion (linear algebra), whereas backpropagation uses strategies such as the stochastic gradient descent (SGD) method [37] to iteratively optimize the parameters.

Compared with GPs, RBFNs are efficient for training and it is less sensitive to the increase of training data size. However, an RBFN cannot directly provide the uncertainty of its predictions like GPs, making it unsuitable for applying an infill criterion for surrogate model management.

Federated learning

Federated learning [33] originates from the attempt to address the privacy concerns in distributed learning [30], which has been widely studied and applied in real-world applications due to its capability of privacy protection and parallel computing [50, 60]. Generally, the global optimization objective of a federated learning system can be written by

$$\begin{aligned} \min _{W_s} F(W_s) = \sum _{k=1}^{\lambda N}p_k F_k(W_k), \end{aligned}$$
(5)

where N is the total number of clients, \(\lambda \) is a coefficient that reflects how many clients will participate in model update in each communication round, and \(p_k\) is the weight that controls the importance of the participating client k, which is usually determined by the size of local dataset \(D_k\),

$$\begin{aligned} p_k = \frac{|D_k|}{\sum _{k=1}^{\lambda N}|D_k|}, \end{aligned}$$
(6)

and \(F_k\) denotes the local objective, which is

$$\begin{aligned} F_k(W_k) = \sum _{i=1}^{n_k} L(W_k;{\varvec{x}}_i,{\varvec{y}}_i), \end{aligned}$$
(7)

where L is the loss function.

As Mcmahan [33] suggested, the global model \(W_s\) can be conducted by averaging a set of local models \(W_k\) \(\left( k=\{1,2, \ldots ,\lambda N\}\right) \) rather than collecting distributed local data, which can be denoted by

$$\begin{aligned} W_s = \sum _{k=1}^{\lambda N} p_k W_k. \end{aligned}$$
(8)

To summarize, federated learning is a distributed learning framework, in which a local model is trained on each client. The trained local models are then uploaded onto the server and aggregated into a global model. The global model is then downloaded to all participating clients to be further trained. Ideally, the global model will converge to the one that is trained on all local data that are centrally stored.

It should be emphasized that the main motivation of the present work is to achieve data-driven optimization of complex systems, in which the data is collected and distributed on multiple clients. Due to privacy concerns and other considerations, the data are not allowed to transmitted to a central server. To the best of our knowledge, all existing work on data-driven evolutionary optimization assumes that the sampled data are available for training a global surrogate model using centralized learning, with one exception reported very recently in Ref. [51], which proposed, for the first time, an algorithm for federated data-driven single-objective optimization. Actually, this work is a natural extension of [51], aiming to propose a federated data-driven evolutionary multi-objective optimization algorithm, FDD-MOEA for short.

Acquisition function

Acquisition function (AF), also known as infill criterion or model management, is designed to decide where to sample new data (new candidate solutions) in the decision space, i.e., to determine which candidate solutions \({\varvec{x}}\) should be selected for calculating their objective values \({\varvec{f}}({\varvec{x}})\), usually by means of time-consuming numerical simulations or physical experiments. AFs were originally developed in Bayesian optimization [38], where the Gaussian process is used as the surrogate, although it can be easily extended to any other types of surrogates capable of providing uncertainty information, such as ensemble surrogates [18], or dropout neural networks [19].

An AF must be able to balance the exploitation and exploration [26], and several successful infill criteria have been widely adopted by surrogate-assisted MOEAs, such as Expectation Improvement (EI) [26] and Lower Confidence Bound (LCB) [44]. In this work, we choose LCB to minimize Eq. (9), which is

$$\begin{aligned} LCB({\varvec{x}}) = \hat{{\varvec{f}}}({\varvec{x}})-\alpha {\hat{s}}({\varvec{x}}), \end{aligned}$$
(9)

where \(\alpha \) is a hyperparameter which is set to 2 as suggested in [16] in the experimental studies.

Federated data-driven multi-objective optimization

In this section, we will briefly introduce the federated construction of the global model, the workflow of the proposed FDD-MOEA, and the used federated acquisition function.

Federated surrogate construction

Clients: Suppose \(W_k=[{\varvec{w}}_k,{\varvec{c}}_k,{\varvec{\delta }}_k,{\varvec{b}}_k]\) represents the surrogate on the \(k^{th}\) client, and let \(\{\hat{{\varvec{y}}}_1,\hat{{\varvec{y}}}_2, \ldots ,\hat{{\varvec{y}}}_{B}\}\) represent the predicted outputs with a batch size of B (\(1\le B \le n_k\)), we have

$$\begin{aligned} \hat{{\varvec{y}}}_i=W_k({\varvec{x}}_i)= \varPhi _i {\varvec{w}} + {\varvec{b}}, \; \text {for}\; i=1,2, \ldots ,B \end{aligned}$$
(10)

then the loss function (L in Eq. (7)) of each local RBFN used in this work can be written as

$$\begin{aligned} L=\frac{1}{2B}\sum _{i=1}^{B}(\hat{{\varvec{y}}}_i-{\varvec{y}})^2, \end{aligned}$$
(11)

and the centers and spreads of the RBFN are determined by K-means maximum distance between centers, then the gradients of weights \({\varvec{w}}_k\) and \({\varvec{b}}_k\) are calculated by

$$\begin{aligned} \frac{\partial L}{\partial {\varvec{w}}_k} = \frac{1}{B}\sum _{i=1}^B \frac{\partial \hat{{\varvec{y}}}_i}{\partial {\varvec{w}}_k}(\hat{{\varvec{y}}}_i-{\varvec{y}}), \end{aligned}$$
(12)
$$\begin{aligned} \frac{\partial L}{\partial {\varvec{b}}_k} = \frac{1}{B}\sum _{i=1}^B \frac{\partial \hat{{\varvec{y}}}_i}{\partial {\varvec{b}}_k}(\hat{{\varvec{y}}}_i-{\varvec{y}}). \end{aligned}$$
(13)

By replacing \(\hat{{\varvec{y}}}_i\) with Eq. (10), we have

$$\begin{aligned} \frac{\partial L}{\partial {\varvec{w}}_k}= & {} \frac{1}{B}\sum _{i=1}^B \varPhi _i(\hat{{\varvec{y}}}_i-{\varvec{y}}), \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial L}{\partial {\varvec{b}}_k}= & {} \frac{1}{B}\sum _{i=1}^B (\hat{{\varvec{y}}}_i-{\varvec{y}}). \end{aligned}$$
(15)
Fig. 1
figure 1

An illustration of local training with server model

Full size image

In this way, each client iteratively trains the weights and biases of the local \(W_k\) with a learning rate \(\eta \) and a local epoch E. In addition, the batch size B is set to 1 in training the local models in this work, mainly because the number of training data on each client is very limited in data-driven optimization.

Server: After the local model on the kth client (\(W_k\)) is obtained and uploaded to the server, the sorted averaging algorithm, as described in Algorithm 1 and first reported in Ref. [51], will be adopted to aggregate all received local models to create the global model \(W_s\). Then, the server will use \(W_s\) to assist an MOEA. Finally, \(W_s\) and the found potential solution \({\varvec{x}}\) to the chosen clients, the kth client will evaluate the \({\varvec{x}}\) by the expensive objectives and update the local dataset to further update local model \(W_k\), which can be illustrated by Fig. 1. The overall framework will be described in “Overall framework”.

figure a

Overall framework

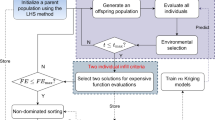
As shown in Fig. 2, the proposed FDD-MOEA differs from those of ensemble-based methods in that it utilizes sorted model averaging to obtain a global model \(W_s\) for fitness approximation instead of averaging predictions of ensemble. In addition, the data partitions for each local models are determined by the operating conditions of the clients and cannot be actively manipulated as done conventional ensemble construction when the data is centrally stored. It also be stress that in principal, any MOEAs can be applied to the proposed framework. In our experimental studies, we choose NSGA-II and RVEA to examine the performance of the proposed framework for MOPs and MaOPs, respectively.

Fig. 2
figure 2

The overall framework of the proposed FDD-MOEA

Full size image

Algorithm 2 summarizes the overall workflow of the proposed FDD-MOEA. Before the optimization starts, Latin hypercube sampling (LHS) is adopted to generate \(11d-1\) points in the decision space, where d is the dimension of the decision space. And these initial points are evaluated by the expensive real objective functions (data collection), the collected data pairs are used as the initial training dataset of for the local models. Then, the kth client will train the local RBFN \(W_k\) with its own dataset and upload the trained \(W_k\) to the server. The server aggregates all uploaded local models by means of sorted averaging to obtain the global model \(W_s\). After that, the acquisition function (AF) will be formed using \(W_s\) and all local models (refer to “Modified LCB”), in which the averaged \(W_s\) will replace the expensive objective functions to predict the objective values, and the local models will collaboratively estimate the uncertainty of the predictions.

figure b

Then, an MOEA is chosen to optimize the acquisition functions, and m new solutions (specified by the user) will be selected from the results of MOEA through clustering. Note, however, that duplicate solutions will be removed before clustering.

  1. (1)

    Removal of redundant solutions. It is very common when the optimization completes, the final population of the MOEA contains redundant solutions or extremely similar solutions. In this work, we calculate the Euclidean distances between solutions of the current population in the decision space and only one will be kept if the distance between two solutions is less than a threshold (\(10^{-6}\) in this work). Note that the number of solutions after removing the redundant solutions may be smaller than m, in particular for high-dimension problems. In this case, we will save the existing solutions and restart the MOEA until the stopping criterion is satisfied.

  2. (2)

    Clustering. After removing the redundant solutions, the remaining ones will be clustered using the K-means algorithm with a center size of m.

In federated optimization, there are many challenges that may lead to difficulties in collecting well distributed data, making it hard to achieve a high-quality global model. For example, in this work, the m selected candidate solutions in each round will be broadcast to all participating clients and each will evaluate all the m samples. As a result, the total FEs will be \(\lambda N m\) (assuming no communication failures), which is \(\lambda N\) times more than in centralized optimization. Note, however, that in federated optimization, the evaluations on different clients are done in parallel, and these additional FEs do not introduce any new data samples compared to the centralized ones. This ensures fair performance comparisons between the federated and centralized optimization. In principle, we can send each of the m solutions to m different clients, in which case the total number of FEs will be m in one round. This will result in two differences. First, the computation time of each client will be approximately 1/m compared to the centralized paradigms. Second, the samples on different clients will become increasingly different as the optimization proceeds, which will result in non-independent and identically distributed (non-iid) data, making the training of a global model challenging [59].

In this work, we consider two main challenges, namely communication failures and client dropout. We define a probability of communication failure \(p_f\) to denote whether the communication between a certain client and the server is successful in one particular iteration of surrogate management. If the communication is successful, then all m candidate solutions selected by the server will be passed to the participating clients, evaluated, and added to the local training dataset for the next round training. Otherwise, the m new solutions will not be evaluated by that particular client. Consequently, the larger the communication failure probability, the stronger the data will be non-iid.

Client dropout is also caused by communication problems. Like in federated learning, we use a participation ratio \(\lambda \) to define the percentage of clients that participate in each round of model update and surrogate management. The smaller participation ratio, the smaller the number of local models, which may result in a poorer global model.

To be consistent with the settings in Ref. [18], the initial number of training data is set to \(11d-1\), and we also limit the maximum number of training data to be \(l=11d-1+25\). A fast non-dominated sorting is applied to select l data for model training.

Table 1 Test instances and their properties
Full size table
Table 2 Mean (std) of the IGD values obtained by FDD-MOEA, HeE-MOEA, GP-MOEA and K-RVEA for different decision dimensions when \(M=3\)
Full size table
Fig. 3
figure 3

The IGD convergence profiles on DTLZ1

Full size image
Fig. 4
figure 4

The IGD convergence profiles on DTLZ2

Full size image
Fig. 5
figure 5

The IGD convergence profiles on DTLZ3

Full size image
Fig. 6
figure 6

The IGD convergence profiles on DTLZ4

Full size image
Fig. 7
figure 7

The IGD convergence profiles on DTLZ5

Full size image
Fig. 8
figure 8

The IGD convergence profiles on DTLZ6

Full size image
Fig. 9
figure 9

The IGD convergence profiles on DTLZ7

Full size image

Modified LCB

As we stated in “Acquisition function”, the acquisition function prefers solutions with high uncertainty and better performance. To achieve this, we utilize the global surrogate model together with the local models to provide predictions of candidate solutions and estimate the uncertainty of the predictions.

First, once the server model \(W_s\) is aggregated, the evaluated objective values \({\hat{f}}({\varvec{x}})\) in Eq. (9) is calculated by

$$\begin{aligned} {{\hat{f}}}({\varvec{x}}) = W_s({\varvec{x}}). \end{aligned}$$
(16)

Similar to the ensemble-based strategy, the variance \({{\hat{s}}}^2({\varvec{x}})\) of the predictions can be estimated by

$$\begin{aligned} {{\hat{s}}}^2({\varvec{x}}) = \frac{1}{\lambda N-1} \left[ \sum _k^{\lambda N}\left( W_k({\varvec{x}}) - {{\hat{f}}}({\varvec{x}})\right) ^2 \right] . \end{aligned}$$
(17)

Consequently, we can easily calculate the LCB values for optimization using the MOEA.

Numerical studies

In the following, the benchmark problems and parameter settings used in the empirical studies are introduced and then the comparative results are presented.

Benchmark problems

As listed in Table 1, we adopt the DTLZ test suite for comparative studies, and 49 test instances in total with different number of decision variables and objectives are used. According to Ref. [22], an MOEA may get trapped in local Pareto front of DTLZ1 and DTLZ3, which will lead to poor performance. And the PF of DTLZ2 are located in an octant of the unit sphere, which is often used to test the performance of an MOEA with a large number of objectives. It is hard for an MOEA to find evenly distributed solutions in the objective space for DTLZ4 due to the biased projection from decision space to the objective space [18], and the mapping parameter \(\alpha \) of DTLZ4 is set to 100 in this work. DTLZ5 and DTLZ6 have degenerate Pareto optimal fronts, and each front is supposed to be an arc in the objective space. The Pareto front of DTLZ7 is disconnected.

Table 3 Mean (std) of the IGD values obtained by FDD-MOEA, HeE-MOEA, GP-MOEA and K-RVEA for different numbers of objectives when \(d=20\)
Full size table
Table 4 Mean (std) of the IGD values obtained using different \(\lambda \) for different numbers of objectives when \(d=30\)
Full size table

Parameter settings

Recall that the number of objectives and the dimension of the decision variable are denoted by M and d, respectively. The basic parameter settings are as follows.

  1. 1.

    The number of independent runs is set to 20 for each test instance, and each time we sample \(11d\;-\;1\) points in the decision space using LHS.

  2. 2.

    NSGA-II is chosen as the MOEA for MOPs, the population size and the number of generations are both set to 50. The crossover distribution index and its probability are set to 20, 1.0. And the corresponding mutation distribution index and probability are 20 and 1/d.

  3. 3.

    RVEA is adopted as the MOEA for MaOPs, and the number of reference vectors are set to 105, 126, 275, 420 for 3, 5, 10, 20 objectives, respectively.

  4. 4.

    As suggested in Ref. [18], the number of RBFN centers is limited to \(\sqrt{M+d}\;+\;3\), the optimization process starts at \(11d-1\) fitness evaluations (FEs) and ends at \(11d-1+120\) FEs, and five new FEs are performed (five new training samples are collected) in each round, which means that the number of iteration R is 24 in a single run. The maximum size of training data l is set to \(11d-1+25\).

  5. 5.

    The hyperparameters of federated learning are set as follows: the local epoch number \(E=20\), the learning rate \(\eta =0.06\), the number of clients \(N=10\), and the participation ratio \(\lambda =0.9\). As previously discussed, for each individual client, the solutions to be sampled at each iteration as identified by the surrogate management strategy by the server may not be implemented on each client with a communication failure probability \(p_f=3\%\). To make a fair comparison with ensemble-based algorithms, the initial solutions are the same on all clients.

  6. 6.

    Inverted generational distance (IGD) [4] is adopted as the performance indicator, which calculates the Euclidean distance between the non-dominated solutions obtained by an algorithm and a set of reference points sampled from the theoretical Pareto front. The result of 20 independent runs are analyzed by the Wilcoxon rank sum at a significance level of 0.05, where symbol ‘\(+\)’ means that FDD-MOEA outperforms the compared method, ‘\(=\)’ indicates the two algorithms perform equally well, and ‘−’ means that the compared method outperforms FDD-MOEA.

Results and discussion

We implement the proposed FDD-MOEA with Python 3.7 [45], and the RBFN is constructed from scratch using the stochastic gradient descent method. The code of NSGA-II is taken from Pymoo [3], and the K-RVEA are implemented by PlatEMO v2.8.0 [43], and the performance indicators are also calculated on PlatEMO. All experiments are conducted on a computer with Intel(R) Core(TM) i7-8700 CPU@3.20GHz 3.19 GHz, Windows 10, version 1909.

Fig. 10
figure 10

Converged IGD values when \(M=20, d=30\) with different \(\lambda \)

Full size image
Table 5 Mean (std) of the IGD values obtained using different \(p_f\) for different numbers of objectives when \(d=30\)
Full size table
Fig. 11
figure 11

Converged IGD values when \(M=20, d=30\) with different \(p_f\)

Full size image

Performance comparison on three-objective test instances

The first set of experiments compares FDD-MOEA with three centralized data-driven MOEAs, namely HeE-MOEA [18], GP-MOEA [18, 19] and K-RVEA [8] on three-objective DTLZ functions with a dimension of the decision space \(d=10,20,40,80\). Specially, HeE-MOEA utilizes a heterogeneous ensemble to assist the optimization, while GP-MOEA is a variant of HeE-MOEA that adopts a GP as the surrogate for approximating each objective function. Note that HeE-MOEA, GP-MOEA and FDD-MOEA use NSGA-II as the baseline optimizer, while K-RVEA is based on RVEA. The parameter settings of the four methods are the same as defined in “Parameter settings”. The average IGD results on all these test instances are summarized in Table 2.

From the results in Table 2, we can observe that FDD-MOEA obtains the best IGD value on 16 out of 28 test instances, compared with HeE-MOEA, GP-MOEA and K-RVEA. These results confirm that the proposed FDD-MOEA works effectively for solving MOPs in a federated system. We also note that K-RVEA performs better than HeE-MOEA and GP-MOEA. It should be stressed that that the purpose of proposing FDD-MOEA is not for developing a new MOEA that performs better than the state-of-the-art data-driven optimization algorithms. Rather, it aims to propose an algorithm that can still work effectively when the data are distributed on different clients and are not allowed to centrally stored.

The convergence profiles of the compared algorithms on DTLZ1–DTLZ7 when \(d=10,80\) over the iterations are plotted in Figs. 3, 4, 5, 6, 7, 8 and 9. From these results, we find that the convergence properties of different algorithms strongly differ on different test instances. One general conclusion is that the performance advantage of FDD-MOEA over the compared algorithms will become stronger as the search dimension increases. This might be attributed to the use of the RBFNs in FDD-MOEA, which has been demonstrated powerful for high-dimensional systems in previous research.

Performance comparison on MaOPs

To further examine the effectiveness of the proposed FDD-MOEA on distributed optimization of many-objective problems, we conduct experiments by setting the number of objectives \(M=5,10,20\) for a fixed dimension \(d=20\). In this case, all algorithms under comparison use RVEA as the baseline optimizer. The parameter settings for all methods are provided in “Parameter settings”. Table 3 presents the statistical results in terms of the IGD values.

Overall, FDD-MOEA performs slightly better than HeE-MOEA and K-RVEA, and much better than GP-MOEA on the MaOP test instances. Compared with HeE-MOEA, FDD-MOEA performs better on 10 out of 21 test instances, equally well and worse on four and seven instances, respectively. Similar to the results presented above, the performance of FDD-MOEA is consistently competitive on all DTLZ1–DTLZ5 instances. FDD-MOEA performs particularly well on DTLZ6 when RVEA is adopted as the optimizer, in contrast to its performance when NSGA-II is used. On DTLZ7, FDD-MOEA is outperformed by HeE-MOEA. In addition, FDD-MOEA outperforms GP-MOEA on 15 out of 21 test instances, achieves similar results on three instances, and is underperformed on four instances.

In general, K-RVEA achieves the second best results on many-objective problems, and K-RVEA outperforms FDD-MOEA on the DTLZ2 and DTLZ7 test instances. Interestingly, when using RVEA as the optimizer, the performance of FDD-MOEA on DTLZ6 problems has a significant improvement and and it outperforms K-RVEA in all cases, which means that using RVEA as the optimizer makes FDD-MOEA more competitive when compared with K-RVEA.

Influence of \(\lambda \)

The participation ratio, \(\lambda \), is an important parameter in federated learning systems. In federated data-driven optimization, a low participation rate will lead to a decrease in the amount of training data on each client. To examine the influence of the participation ratio \(\lambda \) on the performance of FDD-MOEA, empirical experiments are conducted by varying the values of \(\lambda \), while the number of decision variables is fixed to \(d=30\) and RVEA is adopted as the optimizer.

As listed in Table 4, the results indicate that FDD-MOEA is relatively insensitive to the participation ratio and in general, a larger participation ratio contributes to better performance, which is expected. Furthermore, we also investigate the influence of \(\lambda \) on the performance of FDD-MOEA DTLZ1-7 problems in terms of IGD for \(M=20, d=30\). The performance changes of FDD-MOEA over different \(\lambda \) values are presented in Fig. 10. The experimental results show that higher participation ratios will lead to an improvement in the performance of FDD-MOEA, mainly because the total amount of selected solutions is limited, and the amount of local training data on each client may significantly decrease with a lower participation ratio \(\lambda \).

Influence of \(p_f\)

The aim of federated data-driven EAs is to solve of distributed optimization problems without collecting private data stored on local clients [51] and hence, communications between clients and the server when exchanging surrogate information are unavoidable. However, there are many potential reasons that may cause communication failures or packet losses, such as network congestion or when communication network is not available. As mentioned in “Overall framework”, we assume that each client has a failure probability of \(p_f\) when communicating with the server, which means that the m solutions obtained in this iteration cannot be passed to the client. In this part, we study the impact of \(p_f\) on the performance of FDD-MOEA, and the experimental results with \(p_f=1 \%,3 \%,5 \%\) and \(10 \%\) are summarized in Table 5, and the converged IGD values of the compared algorithms are plotted in Fig. 11 when \(M=20\).

Specifically, the dimension of the decision space d and the participation ratio are fixed to 30 and 0.90, respectively, and RVEA is set as the optimizer. As we can see, when \(p_f\) is set to 1% and 3%, the performance of FDD-MOEA does not change much and becomes slightly when \(p_f\) is increased to 5% or 10%. This is also expected since the larger \(p_f\) is, the less data will be available for model management on each client.

Conclusions and future work

It may become unrealistic to assume that all data can be made available for centralized training of surrogates in data-driven evolutionary optimization. To remove this strong assumption, we consider the challenging situation in which data are distributed on different local clients and propose a federated data-driven multi-/many-objective evolutionary optimization algorithm in this work. By leveraging federated learning, a global surrogate is trained collaboratively for fitness approximations, a sorted averaging algorithm is used to aggregate the local models, and the uploaded local surrogates are utilized to provide the uncertainty of solutions. In addition, a modified acquisition function combining local and global information is proposed for surrogate management. Empirical results indicate that the proposed algorithm achieves comparable results on 49 benchmark problems with the state-of-the-art of centralized data-driven evolutionary algorithms.

However, the proposed algorithm does not perform well on the problems with disconnected Pareto fronts, in which case the local model may strongly differ from each other, causing considerable model divergence. Hence, in the future, we will investigate more robust modelling techniques and new acquisition functions for handling strongly non-iid data for data-driven optimization.