Chaos-guided neural key coordination for improving security of critical energy infrastructures

Abstract

In this paper, chaos-guided artificial neural learning-based session key coordination for industrial internet-of-things (IIoT) to enhance the security of critical energy infrastructures (CEI) is proposed. An intruder might pose several security problems since the data are transferred across a public network. Although there have been substantial efforts to solve security problems in the IIoT, the majority of them have relied on traditional methods. A wide range of privacy issues (secrecy, authenticity, and access control) must be addressed to protect IIoT systems against attack. Owing to the unique characteristics of IIoT nodes, existing solutions do not properly address the entire security range of IIoT networks. To deal with this, a chaos-based triple layer vector-valued neural network (TLVVNN) is proposed in this paper. A chaos-based exchange of common seed value for the generation of the identical input vector at both transmitter and receiver is also proposed. This technique has several advantages, including (1) it protects IIoT devices by utilizing TLVVNN synchronization to improve CEI security. (2) Here, artificial neural coordination is utilized for the exchange of neural keys between two IIoT nodes. (3) Using this suggested methodology, chaotic synchronization can be achieved, enabling the chaos-based PRNG seed exchange. (4) Vector-valued inputs and weights are taken into consideration for TLVVNN networks. (5) The deep internal architecture is made up of three hidden layers of the neural network and a vector value as input. As a result, the attacker would have great difficulty interpreting the internal structure. Experiments to verify the performance of the proposed technique are conducted, and the findings demonstrate that the proposed technique has greater performance benefits than the existing related techniques.

Introduction

The energy industry’s digitization is transforming transportation, telecommunications, healthcare, banking, and defense. Critical energy infrastructures (CEI) are rapidly dispersed, resulting in complex cyber-physical networks that require vigilant protection and fast recovery to prevent cyberattacks. Reliable and consistent energy infrastructure is essential for modern societies. Electricity, gas, and oil are used not only in our everyday lives but also in the service of other CEI. This is the most important infrastructure for deep industrialization and information integration. The latest technological advancement in the industrial internet of things (IIoT) era promotes better approaches to magnify the monitoring of energy quality and reliability problems, as well as smart grid initiatives. Resource use, on the other hand, is becoming more ‘smart,’ thanks to internet-connected smart appliances, smart houses, and smart electricity and gas meters. These would help with grid management and better aligning electricity production and demand, but they also open the door to cyberattacks. A smart meter in a smart grid infrastructure uses an insecure channel to access services securely. Since the information is transmitted over a public channel, an intruder may pose several security threats. Distributed wind and solar electricity generation, energy storage systems, and electric cars that are connected to both the internet and the electricity grid are all examples of this. Hackers have made these systems a favorite target. With the spread of the IIoT allowed by the rollout of 5G wireless communication networks, the number of networked devices in the energy system is expected to increase.

The majority of the existing methodology fails to offer the necessary security features, that are deemed to be significant needs in the IIoT security. The foregoing facts point to the development of a robust key exchange strategy that can meet many security requirements while avoiding the security flaws and disadvantages that currently exist in IIoT key exchange techniques. As a result, this paper proposed a robust triple layer vector-valued neural network (TLVVNN) enabling key exchange between the two IIoT nodes. Since this TLVVNN’s input and weight values are vector in nature, a complete neural synchronization can generate multiple pairs of session keys, improving security and maintaining performance. Although this proposed approach would regulate the length of the session key by changing the size of the vectors, the TLVVNN can preserve an appropriate protection standard to apply to real-life systems.

This article addresses the following issues:

• 1. IIoT safety and reliability toward Woman-In-The-Middle attacks must be enhanced. Whenever an assailant intercepts communication between two systems. It is a dangerous assault because the assailant is masked as the actual originator of the message. Because the assailant has the first line of communication, they would confuse the receiver into trusting that they are getting a piece of authentic information.

• 2. It is necessary to create a reliable key exchange method. Rather than transferring the complete key over a dedicated channel, a key must be automatically created at both network nodes via synchrony over a public network.

• 3. A cryptographic keys exchange scheme with high-security toughness which can withstand geometric and majority threats must be constructed.

The following is a summary of the several contributions made by this paper:

• 1. This paper aims to explain basic principles and reveal alternatives for efficient, cost-effective IIoT network security to overcome the problems posed by security complexity.

• 2. It proposes a neural key exchange method for enhancing the security of IIoT nodes. The cryptographic keys are not provided directly to the other node; instead, it is produced by swapping only a few variables over the unprotected network while both nodes use the neural coordination process.

• 3. This proposed method offers vector-valued inputs and weights to the TLVVNN. This technique prevents geometric and majority attacks.

• 4. A chaos-based seed exchange technique is used for generating the TLVVNN’s input vector using common seed value.

• 5. Using chaotic synchronization, both parties may create identical secret seed values (z). The same seed value is utilized to produce the common input vector. Two TLVVNNs synced with each other to generate a common seed value (z) in the sender and receiver sides by sharing specific parameters between sender and recipient. Since some of the variables that serve important components for the shared seed value (z) are not communicated via the public network, the sender keeps these variables hidden.

• 6. The proposed strategy addresses many attacks such as majority, replay, geometric, and session hijacking threats.

• 7. The key exchange mechanisms proposed by Dong and Huang [3], Jeong et al. [6], and Teodoro et al. [30] were first looked at in this study. Their shortcomings were also mentioned in this study. This present study provides a chaos-based TLVVNN synchronized key exchange strategy to provide a scalable length secret key to address the existing difficulties.

• 8. The proposed TLVVNN’s synchronization periods in random walk, anti-Hebbian, and Hebbian learning are significantly shorter than the present CVTPM, VVTPM, and TPM-FPGA methods.

The next section explains related work. The proposed method is discussed in the subsequent section followed by which the computational complexity analysis is discussed. Then TLVVNN’s security attacks are discussed. In the penultimate section, the results and analysis are given. The final section contains the conclusions and future scope, with references at the end.

Related work

Pham et al. [20] presented the foundations of the Whale Optimization Algorithm (WOA) and its applicability in wireless and communications system allocation of resources. They explored three challenges to show the application of WOA in wireless and communication systems, and initial findings are reported. WOA might be used to optimize allocation of resources in wireless networks and other technical areas, according to this article. Numan et al. [17] have emphasized the cloned nodes assault mechanism and given a quick study of clone detection mechanisms employed in fixed wireless sensor. The sensor networks are vulnerable to numerous assaults such as clone node or node duplication due to the characteristics of WSNs like restricted processor, storage, power, and lack of tamper resistance hardware, among others. They also offered a theoretical and conceptual analysis of current centralized and decentralized strategies for detecting clone nodes, as well as their limitations and problems. Moonsamy et al. [13] highlighted that several Android apps reveal facts about the user’s device without the user’s permission. They investigate why certain apps breach, how they leak, and where the information is released. They discovered that three most popular Games apps, that were previously classed as safe, exposed critical device identifiers, such as the IMEI and the IMSI, to third parties. They discovered that third-party advertisement modules were the primary source of all breaches found in their dataset. Lanir et al. [28] presented a strategy that might be used in concert with stochastic, genetic, and geometric threats to ensure that the length of the synaptic does not affect the assailants’ likelihood of succeeding. TPM synchronization, in particular, was demonstrated as a cryptographic key exchange method [21]. Ruttor et al. [24], Rosen-Zvi et al. [22], and Lanir et al. [28] demonstrated that cooperative learning laws can be used to synchronize two tree parity machines (TPMs). Neural cryptography has been the focus of considerable research. Ruttor et al. [23] suggested the coordination technique in the overall TPM system and discovered two major stages: attractive and repulsive steps. Neural networks are being frequently utilized in cybersecurity for a number of years [1, 5, 21]. According to Lu et al. [10], the blockchain enables multi-party collaborative secure data-sharing technology. In Niemiec et al. [15], the impact of changing parameters on the security and availability of various quality training laws was investigated. Edgar et al. [25] suggested a technique for identifying the appropriate TPM setup, which would result in a far more accurate and scalable neural key exchange method. Niemiec  [14] develop a simple solution involving the use of a TPM to solve inaccuracies in the quantum key exchange procedure during transfer. Pal et al. [18] developed a learning algorithm which might improve key effectiveness while also speeding up coordination. For the swap of keys, Chourasia et al. [2] proposed a vectored neuronal syncing.

Sarkar et al. [26, 27] presented techniques that enhanced TPM’s weight range, thus improving the privacy of the key exchange. The data exchange problem was turned into ML problem by incorporating learning with privacy. AAS-IoTSG, an anonymous session key agreement mechanism for the smart grid system, was proposed by Jo et al. [7].

Makkar et al. [11] suggested IoT device protection by identifying spam using machine learning. Gao et al. [4] presented a graph-based procedure to collect the flow of data and flow control information. Shishniashvili et al. [29] recommended using components of the coordinated synaptic weight vector as a cryptographic key rather than a complete weight vector. In quantum key management procedures, coordination of two systems could be used to eliminate errors [12]. The complex-valued tree parity machine (CVTPM) was suggested by the authors in Dong and Huang [3], which utilizes complex numbers for all control parameters. Although they only examined only the geometric attack, it is uncertain whether the CVTPM can withstand a majority attack. Jeong et al. [6] have proposed a VVTPM scheme. However, this method does not provide an effective syncing evaluation. To perform key exchange through reciprocal training of these systems, Teodoro et al. [30] recommended to put TPM architecture on an FPGA.

Proposed methodology

Generation and exchange of TLVVNN’s seed through chaos synchronization

Chaos helps to generate identical secret seed values (z) at both ends using chaos synchronization. This identical seed value is used to generate an identical input vector. For generating common seed value (z) on the sender and receiver side, two TLVVNNs synchronized with each other by exchanging certain parameters between sender and receiver. The sender holds these parameters secret because some of the parameters that play important functions for the common seed value (z) are not transmitted over the public channel. This handling mechanism prevents any attack while exchanging parameters such as sniffing, spoofing, phishing attack. Here, the common seed is produced by synchronizing two TLVVNNs by following the Pecora and Caroll (PC) method. This technique exchanges tuning parameters ($\sigma ,\;b,r,\;x_1,y_2$ and $z_2$) between sender and receiver TLVVNNs for synchronization purposes. Using Eqs. (1), (2), and (3), two secure TLVVNNs, i.e., sender and receiver, has been designed

$$\begin{aligned}&\dot{x}=\sigma \left( x-y\right) \end{aligned}$$

(1)

$$\begin{aligned}&\dot{y}=rx-y-xz \end{aligned}$$

(2)

$$\begin{aligned}&\dot{z}=xy-bz. \end{aligned}$$

(3)

The organization of two TLVVNNs is the main objective of this technique. This refers to a process in which, due to the pairing or to a forcing (periodic or noisy), two (or more) chaotic-TLVVNN (either identical or not identical) control their motion to a similar result. The proposed technique uses the PC method to assume a dynamical system characterized by Eq. (4)

$$\begin{aligned} \overset{-}{\dot{x}}=f\left( \overset{-}{x}\right) , \end{aligned}$$

(4)

where $\dot{x}=\left( x_1,\;x_2,\;\dots ,\;x_n\right)$ is the vector and f is a random mapping. This scheme is broken down into two sub-systems of Eqs. (5) and (6).

$$\begin{aligned}&\left. \begin{array}{r} \overset{-}{\dot{k}}=f\left( \overset{-}{k},\;\overset{-}{l}\right) \\ \overset{-}{\dot{i}}=g\left( \overset{-}{k},\;\overset{-}{l}\right) \end{array}\right\} \mathrm{Driver} \end{aligned}$$

(5)

$$\begin{aligned}&\overset{-}{\dot{m}}=h\left( \overset{-}{k},\;\overset{-}{m}\right) \;\mathrm{Response}. \end{aligned}$$

(6)

The response mechanism is drive by the driver $\overset{-}{\dot{k}}(t)$. The chaotic coordination between the driver and the response system is possible with the Lyapunov exponents and the driver’s adverse behavior. The next equations are to be used using Lorenz system for two secure sub-systems i.e. initiator and responder. Equations (7) and (8) can be described as initiators $(\dot{x}_{1},\dot{z}_{1})$.

$$\begin{aligned}&\dot{x}_{1}=\sigma (x_1-y) \end{aligned}$$

(7)

$$\begin{aligned}&\dot{z}_{1}=x_1y-bz_1. \end{aligned}$$

(8)

Equations (9) and (10) can be identified as the receiver $(\dot{y}_{2},\dot{z}_{2})$

$$\begin{aligned}&\dot{y}_{2}=rx-y_2-xz_2 \end{aligned}$$

(9)

$$\begin{aligned}&\dot{z}_{2}=xy_2-bz_2. \end{aligned}$$

(10)

Response sub-systems for sender and receiver are driven by y(t) and x(t) . If $t\rightarrow \infty$ then the value of $\left| z_2-z_1\right| \rightarrow 0$. Since all systems have been synchronized, a shared value for the device is received.

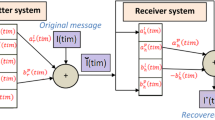
The sender initializes the value of $\sigma$ and b in this method, after which the value of b is sent to the receiver. The receiver initializes the r value and sends it to the sender. For points $x_1$ and $z_1$, the sender produces a random value. The sender gives $x_1$ to the receiver. Initially, the receiver produces random $y_2$, $z_2$ value and sends them to the sender. Therefore, the sender receives $y_2$, $z_2$ from the receiver and receives b and $x_1$ from the sender. Figure 1 shows the initial parameters exchange.

Fig. 1

Initial parameter exchange

The receiver calculates the new value of $\dot{y}_{2}$ and $\dot{z}_{2}$ with the help of r and b and $x_1$ (received from sender) using Eqs. (11) and (12) and returns the value of$\dot{y}_{2}$ and $\dot{z_2}$ to the sender. In Eqs. (11) and (12) the value of $x=x_1$ (current value received from sender).

$$\begin{aligned}&\dot{y}_{2}=rx-y_2-xz_2 \end{aligned}$$

(11)

$$\begin{aligned}&\dot{z}_{2}=xy_2-bz_2. \end{aligned}$$

(12)

Sender calculates the new value of $\dot{x_1}$ and $\dot{z_1}$ with the help of receives value $y_2$ from the receiver and own generated values $\sigma$ and b using Eqs. (13) and (14) and sends the value of new $\dot{x_1}$ to the receiver and so on. In Eqs. (13) and (14), the value of $y=y_2$ (current value received from the receiver). Figure 2 illustrates the exchange of calculated values between sender and receiver.

$$\begin{aligned}&\dot{\;x_1}=\sigma \left( x_1-y\right) \end{aligned}$$

(13)

$$\begin{aligned}&\dot{z}_{1}=x_1y-bz_1. \end{aligned}$$

(14)

Fig. 2

Exchange of calculated values

The sender produces a Nonce which is a random number after a predefined amount of parameter exchange. This Nonce is encrypted with the symmetric $z_1$ cipher and sends the results using Eq. (15).

$$\begin{aligned} {\mathrm{En}}\_{\mathrm{Nonce}}={\mathrm{Encrypt}}_{z_1}\left( \mathrm{Nonce}\right) . \end{aligned}$$

(15)

The receiver receives En_Nonce from the sender. Then decrypts En_Nonce using $z_{2\;}$ and performs $f\left( \;\right)$ using Eqs. (16) and (17), respectively.

$$\begin{aligned} {\mathrm{De}}\_{\mathrm{Nonce}}= & {} {\mathrm{Decrypt}}_{z_2}\left( \mathrm{En}\_{\mathrm{Nonce}}\right) \end{aligned}$$

(16)

$$\begin{aligned} \mathrm{Fn}\_\mathrm{Nonce}= & {} f\left( \mathrm{De}\_\mathrm{Nonce}\right) . \end{aligned}$$

(17)

The receiver encrypts the result of the previous step using $z_2$ and transmits to the sender using Eq. (18). Figure 3 shows the encrypted transmission Nonce.

$$\begin{aligned} \mathrm{En}\_{\mathrm{Fn}}\_{\mathrm{Nonce}}={\mathrm{Encrypt}}_{z_2}\left( \mathrm{Fn}\_\mathrm{Nonce}\right) . \end{aligned}$$

(18)

Fig. 3

Transmission of encrypted nonce

The sender is sent En_Fn_Nonce message from the receiver, attempting to deciphering with $z_1$ and executing reverse function $f^{-1}(\;)$ and checking if it is obtained or not in the original Nonce using Eq. (19).

$$\begin{aligned} \mathrm{Nonce}=f^{-1}\left( \mathrm{Decrypt}_{z_1} \left( \mathrm{En}\_\mathrm{Fn}\_\mathrm{Nonce}\right) \right) . \end{aligned}$$

(19)

If we generate the original ‘Nonce,’ it is possible to infer that both TLVVNNs have the same z value, i.e. ${z}_1=z_2$, where they are synchronized. $z_1$ is then used as a hidden seed to construct an equivalent sender and receiver input vector. When the original Nuncio is not received, a predefined sum of the message is exchanged for chaos synchronization between the sender and the recipient.

TLVVNN’s synchronization

In this article each IIoT node has a TLVVNN. The underlying framework comprises $\chi 1,\;\chi 2,\;\chi 3,\;M$, and $\psi$ values. M denotes the amount of required nodes in the 1st input layer at each artificial node in the 1st hidden layer, and $\chi 1,\;\chi 2,\;\chi 3$ represents the set of nodes in the 1st, 2nd, and 3rd hidden layers, respectively. Consequently, $\alpha _u$ is the input vector of the uth hidden node, $\beta _u$ is the weight matrix of the uth hidden node, $\alpha _{u,v}$ is the $\alpha _u$’s vth component, $\beta _{u,v}$ is the $\beta _u$’s vth component i.e. $\beta _{u,v}\in \{-\psi ,-\psi +1,\;\dots , +\psi \}$, and $\vartheta _u$ is the uth hidden node’s result, the real outcomes of the VNN is $\delta$, the localized field of the uth hidden neuron is $\tau _u$, the order variable is $G_u$, the maximum number of nodes concealed in a single hidden layer is $\sigma$, and the standardized overlap is $\varsigma _u$.

The TLVVNN’s internal parameters are vectorized variables. The input values in this architecture are defined in Eq. (20).

$$\begin{aligned} A^{p}=\left[ \begin{array}{c} \alpha _1^{p}\\ \alpha _2^{p}\\ \vdots \\ \alpha _\eta ^{p}\\ \end{array}\right] =\left[ \begin{array}{cccc} \alpha _{11}^{p}&{}\alpha _{12}^{p}&{}\cdots &{}\alpha _{1M}^{p}\\ \alpha _{21}^{p}&{}\alpha _{22}^{p}&{}\cdots &{}\alpha _{2M}^{p}\\ \alpha _{31}^{p}&{}\alpha _{32}^{p}&{}\cdots &{}\alpha _{3M}^{p}\\ \alpha _{\eta 1}^{p}&{}\alpha _{\eta 2}^{p}&{}\cdots &{}\alpha _{\eta M}^{p} \end{array}\right] , \end{aligned}$$

(20)

where $p=1,\;2,\;\ldots ,\;\sigma$ and $\eta$ denotes the amount of vectors. Equation 21 describes the weight values that are used to mapping input data to hidden units.

$$\begin{aligned} B^{p}=\left[ \begin{array}{c} \beta _1^{p}\\ \beta _2^{p}\\ \vdots \\ \beta _\eta ^{p} \end{array}\right] =\left[ \begin{array}{cccc} \beta _{11}^{p}&{}\beta _{12}^{p}&{}\cdots &{}\beta _{1M}^{p}\\ \beta _{21}^{p}&{}\beta _{22}^{p}&{}\cdots &{}\beta _{2M}^{p}\\ \beta _{31}^{p}&{}\beta _{32}^{p}&{}\cdots &{}\beta _{3M}^{p}\\ \beta _{\eta 1}^{p}&{}\beta _{\eta 2}^{p}&{}\cdots &{}\beta _{\eta M}^{p} \end{array}\right] . \end{aligned}$$

(21)

Here $\beta _{u,v}^{p}\in \{-\psi ,-\psi +1,\;\ldots ,\;+\psi \}$ , $u=1,\;2,\;\ldots ,\;\eta$ represents the uth vector of the weight, $v=1,\;2,\;\ldots ,\;M$ represents the vth input value. Weight range is denoted by $\psi$. The pth hidden unit vector $\vartheta ^{p}$ calculated using Eq. (22).

$$\begin{aligned} \vartheta ^{p}=\left[ \begin{array}{c} \vartheta _1^{p}\\ \vartheta _2^{p}\\ \vdots \\ \vartheta _\eta ^{p} \end{array}\right] =\mathrm{sgn}\left( \tau ^{p}\right) \overset{\triangle }{=}\left[ \begin{array}{c} \mathrm{signum}\left( \tau _1^{p}\right) \\ \mathrm{signum}\left( \tau _2^{p}\right) \\ \vdots \\ \mathrm{signum}\left( \tau _\eta ^{p}\right) \end{array}\right] . \end{aligned}$$

(22)

As a consequence, the TLVVNN and the CVTPM are the same in this situation. As a result, this paper emphasizes the TLVVNN’s ability to generalize systemic extended models such as TPM and CVTPM. Algorithm 1 explains the full TLVVNN sync procedure.

Algorithm 1:

Input : Identical vector input $A^{p}$ and the arbitrary vector weight vector $B^{p}$.

Output : Both communicating IIoT devices have coordinated TLVVNN with the same session key.

Step 1: Set the arbitrary vector-valued weight vector $B^{p}$. Where, $\beta _{u,v}^{p}\in \{-\psi ,-\psi +1,\dots ,+\psi \}$.

Steps 2 through 5 should be repeated once complete coordination is obtained.

Step 2: The result of each hidden node is determined by a weighting factor of the present state of inputs. Equation (23) provides the computation for the first hidden layer.

$$\begin{aligned} \tau _u^{p}=\frac{1}{\sqrt{M}}\alpha _u^{p}.\beta _u^{p} =\frac{1}{\sqrt{M}}\sum _{v=1}^{M}{\alpha _{u,v}^{p}}_{\;\beta _{u,v}^{p}} \end{aligned}$$

(23)

In Eq. (24), $\mathrm{signum}(\tau _u)$ denotes the output $\vartheta _u^{p}$ of the uth hidden unit.

$$\begin{aligned} \vartheta _u^{p}= \mathrm{signum}(\tau _u) \end{aligned}$$

(24)

If $\tau _u=0$ is true, $\vartheta _u^{p}$ is set to $-1$, resulting in binary output. If $\tau _u>0$ is true, $\vartheta _u^{p}$ is mapped to $+1$, representing that the hidden neuron is operational. If the value is $\vartheta _u^{p}\;=-1$, the hidden node is disabled. This is represented in Eq. (25).

$$\begin{aligned} \mathrm{signum}(\tau _u)=\left\{ \begin{array}{lc} -1&{}if\; \tau _u\le 0\\ +1&{}if\; \tau _u>0 \end{array}\right. . \end{aligned}$$

(25)

Step 3: Compute the final outcome of TLVVNN. The TLVVNN’s final outcome is the product of the hidden nodes in the final layer. This is denoted by $\delta$ (Eq. 26).

$$\begin{aligned} \delta =\overset{\chi 3}{\underset{u=1}{\prod \vartheta _1^{u}}} \;\overset{\chi 3}{\underset{u=1}{\prod \vartheta _2^{u}}} \;\vdots \;\overset{\chi 3}{\underset{u=1}{\prod \vartheta _\eta ^{u}}}. \end{aligned}$$

(26)

Equation (27) represents how the value of $\delta$ is represented.

$$\begin{aligned} \delta =\left\{ \begin{array}{lc} -1&{} \quad {\mathrm{if}}\; \gamma \vartheta u=-1,\;\mathrm{{is}}\;{\mathrm{odd}}\\ +1&{}\quad {\mathrm{if}}\; \vartheta _u=-1,\;{\mathrm{is}}\;{\mathrm{even}} \end{array}\right. . \end{aligned}$$

(27)

If TLVVNN has a single hidden node then $\delta =\vartheta _1^{p}$. The $\delta$ value is same for$\;2^{\sigma -1}$ different $(\vartheta _1^{p},\;\;{\vartheta _2^{p}}_{,\;\ldots ,\;}\vartheta _\sigma ^{p})$ representations.

Step 4: When the outcomes of two TLVVNNs A and B are in agreement, $\delta ^{A}=\delta ^{B}$, then, to use one of the three rules, adjust the weight vector.

Both TLVVNN will be learned from one another using the Hebbian (Eq. 28).

$$\begin{aligned} \beta _{u,v}^{p+}=fn\left( \beta _{u,v}^{p}+\alpha _{u,v}^{p}\delta \varTheta \left( \vartheta _u^{p}\delta \right) \varTheta \left( \delta ^{A}\delta ^{B}\right) \right) . \end{aligned}$$

(28)

Both TLVVNNs are learned with the reversal of their output in the anti-Hebbian (Eq. 29).

$$\begin{aligned} \beta _{u,v}^{p+}=fn\left( \beta _{u,v}^{p}-\alpha _{u,v}^{p}\delta \varTheta \left( \vartheta _u^{p}\delta \right) \varTheta \left( \delta ^{A}\delta ^{B}\right) \right) . \end{aligned}$$

(29)

When the set value of output is not important for tuning because it is the same for both TLVVNNs, the random-walk learning rule is utilized (Eq. 30).

$$\begin{aligned} \beta _{u,v}^{p+}=fn\left( \beta _{u,v}^{p}\;+\alpha _{u,v}^{p}\varTheta \left( \vartheta _u^{p}\delta \right) \varTheta \left( \delta ^{A}\delta ^{B}\right) \right) . \end{aligned}$$

(30)

If $P=Q$ is true, then $\varTheta \left( P,Q\right) =1$ is true. Otherwise, if $P\ne Q$ is true, $\varTheta \left( P,Q\right) =0$ is true. Only weights in hidden nodes are modified with $\vartheta _u^{p}=\delta$, and $fn(\beta )$ are used for each learning rule. Equation (31) depicts this.

$$\begin{aligned} fn(\beta )=\left\{ \begin{array}{lc} \mathrm{signum}(\beta )\psi &{}\quad {\mathrm{for}}\; \left| \beta \right| >\psi \\ \beta &{}\quad \mathrm{otherwise}\end{array}.\right. \end{aligned}$$

(31)

Proceed to step 6 if the weight vectors are identical for both TLVVNN.

Step 5: If the output of both TLVVNNs differs, $\delta ^{A}\ne \delta ^{B}$, then the weights cannot be updated. Proceed to step 2.

Step 6: As an IIoT session key, use this synchronized weight vector.

In comparison, although the CVTPM and VVTPM can share $M\times H$ -sized and $\eta \times M\times H$-sized secret key pairs after the full synchronization, the VNN exchange variable-length session key (i.e., $\eta \times \left( M\times \chi 1+\chi 1\times \chi 2+\chi 2 \times \chi 3\right)$-sized keys). As a result, protection can be improved over CVTPM and VVTPM while maintaining performance.

TLVVNN synchronization is used as an IIoT key swap over technique for either block or stream ciphers. However, by changing the number of vectors $\eta$, the TLVVNN can generate different key sizes and exchange a key in polynomial time.

The probability to see $\vartheta _u^{p}\alpha _{u,v}^{p}=+1$ or $\vartheta _u^{p}\alpha _{u,v}^{p}=-1$ are not really similar, but they are influenced by the weight $\beta _{u,v}^{p}$ shown in Eq. (32)

$$\begin{aligned}&P\left( \vartheta _{u,v}^{p}\alpha _{u,v}^{p}=1\right) \nonumber \\&\quad =\frac{1}{2} \left[ 1+erf\left( \frac{\beta _{u,v}^{p}}{\sqrt{MG_u^{p}-\beta _{u,v}^{2p}}}\right) \right] . \end{aligned}$$

(32)

The static probability representation of the weights for $t\rightarrow \infty$ is calculated for the transition probability, and it shows that $\vartheta _{u,v}^{p}\alpha _{u,v}^{p} =\mathrm{signum}(\beta _{u,v}^{p})$ happens frequently than $\vartheta _{u,v}^{p}\alpha _{u,v}^{p}=-\mathrm{signum} (\beta _{u,v}^{p})$. Equation (33) illustrates how to represent this

$$\begin{aligned}&P\left( \beta _{u,v}^{p}=\beta \right) \nonumber \\&\quad =R_0\prod _{i=1}^{\left| \beta \right| } \frac{1+erf\left( \frac{i-1}{\sqrt{MG_u^{p} -\left( i-1\right) ^{2}}}\right) }{1-erf\left( \frac{i}{\sqrt{MG_u^{p}-i^{2}}}\right) }. \end{aligned}$$

(33)

Equation (34) gives the normalization constant $R_0$ in this case

$$\begin{aligned} R_0=\left( \sum _{\beta =-\psi }^\psi \prod _{i=1}^{\left| \beta \right| } \frac{1+erf\left( \frac{i-1}{\sqrt{MG_u^{p}-\left( i-1\right) ^{2}}}\right) }{1-erf\left( \frac{i}{\sqrt{MG_u^{p}-i^{2}}}\right) }\right) ^{-1}. \end{aligned}$$

(34)

The variable of the error functions would be eliminated for $M\rightarrow \infty$, ensuring that the weights are evenly distributed as illustrates in Eq. (35)

$$\begin{aligned} \sqrt{G_u(t=0)}=\sqrt{\frac{\psi (\psi +1)}{3}}. \end{aligned}$$

(35)

If M is not infinite, the probability range can be described with the help of the ordering variable $G_u$, as given in Eq. (36)

$$\begin{aligned} G_u^{p}=\sum _{\beta =-\psi }^\omega \beta ^{2}P\left( \beta _{u,v}^{p}=\beta \right) . \end{aligned}$$

(36)

Equation (37) is obtained by increasing it in respect to $M^{-1/2}$

$$\begin{aligned} G_u^{p}= & {} \frac{\psi (\psi +1)}{3}\nonumber \\&-\frac{8\psi ^{4}+16\psi ^{3}-10\psi ^{2}-18\psi +9}{15\sqrt{3\pi \psi (\psi +1)}}\frac{1}{\sqrt{M}}\nonumber \\&+O\left( \frac{\psi ^{4}}{M}\right) . \end{aligned}$$

(37)

Equation (38) is used to describe the asymptotic efficiency of the order parameter in the context of $1\ll \kappa \ll \sqrt{M}$

$$\begin{aligned} G_u^{p}\sim \frac{\psi (\psi +1)}{3}\left( 1+\frac{8}{5\sqrt{3\pi }} \frac{\psi }{\sqrt{M}}\right) . \end{aligned}$$

(38)

Equation (39) is a first-order estimate of $G_u^{p}$

$$\begin{aligned} G_u^{p}= & {} \frac{\psi (\psi +1)}{3}\nonumber \\&-\frac{8\psi ^{4}+16\psi ^{3}-10\psi ^{2} -18\psi +9}{15\sqrt{3\pi \psi (\psi +1)}}\frac{1}{\sqrt{M}}\nonumber \\&+O\left( \frac{\psi ^{4}}{M}\right) . \end{aligned}$$

(39)

This leads to a logical conclusion (Eq. 40)

$$\begin{aligned} G_u^{p}\sim \frac{\psi (\psi +1)}{3} \left( 1-\frac{8}{5\sqrt{3\pi }}\frac{\psi }{\sqrt{M}}\right) . \end{aligned}$$

(40)

Computational complexity analysis

The setup of the weights in the neural coordination approach requires $(M\times \chi 1+\chi 1\times \chi 2 +\chi 2\times \chi 3)$ calculations. If $M=3,\;\chi 1=3,\;\chi 2=4,$ and $\chi 3=3$, the overall amount of synapse linkages (weights) is ($3 \times 3+3 \times 4+4 \times 3) = 33$. As a result, thirty-three calculations are required. It needs $(M\times \chi 1)$ calculations to generate M set of inputs for each $\chi 1$ amount of hidden nodes. The hidden node outputs need $\left( \chi 1+\chi 2+\chi 3\right)$ number of operations to compute. The amount of hidden nodes in the first, second, and third layers is represented by $\chi 1,\;\chi 2,\;\chi 3$ accordingly. The calculation of the resulting output requires a unit amount of time since it only requires a single operation.

Two parties’ randomly determined weights are equal in the perfect scenario of the neural coordination technique. As a result, TLVVNNs that are coordinated at the start should not use the learning to adjust the weights. In the best scenario, O(generation of identical seed + setup of inputs + construction of weights + processing of hidden node’s outputs) number of calculation is required. If weights generated by the two communications systems are not equivalent, the weights of the hidden nodes with a value equal to the final outcome are modified as per the learning algorithm in each iteration. This situation provides a mean and the worst scenarios in which I iterations are required to construct matching weights on both sides. Therefore, for the mean and worst cases, the overall calculation is $\begin{array}{l} (\;(M\times \chi 1)+(M\times \chi 1+\chi 1\times \chi 2 +\chi 2\times \chi 3)\\ +(\chi 1+\chi 2+\chi 3))+(I\times {\mathrm{No.}}\;{\mathrm{of}}\;\mathrm{weight}\;\mathrm{updation}) \end{array}$, that could be represented as O(time complexity during the 1st iteration + (no. of iterations $\times$ no. of weight changes)).

Security attacks on TLVVNN

Majority attack

To demonstrate TLVVNN’s safety, this article explores the majority assault condition, that is the most successful assault. As a consequence, Eq. (41) may be used to determine the likelihood of a successful attack.

(41)

If the two sync times are believed to be non-overlapping variable elements, and what’s the probability of Sntm_atk $\le$ Sntm? The intruder’s and both participants’ sync timings, and the coordinating period between both the two TLVVNNs, are denoted by Sntm_atk $\le$ Sntm and Sntm. The $P_{\mathrm{Sntm}}^\mathrm{{atk}}\left( t\right)$ and $P_{\mathrm{Sntm}}\left( t\right)$ are the summed likelihood distributions of each sync period. It is seen in Eq. (42)

$$\begin{aligned}&P\left( \mathrm{Sntm}\_\mathrm{{atk}}\le \mathrm{{Sntm}}\right) \nonumber \\&\quad \approx 1-\mathrm{{exp}}\left( \frac{\mathrm{Sntm}\_\mathrm{{atk}}}{\mathrm{Sntm}}\right) . \end{aligned}$$

(42)

The percentage of the mean obtained from the two synchronization gaps, which are factors of the weight range $\psi$, determines the likelihood of a majority assault occurring. The proportion of the two coordinating times, which is a factor of $\psi$, may be calculated using Eqs. (41) and (42) (Eq. 43).

$$\begin{aligned} \left( \frac{\mathrm{Sntm}\_\mathrm{atk}}{\mathrm{Sntm}}\right) \propto \frac{\psi ^{2}}{e^{c_1\psi +c_2\psi ^{2}}} \end{aligned}$$

(43)

Also, as consequence, the session key communication technique management involves the weight range $\psi$. If $\psi \gg 1$, the fraction of the two cooperation periods, is small (Eq. 51), the assailant’s chances of success can be calculated as follows (Eq. 44):

$$\begin{aligned} P\left( \mathrm{Sntm}\_\mathrm{{atk}}\le \mathrm{Sntm}\right) \propto \psi ^{2}e^{-c_1\psi }e^{-c_2\psi ^{2}}. \end{aligned}$$

(44)

So the assailant’s rate of success drops rapidly as the weight ranges $\psi$ increases, the two TLVVNNs engaged would alter $\psi$ to enhance the existing level of safety. As illustrated below, the probability of a majority assault prevailing decreases drastically in relation to $\psi$ (Eq. 45)

$$\begin{aligned} P_{\mathrm{attacker}}\approx e^{-0.17\left( \psi -2.0\right) }. \end{aligned}$$

(45)

The TLVVNN ’s attack probability of a majority attack is determined using Eq. (46)

$$\begin{aligned} P_\mathrm{{atk}}^{\mathrm{TLVVNN}}= & {} P_\mathrm{{atk}}^{\delta ^{1}} \;P_\mathrm{{atk}}^{\delta ^{2}}\; \ldots \;P_\mathrm{{atk}}^{\delta ^\eta }\nonumber \\&\approx \left( P_\mathrm{{atk}}^{\mathrm{CVTPM}}\right) ^\eta . \end{aligned}$$

(46)

Here $P_\mathrm{{atk}}^{\delta ^{u}}$ is the likelihood of a majority assault on each of TLVVNN’s weights succeeding. The probability of a majority attack on CVTPM is given by $P_\mathrm{{atk}}^\mathrm{{CVTPM}}$.

Fig. 4

The relation between the number of rounds and the Frobenius norm of CVTPM, VVTPM, and TLVVNN

Fig. 5

Synchronization time for different weight range (average of 10,000 tests with synaptic depth 10, 15, and 20)

Replay attack

Replay attacks are a type of cyberattack that targets information sent through the web. For this assault, an adversary or another entity with identity theft accesses communication and impersonates the originator to transmit it to the recipient. The recipient believes the communication is genuine, however, it was delivered by an assailant. The essential element of a replay assault is that the information is sent repeatedly to the recipient, hence the term “replay attack.” A neuronal key is used in the suggested approach to counteract this assault. The key can only be used per transaction and never reused.

Table 1 The average and median number of cycles required to achieve perfect coordination

Geometric attack

This suggested methodology considers a geometric assault on TLVVNN. The adversary in this case is E. The probability of $\vartheta _u^{E}\ne \vartheta _u^{A}$ is expressed in Eq. (47) with the aid of the TLVVNN’s error rate $(\omega )$.

$$\begin{aligned} \omega _u^{p}=\frac{1}{2}\left[ 1-erf\left( \frac{\varsigma _u}{\sqrt{2\left( 1-\varsigma _u^{2}\right) }}\frac{\left| \tau _u\right| }{\sqrt{G_u}}\right) \right] . \end{aligned}$$

(47)

Equation (48) shows the likelihood of a modification using a geometric assault if the uth hidden node does not entirely agree and also the remaining of the hidden nodes are in a status of $\vartheta _v^{E}\ne \vartheta _v^{A}$.

$$\begin{aligned} P_g= & {} \int _0^\infty \prod _{v\ne u}\nonumber \\&\left( \int _{\tau _i}^\infty \frac{2}{\sqrt{2\pi G_v}} \;\frac{1-\omega _v^{P}}{1-\omega _v}e^{-\frac{\tau _v^{2}}{2G_v}}\mathrm{{d}}\tau _v\right) \nonumber \\&\frac{2}{\sqrt{2\pi G_v}}\frac{\omega _u^{P}}{\omega _u} e^{-\frac{\tau _u^{2}}{2G_u}} \mathrm{{d}}\tau _u. \end{aligned}$$

(48)

If the $\vartheta _v^{E}\ne \vartheta _v^{A}$ requirement is fulfilled there have been an even amount of hidden neurons that match the conditions, there will be no geometric alteration. Equation 49 is used to express this

$$\begin{aligned} P_{r,1}^{E}=\sum _{u=1}^{\sigma /2} \left( \frac{\sigma -1}{2u-1}\right) \left( 1-\omega \right) ^{\sigma -2u}\epsilon ^{2u}. \end{aligned}$$

(49)

Second component of $P_r^{E}$ can be represented using Eq. (50)

$$\begin{aligned} P_{r,2}^{E}= & {} \sum _{u=1}^{\sigma /2} \left( \frac{\sigma -1}{2u-1}\right) \nonumber \\&P_{2u-1}^{-}\left( 1-\omega \right) ^{\sigma -2u+1}\omega ^{2u-1}. \end{aligned}$$

(50)

The third element of $P_r^{E}$ may be represented using Eq. (51)

$$\begin{aligned} P_{r,2}^{E}= & {} \sum _{u=1}^{\sigma /2} \left( \frac{\sigma -1}{2u-1}\right) \nonumber \\&P_{2u-1}^{-}\left( 1-\omega \right) ^{\sigma -2u+1}\omega ^{2u-1}. \end{aligned}$$

(51)

If $\alpha \;>\;1$, the chance of attracting and repulsion stages in the uth hidden node is expressed using Eqs. (52) and (53)

$$\begin{aligned}&P_a^{E}=\frac{1}{2}\left( 1-\sum _{v=1}^{3}P_{r,v}^{E}\right) \end{aligned}$$

(52)

$$\begin{aligned}&P_r^{E}=\sum _{v=1}^{3}P_{r,v}^{E}. \end{aligned}$$

(53)

Session hijacking attack

A further sort of MITM assault is session hijacking, sometimes known as cookie side-jacking. The attacker obtains the customer’s session identifier and exploits it to get entry to the customer’s profile in a session hijacking operation. Session hijacking occurs when a hacker takes full advantage of a breached active session by hijacking or acquiring the cookies required to administrate it. This suggested solution provides end-to-end encryption between both the sender and the recipient, preventing inadvertent session ID acquisition. The neuronal coordination mechanism generates lengthy and random session cookies, lowering the danger of an opponent guessing or forecasting what such a session cookie is. The TLVVNN begins a fresh syncing of every session to generate a fresh session key, resulting in very brief sessions. TLVVNNs are re-authenticated using a new session ID. TLVVNN also deletes a session cookie at the conclusion of each session to minimize the amount of times a session cookie is accessible in the networks.

Results and analysis

The variance of the overlap is shown in this paper using the Frobenius norm of a matrix to illustrate that the coordination periods of the proposed TLVVNN and existing VVTPM grow is proportional to the very same order $\psi ^{2}$. Using Eq. (54) the Frobenius norm is represented as follows:

$$\begin{aligned} {\left\| B^{p^{A}}-B^{p^{B}}\right\| }_F \overset{\triangle }{=}\sqrt{\sum _{u=1}^{n}}\sum _{v=1}^{M} \left| \beta _{u,v}^{p^{A}}-\beta _{u,v}^{p^{B}}\right| ^{2}. \end{aligned}$$

(54)

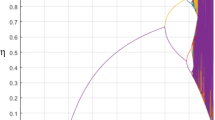
The Frobenius norm decreases to 0 when the two weight vectors are completely coordinated. Here, the vector values are set to 1, 2, and 5 to equate CVTPM, VVTPM, and TLVVNN without losing generality. The relation between the number of rounds and the Frobenius norm is illustrated in Fig. 4. Each line reflects a single synchronization procedure, and since the replicated experimental effects all follow the same sequence, only one outcome is shown for each $\eta$ value.

Figure 5 illustrates the amount of iterations that happened for all users to complete the synchronization. Experiments were carried out on three different ranges of weight, with each reflecting the total significance of 10,000 trials.

Despite the rise in the value of $\eta$, the mean amount of iterations barely matters when considering the initial CVTPM $\left( \eta =1\right)$, VVTPM $\left( \eta =2\right)$, and TLVVNN. This reveals an identical feature not just in the mean value, as well as in the median value (Table 1). The number of vectors $\eta$ has no significance on the synchronization time as each of them can be calculated separately.

Figure 6 depicts the distribution of the overlap $U^\mathrm{{AC}}$ with 100 pairs of networks A and C. Here, 1000 simulations are considered and $M=100$, $\chi _1=\chi _2\;=\chi _3=3,$ and $\psi =3$ .

Fig. 6

The distribution of the overlap $U^\mathrm{{AC}}$ with 100 pairs of networks

Figure 7 depicts a graph depicting the likelihood of a majority attacker succeeding based on the scale of the variable $\eta$. This paper uses random walk and 100 TLVVNNs for the majority attack with 10,000 repeated tests.

Fig. 7

With 10,000 repeated tests, the likelihood of a majority attack success

Figure 8 represents the likelihood of success in various attacks for different weight ranges using the random walk. Here, 1000 simulations are considered and $M=1000$. For genetic and geometric attacks 4096 and 100 assault networks are considered.

Fig. 8

Likelihood of success in geometric, majority and genetic attacks for different weight range using random walk learning

Table 2 shows the success probability of a majority assault. In the 10,000 attack trials, the value 0.0000 indicates that the attack was unsuccessful. In this paper, the desire security standard is set to $10^{-4}$. TLVVNN with $\eta \ge 3$ has $10^{-4}$ attack likelihood. CVTPM with $\eta =1$ and $\psi =15$ has 3% attack likelihood. To achieve the standard security level the CVTPM should set $\psi =57$ .

Table 2 The likelihood of a majority attack succeeding

However, if $\psi =57$ is set, full synchronization takes a very long time, making it nearly difficult for the practical scenario. The synchronization takes approximately 1,270,000 rounds in the case of $\psi =40$. When the TLVVNN is used with $\eta =3$, $\psi =15$, it requires approximately 23,000 rounds. Furthermore, by increasing the parameters $\eta$ and $\psi$ in real-world systems, while the participants use the TLVVNN, an acceptable degree of protection can be obtained.

Figure 9 illustrates a graph depicting the possibility of a majority attacker progressing depending on the learning rules. In an attack situation, the TLVVNN, like previous results, will improve protection regardless of the learning rule.

Fig. 9

Probability of majority attack (the values of the result after 10,000 iterations)

Figure 10 depicts the likelihood of success in the attack using the random walk. Here, 1000 simulations are considered and $M=1000$.

Fig. 10

Likelihood of success in the attack using random walk learning rule for 1000 simulations

Fig. 11

Comparison of number of iterations needed for TLVVNN coordination and existing CVTPM coordination

Fig. 12

Comparison of number of iterations needed for TLVVNN coordination and existing VVTPM coordination

Figure 11 contrasts the speed of CVTPM and chaos-based TLVVNN coordination depending on parameters $\chi 1,\;\chi 2$, and $\chi 3$. Here, Hebbian learning rules are applied. Figure 12 depicts the speed of VVTPM and chaos-based TLVVNN coordination depending on parameters $\chi 1,\;\chi 2,$ and $\chi 3$ with $M=35$. Chaos-based TLVVNN needs much fewer iterations than existing CVTPM and VVTPM, according to all of the cases. The degree of security is substantially enhanced by this feature. Present VVTPM and CVTPM methods, which employ arbitrary weights at the beginning of the coordination stage, are substantially less dependable than the suggested alternative.

The probability value ($\mathrm{P}_\mathrm{Value}$) decides the neural session key’s acceptance or rejection. Table 3 presents the results of the NIST test suite  [16] on the synchronized neural session key. The $\mathrm{P}_\mathrm{Value}$ calculation is performed for the proposed TLVVNN and existing VVTPM  [6] and CVTPM  [3] techniques. The $\mathrm{P}_\mathrm{Value}$ of the proposed TLVVNN has been found to exceed CVTPM.

Table 3 $\mathrm{P}_\mathrm{Value}$ TLVVNN, VVTPM, and CVTPM

In the synchronized neural key, the outcome of the frequency test denotes a proportion of 1 and 0. The frequency test outcome of the TLVVNN technique is 0.711478, that is better than the outcome 0.538632 in Jeong et al. [6], 0.512374 in n Dong and Huang [3], 0.1329 in Karakaya et al. [8], 0.632558 in Patidar et al. [19], and 0.629806 in Liu et al. [9]. The frequency test’s $\mathrm{P}_\mathrm{Value}$ comparison is presented in Table 4.

Table 4 $\mathrm{P}_\mathrm{Value}$ measurements for frequency test

Figures 13 and 14 show TLVVNN synchronizations in two different scenarios: using randomly generated identical input vector and with chaos-guided identical input vector at the beginning of the coordination stage. 20,000 times, coordination was repeated. The mean value is shown by the dashed lines that connect the graph’s points, which may be used to compare disparities. The result in the range $M=\left[ 25,\;30\right]$, $\psi =3$ in Hebbian learning algorithms were addressed. The amount of iterations in the coordination process is strongly affected by the value of $\chi 1-\chi 2-\chi 3$. Here, $\chi 1=\chi 2=\chi 3=6,\;8,\;12$ is considered. The amount of steps required to coordinate TLVVNNs in the chaos-guided identical input vector scenario is significantly smaller. Significantly more iterations are required to coordinate the weights of TLVVNNs using non-chaotic input vector.

Fig. 13

TLVVNN coordination without chaos-based identical input vector

Fig. 14

TLVVNN coordination with chaos-based identical input vector

The simulation results for various $\chi 1-\chi 2-\chi 3-M-\psi$ are represented in Table 5. Two separate columns are used to represent the min and max coordination period. Effective attacker synchronization (E column) indicates the success of the attacker in correctly imitating the actions of the authenticated TLVVNNs. In the last column of the table, the percentage of successful attacker synchronization is shown.

Table 5 Results of 70,0000 simulations of varying $\chi 1-\chi 2-\chi 3-M-\psi$

Figure 15 depicts the sync time needed for 512-bit key creation using different weight ranges. It is discovered that, for big networks, Random Walk outperforms the other two learning methods.

Fig. 15

512-bit key generation with a diverse weight range and fixed TLVVNN size

Table 6 compares the coordination times of TLVVNN and CVTPM approaches for varied learning, weight distributions, and static network size. As the range of weight values of $\psi$ grows in all 3 rules, a tendency towards an increase in the synchronization step has been seen. Hebbian takes less synchronization steps for small $\psi$ values than the other two learning rules in the $\psi$ value of 5–15, but when the $\psi$ raises, more synchronization steps are taken by the Hebbian rule than the other rules.

Table 6 Comparison of synchronization time between TLVVNN and CVTPM

Table 7 compares the TLVVNN and the VVTPM methods for synchronization time using the random walk. The coordination time of the TLVVNN employing the random walk learning is substantially better than the current VVTPM, as seen in this table.

Table 7 Comparison of synchronization time between TLVVNN and VVTPM

Table 8 examines the anti-Hebbian coordination time of the TLVVNN, and TPM-FPGA approaches. As demonstrated in the table, the TLVVNN’s synchronization period is significantly shorter than the present TPM-FPGA. Under the $\psi$ of 20–30, the anti-Hebbian rule requires the least amount of time compared to the other two rules.

Table 8 Comparison of synchronization time in anti-Hebbian rule between TLVVNN and TPM-FPGA

Conclusion and future scope

This paper first examined the key exchange schemes proposed by Dong and Huang [3], Jeong et al. [6], and Teodoro et al. [30] quite recently. This paper also indicated their limitations. Second, to address the existing issues, this paper has presented a chaos-based TLVVNN synchronized key exchange scheme to produce a scalable length secret key. Chaos helps to exchange the seed value for the input vector generation of the TLVVNN. TLVVNN not only has the necessary security mechanisms, but it does have a high level of effectiveness. Third, this paper presents the systematic security assessment. The most powerful geometric and majority attacks have been considered. Also, this paper has shown that TLVVNN can achieve greater levels of security in real-world systems by altering the size of vectors. Fourthly, an analysis of the effectiveness of the scheme is undertaken and the characteristics of existing CVTPM and VVTPM systems are compared. Finally, simulations that prioritize defense over an invading network are used to determine optimized values for $\chi 1,\;\chi 2,\;\chi 3,\;M$ and $\psi$. This demonstrates that two authorized TLVVNNs will swap a key in a channel with a 0.00004% chance, permitting an invading TLVVNN to imitate the network’s real behavior. A geometric technique is created and managed with a 0% accuracy. A secret key of variable sizes can be created by adjusting the TLVVNN’s $\chi 1,\;\chi 2,\;\chi 3,\;M$ and $\psi$. Finally, the results indicate that this proposed methodology is a good key exchange protocol for IIoT nodes in terms of both effectiveness and security in the CEI. There is one problem in the work: no appropriate optimization strategy for generating optimal weight vectors is investigated to improve the speed of neural coordination and improve security. A more comprehensive security examination of the network is planned. By optimizing the weights of the TLVVNN for quicker coordination, considerable research is needed to enhance or strengthen the existing state of research in this field. Two vital components will have to be upgraded in the future. The first is to minimize the neural coordination latency even further, and the second is to perform new neural coordination instead of just a longer one.