Introduction

The multi-objective optimization algorithm (MOA) has been a hot issue in recent years because of its balance on each aspects of the problem, which mainly consists of the particle swarm optimization (PSO) algorithms [1,2,3], the immune clonal algorithms (ICA) [4], the evolutionary algorithms (EA) [5,6,7], the differential evolution (DE) algorithms [8, 9], and other hybrid heuristic algorithms [10,11,12,13,14]. These biological heuristics algorithms obtain better solutions through a continuous iterative process,in which a set of search rules are proposed. To obtain a satisfactory solution, it is necessary to constantly absorb new information and improve the performance of initial solutions through some type of search strategy during the entire iterative process [15,16,17,18,19]. Besides the heuristic mechanism, when it comes to solving multi-objective problems, there are also other special strategies. In 1994, Srinivas et al. presented the non-dominated sorting genetic algorithm (NSGA) [20], the non-dominant layered approach of which enabled good individuals to have greater opportunities to pass on to the next generation the ability to produce a new genetic model of the same species. In 2002, the NSGA-II based on NSGA was proposed, which used the elitism strategy [21]. In addition, the crowded distance sort was also an important aspect in obtaining a set of nice solutions with distribution. Algorithms which also used elitism strategies were SPEA and its improved version SPEA-II [22, 23]. In 2008, Gong et al. proposed a multi-objective immune algorithm with non-dominant neighbor-based selection (NNIA) [24]. The NNIA simulated the phenomenon of symbiosis with multifarious antibodies and activation of minority antibodies in immune responses. However, each of the above related algorithms can only focus on the global search and the local search of the solutions, respectively, without performing deep local search for a partial solution simultaneously. In this paper, we propose to design an improved multi-objective immune algorithm which combines the advantages of the NNIA and the Tabu search algorithm (TSA) (NNITSA) to improve the climbing performance of the algorithm. The NNITSA is used to solve the static partitioning optimization and dynamic cross-regional co-operative scheduling problems of agricultural machinery. Agricultural machinery services are usually performed through fixed political districts. Under the existing management system of agricultural machinery operations, machinery services are overall designed by professional agricultural specialists and organized implementations such as ploughing, planting, harvesting and field management. NSGA-II alleviates all the above three difficulties. Specifically, a fast non-dominated sorting approach with O(MN2) computational complexity is presented. Also, a selection operator is presented that creates a mating pool by combining the parent and offspring populations and selecting the best solutions [25, 26].

This involves multiple field units of different districts that need to be managed uniformly and assigned evenly. However, the political distributions of fields are not balanced, which in turn leads to poor efficiency and a high distribution cost. Therefore, it is necessary to break the fixed partitioning, while optimizing the distribution of fields to improve the efficiency of agricultural machinery and services.

Districting problem is defined as re-dividing geographical districts into new ones to conform to the current system. It is a kind of typical multi-objective optimization problem (MOP) which involves several criteria [27,28,29,30]. The effect of partitioning is said to be even greater than the effect of partitioning other partitions. So, we aim to find all the best solutions that constitute a balanced set. There is no ideal solution to this set, but a better solution can be found in many different of conditions. In addition to the actual operation of agricultural production, several problems with the operation of fields affect the efficiency of field service and completion times. Thus, the scheduling system must to be adapted to give the rational scheduling decision, and to performs cooperative scheduling to maintain the overall of the operating system while maintaining the overall benefits of the scheduler and operating system in the same manner as the operating system.

There are a few of researches on districting and dynamic cooperative scheduling problems so far, mainly focusing on the evolutionary algorithm (EA) [31,32,33], co-evolutionary algorithm (CEA) [34], goal programming [35], and the Tabu search algorithm (TSA) [36], which can basically solve the corresponding problems. What is more, there have been some researches on scheduling of agricultural machineries [37,38,39,40]. Based on most of the algorithms mentioned above, multi-objective optimization algorithm (MOA) plays an important role in solving districting problems. What is more, we already have related work in clonal selection algorithm [41], robust optimization of multi-objective approach [42], dynamic immune clustering for event-driven wireless sensor networks [43] and immune system-inspired rescheduling algorithm [44].

The main contributions of this paper are as follows:

  1. (1)

    A TSA operator is designed to perform parallel mutations with a specific mutation to boost the performance of the algorithm.

  2. (2)

    A local search strategy was introduced to improve the performance of the immune algorithm in local search results, and to improve the accuracy of local search results.

  3. (3)

    A robust evaluation mechanism is introduced, with which, the proposed algorithm solves the dynamic cross-regional cooperative scheduling problem of agricultural machinery.

The remaining content of this paper is organized as follows. In “The improved multi-objective immune algorithm combining NNIA and TSA”, the proposed NNITSA is developed based on NNIA and TSA operators, respectively. In “NNITSA for partitioning optimization of agricultural machinery”, the NNITSA is presented to solve the static partitioning optimization problem and the dynamic cross-regional cooperative problem of agricultural machinery. What is more, the performance of NNIT-SA is analyzed and proved. In “Conclusions”, a summary of the work and the perspectives considered are given.

The improved multi-objective immune algorithm combining NNIA and TSA

Using the strategy of selecting the no-dominant neighborhood individuals, with the proportional cloning strategy according to the crowding distance which strengthens the search of sparse areas of the current Pareto frontier surface, NNIA obtains good solutions for cross-over and mutation processing, so as to ensure that high quality solutions can be generated. Thus, NNIA can obtain a uniformly distributed Pareto optimal solution. Moreover, compared with the existing multi-objective evolutionary optimization methods, NNIA does not rank the non-dominated solution, which reduces the computational complexity. The implementation procedure of NNIA is depicted as follows [24].

Step 1: Initialization. At iteration \(i=1\), generate an initial antibody population POP with size NM.

Step 2: Update dominant population. Select dominant antibodies from POP.

Step 3: Termination. When reaching the stopping criteria (iteration \(i=IMAX\)), stop further iteration and output the dominant population. Otherwise, go on.

Step 4: No-dominated neighbor-based selection: update active population. Calculate the crowing distance of all individuals in NEPOP, sort NEPOP in the descending order of crowing distance, then extract the first NM (maximum size of active population) antibodies to constitute the active population in the genetic stage denoted by APOP.

Step 5: Genetic operation. Apply proportional cloning to the active population. The probability of which is calculated related to the crowding distance. Apply crossover and mutation to the cloned population. Denote the population as genetic population.

Step 6: Get the result antibody population by combining genetic population and dominated population; go to Step 2.

However, the result of non-dominated neighbor-based selection is implemented only in clonal selection stage. Due to the randomness of mutation and crossover, fewer searches conducted within an individual’s neighborhood while expanding the global search scope. So it is important to adopt the neighborhood search strategy, which can not only ensure the diversity of the population, but also speeds up the search process and improves the efficiency of the search.

This neighborhood solution is a key point for the TSA. To get into the optimal solution set, TSA uses a journalist to record the several movements conducted during the several iterations of the program. Any movement in the Tabu list is forbidden in the current iteration. Thus, the same solutions will not appear twice in the latest iteration, which can prevent the evolution of time-consuming circulation and is helpful in finding the local optimum. What is more, TSA also has aspiration criterion in order not to miss the movement of the best solution; the TSA also has aspiration criteria to ensure that it does not miss out on the best solution.The procedure of Tabu search strategy used in this paper is as shown in Algorithm 1.

figure a

As the Tabu search strategy uses two kinds of movements: the migration and swap of units, a boundary algorithm is needed.

  1. (1)

    Given two unit sets A and B of two districts.

  2. (2)

    Calculate the distances between each two units belonging to A and B, denoted by BD. Sort BD in the ascending order of distances.

  3. (3)

    Select the first k pairs of units to constitute the boundary unit sets of A and B.

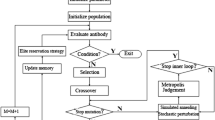
Considering the high quality of local search by the TSA, we use the TSA operator to enhance the local searching capability in the procedure of iterations. In the mutation stage of NNIA, we set the TSA operator as a mutation operator and propose NNITSA. The overall procedures of NNITSA are illustrated in Fig. 1.

Initialize all the units: Load the input parameters, as well as the necessary parameters of NNITSA, such as the dominant population size NM, active population size NA, cloning population size CS, the current iteration number G, the maximum number of iterations GMAX, the crossover probability pc and the mutation probability pm.

Initialize the antibodies: At iteration i=1, an initial antibody population POP with size NM is generated.

Update dominant population: Calculate the objective function value of all individuals in POP. Update dominant antibodies to form the temporary dominant population, denoted by MEPOP.

No-dominated neighbor-based selection: Calculate the crowding distance of all individuals in MEPOP and sort MEPOP in the descending order of crowing distance, then extract the first NA antibodies as the active population.

In most of the multi-objective algorithms, the dominant antibodies are ranked according to crowding distance, which represents how much they contribute to the diversity of objective function values [45].

Fig. 1
figure 1

The overall procedures of NNITSA

Full size image

The definition of crowding distance of is given by:

$$\begin{aligned} Cd(d,D)= & {} \sum \limits _{i=1}^{k}\frac{Cd_i(d,D))}{f_i^{\max }-f_i^{\min }}, \end{aligned}$$
(1)
$$\begin{aligned} Cd_i(d,D)= & {} \left\{ \begin{array}{ll} {\infty ,} if\ f_i(d)=\min \{f_i(d^{'})|d^{'}\in {D}\} \\ \ \ \ \ or\ f_i(d)=\max \{f_i(d^{'})|d^{'}\in {D}\} \\ {\text {otherwise},} \min {f_i(d^{'})-f_i(d^{"})|d^{'}} \\ \ \ \ d^{"}\in {D}:f_i(d^{"})<f_i(d)<f_i(d^{'}) \\ \end{array}\right. , \end{aligned}$$
(2)

where d and D are each dominant antibody and the corresponding population, k is the size of the population, \(f_i^{\max }\) and \(f_i^{\min }\) are the maximum and minimum values of the ith objective function, respectively.

The value of the crowding distance shows the density of the distribution of antibodies in one solution, based on which we can extract active population from dominant population.

Local search: Comparing the current active antibody population with those of the previous iteration, determine whether they are the same, if not, go to Step 6, else, implement local search.

Randomly choose one antibody in the current active antibody population, implement the TSA operator. Replace the chosen antibody with the result of neighbor search; go to Step 6.

Termination: When reaching the stopping criteria (iteration G=GMAX), stop further iteration. Otherwise, go on.

Immunization operations: Special immunization operations, including cross-over and mutation operations, are used to generate the subsequent population.

Proportional cloning: Applying proportional cloning to the selected active population MEPOP. The probability of which is calculated related to the crowding distance.

Select one antibody \(a_i\) from the active population to illustrate, \(a_i\) will be implemented proportional cloning following the equation below:

$$\begin{aligned} \text {CS}_i=\text {CS}\times \frac{Cd(a_i,\text {MEPOP})}{\sum \nolimits _{i=1}^{|A|}Cd(a_j,\text {MEPOP})}, \end{aligned}$$
(3)

where CS is the cloning population size and \(\text {CS}_i\) is calculated by the crowding distance of each active antibody in MEPOP.

Crossover: Denote the antibodies generated by cloning procedure described above as CPOP. Two antibodies are randomly selected from CPOP and MEPOP. Then select two gene bits within the range of antibody length n and cross all gene bits in range of those two. After NM cycles, the crossed population is obtained.

Mutation (TSA): We introduce a TSA operator to improve the climbing performance of NNIA, by taking the dominant local solution of the TSA as the mutated antibody. Only when the solutions found by the TSA are superior to the current antibodies, they will be taken as the antibodies mutated.

Combination: Get the result antibody population by combining immunization population and dominated population; go to Step 3.

The TSA operator is utilized in two aspects:

(1) Mutation: When the Pareto solutions of the algorithm keep the same for several iterations, TSA operator would replace traditional mutation to obtain a better solution instead of randomness mutation. The probability of TSA mutation changes by the increasing of scale of Pareto solutions. Under other circumstance, random mutation is operated to ensure the searching scope of the algorithm.

The adaptive parameter is defined as below:

$$\begin{aligned} c_a=\sqrt{|\text {MEPOP}|}, \end{aligned}$$
(4)

where \(|\text {MEPOP}|\) is the scale of MEPOP, when MEPOP remains the same for \(c_a\) iterations, we adopt TSA mutation.

(2) Local search: As long as the Pareto solutions changes, which means a better solution set is obtained, a local search strategy would be performed. Based on TSA operator, choosing one of the solution set, a better solution would be found. Then if the solutions did not change, the local search would not go deeper, so that the algorithm can be prevented from getting into the local best solution.

NNITSA for partitioning optimization of agricultural machinery

The problem of static partitioning optimization can be described as: there is a randomly distribution of n fields in a certain range, the required service of each field is different. The center of agricultural machinery is located in the center of the range. A redistrict scheme is needed to break the limits of historical partitioning. This is obviously a multi-objective optimization problem because of several conditions that need to be considered for partitioning. We have identified the target of the problem as below.

The goal is to obtain a dominant set of the partitioning of the given field units. Two objectives are considered in this model.

A balanced partitioning scheme must ensure the optimization result of total path. It is assumed that all machines are managed uniformly by the agricultural machinery center and distributed to each district. The travel distance of each district is denoted as: starting from the agricultural machinery center, traversing all the fields of a district and returning to the center of the agricultural machinery center.

$$\begin{aligned} \begin{aligned} \text {Minimize} f_1=L(D)&=\sum \limits _{D_i\in {D}}L(D_i)\\&=\sum \limits _{D_i\in {D}}\sum \limits _{u_j^i\in {D_i}}L(u_j^i), \end{aligned} \end{aligned}$$
(5)

where D is the fields set of all the districts, \(u_j^i\) is the j-th field unit in \(D_i\), L means the length of total path.

We wish that all the districts can complete their work at the same time, so it is necessary to keep the balance of the service load of each district. Thus, the other objective function is shown in Eq. (6).

$$\begin{aligned} \begin{aligned} \text {Minimize} f_2&=\text {Std}(Q(D_i))\\&=\text {Std}{{D_i}\in {D}}(Q(D_i))\\&=\text {Std}_{{D_i}\in {D}}(\sum Q(u_j^i)). \end{aligned} \end{aligned}$$
(6)

This objective function is to minimize the variance of service time among all the districts, where Q means the service time. For this problem, there are some particular implementation issues below.

In order to make it convenient to manage and operate, each district should be relatively aggregated and less overlapping. For improving the efficiency of the algorithm, an initial partitioning algorithm is designed to generate the optimized initial solutions, which combines indivisible field units into feasible districts. The procedure of generating initial scheme is as shown in Algorithm 2.

figure b

When it comes to the calculation of the distance between any two fields, the actual traveling paths of the machineries are taken into account. The specific path of the agricultural machine from a field to another field is not likely to be a simple link between the central point of those two fields, so it is optimized to be the sum of distance of the two right-angled sides of the right-angled triangle corresponding to the line connecting the fields center, as shown in Fig. 2, where \(d_{ij}=d_{AB}+d_{BC}\). Furthermore, the traveling sequence of the fields is also optimized to avoid the intersection of the connected graph.

Fig. 2
figure 2

Example of antibody representation

Full size image

For this problem, we design two special movements. The neighborhood of a solution can be obtained by changing any unit in a district, so the movements in TSA operator are as shown in Algorithm 3.

figure c

The description of the antibody population raises some issues which should be illustrated. We use a structure variable to represent a partitioning scheme. This structure variable has four data members: the first three members are arrays of fields number of the three districts, denoted as \(D_1\),\(D_2\),\(D_3\). Another member is a two-dimensional array which represents the fitness of two objective functions.

At the mutation and crossover stage, each antibody is encoded into a district vector \(\mathbf {X}=(x^1,x^2,...,x^n)\), where n is the total number of fields to be partitioned. The value of each bit of \(\mathbf {X}(x^i)\) is the number of district, which the field i is partitioned to, ranging from 1 to 3, represent \(D_1\),\(D_2\),\(D_3\), respectively (Fig. 3).

What is more, to enhance the effect of crossover stage, we encode the partitioning scheme into a ternary sequence with the length of n, as show in Table 1.

Fig. 3
figure 3

Example of antibody representation

Full size image
Table 1 Example of solution encoding
Full size table

The illustration of immunization operations is as shown in Fig. 4.

Fig. 4
figure 4

Illustration of immunization operations

Full size image

After balanced partitioning, choosing one relatively modest solution of “NNITSA for partitioning optimization of agricultural machinery” as shown in Fig. 5, and allocating unified task sequences for agricultural machines in all area. For example, given 12 machines and they are numbered from 1 to 12 where 1–4 belong to D1, 5–8 belong to D2 and 9–12 belong to D3. In Fig. 5, different colors of fields belong to different districts.

Fig. 5
figure 5

Partitioning result of “NNITSA for partitioning optimization of agricultural machinery”

Full size image

Assume that the machines are homogeneous, but some of them would not be able to continue providing services due to the failure. When a dynamic event occurs, a machinery breaks down and cannot continue to provide services. Other agricultural machines need to be scheduled to continue the work of the broken machine. What is more, in order to ensure the overall efficiency of three districts, the rest of the service may not be done by machineries belonging to the corresponding district only, which is the dynamic cross-regional co-operative scheduling problem.

A number of schedule parameters are required involving the number of available machineries and so on (Table 2).

Table 2 Schedule parameters and input parameters
Full size table

In this experiment, the robustness of different schedule is analyzed. Trigger different amount of dynamic machineries at the same time. Dynamic machineries broken at various time are listed in Table 3. RoubstnessC1–RoubstnessC12 denote the experiments of different machines broken at various time, respectively.

The total travel path of all machines needs to be as small as possible. On the one hand, it is to reduce the energy consumption of the agricultural machinery, and on the other hand, the agricultural machinery passing through the fields will have an impact on the compactness of the soil [46].

$$\begin{aligned} \begin{aligned} \text {Minimize}\ f_1&=L(M)\\&=\sum \limits _{m\in {M}L(m)}\\&=\sum \limits _{m\in {M}}\sum \limits _{k\in {H}}\sum \limits _{j\ne k,j\in {H}}x_{jkm}l_{jk}. \end{aligned} \end{aligned}$$
(7)

We wish that all the districts can complete their work at the same time, so the expected end time of each district is ought to be as balanced as possible.

$$\begin{aligned} Minimize\ f_2=\sigma (T(D))=\sigma (\sum \limits _{d_i\in {D}})T_{m}y_{mi}=\sigma . \end{aligned}$$
(8)

For dynamic cross-regional co-operative scheduling problem, there are some constraints as follows:

Constraint1: We assume that the speed of each machinery is the same.

Constraint2: Each field is served by one machine at one time.

Table 3 Dynamic machineries appeared at various time
Full size table

Constraint3: It is allowed that a machine can leave the current field to serve another field before the service of the current field is completed and a field can be served by two or more machineries one after another.

Constraint4: The traveling sequence of each machine always begins at the depot, by way of several fields, and finally comes back to the depot.

Constraint5: If there is only one element in the to-be-served list of an agricultural machinery, it should stay in the field after finishing all the service waiting for the next instruction instead of returning to the machine center. Otherwise, only when the machine gets to the next field, it would perform other dynamic instructions.

In Algorithm 4, movement1 generates \(H(H-1)/2\) neighboring solutions, where H is the number of fields to be served. While each of the movements 2 and 3 generates a maximum of H solutions. These movements result in a maximum of \(H(H-1)/2+2H\) solutions in the neighborhood of a solution. It is revealed that the scale of local search expands, so NNITSA spends more time on local search.

figure d

Experiment results and analysis

Experiment results and analysis of static partitioning optimization

To fully reflect the performance of the proposed algorithm, all test instances are solved by NSGA-II, NNIA and NNITSA respectively on MATLAB 2016a platform. For all the algorithms, the maximum number of iterations is set as 300, the probability of crossover is set as 0.8, the probability of mutation is set as 0.3, the maximum size of population (the dominant population of NNIA and NNITSA) is set as 100, the maximum size of active populations of NNIA and NNITSA are both set as 20 and the maximum size of clone populations of NNIA and NNITSA are both set as 20.

The parameters of TSA operator in NNITSA are set as follows: The iterations of Tabu search are set as 3 and the maximum number of iterations is set as 5.

For traditional multi-objective algorithms, test functions are widely used to show performance of continuous problems based on true Pareto. However, as NNITSA is proposed to solve discrete problems of schedule of agricultural machines, it is hard to determine true Pareto of a problem. So it is not realistic to use classic test functions to invalidate its performance. We employ a performance indicator C-metric [34]. Given two Pareto approximation sets A and B obtained by two algorithms, the definition of C-metric is as follows:

$$\begin{aligned} C(A,B)=\frac{|\{b\in {B}|\exists a\in {A}:a\le b\}|}{|B|}, \end{aligned}$$
(9)

C-metric is a coverage degree of two finite sets, measures how much A covers B or B covers A. For \(b{\in }B\), if \({\exists }a{\in }A:a{\le }b\), which means b is dominated by at least one solution in A. Thus, C(A, B) shows the percentage of solutions in B which are dominated by any solution in A. What is more, when \(C(A,B)=1\), all solutions in B are dominated by some solutions in A; when \(C(A,B)=0\), there is no solution in B dominated by solutions in A.

The location and amount of service required of each field are summarized in Table 4. All algorithms are performed 10 runs, and the comparative results are shown in Table 5 (A: NNITSA, B: NSGA-II, C: NNIA).

We observe that from the first and second columns, all values of C(A, B) are greater than C(B, A) for all runs. Taking the first run for example, \(C(A,B)=1\) and \(C(B,A)=0\) means all solutions obtained by NSGA-II are dominated by those obtained by NNITSA. Taking Table 6 into consideration, NSGA-II has a high time cost compared to two other algorithms. It is because NSGA-II performs dominant ranking on Pareto solutions during each iteration, which takes a lot of time. Experiments show that NNITSA outperforms NSGA-II not only in performance but also in computation time. From the third and fourth columns, similar results are observed for NNITSA and NNIA. There is a big difference between the value of C(A, C) and C(C, A) for all runs. Which means that NNITSA obviously outperforms the NNIA.

Table 4 Parameters of fields
Full size table
Table 5 Results of three algorithms
Full size table

From Table 6, we can see that the time cost of NNITSA is a little greater than that of NNIA on average. This suggests that NNITSA improves search efficiency while cannot avoid the fact that it takes more time for neighborhood searches.

Table 6 Time costs of three algorithms
Full size table

The Pareto front of the three algorithms for one run is shown in Fig. 6. We can see that NSGA-II is obvious not better than the other two algorithms. NNITSA has a better distribution and performance compared to NNIA. What is more, we can take the extreme points of NNIA and NNITSA into consideration. As shown in Table 7, the extreme points and number of Pareto solutions are compared. First, although the number of Pareto solutions of NNITSA is less than that of NNIA in average, the diversity of solutions of NNIA is a litter bad. In most of the runs, NNITSA can always find the best minimum of \(f_1\)(3.3174, 136.1000), while NNIA can only find four times in ten runs. Taking the sixth run for example, NNITSA got a worse minimum of \(f_1\)(3.5697, 28.3000), but it got a better minimum of \(f_2\)(4.0588, 0.1000) in compensation. From the row of Best and Worst, we can see that NNITSA can get a better result than NNIA in the extreme points. So we can still come to the conclusion that NNITSA plays better than NNIA.

Fig. 6
figure 6

Pareto front of three algorithms

Full size image
Table 7 Comparison of the extreme points and number of Pareto solutions
Full size table

Experiments results and analysis of dynamic cross-regional cooperative scheduling

Each arrangement of serving scheme is denoted as the vector \(\mathbf {X}=(x^1,x^2,...,x^H)\), where \(x^j\) is the number of machine serving the j-th field in according district.

The corresponding schedule of Table 8 is shown in Fig. 7.

To fully demonstrate the complexity of the problem, we have considered the situation of one depot, two depots and three depots. The parameters of fields and algorithms are the same with the static problem. All algorithms are also performed 10 runs, and the comparative results are shown in Table 9 (A: NNITSA, B: NSGA-II, C: NNIA). To illustrate the performance of the proposed algorithm in dynamic problem, taking the failure of the agricultural machine 1 in \(t=3\) as an example.

All the travel path and service finished by machines are shown with solid lines and the planned path and service shown with dotted lines in Figs. 8, 10 and 12, where the red triangle represents the location of the depot. The current locations of the machines are shown under Constraint5. By performing NNITSA, one of the cross-regional cooperative schedules is shown in Figs. 9, 11 and 13.

In Figs. 8 and 9, the axis x represent the value of x-coordinate of the field and the axis y represent the value of y-coordinate of the field. It can be seen that (1) \(M_1\) is originally planned to serve field 10, 12, 11 and so on. When \(M_1\) is broken down, the left service of \(M_1\) is assigned to \(M_4\) and \(M_5\). When \(M_5\) finished its service of field 5 in \(D_2\), it will help to serve fields in \(D_1\). (2) Field 8 is in the adjacent of field 9 but they belong to different districts. Machine \(M_2\) of \(D_1\) would help to finish the work in field 7 in \(D_2\) and Machine \(M_6\) of \(D_2\) would help to finish the work in field 10 in \(D_1\). (3)There is no work assigned to \(M_7\), so it can return to the agricultural machineries center.

Taking Tables 9 and 10 into consideration, all the values of \(C(A,B)=1\) and \(C(B,A)=0\) reflect that NNITSA fully triumphs over NSGA-II in terms of both performance and time. And most solutions obtained by NNITSA are better than NNIA, which means NNITSA outperforms NNIA. Although the running time of NNIT-SA is bigger than NNIA, it is worthwhile so that the searching performance can be proved.

From Tables 11 and 12, we can see that the improved algorithm outperforms the other algorithm in all situations of different number of depots.

We use the robustness to measure how much the schedule cost changes compared with that before the dynamic situation occurs [29]. The cost can be the energy of the machines consumed in the schedule. The robustness is denoted as below, where \(i=1,2K,6\) represents different conditions.

$$\begin{aligned} \text {RT}_i=\frac{{\text {Energy\_after}}_i-{\text {Energy\_before}}}{\text {Energy\_before}}. \end{aligned}$$
(10)

According to Eq. (10), \(RT_i{\in }[0,+{\infty })\), the smaller \(RT_i\) is, the more robust the schedule is.

The robustness of Pareto solutions obtained by NNI-TSA in different conditions are compared in Fig. 14. The numerical robustness in Fig. 14 is selected as the minimum value of each solution of the Pareto solution set, which represents the optimal robust solution of the set. Comparisons of the results of one depot show that the robustness improves with the increase of the number of dynamic machines appears, the robustness becomes better in general. What is more, when the number of machines is greater than three in the second condition (t=5), the robustness of the schedules drops to less than zero, which reveals that less machines may cost less. In the situation of two and three depots, the robustness basically tends to a consistent scope, which shows the number of depots affect the robustness of a scheduling scheme.

Table 8 Example of individual schedule
Full size table
Fig. 7
figure 7

Schedule of Table 8

Full size image
Fig. 8
figure 8

The planed path of machines (one depot)

Full size image
Fig. 9
figure 9

The schedule after a machine is broken (one depot)

Full size image
Fig. 10
figure 10

The planed path of machines (two depots)

Full size image
Fig. 11
figure 11

The schedule after a machine is broken (two depots)

Full size image
Fig. 12
figure 12

The planed path of machines (three depots)

Full size image
Fig. 13
figure 13

The schedule after a machine is broken (three depots)

Full size image
Table 9 Results of three algorithms
Full size table
Table 10 Time costs of three algorithms
Full size table
Table 11 Results of three algorithms
Full size table
Table 12 Time costs of three algorithms
Full size table

Conclusions

In this paper, a multi-objective optimization algorithm NNITSA is proposed for static partitioning optimization and dynamic cross-regional co-operative scheduling problem of agricultural machinery. To increase the searching efficiency, a local search TSA operator is introduced based on the Tabu search algorithm. In addition to solving a dynamic cross-regional co-operative scheduling problem, an evaluation is adopted to estimate different schedules and help to choose the appropriate solution from the Pareto solutions. The route in practical production environment is also considered to refine of machineries. Finally, NNITSA is applied to one static case and one dynamic case. The results compared with NNIA and NSGA-II indicate that NNITSA outperforms the other two algorithms.

Fig. 14
figure 14

Robustness as different number of dynamic machines

Full size image

In the current complex agricultural production environment, such as biomass production,, the demand for fleet management will increase and the cost of the production will be reduced [47]. In future, we will design a multi-operational scheduling algorithm which focuses on the optimization of task sequence of agricultural machineries.