Introduction

The rapid urbanization and modernization have triggered many chronic diseases which creates a colossal threat to public health globally. Diabetes mellitus (DM) also called diabetes is one such disease. It has become one of the most common diseases nowadays in all age groups and habitats [1]. The number of diabetes patients (aged over 18 years) has increased rapidly from 4.7 to 8.5% from 1980 to 2014 which imposes crucial challenges in both developed and developing nations [2]. It has been considered as the seventh major reason for the premature death rate and because of this only, 1.6 million people died every year [3]. Statistical studies reveal that in 2019, 463 million people are living with diabetes worldwide and it has been estimated to reach 578 million by 2030, and 700 million by 2045. Therefore, the number of diabetes patients are projected to increase exponentially by 25% in 2030 and 51% in 2045 [4]. However, this growth is asynchronously distributed as this rate is predicted as 143% in Africa compared to 15% in Europe whereas China, India, and the United States of America are the most affected countries as shown in Fig. 1.

Fig. 1
figure 1

Top 10 most affected countries with diabetes

Full size image

Diabetes is a kind of endocrine disease that is associated with the reduced glucose acceptability by the body either because of absolute or relative insufficiency of insulin produced by the pancreas. Generally, it has been classified into four types: type-1 diabetes (T1D) or juvenile diabetes or insulin-dependent diabetes, type-2 diabetes (T2D) or DM, gestational DM, and specific types of diabetes due to other causes [5]. Amongst them, T1D and T2D are the two most common types of diabetes. The former is irreversible and is developed due to the deficiency of insulin as a result of damaged beta cells of the pancreas whereas, the latter is because of insufficient transportation of insulin into the cells. Both T1D and T2D can lead to serious life-threatening complications, such as diabetic foot syndrome, strokes and heart attacks, cirrhosis of the liver, chronic renal failure, etc. [6]. Therefore, to mitigate these complications, direct cost of diabetes has been increased significantly from $ 232 billion in 2007 to $ 760 billion in 2019 (228%) worldwide and is estimated to reach $ 845 billion by 2045 [7]. However, in the absence of any permanent and long-term cure for diabetes, early and accurate prediction is the only possible way to overcome the above-mentioned issues.

Currently, the early diagnosis and prediction of the disease have been done manually by a doctor which is based upon their knowledge, experience, and observations. Although the healthcare industry already collects a huge amount of data, it does not always reveal inherited hidden patterns. Consequently, these manual decisions can be highly misleading and dangerous especially, for early diagnosis as some parameters may remain hidden and have a devastating impact on the observations and outcomes. Therefore, there is an urgent need for advanced mechanisms for early and automated diagnosis to ensure higher accuracy. Further, as machine learning (ML) and deep learning (DL) techniques have shown promising results in identifying hidden patterns, they have been employed in various complex problems to obtain efficient results with reliable accuracy [8,9,10].

Being motivated by this, in recent years, a number of ML and DL based frameworks have been proposed for the prediction of diabetes such as logistic regression, artificial neural network (ANN), linear discriminant analysis (LDA), naive Bayes (NB), support vector machine (SVM), decision tree (DT), AdaBoost (AB), J48, k-nearest neighbors (k-NN), quadratic discriminant analysis (QDA), random forest (RF), multilayer perceptron (MLP), general regression neural network, and radial basis function (RBF) [11]. These techniques have been employed with various dimensionality reduction (such as principal component analysis) and cross-validation (for example k-fold cross-validation) techniques along with the mechanism for filling missing values and rejecting outliers to uplift the performance of ML and DL models. To predict the likelihood of diabetes with maximum accuracy, three different ML classifiers (DT, SVM, and NB) have been employed, and obtained results reveal that NB provides the maximum accuracy of 82% [12]. Further, the probabilistic neural network achieved an accuracy of 81.49% on the test dataset [13]. Meanwhile, a Gaussian process (GP) based classification technique has been proposed with three different kernels (linear, polynomial, and RBF) to classify the positive and negative diabetes samples. The extensive experiments demonstrate that the GP classifier with tenfold cross-validation outperforms the traditional classifiers (LDA, QDA, and NB) with an accuracy of 81.97% [14]. Furthermore, sequential minimal optimization, SVM, and elephant herding optimizer have been applied to predict diabetes based on multi-objective optimization and yield an accuracy of 78.21% [15].

Although these ML and DL models have shown adequate results but their accuracy is still on the lower side because they learn the relation between input (features) and output (class) based on the classical theories of probability and logic [16, 17]. Therefore, they require a lot of improvements to have general acceptability for diabetes prediction. Further, Quantum Mechanics (QM) has already shown its effectiveness in various domains (such as classification, prediction and, object detection and tracking) and achieved remarkable performance over classical theory-based models. With the motivation of this advent, previously reported work employed QM to uplift the ML and DL models performance [18]. The quantum particle swarm optimization has been employed to diagnose T2D and achieved the precision of 82.18% [19]. The quantum nearest mean classifier has been utilized for binary classification where the quantum version has been used to estimate the optimal performance measures [20]. A quantum-inspired evolutionary algorithm with binary-real representation has been implemented to improve the ANN by providing self-configuring capability based on the data [21]. A quantum-inspired binary classifier (QIBC) has been proposed to enhance the performance metrics in visual object detection tasks [16]. The obtained results reveal that QIBC outperforms current state-of-the-art techniques in most of the tasks. The QM-based framework has been utilized for feature extraction and classification from the electroencephalogram signal and achieved an accuracy of 0.95 with Gaussian kernel [22]. Further, the classification of osteoarthritis has been accomplished by utilizing classical ML and DL models [23]. However, to reduce the computational burden they proposed to use QM as a future work. Therefore, it may be concluded that there is an enormous scope to test and validate the performance of QM. Hence, the research fraternity is now trying to employ this newly advent QM on various benchmark datasets and compare the performance with conventionally used ML and DL techniques.

Under the umbrella of the above discussion, the present investigation explores the employability of QM for the prediction of diabetes amongst people. Further, another prediction model based on DL has been developed. The developed quantum machine learning (QML) and DL models have been trained by employing PIMA Indian diabetes dataset (PIDD) [24]. Finally, the performance of the developed QML and DL models have been compared against the classical models to investigate the effectiveness of these models for the classification task. Therefore, based on the above framework, the main contributions of this work can be sketched as follows:

  • Firstly, the proposed work employs various preprocessing techniques for the cleaning of the PIDD and investigates the effectiveness of these techniques by statistical parameters.

  • Secondly, QML has been employed for the prediction of diabetes in PIDD.

  • Thirdly, the optimized number of layers required to predict diabetes in PIDD for both QML and DL models has been analyzed by extensive experimentation.

  • Finally, the developed models have been exhaustively compared against the state-of-the-art techniques to validate the appropriateness of the developed models based on the prediction accuracy.

The remainder of this paper is organized as follows. The next section describes the methodology utilized in the present investigation. This section also deliberates about the dataset used for the analysis, proposed framework, and simulation setup and metrics. Then, detailed results and discussion have been presented in the following section. To end with, the last section gives the concluding remarks of the present work.

Methodology

This section focuses on the methodology used for the present investigation. In this regard, subsections 2.1, 2.2, and 2.3 explain the dataset utilized, proposed framework and, simulation setup and metrics used to assess the performance of the developed models respectively.

Dataset

In the literature, a number of public datasets for the prediction and classification of diabetes are available. However, it has been found that the lethality of diabetes is more in women as compared with men because the deaths associated with them in 2019 are 2.3 million and 1.9 million respectively [7]. Further, most of today’s world population greatly relies on processed foods with lesser physical activities. Therefore, to properly investigate the risk of diabetes among females, PIDD (developed by the National Institute of Diabetes and Digestive and Kidney Diseases) has been employed for this study. This dataset is one of the most versatile and reliable datasets for diabetes prediction. The PIDD contains a total of 768 instances of females aged above 21 years, out of which 500 samples were non-diabetic (negative) and 268 were diabetic (positive). The PIDD has been extensively utilized to predict the possibility of diabetes for any particular observation based upon 8 most influencing independent features: pregnancies (P), glucose (G), blood pressure (BP), skin thickness (ST), insulin (I), body mass index (BMI), diabetes pedigree function (DPF), and Age. The description of these features with a brief statistical analysis of PIDD has been presented in Table 1. Further, on the basis of class-specific density distribution these features have been also illustrated in Fig. 2 for better understanding of the dataset.

Table 1 Description of PIMA Indian Diabetes dataset
Full size table
Fig. 2
figure 2

Density distribution of attributes in PIMA Indian Diabetes dataset (PIDD)

Full size image

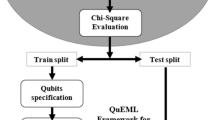
Proposed framework

The proposed methodology for accurate prediction of diabetes has been illustrated in Fig. 3 which includes preprocessing of the dataset, sampling, classification, and performance evaluation. However, preprocessing is one of the most important and crucial features amongst them because the quality of data has a direct impact on the performance of the classifier.

Fig. 3
figure 3

Block diagram of the proposed automatic diabetes prediction methodology

Full size image

Exploratory data analysis and preprocessing

Exploratory data analysis (EDA) and data preprocessing have been considered the most essential step in any data-driven analysis. The EDA deals with the better understanding of the data by visualizing various aspects of it whereas, data preprocessing takes care of duplicate and imbalanced data, highly correlated and low variance attributes in the dataset, missing values, outliers in the dataset, etc. After performing EDA, it has been observed that the PIDD contains many missing values, outliers, and the values of attributes are also not normalized. Therefore, the present investigation utilizes outlier rejection (OR), filling missing values (MV), and normalization (N) in preprocessing which are briefly described as follows:

The extremely deviated observations from other observations have been considered as outliers and must be rejected from the dataset because the classifiers are very sensitive to the distribution as well as data range of features [25]. In the current work, quartiles have been employed to detect and reject the outlier which has been mathematically formulated in Eq. (1).

$$ {\text{OR}}\left( x \right) = \left\{ {\begin{array}{*{20}c} {x,} & {{\text{if}} Q_{1} - 1.5 \times {\text{IQR}} \le x \le Q_{3} + 1.5 \times {\text{IQR}}} \\ {\text{reject, }} & {{\text{otherwise}}} \\ \end{array} } \right., $$
(1)

where, x represents the occurrences of the feature vector which lies in n-dimensional feature space (\(x \in {\mathbb{R}}^{n}\)). \(Q_{1}\),\( Q_{3}\) and \({\text{IQR}}\) denotes the first, third, and interquartile range of the features subjected to \(Q_{1} ,Q_{3} , {\text{IQR}} \in {\mathbb{R}}^{n}\) respectively.

The next step in preprocessing is to carefully find and, fill the missing and null values for appropriate attributes only. Although, it has been found that all the attributes have null values (replaced by zero) but some attributes like G and BP cannot be zero whereas, attributes such as P may have zero value. Therefore, missing values have been handled by employing median by target (outcome) in the remaining seven features (G, BP, ST, I, BMI, DPF, and Age) which can be formulated as shown in Eq. (2). The main reason for employing median by target over mean to handle missing values is that in mean the average value of the attribute has been utilized to fill the missing value. In contrast to this, median by target first analyzed the corresponding outcome against the missing value attribute and then, fill the missing value by the median value of the attribute for that target.

$$ {\text{MV}}\left( x \right) = \left\{ {\begin{array}{*{20}c} {{\text{median}}\left( x \right),} & {{\text{if}} x = {\text{missed/null}}} \\ {x, } & {{\text{otherwise}}} \\ \end{array} } \right.. $$
(2)

Lastly, the normalization has been performed by rescaling the feature values to achieve the standard normal distribution with zero mean and unit variance (\(\sigma^{2}\)). The normalization (Eq. (3)) also reduces the skewness of the data distribution:

$$ N\left( x \right) = \frac{{x - \overline{x}}}{\sigma }, $$
(3)

where \(\overline{x}\) and \(\sigma\) represents the mean and standard deviation respectively (\(\overline{x}\), \(\sigma \in {\mathbb{R}}^{n}\)).

Further, the sampling technique, a vital step in any data-driven analysis, has been employed to obtain train, validate, and test subset. It is a process by which a representative portion of data has been utilized for extracting the characteristics and parameters from large datasets hence, it helps in better training of the model. It is of four types: linear sampling, shuffled sampling, stratified sampling, and automatic sampling. These techniques randomly split the collected data into various sets of representative information by employing dissimilar permutation and combination. The linear sampling technique linearly divides the collected data into a representative set of information without changing the sequence. The shuffled sampling randomly splits the dataset and constructs a subset from the available dataset. It also employs arbitrary data selection for assembling the subsets. The stratified sampling is similar to the shuffled sampling with the difference is that it retains the class distribution all over the dataset. The automatic sampling employs stratified sampling as default however, depending upon the data other suitable sampling techniques can also be utilized.

DL model

DL, a subset of ML, is a kind of black box which learns the relationship between features and target on its own. In this work, a multilayer feed-forward perceptron (MLP) model has been employed to build a DL model and trained with root mean square propagation (RMSprop) using back-propagation. The MLP consists of a single input–output layer and may have several hidden layers whereas, each layer contains many neurons that are connected with each other in the unidirectional manner of different weights [26]. The proposed model has been developed by utilizing Keras sequential library of TensorFlow which contains one input layer, four hidden layers, and one output layer. The model summary and architecture of the developed model have been presented in Table 2 and Fig. 4 respectively for better understanding.

Table 2 Model summary of developed DL model
Full size table
Fig. 4
figure 4

The MLP architecture for diabetes prediction

Full size image

The K-dimensional input vector of any layer of MLP produces O-dimensional output vector where K and O represents the input–output dimension of the respective layer subjected to \(f\left( x \right) : {\mathbb{R}}^{K} \to ^{ } {\mathbb{R}}^{O}\). The output of each processing unit for k neurons can be mathematically represented by Eq. (4):

$$ f\left( x \right) = \emptyset \left( {\mathop \sum \limits_{k} w_{k} x_{k} + b} \right), $$
(4)

where \(w_{k}\), \(x_{k}\), \(b\), and \(\emptyset\) are the weights, input, bias, and the activation function respectively.

The proposed model has been trained with the goal to minimize a cost function which also uses L2 regularization to avoid overfitting and has been mathematically formulated in Eq. (5):

$$ L = \mathop \sum \limits_{i = 0}^{K} \left( {y_{i} - \mathop \sum \limits_{j = 0}^{O} x_{ij} w_{j} } \right)^{2} + \lambda \mathop \sum \limits_{j = 0}^{O} w_{j}^{2} , $$
(5)

where L represents the cost function and \(\lambda\) is the regularization parameter. Further, during the entire training process weights are updated regularly by employing the RMSprop optimization technique to achieve the desired target value as expressed in Eq. (6):

$$ \begin{gathered} w_{t} = w_{t - 1} - \frac{\eta }{{\sqrt {\rho_{t} } }} \times \frac{{{\text{d}}L}}{{{\text{d}}w}}, \hfill \\ \rho_{t} = \beta \rho_{t - 1} + \left( {1 - \beta } \right)\left( {\frac{{{\text{d}}L}}{{{\text{d}}w}}} \right)^{2} , \hfill \\ \end{gathered} $$
(6)

where \(w_{t}\) and \(w_{t - 1}\) represents the new and old weights respectively with \(\rho_{t}\) and \(\rho_{t - 1}\) the new and old exponential average of the squared gradient respectively. However, \(\beta\) and \(\eta\) represent the moving average parameter and learning rate respectively. The hyperparameters such as the number of hidden layers, number of neurons in each hidden layer, learning rate, epochs, and activation functions for each layer have been empirically (hit and trial) chosen in the present work and have been illustrated in Table 3.

Table 3 Hyperparameters of developed DL model
Full size table

QML model

In the recent past, the world has witnessed enormous growth in the field of ML and DL. The models developed using these techniques have been applied in almost all imaginable sectors such as military, aerospace, agriculture, finance, and healthcare. However, with the increasing number of features, they require millions of parameters to learn and therefore, struggles to train efficiently and create lots of computational burden. On the contrary side, quantum computers have been found capable to solve such problems effectively with existing technologies by computing multiple states simultaneously. They utilize the three basic properties of quantum physics: superposition, Entanglement, and Interference. Because of these inherited properties qubits (the basic unit of quantum computers) can be in multiple states concurrently (superposition), extremely correlated even if separated by great distances (entanglement), and bias towards the desired state (interference). Therefore, quantum computing has the potential by which the research community has reached an inch closer towards achieving Artificial General Intelligence.

The superposition is the main property of QM which can be expressed by Eq. (7) [27].

$$ \left| \psi \right\rangle = \delta \left| 0 \right\rangle + \vartheta \left| 1 \right\rangle , $$
(7)

where, \(\left| \psi \right\rangle\) represents any arbitrary state between 0 and 1. \(\delta\) and \(\vartheta\) are complex numbers such that \(\left| \delta \right|^{2} + \left| \vartheta \right|^{2} = 1\). The qubit remains in this state until measured and after that, it collapses into either state \(\left| 0 \right\rangle\) or state \(\left| 1 \right\rangle\) with the probability of \(\left| \delta \right|^{2}\) or \(\left| \vartheta \right|^{2}\) respectively. The number of qubits required to perform the given task has been calculated by Eq. (8) which in the present work has been computed as 3.

$$ {\text{number of qubits}} = \log_{2} \left( {\text{number of attributes}} \right). $$
(8)

The present work utilizes a variational quantum circuit (VQC) with tunable hyperparameters to develop QML based classifier for diabetes prediction in PIDD [28]. The developed quantum circuit has three main components: (1) Encoder to encode the input data into quantum states (2) Decoder which produces output states, and (3) Evaluator which is used to compare the output values from the circuit with the corresponding input labels. The evaluation has been performed with the Pauli-Z operators and the average evaluated value has been used to improve the statistical accuracy [29]. The decoder quantum gates have been parameterized to model the input training data by optimizing the cost function which can be mathematically formulated as in Eq. 9.

$$ \begin{gathered} L\left( {x,y} \right) = \mathop \sum \limits_{j \ne y} \max \left( {0,g_{j} - g_{y} + \Delta } \right), \hfill \\ g_{i} = c_{i} \left( {x;\alpha } \right), \hfill \\ \end{gathered} $$
(9)

where \(\Delta\) represents the safe margin and \(g_{i}\) the interpreted score of ith classifier (\(c_{i}\)) on input x such that \(g_{i} \in \left[ { - 1,1} \right]\). The parameters have been tuned using Adam optimizer with a learning rate of 0.01 and batch size 10. Further, mini-batch training has been employed and hence, used to optimize the average loss of the generated mini-batch. The parameters used for the developed QML model has been represented in Table 4.

Table 4 Parameters of developed QML model
Full size table

Simulation setup and metrics

All the proposed models in the reported work have been implemented on Pycharm using Python 3.8 programming environment with various APIs of Python and Keras. The specifications of the simulation platform have been presented in Table 5 with their associated configurations.

Table 5 Specifications of the simulation platform
Full size table

The performance of the developed models has been regularly measured in terms of various evaluation metrics such as precision, accuracy, recall, F1 score, specificity, balanced accuracy, false detection rate (FDR), missed detection rate (MDR), and diagnostic odds ratio (DOR) [30,31,32]. Amongst all these performance parameters, precision, accuracy, recall, and F1 score represent how accurate the predictions are, percentage of true predictions, number of true positives that are correctly identified, and the balance between precision and recall respectively. However, Specificity signifies the number of true negatives whereas, balanced accuracy is the average of recall and specificity. Moreover, FDR and MDR have been used to evaluate the ratio of false-positive and false-negative in the detected objects. Additionally, DOR has been evaluated to find the effectiveness of the diagnostic test. Mathematically, these metrics can be computed using Eq. (10)-(19).

$$ {\text{Precision}} = \frac{{N_{{{\text{TP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{FP}}}} }}, $$
(10)
$$ {\text{Accuracy}} = \frac{{N_{{{\text{TP}}}} + N_{{{\text{TN}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{TN}}}} + N_{{{\text{FP}}}} + N_{{{\text{FN}}}} }} \times 100, $$
(11)
$$ {\text{Recall}} = \frac{{N_{{{\text{TP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{FN}}}} }}, $$
(12)
$$ {\text{F}}_{1} \;{\text{score}} = \frac{{2 \times {\text{Precision}} \times {\text{Recall}}}}{{{\text{Precision}} + {\text{Recall}}}}, $$
(13)
$$ {\text{Specificity}} = \frac{{N_{{{\text{TN}}}} }}{{N_{{{\text{TN}}}} + N_{{{\text{FP}}}} }}, $$
(14)
$$ {\text{Balanced accuracy}} = \frac{1}{2}\left( {{\text{Recall}} + {\text{Specificity}}} \right), $$
(15)
$$ {\text{False detection rate}} = \frac{{N_{{{\text{FP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{TN}}}} }}, $$
(16)
$$ {\text{Missed detection rate}} = \frac{{N_{{{\text{FN}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{TN}}}} }}, $$
(17)
$$ {\text{False detection rate}} = \frac{{N_{{{\text{FP}}}} }}{{N_{{{\text{TP}}}} + N_{{{\text{TN}}}} }}, $$
(18)
$$ {\text{Diagnostic odds ratio}} = \frac{{N_{{{\text{TP}}}} \times N_{{{\text{TN}}}} }}{{N_{{{\text{FP}}}} \times N_{{{\text{FN}}}} }}, $$
(19)

where, NTP is the number of true positives, i.e., number of desired objects detected correctly, NFP is the Number of false positives, i.e., number of detected objects which could not correspond to the ground truth objects, NTN is the number of true negatives, i.e., number of undesired objects detected correctly, NFN is the number of false negatives, i.e., number of ground truth objects that could not be detected.

Result and discussion

This section presents the various results obtained in different subsections using proposed methodologies. The results obtained after preprocessing have been described in the next section whereas, the results for prediction of diabetes in PIDD by employing the developed DL and QML models have been shown in subsequent sections respectively. Finally, the obtained results using proposed QML and DL have been compared with previously reported results using various conventional ML techniques in the next section.

Results for preprocessing

The class-wise density distribution of features in PIDD represents the complexity in identifying the positive and negative samples. Further, the presence of outliers incorporates skewness and kurtosis which in turn make the model to underestimate or overestimate the predicted value respectively. After OR, the number of samples has been reduced from 768 to 639 in PIDD. Thereafter, the MV has been replaced by their target-based median values. It has been observed that these operations make the skewness of distribution move towards zero because the mean and median values of the attributes coincide approximately. The results of OR and filling MV have been presented in Table 6.

Table 6 Description of PIDD after preprocessing
Full size table

Additionally, the correlation plot between various attributes of PIDD without and, with OR and filled MV have been illustrated in Fig. 5a, b respectively. Evidently, the preprocessing significantly improved the correlation of attributes with target outcome, especially for BP, ST, and I attribute.

Fig. 5
figure 5

Correlation matrix of PIDD a original, b preprocessed

Full size image

Further, the obtained and preprocessed PIDD has been divided into training, validation, and test subset by employing the shuffled sampling technique because of its simplicity and lack of bias which results in the generation of the balanced dataset. For this purpose, a policy of 70:20:10 has been adopted, and therefore 447, 128, and 64 samples have been randomly picked as train-, validate-, and test subset respectively.

Results for DL model

The performance of any DL model has been greatly affected by the number of hidden layers and the number of neurons in each layer. However, the addition of these parameters not only increases the complexity of the model but also does not always produces the optimum results. Therefore, to develop the best DL model in the present work, extensive experiments have been carried out on the PIDD. Six different DL models with varying hidden layers (1–6) have been implemented and tested, where the optimum number of neurons have been chosen empirically. The experimentally obtained results demonstrate that out of these six DL models, the model developed using four hidden layers with the number of neurons in each hidden layer as 16, 32, 8, and 2 respectively, produced the maximum validation accuracy. This may be because the higher number of hidden layers with a greater number of neurons will tend to limit the generalization capability of the model. Also, it may be affected by the problem of vanishing gradients, which often lead the model towards overfitting particularly in the case of smaller datasets such as PIDD. Further, it has been observed that the models developed using a lesser number of hidden layers are also unable to provide optimum results which might be because of underfitting. The comparative analysis of all the developed DL models has been presented in Fig. 6 for better clarity.

Fig. 6
figure 6

Performance comparison of developed DL models

Full size image

The obtained results reveal that the DL model developed using four hidden layers MLP architecture outperforms other developed DL models by a minimum margin of 7.36%. Further, the confusion matrix has been obtained for original and preprocessed PIDD, as presented in Fig. 7.

Fig. 7
figure 7

Confusion matrix for developed DL model a original, b OR, c OR + MV, d OR + MV + N

Full size image

Based on the obtained confusion matrix, other performance metrics (mentioned in “Simulation setup and metrics”) of the developed DL model have been evaluated and presented in Table 7. It has been observed that OR and OR + MV significantly boost the performance of developed model as compared with original raw data by 0.10 (16.43%) and 0.29 (47.64%) for precision, 0.06 (8.16%) and 0.18 (23.51%) for accuracy, 0.05 (7.14%) and 0.25 (35.71%) for recall, 0.08 (12.37%) and 0.28 (42.33%) for F1 score, 0.06 (7.54%) and 0.15 (18.86%) for specificity, 0.06 (7.90%) and 0.20 (27.36%) for balance accuracy, − 0.07 (− 38.36%) and − 0.15 (− 82.15%) for FDR, − 0.03 (− 22.96%) and − 0.10 (− 81.67%) for MDR, and 9.93 (109.39%) and 389.93 (4297.14%) for DOR respectively. It has been also very evident that in spite of improving the result, the incorporation of N in OR + MV reduces the values of these metrics which might be because of losing information due to less variability in PIDD.

Table 7 Performance evaluation of developed DL model under various preprocessing steps
Full size table

Results for QML model

The performance of the QML model greatly relies on the number of layers being employed. Therefore, exhaustive experimentation has been done by varying the number of layers (2, 4, 6, and 8) to find the optimum number of layers. It has been observed that the QML model with 4 layers provides optimum validation accuracy (Fig. 8). This may be because the higher number of layers leads towards overfitting whereas, lesser layers to underfitting particularly for a small dataset like PIDD. Therefore, the QML model developed using four layers dominates other models by a minimum margin of 3.70%.

Fig. 8
figure 8

Comparison of developed QML models

Full size image

The developed QML model with the optimum number of layers has been used to evaluate the performance of both the original and preprocessed dataset. Since, the norm square is always equal to one in QM which is the prime requirement and has to be taken care while state preparation. Hence, normalization is the inherent property of quantum computing therefore, the performance of the developed QML model has been evaluated on the original, OR + N, and OR + MV + N dataset which has been illustrated in the form of confusion matrix’s in Fig. 9.

Fig. 9
figure 9

Confusion matrix for developed QML models: a Original data, b OR + N, c OR + MV + N

Full size image

Based upon these confusion matrix’s performance of developed QML models have been computed and presented in Table 8. It has been observed that both the OR + N and OR + MV + N preprocessing techniques greatly uplift the performance of developed QML model as compared with original PIDD by 0.19 (38.46%) and 0.26 (53.51%) for precision, 0.14 (20.93%) and 0.19 (27.91%) for accuracy, 0.15 (23.08%) and 0.20 (30.77%) for recall, 0.18 (32.54%) and 0.24 (42.93%) for F1 score, 0.14 (20.00%) and 0.18 (26.67%) for specificity, 0.14 (21.50%) and 0.19 (28.67%) for balanced accuracy, − 0.18 (− 55.29%) and − 0.22 (− 66.49%) for FDR, − 0.08 (− 49.14%) and − 0.11 (− 66.49%) for MDR, and 14.02 (352.31%) and 31.91 (801.82%) for DOR respectively.

Table 8 Performance metrics of developed QML model under various preprocessing steps
Full size table

Results comparison

In this subsection, the simulated results of optimized developed models for the prediction and classification of diabetic person has been compared against each other and also with the previously reported results. It has been observed that the developed DL model yields better prediction on all the performance metrics and therefore, completely outperforms the QML model as illustrated in Table 9. The main reason for the underperformance of QML may be considered as the smaller PIDD along with the normalization of data. The developed DL model achieves higher values of precision (21.62%), accuracy (10.46%), recall (11.76%), and F1 score (17.72%). It also provides a margin of 10.46% for both specificity and balanced accuracy than to QML model. Further, the lower values of FDR and MDR for DL model as compared to QML model indicates that the DL model predicts less false positive and negative values. Additionally, much higher values of DOR have been also observed which clearly reveals that the developed DL model has a very high test performance. Therefore, the proposed DL model appears to be the most appropriate for the classification and prediction of diabetes from the PIDD.

Table 9 Comparison of developed models
Full size table

Further, the performance (precision, accuracy, recall and, F1 score) of developed models has been compared against the reported ML and DL model's performance and their comparison has been presented in Table 10. It has been observed that all the models perform better and provides acceptable prediction results. However, the developed DL establishes its supremacy and attains the best values for most of the performance metrics. Furthermore, it enhances the state-of-the-art performance in terms of accuracy, recall, and F1 score by a minimum margin of 0.01 (1.06%), 0.01 (1.06%), and 0.02 (2.20%) respectively with a very slight drop in precision.

Table 10 Comparative analysis of proposed and already developed diabetes prediction models
Full size table

Conclusion

In the proposed work, the diabetes prediction model has been accomplished by employing QML and DL framework. The importance of preprocessing and EDA has been explored and it has been found that they play an important role in robust and precise prediction. Further, the optimum number of layers have been obtained for both QML and DL models. The results obtained by utilizing optimum QML and DL models have been compared against the state-of-the-art models and the comparative analysis reveals that the developed DL model outperformed all the other models. Therefore, the developed DL model has shown great potential for the prediction of diabetes from PIDD. Further, although the performance of employed QML is still struggling as compared to the proposed DL but, compared with the existing models. In the future, the developed DL model will be examined on other diabetes datasets to examine the robustness of the model and a user-friendly web application will be developed. Moreover, the proposed QML model needs to integrate with the deep learning framework which may boost the performance against the developed models and state-of-the-art techniques.