Introduction

When a firm is going to locate some facilities into a market, while there already exists or will exist some facilities belongs to other firms, the competitive reaction should be analyzed in detail. Among such a market environment, firms seeking for maximizing their profit will make location-then-quantity decisions of their facilities. Unlike most location models regarding the facility quantity as a predefined value, we assume that competing firms also make quantity decisions as well as location decisions. Optimal facility location may be affected by different factors, service price, facility attractiveness, customer behavior, etc. Adjusting facility locations has a great effect on supply chain management by changing transportation cost, material allocation, and logistic operation. Melo et al. [1] reviewed the facility location literatures in the context of supply chain management from the perspective of network structure, decision variables, and other supply chain characteristics. The location site could also be a crucial determinant of market share and profit, further influence the quantity decision. Since submodularity is the basic property of the facility location models, the quantity of facilities also plays a vital role in firm profit. The competitive location model is widely applied in various areas in which the location of service could be spatial or temporal, such as the position of chain stores [2, 3], shopping malls [4], or as in the case of a timetable schedule, like transport scheduling [5,6,7], and TV news scheduling [8]. Some bibliography papers make detailed surveys [9,10,11,12].

Since Hotelling [13] first proposed a specific case of competitive location model, we realized location and service price are important for a facility, they both have a significant impact on customers, and further influence market share and revenue of an individual competing firm. For a review of major contributions on extensions of the Hotelling model, please see Eiselt [14]. Most of the initial locational studies discussed the optimal location of a single facility with various market assumptions, while current literatures focus mainly on more realistic and practical problems. Fan et al. [15] proposed a facility location design model including the interdependency of infrastructure systems which was estimated by a heterogeneous flow scheme, investigated the model performance by sensitivity analysis in the numerical study. In a competitive market, Fernández et al. [16] assumed customer choice obeys the Huff proportional rule, split the customer demand with respect to the facility quality and distance, and solved the large size case by a ranking-based discrete optimization algorithm. Ni et al. [17] improved existing location models by removing the assumption that facility cost is either a fixed setup or a simple cost function, substituted it as general nonlinear costs in the facility location framework. Yavari and Mousavi‑Saleh [18] proposed the Extended Radius bi-levels restructuring capacitated facility location problem (ER-RCFLP), including opening, closing down and resizing new facilities, extended the location model as a hierarchical problem. In the two-stage capacitated facility location model, Mauri et al. [19] proposed two hybrid metaheuristics for solving the multiproduct problem, the transportation cost and customer behavior were considered in computational experiments. Filippi et al. [20] incorporated cost minimization and customer satisfaction as the objectives and constructed a fair single source capacitated facility location (F-SSCFL) problem, a weighted sum method was applied to generate a small set of solutions, and then, they implemented a Benders decomposition approach to handle large-scale instances.

When both firms have more than one facility in the market, solving for exact optimal or equilibrium locations quickly becomes computationally intractable. The enumeration method was frequently used to search for the true solution of multiple facilities but always accompanied by too much redundant calculation. By incorporating prospect theory, Xu et al. [21] defined both theoretical model and mathematical model of location problems of single facility and multiple facilities. Mehrez and Stulman [22] tried to solve the maximal covering location problem within a planar market with the enumeration method by dynamically list all potential location sets. Ghosh and Craig [23] develop a location-allocation model that solved the multiple site selection problem in a competitive environment, developed an enumerate search algorithm to finding desirable locations of centroids problem. Dobson and Karmarkar [24] defined several concepts of stabilities in a linear competitive location problem and utilized an enumeration algorithm for solving the model. By doing this, he concluded the set of locations that maximize the profit of existing facilities is stable under competition. Drezner et al. [25] incorporated the anticipation of future entry of competitor’s facility into competitive location model in continuous planar space. One of the three algorithms they applied is the enumeration method which was named the brute force approach.

Some recent developments focus mainly on the heuristic algorithms which fast and accurately obtain the combinatorial location sites. The greedy algorithm and the branch and bound algorithm are the two most widely used methods. It is the simplest method to solve location problems with the fastest running speed. Huff [26] proposed a greedy procedure to seek multiple retail locations, approximated the optimum location of retail stores by incorporating probabilistic customer behavior. Corneuejols et al. [27] constructed an account location problem for a bank to maximize its available funds. They reviewed various heuristics and algorithms, results showed that greedy heuristic can get superior performance with reasonable computation. Revelle [28] constructed a maximum capture problem (MAXCAP) with the restriction that potential facility location can only be the vertices in a network, a greedy adding heuristic was applied to solve the model. Benati and Hansen [29] formulated the competitive location problem into an integer nonlinear programming model by incorporating random customer utility. Several methods and heuristic algorithms were compared. They found that variable neighborhood search heuristic solution is quite close to the greedy solution. Drezner et al. [30] proposed a leader–follower location design model with the budget constraint, and the optimal leader action was obtained by the greedy algorithm based on the follower’s choice. Kress and Pesch [31] have solved two-stage competitive location optimization by a greedy algorithm and tabu search heuristic. They found pricing stage has a strong effect on location solutions. Nevertheless, people found greedy only obtained an inferior feasible solution, and branch and bound algorithm can get more accurately optimal solutions with the cost of larger computation. Benati [32] provides two branch and bound heuristic algorithms to solve the competitive location problem with random utility customers. The first one using Lagrangian relaxation, while the second one relies on the submodular feature of the competitive location model. Benati [33] again solved the integer nonlinear programming model of competitive location problem by advanced branch and bound methods named data-correcting method, heuristic-concentration method. He found larger size problem still needed to be tackled by heuristic-concentration methods. Saidani et al. [34] formulated the location and design problem in a planar market as a two-stage quality-location model. They solved the location stage by an interval branch and bound algorithm. There are also other innovative algorithms, for example, the improved whale optimization algorithm (IWOA) in the locating problem of electric vehicle (EV) charging stations [35].

In this paper, we incorporate the two-stage competitive location model applied in Kress [31] to simulate the behavior of both firms, and assume that in short-term competition, the incumbent firm can only adjust its service price but not relocate its facilities. The whole decision procedure is divided into two stages: the entrant firm makes location decision in the first stage, and both firms adjust their price in the second stage. The essential problem is competing firms make location and price decisions intending to maximize their profit in a competitive market environment. The two-stage location model integrates location and pricing process, and it is better applicative for the industries with frequent location competition and price adjustment, civil aviation industry for instance. To simulating different location decision behavior, a greedy algorithm and an approximate branch and bound heuristic are applied to solve optimal entrant location. Then, we conduct a marginal analysis to make quantity decisions of facilities. We improved previous work in the following ways: propose an approximate branch and bound heuristic by introducing a covering range variable into the branch and bound algorithm to accelerate calculation speed. Relax the assumption that entrant firms have a given exogenous quantity of facilities, and make it feasible to adjust the number of facilities. Compare the decision effects of two mainstream location modes.

The paper is organized as follows. The next section introduces the model framework of the two-stage competitive location model and quantity decision model. Different location decision modes along with algorithms are given in the following section. The next section provides algorithm performance and results of numerical experiments using the models and decision modes in the following sections. This paper ends up in the last section with the conclusion and future works.

Model framework

Now, we define a model with two types of firms \(q\), incumbent firm (\(I\)) and entrant firm (\(E\)), facing a finite market consisting of a location set \(V\) and a linear segment \(L\) seeking for maximizing their revenue by determining the number of facilities and locating them. Discrete locations in location set \(V\) uniformly distributed along market space \(L\), for location \(i\), \(j\) in \(V\), the distance between \(i\), \(j\) is labeled as \(d_{ij}\). The incumbent firm has \(s > 0\) facilities already located in location set \(X_{s}^{I}\), \(X_{s}^{I} \subseteq V\), entrant firm has \(r > 0\) facilities will be located in location set \(X_{r}^{E}\) in the future, \(X_{r}^{E} \subseteq V\), define \(Z\) as the facility location set, \(Z \subseteq V\), \(Z = X_{s}^{I} \cup X_{r}^{E}\). For both incumbent and entrant firm’s location set \(X_{s}^{I}\), \(X_{r}^{E}\), define the binary variable \(x_{j}^{I}\), \(x_{j}^{E} \in \left\{ {0,{ }1} \right\}\) as their location variable. The variable equals 1 when the firm locates a facility at location \(j\), \(j \in V\).

Each location \(i\). has finite customer demand \(w_{i}\), representing the number of customers who are willing to take service at \(i\). Unlike most of the competitive location models utilize a deterministic behavior that customers only patronize the facility with the lowest patronize cost, which sometimes consists of transportation cost (positively correlated to distance) and mill price sometimes only distance, we will take customer’s personal preference and taste into consideration. Based on the assumption that customers obey the probabilistic choice rule, we define they make the patronizing decision with a random utility. The utility of a customer located in \(i\) (\(i \in V\).) to patronize a facility of firm \(q\) located in \(j\) (\(u_{ij}^{q}\)) can be divided into two parts: \(v_{ij}^{q}\) and \(\mu_{ij}^{q}\), which means the deterministic term and the random (unobservable) term, respectively:

$$ u_{ij}^{q} = v_{ij}^{q} + \mu_{ij}^{q} $$
(1)

Because of the lack of information of an individual customer, we introduce a continuous random variable \(\mu_{ij}^{q}\). When customers value both the distance from a facility and the unit mill price of that facility, the deterministic term can be defined as

$$ v_{ij}^{q} = a_{j}^{q} - \alpha d_{ij} - \beta p^{q} , $$
(2)

where \(d_{ij}\): distance between customer located in location \(i\) and facility located in location \(j\), \(d_{ij} = \left| {i - j} \right|\), \(p^{q}\): unit mill price of firm \(q\)’s facilities, \(a_{j}^{q}\): the average quality of firm \(q\) located in \(j\), related to facility design [26, 36] including floor area, business hours, etc. Since the quality variable is not considered in this research, we will take it as 0 in the following paragraph. α: positive preference parameter for the distance, denotes the distance sensitivity of customers (spatial friction coefficient [29, 33]). \(\beta\): positive preference parameter for the price, denotes the price sensitivity of customers.

Although competing firms cannot estimate the patronizing decision of every individual customer, they can obtain the integral choice probability by assuming the distribution of the random variable. It is widely accepted when random variable \(\mu_{ij}^{q}\) is independent identically distributed according to the extreme value Gumbel distribution. The probability that a customer located in \(i\) patronizes a facility located in \(j\) belongs to firm \(q\) (\(P_{ij}^{q}\)) can be formulated as a multinomial logit expression [37]. It is algebraically derived from random customer utility. Where \(N_{0}\) is a no purchase option, which means that customers can choose not to take any facility at all, \(N_{0} = e^{{u_{0} }}\). \(u_{0}\) is the utility of customers obtained from not patronizing any facility or patronizing an external facility. We will set it as 0.01 in numerical instances, because we focus mostly on the intra-market competition:

$$ P_{ij}^{q} = \frac{{{\text{e}}^{{\left( { - \alpha d_{ij} - \beta p^{q} } \right)}} }}{{\mathop \sum \nolimits_{{j \in X_{s}^{I} }} {\text{e}}^{{\left( { - \alpha d_{ij} - \beta p^{I} } \right)}} x_{j}^{I} + \mathop \sum \nolimits_{{j \in X_{r}^{E} }} {\text{e}}^{{\left( { - \alpha d_{ij} - \beta p^{E} } \right)}} x_{j}^{E} + N_{0} }},\forall i \in V, j \in Z. $$
(3)

Then, we could mathematically formulate the revenue function of firm \(q\) by function \({\text{Rev}}^{q} = \sum\nolimits_{i \in V} {\sum\nolimits_{j \in Z} {w_{i} } } P_{ij}^{q} x_{j}^{q} p^{q}\). Kress and Pesch [31] first constructed a two-stage location model that well depicted the location-then-pricing behavior of competing firms in a network. Next, we will decompose the two-stage competitive location model into pricing stage and location stage to explain this model in detail.

Now, considering there is a firm getting ready to enter the market. Since the entrant firm can make full investigation and preparation before making decisions, we assume that he can have complete information of the incumbent firm’s location and pricing. Taking the incumbent firm’s facility location and service price into account, the entrant firm can make decisions from the perspective of both price and location. In the short-term competition between two firms, the incumbent firm has no flexibility to change its facility location, because there would have fixed cost be paid for locating a facility in the market.

Pricing stage

The only response of the incumbent firm toward the competition of the entrant firm is adjusting its price to maximize revenue. Assume the price competition can occur all the time, competing firms can change price anytime they want during the pricing stage, every step taken by the entrant will trigger price adjustment of the incumbent firm. Since price information is public in the market, both the incumbent and entrant firm can adjust its price to generate maximal revenue based on the locations of all facilities and the price of the other firm. Every single adjustment can be seen as the best response to the other player’s new price. They will keep competing by changing their prices until no one has further incentive to change its price anymore. Then, we can conclude they have reached the pricing equilibrium state. This is a non-cooperative game process with the pricing decision as strategy and revenue function as payoff function. For a given incumbent firm location sets \(X_{s}^{I}\) (\(X_{s}^{I} \subseteq V\)) and a specific entrant firm location sets \(\overline{{X_{r}^{E} }}\) (\(\overline{{X_{r}^{E} }} \subseteq V\)), we can get equilibrium price of the incumbent firm \(p^{I*}\) and entrant firm \(p^{E*}\). We assume they have to keep the services in different locations at the same price:

$$ p^{I*} \in \mathop {\arg \max }\limits_{{p^{I} }} {\text{Rev}}^{I} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in \overline{Z}}} w_{i} P_{ij}^{I} \left( {p^{I} ,p^{E} } \right)x_{j}^{I} p^{I} , $$
(4)
$$ p^{E*} \in \mathop {\arg \max }\limits_{{p^{E} }} {\text{Rev}}^{E} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in \overline{Z}}} w_{i} P_{ij}^{E} \left( {p^{I} ,p^{E} } \right)x_{j}^{E} p^{E} , $$
(5)
$$ \overline{Z} = X_{s}^{I} \cup \overline{{X_{r}^{E} }} , $$
(6)
$$ p^{q} \ge 0\quad \forall q \in \left\{ {I,E} \right\}. $$
(7)

Function (4) and (5) mean that the resulting prices from the pricing stage are Nash equilibrium price obtained from a repeated game, and two firms adjust their price in turn to maximize revenue, until both firms do not have further incentives to change the price. Constraint (6) restricts the facilities of incumbent and entrant should be located in current combinatorial sets respectively. Constraint (7) restrict price should be non-negative.

Location stage

With the current equilibrium prices of both sides, the entrant firm can choose the optimal locations for maximizing its revenue with the fixed incumbent location. For a given incumbent location set \(X_{s}^{I}\) and entire potential entrant facility location set \(\widetilde{{X_{r}^{E} }}\) (\(|\widetilde{{X_{r}^{E} |}} = C_{n}^{r}\)), entrant firm has a perfect knowledge of the price response taken by the incumbent firm. According to all such information, he can calculate the revenue of every specific location set \(\overline{{X_{r}^{E} }}\) (\(\overline{{X_{r}^{E} }} \in \widetilde{{X_{r}^{E} }}\)), and then choose to locate the facilities in optimal location set \(X_{r}^{E*}\) which can obtain the maximized revenue:

$$ \mathop {\max {\text{Rev}}^{E} }\limits_{{X_{r}^{E} }} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in \overline{Z}}} w_{i} P_{ij}^{E} \left( {p^{I*} ,p^{E*} } \right)x_{j}^{E} p^{E*} , $$
(8)
$$ {\text{subject to:}} $$
$$ \mathop \sum \limits_{{j \in \overline{{X_{r}^{E} }} }} x_{j}^{E} = r, $$
(9)
$$ \overline{{X_{r}^{E} }} \in \widetilde{{X_{r}^{E} }}, $$
(10)
$$ x_{j}^{E} \in \left\{ {0, 1} \right\}. $$
(11)

Objective (8) ensures the entrant firm maximized revenue by locating its facilities. Constraint (9) restricts the number of facilities is \(r\). Constraint (10) restricts the optimal entrant location set has to be generated from all potential location sets. Constraint (11) ensures the location decision of a specific location has to be one or nothing. Then, we can compose the whole competitive location optimization process. First, take a specific entrant firm location set \(\overline{{X_{r}^{E} }}\) from all potential facility location set \(\widetilde{{X_{r}^{E} }}\) by some technique, along with the initial price for both firms \(p^{I}\), \(p^{E}\), fixed incumbent firm location set \(X_{s}^{I}\). Insert them into pricing stage calculation and get equilibrium price \(p^{{I{*}}}\), \(p^{{E{*}}}\), entrant firm’s revenue \({\text{Rev}}^{E}\). Compare all revenue with different entrant firm location sets, select the optimal location set by which entrant firm can get maximal revenue. The techniques of extracting \(\overline{{X_{r}^{E} }}\) from \(\widetilde{{X_{r}^{E} }}\) are explained in the next chapter.

Quantity decision

Economically speaking, the benefit from adding additional production factors would eventually become smaller and smaller; this is the so-called feature of diminishing marginal returns. Of competitive location models, such feature still holds. Benati [29, 32] proved the objective function of various location models was a submodular function, such function has natural diminishing marginal returns by definition, i.e., within a market with finite customer demand, and the gained market share of an additional facility will decrease with the increase of facility quantity. So that the facility quantity is also a crucial decision to keep marginal revenue larger than marginal cost. Only a few models include the optimal quantity of two firms. Ghosh and Craig [38] used the multiplicative competitive interaction (MCI) formulation to estimate the market share of the entrant and incumbent facilities, they considered both the number and locations of facilities. Ghosh and Craig [23] developed a location-allocation model that solved multiple site selection problem, found optimal locations and number of facilities. We incorporate the facility quantity variable into the two-stage competitive location model, make quantity decisions based on the optimal facility locations and price. Please see functions (12)–(18):

$$ \mathop {\max }\limits_{r} \pi^{E} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in Z^{*} }} w_{i} P_{ij}^{E} \left( {p^{I*} ,p^{E*} } \right)x_{j}^{E} p^{E*} - \mathop \sum \limits_{{j \in X^{E*} }} c^{E} x_{j}^{E} , $$
(12)
$$ {\text{subject to:}} $$
$$ p^{I*} \in \mathop {\arg \max }\limits_{{p^{I} }} {\text{Rev}}^{I} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in Z^{*} }} w_{i} P_{ij}^{I} \left( {p^{I} ,p^{E} } \right)x_{j}^{I} p^{I} , $$
(13)
$$ p^{E*} \in \mathop {\arg \max }\limits_{{p^{E} }} {\text{Rev}}^{E} = \mathop \sum \limits_{i \in V} \mathop \sum \limits_{{ j \in Z^{*} }} w_{i} P_{ij}^{E} \left( {p^{I} ,p^{E} } \right)x_{j}^{E} p^{E} , $$
(14)
$$ Z^{*} = X_{s}^{I} \cup X_{r}^{E*} , $$
(15)
$$ p^{q} \ge 0 \quad\forall q \in \left\{ {I,E} \right\} , $$
(16)
$$ \mathop \sum \limits_{{j \in X_{r}^{E*} }} x_{j}^{E} = r, $$
(17)
$$ x_{j}^{E} \in \left\{ {0,{ }1} \right\}. $$
(18)

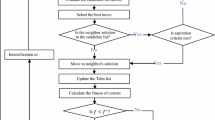
Here, \(c^{E}\) represents the cost of the additional facility, we assume fixed opening cost here. Objective (12) is based on profit function, total revenue minus total cost of entrant firm. For constraint (13)–(17), please see explanation in Sects. 2.1 and 2.2. The only difference quantity decision should be made corresponds to the optimal location set \(X_{r}^{E*}\). Entire facility location \(Z^{*}\) consists of \(X_{s}^{I}\) and \(X_{r}^{E*}\). Figure 1 illustrates the entire process.

Fig. 1
figure 1

Two-stage competitive location model with quantity decisions

Full size image

Location decision modes

Location stage calculation is nonlinear integer programming, Hakimi [39] proved searching the optimal location set is an NP-hard problem, and notoriously complicated to solve, and some heuristic algorithms must be used in the calculation[40]. In the current model, the entire possible location set \(\widetilde{{X_{r}^{E} }}\) consists of \(C_{n}^{r}\) location set \(\overline{{X_{r}^{E} }}\), and it is unrealistic to try all the location sets and obtain the best one when solving a large-scale problem. We have to choose a reasonable technique that could solve the location stage rapidly and accurately. The most widely used location decision modes are sequential decision and simultaneous decision, and they select location set by different techniques, respectively. We will evaluate two branch and bound algorithms of simultaneous decision mode by running speed and result accuracy which are the two most important factors when evaluating a calculation algorithm.

Sequential location mode

Sequential decision mode locates the facilities sequentially one by one in the market, and then gets the local optimum solution, also known as the greedy algorithm. It can fast obtain a feasible solution, since sequential decisions decompose the original combinatorial location problem as \(r\) single location problem, and thus accelerate the procedure to the most extend. For a new facility, put it at any potential location and get the equilibrium price, and then calculate the revenue with equilibrium prices. Iterate for \(r\) times, obtain the revenue of all potential locations, and set the new service at the location with maximal revenue. Repeat the last process with all previous facilities fixed until all facilities find optimal location.

In a specific iteration of the pricing stage, we have to get optimal price (both mill price and differential price) which maximizes the firm’s revenue. The pricing equilibrium problem can be solved by a Python module SciPy which has a function optimize. Minimize that can quickly solve this one-dimensional convex optimization problem by BFGS method. After several iterations, we can get the equilibrium price of both firms. The pseudocode sequential decision algorithm works as Algorithm 1.

figure a

Simultaneous location mode

Unlike the mixed location and price interactive of sequential decision mode, the entrant firm makes a location-price decision in simultaneous decision mode, i.e., in the location stage, there is no dynamic price competition, and only the initial price is accounted rather than the equilibrium price. The whole process can be described as a separated location-price process during which firms make the location-then-price decision, while the process of a sequential decision can be described as an integrated location-price process.

Both the enumeration method and branch and bound method can represent the idea of simultaneous decision mode, but as mentioned before, the enumeration method has a natural defect in the large-scale calculation. The branch and bound algorithm was widely applied in mixed-integer programming models. It is well accepted that Land and Doig [41] first initiated this systematic searching method in solving discrete programming problems in 1960, Little et al. [42] named it “branch and bound” method. Compared with the greedy algorithm, the branch and bound method have different solving logic. It simultaneously searches for the optimal combinatorial solutions of all facilities instead of setting up facilities one by one in the market. By constructing a paradigmatic enumeration tree with branches of all variables, the algorithm investigates the upper and lower bounds of such branches, and substitutes the optimal solution with the branch which produces a better solution while eliminates the branches with inferior solutions than the current one. For detailed algorithm, please see Land and Doig [41].

Classic branch and bound algorithm can solve small-scale calculations efficiently. However, when we apply it to a large-scale competitive location model, it always costs too much time because of the calculation complexity, even cost similar time as enumeration method in some extreme situation. To accelerate calculation speed, we generalized the method as an approximate branch and bound method by incorporating the idea of distance correction from Drezner [25] and interval analysis from Saidani [34]. We introduce a range variable \(R\) into analysis, merge the original potential locations as new joint locations covered by range \(R\), run the model and get optimal location by classic branch and bound algorithm with joint locations, and then convert the optimal joint locations into original locations.

Figure 2 demonstrates the conversion of market setting with cover range variable. Specifically, for a given number of potential \(n\) locations and range value \(R\), generate joint new locations set \(V^{\prime}\) by combining original locations within the range, the number of joint locations is n′ (\(n^{\prime} = n/R\) ). Customer demand \(w_{i}\) at original locations also added up segmentally as the customer demand at the new location \(w_{i\prime }\). Define the gravity center location (\(g\)) of every range segment as the joint location point, calculate the distance between customer and facilities with location point i′, j′, distance is labeled as \(d_{i\prime j\prime }\). Here, distance \(d_{i\prime j\prime }\) equals to \(\left| {g_{i\prime } - g_{j\prime } } \right|\) instead of \(\left| {i^{\prime} - j^{\prime}} \right|\) . Then obtain an approximate optimal solution by branch and bound method. After entrant facilities are set up, both firms will proceed with the pricing competition. Please notice the condition of applying the approximate range covered heuristic is the number of joint locations n′ should be larger than the number of facilities \(r\), range variable need to guarantee \(n/R \ge r\). For detailed pseudocode process, please see Algorithm 2.

Fig. 2
figure 2

Market setting conversion with a cover range

Full size image
figure b

Numerical results

In this section, we will run numerical experiments in a competitive market with two firms and provide computational results from the aforementioned models. All the experiment scenarios and algorithms are compiled in Python programming language and implemented on the macOS platform.

According to the assumption, all the firms seek for maximal profit. When an incumbent firm monopolizes the market, its location behavior was simulated by the enumeration method to find the true optimal solutions. After an entrant firm entering the market, both firms start to compete by adjusting prices, and then, the entrant firm determines the quantity and location of facilities, while the incumbent firm has to keep facilities fixed. Function (4)–(18) will be calculated with the location stage implemented by sequential decision mode and simultaneous decision mode. Assume that the linear market consists of 100 potential locations with 1000 customer demand, \(w\left( i \right)\) obey a specific normal distribution \(N\left( {50,25} \right)\), \(0 < i \le 100\). Set initial price as \(p^{I} = p^{I} = 10\).

Parameter settings

The most reasonable parameter setting is affected by market type and variables considered in the model, and different settings of parameters will cause some deviation in the calculation. In a planar market, with only location stage be considered, spatial friction coefficient \(\alpha\) was estimated to be 0.195 [29, 37]. When including the pricing stage, parameter setting was becoming more complex, distance parameter (\(\alpha\)), price parameter (\(\beta\)), no purchase option (\(N_{0}\)) should be determined simultaneously before running the model. There is still no widely accepted parameter setting of the two-stage competitive location model. Kress and Pesch [31] randomly generate six sets of test instances from both distance parameter and price parameter ranged from 0.015 to 4. In the empirical analysis, different industries may have more reliable results. For example, Lurkin et al. [43] take price endogeneity into passenger utility model, and estimate two parameters for airlines of the civil aviation industry, ranging from 0.003 to 2.5, but still lack sufficient accuracy. In summary, we can recognize that the parameter value has substantial uncertainty.

To obtain the general conclusion, we will use three sets of parameters for theoretical analysis. When two coefficient parameters are to determine in the logit model, change one parameter while setting the other fixed is equivalent to simultaneously determine two parameters. Make transformation of patronizing probability by calculating the \(e^{\beta }\)th root:

$$ P_{ij}^{q} = \frac{{{\text{e}}^{{\left( { - \frac{\alpha }{\beta }d_{ij} - p^{q} } \right)}} }}{{\mathop \sum \nolimits_{{j \in X_{s}^{I} }} {\text{e}}^{{\left( { - \frac{\alpha }{\beta }d_{ij} - p^{I} } \right)}} x_{j}^{I} + \mathop \sum \nolimits_{{j \in X_{r}^{E} }} {\text{e}}^{{\left( { - \frac{\alpha }{\beta }d_{ij} - p^{E} } \right)}} x_{j}^{E} + {\text{e}}^{{\frac{{u_{0} }}{\beta }}} }}, $$
(19)

Then, we can define \(\alpha^{\prime} = \alpha /\beta\) , \(N_{0}^{^{\prime}} = e^{{\frac{{u_{0} }}{\beta }}}\), original parameter setting problem is converted to set the relative value of \(\alpha\) to \(\beta\). By keeping \(\alpha\) fixed to \(0.1\), first, we assume that the price preference of customers is equal to distance preference, and next, we assume price preference is half and two times of distance preference, respectively, represent heterogeneous customers’ preference. Then, three sets of parameters are created, \(\alpha = 0.1, \beta = 0.05\), \(\alpha = \beta = 0.1\), \(\alpha = 0.1, \beta = 0.2\). All the results hereafter are the average value from numerical cases with three sets of parameters.

Performance of simultaneous decision

In this section, we will examine the performance of the approximate branch and bound heuristic. Generate 1–5 true optimal incumbent facility locations, calculate 1–10 optimal locations of entrant facility by traditional branch and bound algorithm, and approximate branch and bound algorithm of Algorithm 2. Taking the results from the traditional branch and bound algorithm as standard, compare two algorithms with two criteria: Running time and location accuracy. We will introduce average absolute distance as the accuracy indicator. For \(m\) instance location set \(X_{m}\), if location variable \(x_{j}\) within this set equals to 1, absorb index \(j\) into the location index set \(J_{m}\). Average absolute distance (\(\sigma\)) with standard location set \(X_{m}^{*}\) can be defined as:

$$ \sigma = \frac{{\mathop \sum \nolimits_{k = 1}^{m} \left| {j_{k} - j_{k}^{*} } \right|}}{m}. $$
(20)

Here, \(j_{k}^{*}\) represents the index in standard location index set \(J_{m}^{*}\) of \(X_{m}^{*}\). Table 1 presents the running time of 1–10 entrant facilities, and we use the average running time from experiments with 1–5 incumbent facilities. Select 2, 4, 5, 10 as range value, since we have 100 potential locations and we are not willing to have any fractional numbers in the calculation. Please notice traditional branch and bound algorithm could be considered equivalent to the approximate heuristic with range 1, the result from which was employed as the location benchmark to show the efficiency of the approximate heuristic [44]. From Table 1, we can see a huge acceleration in searching for optimal locations with the range value increase. The running time of branch and bound algorithm is not stable and always larger than 10 min. With the increase of entrant facility, approximate heuristic has more moderately increasing running time. When the range value equals to 4, we can get an approximately optimal solution within 10 s. The lower accuracy (larger range value), the faster speed of solution searching.

Table 1 Running time of different range value
Full size table

Next, we will investigate the location accuracy of the approximate branch and bound algorithm. Since branch and bound can obtain the global optimal solution of the integer programming model, the average absolute distance of the traditional branch and bound would be 0 all the time. With the optimal solution of 1–10 entrant facilities by branch and bound algorithm, we calculate the average absolute distance of different cover ranges by function (20). Results are displayed in Fig. 3, and different lines represent different range values. Generally speaking, running speed and calculation accuracy are contradictory, faster speed is always accompanied by lower accuracy, and such a phenomenon is obviously appeared in Fig. 3. Approximate heuristic with \(R\) equals 10, which has the fastest speed, is the least accurate method. With the increase of range value, the location accuracy decreased. After a comprehensive analysis, the approximate heuristic with \(R\) equals to 2 has the best performance, since it has reasonable calculation speed with only a little loss in accuracy.

Fig. 3
figure 3

Average absolute distance of different range value

Full size image

Optimal quantity

After comparing the performance of different algorithms, in this section, we will run the entire two-stage competitive location model, and then determine the optimal quantity and location of the entrant facility. Based on the analysis from “Performance of simultaneous decision”, approximate branch and bound heuristic with range 2 and sequential location mode in Algorithm 1 will be adopted in the location stage, respectively, represents two location decision modes. In the current model, we determine the facility quantity by marginal analysis. Optimal quantity should ensure the entrant firm obtain maximal profit, i.e., \(r^{*} = \arg \max \pi^{E} = {\text{Rev}}^{E} - C^{E}\). The marginal revenue of the additional facility should strictly greater than or equal to marginal cost.

From the marginal profit of the additional facility, a competing firm can conclude if it could keep expanding its business scale. Only non-negative marginal profit can ensure the non-decreasing of total profit, and the firm should cut off the quantity immediately as long as marginal revenue of the last facility is lower than marginal cost. Figures 4 and 5 display the marginal revenue of the entrant firm with sequential location and simultaneous location decisions. Calculate location, price, and revenue of 1–10 entrant facilities by two-stage competitive location model, function (4)–(11), and then get marginal revenue of the additional facility. Different lines represent experiments with the different numbers of incumbent facilities. We can see diminishing marginal revenue with the increased number of entrant facilities in both figures. Compared with sequential location mode, simultaneous location mode is not as smooth in the descent process. In sequential location mode, marginal revenue with the less incumbent facility is strictly higher than marginal revenue with the more incumbent facility. However, simultaneous location mode does not hold such results.

Fig. 4
figure 4

Marginal revenue of sequential decision

Full size image
Fig. 5
figure 5

Marginal revenue of simultaneous decision

Full size image

Table 2 presents exact locations of optimal quantity based on different marginal costs. Keep the principle of marginal analysis and confirm the quantity of facility, and then output the corresponding optimal location. Table 3 presents the profit of the entrant firm corresponding to optimal quantity and location. Calculate profit of 1–10 entrant facilities by two-stage competitive location model with quantity decision, function (12)–(18). From Table 2, we realize that there are differences in exact location between the two decision modes. With the marginal cost increases, the optimal strategy of quantity decision for entrant firm is cutting down the facility with lower marginal revenue, so that the optimal quantity is decreased. Compared the two decision modes, we can see the sequential mode always has no fewer quantity facilities than the simultaneous mode, which means that the additional facilities’ marginal revenue of sequential mode is no less than that of simultaneous mode. Table 3 holds the claim and profit of sequential mode always larger than or equal to the profit of simultaneous mode, sequential location mode is the advantage strategy.

Table 2 Locations of optimal quantity based on different marginal cost
Full size table
Table 3 Profit of entrant firm corresponding to optimal locations
Full size table

Conclusion

In this paper, we assumed that the entrant firm can adjust its number of facilities to obtain maximal profit, introduced facility quantity as a decision variable into a two-stage competitive location model which consists of the pricing stage and location stage. During the location stage, sequential location mode and simultaneous location mode were applied to simulate different location behavior. We developed an approximate branch and bound method to accelerate the searching process under the premise of accuracy. Quantity decision was made based on marginal analysis, and then, corresponding location and profit were calculated.

We design several experiments in a linear market with normally distributed customers to examine the calculation performance of approximate heuristic and compare the results of two location modes. From numerical experiments, we found that the approximate branch and bound method is an ideal supplement of the traditional branch and bound method, especially for location problems with large-scale potential locations. It accelerated running speed tremendously with only a little loss in accuracy, and the key point is the balance between running speed and accuracy which depends on the selection of range value (\(R\)). According to optimal quantity, location, and profit of both sequential and simultaneous location modes, we concluded that when a new firm is going to enter a market with both price and location competition (for instance, civil aviation industry), and sequential location mode can produce more profit than simultaneous location mode; it is an advantage strategy.