Introduction

Multi-objective optimisation has been widely applied to diverse real-world problems [12, 24], while many-objective optimisation problems are under-exploited but commonly seen in real life [17]. An important example is the engine calibration within car engine design [28].

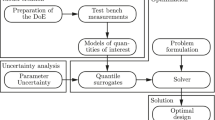
Engine calibration aims at simultaneously adjusting a set of parameters to ensure the performance of an engine under various working conditions using an engine simulator. A working condition is often described by a number of parameters depending on the actual usage of engine, such as the speed. Traditional calibration process is achieved by manually changing the engine parameters, simulating its state under different working conditions, comparing its states on engine maps [23], and repeating the above steps until the states are closed to some desired states. Figure 1 illustrates the manual process of adjusting engine parameters. The calibration process is usually time-consuming and highly relies on the human knowledge. Ma et al. [22, 23] proposed a multi-objective optimisation approach to automate the gasoline direct injection engine calibration process, in which five engine parameters were adjusted under four cases and three evaluation criteria were considered for each case. However, some of the engines, such as aero-engines, are controlled by dozens of parameters. To achieve optimal performance, the engines should be examined under more working conditions. Due to the large number of engine parameters to be adjusted, the performance measurements to be considered, as well as the working conditions to be tested, the calibration process is a crucial many-objective optimisation problem.

In this work, we consider a real aero-engine with non-convex search space of 27 parameters (e.g., compressor pressure ratio, compressor efficiency, and combustion efficiency) and its expected performance under 33 different flight conditions. An engine state is described by 15 measurements, such as compressor exit pressure and fuel flow parameters. Therefore, 27 parameters need to be adjusted at the same time to make the engine’s states as closed to the given measurement data as possible.

We model this calibration process as a many-objective optimisation problem. A fast many-objective evolutionary optimisation algorithm with shift-based density estimation is designed to search for parameter setting with acceptable performance accuracy and improve the calibration speed. During optimisation, a numerical simulation program is used to simulate the performance of the engine given a parameter setting and a working condition. Our approach is compared to several state-of-the-art many- and multi-objective optimisation algorithms on this real-world engine calibration problem and achieves superior performance.

The main contributions of this paper are as follows.

  • Efficient calibration of a real aero-engine: a real aero-engine model and real data of performance measurements are used in this work.

    • Large parameter search space: We consider 27 parameters of this aero-engine. To our best knowledge, no existing work has ever calibrated a such big number of parameters.

    • Large number of criteria to be optimised: Four hundred and ninety-five criteria are considered in our aero-engine calibration process. To our best knowledge, no existing work on engine calibration has ever considered a such large number of criteria to be optimised.

    • Non-convex constrained parameter space: The calibration of model parameter is a constrained optimisation problem. The parameter space of our aero-engine model is non-convex and black-box. Given a parameter setting, the computational fluid dynamics (CFD) simulation of engine dynamics is able to determine if a given parameter setting is feasible or not, but it is time-consuming as an evaluation of a parameter setting.

  • Two optimisation approaches for automating the calibration process:

    • Many-objective optimisation with a simple yet effective fSDE: We model the calibration process as a many-objective optimisation problem and propose a fast many-objective evolutionary algorithm with Shift-based Density Estimation (fSDE) for automating and speeding up the calibration process. The proposed fSDE shows its superior or competitive performance to some state-of-the-art many- and multi-objective evolutionary algorithms on our real aero-engine calibration problem and a well-known many-objective optimisation benchmark test suite.

    • Single-objective optimisation: To further validate our approach, the process is also modelled as a single-objective optimisation problem with a linear aggregation of criteria to be optimised. Several classic and state-of-the-art evolutionary algorithms have been applied, but their efficiency is worse than our proposed fSDE, probably due to the infeasible parameter settings.

  • Inspiration to human engineers:

    • Fault diagnosis assistant: It has been observed that very different engine parameter settings lead to similar performance, which motivates human engineers to seek for the reasons and understand why it happened (e.g., sensibility of parameter, faults, or bias in computational model).

    • Additional parameters and measurements: As different settings lead to similar performance given the current parameters, measurements, and operation points, human decision makers can consider additional calibration parameters, measurements, or operation points.

    • Novelty of design: From a perspective of discovering engines, instead of problem solving, diverse settings found by fSDE inspire human engineers to design novel engines.

Fig. 1
figure 1

Manual engine calibration process. An acceptable parameter setting \(\varvec{x}\) should ensure measurement errors within certain threshold at several given operation points \(s_1, s_2, \dots , s_k\)

Full size image

In the remainder of this paper, “Background” discusses the background and related work. “A real-world aero-engine calibration problem” presents the real aero-engine calibration problem studied in this paper. The many- and single-objective evolutionary optimisation for calibration are provided in “Many-objective evolutionary optimisation for aero-engine calibration” and “Single-objective evolutionary optimisation for aero-engine calibration”, respectively. In particular, “fSDE: fast MaOEA with shift-based density estimation” introduces our proposed fSDE. Our fSDE is compared to some state-of-the-art many- and multi-objective evolutionary algorithms on a well-known many-objective optimisation benchmark test suite (“Efficiency verification of fSDE on benchmark test suite”) and our real aero-engine calibration problem (“fSDE for aero-engine calibration”). Finally, “Conclusion” concludes.

Background

Engine calibration

Engine calibration refers to the process of adjusting a set of parameters of a given engine model, denoted as \(\varvec{x}=(x_1, x_2,\dots , x_d)\), to ensure its performance at several operation points or working conditions (illustrated in Fig. 1). An operation point s is often determined by a number of values that describe the actual usage of the engine. Taking aero-engines as an example, an operating point is specified by a Mach number, a flight altitude, and a flight state (e.g., taking-off and cruising), which is quantified by a mechanical spool speed [14]. The quality of a parameter setting is indicated by the distances between a number of measurements, denoted as \(m_1, m_2, \dots , m_h\), and their theoretically optimal values, denoted as \(m^*_1, m^*_2, \dots , m^*_h\). Usually, dozens of measurements are considered at each operation point. The lower the distance is, the better the engine parameters are. It is worth mentioning that the engine parameters remain unchanged at different operation points.

Fig. 2
figure 2

Schematic diagram of the engine model studied in this paper. The numbers between brackets are the indices of measurements described in Table 2

Full size image

Model-based engine calibration with meta-heuristics

The engine calibration process, illustrated in Fig. 1, can be formalised as an optimisation problem given a computational engine model, which simulates the model and calculates the measurements given a parameter setting and an operation point. Applying black-box optimisation algorithms, such as meta-heuristics, to automate the engine calibration process is straightforward. [28] reviewed the applications of meta-heuristics in car engine calibration published till 2013. In the reviewed work [28], multi-objective evolutionary algorithms have often been applied to optimise at most six objectives at the same time [15, 21, 26], while single-objective algorithms, such as particle swarm optimisation (PSO), have also been used [25, 32]. More recently, Ma et al. [22, 23] proposed a multi-objective optimisation approach to automate the gasoline direct injection engine calibration process, in which five engine parameters were adjusted under four operation conditions and three measurements were considered for each operation condition.

Multi- and many-objective optimisation

Various multi-objective evolutionary algorithms (MOEAs) and many-objective evolutionary algorithms (MaOEAs) have been proposed to deal with multi- and many-objective optimisation problems [12, 24], mainly categorised into three groups: (i) Pareto dominance-based, (ii) decomposition-based, and (iii) indicator-based. Pareto dominance-based MOEAs aim to use Pareto dominance mechanisms to select non-dominated solutions and apply some additional strategies to improve the diversity of solutions. The non-dominated sorting genetic algorithm II (NSGA-II) [10] is one typical MOEA, and other examples include the Pareto envelope-based selection algorithm II (PESA-II) [5] and the improved version of the Strength Pareto Evolutionary Algorithm (SPEA2) [36]. Although Pareto dominance-based MOEAs have good capability, the performance can be worsen rapidly with the increased number of objectives due to the dominance resistance phenomenon [17]. To overcome this issue, relaxed dominance-based MOEAs are proposed which aim to design new dominance relations, such as \(\epsilon \)-dominance [16] and GrEA [33]. Examples of decomposition-based MOEAs/MaOEAs include the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [34], the non-dominated sorting genetic algorithm III (NSGA-III) [9], and the reference vector-guided evolutionary algorithm (RVEA) [2]. These algorithms tend to decompose the original problem into some simpler multi-objective or single-objective optimisation problems. The two-archive algorithm (Two_Arch2) [31], the indicator-based evolutionary algorithm (IBEA) [35], and the fast hypervolume-based evolutionary algorithm (HypE) [1] are popular indicator-based MOEAs/MaOEAs.

A real-world aero-engine calibration problem

We consider a real aero-engine model parameterised by 27 parameters which need to be adjusted at 33 operation points. The considered engine model is illustrated in Fig. 2.

Twenty-seven engine parameters A total number of 27 engine parameters are adjusted, such as compressor pressure ratio, compressor efficiency, fan inner/outer pressure ratio, high-/low-pressure turbine efficiency, bypass ratio, and heat-transfer coefficient. Table 1 provides the lower and upper bounds of those parameters.

Table 1 Lower bound (LB) and upper bound (UB) of the aero-engine model parameters and a known optimum provided by a human engineer
Full size table

Fifteen measurements per operation point At each operation point, the computational model outputs 15 measurements of the considered real aero-engine, described in Table 2. These measurements describe the environmental condition, the working status, and the performance of the engine. The numbers between brackets in Fig. 2 correspond to the indices of measurements described in Table 2. Their desired values (called “targets” in this paper) for an engine of optimal status vary at different operation points. The targets of 33 operation points are available in our real problem.

Table 2 Considered measurements at each operation point
Full size table

Thirty-three operation points The measurements at 33 different operation points are provided. These operation points are carefully selected by a human engineer to represent various states of an aircraft.

Computational engine model A computational engine model (a Windows executable file with extension .exe) is available. It takes a parameter setting \(\varvec{x}\) and an operation point s as two inputs. During a simulation, several CFD calculations are performed inside the computational model to simulate the dynamics. If the CFD simulation does not converge, then the input setting is labelled as “infeasible” and the simulated measurement values are considered “unbelievable”; otherwise, the input setting is labelled as “feasible” and the simulated measurements \(m_1, m_2, \dots , m_h\) are considered “believable”. The label and simulated measurements are returned, as shown in Algorithm 1. Each simulation consumes approximately 0.2 s. Note that this is not the case of expensive optimisation problem, but the real-time optimisation efficiency is very important in this real-world application.

figure a

Evaluation criterion Given a number of operation points \(s_j\), \(j \in \{1,\dots ,33\}\), the quality of an engine parameter setting \(\varvec{x}\) is often evaluated with the root-mean-square error (RMSE) computed as follows:

$$\begin{aligned}&RMSE(\varvec{x}) \nonumber \\&\quad =\sqrt{\frac{1}{33*15}\sum _{j=1}^{33} \sum _{i=1}^{15} \left( \frac{Simulate(\varvec{x},s_j)-m^*_{i,j}}{m^*_{i,j}}\right) ^2},\nonumber \\ \end{aligned}$$
(1)

where \(m^*_{i,j}\) refers to the target value of the \(i^{th}\) measurement of the optimal engine at operation point \(s_j\) for any \(i \in \{1,\dots ,15\}\) and \(j \in \{1,\dots ,33\}\). The error rate of the \(i^{th}\) measurement at the \(j^{th}\) operation point is calculated as the normalised distance between the simulated value and its target value:

$$\begin{aligned} e_{i,j}(\varvec{x})=\left| \frac{Simulate(\varvec{x},s_j)-m^*_{i,j}}{m^*_{i,j}}\right| . \end{aligned}$$
(2)

In our real-world scenario, an engine parameter setting \(\varvec{x}\) with \(RMSE(\varvec{x})\) lower than \(0.5\%\) is considered acceptable. For a better performance, an \(RMSE(\varvec{x})\) lower than \(0.3\%\) is favourable. To achieve a such quality, it takes on average 3 h manual work (as illustrated in Fig. 1) by an experienced human engineer.

Many-objective evolutionary optimisation for aero-engine calibration

fSDE: fast MaOEA with shift-based density estimation

In the field of multi-/many-objective optimisation, a performance indicator refers to the measure used to evaluate the quality of a solution set provided by an optimiser (e.g., an MOEA) [19]. The quality of a solution set can be described by the extent of its approximation of the Pareto front, in terms of four aspects [19], namely convergence, spread, uniformity, and cardinality. Similarly, indicators can also be applied to approximate the contribution of each individual (i.e., solution) in a population, and then used as a criterion to differentiate the individuals.

Indicator-based MaOEAs have a significant advantage. They can avoid low selection pressure towards Pareto front via non-dominated sorting thanks to a high proportion of non-dominated solutions [17]. The studies of [17, 19] showed that generally the performance of an indicator-based MaOEA strongly depends on the selection of appropriate indicators and strategies to use them. On one hand, different indicators have a different bias towards the Pareto front. For instance, the work of [18, 31] showed that IBEA using \(I_{\epsilon }\) indicator may make the population converge to sub-regions of the Pareto front with bad diversity. On the other hand, strategies using indicators imply large computational consumption and may lead to inefficiency of algorithms [1].

Due to the large number of objectives in this aero-engine calibration problem and the requirement of real-time efficiency in real-world application, we intend to design an indicator-based MaOEA to achieve better performance with acceptable time cost.

Shift-based density estimation (SDE)

Li et al. [20] showed that the shift-based density estimation (SDE) is able to detect individuals with good convergence and diversity. Therefore, SDE [20] is chosen as the indicator to guide search processes as finding more diverse parameter settings of high quality is favourable in our case. The shifted density \(D(p,{\mathcal {P}})\) of an individual p corresponding to its belonging population \({\mathcal {P}}\) is formalised as follows [20]:

$$\begin{aligned} D(p,{\mathcal {P}})=\min _{q \in {\mathcal {P}}, q \ne p}\left\{ \sqrt{\sum _{i=1}^{m}{({p_i-\max {(q_i,p_i)})}^2}} \right\} , \end{aligned}$$
(3)

where m is the number of objectives. \(q_i\) and \(p_i\) (\(i \in \{1,2,...,m\}\)) denote the ith objective value of individuals q and p, respectively. The value \(D(p,{\mathcal {P}})\) is used as the fitness of individual p, thus \(fitness_{p} = D(p,{\mathcal {P}})\).

Framework of fSDE: less is more

SDE has been integrated into NSGA-II, SPEA2, and PESA-II, and shown to improve the performance of the aforementioned algorithms [20]. However, the aforementioned algorithms are complex and the required operations, such as non-dominate sorting, are time-consuming; while in our scenario, real-time efficiency is crucial. Therefore, we proposed a simple MaOEA framework with SDE, called fSDE, presented in Algorithm 2. First, N solutions are randomly generated as the initial population \({\mathcal {P}}\). Then, at every generation, a binary tournament selection strategy is processed to generate a mating pool B of size N based on the fitness of individuals in \({\mathcal {P}}\). After reproducing N offspring, denoted as O, through simulated binary crossover [7] and polynomial mutation [8], an environmental selection is processed to delete the N worst solutions from \({\mathcal {P}}\bigcup {\mathcal {O}}\) and keep the remained N solutions as the new population. The above steps are repeated until termination criteria are reached. Considering a population of N individuals for a multi-objective optimisation problem with m objectives, calculating the fitness values (i.e., shifted density values) costs \(O(mN^2)\). The deletion step in the environmental selection costs \(O(N\log {N})\). Therefore, the total complexity is \(O(mN^2)\).

figure b

Efficiency verification of fSDE on benchmark test suite

To verify the effectiveness of our proposed fSDE, we compare it to state-of-the-art many- and multi-objective evolutionary algorithms on a commonly used benchmark function set, MaF [3]. The baseline algorithms considered in our comparison study are MOEA/D [34], NSGA-III [9], Two_Arch2 [31], and IBEA [35], taken from the MATLAB-based MOEA platform, PlatEMO-v2.5 [30]. The proposed fSDE is also implemented in MATLAB and integrated into PlatEMO-v2.5. MaF contains 15 test functions, designed for many-objective optimisation aiming to represent various real-world scenarios with many different shapes of Pareto fronts [3]. Table 3 shows the number of objectives considered in this comparison study, the corresponding number of reference vectors, and the corresponding number of function evaluations [29], determined by Das and Dennis’s systematic approach [6, 9]. For all algorithms, its population size is set as the number of reference points.

The hypervolume (HV) is adopted as the performance metric. Normalised objective values are used to compute HV values, and then, the reference point \((1.1,1.1,\dots ,1.1)\) is used for computing HV. On each benchmark function of MaF, 30 independent optimisation trials have been performed by each algorithm. The averaged HV values, standard deviations, and the results of Wilcoxon rank sum test [4] in solving MaF with 5, 10, and 20 objectives are reported in Tables 4, 5, and 6, respectively.

Table 3 Experimental setting of tests on MaF, where d is the number of decision variables
Full size table

According to Table 4 (5 objectives), Two_Arch2 performs better than fSDE and its pairwise win/tie/loss counts against fSDE are 8/4/3. fSDE outperforms MOEA/D and NSGA-III in terms of HV values. In addition, the performance of IBEA and NSGA-III is similar to that of fSDE. In solving MaF test suite with ten objectives (cf. Table 5), fSDE has the best overall performance in terms of convergence and diversity among the compared MaOEAs. fSDE achieves significantly better HV values than MOEA/D in 12 out of 15 functions. When solving MaF with 20 objectives (cf. Table 6), NSGA-III obtains better HV values than fSDE, while fSDE achieves better quality (HV) than MOEA/D. Moreover, IBEA and Two_Arch2 have similar performance compared to fSDE. To summarise, fSDE achieves superior or competitive performance on MaF compared to the considered baseline algorithms.

Table 4 Averaged HV values in solving MaF with five objectives
Full size table
Table 5 Averaged HV values in solving MaF with ten objectives
Full size table
Table 6 Averaged HV values in solving MaF with 20 objectives
Full size table

fSDE for aero-engine calibration

We model the aero-engine calibration process as a many-objective optimisation problem, aiming at minimising simultaneously all the error rates, Eq. (2). To do so, two naive but effective dimensionality reduction methods (“Naive but effective dimensionality reduction”) and dimensionality reduction via principal component analysis (“Failure of dimensionality reduction via principal component analysis”) have been performed.

Naive but effective dimensionality reduction

Two naive dimensionality reduction methods have been considered: (i) modelling \(\frac{1}{15}\sum _{i=1}^{15} e_{i,j}(\varvec{x})\) with \(j \in \{1,\dots ,33\}\) as 33 objectives; and (ii) modelling \(\frac{1}{33}\sum _{j=1}^{33} e_{i,j}(\varvec{x})\) with \(i \in \{1,\dots ,15\}\) as 15 objectives. As a baseline, we also (iii) model all the error rates as \(33*15\) objectives. Twenty independent optimisation trials of fSDE with 20,000 simulation calls to the computational model as optimisation budget are applied to each of the above three many-objective optimisation problems, denoted as fSDE-33, fSDE-15, and fSDE-495, respectively.

Quality assessment in objectives Figure 3 illustrates the averaged RMSE, calculated with Eq. (1), over 20 independent trials with respect to the simulation number (left) and time in seconds (right). No obvious difference has been observed among the three cases at the early optimisation stage. However, along with the optimisation time, fSDE-15 (solid black curve) converges slightly better than fSDE-33 and fSDE-495. Figure 4 illustrates the lowest error rate among the 495 error rates among the 20 trials, named as minmax error. Lower minmax error implies overall better parameter setting. According to Figs. 3 and 4, although fSDE-33 achieves similar RMSE as the other two cases, its minmax error is higher after 5, 000 model simulations. The experimental result is coherent with an engineering perspective, and thus, the values of an identical measurement at various operation points is highly correlated and can be aggregated to a single value, as in case (i), thus fSDE-15.

Fig. 3
figure 3

Averaged RMSE over 20 independent trials with respect to the simulation number of the computational model (left) and time (right)

Full size image
Fig. 4
figure 4

Averaged minmax error over 20 independent trials with respect to the simulation number of the computational model (left) and time (right)

Full size image

Quality assessment in decisions Four aero-engine parameter settings with RMSE lower than \(0.5\%\) found by fSDE-15, denoted as \(\varvec{x}_a\), \(\varvec{x}_b\), \(\varvec{x}_c\), and \(\varvec{x}_d\), are illustrated in Table 7. For reference, a known optimum parameter setting of this problem, denoted as \(\varvec{x}^*\), is given on the second column. On most of the coordinates, the illustrated parameter settings are very closed to the optimum, except for the parameters at coordinates 15–17. Those parameters at coordinates 15–17 are the volume of cooling flow of the high-pressure turbine guide vane, the high-pressure turbine rotor, the low-pressure turbine guide vane, and the low-pressure turbine rotor. The model is less sensitive to those four parameters.

Table 7 Four aero-engine parameter settings with RMSE lower than \(0.5\%\) found by fSDE
Full size table

Quality assessment in efficiency As mentioned previously, in this calibration problem, an experienced human engineer needs approximately 3 h to find a parameter setting with an RMSE value lower than \(0.3\%\). With fSDE, it takes less than 15 min to achieve a such RMSE value and 22 min to achieve an RMSE value of \(0.2\%\). All the experiments in this paper were ran on an i7-8700 Intel processor desktop with 8 cores.

Failure of dimensionality reduction via principal component analysis

To reduce the dimensionality of objectives, principal component analysis (PCA) has been performed. First, we sample 20,000 parameter settings uniformly at random in the legal ranges provided in Table 1 and simulate them at the given operation points. Among the 20,000 samples, only 13,331 settings are feasible. PCA is performed on the 15 averaged measurements over operation points of feasible samples, according to the results of which the number of objectives is reduced to 7. Again, fSDE is applied to optimise the resulted 7-objective problem, denoted as fSDE-7. However, after dimensionality reduction via PCA, the percentage of infeasible settings sampled by fSDE (left of Fig. 5) increases along with the increased generation number, while without dimension reduction, the percentage of infeasible settings sampled by fSDE-15 (cf. Sect. 4.3.1) decreases, as shown in the right of Fig. 5. Due to the large number of sampled infeasible parameter settings, the fSDE fails and does not converge given more optimisation time. The dimensionality reduction via PCA loses the implicit information of parameter feasibility and infeasibility.

Fig. 5
figure 5

Percentage of infeasible parameter settings sampled by fSDE-7 (left) and fSDE-15 (right) at every generation

Full size image

Comparison with baselines

As a supplementary verification, IBEA, MOEA/D, NSGA-III, and Two_Arch2 with the second dimensionality reduction method, i.e., case (i), have also been applied given the same number of simulations and the results are illustrated in Figs. 3 and 4. Our proposed fSDE outperforms NSGA-III and Two_Arch2 in terms of solutions quality (RMSE) and outperforms MOEA/D in terms of real-time performance (right of Fig. 3) on our real aero-engine calibration problem.

Discussion

When modelling our aero-engine calibration as a many-objective optimisation problem, the usage of sophisticated dimensionality reduction method should be reconsidered. On the contrary, naive dimensionality reduction methods meet better the needs in engineering and lead to better results. Many-objective evolutionary algorithms are able to find diverse solutions of high quality. However, their computational cost is sometimes relatively high if an evaluation of solution is not feasible. As in our case, an evaluation takes only around 0.2 s and the optimisation efficiency is a more important indicator to be considered when selecting an optimisation algorithm. Our proposed fSDE with a simple framework outperforms the baseline algorithms in terms of real-time performance on the aero-engine calibration.

Single-objective evolutionary optimisation for aero-engine calibration

For a further verification of our approach, we model the calibration process as a single-objective optimisation problem with a linear aggregation of the distance between the target values and the simulated values of measurements given a setting. The fitness function is designed as follows:

$$\begin{aligned} fitness(\varvec{x})=1-RMSE(\varvec{x}), \end{aligned}$$
(4)

where \(RMSE(\cdot )\) is defined in Eq. (4). A huge negative value is returned as fitness in case of invalid calculation or constraint violation in CFD calculations.

Failure of PSO, DE, and CMA-ES Although classic single-objective evolutionary algorithms can be applied directly to a such problem, two issues arise: (i) sampling infeasible settings leads to slow convergence due to the time consumed to determine the feasibility of sampled settings, and (ii) re-samplings due to sampled out-of-range settings lead to divergent values. The optimisation results by a classic PSO [13], a differential evolution (DE) [27], and a covariance matrix adaptation evolution strategy (CMA-ES) [11] shown in Figs. 6 and 7 and Table 8 illustrate examples of the above two issues. Therefore, particular operations should be taken for tackling the above issue.

Table 8 Optimised aero-engine parameter settings by single-objective evolutionary algorithms
Full size table

The classic PSO and DE are implemented by us. The PSO uses \(\lambda = 90\), \(\omega =0.5\), and \(C_1=C_2=0.5\), and the DE uses \(\lambda = 90\), \(C_r=0.3\) and \(F=1\). The program of CMA-ES is taken from https://github.com/AlexanderFabisch/CMA-ESpp, and uses \(\mu =\lambda =13\), while the other parameters use the default setting. Each curve in Figs. 6 and 7 is an averaged result over 20 independent optimisation trials with 20,000 model simulations as budget.

Self-adaptive particle swarm optimisation (saPSO)

In the classic PSO, the location of particles (\(\varvec{x}\)) is updated by the following equations:

$$\begin{aligned} v_i= & {} \omega * v_{i} + C_1* r_1*(gbest - \mathbf{{x}}_{i}) \nonumber \\&+ C_2 *r_2* (pbest_{i}-\mathbf{{x}}_{i}), \end{aligned}$$
(5)
$$\begin{aligned} \mathbf{{x}}_i= & {} \mathbf{{x}}_{i} + v_i, \end{aligned}$$
(6)

where \(\varvec{x}_i\) is the \(i^{th}\) individual, and \(r_1\) and \(r_2\) are two random vectors \(\in (0,1)^d\), where d is the dimension. Each coordinate of the velocity \(v_i\) is the sum of three items: inertia (\(\omega * v_{i}\)), the vector with random weight pointing to the global best location of all particles found during optimisation (\(C_1 * r_1 * (gbest - \mathbf{{x}}_{i})\)) and the vector with random weight pointing to the best location of this particle found during optimisation (\(C_2 * r_2 * (pbest_{i}- \mathbf{{x}}_{i})\)).

Fig. 6
figure 6

Averaged RMSE over 20 independent trials with respect to the simulation number of the computational model (left) and time (right)

Full size image
Fig. 7
figure 7

Averaged minmax error over 20 independent trials with respect to the simulation number of the computational model (left) and time (right)

Full size image

To avoid the change of sampling distribution, the way to handle the out-of-range or infeasible solutions is re-sampling. However, when a particle is close to the boundary of feasible area in solution space and the inertia (\(\omega *v_{i}\)) points out to the boundary, the updated location (\(\mathbf{{x}}_i\)) is likely to be infeasible. Larger the inertia is, lower the possibility of sampling a feasible solution is. As a consequence, more computational resource will be consumed by re-sampling. In PSO, the waste of resource on re-sampling leads to a significant reduction of final solution’s quality given limited optimisation budget.

We propose a self-adaptive PSO (saPSO) to handle this situation. In saPSO, for each re-sampling, \(\omega \) is assigned as \(\omega ^2\). As \(\omega \in (0,1)\), the inertia is attractively reduced during re-sampling. Therefore, the possibility that the generated location is feasible is increasing. Algorithm 3 describes the process of our saPSO. The saPSO with the same parameters as PSO and \(\omega =0.9\) is performed on the engine calibration using the fitness defined in Eq. (4). Experimental results are shown in Figs. 6 and 7, as well as Table 8. It is observed that the saPSO converges as fast as CMA-ES, but does not lead to solution value far from the optimum on the \(18^{th}\) coordinate as the CMA-ES, PSO, and DE do. The extremely poor values found by CMA-ES, PSO, and DE on the 18th coordinate can be explained by the sampled out-of-range or infeasible parameter settings. When an out-of-range parameter setting is sampled, CMA-ES, PSO, and DE will re-sample a setting uniformly at random within the ranges given in Table 1. Although the particular design of saPSO successfully reduces the probability of sampling out-of-range or infeasible parameter settings, its final recommended parameter setting is not as good as the ones recommended by fSDE given the same amount of model simulations (cf. Fig. 8).

figure c
Fig. 8
figure 8

Comparison among saPSO, CMA-ES, and fSDE. Figures on the bottom are the cropped version of the ones on top for better visualising the difference

Full size image

Discussion

Modelling the aero-engine calibration process as a single-objective optimisation problem is straightforward. However, due to the characteristics of our real-world calibration problem, the single-objective evolutionary algorithms are not efficient due to the sampling of out-of-range or infeasible parameter settings. Although we have proposed a simple self-adaptive PSO particularly to tackle this issue and obtained better performance comparing to some classic single-objective evolutionary algorithms, the efficiency of the self-adaptive PSO is still lower than the fSDE (cf. Fig. 8). This observation can be explained by the mechanics of fSDE. The crossover and mutation operators of fSDE will not lead to out-of-range samples.

Conclusion

In this paper, we consider a real aero-engine calibration problem with 27 parameters to be calibrated, 15 measurements at each operation point as quality criteria, and their values at 33 operation points as calibration data. The calibration process is modelled as a black-box optimisation problem aiming at minimising the distance between the simulated measurement values using a computational engine model and their calibration data. Both many- and single-objective evolutionary algorithms have been applied to calibrate the parameters. A fast many-objective evolutionary optimisation algorithm with shift-based density estimation, called fSDE, and a novel single-objective evolutionary algorithm, called saPSO, have been proposed and compared to several classic and state-of-the-art algorithms. The performance of fSDE has been assessed in terms of objective values, recommended decisions, and efficiency. Without parallelising the calculation or evaluation of population, the proposed fSDE consumes ten times less time to find diverse parameter settings of high quality, compared to the time needed to find one single setting by an experienced human engineer using the traditional manual calibration process. fSDE not only provides diverse solutions but also finds solutions of high-quality faster, compared to some state-of-the-arts, thank to its simple operations.

Besides problem solving, our work also contributes in various ways. When finding different engine parameter settings with similar performance, human engineers may be assisted to diagnose the computational engine model and the measurements, and inspired to discover novel engine models. As a future work, we are interested in training a predictor to determine the feasibility of a sampled parameter setting to further reduce the required number of model simulations and improve the optimisation efficiency.