Hybridization of ring theory-based evolutionary algorithm and particle swarm optimization to solve class imbalance problem

Abstract

Many real-life datasets are imbalanced in nature, which implies that the number of samples present in one class (minority class) is exceptionally less compared to the number of samples found in the other class (majority class). Hence, if we directly fit these datasets to a standard classifier for training, then it often overlooks the minority class samples while estimating class separating hyperplane(s) and as a result of that it missclassifies the minority class samples. To solve this problem, over the years, many researchers have followed different approaches. However the selection of the true representative samples from the majority class is still considered as an open research problem. A better solution for this problem would be helpful in many applications like fraud detection, disease prediction and text classification. Also, the recent studies show that it needs not only analyzing disproportion between classes, but also other difficulties rooted in the nature of different data and thereby it needs more flexible, self-adaptable, computationally efficient and real-time method for selection of majority class samples without loosing much of important data from it. Keeping this fact in mind, we have proposed a hybrid model constituting Particle Swarm Optimization (PSO), a popular swarm intelligence-based meta-heuristic algorithm, and Ring Theory (RT)-based Evolutionary Algorithm (RTEA), a recently proposed physics-based meta-heuristic algorithm. We have named the algorithm as RT-based PSO or in short RTPSO. RTPSO can select the most representative samples from the majority class as it takes advantage of the efficient exploration and the exploitation phases of its parent algorithms for strengthening the search process. We have used AdaBoost classifier to observe the final classification results of our model. The effectiveness of our proposed method has been evaluated on 15 standard real-life datasets having low to extreme imbalance ratio. The performance of the RTPSO has been compared with PSO, RTEA and other standard undersampling methods. The obtained results demonstrate the superiority of RTPSO over state-of-the-art class imbalance problem-solvers considered here for comparison. The source code of this work is available in https://github.com/Sayansurya/RTPSO_Class_imbalance.

Introduction

In classical machine learning, the direct application of standard classifiers is logical only when the number of samples found in each class of the considered classification problem is balanced which is an ideal case. But in some real-life datasets like disease prediction datasets the number of samples in each class is often unequal i.e., the problem of class imbalance is present therein. Standard classifiers are not enough to predict the results precisely on these datasets. Imbalance class means there is a disproportionate ratio of observations in each class. Training the classifiers directly on such datasets may affect the model performance [69]. In many cases, the imbalanced ratio is so extreme that the standard classifiers in use are often become biased towards the majority class (sometimes called as “negative” class) and overlook the minority class (sometimes called as “positive” class) examples during training for estimating class separating hyperplane(s) and as a result, these classifiers tend to predict samples of majority class as minority class.

This class imbalance problem is very common in many applications like medical diagnosis or monitoring, detection of oil spills in satellite radar images, fraud detection [33], text classification [41], information retrieval and filtering [16, 36], twitter spam detection [42], detection of adverse drug reaction [53], 5G future network [2] and many more. In this scenario, standard classifiers become almost biased towards the majority class (class having more samples) instances and try to predict them correctly, whereas treating the samples from minority class as noise or sometimes ignore them [27]. As a result, the minority class samples are often misclassified as the members of the majority class. To be specific, here the challenge is how precisely these minority class samples can be predicted, also to preserve the accuracy in the prediction of the majority class samples.

Throughout the years, many researchers have used different approaches to deal with the class imbalance problem. Two categories of techniques are mainly followed to cope up with the class imbalanced datasets that are cost sensitive techniques and sampling techniques [65]. A cost sensitive technique is a sub-field of machine learning and it is used to minimize the cost of training by taking the costs of prediction errors and potentially other costs into account. These techniques can be divided into three groups: data resampling, algorithm modification, and ensemble method. A cost-sensitive technique does not improve the data distribution [13]. Rather the goal of the cost sensitive learning is to minimize the cost of a model on a training dataset. The other category of techniques i.e., sampling techniques encompass two different methods: oversampling and undersampling. In oversampling, the minority class instances are increased by adding more synthesized training data to balance the ratio of the two classes. It can be random oversampling or synthetic minority oversampling technique (SMOTE) [14]. But SMOTE is not beneficial for high-dimensional data [9]. In undersampling techniques, the majority class instances are merged or removed to make a good balance between the number of samples of the two classes. Some of the undersampling techniques are random undersampling (RU) [47], edited nearest neighbors (ENN) rule [70], nearmiss undersampling (NMU) [7], Condensed nearest neighbors (CNN) [55] etc. However, the limitation of using only one of these undersampling methods is that it may not be able to select the most important data samples from the majority class and thereby it might remove some of the crucial and important data from the majority class samples.

Moreover, the above techniques are largely data-dependent and may fail if the same algorithm is applied to other datasets. Hence, a more flexible and self-adaptable algorithm that considers the essence of the majority class data in the underlying classification problem prior to removal is required [65]. To fulfill the requirement, in the recent past, some researchers have applied different optimization algorithms because optimization algorithms are more self-adaptable and can upgrade their fitness value in each iteration. The mostly used optimization algorithms for this problem are Genetic Algorithm (GA) [37], Particle Swarm Optimization (PSO) [39], Ant Colony Optimization [22] [66] etc.

Considering the success of these methods over the traditional ones, we have proposed a hybrid method, termed RTPSO, where two meta-heuristic algorithms Ring Theory (RT)-based Evolutionary Algorithm (RTEA) [34] and PSO are used. RTEA has been used for feature selection (FS) by Ahmed et al. [1] with Harmony Search (HS) algorithm [30] and produced promising results, which has inspired us to apply it with PSO for solving the problem in hand. From the best of our knowledge, the proposed method is completely original and it has been used for the first time to solve said problem. We have used Area Under Curve (AUC) of the ROC (ROC-AUC) score, precision-recall (PR) of AUC (PR-AUC) and F1 score of the AdaBoost classifier [35] for evaluation of our proposed model because typical recognition accuracy score does not reflect the misclassification rate of the minority class samples. The proposed RTPSO algorithm has been experimented on 15 standard and publicly available class imbalance datasets. We have also compared our method with some classic as well as recently proposed methods related to the class imbalance problem.

The entire process of our work is organized as follows: we have discussed some past works in this domain in section “Literature survey” and we have discussed some preliminary techniques used for this research work in section “Preliminaries”. In section “Proposed method” the proposed method has been described in detail. We have discussed the datasets and analysed the experimental results elaborately in section “Experimental results and discussion”. In section “Experimental results and discussion” we have also compared performance of our method with other state-of-the-art methods and in section “conclusion” we have concluded our work.

Literature survey

Over the years many researchers have developed different methods to deal with this class imbalance problem. In this section, we have discussed some popular algorithms that have been used to solve the class imbalance problem.

Chawla et al. [14] introduced the combination of undersampling on majority class samples and oversampling on minority class samples. They oversampled the minority class samples by creating “synthetic” examples. The authors claimed to get a better classification performance on receiver operating characteristic (ROC) curve than normal undersampling technique on Pima Indian diabetes, Phoneme datasets etc. Selecting the nearest neighbors with a focus on examples improved the misclassification rate. But, this approach was not able to handle datasets with all nominal features. Yang et al. [65] proposed a method using PSO with multiple classifiers and evaluation metrics. They experimented on class imbalanced datasets like breast cancer, diabetes etc. But the method did not consider highly imbalanced datasets, hence the performance of the proposed method on such datasets can not be ensured. Liu et al. [43] used RU on SEER breast cancer datasets to balance it. They used the Bagging algorithm to construct an integration of the decision tree model. However, the use of only RU in data preprocessing stage might not be enough because the samples which were removed from the majority class might hold important data, and as a result, the model might fail to produce correct results on the unknown samples.

Anand et al. [3] used the undersampling technique on highly imbalanced datasets with support vector machine (SVM) as classifier to improve the sensitivity. The authors selected the “boundary samples” from the majority classes i.e., the samples of two classes lying close to each other. They used their proposed method on four datasets: micropred, xwchen, active-site and cysteine. In another work, Thomas [57] proposed prototype generation using K-means clustering algorithm and claimed that it can be used in high dimensional datasets also. But, if the variances of the clusters are not so different, the proposed method’s performance is quite similar to normal K-means approach and the border region development could be more improved. Gao et al. [28] proposed a method in their paper, where a combination of SMOTE and PSO with radial basis function (RBF) classifier used on Pima Indian diabetes, ADI and Haberman survival datasets. In this work, the authors had considered only a few datasets to evaluate their proposed method and hence the method may be dataset dependant. Cao et al. [12] proposed a wrapper approach along with cost-sensitive neural network model, where the optimization was based on the PSO. They claimed that the experimental results on datasets like hepatitis, abalone and segment are effective than normal sampling methods. Samma et al. [52] introduced a model using PSO and Fuzzy SVM (FSVM), named as PSO-FSVM model for tackling the class imbalance problem. The experiment was performed only on MIAS mammogram dataset which indicates that the algorithm might be dataset dependant.

Prusa et al. [47] used RU method and claimed to have a significant improvement in classification performance. Zhu et al. [70] implemented ENN undersampling method and adaptive synthetic oversampling approach to solve the class imbalance problem and they also used the two-step FS technique to optimize the feature set. The technique mentioned by Bunkhumpornpat and Sinapiromsaran [11], used the density-based majority undersampling technique (DBMUTE) that has the ability to adapt directly density reachable graph. They showed improved results on UCI health monitoring datasets: Haberman’s survival and diabetes.

Bao et al. [7] proposed a new method called: Boosted Near-miss Under-sampling on SVM ensembles (BNU-SVMs) and they also used a kernel-distance pre-computation technique to improve the model performance in high dimensional features. Shekarforoush et al. [55] performed a case study in the resampling techniques like CNN, Cluster Centroids (CC) and SMOTE. Vu et al. [60] introduced an application of the deep learning-based approach, called Auxiliary Classifier Generative Adversarial Network, to address the class imbalance problem by generating synthesized data samples in network traffic data classification. But, in general, deep learning models need a huge amount of data to get trained properly which may not be available for many real-world datasets. To handle the class imbalance problem, Rayhan et al. [48] introduced a new clustering-based undersampling approach with boosting (AdaBoost) algorithm i.e., CUSBoost. The authors claimed that CUSBoost algorithm is capable to handle highly imbalanced datasets effectively. They evaluated the proposed method on 13 imbalance datasets.

In the paper, Aydogan et al. [5] reported a new cost-sensitive classification method (CBR-PSO) using PSO and rough set theory. The algorithm tested on datasets like a brain tumour, leukaemia and lung cancer. The proposed method could be combined with other multi-objective heuristic algorithms or extended with rule pruning approaches to produce a better result. Zhang and Chen [68] proposed a method by incorporating random oversampling, K-means and SVM, dubbed as RK-SVM model. The authors worked on the imbalanced WDBC, Pima and Iris datasets. But this approach is computationally expensive and the algorithm is not tested on highly imbalanced datasets.

In the recent past, many researchers used evolutionary algorithms to improve prediction accuracy. Yu et al. [67] worked with accelerating evolutionary computation, Cheng et al. [17] introduced various model-based evolutionary algorithms (MBEAs) and He et al. [34] proposed evolutionary multi-objective optimization and used it on real-world applications. Gautheron et al. [29] introduced Mahalanobis metric learning (IML) algorithm. The authors have used the datasets like Pima, Balance, Splice and Heart to evaluate their model’s performance. The proposed algorithm could be adapted to learn non-linear metrics. Unal et al. [59] created diversity in using Multi-Objective PSO (MOPSO) by using random immigrants approach. The application of the proposed solution is tested in four different sets using Generational Distance, Spacing, Error Ratio, and Run Time performance measures. Wang et al. worked with Multiple-Strategy Learning PSO (MSL-PSO) algorithm [61] to solve the problem efficiently with large scale variables.

Li et al. [40] proposed adaptive cost-sensitive learning, by developing the model on a sparse cost matrix with a diagonal form. They also used evolutionary extreme learning machine with multi-objective function to optimize the solution. They experimented with their method on real-world datasets like yeast, hayes-roth, ecoli and page blocks. In another work, Wang et al. [62] used a sampling approach for an imbalanced dataset via self-placed learning (ISPL). ISPL is so designed that it can select high-quality samples from the majority class to balance between majority and minority classes. They executed the proposed method on four publicly available breast cancer datasets. But the imbalance ratio was low in all the cases. Therefore, the proposed method did not guarantee to work the same on highly imbalanced datasets. Ghosh et al. [31] proposed a meta-heuristic algorithm, namely adaptive $\beta$-hill climbing (A$\beta$HC) with BSF optimizer (A$\beta$BSF) in solving FS problem. Ahmed et al. [1] also introduced a new hybrid meta-heuristic FS model based on a well-known meta-heuristic HS algorithm and a recently proposed RT-based Evolutionary Algorithm (RTEA), which was named as RT-based HS (RTHS). Both the methods achieved decent results in the FS domain. Therefore, we have implemented these two algorithms on class imbalance problem and have compared them with our proposed method.

From the above discussion, it can be observed that if we can apply a generalized and self-adaptable method in the data preprocessing stage before classifying data in the imbalanced datasets, the classification result would be much better. With this line of thought, we have proposed a hybrid optimization method, called RTPSO, to balance the imbalanced dataset more intelligently, and evaluated our model performance by AdaBoost classifier. Highlights of this work are as follows:

• 1. Well-known swarm intelligence based optimization algorithm PSO is hybridized with RTEA, a recently proposed optimization algorithm, to solve the class imbalance problem for the first time to the best of our knowledge.

• 2. The proposed method, called RTPSO, has been assessed in terms of ROC-AUC, PR-AUC or F1 score using AdaBoost classifier and evaluated on 15 standard and publicly available datasets where imbalance ratio varies from moderate to extremely high.

• 3. The performance of the proposed method has been compared with some conventional as well as recently published methods.

Preliminaries

Particle swarm optimization

PSO, proposed by Kennedy and Eberhart [39], is a swarm intelligence-based meta-heuristic algorithm that can solve complex optimization problems. It is inspired by the social behavior of a flock of birds, school of fishes etc. [18]. PSO algorithm uses a bunch of particles that are called swarm. Each particle, denoted by a point in a D dimensional space, is initialized with random velocity, which can move around and explore the search space. Here, D represents the dimension of the search space. In every iteration, each particle keeps track of their individual best fitness value and the best fitness value acquired by the whole population. By simultaneous updating of the best position (position with the best fitness value), it moves towards the global optimum position [6].

This algorithm also encompasses some tuning parameters that make a great impact on the performance of this algorithm, often expressed as exploration-exploitation trade-off [58]. Exploration implies of probing various regions in the search space with the hope of finding a better solution, maybe the global one. Exploitation means searching only on promising candidates to find the local optimum solution accurately. The mathematical illustration of the PSO algorithm is as follows.

Let, $X_i$ is the $i^{th}$ particle in the D dimensional space S and it is denoted as below.

$$\begin{aligned} X_i = (X_{i_1} X_{i_2} X_{i_3} X_{i_4} \ldots X_{i_D}) \end{aligned}$$

(1)

Let, there are N particles in S. Now, the whole population can be presented as:

$$\begin{aligned} X = \{X_1, X_2, X_3, X_4,\ldots , X_N\} \end{aligned}$$

(2)

The velocity ($v_i$) and position ($X_i$) of $i^{th}$ particle at time $k+1$ are estimated using Eqs. 3 and 4 respectively [25].

$$\begin{aligned} v^{k+1}_i= & {} wv^k_i + c_1r_1(P^k_i - X^k_i) + c_2r_2(P^k_g - X^k_i) \end{aligned}$$

(3)

$$\begin{aligned} X^{k+1}_i= & {} X^k_i + v^{k+1}_i \end{aligned}$$

(4)

In Eq. 3, $w \in [0.8, 1.4]$ is called as inertia factor that decides the contribution rate of the velocity of the particle from previous to current time [23]. $v^k_i$ represents the velocity of the $i^{th}$ particle at time k. $c_1\in [1.5, 2]$ and $c_2\in [2, 2.5]$ are the cognitive coefficient and social coefficient respectively. $P^k_i$ and $P^k_g$ represent the personal and global best solution at time k respectively. $r_1$ and $r_2$ are two diagonal matrices of dimension D with uniform random numbers between 0 and 1. In Eq. 4, $X^k_i$ represents the position of the $i^{th}$ particle at time k.

Inertia weight (i.e., w) plays an important role while PSO searches for the global best solution. With the larger value of w, the searching ability of PSO is improved while considering the whole search space. On the contrary, the searching ability of it is improved with a smaller value of w while considering partial space. According to the work mentioned in [6], this algorithm can quickly converge to the near optimal solution from a bigger search space when the value of w decreases linearly from 0.9 to 0.4. Altogether the iteration of the process is controlled by Eqs. 3 and 4 and continues until it reaches either the predefined fitness value (i.e., global optimum) or exceeds the maximum number of iterations [46].

Ring theory-based evolutionary algorithm

RTEA, proposed by He et al. [34], is a physics-based meta-heuristic algorithm. It is inspired by the RT in mathematics. It is based on the algebraic theory and is mainly used in the combinatorial optimization problem. Two evolution parameters global exploration operator (R-GEO) and local development operator (R-LDO) are used for generating a new population following a greedy strategy.

Ring

Definition: A nonempty set R (i.e., $R\ne \emptyset$) equipped with two binary operations, addition (+) and multiplication (.), is called a ring (mathematically represented as (R, +, .)) if it follows the ring axioms [26] [50] defined below.

Ring axioms:

• $\forall c,d \in R, c + d = d + c$

• $\forall c,d,e \in R, (c + d) + e = c + (d + e)$

• $\exists 0 \in R$ such that $\forall c \in R, c + 0 = 0 + c = c$, here this 0 is called additive identity.

• $\forall c \in R, \exists d \in R$ such that $c + d = d + c = 0$, here this d is called additive inverse of c, can be written as $-c$.

• $\exists 1 \in R$ such that $\forall c \in R, c . 1 = 1 . c = c$, here 1 is called multiplicative identity

• $\forall c,d,e \in R, (c . d) . e = c . (d . e)$

• $\forall c,d,e \in R, c . (d + e) = c.d + c.e; (d + e).c = d.c + e.c$

Let, $W_q = \{[0],[1],\ldots .,[q-1]\}$ be a collection of remainder classes of modulo q, where [f]= $\{ u \in W | u\cong f(mod$ $q)\}$, where $0\leqslant u \leqslant q-1$, $q > 1$, and W is the set of integers. Here additive and multiplicative, two binary operations can be defined as following:

[i] $\oplus$ [j] = [$(i + j)mod$ q], [i] $\odot$ [j] = [(ij)mod q], $\forall i,j \in W_q$

Now, we can easily show that $W_q$ along with the binary operations $\oplus$ and $\odot$ satisfies all the ring axioms and hence we can say ($W_q$, $\oplus$, $\odot$) is a ring.

Direct product of rings

The direct product of rings can be used as a method to construct a new ring with the help of two or more rings. It is a special type of ring, where every element is an ordered m-tuple (i.e., m number of rings are used to generate new ring). If $R_j$ ($j \in \tau = \{1, 2, 3, \ldots , q\}$ and $q\ge 2$) are rings, then $\prod _{j \in \tau }R_j = R_1 \times R_2 \times \cdots \times R_q$ is a ring consists of two binary operations ($\odot$ and $\oplus$) that can be defined by $\langle c_1, c_2, \ldots , c_q \rangle \odot \langle d_1, d_2, \ldots , d_q \rangle = \langle c_1d_1, c_2d_2, \ldots , c_qd_q \rangle$ and $\langle c_1, c_2, \ldots , c_q \rangle \oplus \langle d_1, d_2, \ldots , d_q \rangle = \langle c_1+d_1, c_2+d_2, \ldots , c_q+d_q \rangle$. Here $\prod _{j \in \tau }$ is the direct product of $R_j, j\in \tau$ [1].

Overview of RTEA

There exists a bijection $V: \prod _{j=1}^q {\mathbb {A}}_{s_j} \longrightarrow {\mathbb {A}} [s_1, s_2, \ldots , s_q]$. So ${\mathbb {A}}[s_1, s_2, \ldots , s_q] = \{0, 1, \ldots , s_1-1\} \times \{0, 1, \ldots , s_2-1\} \times \cdots \times \{0, 1, \ldots , s_q-1\}$. Then RTEA has been proposed after drawing supports from addition, multiplication and inverse operations on $\prod _{j=1}^q$.

Let us have four randomly selected q-dimensional integer vectors: $L_1, L_2, L_3$ and $L_4$ from ${\mathbb {A}}[s_1, s_2, \ldots , s_q]$, where $L_1 = \langle l_{11}, l_{12}, \ldots , l_{1q} \rangle , L_2= \langle l_{21}, l_{22}, \ldots , l_{2q} \rangle , L_3 = \langle l_{31}, l_{32} ,\ldots , l_{3q} \rangle , L_4= \langle l_{41}, l_{42}, \ldots , l_{4q} \rangle$. These four vectors can be used to create a new q- dimensional integer vector $L = \langle l_1, l_2, \ldots , l_q \rangle \in {\mathbb {A}}[s_1, s_2, \ldots , s_q]$ using Eq. 5

$$\begin{aligned} L_j = {\left\{ \begin{array}{ll} \{L_{1j} + L_{4j} \times [L_{2j} + (s_j - L_{3j})]\}(mod \quad s_j ) &{} \\ \text {if } rndm(k) \leqslant 0.5; &{} \\ \{L_{1j} + [L_{2j} + (s_j - L_{3j})]\}(mod \quad s_j) \text { else }\\ \end{array}\right. } \end{aligned}$$

(5)

In Eq. 5, the procedure that generates a new q-dimensional integer vector, which has the ability of global learning, is called R-GEO. But the local exploration ability is also required with the global exploration to maintain the balance between local and global search abilities of the algorithm [4]. The new operator used to implement local search is called R-LDO in Algorithm 1.

Proposed method

Proposed model and solution representation

As the optimization algorithms have been proving their capabilities to solve problems efficiently of different domains for a long time, researchers are trying to come up with some new ideas to contribute more to the field of optimization. Because of such huge interest of the researchers, several new optimization algorithms have been proposed in the past decade. It may seem like there is no need for any such algorithm anymore. But, as per No Free Lunch (NFL) theorem [64], there is no such algorithm that is capable enough to solve every type of optimization problem efficiently. This conclusion of NFL theorem keeps the research area as active as earlier, and also keeps us motivated to come up with a new idea to solve a specific optimization problem, we have considered here i.e., class imbalance problem. In the present work, we have hybridized one of the most popular meta-heuristic algorithms PSO with a recently proposed meta-heuristic RTEA. Applicability of these two algorithms have already been shown in various optimization related problems.

The main reason for proposing a hybridization of two algorithms that work well in isolation is to fix some issues such as premature convergence and stagnation at local optima. Meta-heuristic algorithms suffer mainly from these two problems. Whereas, hybrid algorithms try to converge the solution and find the global optima with the help of exploration and exploitation operators of both the algorithms. Since the hybrid algorithm can be viewed as a union of the underlying algorithms so we expect it to perform better. In PSO algorithm, the particles update their position based on the past best positions and present the global best candidate in the solution. This strategy is used to explore as well as exploit the search space properly. RTEA uses the R-GEO operator for exploration and R-LDO operator for exploitation. However, the core searching strategies of PSO and RTEA may not be efficient. Here, the RTPSO is superior as it takes advantage of the exploration and the exploitation phases of its parent algorithms for strengthening the search process. Not only does it come up with strong exploration and exploitation phases, but also successfully balances these two important phases. Since RTEA updates the solution using four randomly chosen solutions so it may mislead the search process without exploiting the neighbour. On the contrary, PSO has extensive exploitation capabilities but lacks of proper exploration ability and hence may lead to immature convergence. The union of these two helps us to overcome the disadvantages of the individual algorithms.

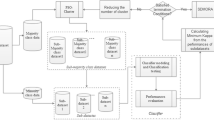
Normally, there are two ways of hybridizing meta-heuristic algorithms: high-level approach and low-level approach [56]. In the high-level approach, we use the output of one algorithm as the input to the other to form a pipeline model. In this approach, methods are executed one after another until the termination condition is reached. The low-level style addresses the functional configuration of a single optimization algorithm. In this approach, one meta-heuristic is embedded into the other in such a way that a function in a meta-heuristic is replaced by another meta-heuristic. The proposed RTPSO follows the high-level approach of hybridization between PSO and RTEA. RTPSO is created in the anticipation of finding better solutions and a better convergence rate than PSO and RTEA. The flowchart of the proposed method is depicted in Fig. 1.

Fig. 1

Flowchart of the proposed RTPSO used for solving class imbalance problem

Working procedure

Initially, we divide our datasets into train and test sets. Then, we further divide the train set into temporary train and validation sets. The test set is utilized at the end to evaluate the model performance. First, the samples belonging to the majority class and minority class in the train set are identified and then from the samples of these majority class, we try to find out the samples (same in the number of minority class samples) which can represent the characteristics of whole majority class samples in the best way possible. In this context, we would like to mention that we have kept minority class samples intact. To guide this process, we take the help of the validation set for evaluating performance in each iteration of RTPSO. In short, in each iteration, we train the classifier on the selected train set and evaluate the performance of the learned module on the validation set. This performance score is used to calculate the fitness value of RTPSO algorithm.

At the initial phase, randomly generated population represents potential solutions which are updated in every iteration using the operators of PSO and RTEA. These solutions represent the combination of some samples that belong to the majority class of the train set.

To check the quality of a solution we take the help of ROC-AUC, PR-AUC score or F1 score. To calculate the fitness value in each iteration of RTPSO we follow the following steps.

• Initially, selected majority class samples and existing minority class samples of train set are combined to form a temporary train dataset.

• Temporary train dataset is used to train AdaBoost classifier and then evaluated on samples of the validation set to calculate the ROC-AUC, PR-AUC and F1 score.

After finding the near optimal solution i.e., the best combination of majority class samples from the train set, we create the final dataset by combining the selected majority class samples and the existing minority class samples of the train set. Next, we train our model based on this dataset and evaluate it on the test set which we have created at the beginning.

Fitness function

Fitness function is the guide of any optimization algorithm. The goal of the fitness function is to find a test datum that fits a given test criterion [8]. A well-constructed fitness function can increase the chance of finding a better solution by less number of iterations. In our case, it governs the update of the personal best value and global best value in each iteration. From [10] we can observe that ROC-AUC score exhibits some preferable properties than the typical accuracy score. It gives the correct indication of classification result as it is scale-invariant. ROC-AUC score is also decision threshold independent. F1 score is the weighted average of precision and recall. It takes both false positive and false negative into account for evaluation. For these aforementioned reasons, we have used both the AUC scores and F1 score as fitness function alternatively. We have used each metric individually as fitness function.

ROC-AUC score: ROC-AUC is the measurement of the model’s classification performance. It indicates to which extent the model can classify the positive and negative classes accurately, thus it ranks them correctly [49]. ROC-AUC curve is given by Eq. 6:

$$\begin{aligned} ROC-AUC = \frac{1 + TP_{rate} - FP_{rate}}{2} \end{aligned}$$

(6)

where, $TP_{rate}$ represents the true positive rate and $FP_{rate}$ is the false positive rate. Equation 7 depicts the fitness function which uses ROC-AUC score:

$$\begin{aligned} fitness_1 = ROC-AUC Score(particle) \end{aligned}$$

(7)

F1 score: Harmonic mean of precision and recall. It can be defined by:

$$\begin{aligned} F1\,score = \frac{2 \times recall \times precision}{recall + precision} \end{aligned}$$

(8)

In Eq. 8precision = $\frac{TP}{TP + FP}$ and recall = $\frac{TP}{TP + FN}$ where TP, FP and FN represent true positive, false positive and false negatives respectively [32, 45]. Equation 9 represents the fitness function which uses F1 score as fitness measurement:

$$\begin{aligned} fitness_2 = F1 Score(particle) \end{aligned}$$

(9)

However, when dealing with highly skewed datasets, PR curves give a more informative picture of an algorithmś performance. So, we have also calculated the PR-AUC score to evaluate the performance of the proposed method more precisely.

PR-AUC score: It is the score that combines precision and recall in single variable. The PR curve shows the trade-off between precision and recall for different threshold values [20, 51]. We can compute PR-AUC [38] by parameterizing the PR curve by Eq. 10.

$$\begin{aligned} PR-AUC = \int _{0}^{1} p(r)dr \end{aligned}$$

(10)

where p and r denote precision and recall respectively. ROC-AUC looks at true positive and false positive cases while PR-AUC looks at positive predictive value and true positive score. Equation 11 depicts the fitness function which uses PR-AUC score:

$$\begin{aligned} fitness_3 = PR-AUC Score(particle) \end{aligned}$$

(11)

Transfer function

Since class imbalance is a binary optimization problem [65] so to convert the continuous optimization to a binary variant, a transfer function is used. We use ’0’ and ’1’ for non-selection and selection of a sample to prepare the final training dataset. To perform this action, the sigmoid function has been used in the present work. A sigmoid curve is an S-shaped curve (see Fig. 2) whose output range $\in$ [0, 1]. This transfer function is defined as:

$$\begin{aligned} T(x) = \frac{1}{1+e^-x} \end{aligned}$$

(12)

Now, based on the output of the sigmoid function, we update the positions of the particle as:

$$\begin{aligned} X_{i,j} = {\left\{ \begin{array}{ll} 1 &{} \text {if } T(X_{ij}) > 0.5\\ 0 &{} \text {if } T(X_{ij}) \le 0.5 \end{array}\right. } \end{aligned}$$

(13)

where, $X_{ij}$ is the position of $i^{th}$ particle in $j^{th}$ dimension.

Fig. 2

Graphical representation of the sigmoid transfer function used in the present work

Experimental results and discussion

This section presents the results of the proposed method. A set of experiments are conducted to evaluate the performance of the proposed method. Firstly, we have shown the effect of different population sizes on the performance, and then convergence curves are plotted to show the process of converging towards the near optimal solution. Secondly, results of the RTPSO are compared with the parent optimization techniques i.e., PSO and RTEA. The results are compared based on ROC-AUC and PR-AUC as they represent the best decision boundary between values of true positive (TP) and false positive (FP) [48]. Finally, we have compared performances with the state-of-the-art techniques and made statistical test to justify the worth of our work.

Dataset description

We have considered 15 real-world class imbalance datasets to evaluate the performance of our proposed method. The datasets are taken from three different popularly used repositories namely, namely, UCI¹, Keel² and LIBSVM³. These datasets are selected from different domains like disease detection, predicting the cellular localization sites of proteins, and prediction of the age of abalone. We have included the datasets with low (e.g., like WDBC and heart datasets) to moderate (e.g., Hayes-roth and Page-blocks0 datasets) imbalance ratio as well as with very high imbalance ratio (e.g., Abalone19 and Yeast5 datasets) to establish the robustness of our model i.e., how well RTPSO behaves on the datasets having low to very high imbalance ratio. Hayes-roth, New-thyroid, SPECTF and Heart are small datasets having the number of samples 160, 215, 267 and 270 respectively. There are also some large datasets like Page-blocks0, Abalone, Abalone19 and Segment0 having the number of samples 5472, 4177, 4174 and 2308 respectively. Most of the datasets are used for binary classification problems. For simplicity, we have divided these datasets into two groups, one with imbalance ratio $\le$ 6 and the other with imbalance ratio > 6.

We have redefined the multi-class problems as binary class problems since class imbalance problem is mainly designed for binary classification problem [44]. For this, we have converted a certain combination of classes into minority class and the rest of the classes into the majority class following the similar convention as described in the work [29]. Related information of these two categories of datasets is provided in Tables 1 and 2.

For experimental need, we have initially divided each of the datasets into a training set and a test set having 80% and 20% of samples of the corresponding dataset respectively. The division is made by maintaining the original imbalance ratio in both sets. However, later during optimization of majority class samples using RTPSO, we have considered 20% of training samples as validation samples i.e., for calculating the fitness value of an optimization algorithm. Finally, the optimal sample set generated from RTPSO is used to train AdaBoost classifier and the model is evaluated on the test set samples.

The code is written in Python 3 and the graphs are plotted using matplotlib.

Table 1 Description of the datasets having imbalance ratio $\le$ 6 used to evaluate the proposed method

Table 2 Description of the datasets having imbalance ratio > 6 used to evaluate the proposed method. In all the datasets class 1 is taken as a minority class

Parameter tuning

In meta-heuristic, the parameters play an important role in determining the end result. So, it is very important to find the proper parameter values. Since with the increase of population size and iteration number, the computational time also increases so we have performed some experiments to test the effect of population sizes on the performance and the rate of convergence concerning the number of iterations. Experiments are also performed to find out the proper values of $c_1$, $c_2$ and $P_m$.

During the experiment, we have varied one parameter and kept others constant. The effect of different population sizes on the performance of the model is plotted in Fig. 3 using ROC-AUC vs population size graph. To show the convergence of solutions we have plotted graphs for fitness values vs iteration number that are shown in Fig. 4. We have varied the value of $c_1$ from 0 to 2 with step size 0.25. The obtained ROC-AUC scores are exhibited in Fig. 5. $c_2$ is also varied from 0 to 2 with a step size of 0.25. The findings of the experiments are shown in Fig. 6. The value of $P_m$ is varied from 0 to 0.9 with step a size of 0.1. The ROC-AUC values obtained are exhibited in Fig. 7.

The graphs in Fig. 3 confirm that RTPSO attains peak accuracy with a population size around 20 while the graphs in Fig. 4 depict that RTPSO converges around $50^{th}$ iteration in most of the cases. Based on this observation and keeping the computational time in mind, we have chosen population size as 20 and iteration number as 50 for further experiments. From Figs. 5 and  6 we can observe that $c_1 = 2$ and $c_2 = 2$ produce relatively better results. Similarly, from Fig. 7 we can conclude that $P_m = 0.2$ produces relatively better results than other values. So for further experiments, we have set $c_1 = 2$, $c_2 = 2$ and $P_m = 0.2$.

Fig. 3

Graphs for achieved ROC-AUC scores using different population size for 15 datasets using PSO, RTEA and RTPSO

Fig. 4

Graphs showing the convergence of the solutions over numbers of iterations for 15 datasets using PSO, RTEA and RTPSO

Table 3 Comparison of RTPSO with PSO and RTEA in terms of ROC-AUC score. Best result achieved for each dataset is highlighted in bold font

Table 4 Comparison of RTPSO with PSO and RTEA in terms of average and standard deviation of ROC-AUC score. Best result achieved for each dataset is highlighted in bold font

Table 5 Comparison of RTPSO with PSO and RTEA in terms of F1 score. Best result achieved for each dataset is highlighted in bold font

Table 6 Comparison of RTPSO with PSO and RTEA in terms of average and standard deviation of F1 score. Best result achieved for each dataset is highlighted in bold font

Table 7 Comparison of RTPSO with PSO and RTEA in terms of PR-AUC score. Best result achieved for each dataset is highlighted in bold font

Table 8 Comparison of RTPSO with PSO and RTEA in terms of average and standard deviation of PR-AUC score. Best result achieved for each dataset is highlighted in bold font

Analysis of results

This section reports the results obtained by the proposed RTPSO algorithm on the datasets mentioned in Tables 1 and 2. We run PSO, RTEA and RTPSO algorithms for 15 times on the present datasets and recorded the performance scores. Table 3 reveals the results of the RTPSO algorithm and comparison with the original PSO and RTEA algorithms in terms of ROC-AUC score. From Table 3, we can clearly observe that the RTPSO achieves the best ROC-AUC score for most of the datasets. For example, on SPECTF dataset using RTPSO, the best result has been obtained i.e., 0.8974 which is better than the original (0.8351), PSO (0.8731) and RTEA (0.8583) results. On Hayes-roth and New-thyroid, all the methods have obtained 1 as ROC-AUC score. The proposed method is also performing well for Abalone dataset compared to the rests. On Segment0 dataset, only RTPSO has achieved 1 as ROC-AUC score. We have achieved 0.9917 score using PSO, 0.9957 by RTEA and 0.9987 by RTPSO while evaluating on WDBC dataset. Our proposed RTPSO technique has acquired 0.9451 as ROC-AUC score in the Heart dataset. Abalone19 is the most imbalanced dataset with an imbalance ratio 129.44 and on that also our proposed method obtains 0.9295 as ROC-AUC score, and outperforms the other methods. The result of Poker-9_vs_7 dataset is 1 by RTPSO while 0.8404 by original, 0.9574 by PSO and 0.9308 by RTEA. For Kddcup-guess_passwd_vs_satan dataset, RTPSO and PSO have obtained 1 as ROC-AUC score. In case of Page-blocks0, we have obtained 0.9954 as ROC-AUC score using RTPSO, 0.9850 by original, 0.9895 by PSO and 0.9927 by RTEA.

Table 9 p-values produced by the ANOVA test considering ROC-AUC, F1 score and PR-AUC score using RTPSO, PSO and RTEA

Table 10 Comparison of RTPSO with the state-of-the-art class imbalance problem-solving methods on the datasets having imbalance ratio $\le 6$. The comparison is made based on F1 score. Best result achieved for each dataset is highlighted in bold font

Table 11 Comparison of RTPSO with state-of-the-art class imbalance problem-solving methods on the datasets having imbalance ratio > 6. The comparison is made based on ROC-AUC score. Best result achieved for each dataset is highlighted in bold font

Table 12 p-values produced by the ANOVA test for the F1 scores achieved by the RTPSO algorithm, PSO algorithm and RTEA as compared with 9 other state-of-the art methods considered here

Table 13 p-values produced by the ANOVA test for the ROC-AUC scores achieved by the RTPSO algorithm, PSO algorithm and RTEA with 9 other state-of-the art methods considered here

The proposed method has obtained 1 as ROC-AUC score for 5 datasets (33.33% of all datasets): Hayes-roth, New-thyroid, Kddc-up-guess_passwd_vs_satan and Poker-9_vs_7. However, in case of BUPA, Abalone9-18 and Led7digit-0-2-4-5-6-7-8-9_vs_1, RTPSO can not outperform PSO and RTEA in terms of ROC-AUC score. Out of 15 datasets, RTPSO achieves the highest score for 12 datasets (80% of all the datasets). Also, for 12 datasets (80%) the proposed method has acquired greater than 0.9 ROC-AUC score. We have also shown the comparisons of RTPSO with PSO and RTEA in terms of average and standard deviation (SD) of ROC-AUC score in the Table 4. From the table, we can clearly observe that RTPSO is achieving the best results most of the time. Similarly, Tables 5 and 6 represent the comparisons of results in terms of F1 score. From Table 5 RTPSO has acquired 1 as F1 score in Hayes-roth, Kddcup-guess_passwd_vs_satan and Poker-9_vs_7 datasets. We have also achieved the best F1 score in most of the datasets. In Table 6 also the proposed technique is executing well in terms of average and SD.

From the Table 7 we can observe that, the proposed method is performing really well in terms of PR-AUC score as compared to PSO and RTEA. RTPSO has acquired 1 as PR-AUC score in Hayes-roth, Kddcup-guess_passwd_vs_satan datasets. RTPSO has achieved the highest PR-AUC score except for New-thyroid, BUPA, Yeast5 and Page-blocks0 datasets. We have also compared the results of RTPSO with PSO and RTEA in terms of average and standard deviation of PR-AUC score in Table 8. Here also the proposed method is achieving the best results in most of the cases. Although, in general, it is quite difficult for any particular algorithm to handle the datasets with low to extremely high imbalance ratio, but the results in Tables 3, 5 and 7 confirm that the current RTPSO performs really well for all these said datasets. Hence we can safely comment that RTPSO is more effective than the individual algorithms (i.e., PSO and RETA) to solve the class imbalance problem.

Factorial analysis of variance (ANOVA) test [19] is performed as statistical test to ensure that the obtained results are statistically significant. The null hypothesis is that the two sets of results have same group means. A factorial ANOVA works with more than one independent variable [21, 24]. It has two or more independent variables that split the samples in four or more groups. The simplest case of a factorial ANOVA uses two binary variables as independent variables, thus creating four groups within the samples. If the obtained p-values are < 0.05, then we can conclude that there are significant differences among the treatments at 5% significance level. Now, from Table 9, we can see that the obtained p-values produced by factorial ANOVA test considering ROC-AUC, F1 and PR-AUC score separately confirms that the analysis is significant and hence we reject the null hypothesis.

Comparison with state-of-the-art methods

To validate the effectiveness of our proposed method, in this section we have compared our results with different methods applied on these same datasets according to ROC-AUC score and F1 score (as discussed in the section “Fitness function”) which are taken from literature.

For the datasets with imbalance ratio $\le$ 6, using F1 score we have compared the results with the other standard methods which are frequently used in class imbalance problem in Table 10. The methods include RU [47], ENN [70], NMU [7], CNN [55], prototype generation using K-means clustering (PK) [57], SMOTE [14], Imbalanced Metric Learning (IML) [29], which follows Mahalanobis metric learning algorithm [63], RTHS [1] and A$\beta$BSF [31]. Some of these methods are very popular and useful to deal with the class imbalance problem. RTHS and A$\beta$BSF are recently used evolutionary algorithms. From the Table 10, it is clear that for all the datasets, our proposed method has achieved the best F1 score than state-of-the-art methods with which present method is compared. It has also obtained 1 as F1 score in Hayes-roth dataset.

For the datasets which have the imbalance ratio > 6, we have added some more standard methods compared to the previous case. We have compared the results in terms of AUC score with RU [47], ENN [70], NMU [7], PK [57], SMOTEBoost (SB) [15], CUSBoost (CB) [48], RUSBoost (RB) [54], RTHS [1] and A$\beta$BSF [31] methods. From the Table 11, it is obvious that our proposed method has acquired the highest ROC-AUC score in all of the datasets. we have obtained above 0.9 as ROC-AUC score for all the datasets. We have also achieved 1 as ROC-AUC score for 3 datasets: Kddcup-guess_passwd_vs_satan, Poker-9_vs_7 and Segment0 .

A statistical test is performed to ensure that our obtained results are statistically significant. The goal is to determine whether there is enough evidence to “reject” a conjecture or hypothesis about the process. The conjecture is called the null hypothesis. For our case, the null hypothesis states that the two sets of results have the same distribution. So, to determine the statistical significance of RTPSO algorithm, ANOVA test has been performed. From the test results provided in Table 12 (in terms of F1 score) and Table 13 (in terms of ROC-AUC score), we can conclude that the results of the proposed RTPSO algorithm are found to be statistically significant.

Fig. 5

Graphs for achieved ROC-AUC scores using different values of c1 for 15 datasets using RTPSO

Conclusion

In this work, we have proposed a hybrid meta-heuristic method, called RTPSO, to deal with class imbalance problem. RTPSO is based on a popular swarm-intelligence based meta-heuristic algorithm PSO and a recently proposed meta-heuristic algorithm RTEA. This hybrid method is proposed to overcome the demerits of PSO and RTEA. From the best of our knowledge, the proposed approach is totally original and it has been used for the first time to solve the class imbalance problem. As RTPSO is self-adaptable to different datasets, so it can be integrated with different classifiers and evaluation parameters easily for any class imbalance datasets. The proposed method has experimented on 15 standard real-life datasets having low to extreme class imbalanced ratio. It has been compared with its parent algorithms PSO and RTEA along with some standard sampling methods using AdaBoost classifier. From the Tables 3, 5, 7, 10 and 11 we can clearly observe that RTPSO achieves better results in most of the cases than the other methods. We have acquired the highest score in 12 datasets (80.00%) out of 15 datasets in Table 3. RTPSO has also obtained 1 as ROC-AUC score for 5 datasets (33.33%). These results verify the advantages and the excellent performance of the proposed approach, which helps us to conclude that it can be used for any class imbalance datasets. As a future scope of the work, we can add more powerful and advanced classifiers to our proposed algorithm to reach better solutions. Additionally, it can be used in more interesting and popular research problems. Finally, RTPSO can be successfully applied on high dimensional datasets also.

Appendix

See Figs. 5, 6 and 7

Fig. 6

Graphs for achieved ROC-AUC scores using different values of c2 for 15 datasets using RTPSO

Fig. 7

Graphs for achieved ROC-AUC scores using different values of $P_m$ for 15 datasets using RTPSO