Introduction

Reliability is the probability that an object will continuously perform a specified task or mission satisfactorily under a certain condition, for at least a given time or interval. Therefore, the probability of a successful performance of a system as designed is termed system reliability. A system is an integration of different components performing one or more operational functions [30]. The system reliability may depend on the system configurations, operational rules, the state of the failure and the failure process, which can be describe by certain law of probability. In any system, the reliability of individual components plays an important role in the proper functioning of the system. All the manufacturing companies rely on the reliable performance of components of the system to complete missions successfully. Selective maintenance problem arise when a firm desire to make an optimal decision on which component or subsystem to be maintain first, keeping in mind the scarce resources. An interested great research problem in reliability engineering is that of how, when and where to allocate, repair and or replace components of a system [29, 31, 33].

Fig. 1
figure 1

Graphical representation of the proposed model

Full size image

The main objective of selective maintenance is to find out the most important component or subsystem to maintain to minimize the production lost by avoiding frequent system failures. A system or component can be maintain selectively if and only if it has just finished a task and ready for the next. This means that, no component or subsystem can be selected for maintenance during the operation, some components are repairable and replaceable while others are not. The deterioration or failure of a system’s mechanism has a wide spectrum effect on the entire system. Many numerical, heuristic and metaheuristic algorithms were employed in studying this problem as can be seen in the next section. However, most of the existing algorithms have computational difficulties, time consuming when dealing with large problems and at times exact solutions are not easily obtainable. In light of this, devising an optimization technique that is both efficient and effective remain a hot topic in this regard [10].

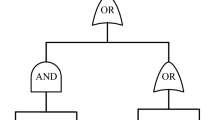
The purpose of this article is to bring to the fore, a new approach of multi-objective system reliability optimization for selective maintenance allocation problem under neutrosophic environment. Considering the nature of uncertainty in the failure of a system or its component, this research sought to incorporate fuzzy programming, Intuitionistic Fuzzy Programming and neutrosophic fuzzy goal programming. The whole system is divided into two groups X and Y each having subsystems with independent identical components. In each subsystem, there are two types of components involved (replaceable and repairable) (see Fig. 1). The overall objective is to optimally allocate the deteriorating components in the subsystems that would maximize its reliability. The system performs next mission after a limited time within which, the selective maintenance on the involved components of the subsystem is performed. The parameters of the proposed model are considered to be fuzzy, which are explained by the triangular fuzzy number. Neutrosophic goal programming technique is used to obtain the compromise allocation of replaceable and repairable components of the subsystem. Most of the real-life problematic situation are complex and have more than a single objective, especially in complex system reliability; hence, the use of MOSMAP becomes imperative. Using NFG, the best possible compromise solution of MO-SMAP under the fuzzy environment are obtained.

The significant advantage of this concept is that the decision-maker has three different degrees of information at his disposal to consider before making a final decision regarding the problem at hand. They are the truthhood, indeterminacy, and falsity. However, the existing approaches use only the truthness function as bases to the problem solution. Unlike in a real-life situation, decision outcome can be agreed, not sure, and disagreement. Therefore, the proposed concept of neutrosophic logic washes away this drawback; hence, all the aspects of decision-making are considered. Also, the indeterminacy part of the model allows experts to present their opinions about unclear preferences.

Moreover, the proposed methodology is very comfortable; goals can be easily and quickly achievable and useful in solving any multiple objective decision-making optimization problem under crisp and uncertain environment. Most of the problematic real-life situations are complex and have more than a single goal, especially in system reliability; hence, the use of MOSMAP becomes imperative. The NFG gives the best possible compromise solution of MO-SMAP under the fuzzy environment.

In the past decade, researches have studied selective maintenance problem in fuzzy environment. However, none of them has considered MO-SMAP under neutrosophic environment; and this is perceived to be the significant drawback that we have noticed in all previous research. Motivated by such research, we have formulated a MO-SMAP model under neutrosophic environment. The concept aims to present an algorithmic solution to the MO-SMAP, which should be relatively simple and efficient in real-world circumstances. In light of that, we propose a new MO-SMAP with fuzzy parameters. To the best of our knowledge, for the first time, MO-SMAP is studied under a neutrosophic environment. NGP is an innovative technique for dealing with uncertain, imprecise incomplete and contradictory information that is highly common in science and engineering situations. A new defuzzification technique is also discussed based on beta distribution to convert fuzzy parameters into crisp values.

The paper is arranged as follows: “Literature review” section reviews the literature on the system reliability and selective maintenance. In “Multi-objective selective maintenance allocation problem” section, a non-linear multi-objective selective maintenance allocation problem has been considered in a crisp and fuzzy nature. In “Conversion technique of fuzzy numbers” section, the defuzzification technique has been discussed for converting the fuzzy parameters into crisp form. In “Solution techniques” section, three solution approaches have been discussed and the stepwise algorithm for the optimal solution are presented. In “Numerical illustration” section, a numerical example is considered to illustrate the effectiveness of the proposed model under neutrosophic environment. Also, a comparative study with two other techniques are presented. “Conclusion” section summarizes the conclusion and suggest the future work.

Literature review

Research on selective maintenance and system reliability allocation has a long tradition. Reliability allocation can be referred to as the process whereby different values of reliability are assigned to different components of a system. Many authors proposed various approaches and techniques for optimal reliability allocation. Some minimize system cost subject to reliability constraints, others maximize the system reliability under a limited budget. First work on selective maintenance has been reported in Rice et al. [39]. They considered a selective maintenance model for maximizing the reliability of the system. Cassady et al. [7, 8] extended the work in three different ways, viz., they considered three different models of selective maintenance, i.e. maximizing the reliability of the system subject to maintenance time and maintenance cost; minimizing the repair cost of the components of a system subject to minimum required reliability level and time constrain; and finally, minimizing repair time of the components subject to the cost and reliability constraints. Gupta et al. [22] considered two cases of reliability optimization problem, a maintenance and redundancy cases using interval programming. Selective maintenance for multi-state system has been investigated by Liu and Huang [32] where they considered the imperfect maintenance quality of the binary state elements. Many authors work on selective maintenance, we refer to Ali et al. [3], Ali and Hasan [1, 2]; Chern [10], Cheng et al. [9], Painton and Campbell [34], Pandey et al. [35], Rajagopalan and Cassady [38], Khatab and Aghezzaf [27], Khatab et al. [28], Xu et al. [43], Zhao et al. [44], Diallo et al. [13, 14], Wang and Li [42], Galante et al. [15], Jiang and Liu [24] among others. Intuitionistic fuzzy optimization has been used intensively in reliability optimization and multi-criteria decision-making problems under neutrosophic environment. Recent work includes [16,17,18,19] and many others.

Some existing work on selective maintenance problem according to the types of models, optimizations, approaches and techniques used by different authors are summarized in Table 1.

Table 1 Characteristics of previously proposed models
Full size table
Table 2 Characteristics of previously proposed models (Cont’d)
Full size table

Multi-objective selective maintenance allocation problem

One of the most important aspects in manufacturing industries is the system maintenance. It plays a vital role to the performance and reliability of the system. In this section, we consider a system containing several subsystems with replaceable and repairable components. We assume the system has to perform several missions in a sequence with a known break after a limited (fixed) time interval between missions. Also, repairing and replacement/maintenance technology is assume to be available before failure. The whole system is divided into two main groups X and Y each having m subsystems with independent identical components (\(n_r~~and~n_q\)). The two groups of the system (X and Y), and all the subsystems in them are configured in series while the independent identical components are connected in parallel (see Fig. 1). This types of configurations are known as series-parallel system, and can be easily found in communication network, nuclear system, military weapons, heavy machines, power generation systems, and gas turbine engine of an aircraft among others.

Assumption for the proposed model

  1. 1.

    All the subsystems’ components are independently and identically distributed (iid)

  2. 2.

    The whole system is divided into two groups X and Y and is connected in series (see Fig. 1).

  3. 3.

    In group X, the components are connected in parallel in the subsystems from 1  to  r.

  4. 4.

    In group Y, the components are connected in parallel in the subsystems from \(r+1~~ to~~ q\).

  5. 5.

    The system has two different types of components, type I (replaceable components) and type II (repairable components).

  6. 6.

    Type I components are very sensitive and any failure of such components are immediately replaced by another new one.

  7. 7.

    Type II components are at low risk and any failure in such components can be repaired and then put back for use.

  8. 8.

    All components in the subsystems are restricted to be repaired and replaced before the next mission.

  9. 9.

    The failures of the components in the subsystem are statistically independent in the time interval.

The diagrammatic representation of the proposed selective maintenance model is given in Fig. 1 and the notations used in the reliability models are presented in Table 3.

Table 3 Nomenclature
Full size table

The total failed components (repairables and replaceables) in the subsystems can only be selected for maintenance during the interval or break time and before the starting next production run. Therefore, the number of components available for the next mission in the subsystem will be \((l_i - \text {g}_i) + m_i, i= 1,2, \dots , q\). The reliability of the subsystem X and Y for the next production run can be calculated as

$$\begin{aligned} \left\{ \begin{array}{lr} R_X(m_i) = \prod _{i=1}^{r}\left[ 1 - (1 - r_i)^{l_i - \text {g}_i + m_i}\right] ,\\ \qquad The~~reliability~~ of~~ subsystem~~ X\\ &{}\\ R_Y(m_i) = \prod _{i=r+1}^{q}\left[ 1 - (1 - r_i)^{l_i - \text {g}_i + m_i}\right] ,\\ \qquad The ~~reliability~~ of~~ subsystem~~ Y\\ &{}\\ \sum _{i=1}^{q}c_i\left[ m_i + exp(\alpha _im_i)\right] \le C,\\ \qquad The~~ repairing~~ cost~~ of ~~the ~~system. \end{array} \right. \end{aligned}$$
(1)

where \(exp(\alpha _i m_i\)) is the extra cost spent due to the interconnection between parallel components. Then the mathematical formulation of the problem is

$$\begin{aligned} Maximize~~~\left\{ \begin{array}{lr} R_X(m_i) = \prod _{i=1}^{r}\left[ 1 - (1 - r_i^{l_i - \text {g}_i + m_i})\right] ,\\ R_Y(m_i) = \prod _{i=r+1}^{q}\left[ 1 - (1 - r_i^{l_i - \text {g}_i + m_i})\right] , \\ subject~~to: &{}\\ \sum _{i=1}^{q}c_i\left[ m_i + exp(\alpha _im_i)\right] \le C,\\ 1\le m_i \le \text {g}_i,~~l_i\ge \text {g}_i, \\ \quad i=1,2,\cdots , q ~~~and~~integer \end{array} \right. \end{aligned}$$
(2)

Estimating the number of components using stochastic process

Let the number of components failures X in an interval time t, follows a Poisson distribution with mean \(\mu t\). The probability of failure at time t equal to n can be given by

$$ Pr\lbrace X=n \rbrace = (\mu t)^ne^-{\mu t}/n!,~~~n\ge 0. $$

Since we assume the components failure are statistically independent in the time interval, and that the failure rate is not constant, then the process is a typical non-homogeneous Poisson process [11], and the number of failures between time interval (a,b] will follow a Poisson distribution with mean (MTBF)

\(\int _{a}^{b}v(t)dt\), v(t) is the intensity function. Therefore, the probability of no failure in the time interval (a, b] can be calculated using the relation:

$$\begin{aligned} exp\left\{ -\int _{a}^{b}v(t)dt\right\} \end{aligned}$$

Multi-objective selective maintenance allocation problem under uncertainty

In real-world systems, the components failure nature and the uncertainty of the mission duration together, result in the operational time uncertainty of components in the mission. Several situations such as uncertain judgments, unpredictable conditions or human error, incomplete knowledge and information, may occur. The uncertainty associated with a component of a systems at the end of a mission can be trace from the uncertainty associated with the operational time originally. The relationship among the mission duration, failure time, and operational time in terms of uncertainty from previous to the next mission are presented in Fig.  2

Fig. 2
figure 2

Relationships among uncertainties in a system

Full size image

Considering the imprecision and uncertainty in the system reliability, we employ fuzzy numbers to address such type of problems. In light of this, model 2 can be formulated as a fuzzy nonlinear programming problem by assuming the parameters to be fuzzy. Since the available cost for repairing and replacing the components varies from time to time, it cannot be fixed and therefore it has been considered as independent factor that can be estimated. Thus, we have

$$\begin{aligned} Maximize\,\left\{ \begin{array}{lr} R_X(m_i) = \prod _{i=1}^{r}\left[ 1 - (1 - \tilde{r_i})^{l_i - \tilde{\text {g}_i} + m_i}\right] ,\\ R_Y(m_i) \!=\! \prod _{i=r+1}^{q}\left[ 1 - (1 \!-\! \tilde{r_i})^{l_i - \tilde{\text {g}_i} \!+\! m_i}\right] , \\ subject~~to: &{}\\ \sum _{i=1}^{q}\tilde{c_i}\left[ m_i + exp(\alpha _im_i)\right] \le {\tilde{C}},\\ 1\le m_i \le \text {g}_i,~~l_i\ge \text {g}_i, \\ \quad i=1,2,\cdots , q~~and~~integer, \end{array} \right. \nonumber \\ \end{aligned}$$
(3)

where the parameters \({\tilde{C}},\tilde{c_i},\tilde{r_i},\)and \(\tilde{\text {g}_i}\) are assumed to be fuzzy. The fuzzy numbers are then converted to its crisp equivalent form in the next section.

Conversion technique of fuzzy numbers

In this section, we consider a statistical beta distribution to defuzzify the fuzzy numbers into a crisp value based on the concept of Rahmani et al. [37].

Let there be a continuous random variable Y that follow a Beta distribution with mean \(\alpha \) and standard deviation \(\sigma \), then its follows that the probability density function (pdf) is defined as

$$\begin{aligned} f(y) =\left\{ \begin{array}{lr} \dfrac{\Gamma (\mu + \sigma )}{\Gamma (\mu )\Gamma (\sigma )}y^{\mu - 1}(1-y)^{\sigma -1}, ~~~~0\le y\le 1\\ 0 \end{array} \right. \end{aligned}$$
(4)

where, \(\mu \) , \(\sigma \) > 0 are the Beta distribution parameters. Therefore, the mean value of the distribution is given by:

$$\begin{aligned} \alpha = \dfrac{\mu }{\mu + \sigma } \end{aligned}$$
(5)

If \(\mu \), \(\sigma \) \(\ge \) 1, then the beta function will have a unimodal curve, whereas if \(\mu < \sigma \) or \(\mu > \sigma \), the beta curve will exhibit a negative and positive skewness, respectively. Otherwise the function will be symmetric.

Let \({\tilde{p}} = (a,b,c)\) be a triangular fuzzy number (TFN) and lies in between (0, 1) . This will be in the form of \({\tilde{p}}' =\left\{ \left( \frac{a-b}{c-a}\right) ,\left( \frac{b-a}{c-a}\right) ,\left( \frac{c-a}{c-a}\right) \right\} \) = \(\left\{ o, \left( \frac{b-a}{c-a}\right) ,1 \right\} \).

The beta parameters can be defined as

$$\begin{aligned} \mu = \frac{b-a}{c-a} + 1, ~~~~~~~~~~ \sigma = \frac{c-b}{c-a} +1 \end{aligned}$$
(6)

Then, the mean value of the beta distribution according to a fuzzy number can be calculated as:

$$\begin{aligned}&\alpha ' = \dfrac{\mu }{\mu + \sigma } = \frac{(b-a)/(c-a) + 1}{(b-a)/(c-a) + 1 (c-b)/(c-a) + 1} \nonumber \\&\qquad = \frac{b+c -2a}{3(c-a)}. \end{aligned}$$
(7)

The crisp number of \(\alpha _{{\tilde{p}}}\) corresponding to TFN \({\tilde{p}} = (a,b,c)\) is calculated by the following relation:

$$\begin{aligned} \alpha _{{\tilde{p}}} = \frac{a+b+c}{3}. \end{aligned}$$
(8)

Solution techniques

In this section, we reviewed and defined some important aspects of the methodologies used in this study for solving the selective maintenance allocation problem in system reliability. We have considered three types of techniques, viz., neutrosophic goal programming approach, fuzzy programming, and intuitionistic fuzzy programming. With the help of these approaches, the formulated multi-objective selective maintenance problem is converted into a single-objective problem. The complete process is given in the stepwise procedure below (“Computational algorithm” section), this procedure can be generally use for converting any multi-objective optimization problem to a single-objective in different domain of study.

Neutrosophic goal programming approach (NGPA)

Recently, the expanded fuzzy and intuitionistic fuzzy set has been considered as a neutrosophic set (NS) with additional membership function known as indeterminacy. In many real-life decision-making problems, it has been observed that, many situations exist where decision-makers have indeterminacy or unbiased thoughts on making a decision. Indeterminacy values always lie between the truthhood and falsehood values. The term neutrosophic means ”knowledge of indeterminacy or natural thoughts” and is coiled from a French word ”neuter” meaning natural and a Greek word ”Sophia” meaning skill. It is enough evidence to consider a NS differently from the fuzzy and intuitionistic sets. The former considers three different types of membership functions. Viz; the truthhood, indeterminacy, and falsehood. While the later, considers maximizing the degree of membership and non-membership function in case of fuzzy and intuitionistic sets respectively.

Alternatively, NS maximizes the degree of truthhood and indeterminacy, and minimizes the degree of falsehood membership functions respectively. A significant touchstone in the judgment-making process reflect the NS, where by a decision -maker may completely satisfied (truth), somehow satisfied (indeterminacy) and completely dissatisfied (falsehood). These types of consideration in any decision-making problems provide more strength to make the best decision or obtained an optimal solution.

In real-life decision-making problems involving multiple objectives, the job of obtaining the optimal solution is a challenging task. However, neutrosophic goal programming (NGP) can be use in obtaining the best compromise (satisfying) solution of multi-objective problem having conflicting goals. The NGP is generally a reflective on the three conditions: the degree of truth; indeterminacy; and falsity present in any decision-making optimization problems.

Below are some basic definitions and terms:

Definition 1

Fuzzy Set\(:\) A fuzzy set \({\tilde{A}}\) is defined by

$$\begin{aligned} {\tilde{A}} = \left\{ \left( x, \mu _{{\tilde{A}}}(x)\right) :x \in A, \mu _{{\tilde{A}}}(x) \in [0,1]\right\} . \end{aligned}$$
(9)

In the pair of (9), the first element x belongs to the classical set A; the second element \(\mu _{{\tilde{A}}}(x)\), belongs to the interval [0, 1], called membership function or grade of membership. The membership function is also a degree of compatibility or a degree of truth of x in A. The elements with a zero degree of membership are normally not listed.

Definition 2

Intuitionistic fuzzy set\(:\) Let X be a universe of discourse. Then an intuitionistic fuzzy set \({\tilde{A}}^I\) in X is defined by a set of ordered triples given by

$$\begin{aligned} {\tilde{A}}^I = \left\{ < x, \mu _{{\tilde{A}}^I}(x), \gamma _{{\tilde{A}}^I}(x)> :x \in X \right\} . \end{aligned}$$
(10)

where \(\mu _{{\tilde{A}}^I}, \gamma _{{\tilde{A}}^I} :X \rightarrow [0,1]\) are functions such that \(0 \le \mu _{{\tilde{A}}^I}(x) + \gamma _{{\tilde{A}}^I}(x) \le 1, \forall x \in X\). The value \(\mu _{{\tilde{A}}^I}(x)\) represents the degree of membership and \(\gamma _{{\tilde{A}}^I}(x)\) represents the degree of non-membership of the element \(x\in X\) being in \({\tilde{A}}^I\cdot h(x) = 1-\mu _{{\tilde{A}}^I}-\gamma _{{\tilde{A}}^I}\) is the degree of hesitation of the element \(x \in X\) being in \({\tilde{A}}^I.\)

Definition 3

Neutrosophic Set (NS)\(:\) Let Z be a universe of discourse and \(z \in Z\), then a neutrosophic set \(P \in Z\) with three different types of membership functions defined as; Truth \(T_P(z)\), Indeterminacy \(I_P(z)\) and False \(F_P(z)\) and presented by:

$$\begin{aligned} P = \left[ \lbrace z, T_p(z), T_P(z), F_P(z)\right\} z: \in Z] \end{aligned}$$
(11)

Where \(T_P(z), I_P(z), ~and~ F_P(z)\) are real non-standard or real standard with range ]\(0^-, 1^+\)[. That is , \(T_P(z): Z \longrightarrow \) ]\(0^-, 1^+\)[,\(~~~~ I_P(z): Z \longrightarrow \) ]\(0^-, 1^+\)[,\(~~~~ F_P(z): Z \longrightarrow \) ]\(0^-, 1^+\)[ and no restrictions on the sum of the memberships, hence

$$\begin{aligned} 0^- \le sup T_p(z)+ T_p(z)+ sup F_p(z) \le 3^+. \end{aligned}$$
(12)

Definition 4

Single-valued neutrosophic set (SVNS)\(:\) A single value neutrosophic set (SVNS) P over the universe of discourse Z is presented as

$$\begin{aligned} P = \lbrace < z, T_p(z), T_P(z), F_P(z)>\rbrace z \in Z ], \end{aligned}$$
(13)

where \(T_P(z), I_P(z), ~and~F_P(z) \in (0,1) ~sum~0 \le T_p(z)+ T_p(z)+ sup F_p(z) \le 3\) for every \(z \in Z\).

Definition 5

Union of neutrosophic set\(:\) Let P and Q be the two NS, then \(R= P \bigcup Q\) with truth \(T_R(z)\), indeterminacy \(I_R(z)\) and false \(F_R(z)\) membership functions are defined as

$$\begin{aligned} \bigcup _R =\left\{ \begin{array}{lr} T_R(z) = \max (T_P(z), T_Q(z)\\ I_R(z) = \min (I_P(z), I_Q(z)\\ F_R(z) = \min (F_P(z), F_Q(z) &{}\\ \forall z \in Z \end{array} \right. \end{aligned}$$
(14)

Definition 6

Intersection of neutrosophic set\(:\) Let P and Q be the two NS, then \(R= P \bigcap Q\) with truth \(T_R(z)\), indeterminacy \(I_R(z)\) and false \(F_R(z)\) membership functions are defined as

$$\begin{aligned} \bigcap ^R =\left\{ \begin{array}{lr} T_R(z) = \min (T_P(z), T_Q(z)\\ I_R(z) = \max (I_P(z), I_Q(z)\\ F_R(z) = \max (F_P(z), F_Q(z) &{}\\ \forall z \in Z \end{array} \right. \end{aligned}$$
(15)

The first concept of the fuzzy decision (D), fuzzy goal (G) and fuzzy constraints (C) are proposed by Bellman and Zadeh [6]. The concept proved to efficient for solving real-life decision making optimization problems under uncertainty. Thus, a fuzzy decision set may be described as \(D= G \cap C\).

Therefore, a neutrosophic decision set \(D_N\) with neutrosophic goal set and neutrosophic constraints set can be stated as

\(D_N \!=\! \{(\cap ^J_{j=1}G_j)\cap (\cap ^K_{k=1}C_k)= (z, T_D(z), I_D(z), F_D(z)) \}\), where

$$\begin{aligned}&T_D(z)=\min \begin{bmatrix} T_{G_1}(z), T_{G_2}(z), \dots , T_{G_j}(z)\\ T_{C_1}(z), T_{C_2}(z), \dots , T_{C_k}(z)\\ \end{bmatrix} \forall z \in Z \end{aligned}$$
(16)
$$\begin{aligned}&I_D(z)=\max \begin{bmatrix} I_{G_1}(z), I_{G_2}(z), \dots , I_{G_j}(z)\\ I_{C_1}(z), I_{C_2}(z), \dots , I_{C_k}(z)\\ \end{bmatrix} \forall z \in Z \end{aligned}$$
(17)
$$\begin{aligned}&F_D(z)=\min \begin{bmatrix} F_{G_1}(z), F_{G_2}(z), \dots , F_{G_j}(z)\\ F_{C_1}(z), F_{C_2}(z), \dots , F_{C_k}(z)\\ \end{bmatrix} \forall z \in Z \end{aligned}$$
(18)

and \(D_N\) is the neutrosophic decision set with truth \(T_D(z)\), indeterminacy \(I_D(z)\) and false \(F_D(z)\) membership functions, respectively.

Compromise solution for multi-objective optimization under NGPA

To obtain the compromise solutions for multi-objective decision making optimization problems, we formulate the membership functions for each objective and calculate the lower and upper bounds by solving it individually under the defined constraints of the problem.

Let \(U_j\) and \(L_j\) denotes the upper and lower bound for every objective function of the problem, and define by

\(U_j = \{\max (M_j(X))\}\) and \(L_j = \{\min (M_j(X))\}\) \(\forall \) \(j = 1,2,\dots J\).

Under neutrosophic domain, the bounds for \(j^{th}\) objective functions can be calculated as:

$$\begin{aligned} Bounds = \left\{ \begin{array}{lr} U^T_j =U_j,~~~~~~~ L_j^T =L_j&{} \\ ~~ {\textit{for truth membership function}},\\ U^I_j =L_j + a_j, ~~~~~~L_j^T =L_j&{}\\ ~~ {\textit{for indeterminacy membership function}}\\ U^F_j =U_j^T,~~~~~~~~ L_j^F =L_j^T+ b_j&{} \\ ~~ {\textit{for falsity membership function}}\\ \end{array} \right. \nonumber \\ \end{aligned}$$
(19)

\(U^T_j =U_j\),        \(L_j^T =L_j\) for truth membership function,

\(U^I_j =L_j + a_j\),       \(L_j^T =L_j\) for indeterminacy membership function,

\(U^F_j =U_j^T\),         \(L_j^F =L_j^T+ b_j\) for false membership function,

where the values of \(a_j\) and \(b_j\) are real numbers between (0, 1) assigned by the DM. The linear membership functions for each objective under the neutrosophic domain is then constructed as follows:

$$\begin{aligned}&\mu _j^T(M_j(x)) = \left\{ \begin{array}{lr} 0, &{} M_j(x) \le L_j^T\\ \dfrac{M_j(x) -L_j^T}{U_j^T -L_j^T}, &{}~~~~~~ L_j^T \le M_j(x) \le U_j^T\\ 1,&{} M_j(x) \ge U_j^T \end{array} \right. \end{aligned}$$
(20)
$$\begin{aligned}&\mu _j^I(M_j(x)) = \left\{ \begin{array}{lr} 0, &{} M_j(x) \le L_j^I\\ \dfrac{M_j(x) -L_j^I}{U_j^I -L_j^I}, &{}~~~~~~ L_j^I \le M_j(x) \le U_j^I\\ 1,&{} M_j(x) \ge U_j^I \end{array} \right. \end{aligned}$$
(21)
$$\begin{aligned}&\mu _j^F(M_j(x)) = \left\{ \begin{array}{lr} 0, &{} M_j(x) \le L_j^F\\ \dfrac{U_j^F - M_j(x)}{U_j^F -L_j^F}, &{}~~~~~~ L_j^F \le M_j(x) \le U_j^F\\ 1,&{} M_j(x) \ge U_j^F \end{array} \right. \end{aligned}$$
(22)

In all cases, \(U_j \ne L_j, \forall j= 1,2, \dots , J\) for all objective functions. If in any situations \(U_j = L_j, \forall j= 1,2, \dots , J\) then membership value will assume the value 1. The graphical presentation of the different membership functions in the neutrosophic environment is defined in Fig. 3.

Therefore, the membership functions Eqs. (20–22) are converted into goals in Eq. 23. DM may set a target of achieving the highest possible degree of satisfaction (truthhood = 1) and that of indifference threshold (indeterminacy = 0.5), and may wish to minimize the degree of falsehood (0) as much as possible in the decision-making process. The mathematical expression of the conversion is given in Eq. 23

$$\begin{aligned} \left\{ \begin{array}{lr} \mu _j^T(M_j(x))+ D_{jT}^- + D_{jT}^+ = 1,\\ \mu _j^I(M_j(x))+ D_{jI}^- + D_{jI}^+ = 0.5,\\ \mu _j^F(M_j(x))+ D_{jF}^- + D_{jF}^+ = 0\\ where\\ D_{jT}^- , D_{jT}^+,~~ \\ {\textit{Deviations related to truth membership function}}\\ D_{jI}^- , D_{jI}^+,~~ \\ {\textit{Deviations related to indeterminacy membership function}} \\ D_{jF}^- , D_{jF}^+, ~~ \\ {\textit{Deviations related to false membership function}} \\ and\\ D_{jT}^- \cdot D_{jT}^+ =0,~~~~D_{jI}^- \cdot D_{jI}^+ =0,~~~~D_{jF}^- \cdot D_{jF}^+ =0, \end{array} \right. \end{aligned}$$
(23)

Consequently, the DM’s target may be under achieve, over achieve or perfectly satisfied. Due to this inherent features in the process, the deviations from both the under and over achievements are minimized, and the general mathematical model of the NGP for multi-objective decision-making problem is given in Eq. (24)

$$\begin{aligned} \left\{ \begin{array}{lr} Minimize~~ M =\sum _{j=1}^{J}W_{jT} \cdot D_{jT}^- \\ + \sum _{j=1}^{J}W_{jI} \cdot D_{jI}^- + \sum _{j=1}^{J}W_{jF} \cdot D_{jF}^+\\ subject~~to:\\ \mu _j^T(M_j(x))+ D_{jT}^- + D_{jT}^+ \ge 1,\\ \mu _j^I(M_j(x))+ D_{jI}^- + D_{jI}^+ \ge 0.5,\\ \mu _j^F(M_j(x))+ D_{jF}^- + D_{jF}^+ \le 0\\ \mu _j^T(M_j(x)) \ge \mu _j^I(M_j(x))\\ \mu _j^T(M_j(x)) \ge \mu _j^F(M_j(x))\\ \mu _j^F(M_j(x)) \ge 0\\ \mu _j^T(M_j(x)) + \mu _j^I(M_j(x)) + \mu _j^F(M_j(x)) \le 3\\ D_{jT}^- \cdot D_{jT}^+ =0,~~~~D_{jI}^- \cdot D_{jI}^+ =0,~~~~D_{jF}^- \cdot D_{jF}^+ =0,\\ f_k(x) \le , =, \ge \text {g}_k,~~~k=1,2. \cdots , K\\ x_i \ge 0, ~~~i=1,2, \cdots , m,~~~x_i \in X\\ D_{jT}^-, D_{jT}^+,~~~~D_{jI}^-, D_{jI}^+,~~~~D_{jF}^-, D_{jF}^+ \ge 0,~~~\forall j \end{array} \right. , \end{aligned}$$
(24)
Fig. 3
figure 3

Graphical presentation of the degree of truth, indeterminacy and false membership functions for the objective functions

Full size image

where \(W_{jT}, W_{jI},~~and~~ W_{jF}\) are the weights associated with the deviations of the membership goals and are defined as:

$$\begin{aligned}&W_{jT}= \frac{1}{U_j^T - L_j^T},~~W_{jI}= \frac{1}{U_j^I - L_j^I}, and \\&W_{jF}= \frac{1}{U_j^F - L_j^F}. \end{aligned}$$

In light of Eq. (24), the proposed multi-objective non-linear selective maintenance model can be stated in model (25) as follows:

$$\begin{aligned} Minimize~~~\left\{ \begin{array}{lr} M= (W_{1T} \cdot D_{1T}^- +W_{2T} \cdot D_{2T}^-)\\ \quad +(W_{1I} \cdot D_{1I}^- +W_{2I} \cdot D_{2I}^-)\\ \quad + (W_{1F} \cdot D_{1F}^- +W_{2F} \cdot D_{2F}^-)\\ subject~~to:\\ \dfrac{\left\{ \prod _{i=1}^{r}\left[ 1 - (1 - r_i)^{l_i - \text {g}_i + m_i}\right] \right\} - L^T_j}{U^T_j -L^T_j} +D_{1T}^- -D_{1T}^+ \ge 1 \\ \dfrac{\left\{ \prod _{i=1}^{r}\left[ 1 - (1 - r_i)^{l_i - \text {g}_i + m_i}\right] \right\} - L^I_j}{U^I_j -L^I_j} +D_{1I}^- -D_{1I}^+ \ge 0.5 \\ \dfrac{U^F_j - \left\{ \prod _{i=1}^{r}\left[ 1 - (1 - r_i)^{l_i - \text {g}_i + m_i}\right] \right\} }{U^F_j - L^F_j} +D_{1F}^- -D_{1F}^+ \le 0 \\ \dfrac{\left\{ \prod _{i=1}^{r}\left[ 1 - (1 - \tilde{r_i})^{l_i - \tilde{\text {g}_i} + m_i}\right] \right\} - L^T_j}{U^T_j -L^T_j} +D_{1T}^- -D_{1T}^+ \ge 1 \\ \dfrac{\left\{ \prod _{i=1}^{r}\left[ 1 - (1 - \tilde{r_i})^{l_i - \tilde{\text {g}_i} + m_i}\right] \right\} - L^I_j}{U^I_j -L^I_j} +D_{1I}^- -D_{1I}^+ \ge 0.5 \\ \dfrac{U^F_j - \left\{ \prod _{i=1}^{r}\left[ 1 - (1 - \tilde{r_i})^{l_i - \tilde{\text {g}_i} + m_i}\right] \right\} }{U^F_j - L^F_j} +D_{1F}^- -D_{1F}^+ \le 0 \\ \mu _j^T(M_j(x)) \ge \mu _j^I(M_j(x))\\ \mu _j^T(M_j(x)) \ge \mu _j^F(M_j(x))\\ \mu _j^T(M_j(x)) + \mu _j^I(M_j(x)) + \mu _j^F(M_j(x)) \le 3\\ D_{jT}^- \cdot D_{jT}^+ =0,~~~~D_{jI}^- \cdot D_{jI}^+ =0,~~~~D_{jF}^- \cdot D_{jF}^+ =0,\\ \sum _{i=1}^{q}\tilde{c_i}\left[ m_i + exp(\alpha _im_i)\right] \le {\tilde{C}},\\ 1\le m_i \le \text {g}_i,~~l_i\ge \text {g}_i, ~~~~~~i=1,2,\cdots , q~~and~~integer\\ D_{jT}^-, D_{jT}^+,~~~~D_{jI}^-, D_{jI}^+,~~~~D_{jF}^-, D_{jF}^+ \ge 0,~~~\forall j \end{array} \right. \end{aligned}$$
(25)

Computational algorithm

For any mathematical model, there exist a computational procedures to guide the formulation of the real-life situation into optimization model. The proposed work is not an exceptional, hence, the following steps are followed in solving the proposed non-linear multi-objective selective maintenance model using NGP.

  1. Step 1

    Let a non-linear multiobjective programming problem (MO-NLPP) with j objectives functions be given as:

    $$\begin{aligned} \begin{array}{ll} Optimize \, \, \left( f_1(X), f_2(X), \ldots f_j(X)\right) \\ subject \, \, to;\\ g_i(x)\le b_i, \, \, \, i=1, 2, \ldots , m; \, \, x\ge 0. \end{array} \end{aligned}$$
  2. Step 2

    Using Step 1, formulate the real-life MO-SMAP incorporating the fuzzy parameters in light of model (3).

  3. Step 3

    Transform each fuzzy parameter defined in Step 2 into crisp by applying the defuzzification technique discussed in section 4.

  4. Step 4

    Solve the MO-SMAP in Step 2, taking one objective function under the set of constraints at a time and ignored the others. After computing the ideal solutions, construct a pay-off matrix given as

    $$\begin{aligned} \begin{bmatrix} f^*_1(x^1)&{} f_2(x^1)&{} \cdots &{} f_j(x^1)\\ f_1(x^2) &{} f^*_2(x^2)&{} \cdots &{} f_j(x^2)\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ f_1(x^j) &{} f_2(x^j)&{} \cdots &{} f^*_j(x^j) \end{bmatrix} \end{aligned}$$
  5. Step 5

    Obtained the lower (\(L_j\)) and upper (\(U_j\) ) bounds for each objective functions in light of model (19) and construct the truth, indeterminacy and false linear membership functions in light of Eqs. (20)–(22).

  6. Step 6

    Convert the membership functions constructed in Step 5 into goals and develop a NGP model in light of Eq. (23), Minimize the decision-makers’ deviational goals (under and over achievement) in light of Eq. (24.) and convert it into a crisp equivalent using the propose NGP technique given in model (25).

  7. Step 7

    Solve the proposed non-linear multi-objective selective maintenance problem to obtain the optimal allocation (compromise solution).

  8. Step 8.

    Solve the resulting model in Step 6 with any available commercial packages such as GAMS, LINDO/LINGO, etc. to obtain the compromise solution (Pareto solution).

Fuzzy programming (FP)

Fuzzy programming (FG) is one of the several models for optimization under uncertainty. It is well suited for multi-objective modelling problems. The general mathematical model of a multi-objective optimization problem with j objectives and k constraints for the m decision variables can be defined as

$$\begin{aligned} Optimize~~~\left\{ \begin{array}{lr} M= (M_1, M_2, \cdots , M_j)\\ subject~~to:\\ \text {g}_k \le 0, ~~ k=i, 2, \dots , K \\ x_i \ge 0,~~ i= 1, 2, \dots , m. \end{array} \right. \end{aligned}$$
(26)

The technique was employed by Zimmermann [45] to solve a multi-objective optimization problem. The general formulation of fuzzy programming can be defined as

$$\begin{aligned} \left\{ \begin{array}{lr} Maximize~~\alpha \\ subject~~to:\\ \mu _j(x) \ge \alpha ~~~~~~~~\forall j\\ \text {g}_k \le 0, ~~ k=i, 2, \dots , K \\ x_i \ge 0,~~ i= 1, 2, \dots , m. \end{array} \right. , \end{aligned}$$
(27)

where \(\mu _j (x)\) is the membership function of the objective function.

Intuitionistic fuzzy programming (IFP)

A new concept for optimization under uncertainty known as IFP was proposed by Angelov [5] as an extension of the traditional fuzzy optimization. The concept incorporate the degrees of rejections of the objective(s), the constraints and the satisfaction all together based on intuition. The general mathematical formulation of the IFP technique for solving the multi-objective optimization problem can be stated as:

$$\begin{aligned} \left\{ \begin{array}{lr} Maximize~~(\alpha - \beta )\\ subject~~to:\\ \mu _j(x) \ge \alpha ,~~ \gamma _j(x)\le \beta ~~~~~~~~\forall j\\ \alpha + \beta \le 1,~~ \alpha \ge \beta ,~~ \beta \ge 0,\\ \text {g}_k \le 0, ~~ k=i, 2, \cdots , K \\ x_i \ge 0,~~ i= 1, 2, \dots , m. \end{array} \right. \end{aligned}$$
(28)

Where, \(\mu _j (x), \gamma _j(x)\) is the membership function of the objective function.

Numerical illustration

We considered a system divided into two groups X and Y having seven subsystems altogether. Group X contained three and group Y contain four subsystems, and in each subsystem, some components are replaceable while others are repairable. Let assume the performance of the system in the next mission depends on its previous mission. We use the non-homogeneous stochastic Poisson process discussed in section 3.1 to estimate the average number of components failing before the next run given the maintenance cost. In the first run, 3 components were estimated to failed, 2 components in the second run, 4 components in the third and fourth run, and 6 components in the fifth production run. The failed components are presented as triangular fuzzy numbers. Also, the total maintenance cost for repairing and replacing of the available components for the next run is considered to be a triangular fuzzy number with values (2500, 3000, and 3500) units. The available cost for the repairing and replacing, several failed components, reliability of each component and the total number of components in the subsystems for group X and Y are shown in Table 4 and 5 .

Table 4 The data for group X sub-systems
Full size table
Table 5 The data for group Y sub-systems
Full size table

The defuzzification technique discussed in section 4, is used to obtain the crisp value of Tables 4 and 5 as shown in Table 6, also the crips equivalent of model (2) is presented in Eq. (30) using same defuzzification.

Numerical presentation Table 6 data are input into model (3) which is shown in Eq. (29).

$$\begin{aligned}&Maximize~~~\left\{ \begin{array}{lr} R_X = \left[ 1 - (1 - (0.62, 0.65,0.69))^{8-(3,4,5) + m_1}\right] \times \\ \left[ 1 - (1 - (0.51, 0.55,0.58))^{6-(3,4,5) + m_2}\right] \times \left[ 1 - (1 - (0.64, 0.70,0.76))^{10-(6,7,8)+ m_3}\right] \\ R_Y = \left[ 1 - (1 - (0.64, 0.70, 0.76))^{8-(4, 5,6) + m_4}\right] \times \left[ 1 - (1 - (0.51, 0.55,0.58))^{10-(7,8,9) + m_5}\right] \times \\ \left[ 1 - (1 - (0.56, 0.60,0.66))^{12-(9,10,11) + m_6}\right] \times \left[ 1 - (1 - (0.62, 0.65,0.69))^{10-(6,7,8) + m_7}\right] \\ subject~~to: (145,140,145)\times \left[ m_1 + exp(0.25*m_1)\right] + (105,110,115)\times \left[ m_2 + exp(0.25*m_2)\right] +\\ (145,150,155)\times \left[ m_3 + exp(0.25*m_3)\right] +(65,70,75)\times \left[ m_4 + exp(0.25*m_4)\right] +\\ (25,30,35)\times \left[ m_5 + exp(0.25*m_5)+(40,45,50 )\right] \times \left[ m_6 + exp(0.25*m_6)\right] +\\ (60,65,70)\times \left[ m_7 + exp(0.25*m_7)\right] \le (2500, 3000, 3500),\\ 1\le m_1 \le (3,4,5),~~1\le m_2 \le (3,4,5),~~1\le m_3 \le (3,7,8),~~1\le m_4 \le (4,5,6),\\ 1\le m_5 \le (37,8,9),~~1\le m_6 \le (9,10,11),~~1\le m_7 \le (6,7,8) \end{array} \right. \nonumber \\\end{aligned}$$
(29)
$$\begin{aligned}&Maximize~~~\left\{ \begin{array}{lr} R_X =\left[ 1 - (1 - (0.65))^{8-4 + m_1}\right] \times \left[ 1 - (1 - (0.54))^{6-4 + m_2}\right] \times \left[ 1 - (1 - (0.70))^{10-7 + m_3}\right] \\ R_Y = \left[ 1 - (1 - (0.70))^{8-5 + m_4}\right] \times \left[ 1 - (1 - (0.54))^{10-8 + m_5}\right] \times \left[ 1 - (1 - (0.60))^{12-10 + m_6}\right] \times \\ \left[ 1 - (1 - (0.65))^{6-4 + m_7}\right] \\ subject~~to: &{}\\ 140\times \left[ m_1 + exp(0.25*m_1)\right] + 110\times \left[ m_2 + exp(0.25*m_2)\right] +\\ 150\times \left[ m_3 + exp(0.25*m_3)\right] + 70\times \left[ m_4 + exp(0.25*m_4)\right] +\\ 30\times \left[ m_5 + exp(0.25*m_5)+ 45\right] \times \left[ m_6 + exp(0.25*m_6)\right] +\\ 65\times \left[ m_7 + exp(0.25*m_7)\right] \le 3000\\ 1\le m_1 \le 4,~~1\le m_2 \le 4,~~1\le m_3 \le 7,~~1\le m_4 \le 5,\\ 1\le m_5 \le 8,~~1\le m_6 \le 10,~~1\le m_7 \le 7 \end{array} \right. \end{aligned}$$
(30)
Table 6 Values of the crisp parameters
Full size table

The above multi-objective non-linear programming model Eq. (30) is solved by the Lingo version 16.0 optimization software. The resulting pay-off matrix of the problem is given in Eq. (31).

$$\begin{aligned} \begin{Bmatrix} Z_1&Z2\\ 0.9908414&~~~0.8311538\\ 0.8967782&~~~ 0.9989539 \end{Bmatrix} \end{aligned}$$
(31)

Therefore, the best and worst values for every objective can be defined as: \(0.8967782 \le Z_1 \le 0.9908414\), and \(0.8311538 \le Z_2 \le 0.9989539\).

In light of the equivalent crisp model Eq. (25), the Lingo optimization software version 16.0 is employed to obtain the compromise solution of the proposed model.The compromise solutions of all the three discussed techniques in section 5 are given in Table 7. The result indicated that the reliability of group x systems is \(R_X= 0.9903905\) and that of group Y is \(R_Y=0.9924332\) with various repaired components in the subsystems before the next production run as   \(m_1=1,~~m_2=4,~~m_3=2,~~m_4=2,~~m_5=6,~~m_6=5,~~m_7=3.\) It implies from Table 7 that components 1, 4 and 2 in subsystem 1, 2 and 3 have to be replaced, respectively. Likewise, components 2,6,5 and 3 in subsystem 4, 5, 6 and 7 have to be repaired, respectively.

Table 7 Compromise allocation for the repairable and replaceable components
Full size table

Comparison with the existing methods

The selective maintenance allocation problem of the reliability optimization problem is a fundamental decision making problem which occurs in real-life situations. From this viewpoint of the problem, our main objective is to find the compromise allocation of replaceable and repairable components while maximizing the reliability of the system. In this section, our main objective it shows the advantages of the proposed model and approach concerning some existing methods and related models. For instance, Cassady et al. [7, 8]; Rajagopalan and Cassady [38]; Liu and Huang [32]; Pandey et al. [35]; Khatab and Aghezzaf [27]; Galante et al. [15], solved a single objective selective maintenance problem. Still, we established and solve our model under the multiobjective case, which is more realistic for real-life reliability optimization problems. Khan et al. [26]; Ali and Hasan [1], Ali et al. [4]; Gupta et al. [22], have considered MO-SMAP under certainty environment. However, this research evaluated the proposed model under uncertainty environment because, in decision-making issues, the available data (i.e. the possible values of the system parameters) cannot always be precisely determined and known. In real-world situations, several different problems arise, such as uncertain judgments, unpredictable conditions or human error, partial or incomplete information in which decision-makers make decisions with available accurate data on the parameters of the problem. To overcome this drawback, the proposed model considered under uncertainty environment. From this perspective, our is more superior to tackle real-life reliability optimization problems.

Furthermore,the non-linear multi-objective selective maintenance optimization in the fuzzy environment has been formulated and solved by the proposed NGP. The problem are aslo solved by two other techniques discussed in section 5.4 and 5.5 . The results are presented in Table 7. The compromise solutions are compared with the proposed technique and are shown in Fig. 4. It can be observed that, the FP and IFP techniques have the same values while the propose NGP have different and better values of the compromise solution. Thus, we conclude that the NGP gives better results over the existing FP and IFP techniques.

Additionally, Ali and Hasan [1], Gupta et al. [21], Hassen et al. [23], Quddoos et al. [36], Diallo et al. [13], have considered different types of selective maintenance models and solved it using fuzzy programing and some other existing techniques. The fuzzy set concept, and the intuitionistic fuzzy set, can only handle incomplete or imprecise information. However, information related to indeterminacy or inconsistency cannot be address by those methods. The concept of the neutrosophic set is introduced to overcome this kind of information in the decision-making process. Neutrosophic logic is a non-standard research technique that reflects a mathematical model of complexity, vagueness, ambiguity, incompleteness and inconsistency. In Neutrosophic, indeterminacy is quantified directly, while truth, indeterminacy, and falsehood membership are independent. In some instances, this plays a crucial role in coping with inconsistent and incomplete information. Hence this research builds a new MO-SMAP model and solved using a new technique NGP and compared it with FG and IFG. From Table 7, it can quickly be seeing that NGP gives a better result.

Also, Ali et al. [4] considered a MO-SMAP under a stochastic environment to find the optimum number of replaceable and repairable components while maximizing the system reliability. After comparing the results, we can conclude that the proposed NGP technique for solving MO-SMAP is better. Application of NS concept is scorching and attractive research area nowadays, see [20].

Fig. 4
figure 4

Comparison among FP, IFP and NGP approaches

Full size image

Conclusion

In this paper, we have proposed a model under a non-deterministic environment. The main objective of the manuscript is to consider situations where the decision-makers have some neutral thoughts about whether the deteriorating components have to be replaced or repaired. The problem is modelled as a MO-SMAP, a new defuzzification technique based on beta distribution is introduced and used to convert the MO-SMAP fuzzy parameters into crips form. We then used the NGP technique to obtain the compromise allocation while maximizing the reliability of the system. The solution of the NGP is compared with that of FG and IFG techniques. Table 7 shows the solution comparison of the proposed method and the two other approach. It can be observed that the reliability values for the considered systems resulting from our model are better than the two different techniques; and hence, proofs to be more efficient. The proposed model is computational simple, and any available commercial optimization package can be easily used to solve the problem. The degree of satisfaction can be maximized and dissatisfaction is minimized using this concept. In future, we can consider the stochastic model for the selective maintenance allocation problems and used some other approaches. Also, A more extensive system can be used to explore more applicability of the model in system reliability.