Abstract
Topological index is a numerical value associated with a chemical constitution for correlation of chemical structure with various physical properties, chemical reactivity or biological activity. In this work, some new indices based on neighborhood degree sum of nodes are proposed. To make the computation of the novel indices convenient, an algorithm is designed. Quantitative structure property relationship (QSPR) study is a good statistical method for investigating drug activity or binding mode for different receptors. QSPR analysis of the newly introduced indices is studied here which reveals their predicting power. A comparative study of the novel indices with some well-known and mostly used indices in structure-property modelling and isomer discrimination is performed. Some mathematical properties of these indices are also discussed here.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The graph theory is a significant part of applied mathematics for modeling real life problems. The chemical graph theory, a fascinating branch of graph theory, provides many information on chemical compounds using an important tool called the topological index [4, 43]. Theoretical molecular descriptors alias topological indices are graph invariants that play an important role in chemistry, pharmaceutical sciences, materials science, engineering and so forth. Its role on QSPR/QSAR analysis [2, 22, 23, 37, 38], to model physical and chemical properties of molecules is also remarkable. Among several types of topological indices, vertex degree based [15] topological indices are most investigated and widely used. The first vertex degree based topological index is proposed in 1975 by Randić [36] known as Connectivity index or Randic index. Connectivity index is defined by
where \(d_{G}(u)\), \(d_{G}(v)\) represent the degree of nodes u,v in the vertex set V(G) of a molecular graph G. By molecular graph, we mean a simple connected graph considering atoms of chemical compound as vertices and the chemical bonds between them as edges. E(G) is the edge set of G. The inverse Randic index [19] is given by
The Zagreb indices, introduced by Gutman and Trinajestić [20], are defined as follows:
Furtula et al. [12] have introduced the forgotten topological index as follows:
Zhou and Trinanjstić have designed the sum connectivity index [49] which is as follows:
The symmetric division degree index [44] is defined as
The redefined third Zagreb index [39] is defined by
For more study about degree based topological indices, readers are referred to the articles [5, 10, 24, 25, 27, 32]. Recently, the present authors introduced some new indices [30, 31] based on neighborhood degree sum of nodes. As a continuation, we present here some new topological indices, named as first NDe index (\(\mathrm{ND}_{1}\)), second NDe index (\(\mathrm{ND}_{2}\)), third NDe index (\(\mathrm{ND}_{3}\)), fourth NDe index (\(\mathrm{ND}_{4}\)), fifth NDe index (\(\mathrm{ND}_{5}\)), and sixth NDe index (\(\mathrm{ND}_{6}\)) and defined as
where \(\delta _{G}(u)\) is the sum of degrees of all neighboring vertices of \(u \in V(G)\), i.e, \(\delta _{G}(u)=\sum \nolimits _{v \in N_{G}(u)}d_{G}(v)\), \(N_{G}(u)\) being the set of adjacent vertices of u. The goal of this article is to check the chemical applicability of the above newly designed indices and discuss about some bounds of them in terms of other topological descriptors to visualize the indices mathematically.
We construct the results into two different parts. We start the first part with an algorithm for computing the indices and then some statistical regression analysis have been made to check the efficiency of the novel indices to model physical and chemical properties. Then, we would like to test their degeneracy. It follows a comparative study of these indices with other topological indices. This part ends with a discussion about the applications of the present work. The second part deals with some mathematical relation of these indices with some other well-known indices.
Computational aspects
In this section, we have designed an algorithm to make the computation of the novel indices convenient.

To make it simple and understandable, we have considered some variables and matrices. We have used conn [E][2] matrix to store the connection details among vertices, whereas deg [V][2] and \(\delta [V][2]\) is the matrix to store degree of each vertex and neighborhood degree sum of vertex respectively. The novel indices can be considered as function of \(\delta _{G}(u)\),\(\delta _{G}(v)\),\(d_{G}(u)\), and \(d_{G}(v)\) i.e., f(\(\delta _{G}(u)\),\(\delta _{G}(v)\),\(d_{G}(u)\), \(d_{G}(v)\)).
Newly introduced indices in QSPR analysis
In this section, we have studied about the newly designed topological indices to model physico-chemical properties [Acentric Factor (Acent Fac.), entropy (S), enthalpy of vaporization (HVAP), standard enthalpy of vaporization (DHVAP), and heat capacity at P constant (CP)] of the octane isomers and physical properties [boiling points (bp), molar volumes (mv) at 20\(^\circ \)C, molar refraction (mr) at 20 \(^\circ \)C, heats of vaporization (hv) at 25 \(^\circ \)C, critical temperature (ct), critical pressure (cp) surface tensions (st) at 20 \(^\circ \)C and melting points (mp)] of the 67 alkanes from n-butanes to nonanes. The experimental values of physico-chemical properties of octane isomers (Table 1) are taken from http://www.moleculardescriptors.eu. The data related to 67 alkanes (Table 9) are compiled from [27]. For comparative study, different well-known existing descriptors are collected form http://www.moleculardescriptors.eu/books/books.htm. First, we have considered the octane isomers (Table 2) and then the 67 alkanes are taken into account.
Regression model for octane isomers
We have tested the following linear regression models
where P is the physical property and TI is the topological index. Using the above formula, we have the following linear regression models for different neighborhood degree sum based topological indices.
1. \(\mathrm{ND}_{1}\) index:
2. \(\mathrm{ND}_{2}\) index:
3. \(\mathrm{ND}_{3}\) index:
4. \(\mathrm{ND}_{4}\) index:
5. \(\mathrm{ND}_{5}\) index:
6. \(\mathrm{ND}_{6}\) index:
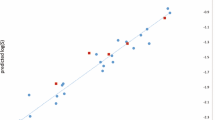
The correlations of the novel descriptors with different physico-chemical properties are depicted in the Figs. 1, 2, 3, 4, 5 and 6.
Now we describe above linear models in the Tables 3, 4, 5, 6, 7 and 8. Here c, m, r, SE, F, SF stands for intercept, slope, correlation coefficient, standard error, F test, and significance F respectively. Correlation coefficient tells how strong the linear relationship is. The standard error of the regression is the precision that the regression coefficient is measured. To check whether the results are reliable, Significance F can be useful. If this value is less than 0.05, then the model is statistically significant. If significance F is greater than 0.05, it is probably better to stop using that set of independent variable.
Regression model for 67 alkanes
We have tested here the model described in (1) for 67 alkanes from n-butanes to nonanes. we have the following linear regression models for different neighborhood degree sum-based topological indices.
1. \(\mathrm{ND}_{1}\) index:
2. \(\mathrm{ND}_{2}\) index:
3. \(\mathrm{ND}_{3}\) index:
4. \(\mathrm{ND}_{4}\) index:
5. \(\mathrm{ND}_{5}\) index:
6. \(\mathrm{ND}_{6}\) index:
The statistical parameters like previous discussion are used in Tables 11, 12, 13, 14, 15 and 16 to interpret the above regression models, where N denotes the total number of alkanes under consideration.
Several interesting observations on the data presented in Table 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16 can be made. From Table 3, the correlation coefficient of \(\mathrm{ND}_1\) index with entropy, acentric factor and DHVAP for octane isomers are found to be good (Fig. 1). Specially, it is strongly correlated with acentric factor having correlation coefficient \(r=-0.9904\). Also, the correlation of this index is good for the physical properties of 67 alkanes except for cp and mp having correlation coefficient values − 0.6941 and 0.2516, respectively. The range of correlation coefficient values lies from 0.7436 to 0.8981.
The QSPR analysis of \(\mathrm{ND}_2\) index reveals that this index is suitable to predict entropy, acentric factor and DHVAP of octane isomers (Fig. 2). In addition, one can say from Table 12 that, this index have remarkably good correlations with the physical properties of alkanes except mp. The correlation coefficients lies from 0.809 to 0.9638 except mp (\(r=0.2862\)). Surprisingly, the correlation of \(\mathrm{ND}_2\) with hv is very high with correlation coefficient value 0.9638.
Table 13 shows that \(\mathrm{ND}_3\) index is inadequate for any structure property correlation in the case of alkanes having the correlation coefficient values from 0.2036 to 0.7318. But, from Table 5, we can see that \(\mathrm{ND}_3\) is well correlated with entropy and acentric factor with correlation coefficients \(-0.9387\) and \(-0.9765\) respectively.
The QSPR analysis of \(\mathrm{ND}_4\) index shows that this index is well correlated with entropy, acentric factor, DHVAP, and HVAP for octane isomers (Table 6). Table 14 shows that \(\mathrm{ND}_4\) index is inadequate for structure property correlation in case of alkanes except cp and hv having correlation coefficients -0.8634 and 0.8679, respectively.
From Table 7, one can say that \(\mathrm{ND}_5\) does not sound so good except CP having correlation coefficient 0.8478. But this index can be considered as an useful tool to predict the physical properties of alkanes except cp and mp. This index is suitable to model bp, ct, mv, mr, hv, st with correlation coefficients 0.9166, 0.9779, 0.8881, 0.9319, 0.8950, and 0.9267, respectively.
The QSPR analysis of \(\mathrm{ND}_6\) index reveals that the correlation coefficient of this index with the physical properties of alkanes are very poor (Table 16). The range of correlation coefficient values lies from 0.2192 to 0.7823. But, when we look into the Table 8, we can say that this index has the ability to model entropy, acentric factor, and DHVAP for octane isomers.
Now we compare the modelling ability of the novel indices with some well-known and mostly used indices that include: First Zagreb index (\(M_1\)), second Zagreb index (\(M_2\)), Forgotten topological index (F), Sum connectivity index (SCI), Randić index (R), symmetric division deg index (SDD), Weiner index (W) [47], hyper Weiner index [37] (WW), terminal Wiener index (TW) [18], Schultz index (Sc) [41], first (\(S_1\)) and second status connectivity index (\(S_2\)) [34], Gutman index (GI) [16], degree distance index (DD) [6], inverse sum indeg status (ISIS) index [7], total eccentricity connectivity index (TECI) [1], first Zagreb eccentricity connectivity Index (ZECI\(_1\)) [13], first (\(\xi _1\)) and second eccentricity connectivity index (\(\xi _2\)) [29, 46], connective eccentricity index (CEI) [29, 46], vertex adjacency energy (E) [17], Laplacian energy (LE) [21], atom bond connectivity index (ABC) [8], augmented Zagreb index (AZI) [11], geometric arithmetic index (GA) [45], harmonic index (H) [9], Ashwini Index (A) [33], SM-index (SM) [42], vertex Zagreb energy (\(Z_{1}E\)) [26], forgotten energy (FE) [26], harmonic energy (HE) [26], geometric-arithmetic energy (GAE) [40], degree-sum energy (DSE) [35], sum-connectivity energy (SCE) [48], and Randić energy (RE) [3]. From Tables 3, 4, 5, 6, 7 to 8, it is clear that among six new indices, the \(\mathrm{ND}_1\) index can model acentric factor of octane isomers with excellent accuracy. To investigate the predictability of different well-established descriptors for acentric factor of octanes, linear regression analysis is performed and the outcomes are reported in Tables 17, 18, 19 and 20. From those findings, several observations can be made. The modulus of the correlation coefficient and the F value of \(\mathrm{ND}_1\) index is significantly high compared to the existing indices listed in Tables 17, table:comp2, table:comp3 and 20. The standard error and the SF value of the \(\mathrm{ND}_1\) index is lower than that of the indices reported in Tables 17, 18, 19 and 20. Thus, it can be concluded that the \(\mathrm{ND}_1\) index is efficient in predicting acentric factor of octanes with high accuracy compared to several well-known and mostly utilised molecular descriptors.
Now we are going to compare the new descriptors with the existing descriptors in structure-property modelling for 67 alkanes. Statistical parameters of linear regression models of different degree based indices, distance based indices and spectral indices are reported in [24, 26, 42]. We listed the correlation coefficients of those models in Tables 21, 22 and 23 for critical temperature (ct), critical pressure (cp) and surface tension (st). Form Tables 11, 12, 13, 14, 1516, 21, 22, 23, one can draw the following observations. Among all the newly proposed indices and the already existing indices listed in Tables 21, 22 and 23, the \(\mathrm{ND}_5\) index has remarkable correlation with ct and st, whereas for cp, the \(\mathrm{ND}_2\) index sounds the best. The rest parameters [24, 26, 42] are also in favour of \(\mathrm{ND}_2\) and \(\mathrm{ND}_5\) indices. Therefore, we can conclude that \(\mathrm{ND}_2\) and \(\mathrm{ND}_5\) indices outperform several well-established and mostly utilised descriptors in modelling cp, ct, and st for alkanes.
Correlation with some well-known indices
In this section, we investigate the correlation between the new indices and some well-known indices for octane isomers. It is clear from Table 24, that the new indices have a high correlation with the well-established indices except \(\mathrm{ND}_5\) index. Highest correlation coefficient (\(r=0.9977\)) is between \(\mathrm{ND}_1\) and \(M_{2}\). From Table 25, one can say that \(\mathrm{ND}_5\) has significantly low correlation coefficient with other indices. So we can conclude that \(\mathrm{ND}_5\) is independent among five indices. A correlation graph (Fig. 7) is drawn considering indices as vertices and two vertices are adjacent if and only if \(\vert r \vert \ge 0.95\).
Degeneracy
The objective of a topological index is to encipher the structural property as much as possible. Different structural formulae should be distinguished by a good topological descriptor. A major drawback of most topological indices is their degeneracy, i.e., two or more isomers possess the same topological index. Topological indices having high discriminating power captures more structural information. We use the measure of degeneracy known as sensitivity introduced by Konstantinova [28], which is defined as follows:
where N is the total number of isomers considered and \(N_I\) is the number of them that cannot be distinguished by the topological index I. As \(S_I\) increases, the isomer-discrimination power of topological indices increases. The vertex degree-based topological indices have more discriminating power in comparison with other classes of molecular descriptors. For octane and decane isomers, the newly introduced indices exhibit better response compared to some well-known degree-based indices (Table 26).
Applications
QSPR analysis is a powerful investigation for breaking down a molecule into a series of numerical values describing its relevant physico-chemical properties and biological activities. Descriptors having the strongest correlation in this study give information about essential functional groups of compounds under consideration. Accordingly, we can regulate pharmacological action or physico-chemical properties of drugs by modifying certain groups in the structure of medications. It is usually very costly to test a compound using a wet lab, but the QSPR study allow that cost to be reduced. This is generally used to analyze biological activities with specific properties associated with the structures and is helpful in understanding how molecular attributes in a drug effect biological activities. QSPR approaches can be used to develop models which can predict properties or activities of organic chemical. An efficient way of encoding structures with determined topological index is, therefore, necessary for the construction of accurate models. The indices used for the creation of model can offer a chance to concentrate on particular characteristics that account for the activity or property of interest in the compounds. QSPR analysis of some newly designed indices using octane isomers and alkanes is performed in this work. It has been shown that these indices can be considered as useful molecular descriptors in QSPR research. They yield excellent correlation with S, Acent Fac, HVAP, DHVAP, CP for octane isomers and bp, ct, cp, mv, mr,hv, st, mp for alkanes. Their isomer discrimination ability is also remarkable for octane and decane isomers. These indices are an extension of some well-known degree-based topological indices namely R, \(\mathrm{SCI}\), \(\mathrm{SDD}\), and \(\mathrm{ReZG}_{3}\). Sometimes the predictive power of these indices is superior, sometimes little bit inferior than that of the old indices. But the degeneracy test on Table 26, assures the supremacy of newly designed indices in comparison to the old indices. It is worth discussing the mathematical properties of the novel descriptors discussed in the following section.
Mathematical properties
In this section, we discuss about some bounds of the newly proposed indices with some well-known indices. Throughout this section, we consider simple connected graph. We construct this section with some standard inequalities. We start with the following inequality.
Lemma 1
(Radon’s inequality) If \(x_{i}, y_{i}> 0, i=1,2, \ldots ,n, t>0\), then
where equality holds iff \(x_i=ky_i\) for some constant k, \(\forall i=1,2, \ldots ,n.\)
Proposition 1
For a graph G having m edges with neighborhood version of second Zagreb index \(M_2^{*} (G)\) [31], we have
where equality holds iff G is regular or complete bipartite graph.
Proof
For a graph G, \(M_2^{*} (G)= \sum \nolimits _{uv \in E(G)}\delta _{G}(u)\delta _{G}(v)\). Now considering \(x_{i} =1, y_{i} =\delta _{G}(u)\delta _{G}(v), t = \frac{1}{2}\), in (2), we obtain
Now using the definition of \(\mathrm{ND}_{1}\) and \(M_2^{*}\) indices, we can easily obtain the required bound (3). Equality in (4) holds iff \(\delta _{G}(u)\delta _{G}(v)=k\), a constant \(\forall uv \in E(G)\). So the equality in (3) holds iff G is regular or complete bipartite graph.
Lemma 2
Let \(\mathbf {x}=(x_1,x_2, \ldots ,x_n)\) and \(\mathbf {y}=(y_1,y_2, \ldots ,y_n)\) be sequence of real numbers. Also let \(\mathbf {z}=(z_1,z_2, \ldots ,z_n)\) and \(\mathbf {w}=(w_1,w_2, \ldots ,w_n)\) be non-negative sequences. Then
In particular, if \(z_i\) and \(w_i\) are positive, then the equality holds iff \(\mathbf {x}=\mathbf {y}=\mathbf {k}\), where \(\mathbf {k}=(k,k,\ldots ,k)\), a constant sequence.
Proposition 2
For a graph G having m edges with neighbourhood version of second Zagreb index \(M_2^{*}(G)\), we have
where equality holds iff G is \(P_2\).
Proof
Considering \(x_{i} =\delta _{G}(u)\delta _{G}(v), y_{i} =1, z_{i} =1, w_{i} =1\), in (5), we get
After using the definition of \(\mathrm{ND}_1\) and \(M_2^{*}\) indices we can obtain
After simplification, the required bound is obvious.
From Lemma 2, the equality in (6) holds iff \(\delta _{G}(u)\delta _{G}(v)=1 \forall uv \in E(G)\),i.e. G is \(P_2\).
Remark
By arithmetic mean \(\ge \) geometric mean, we can write
So the upper bound of \(\mathrm{ND}_1 (G)\) obtained in Proposition 1, is better than that obtained in Proposition 2.
Proposition 3
For a graph G having second Zagreb index \(M_2 (G)\), forgotten topological index F(G) , neighbourhood version of hyper Zagreb index \(HM_N (G)\) [31], neighbourhood Zagreb index \(M_N (G)\) [30], we have
equality holds iff G is \(P_{2}\).
Proof
For a graph G, we have \(M_{N}(G) =\sum \nolimits _{v \in V(G)}\delta _{G}(v)^{2} =\sum \nolimits _{uv \in E(G)}[\delta _{G}(u)d_{G}(v)+\delta _{G}(v)d_{G}(u)]\), \(HM_{N}(G) = \sum \nolimits _{uv \in E(G)}[\delta _{G}(u)+\delta _{G}(v)]^{2}\). We know that for any two non-negative numbers x, y, arithmetic mean \(\ge \) geometric mean, i.e., \(\frac{x+y}{2} \ge \sqrt{xy},\) equality holds iff \(x=y\). Now considering \(x=d_G (u)+d_G (v)\), \(y=\delta _G (u)+\delta _G (v)\), we get
squiring both sides, we have
which gives
After simplifying and using the formulation of \(\mathrm{ND}_6\), F, \(M_2\), \(\mathrm{HM}_N\), and \(M_N\) indices, the required bound is clear. The equality in (7) occurs iff \(d_G (u)+d_G (v)= \delta _G (u)+\delta _G (v)\), i.e., G is \(P_2\). Hence the proof. \(\square \)
For a graph G consider
Thus \(\delta _{N} \le \delta _{G}(u) \le \Delta _{N}\) for all \(u \in V(G)\). Equality holds iff G is regular or complete bipartite graph. Clearly we have the following proposition.
Proposition 4
For a graph G with m number of edges, we have the following bounds.
-
(i)
\(m\delta _{N} \le \mathrm{ND}_{1}(G) \le m\Delta _{N}\),
-
(ii)
\(\frac{m}{\sqrt{2\Delta _{N}}} \le \mathrm{ND}_{2}(G) \le \frac{m}{\sqrt{2\delta _{N}}}\),
-
(iii)
\(2m\delta _{N}^{3} \le \mathrm{ND}_{3}(G) \le 2m\Delta _{N}^{3}\),
-
(iv)
\(\frac{m}{\Delta _{N}} \le \mathrm{ND}_{4}(G) \le \frac{m}{\delta _{N}}\),
-
(v)
\(\frac{F_{N}^{*}(G)-2M_{2}^{*}(G)}{\delta _{N}^{2}}+2m \le \frac{F_{N}^{*}(G)-2M_{2}^{*}(G)}{\Delta _{N}^{2}}+2m\),
where [31] \(F_{N}^{*}(G)= \sum \nolimits _{uv \in E(G)}[d_{G}(u)^{2}+d_{G}(v)^{2}].\)
Equality holds in each case iff G is regular or complete bipartite graph.
Lemma 3
Let \(a_i\) and \(b_i\) be two sequences of real numbers with \(a_i \ne 0\) (\(i=1,2, \ldots ,n\)) and such that \(pa_i \le b_i \le Pa_i\). Then
Equality holds iff either \(b_i=pa_i\) or \(b_i=Pa_i\) for every \(i=1,2, \ldots ,n.\)
Proposition 5
For a graph G with m edges having neighbourhood version of second Zagreb index \(M_2^{*}(G)\), we have
Equality holds iff G is regular or complete bipartite graph.
Proof
Putting \(a_{i}=1\), \(b_{i}=\sqrt{\delta _{G}(u)\delta _{G}(v)}\), \(p=\delta _{N}\), \(P=\Delta _{N}\) in 8, we get
Now applying the definition of \(M_2^{*}(G)\), \(\mathrm{ND}_1(G)\) in the above inequation, we obtain
Which implies
Equality holds iff \(\sqrt{\delta _{G}(u)\delta _{G}(v)} = \delta _{N}\) or \(\sqrt{\delta _{G}(u)\delta _{G}(v)} = \Delta _{N}\) for all \(uv \in E(G)\), i.e. G is regular or complete bipartite graph. Hence the proof. \(\square \)
Proposition 6
For a graph G of size m with fifth version of geometric arithmetic index \(GA_{5}\), and second Zagreb index \(M_{2}(G)\), we have
-
(i)
\(\mathrm{ND}_{5}(G) \ge \frac{2m^{2}}{ GA_{5}}\),
-
(ii)
\(\mathrm{ND}_{5}(G) \ge \frac{4M_{2}(G)^{2}}{m\Delta _{N}^{2}}-2m\).
Equality in both cases hold iff G is regular or complete bipartite graph.
Proof
-
(i)
For a graph G, we know that [14] \(GA_{5}(G)=\sum \nolimits _{uv \in E(G)}\frac{2\sqrt{\delta _{G}(u)\delta _{G}(v)}}{\delta _{G}(u)+\delta _{G}(v)}\). Now by Cauchy–Schwarz inequality, we have
$$\begin{aligned}&\left( \sum \limits _{uv \in E(G)}1 \right) ^{2} = \bigg (\sum \limits _{uv \in E(G)}\sqrt{\frac{\delta _{G}(u)+\delta _{G}(v)}{\sqrt{\delta _{G}(u)\delta _{G}(v)}}} \\&\qquad \times \frac{1}{\sqrt{\frac{\delta _{G}(u)+\delta _{G}(v)}{\sqrt{\delta _{G}(u)\delta _{G}(v)}}}}\bigg )^{2} \\&\quad \le \sum \limits _{uv \in E(G)}\frac{\delta _{G}(u)+\delta _{G}(v)}{\sqrt{\delta _{G}(u)\delta _{G}(v)}}\sum \limits _{uv \in E(G)}\frac{\sqrt{\delta _{G}(u)\delta _{G}(v)}}{\delta _{G}(u)+\delta _{G}(v)}. \end{aligned}$$Thus,
$$\begin{aligned} 2m^{2} \le GA_{5}(G)\sum \limits _{uv \in E(G)}\frac{\delta _{G}(u)+\delta _{G}(v)}{\sqrt{\delta _{G}(u)\delta _{G}(v)}}. \end{aligned}$$(9)We know that
$$\begin{aligned} \frac{\delta _{G}(u)}{\delta _{G}(v)}+\frac{\delta _{G}(v)}{\delta _{G}(u)} \ge \sqrt{\frac{\delta _{G}(u)}{\delta _{G}(v)}}+\sqrt{\frac{\delta _{G}(v)}{\delta _{G}(u)}}. \end{aligned}$$From 9, we obtain \(2m^{2} \le GA_{5}(G)\mathrm{ND}_{5}(G)\), i.e.
$$\begin{aligned} \mathrm{ND}_{5}(G) \ge \frac{2m^{2}}{ GA_{5}}. \end{aligned}$$Equality holds iff \(\frac{\delta _{G}(u)+\delta _{G}(v)}{\sqrt{\delta _{G}(u)\delta _{G}(v)}} = k\), a constant \(\forall uv \in E(G)\). That is, \(\delta _{G}(u) = {\text {some constant}} \times \delta _{G}(v)\) \(\forall uv \in E(G)\), i.e., G is regular or complete bipartite graph.
-
(ii)
By Cauchy–Schwarz inequality, we have
$$\begin{aligned} \mathrm{ND}_{5}(G)= & {} \sum \limits _{uv \in E(G)}\frac{[\delta _{G}(u)+\delta _{G}(v)]^{2}}{\delta _{G}(u)\delta _{G}(v)}-2m \\\ge & {} \frac{1}{\Delta _{N}^{2}}\sum \limits _{uv \in E(G)}[\delta _{G}(u)+\delta _{G}(v)]^{2}-2m\\= & {} \frac{1}{m\Delta _{N}^{2}}\sum \limits _{uv \in E(G)}1^{2}\sum \limits _{uv \in E(G)}[\delta _{G}(u)+\delta _{G}(v)]^{2} -2m \\\ge & {} \frac{1}{m\Delta _{N}^{2}}[\sum \limits _{uv \in E(G)}(\delta _{G}(u)+\delta _{G}(v))]^{2}-2m \\= & {} \frac{4M_{2}(G)^{2}}{m\Delta _{N}^{2}}-2m. \end{aligned}$$
Equality holds iff \(\delta _{G}(u)=\Delta _{N} = \delta _{G}(v)\) and \(\delta _{G}(u)+\delta _{G}(v) = c, \) a constant occur simultaneously for all \(uv \in E(G).\) That is, G is regular or complete bipartite graph.
Hence the proof \(\square \)
It is obvious that, \(\delta _G (u)\ge d_G (u)\) and \(\delta _G (v) \ge d_G (v)\), \(\forall uv \in E(G)\). Equality appears for \(P_2\) only. Keeping in mind this fact, we have the following proposition.
Proposition 7
For a graph G, having Randic index R(G), second Zagreb index \(M_2 (G)\), reciprocal Randic index \(\mathrm{RR}(G)\), sum-connectivity index \(\mathrm{SCI}(G)\), we have
-
(i)
\(\mathrm{ND}_{1}(G) \ge \mathrm{RR}(G)\)
-
(ii)
\(\mathrm{ND}_{2}(G) \ge \mathrm{SCI}(G)\)
-
(ii)
\(\mathrm{ND}_{3}(G) \ge \mathrm{ReZG}_{3}(G)\)
-
(iii)
\(\mathrm{ND}_{4}(G) \ge R(G)\)
-
(iv)
\(\mathrm{ND}_{5}(G) \le 2M_{2}(G)\)
-
(v)
\(\mathrm{ND}_{6}(G) \le 2M_{2}(G)\)
Equality holds in each case iff G is \(P_2\).
Conclusion
In this article, we have proposed some novel topological indices based on neighborhood degree sum of end vertices of edges. Their predictive ability have tested using octane isomers and alkanes from n-butanes to nonanes. These indices have demonstrated as useful molecular descriptors in QSPR study. These indices are an extension of some well established indices based on degree. The correlations between these new indices and the different properties and activities are often stronger, sometimes slightly weaker than the old indices. For octane isomers, the \(\mathrm{ND}_{1}\) index can model acentric factor with high precision compared to the existing indices under consideration. For alkanes, the \(\mathrm{ND}_{5}\) index is more effective in predicting ct and st compared to other well-known indices. The predictability of \(\mathrm{ND}_2\) index is remarkable for cp compared to the existing and often used topological indices. The sensitivity test (Table 26) confirms the supremacy of the novel indices compared to the old indices. We have also correlated these indices with other degree-based topological indices. This investigation on Tables 24, 25 concludes that \(\mathrm{ND}_{5}\) index is independent among all novel indices. This work ends with computing some bounds of these novel indices. For further research, these indices can be computed for various graph operations and some composite graphs and networks.
References
Ashrafi AR, Ghorbani M, Hossein-Zadeh MA (2011) The eccentric connectivity polynomial of some graph operations. Serdica J Comput 5:101–116
Balaban AT, Mills D, Ivanciuc O, Basak SC (2000) Reverse Wiener Indices. Croat Chem Acta 73:923–941
Bozkurt SB, Gutman I, Cevik AS (2010) Randić matrix and Randić energy. MATCH Commun Math Comput Chem 64:239–250
Devillers J, Balaban AT (1999) Topological indices and related descriptors in QSAR and QSPR. Gordon and Breach, London
De N, Nayeem SMA, Pal A (2016) F-index of some graph operations. Discrete Math Algorithms Appl 8:1650025
Dobrynin AA, Kochetova AA (1994) Degree-distance of a graph: a degree analogue of the Wiener index. J Chem Inf Comput Sci 34:1082–1086
Doley A, Buragohain J, Bharali A (2020) Inverse sum indeg status index of graphs and its applications to octane isomers and benzenoid hydrocarbons. Chemom Intell Lab Syst 203:104059
Estrada E (2008) Atom-bond connectivity and the energetic of branched alkanes. Chem Phys Lett 463:422–425
Fajtlowicz S (1987) On conjectures of graffiti II. Congr Numer 60:189–197
Furtula B, Das KC, Gutman I (2018) Comparative analysis of symmetric division deg index as potentially useful molecular descriptor. Int J Quantum Chem 118:e25659
Furtula B, Graovac A, Vukicević D (2010) Augmented Zagreb index. J Math Chem 48:370–380
Furtula B, Gutman I (2015) Forgotten topological index. J Math Chem 53:1184–1190
Ghorbani M, Hosseinzadeh MA (2012) A new version of Zagreb indices. Filomat 26:93–100
Graovac A, Ghorbani M, Hosseinzadeh MA (2011) Computing fifth geometric-arithmetic index for nanostar dendrimers. J Math Nanosci 1:32–42
Gutman I (2013) Degree-based topological indices. Croat Chem Acta 86:351–361
Gutman I (1994) Selected properties of the Schultz molecular topological index. J Chem Inf Model 34:1087–1089
Gutman I (1978) The energy of graph. Ber Math Stat Sekt Forshungsz Graz 103:1–22
Gutman I, Furtula B, Petrović M (2009) Terminal Wiener index. J Math Chem 46:522–531
Gutman I, Furtula B, Elphick C (2014) Three new/old vertex-degree-based topological indices. MATCH Commun Math Comput Chem 72:617–632
Gutman I, Trinajstić N (1972) Graph theory and molecular orbitals. Total \(\pi \)-electron energy of alternate hydrocarbons. Chem Phys Lett 17:535–538
Gutman I, Zhou B (2006) Laplacian energy of a graph. Lin Algebra Appl 414:29–37
Hawkins DM, Basak SC, Mills D (2003) Assessing model fit by cross-validation. J Chem Inf Comput Sci 43:579–586
Hawkins DM, Basak SC, Shi X (2001) QSAR with few compounds and many features. J Chem Inf Comput Sci 41:663–670
Hosamani SM (2017) Computing Sanskruti index of certain nanostructures. J Appl Math Comput 54:425–433
Hosamani SM, Malghan SH, Cangul IN (2015) The first geometric-arithmetic index of graph operations. Adv Appl Math Sci 14:155–163
Hosamani SM, Kulkarni BB, Boli RG, Gadag VM (2017) QSPR analysis of certain graph theocratical matrices and their corresponding energy. Appl Math Nonlinear Sci 2:131–150
Hosamani S, Perigidad D, Maled SJY, Gavade S (2017) QSPR analysis of certain degree based topological indices. J Stat Appl Pro 6:1–11
Konstantinova EV (1996) The discrimination ability of some topological and information distance indices for graphs of unbranched hexagonal systems. J Chem Inf Comput Sci 36:54–57
Li SC, Zhao LF (2016) On the extremal total reciprocal edge-eccentricity of trees. J Math Anal Appl 433:587–602
Mondal S, De N, Pal A (2020) On neighbourhood Zagreb index of product graphs. J Mol Struct 1223:129210
Mondal S, De N, Pal A (2019) On some new neighbourhood degree based indices. Acta Chem Iasi 27:31–46
Mondal S, De N, Pal A (2019) The M-polynomial of line graph of subdivision graphs. Commun Fac Sci Univ Ank Ser Al Math Stat 68:2104–2116
Plavsic D, Nikolić S, Trinajstić N (1993) On the Harary index for the characterization of chemical graphs. J Math Chem 12:235–250
Ramane HS, Yalnaik AS (2017) Status connectivity indices of graphs and its applications to the boiling point of benzenoid hydrocarbons. J Appl Math Comput 55:609–627
Ramane HS, Revankar DS, Patil JB (2013) Bounds for the degree sum eigenvalues and degree sum energy of a graph. Int J Pure Appl Math Sci 6:161–167
Randić M (1975) On Characterization of molecular branching. J Am Chem Soc 97:6609–6615
Randić M (1993) Comparative structure-property studies: regressions using a single descriptor. Croat Chem Acta 66:289–312
Randić M (1996) Quantitative structure-property relationship: boiling points and planar benzenoids. New J Chem 20:1001–1009
Ranjini PS, Lokesha V, Usha A (2013) Relation between phenylene and hexagonal squeeze using harmonic index. Int J Graph Theory 1:116–121
Rodríguez JM, Sigarreta JM (2015) Spectral study of the geometric-arithmetic index. MATCH Commun Math Comput Chem 74:121–135
Schultz HP (1989) Topological organic chemistry 1. Graph theory and topological indices of alkanes. J Chem Inf Comput Sci 29:227–228
Shirakol S, Kalyanshetti M, Hosamani SM (2019) QSPR analysis of certain distance based topological indices. Appl Math Nonlinear Sci 4:371–386
Todeschini R, Consonni V (2000) Handbook of molecular descriptors. Wiley-VCH, Weinheim
Vukicevic D (2010) Bond additive modeling 2 mathematical properties of max-min rodeg index. Croat Chem Acta 54:261–273
Vukicević D, Furtula B (2009) Topological index based on the ratios of geometrical and arithmetical means of end-vertex degrees of edges. J Math Chem 46:1369–1376
Wang G, Yan L, Zaman S, Zhang M (2020) The connective eccentricity index of graphs and its applications to octane isomers and benzenoid hydrocarbons. Int J Quantum Chem 2020:e26334
Wiener H (1947) Structural determination of paraffin boiling points. J Am Chem Soc 69:17–20
Zhou B, Trinajstić N (2010) On sum-connectivity matrix and sum-connectivity energy of (molecular) graphs. Acta Chim Slov 57:518–523
Zhou B, Trinajstić N (2009) On a novel connectivity index. J Math Chem 46:1252–1270
Acknowledgements
Funding was provided by the Department of Science and Technology (DST), Government of India (Grant no. IF170148).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mondal, S., Dey, A., De, N. et al. QSPR analysis of some novel neighbourhood degree-based topological descriptors. Complex Intell. Syst. 7, 977–996 (2021). https://doi.org/10.1007/s40747-020-00262-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-020-00262-0