Abstract
Genetic Programming (GP) is a popular and powerful evolutionary optimization algorithm that has a wide range of applications such as symbolic regression, classification and program synthesis. However, existing GPs often ignore the intrinsic structure of the ground truth equation of the symbolic regression problem. To improve the search efficacy of GP on symbolic regression problems by fully exploiting the intrinsic structure information, this paper proposes a genetic programming with separability detection technique (SD-GP). In the proposed SD-GP, a separability detection method is proposed to detect additive separable characteristics of input features from the observed data. Then based on the separability detection results, a chromosome representation is proposed, which utilizes multiple sub chromosomes to represent the final solution. Some sub chromosomes are used to construct separable sub functions by using separate input features, while the other sub chromosomes are used to construct sub functions by using all input features. The final solution is the weighted sum of all sub functions, and the optimal weights of sub functions are obtained by using the least squares method. In this way, the structure information can be learnt and the global search ability of GP can be maintained. Experimental results on synthetic problems with differing characteristics have demonstrated that the proposed SD-GP can perform better than several state-of-the-art GPs in terms of the success rate of finding the optimal solution and the convergence speed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Genetic programming (GP) is a popular and powerful evolutionary optimization algorithm that solves user-defined tasks by the evolution of computer programs [7, 10, 23]. It has attracted increasing attention from researchers in various research fields and a number of enhanced GP variants have been proposed recently, such as Cartesian genetic programming [14], Semantic Genetic Programming (SGP) [4, 9, 15], Grammatical evolution (GE) [16], Gene Expression Programming (GEP) [8, 22, 23], Linear Genetic Programming (LGP) [3] and Multiple Regression Genetic Programming (MRGP) [1]. So far, GP and its variants have been applied to a number of practical applications, including symbolic regression [24], classification [7], time series prediction problem [23] and program synthesis [11, 20].
In GPs, a solution is constructed by combining a set of primitives consisting of functions and input features. Thus, without exploiting the structure information in advance, to some extent, the searching process is merely recombination with the given building blocks. Most existing GPs [4, 8, 14, 16] search solutions in the entire search space directly without utilizing the relationships among input features to accelerate the search. As a result, they often suffer from low search efficacy on complicated symbolic regression problems.
In practical applications, however, the physical system that generates the observed data usually can be decomposed into a number of separable sub systems. Accordingly, the analytical function to model the system can be decomposed into a number of separable sub functions. By searching the sub functions in smaller sub spaces first and then building the final analytical function in a bottom-up manner, the solution structure can be fully exploited and the search efficacy could be improved significantly. Inspired by this, Luo et al. [12] recently proposed a block building programming (BBP) for symbolic regression. The BBP adopted a separability detection method to judge whether the target function is separable. Then, based on the detection results, the original target function is divided into several blocks and further into factors. The factors are then modeled by an optimization engine such as GP. However, to accomplish the separability detection task, the BBP requires the system being able to generate desired training data that satisfy certain constrains, which limits its application scopes. Udrescu and Tegmark [19] recently also developed a symbolic regression system (named AI Feynman) with a separability detection method. However, the separability detection method in AI Feynman requires a highly accurate neural network to predict the output of given input features, which is hard to construct. Besides, the separability detection method in AI Feynman has not yet been integrated with GP to improve the performance of GP.
To address the aforementioned issues, this paper proposes an efficient Genetic Programming with Separability Detection (SD-GP) for symbolic regression. In the proposed SD-GP, the separability detection method in BBP is extended to detect additive separable characteristic of the target model. Besides, by using a gaussian process surrogate model, the proposed method does not require the system be able to generate new data for separability detection, which is more flexible for practical use. Then, based on the separability detection results, a chromosome representation is proposed to encode solutions. The proposed chromosome representation consists of multiple sub chromosomes. These sub chromosomes generally consist of two kinds: the first kind is simply encoded by all the input features, while the second kind is the separated chromosomes that are encoded by the separable features. Notably, the chromosome encoded by all the input features is still maintained so as to enhance the stability of our method, considering that there can be some ground truth equation having no separable features. The final solution is a weighted sum of all sub functions, and the weights of sub functions are optimized using the least squares method. In this way, the proposed SD-GP can hopefully attain optimal solution efficiently and can ensure the global search ability even when the separability detection is not accurate enough.
The rest of the paper is organized as follows. “Preliminaries” presents related background techniques. “The proposed algorithm” describes the proposed SD-GP algorithm, followed by the experiment study in “Experiments and results”. Finally, “Conclusion” draws the conclusions and future work.
Preliminaries
In [12], Luo et al. proposed a separability detection technique named as the Bi-Correlation Test (BiCT). In this paper, we further extended the BiCT to detect the additive separable characteristics of input features in a more flexible manner. To facilitate reader better comprehend our method, we briefly describe the BiCT technique in this section. Generally, the BiCT aims to detect whether the given system is partially separable by calculating the correlation coefficient of certain sample data generated by the system.
Definition 1
A scalar function \(f(\mathbf {x})\) with n continuous variables \(\mathbf {x}=[x_{1}, x_{2},\) \(\dots , x_{n}]\) (\(f:\mathbb {R}^{n}\mapsto \mathbb {R}\), \(x\in \mathbb {R}^{n}\)) is partially separable if and only if it can be rewritten as
where \(c_{0}\) is a constant, \(\mathbf {x_{i}}\) represents a partition of the vector \(\mathbf {x}\) that contains \(n_{i}\) variables, \(\varphi _{i}\) is a scalar sub function (\(\varphi _{i}:\mathbb {R}^{n_{i}}\mapsto \mathbb {R}\)), and the binary operator \(\otimes _{i}\) can be plus (\(+\)), minus (−) and times (\(*\)), c is the number of separable partitions.
In order to test whether \(\mathbf {x_{test}}\) containing a certain part of the input variables can be separated from the input vector \(\mathbf {x}\) to form \(\mathbf {x_{i}}\) in Eq. (1), BiCT first constructs four input matrices \(\mathbf {X_{A}}\), \(\mathbf {X_{B}}\), \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\) for sampling. The structures of matrices \(\mathbf {X_{A}}\) and \(\mathbf {X_{B}}\) are described in (2).
where m and n are the variable numbers of vector \(\mathbf {x_{test}}=(x_{1},x_{2},\dots ,x_{m})\) and \(\mathbf {x}=(x_{1},x_{2},\dots ,x_{n})\), and N is the number of samples. The values of the first m columns which correspond to the sampling values of the variables in \(\mathbf {x_{test}}\), are the same in both \(\mathbf {X_{A}}\) and \(\mathbf {X_{B}}\) and make up the fixed matrix \(\mathbf {X_{fixed}}\). The rest \(n-m\) columns which represent the samples of remaining variables in \(\mathbf {x}\), are randomly sampled and form random matrices \(\mathbf {X_{random\_A}}\) and \(\mathbf {X_{random\_B}}\), respectively. The structures of matrices \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\) are similar to \(\mathbf {X_{A}}\) and \(\mathbf {X_{B}}\), but the random matrices in \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\) correspond to the variables in \(\mathbf {x_{test}}\), while the fixed matrix represents the samples of the remaining variables in the vector \(\mathbf {x}\).
The corresponding sampled outputs of \(\mathbf {X_{A}}\), \(\mathbf {X_{B}}\), \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\) are represented as \(\mathbf {Y_{A}}\), \(\mathbf {Y_{B}}\), \(\mathbf {Y_{C}}\) and \(\mathbf {Y_{D}}\), respectively. Then, the correlation coefficient \(r_{AB}\) between \(\mathbf {Y_{A}}\) and \(\mathbf {Y_{B}}\) is estimated as follows:
where N is the number of samples in \(\mathbf {Y_{A}}\) and \(\mathbf {Y_{b}}\), \(a_i\) and \(b_i\) are the i-th values in \(\mathbf {Y_{A}}\) and \(\mathbf {Y_{b}}\), \({\bar{a}}\) and \({\bar{b}}\) are the sample mean values of \(\mathbf {Y_{A}}\) and \(\mathbf {Y_{b}}\), and \(\sigma _{a}\) and \(\sigma _{b}\) are the sample standard deviations of \(\mathbf {Y_{A}}\) and \(\mathbf {Y_{b}}\). Similarly, \(r_{CD}\) can be obtained based on \(\mathbf {Y_{C}}\) and \(\mathbf {Y_{D}}\). If both \(r_{AB}\) and \(r_{CD}\) are both equal to 1, then it can be judged that the variables in \(\mathbf {x_{test}}\) can be separated from the input variables as a whole and the original data are partially separable.
Based on the above descriptions, we can find that the BiCT technique could not distinguish whether the system is separable in the form of addition or multiplication. Besides, the BiCT requires that the system can provide the outputs of randomly generated input features (i.e., \(\mathbf {X_{A}}\), \(\mathbf {X_{B}}\), \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\)). This requirement is usually not easy to satisfy when the given problem only provides a fixed set of data for training.
The proposed algorithm
In this section, we first describes the proposed surrogate-assisted additive separability detection method named as Surrogate-assisted Additive Bi-Correlation Test (SAA-BiCT). Then, the proposed genetic programming with SAA-BiCT is presented.
The surrogate-assisted additive bi-correlation test method
Although BiCT can effectively detect the separability from the observed data automatically, there are two shortcomings that limit its application. First, BiCT can only detect the features with separability, but is disable to distinguish whether the separable features are additive or multiplicative. For example, variables in \(f_1(x_{1},x_{2},x_{3})=x_{1}+x_{2}+x_{3}\) and \(f_2(x_{1},x_{2},x_{3})=x_{1}*x_{2}*x_{3}\) are considered to be partially separable when tested by BiCT, but the former function is additive combination and the latter is multiplicative combination. Second, if the problem only provides a fixed set of data for training, the special sampling input and output matrices for detection may not be available, which makes it inapplicable. To overcome the aforementioned issues, we proposed an enhanced additive separability detection method named SAA-BiCT.
In the SAA-BiCT, the same method as mentioned in Sect. 2 is utilized to construct input matrices \(\mathbf {X_{A}}\), \(\mathbf {X_{B}}\), \(\mathbf {X_{C}}\) and \(\mathbf {X_{D}}\). To avoid the limitation caused by insufficient data in the original data set, we adopt a Gaussian process regression (GPR) as the surrogate model to predict the output matrices of the four input matrices. Specially, in this paper, the Squared Exponential with Periodic Element is adopted as the kernel function of the GPR model, which can be expressed as follows:
where \(\sigma _f\), l and \(\sigma _n\) are hyper-parameters of the kernel function. The JADE [21] is adopted as the solver to optimize the hyper parameters of the GPR model.
After generating the input and output matrices, the proposed SAA-BiCT does not directly use their corresponding output matrices to calculate the linear correlation coefficients. Assuming the data dimension is n, and \(x_{1},\) \(x_{2}, \dots ,x_{m}\) are tested variables and \(\mathbf {x_{test}}=(x_{1},x_{2},\dots ,x_{m})\), we define the matrices \({\Gamma _\mathbf{test}}\) and \({\Gamma _\mathbf{rest}}\) as follows:
where N is the number of samples, \(\mathbf {x_{rest}}=(x_{1},x_{2},\dots ,x_{n-m})\) is a vector made up of the remaining input variables, and \(\zeta \) is a nonlinear function. Then matrices \(\mathbf {Y^{'}_{A}}\), \(\mathbf {Y^{'}_{B}}\), \(\mathbf {Y^{'}_{C}}\) and \(\mathbf {Y^{'}_{D}}\) can be obtained by
We use the newly constructed \(\mathbf {Y^{'}_{A}}\) and \(\mathbf {Y^{'}_{B}}\) to calculate the correlation coefficient \(r_{AB}\) and \(\mathbf {Y^{'}_{C}}\), and \(\mathbf {Y^{'}_{D}}\) to calculate \(r_{CD}\) by Eq. (3). If the results of \(r_{AB}\) and \(r_{CD}\) are 1, the variables in \(\mathbf {x_{test}}\) can be considered to be additively separable.
Based on the above mechanism, the proposed SAA-BiCT can distinguish the additive separable structures from the original data model. SAA-BiCT applies an additive separability factor to the process of testing, so that it can only test the model from the perspective of additive separability. For example, function \(f(x_{1},x_{2},x_{3},x_{4})=x_{1}*x_{2}*x_{3}*x_{4}\) is a multiplicative model. When SAA-BiCT tests whether \(x_{1}\) can be additively separable, a factor \(\zeta (x_{1})\) is added to the original model and extends the function to be \(f(x_{1},x_{2},x_{3},x_{4})=x_{1}*x_{2}*x_{3}*x_{4}+\zeta (x_{1})\). Then by calculating the correlation coefficients, SAA-BiCT can judge that \(x_{1}\) is not separable. It is worth pointing out that different \(\zeta \) forms can lead to different detection effects. In this paper, we adopt a simple \(\zeta \) function as shown in (7) which works well based on our empirical test.
Genetic programming with separability detection
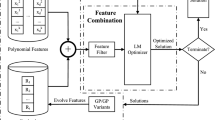
To harness the separability characteristic of the given problem to improve the search performance, the proposed SD-GP adopts a multi-chromosome representation method. In SD-GP, each sub chromosome represents a sub function of the model to be solved, and the final model is the weighted sum of all sub functions. Figure 1 illustrates the general framework of the proposed SD-GP. It first uses the SAA-BiCT to detect the additive separability of the observed model. Then, the original input variables are disassembled for each sub chromosome according to the additive separation features. The least squares estimator method is utilized to optimize the weight of each sub function. The population of chromosomes is repeatedly evolved using genetic operators such as crossover, mutation and selection, until the termination condition is met.
When testing separability on the observed data, traversing all combinations takes a lot of time. However, it is not necessary to perform the SAA-BiCT on all input variable combinations one by one under some circumstances. For instance, if the input variables are \(x_{1},x_{2},x_{3}\), there are 7 combinations, which are \((x_{1})\), \((x_{2})\), \((x_{3})\), \((x_{1},x_{2})\), \((x_{1},x_{3})\), \((x_{2},x_{3})\) and \((x_{1},x_{2},x_{3})\). A data set that contains n input variables contains \(C^{1}_{n}+C^{2}_{n}+\dots +C^{n}_{n}\) combinations of variables. As the number of variables increases, the computational time will increase dramatically. Whereas, in SAA-BiCT, we only need to test \((x_{1})\), \((x_{2})\) and \((x_{3})\) and totally test \(C^{1}_{n}+C^{2}_{n}+\dots +C^{\lfloor {n/2}\rfloor }_{n}\) times to achieve the same detection effect. In this paper, we aim to reduce the number of variables in each separated part so as to reduce the difficulty of searching the sub functions. Therefore, the proposed SAA-BiCT starts with combinations with fewer variables. That is, each single variable is tested at the beginning, and then the combinations of them. In addition, all variables to be tested are put into a vector before detection. Once variables or their combinations is separable, these variables are removed from the vector. If only combinations formed by the variables in the vector are detected, unnecessary detections can be avoided and the separable feature set can be obtained.
The encoded solution I of a chromosome in SD-GP is obtained by
where \(C_{i}\) is one of the sub chromosomes, \(\beta _{i}\) is the weight calculated by the least squares estimator method and k is the number of sub chromosomes. In this paper, we adopts the fixed-length gene expression encoding method to encode each sub chromosome \(C_{i}\).
Basic structure and implementation details of genetic programming
The basic structure of the gene expression chromosome contains a Head section and a Tail section. The Head section can contain both function symbols (e.g., \(+\), \(*\), \(\sin \)) and terminal symbols (e.g., \(x_{1}, x_{2}\)), while the Tail section can only contain terminal symbols. To ensure the whole chromosome can be decoded correctly, the length of Head (h) and Tail (t) must satisfy \(t=h\cdot (u-1)+1\), where u is the number of maximum operands of function symbols.
The process of using a chromosome to represent a mathematical function is as shown in Fig. 2. Given a string-based representation in Fig. 2, one should treat the first operator as the root node in encoding tree. Then, the rest symbols in the string are traversed in a breath-first-search fashion. That is, \(+\) and \(x_1\) should be the children of root node −, and \(*\) and \(\sin \) should be the children of the second symbol \(+\), and so on. With the constructed encoding tree, the equation \(x_1*x_1+\sin (x_2)-x_1\) can be obtained naturally.
The generation of sub chromosomes generally depends on the obtained additive separation features. Each separable group of variables is assigned to a sub chromosome, and the sub chromosome can only utilize the separable group of variables to construct sub function. To ensure the global search ability of the algorithm, an additional sub chromosome is added to each chromosome, which can utilize all variables involved to construct sub function. In SD-GP, the minimum number of sub chromosomes \(K_{min}\) (e.g., \(K_{min} = 5\)) is set in advance. When the number of separable variable sets found by SAA-BiCT is smaller than \(K_{min}\), the remaining sub chromosomes can utilize all variables to construct sub functions.
The SD-GP adopts SL-GEP [22] as the GP solver to evolve the above multi-chromosomes. The SL-GEP is a recently published GP variant which can efficiently search solution by using extended genetic operators borrowed from differential evolution (DE) [17, 21]. It should be noted that the SL-GEP adopts a gene expression chromosome representation with automatically defined functions (C-ADFs). In this paper, we only borrow the genetic operators of SL-GEP to evolve the proposed chromosomes. Generally, the evolutionary process in SL-GEP is composed of four main steps, which are initialization, mutation, crossover and selection. In the initialization, according to the chromosome structure, corresponding symbols are randomly assigned to the Head and Tail sections to form the initial chromosomes. Then the chromosomes are iteratively evolved through mutation, crossover and selection, until the termination condition is satisfied. In this paper, the algorithm will terminate when a pre-defined maximum number of generations is reached or a pre-defined satisfying solution is found.
Experiments and results
This section investigates the performance of the proposed SD-GP algorithm. First, the experimental settings, including the synthetic test problems, the compared algorithms and the parameter settings of all algorithms are described. Then, the comparison results are presented. Finally, the effectiveness of the separability detection of SAA-BiCT is discussed.
Experiment settings
To test the effectiveness of the proposed SD-GP for solving problems with separable additive structure, a synthetic problem set containing 15 symbolic regression problems with different features is designed for testing, as listed in Table 1. The problems can be divided into three categories: Category I is made up of basic multivariate problems. The problems in Category II have more complex forms with more square or even cubic structures, which are harder to be solved. Category III contains more function primitives, including \(\sin \), \(\cos \), \(\exp \) and \(\ln \). The format U[a, b, N] in column Data Set means that the number of samples is N and each input variable is randomly sampled in the interval (a, b).
To better evaluate the performance of the proposed SD-GP, we choose three other GP variants for comparison. The first algorithm is a modified SL-GEP [22] (labelled as S-SLGEP), which removes the ADFs in chromosome representation and uses least squares estimator method to create constants. Since the S-SLGEP is adopted as the fundamental component in the proposed method, comparison with S-SLGEP indicates the effectiveness of the proposed preprocessing component, SAA-BiCT.
The second algorithm is a multi-gene GP (SMGGP), which adopts the chromosome representation and genetic operators in SD-GP but abandons the separability detection technique. Comparison with SMGGP serves as component analysis to indicate the efficacy of the separability component. The last algorithm is the Genetic Programming Toolbox for the Identification of Physical Systems version 2 (GPTIPS-2) [18], a widely used open source genetic programming toolbox for multi-gene symbolic regression on MATLAB platform [2, 5, 6, 13]. SMGGP and GPTIPS-2 are multi-gene algorithms, but unlike SD-GP, they do not use the knowledge obtained from the observed data to assist the searching process, so the total number of their sub chromosomes (K) is fixed in advance. In our experiments, the parameter K of SMGGP and GPTIPS-2 is set to 5. For SD-GP, we set the minimum number of sub chromosomes \(K_{\min }=5\). The length of the string representing the sub chromosome (L) in SD-GP and SMGGP is 21. Because S-SLGEP is a single-chromosome GP algorithm, so to enhance its expression ability, its chromosome can contain more symbols than other three algorithms and its L is set to 81. For GPTIPS-2, the maximum depth (\(D_{\max }\)) of the GP tree is set to 4. In addition, the fitness value V of all algorithms is calculated by
where \(y_{i}\) is the output value calculated by the indicate chromosome and \(o_{i}\) is the real output value in the observed data set. The common parameters of SD-GP and S-SLGEP are set the same as suggested in SL-GEP [22]. Table 2 lists the important parameter settings of the proposed SD-GP.
Results and discussion
For each test problem, we run all algorithms for 30 independent times and count the total successful times for solving problems correctly. The experimental results are recorded in Table 3. Column SAA-BiCT in SD-GP shows whether SAA-BiCT is able to detect all additive separable features correctly from the input variables.
The experimental results show that the proposed SD-GP performs much better than other compared algorithms. In general, SMGGP, GPTIPS-2 and SD-GP, which adopt multi-gene encoding technique, perform significantly better than S-SLGEP which uses only a single chromosome. Among the three multi-gene algorithms, SD-GP performs the best, especially when SAA-BiCT can correctly detect all the additive separable features of the observed data. It is difficult for SMGGP and GPTIPS-2 to solve multivariate problems which contain many additive high-power structures, such as problems in Category II. However, with the detected knowledge, SD-GP can search efficiently on these problems.
In SD-GP, the number of sub chromosomes is determined by the number of separable features detected. In this way, SD-GP can adaptively adjust the chromosome size so as to fit the complexity of the problem. Meanwhile, both SMGGP and GPTIPS-2 use a fixed size of sub chromosomes to solve all problems, which is less flexible than the proposed SD-GP. For example, when they solve Problem 11 that requires 8 sub chromosomes, they cannot automatically increase the number of sub chromosomes, thereby weakening their problem-solving ability. Owing to SAA-BiCT, the SD-GP can overcome the above weakness. It should be noted that even when SAA-BiCT fails to detect correct separable features, SD-GP still has promising anti-interference ability to correct errors, just as what happened during the solution of Problem 3, Problem 10, Problem 11 and Problem 15. On Problem 10, SAA-BiCT wrongly considers that both \(x_{2}\) and \(x_{3}\) can be separated independently, but in reality they are only separable as a whole. However, since SD-GP uses extra sub chromosomes to contain all variables and limits the minimum number of sub chromosomes to 5, the separable part \(sin(x_{2}+x_{3})\) can be found by additional sub chromosomes successfully.
In order to further test the efficiency of SD-GP in finding correct solutions, we plot the convergence graphs of fitness values on nine canonical problems in Fig. 3, and six problems with relatively complex primitives in Fig. 4. The fitness values are obtained by Eq. (9). Thus the closer the fitness is to zero, the better the solution is. The results in Fig. 3 and Fig. 4 show that SD-GP always converges the fastest among the compared algorithms, which indicates that the proposed method is effective to improve the search efficiency of GP.
Finally, we test the additive separability detection capability of SAA-BiCT and BiCT. The variables that are mistakenly judged to be additive separable are listed in Table 4. It can be observed that BiCT has misjudgments on all multiplicative functions, which donates that it has no discerning ability to the multiplicative separation and additive separation. Meanwhile, SAA-BiCT can correctly identify the additive separability features on most cases. It is worth pointing out that the detection accuracy of SAA-BiCT is limited by the prediction accuracy and the calculation error, so misjudgments may occur sometimes.
Conclusion
In this paper, we proposed a genetic programming with separability detection technique (SD-GP) to improve the search efficacy of GP on symbolic regression problems with separable structures. SD-GP uses a separability detection method called SAA-BiCT to discover the additive separable features in the observed model, and then it generates and accelerates the evolution of sub chromosomes with the obtained knowledge. Experiments have indicated that SD-GP has advantages in problems with seperable structures compared to S-SLGEP, SMGGP and the widely used MATLAB toolbox GPTIPS-2. There are several future research directions. First, the proposed method can be further improved by designing a more accurate prediction method to assist the separability detection. Second, different forms of \(\zeta \) in Eq. (7) can be tried to achieve better separability detection results. Hereafter, with the separability detection component, the proposed algorithm can be further extended to high-dimensional scenario by reducing the computation overhead. In addition, the proposed algorithm framework can be further improved by incorporating other useful knowledge learned from the observed data, such as symmetry characteristic of input features.
Data availibility statement
The data sets used and /or analyzed during the present study are available from the corresponding author on reasonable request.
References
Arnaldo I, Krawiec K, O’Reilly UM (2014) Multiple regression genetic programming. In: Proceedings of the 2014 annual conference on genetic and evolutionary computation, GECCO ’14, pp. 879–886. Association for Computing Machinery, New York, NY, USA (2014). https://doi.org/10.1145/2576768.2598291
Astarabadi SSM, Ebadzadeh MM (2019) Genetic programming performance prediction and its application for symbolic regression problems. Inf Sci 502:418–433
Brameier MF, Banzhaf W (2007) Linear genetic programming. Springer, Berlin
Castelli M, Vanneschi L, Silva S (2014) Semantic search-based genetic programming and the effect of intron deletion. IEEE Trans Cybern 44(1):103–113
D’Angelo G, Palmieri F (2020) Knowledge elicitation based on genetic programming for non destructive testing of critical aerospace systems. Future Gen Comput Syst 102:633–642
D’Angelo G, Pilla R, Tascini C, Rampone S (2019) A proposal for distinguishing between bacterial and viral meningitis using genetic programming and decision trees. Soft Comput 23(22):11775–11791
Espejo PG, Ventura S, Herrera F (2010) A survey on the application of genetic programming to classification. IEEE Trans Syst Man Cybern Part C (Applications and Reviews) 40(2):121–144
Ferreira C (2001) Gene expression programming: a new adaptive algorithm for solving problems. Complex Syst 13(2):p8–129
Ffrancon R, Schoenauer M (2015) Memetic semantic genetic programming. In: Proceedings of the 2015 annual conference on genetic and evolutionary computation, pp 1023–1030. ACM
Koza JR (1992) Genetic Programming: vol. 1, On the programming of computers by means of natural selection, vol. 1. MIT press
Langdon WB, Harman M (2015) Optimizing existing software with genetic programming. IEEE Trans Evol Comput 19(1):118–135
Luo C, Chen C, Jiang Z (2017) A divide and conquer method for symbolic regression. arXiv e-prints arXiv:1705.08061
Mehr AD, Jabarnejad M, Nourani V (2019) Pareto-optimal mpsa-mggp: a new gene-annealing model for monthly rainfall forecasting. J Hydrol 571:406–415
Miller JF, Thomson P (2000) Cartesian genetic programming. Genetic programming. Springer, Berlin, pp 121–132
Moraglio A, Krawiec K, Johnson CG (2012) Geometric semantic genetic programming. International conference on parallel problem solving from nature. Springer, Berlin, pp 21–31
O’Neill M, Ryan C (2001) Grammatical evolution. IEEE Trans Evol Comput 5(4):349–358
Price K, Storn R, Lampinen J (2005) Differential evolution: a practical approach to global optimization, natural computing series. Springer, Berlin
Searson DP (2015) GPTIPS 2: an open-source software platform for symbolic data mining. Springer, Cham, pp 551–573. https://doi.org/10.1007/978-3-319-20883-1_22
Udrescu SM, Tegmark M (2020) Ai feynman: a physics-inspired method for symbolic regression. Sci Adv 6:16. https://advances.sciencemag.org/content/6/16/eaay2631
Weise T, Wan M, Tang K, Yao X (2014) Evolving exact integer algorithms with genetic programming. In: 2014 IEEE congress on evolutionary computation (CEC), pp 1816–1823
Zhang J, Sanderson AC (2009) Jade: adaptive differential evolution with optional external archive. IEEE Trans Evol Comput 13(5):945–958
Zhong J, Ong YS, Cai W (2016) Self-learning gene expression programming. IEEE Trans Evol Comput 20(1):65–80
Zhong J, Feng L, Ong Y (2017) Gene expression programming: a survey [review article]. IEEE Comput Intell Mag 12:54–72
Zhong J, Feng L, Cai W, Ong Y (2018) Multifactorial genetic programming for symbolic regression problems. In: IEEE transactions on systems, man, and cybernetics: systems, vol. 50, no. 11, pp. 4492–4505, Nov. 2020
Acknowledgements
This work is partially supported under the Key Project of Science and Technology Innovation 2030 supported by the Ministry of Science and Technology of China (Grant no. 2018AAA0101303), the National Natural Science Foundation of China (Grant no. 62076098), and the Fundamental Research Funds for the Central Universities (Grant no. D2191200).
Funding
This work was supported in part by the Key Project of Science and Technology Innovation 2030 supported by the Ministry of Science and Technology of China (Grant no. 2018AAA0101303) in part by the National Natural Science Foundation of China (Grant no. 62076098), and the Fundamental Research Funds for the Central Universities (Grant no. D2191200).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no competing interests.
Code availability
If published, the custom code described in the paper can be downloaded from https://www.jianguoyun.com/p/DQ5TLQUQrdfiCBj869ED.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, WL., Yang, J., Zhong, J. et al. Genetic programming with separability detection for symbolic regression. Complex Intell. Syst. 7, 1185–1194 (2021). https://doi.org/10.1007/s40747-020-00240-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-020-00240-6