A note on different types of product of neutrosophic graphs

Abstract

Fuzzy set and neutrosophic set are two efficient tools to handle the uncertainties and vagueness of any real-world problems. Neutrosophic set is more capable than fuzzy set to deal the uncertainties of a real-life problem. This research paper introduces some new concept of single-valued neutrosophic graph (SVNG). We have also presented some different operations on SVNG such as rejection, symmetric difference, maximal product, and residue product with appropriate examples, and some of their important theorems are also described. Then, we have described the concept of total degree of a neutrosophic graph with some interesting examples. We have also presented an efficient approach to solve a decision-making problem using SVNG.

Introduction

In 1965, Prof. Zadeh [25] presented a novel concept of fuzzy set theory which has been efficiently used to model the many real-world decision problems, which are generally uncertain. It is an extended version of crisp/classical set, where each and every objects of the fuzzy set have varying grades of membership value. Since, the simple classical set lies in 2 truth values (zero (false) and one (true)). For this reason, crisp set is not properly work with uncertainties of real-world problems. However, the type 1 fuzzy set provides its element to have the grade of membership within 0 and 1 which gives better results, rather of taking single value of 1 or 0. In a fuzzy set, the grade of membership of an object is not similar as the value of probability; however, it describes the belongingness grade of an object to that fuzzy set. The membership grade is a specific single value within zero and one. Decision-maker is unable to deal with the uncertainties of any complex real-life problem properly using those single value of membership grade. To overcome this problem of the type 1 fuzzy set, Atanassov [8] has extended the type 1 fuzzy set to an intuitionistic fuzzy set (IFS) by including a non-membership grade and a hesitancy grade of each and every element of the fuzzy set. It is capable to describe the elements of the fuzzy set from three different aspects of inferiority, superiority, and hesitation, which are generally modeled by the intuitionistic fuzzy numbers (IFNs). To handle more useful information of real-life problem under imprecise, vague, and uncertain environment, Smarandache [20, 21] has presented the novel idea of neutrosophic set, by generalizing the idea of IFS. The neutrosophic set can be used to capture the uncertainties due to inconsistent, vagueness, and indeterminate data of any problem. It is nothing but an extended edition of simple classical set, fuzzy set, and intuitionistic fuzzy set. In neutrosophic set, each object has 3 different types of membership grade: truth, false, and indeterminate. Those 3 membership grades of neutrosophic set are not dependent of each other and always with in ]0, 1[.

Graph is an efficient tool to model the real-life problems. By modeling the graph, the objects and their relations are symbolized by nodes and arcs. There exists many different types of information in real-life problems, and we need several types of graphs to model those problems such as fuzzy graph, intuitionistic fuzzy graphs, and neutrosophic graph theory [1, 6, 7, 9, 11, 23, 24]. Shannon and Atanassov [19] presented the concept of relationship between IFS. Then, they have introduced the concept of intuitionistic fuzzy graphs and presented many theorems in [19]. Parvathi et al. [12,13,14] proposed some operations between two intuitionistic fuzzy graphs. In [17], Rashmanlou et al. proposed many products operations such as lexicographic, direct product, strong product, and semi-strong product on intuitionistic fuzzy graphs. They have described the cartesian production, join, composition and union on intuitionistic fuzzy graphs in their paper. For further study on intuitionistic fuzzy graphs, please refer to [2, 15, 16, 18]. Smarandache [22] has introduced the n-SuperHyperGraph, with super-vertices that is the most general form of graph as today. Akram et al. [3,4,5] have introduced the idea of pythagorean fuzzy graph. They have described the several applications of pythagorean fuzzy graph in their paper. Neutrosophic graph [10] is used to model many real-world problem which consists of inconsistent information. Recently, many scientists have researched on graph in neutrosophic environment, for instance, Yang et al. [23], Arkam [6, 7], Ye [24], Naz et al. [11], and Broumi [9].

The main motivation of this research work is to present some effective methods for modeling and solving the decision-making problem (NSP) using the SVNG. In this paper, we define the regular SVNG, complete SVNG, and strong SVNG. Some different operations on SVNG such as rejection, symmetric difference, maximal product, and residue product are presented with appropriate examples. Then, the idea of degree and total degree of an SVNG are described under these operations with some examples. We have also introduced two new neutrosophic operators (neutrosophic weighted arithmetic average operator and neutrosophic weighted geometric average operator) to solve the neutrosophic decision-making problem. We have modeled a real-life problem for selecting the best hotel of city using SVNG and those two operators are used to solve this problem.

Single-valued neutrosophic set (SVNS)

Definition 2.1

(SVNS) Let X be a universe of discourse. A single-valued neutrosophic set ${\widetilde{S}}$ is defined on X is given by:

$$\begin{aligned} {\widetilde{S}}=\lbrace (x,T_{_{{\widetilde{S}}}}(x),I_{_{{\widetilde{S}}}}(x),F_{_{{\widetilde{S}}}}(x)):x\in X \rbrace , \end{aligned}$$

where $T_{_{{\widetilde{S}}}}(x):X\rightarrow [0,1]$, $I_{_{{\widetilde{S}}}}(x):X\rightarrow [0,1]$, $F_{_{{\widetilde{S}}}}(x):X\rightarrow [0,1]$ are called truth membership degree, indeterminacy membership degree, and falsity membership degree of x on ${\widetilde{S}}$, respectively, satisfy the condition $0\le T_{_{{\widetilde{S}}}}(x)+I_{_{{\widetilde{S}}}}(x)+F_{_{{\widetilde{S}}}}(x)\le 3$, $\forall x\in X$.

Definition 2.2

(Set operation on SVNS) Let ${\widetilde{A}}=\lbrace (x,T_{_{{\widetilde{A}}}}(x),I_{_{{\widetilde{A}}}}(x),F_{_{{\widetilde{A}}}}(x)):x\in X \rbrace$ and ${\widetilde{B}}=\lbrace (x,T_{_{{\widetilde{B}}}}(x),I_{_{{\widetilde{B}}}}(x),F_{_{{\widetilde{B}}}}(x)):x\in X \rbrace$ be two SVNSs. Then, some set operations can be defined as follows:

(i):

${\widetilde{A}}\subseteq {\widetilde{B}}$ iff $T_{_{{\widetilde{A}}}}(x)\le T_{_{{\widetilde{B}}}}(x)$, $I_{_{{\widetilde{A}}}}(x)\le I_{_{{\widetilde{B}}}}(x)$ and $F_{_{{\widetilde{A}}}}(x)\geqslant F_{_{{\widetilde{B}}}}(x)$, $\forall x\in X$;

(ii):

${\widetilde{A}}={\widetilde{B}}$ iff $A\subseteq {\widetilde{B}}$ and ${\widetilde{A}}\supseteq {\widetilde{B}}$;

(iii):

${\widetilde{A}}^{c}=\lbrace (x, F_{_{{\widetilde{A}}}}(x),I_{_{{\widetilde{A}}}}(x),T_{_{{\widetilde{A}}}}(x)):x\in X\rbrace$;

(iv):

${\widetilde{A}}\cup {\widetilde{B}}=\lbrace (x,T_{_{{\widetilde{A}}}}(x)\vee T_{_{{\widetilde{B}}}}(x),I_{_{{\widetilde{A}}}}(x)\vee I_{_{{\widetilde{B}}}}(x), F_{_{{\widetilde{A}}}}(x)\wedge T_{_{{\widetilde{B}}}}(x))\rbrace$;

(v):

${\widetilde{A}}\cap {\widetilde{B}}=\lbrace (x,T_{_{{\widetilde{A}}}}(x)\wedge T_{_{{\widetilde{B}}}}(x),I_{_{{\widetilde{A}}}}(x)\wedge I_{_{{\widetilde{B}}}}(x), F_{_{{\widetilde{A}}}}(x)\vee T_{_{{\widetilde{B}}}}(x))\rbrace$.

Definition 2.3

Single-valued neutrosophic relation (SVNR) Let X and Y be two universe of discourse, and ${\widetilde{P}}=(T_{{\widetilde{P}}},~I_{{\widetilde{P}}},~F_{{\widetilde{P}}})$ and ${\widetilde{Q}}=(T_{{\widetilde{Q}}},~I_{{\widetilde{Q}}},~F_{{\widetilde{Q}}})$ be two SVNS’s on X and Y, respectively. Then, the cartesian product of ${\widetilde{P}}$ and ${\widetilde{Q}}$ is given by: ${\widetilde{P}}\times {\widetilde{Q}}=\left\{ \left( (p,~q),~T_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q),~I_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q), F_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q) \right) :0\le T_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)+I_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)+F_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)\le 1,~\forall ~p\in X,q\in Y\right\}$ Here, $T_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)=T_{{\widetilde{P}}}(p)\wedge T_{{\widetilde{Q}}}(q)$, $I_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)=I_{{\widetilde{P}}}(p)\wedge I_{{\widetilde{Q}}}(q)$ and $F_{{\widetilde{P}}\times {\widetilde{Q}}}(p,~q)=F_{{\widetilde{P}}}(p)\vee F_{{\widetilde{Q}}}(q)$, $\forall ~p\in X,~q\in Y$. Then, an SVNS ${\widetilde{R}}\subseteq {\widetilde{P}}\times {\widetilde{Q}}$ is called an SVNR on ${\widetilde{P}}$ and ${\widetilde{Q}}$.

Single-valued neutrosophic graph (SVNG)

Definition 3.1

Let $G=(V_G,~E_G)$ be a graph containing no self-loop and parallel edges, where $V_G$ be the set of vertices and $E_G$ be the set of edges. Then, a single-valued neutrosophic graph of G is denoted by ${\widetilde{G}}=(V_G,~{\widetilde{\sigma }},~{\widetilde{\mu }})$, where ${\widetilde{\sigma }}=(T_{{\widetilde{\sigma }}},~I_{{\widetilde{\sigma }}},~F_{{\widetilde{\sigma }}})$ is an SVNS on $V_G$ and ${\widetilde{\mu }}=(T_{{\widetilde{\mu }}},~I_{{\widetilde{\mu }}},~F_{{\widetilde{\mu }}})$ is a single-valued neutrosophic symmetric relation on $E_G\subseteq V_G\times V_G$ $\Big ($ $T_{{\widetilde{\sigma }}}:V_G\rightarrow [0,~1]$, $I_{{\widetilde{\sigma }}}:V_G\rightarrow [0,~1]$, $F_{{\widetilde{\sigma }}}:V_G\rightarrow [0,~1]$, $T_{{\widetilde{\mu }}}:V_G\times V_G\rightarrow [0,~1]$, $I_{{\widetilde{\mu }}}:V_G\times V_G\rightarrow [0,~1]$, $F_{{\widetilde{\mu }}}:V_G\times V_G\rightarrow [0,~1]$ $\Big )$, and is defined as follows:

(i):

$T_{{\widetilde{\mu }}}((x,~y))\leqslant T_{{\widetilde{\sigma }}}(x)\wedge T_{{\widetilde{\sigma }}}(y)$, $\forall ~ (x,~y)\in V_G\times V_G$;

(ii):

$I_{{\widetilde{\mu }}}((x,~y))\leqslant I_{{\widetilde{\sigma }}}(x)\wedge I_{{\widetilde{\sigma }}}(y)$, $\forall ~ (x,~y)\in V_G\times V_G$;

(iii):

$F_{{\widetilde{\mu }}}((x,~y))\ge F_{{\widetilde{\sigma }}}(x)\vee F_{{\widetilde{\sigma }}}(y)$, $\forall ~ (x,~y)\in V_G\times V_G$;

If there is no edge between the vertices $\xi$ and $\eta$, then $T_{{\widetilde{\mu }}}((\xi ,~\eta ))=0,~I_{{\widetilde{\mu }}}((\xi ,~\eta ))=0~ \text{ and }~F_{{\widetilde{\mu }}}((\xi ,~\eta ))=0$. The SVNG ${\tilde{G}}$ is called strong SVNG, if $\forall ~ (x,~y)\in E_G$, $T_{{\widetilde{\mu }}}((x,~y))= T_{{\widetilde{\sigma }}}(x)\wedge T_{{\widetilde{\sigma }}}(y)$, $I_{{\widetilde{\mu }}}((x,~y))= I_{{\widetilde{\sigma }}}(x)\wedge I_{{\widetilde{\sigma }}}(y)$, and $F_{{\widetilde{\mu }}}((x,~y))= F_{{\widetilde{\sigma }}}(x)\vee F_{{\widetilde{\sigma }}}(y)$. ${\widetilde{G}}$ is said to be complete SVNG, if $\forall ~ x,~y \in V$, $T_{{\widetilde{\mu }}}((x,~y))= T_{{\widetilde{\sigma }}}(x)\wedge T_{{\widetilde{\sigma }}}(y)$, $I_{{\widetilde{\mu }}}((x,~y))= I_{{\widetilde{\sigma }}}(x)\wedge I_{{\widetilde{\sigma }}}(y)$, and $F_{{\widetilde{\mu }}}((x,~y))= F_{{\widetilde{\sigma }}}(x)\vee F_{{\widetilde{\sigma }}}(y)$. ${\widetilde{G}}$ is said to be regular SVNG, if $~\sum \nolimits _{x\ne y}T_{{\widetilde{\mu }}}((x,~y))= \text {constant}$, $\sum \nolimits _{x\ne y}I_{{\widetilde{\mu }}}((x,~y))= \text {constant}$, and $\sum \nolimits _{x\ne y} F_{{\widetilde{\mu }}}((x, y))= \text {constant}$.

Definition 3.2

(Degree and Total degree) Let ${\widetilde{G}}=(V_G, {\widetilde{\sigma }}, {\widetilde{\mu }})$ be the SVNG defined in Definition 3.1. The degree of a vertex $\xi \in V_G$ is denoted by $d_{{\widetilde{G}}}(\xi )=\left( (d_T)_{{\widetilde{G}}}(\xi ),~(d_I)_{{\widetilde{G}}}(\xi ), (d_F)_{{\widetilde{G}}}(\xi ) \right)$. Here, $(d_T)_{{\widetilde{G}}}(\xi )=\sum \nolimits _{\xi \eta \in E_G}T_{{\widetilde{\mu }}}{\xi \eta }$, $(d_I)_{{\widetilde{G}}}(\xi )=\sum \nolimits _{\xi \eta \in E_G}I_{{\widetilde{\mu }}}{\xi \eta }$ and $(d_F)_{{\widetilde{G}}}(\xi )=\sum \nolimits _{\xi \eta \in E_G}F_{{\widetilde{\mu }}}{\xi \eta }$. The total degree of a vertex $v\in V_G$ is denoted by $td_{{\widetilde{G}}}(v)=\left( (td_T)_{{\widetilde{G}}}(v), (td_I)_{{\widetilde{G}}}(v),~(td_F)_{{\widetilde{G}}}(v) \right)$. Here, $(td_T)_{{\widetilde{G}}}(v)=\sum \nolimits _{v\eta \in E_G}T_{{\widetilde{\mu }}}{vu}+T_{{\widetilde{\sigma }}}(u)$, $(d_I)_{{\widetilde{G}}}(v)=\sum \nolimits _{v\eta \in E_G}I_{{\widetilde{\mu }}}{vu}+I_{{\widetilde{\sigma }}}(u)$ and $(d_F)_{{\widetilde{G}}}(v)=\sum \nolimits _{vu\in E_G}F_{{\widetilde{\mu }}}{vu}+F_{{\widetilde{\sigma }}}(u)$.

Definition 3.3

(Rejection of two SVNG’s) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},~{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},~{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $P_{1}=(V_{P_1},~E_{P_1})$ and $P_{2}=(V_{P_2},E_{P_2})$, respectively, where ${\widetilde{\sigma }}_1=(T_{{\widetilde{\sigma }}_1},~I_{{\widetilde{\sigma }}_1},~F_{{\widetilde{\sigma }}_1})$, ${\widetilde{\mu }}_1=(T_{{\widetilde{\mu }}_1},~I_{{\widetilde{\mu }}_1},~F_{{\widetilde{\mu }}_1})$, ${\widetilde{\sigma }}_2=(T_{{\widetilde{\sigma }}_2},~I_{{\widetilde{\sigma }}_2},~F_{{\widetilde{\sigma }}_2})$, ${\widetilde{\mu }}_2=(T_{{\widetilde{\mu }}_2},~I_{{\widetilde{\mu }}_2},~F_{{\widetilde{\mu }}_2})$. Then, the rejection of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is denoted by ${\widetilde{P}}_{1}|{\widetilde{P}}_{2}=({\widetilde{\sigma }}_{1}|{\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{1}|{\widetilde{\mu }}_{2})$ and defined as:

(i):

$\forall (x,~y)\in V_{P_1}\times V_{P_2}$, $T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}}(x,~y)=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{2}}(y)$, $I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}}(x,~y)=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{2}}(y)$ and $F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}}(x,~y)=T_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{2}}(y)$;

(ii):

$\forall x\in V_{P_1}$ and $yz\notin E_{P_2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((x,~y)(x,~z))=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{2}}(y)\wedge T_{{\widetilde{\sigma }}_{2}}(z)$;

(b) $(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((x,~y)(x,~z))=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{2}}(y)\wedge I_{{\widetilde{\sigma }}_{2}}(z)$;

(c) $(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((x,~y)(x,~z))=F_{{\widetilde{\sigma }}_ {1}}(x)\vee F_{{\widetilde{\sigma }}_{2}}(y)\vee F_{{\widetilde{\sigma }}_{2}}(z)$;

(iii):

$\forall x\in V_{P_2}$ and $yz\notin E_{P_1}$,

(a) $(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((y,~x)(z,~x))=T_{{\widetilde{\sigma }}_{1}}(y)\wedge T_{{\widetilde{\sigma }}_{1}}(z)\wedge T_{{\widetilde{\sigma }}_{2}}(x)$;

(b) $(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((y,~x),(z,~x))=I_{{\widetilde{\sigma }}_{1}}(y)\wedge I_{{\widetilde{\sigma }}_{1}}(z)\wedge I_{{\widetilde{\sigma }}_{2}}(x)$;

(c) $(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((y,~x),(z,~x))=F_{{\widetilde{\sigma }}_{1}}(z)\vee F_{{\widetilde{\sigma }}_{1}}(y)\vee F_{{\widetilde{\sigma }}_{2}}(x)$;

(iv):

$\forall xy\notin E_{P_1}$ and $zw\notin E_{P_2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((x,~z)(y,~w))=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{1}}(y)\wedge T_{{\widetilde{\sigma }}_{2}}(z)\wedge T_{{\widetilde{\sigma }}_{2}}(w)$;

(b) $(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((x,~z)(y,~w))=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{1}}(y)\wedge I_{{\widetilde{\sigma }}_{2}}(z)\wedge I_{{\widetilde{\sigma }}_{2}}(w)$;

(c) $(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((x,~z)(y,~w))=F_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{1}}(y)\vee F_{{\widetilde{\sigma }}_{2}}(z)\vee F_{{\widetilde{\sigma }}_{2}}(w)$.

Example 1

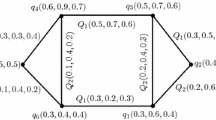
Consider two SVNGs ${\widetilde{P}}_{1}$ (shown in Fig. 1a) and ${\widetilde{P}}_{2}$ (shown in Fig. 1b) of the graphs $P_{1}$ and $P_{2}$, respectively. The rejection ${\widetilde{P}}_{1}|{\widetilde{P}}_{2}$ of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is shown in Fig. 1.

Fig. 1

SVNG ${\widetilde{P}}_{1}|{\widetilde{P}}_{2}$

Theorem 3.4

Let ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ be two SVNGs of the graph’s $G_{1}$ and $G_{2}$, respectively. Then, the rejection ${\widetilde{P}}_{1}|{\widetilde{P}}_{2}$ of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is an SVNG.

Proof

Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},~{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},~{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},~E_{1})$ and $G_{2}=(V_{2},~E_{2})$, respectively.

(i):

Let $\alpha \in V_{1}$ and $(\gamma ,\delta )\notin E_{2}$. Then:

$$\begin{aligned} \begin{aligned}&(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )). \end{aligned} \end{aligned}$$

(ii):

Let $(\alpha ,\beta )\notin E_{1}$ and $\gamma \in V_{2}$. Then:

$$\begin{aligned}&(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )).\\ \end{aligned}$$

(iii):

Let $(\alpha ,\beta )\notin E_{1}$ and $(\gamma ,\delta )\notin E_{2}$. Then:

$$\begin{aligned} \begin{aligned}&(T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((T_{{\widetilde{\sigma }}_{1}}| T_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )),\\&(I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )),\\&(F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee ((F_{{\widetilde{\sigma }}_{1}}| F_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )). \end{aligned} \end{aligned}$$

This completes the proof.

$\square$

Definition 3.5

(Degree of the rejection of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(d_{T})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge T_{{\widetilde{\sigma }}{2}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ),\\&(d_{I})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta )=\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}}\\&\quad I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge I_{{\widetilde{\sigma }}{2}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ),\\&(d_{F})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta ) =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}}\\&\quad F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\gamma )\vee F_{{\widetilde{\sigma }}{2}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta ). \end{aligned}$$

Definition 3.6

(Total degree of the rejection of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(td_{T})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta ) =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge T_{{\widetilde{\sigma }}{2}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{I})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}|I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge I_{{\widetilde{\sigma }}{2}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{F})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}|F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\notin E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\gamma )\vee F_{{\widetilde{\sigma }}{2}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\beta ). \end{aligned}$$

Example 2

We consider the SVNG ${\widetilde{P}}_{1}|{\widetilde{P}}_{2}$, as shown in Fig. 1. Then, the degree of the vertex $(\alpha ,~z)$ is $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z)=\left( (d_{T})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z),~(d_{I})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z),~(d_{F})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z)\right) =\left( 1.2,~0.8,~1.0 \right)$, and the total degree of the vertex $(\alpha ,~z)$ is $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z)=\left( (td_{T})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z),~(td_{I})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z), (td_{F})_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~z)\right) =\left( 1.8,~1.2,~1.5 \right)$. Similarly, the degree and total degree of the remaining vertices is given by: $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~x)=(0,~,0,~0)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~x)=(0.6,~0.4,~0.5)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~x)=(0,~,0,~0)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~x)=(0.7,~0.4,~0.6)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~y)=(1.2,~,0.8,~1.0)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~y)=(1.8,~1.2,~1.5)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~w)=(1.2,~,0.8,~1.0)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\alpha ,~w)=(1.8,~1.2,~1.3)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~y)=(1.4,~,1.0,~1.2)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~y)=(2.1,~1.5,~1.8)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~z)=(1.4,~,1.1,~1.2)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~z)=(2.1,~1.7,~1.8)$, $d_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~w)=(1.4,~,1.0,~1.2)$, $td_{{\widetilde{P}}_{1}|{\widetilde{P}}_{2}}(\beta ,~w)=(2.1,~1.7,~1.8)$.

Definition 3.7

(Symmetric difference) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. Then, the symmetric difference of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is denoted as ${\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}=({\widetilde{\sigma }}_{1}\oplus {\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{1}\oplus {\widetilde{\mu }}_{2})$ and defined as follows:

(i):

$\forall (x,y)\in V_{1}\times V_{2}$, $T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{2}}(y)$, $I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}}(x,y)=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{2}}(y)$ and $F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{2}}(y)$;

(ii):

$\forall x\in V_{1}$ and $(y,z)\in E_{2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\mu }}_{2}}(y,z)$;

(b) $(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\mu }}_{2}}(y,z)$;

(c) $(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=F_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\mu }}_{2}}(y,z)$;

(iii):

$\forall x\in V_{2}$ and $(y,z)\in E_{1}$,

(a) $(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=T_{{\widetilde{\mu }}_{1}}(y,z)\wedge T_{{\widetilde{\sigma }}_{2}}(x)$;

(b) $(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=I_{{\widetilde{\mu }}_{1}}(y,z)\wedge I_{{\widetilde{\sigma }}_{2}}(x)$;

(c) $(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=F_{{\widetilde{\mu }}_{1}}(z,y)\vee F_{{\widetilde{\sigma }}_{2}}(x)$;

(iv):

$\forall (x,y)\notin E_{1}$ and $(z,w)\in E_{2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{1}}(y)\wedge T_{{\widetilde{\mu }}_{2}}(z,w)$;

(b) $(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{1}}(y)\wedge I_{{\widetilde{\mu }}_{2}}(z,w)$;

(c) $(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=F_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{1}}(y)\vee F_{{\widetilde{\mu }}_{2}}(z,w)$;

(v):

$\forall (x,y)\in E_{1}$ and $(z,w)\notin E_{2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=T_{{\widetilde{\mu }}_{1}}(x,y)\wedge T_{{\widetilde{\sigma }}_{2}}(z)\wedge T_{{\widetilde{\sigma }}_{2}}(w)$;

(b) $(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=I_{{\widetilde{\mu }}_{1}}(x,y)\wedge I_{{\widetilde{\sigma }}_{2}}(z)\wedge I_{{\widetilde{\sigma }}_{2}}(w)$;

(c) $(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=F_{{\widetilde{\mu }}_{1}}(x,y)\vee F_{{\widetilde{\sigma }}_{2}}(z)\vee F_{{\widetilde{\sigma }}_{2}}(w)$.

Example 3

Consider two SVNGs ${\widetilde{A}}_{1}$ and ${\widetilde{A}}_{2}$ of the graphs $G_{1}$ and $G_{2}$, respectively, as shown in Fig.2a and Fig.2b. The symmetric difference ${\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}$ is shown in Fig. 2.

Fig. 2

SVNG ${\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}$

Theorem 3.8

Let ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ be two SVNGs of the graph’s $G_{1}$ and $G_{2}$, respectively. Then, the symmetric difference ${\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}$ of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is an SVNG.

Proof

Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively.

(i):

Let $\alpha \in V_{1}$ and $(\gamma ,\delta )\in E_{2}$. Then:

$$\begin{aligned}&(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee F_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )). \end{aligned}$$

(ii):

Let $(\alpha ,\beta )\in E_{1}$ and $\gamma \in V_{2}$. Then:

$$\begin{aligned}&(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =T_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge (T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )) \\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =I_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge (I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )) \\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =F_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee (F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )) \\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )). \end{aligned}$$

(iii):

Let $(\alpha ,\beta )\notin E_{1}$ and $(\gamma ,\delta )\in E_{2}$. Then:

$$\begin{aligned} \begin{aligned}&(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )),\\&(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )),\\&(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee ((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\beta ,\delta )). \end{aligned} \end{aligned}$$

(iv):

Let $(\alpha ,\beta )\in E_{1}$ and $(\gamma ,\delta )\notin E_{2}$. Then:

$$\begin{aligned}&(T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =T_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((T_{{\widetilde{\sigma }}_{1}}\oplus T_{{\widetilde{\sigma }}_{2}})(\beta ,\delta ),\\&(I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =I_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((I_{{\widetilde{\sigma }}_{1}}\oplus I_{{\widetilde{\sigma }}_{2}})(\beta ,\delta ),\\&(F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\delta )\\&\quad =F_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\quad =((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee ((F_{{\widetilde{\sigma }}_{1}}\oplus F_{{\widetilde{\sigma }}_{2}})(\beta ,\delta ). \end{aligned}$$

This completes the proof. $\square$

Definition 3.9

(Degree of the symmetric difference of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(d_{T})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\quad \wedge T_{{\widetilde{\sigma }}{2}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ),\\&(d_{I})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\quad \wedge I_{{\widetilde{\sigma }}{2}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ),\\&(d_{F})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\quad \vee F_{{\widetilde{\sigma }}{2}}(\beta )\wedge F_{{\widetilde{\sigma }}_{2}}(\delta ). \end{aligned}$$

Definition 3.10

(Total degree of the symmetric difference of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(td_{T})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}\oplus T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +T_{{\widetilde{\sigma }}_{1}}|T_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\wedge T_{{\widetilde{\sigma }}{2}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{I})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}\oplus I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\gamma )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\wedge I_{{\widetilde{\sigma }}{2}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{F})_{{\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}\oplus F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +\sum _{(\alpha ,\gamma )\notin E_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\gamma )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},(\beta ,\delta )\notin E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha ,\gamma )\\&\vee F_{{\widetilde{\sigma }}{2}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\delta )\\&\qquad +F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\beta ). \end{aligned}$$

Example 4

We consider the SVNG ${\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}$, as shown in Fig. 2. Then, the degree of the vertex $(v_1,~y_4)$ is $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4)=\left( (d_{T})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4),~(d_{I})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4),~(d_{F})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4)\right) =\left( 0.9,~0.7,~1.0 \right)$ and the total degree of the vertex $(v_1,~y_1)$ is $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4)=\left( (td_{T})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4),~(td_{I})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4), (td_{F})_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_4)\right) =\left( 1.4,~1.1,~1.8 \right)$. Similarly, the degree and total degree of the remaining vertices is given by $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_1)=(1.1,~,0.9,~2.8)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_1)=(1.6,~1.3,~3.5)$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_2)=(1.0,~,0.8,~2.5)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_2)=(1.5,~1.2,~3.2)$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_3)=(0.8,~,0.6,~3.0)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_1,~y_3)=(1.3,~1.0,~3.8)$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_1)=(1.1,~,0.9,~3.0)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_1)=(1.8,~1.3,~3.8$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_2)=(1.0,~,0.8,~3.0)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_2)=(1.7,~1.3,~3.8)$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_3)=(0.8,~,0.6,~3.2)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_3)=(1.5,~1.1,~4.0)$, $d_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_4)=(0.9,~,0.7,~3.2)$, $td_{{\widetilde{A}}_{1}\oplus {\widetilde{A}}_{2}}(v_2,~y_4)=(1.6,~1.1,~4.0)$.

Definition 3.11

(Residue product of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. Then, the residue product of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is denoted as ${\widetilde{P}}_{1}\bullet {\widetilde{P}}_{2}=({\widetilde{\sigma }}_{1}\bullet {\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{1}\bullet {\widetilde{\mu }}_{2})$ and defined as:

(i):

$\forall (x,y)\in V_{1}\times V_{2}$, $T_{{\widetilde{\sigma }}_{1}}\bullet T_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{2}}(y)$, $I_{{\widetilde{\sigma }}_{1}}\bullet I_{{\widetilde{\sigma }}_{2}}(x,y)=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{2}}(y)$ and $F_{{\widetilde{\sigma }}_{1}}\bullet F_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{2}}(y)$;

(ii):

$\forall (x,y)\in E_{1}$ and $z\ne w\in V_{2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}\bullet T_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=T_{{\widetilde{\mu }}_{1}}(x,y)$;

(b) $(I_{{\widetilde{\mu }}_{1}}\bullet I_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=I_{{\widetilde{\mu }}_{1}}(x,y)$;

(c) $(F_{{\widetilde{\mu }}_{1}}\bullet F_{{\widetilde{\mu }}_{2}})((x,z),(y,w))=F_{{\widetilde{\mu }}_{1}}(x,y)$.

Example 5

Consider two SVNGs ${\widetilde{B}}_{1}$ and ${\widetilde{B}}_{2}$ of the graphs $G_{1}$ and $G_{2}$, respectively, as shown in Fig. 3a, b.

The residue product ${\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}$ of SVNGs ${\widetilde{B}}_{1}$ and ${\widetilde{B}}_{2}$ is shown in Fig. 3.

Fig. 3

SVNG ${\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}$

Theorem 3.12

Let ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ be two SVNGs of the graph’s $G_{1}$ and $G_{2}$, respectively. Then, the residue product ${\widetilde{P}}_{1}\oplus {\widetilde{P}}_{2}$ of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is an SVNG.

Definition 3.13

(Degree of the residue product of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned} \begin{aligned}&(d_{T})_{P_{1}\bullet P_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}\bullet T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ),\\&(d_{I})_{P_{1}\bullet P_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}\bullet I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ),\\&(d_{F})_{P_{1}\bullet P_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}\bullet F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ). \end{aligned} \end{aligned}$$

Definition 3.14

(Total degree of the residue product of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(td_{T})_{{\widetilde{P}}_{1}\bullet {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}\bullet T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +T_{{\widetilde{\sigma }}_{1}}\bullet T_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma )\\&\qquad +T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{I})_{{\widetilde{P}}_{1}\bullet {\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}\bullet I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +I_{{\widetilde{\sigma }}_{1}}\bullet I_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma )\\&\qquad +I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{F})_{P_{1}\bullet P_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}\bullet F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +F_{{\widetilde{\sigma }}_{1}}\bullet F_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{(\alpha ,\gamma )\in E_{1},\beta \ne \delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma )\\&\qquad +F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\beta ). \end{aligned}$$

Example 6

We consider the SVNG ${\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}$, as shown in Fig. 3. Then, the degree of the vertex $(s_1,~t_1)$ is $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1)=\left( (d_{T})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1),~(d_{I})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1),~(d_{F})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1)\right) =\left( 0.2,~0.8,~0.4 \right)$ and the total degree of the vertex $(s_1,~t_1)$ is $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1)=\left( (td_{T})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1),~(td_{I})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1), (td_{F})_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_1)\right) =\left( 0.6,~1.3,~1.0 \right)$. Similarly, the degree and total degree of the remaining vertices is given by $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_2)=(0.2,~,0.8,~0.4)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_2)=(0.5,~1.3,~1.0)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_3)=(0.2,~,0.8,~0.4)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_1,~t_3)=(0.9,~1.2,~1.2)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_1)=(0.6,~,1.8,~0.6)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_1)=(0.8,~2.5,~1.1$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_2)=(0.6,~,1.8,~0.6)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_2)=(0.8,~2.4,~0.9)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_3)=(0.6,~,1.8,~0.6)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_2,~t_3)=(0.8,~2.2,~1.4)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_1)=(0.4,~,1.0,~0.2)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_1)=(1.0,~1.6,~0.7)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_2)=(0.4,~,1.0,~0.2)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_2)=(0.9,~1.6,~0.4)$, $d_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_3)=(0.4,~,1.0,~0.2)$, $td_{{\widetilde{B}}_{1}\bullet {\widetilde{B}}_{2}}(s_3,~t_3)=(1.1,~1.4,~1.0)$.

Definition 3.15

(Maximal product) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. Then, the maximal product of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is denoted as ${\widetilde{P}}_{1}* {\widetilde{P}}_{2}=({\widetilde{\sigma }}_{1}* {\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{1}*{\widetilde{\mu }}_{2})$ and defined as:

(i):

$\forall (x,y)\in V_{1}\times V_{2}$, $T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\sigma }}_{2}}(y)$, $I_{{\widetilde{\sigma }}_{1}}*I_{{\widetilde{\sigma }}_{2}}(x,y)=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\sigma }}_{2}}(y)$ and $F_{{\widetilde{\sigma }}_{1}}*F_{{\widetilde{\sigma }}_{2}}(x,y)=T_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\sigma }}_{2}}(y)$;

(ii):

$\forall x\in V_{1}$ and $(y,z)\in E_{2}$,

(a) $(T_{{\widetilde{\mu }}_{1}}* T_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=T_{{\widetilde{\sigma }}_{1}}(x)\wedge T_{{\widetilde{\mu }}_{2}}(y,z)$;

(b) $(I_{{\widetilde{\mu }}_{1}}* I_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=I_{{\widetilde{\sigma }}_{1}}(x)\wedge I_{{\widetilde{\mu }}_{2}}(y,z)$;

(c) $(F_{{\widetilde{\mu }}_{1}}* F_{{\widetilde{\mu }}_{2}})((x,y),(x,z))=F_{{\widetilde{\sigma }}_{1}}(x)\vee F_{{\widetilde{\mu }}_{2}}(y,z)$;

(iii):

$\forall x\in V_{2}$ and $(y,z)\in E_{1}$,

(a) $(T_{{\widetilde{\mu }}_{1}}* T_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=T_{{\widetilde{\mu }}_{1}}(y,z)\wedge T_{{\widetilde{\sigma }}_{2}}(x)$;

(b) $(I_{{\widetilde{\mu }}_{1}}* I_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=I_{{\widetilde{\mu }}_{1}}(y,z)\wedge I_{{\widetilde{\sigma }}_{2}}(x)$;

(c) $(F_{{\widetilde{\mu }}_{1}}* F_{{\widetilde{\mu }}_{2}})((y,x),(z,x))=F_{{\widetilde{\mu }}_{1}}(z,y)\vee F_{{\widetilde{\sigma }}_{2}}(x)$.

Example 7

Consider two SVNGs ${\widetilde{M}}_{1}$ and ${\widetilde{M}}_{2}$ of the graphs $G_{1}$ and $G_{2}$, respectively, as shown in Fig. 4a, b.

The rejection ${\widetilde{M}}_{1}*{\widetilde{M}}_{2}$ of ${\widetilde{M}}_{1}$ and ${\widetilde{M}}_{2}$ is shown in Fig. 4.

Fig. 4

SVNG ${\widetilde{M}}_{1}*{\widetilde{M}}_{2}$

Theorem 3.16

Let ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ be two SVNG’s of the graph’s $G_{1}$ and $G_{2}$, respectively. Then, the maximal product ${\widetilde{P}}_{1}*{\widetilde{P}}_{2}$ of ${\widetilde{P}}_{1}$ and ${\widetilde{P}}_{2}$ is an SVNG.

Proof

Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively.

(i):

Let $\alpha \in V_{1}$ and $(\gamma ,\delta )\in E_{2}$. Then:

$$\begin{aligned} \begin{aligned}&(T_{{\widetilde{\mu }}_{1}}*T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(I_{{\widetilde{\mu }}_{1}}*I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}*I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge ((I_{{\widetilde{\sigma }}_{1}}*I_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )),\\&(F_{{\widetilde{\mu }}_{1}}*F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\alpha ,\delta ))\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\gamma ,\delta )\\&\quad =F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\vee F_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\delta ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}*F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee ((F_{{\widetilde{\sigma }}_{1}}*F_{{\widetilde{\sigma }}_{2}})(\alpha ,\delta )). \end{aligned} \end{aligned}$$

(ii):

Let $(\alpha ,\beta )\in E_{1}$ and $\gamma \in V_{2}$. Then:

$$\begin{aligned}&(T_{{\widetilde{\mu }}_{1}}*T_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =T_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{1}}(\beta ))\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =(T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}(\beta )\wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(I_{{\widetilde{\mu }}_{1}}*I_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =I_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{1}}(\beta ))\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =(I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}(\beta )\wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((I_{{\widetilde{\sigma }}_{1}}*I_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\wedge (I_{{\widetilde{\sigma }}_{1}}*I_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )),\\&(F_{{\widetilde{\mu }}_{1}}*F_{{\widetilde{\mu }}_{2}})((\alpha ,\gamma ),(\beta ,\gamma ))\\&\quad =F_{{\widetilde{\mu }}_{1}}(\alpha ,\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{1}}(\beta ))\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =(F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}(\beta )\vee F_{{\widetilde{\sigma }}_{2}}(\gamma ))\\&\quad =((F_{{\widetilde{\sigma }}_{1}}*F_{{\widetilde{\sigma }}_{2}})(\alpha ,\gamma ))\vee (F_{{\widetilde{\sigma }}_{1}}*F_{{\widetilde{\sigma }}_{2}})(\beta ,\gamma )). \end{aligned}$$

This completes the proof.

$\square$

Definition 3.17

(Degree of the maximal product of two SVNG’s) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(d_{T})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}*T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma ),\\&(d_{I})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\qquad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}*I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma ),\\&(d_{F})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}*F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma ). \end{aligned}$$

Definition 3.18

(Total degree of the maximal product of two SVNGs) Let ${\widetilde{P}}_{1}=({\widetilde{\sigma }}_{1},{\widetilde{\mu }}_{1})$ and ${\widetilde{P}}_{2}=({\widetilde{\sigma }}_{2},{\widetilde{\mu }}_{2})$ be two SVNGs of the graphs $G_{1}=(V_{1},E_{1})$ and $G_{2}=(V_{2},E_{2})$, respectively. For any vertex $(\alpha ,\beta )\in V_{1}\times V_{2}$:

$$\begin{aligned}&(td_{T})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} T_{{\widetilde{\mu }}_{1}}|T_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +T_{{\widetilde{\sigma }}_{1}}*T_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}T_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge T_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +T_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge T_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{I})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} I_{{\widetilde{\mu }}_{1}}*I_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +I_{{\widetilde{\sigma }}_{1}}|I_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}I_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \wedge I_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +I_{{\widetilde{\sigma }}_{1}}(\alpha )\wedge I_{{\widetilde{\sigma }}_{2}}(\beta ),\\&(td_{F})_{{\widetilde{P}}_{1}*{\widetilde{P}}_{2}}(\alpha ,\beta )\\&\quad =\sum _{((\alpha ,\beta ),(\gamma ,\delta ))\in E_{1}\times E_{2}} F_{{\widetilde{\mu }}_{1}}*F_{{\widetilde{\mu }}_{2}}((\alpha ,\beta ),(\gamma ,\delta ))\\&\qquad +F_{{\widetilde{\sigma }}_{1}}|F_{{\widetilde{\sigma }}_{2}}(\alpha ,\beta )\\&\quad =\sum _{\alpha =\gamma \in V_{1},(\beta ,\delta )\in E_{2}}F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\mu }}_{2}}(\beta ,\delta )\\&\qquad +\sum _{(\alpha ,\gamma )\in E_{1},\beta =\delta \in V_{2}}F_{{\widetilde{\mu }}_{1}}(\alpha ,\gamma ) \vee F_{{\widetilde{\sigma }}_{2}}(\gamma )\\&\qquad +F_{{\widetilde{\sigma }}_{1}}(\alpha )\vee F_{{\widetilde{\sigma }}_{2}}(\beta ). \end{aligned}$$

Example 8

We consider the SVNG ${\widetilde{M}}_{1}*{\widetilde{M}}_{2}$, as shown in Fig. 4. Then, the degree of the vertex (a,  x) is $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x)=\left( (d_{T})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x),~(d_{I})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x),~(d_{F})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x)\right) =\left( 1.5,~0.5,~1.7\right)$ and the total degree of the vertex (a,  x) is $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x)=\left( (td_{T})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x), (td_{I})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x), (td_{F})_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~x)\right) =\left( 2.3,~0.7,~2.1 \right)$. Similarly, the degree and total degree of the remaining vertices is given by $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~x)=(0.86,~,1.14,~2.12)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~x)=(1.16,~1.84,~2.62)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~x)=(1.46,~0.94,~2.42)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~x)=(1.96,~1.34,~3.12)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~x)=(2.4,~0.4,~1.8)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~x)=(3.1,~0.5,~2.2)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~y)=(1.4,~0.5,~1.85)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~y)=(2.3,~0.7,~8.85)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~y)=(0.86,~1.14,,~2.6)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~y)=(1.16,~1.74,~3.3)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~y)=(1.46,~0.94,~2.8)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~y)=(1.96,~1.34,~3.5)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~y)=(1.6,~0.3,~1.35)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~y)=(2.1,~0.4,~2.15)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~z)=(1.1,~0.5,~1.55)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(a,~z)=(1.8,~0.7,~2.05)$, $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~z)=(0.86,~ 1.14,~2.02)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(b,~z)=(1.16,~1.74,~2.52)$ $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~z)=(1.36,~0.94,~2.42)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(c,~z)=(1.86,~1.34,~3.12)$ $d_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~z)=(1.5,~0.3,~1.65)$, $td_{{\widetilde{M}}_{1}*{\widetilde{M}}_{2}}(d,~z)=(2.2,~0.4,~2.35)$

Arithmetic average operator and geometric average operator in neutrosophic environment

Definition 4.1

Let ${\widetilde{P}}=(T_{_{{\widetilde{P}}}},~I_{_{{\widetilde{P}}}},~F_{_{{\widetilde{P}}}})$ and ${\widetilde{Q}}=(T_{_{{\widetilde{Q}}}},~I_{_{{\widetilde{Q}}}},~F_{_{{\widetilde{Q}}}})$ be two single-valued neutrosophic sets. Then, the operational relations between ${\widetilde{P}}$ and ${\widetilde{Q}}$ are defined as follows:

(i):

${\widetilde{P}}+{\widetilde{Q}}=\Big (T_{_{{\widetilde{P}}}}(x)+T_{_{{\widetilde{Q}}}}(x)-T_{_{{\widetilde{P}}}}(x)T_{_{{\widetilde{Q}}}}(x),~I_{_{{\widetilde{P}}}}(x)+I_{_{{\widetilde{Q}}}}(x)-I_{_{{\widetilde{P}}}}(x)I_{_{{\widetilde{Q}}}}(x),~F_{_{{\widetilde{P}}}}(x)+F_{_{{\widetilde{Q}}}}(x)-F_{_{{\widetilde{P}}}}(x)F_{_{{\widetilde{Q}}}}(x)\Big )$,

(ii):

${\widetilde{P}}\cdot {\widetilde{Q}}=\Big (T_{_{{\widetilde{P}}}}(x)T_{_{{\widetilde{Q}}}}(x),~I_{_{{\widetilde{P}}}}(x)I_{_{{\widetilde{Q}}}}(x),~F_{_{{\widetilde{P}}}}(x)F_{_{{\widetilde{Q}}}}(x)\Big )$,

(iii):

$a{\widetilde{P}}=\Big (1-(1-T_{_{{\widetilde{P}}}}(x))^a,~1-(1-I_{_{{\widetilde{P}}}}(x))^a,~(F_{_{{\widetilde{P}}}}(x))^a\Big )$, $a>0$,

(iv):

${\widetilde{P}}^a=\Big ((T_{_{{\widetilde{P}}}}(x))^a,~(I_{_{{\widetilde{P}}}}(x))^a,~1-(1-F_{_{{\widetilde{P}}}}(x))^a\Big )$, $a>0$.

Definition 4.2

Let ${\widetilde{P}}_r~(r=1,~2,\ldots ,~n)$ be n numbers single-valued neutrosophic sets. Then, the neutrosophic weighted arithmetic average operator of ${\widetilde{P}}_r$ with weight $w=(w_1,~w_2,\ldots ,~w_n)^t$ is denoted by $NWA^w({\widetilde{P}}_1,~{\widetilde{P}}_2,\ldots ,~{\widetilde{P}}_n)$ and is defined as follows:

$$\begin{aligned} \begin{aligned}&NWA^w({\widetilde{P}}_1,~{\widetilde{P}}_2,\ldots ,~{\widetilde{P}})=\sum _{r=1}^nw_r{\widetilde{P}}_r\\&=\bigg (1-\prod \limits _{r=1}^n(1-T_{_{{\widetilde{P}}_r}}(x))^{w_r},~1 -\prod \limits _{r=1}^n(1-I_{_{{\widetilde{P}}_r}}(x))^{w_r},\\&\quad ~\prod \limits _{r=1}^n(F_{_{{\widetilde{P}}_r}}(x))^{w_r}\bigg ), \end{aligned} \end{aligned}$$

where $\sum \nolimits _{r=1}^nw_r=1$.

Definition 4.3

Let ${\widetilde{Q}}_r~(r=1,~2,\ldots ,~n)$ be n numbers single-valued neutrosophic sets. Then, the neutrosophic weighted geometric average operator of ${\widetilde{Q}}_r$ with weight $w=(w_1,~w_2,\ldots ,~w_n)^t$ is denoted by $NWG^w({\widetilde{Q}}_1,~{\widetilde{Q}}_2,\ldots ,~{\widetilde{Q}}_n)$ and is defined as follows:

$$\begin{aligned} \begin{aligned}&NWG^w({\widetilde{Q}}_1,~{\widetilde{Q}}_2,\ldots ,~{\widetilde{Q}})=\prod _{r=1}^n{\widetilde{Q}}^{w_r}_r\\&=\bigg (\prod \limits _{r=1}^n(T_{_{{\widetilde{Q}}_r}}(x))^{w_r},~\prod \limits _{r=1}^n(I_{_{{\widetilde{Q}}_r}}(x))^{w_r}, 1-\prod \limits _{r=1}^n(1-F_{_{{\widetilde{P}}_r}}(x))^{w_r}\bigg ), \end{aligned} \end{aligned}$$

where $\sum \nolimits _{r=1}^nw_r=1$.

Score and accuracy value

Let ${\widetilde{P}}=(T_{_{{\widetilde{P}}}},~I_{_{{\widetilde{P}}}},~F_{_{{\widetilde{P}}}} )$ be a single-valued neutrosophic number. Then, its score and accuracy value is denoted by $S({\widetilde{P}})$ and $H({\widetilde{P}})$, respectively, and is defined as follows:

$$\begin{aligned} S({\widetilde{P}})=\frac{2+T_{_{{\widetilde{P}}}}-I_{_{{\widetilde{P}}}}-F_{_{{\widetilde{P}}}}}{3}~\text{ and }~H({\widetilde{P}})=(T_{_{{\widetilde{P}}}}-F_{_{{\widetilde{P}}}}). \end{aligned}$$

Comparison between neutrosophic numbers

Let ${\widetilde{P}}$ and ${\widetilde{Q}}$ be two neutrosophic numbers on the universe of discourse X. Then relation between ${\widetilde{P}}$ and ${\widetilde{Q}}$ is defined as follows:

(i):

if $S({\widetilde{P}})>S({\widetilde{Q}})$, ${\widetilde{P}}\succ {\widetilde{Q}}$

(ii):

if $S({\widetilde{P}})<S({\widetilde{Q}})$, ${\widetilde{P}}\prec {\widetilde{Q}}$

(iii):

if $S({\widetilde{P}})=S({\widetilde{Q}})$, then we have considered the following cases:

(a):

if $H({\widetilde{P}})>H({\widetilde{Q}})$, ${\widetilde{P}}\succ {\widetilde{Q}}$,

(b):

if $H({\widetilde{P}})<H({\widetilde{Q}})$, ${\widetilde{P}}\prec {\widetilde{Q}}$

(c):

if $H({\widetilde{P}})=H({\widetilde{Q}})$, ${\widetilde{P}}\approx {\widetilde{Q}}$.

Let ${\widetilde{A}}=\{{\widetilde{A}}_1,~{\widetilde{A}}_2,\ldots ,~{\widetilde{A}}_m\}$ be the set of alternatives and $C=\{C_1,~C_2,\ldots ,~C_n\}$ be the set of criteria. We consider that $w_j$ be the weight corresponding to the criteria $C_j$ $(j=1,~2,\ldots ,~n)$, such that $\sum \nolimits _{j=1}^nw_j=1$. In the decision-making problem, the evaluation information of the alternative ${\widetilde{A}}_i$ $(i=1,2,\ldots ,m)$ on the criteria is represented by the form of a single-valued neutrosophic number:

$$\begin{aligned} \begin{aligned} {\widetilde{A}}_i&=\{(C_j,~T_{_{{\widetilde{A}}_i}}(C_j),~I_{_{{\widetilde{A}}_i}}(C_j),~F_{_{{\widetilde{A}}_i}}(C_j)):0\le T_{_{{\widetilde{A}}_i}}(C_j)\\&\quad +I_{_{{\widetilde{A}}_i}}(C_j)+F_{_{{\widetilde{A}}_i}}(C_j)\le 3,~\forall ~ j=1,2,\ldots ,n\}\\&=(T_{i,j},I_{i,j},F_{i,j}). \end{aligned} \end{aligned}$$

Let ${\widetilde{a}}_{i,j}=(T_{i,j},I_{i,j},F_{i,j}),~i=1,2,\ldots ,m,~j=1,2,\ldots ,n.$

• Step 1. We construct single-valued neutrosophic decision matrix:

  $$\begin{aligned}&{\widetilde{D}}_{m,n} = ({\widetilde{a}}_{i,j})_{m,n}\\&\quad = \begin{pmatrix} (T_{1,1},I_{1,1},F_{1,1}) &{} (T_{1,2},I_{1,2},F_{1,2}) &{} \cdots &{} (T_{1,n},I_{1,n},F_{1,n}) \\ (T_{2,1},I_{2,1},F_{2,1}) &{} (T_{2,2},I_{2,2},F_{2,2}) &{} \cdots &{} (T_{2,n},I_{2,n},F_{2,n}) \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ (T_{m,1},I_{m,1},F_{m,1}) &{} (T_{m,2},I_{m,2},F_{m,2}) &{} \cdots &{} (T_{m,n},I_{m,n},F_{m,n}). \end{pmatrix} \end{aligned}$$

• Step 2. We aggregate the elements of each row of the decision matrix using neutrosophic arithmetic average operator:

  $$\begin{aligned} \begin{aligned} {\widetilde{R}}_i&=NWA^w({\widetilde{a}}_{i,1}, {\widetilde{a}}_{i,2}, \dots ,{\widetilde{a}}_{i,n})\\&=\bigg (1-\prod \limits _{j=1}^n(1-T_{i,j})^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-I_{i,j})^{w_j},~\prod \limits _{j=1}^n(F_{i,j})^{w_j}\bigg )\\&=\bigg (1-\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-I_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~\prod \limits _{j=1}^n(F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\bigg ). \end{aligned} \end{aligned}$$

• Step 3. Now, we evaluate score and accuracy value of ${\widetilde{R}}_i$:

$$\begin{aligned} \begin{aligned} S({\widetilde{R}}_i)&=\frac{2+\Big \{1-\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\Big \}-\Big \{1-\prod \limits _{j=1}^n(1-I_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\Big \}-\prod \limits _{j=1}^n(F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}}{3}\\&=\frac{2-\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}+\prod \limits _{j=1}^n(1-I_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-\prod \limits _{j=1}^n(F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}}{3} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} H({\widetilde{R}}_i)=1-\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-\prod \limits _{j=1}^n(F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}. \end{aligned} \end{aligned}$$

• Step 4. According to score and accuracy value, we ranking ${\widetilde{R}}_i$, i.e., ${\widetilde{A}}_i$, $i=1,2,...,n.$

Now, using neutrosophic arithmetic average operator on the neutrosophic decision matrix, we have solved the decision-making problem.

• Step 2. We aggregate the elements of each row of the decision matrix using neutrosophic geometric average operator:

  $$\begin{aligned} \begin{aligned} {\widetilde{Q}}_i&=NWG^w({\widetilde{a}}_{i,1}, {\widetilde{a}}_{i,2}, \cdots ,{\widetilde{a}}_{i,n})\\&=\bigg (\prod \limits _{j=1}^n(T_{i,j})^{w_j},~\prod \limits _{j=1}^n(I_{i,j})^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-F_{i,j})^{w_j}\bigg )\\&=\bigg (\prod \limits _{j=1}^n(T_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~\prod \limits _{j=1}^n(I_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\bigg ). \end{aligned} \end{aligned}$$
• Step 3.
  $$\begin{aligned} \begin{aligned}&S({\widetilde{Q}}_i)=\frac{2+\prod \limits _{j=1}^n(T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-\prod \limits _{j=1}^n(I_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-\Big \{1-\prod \limits _{j=1}^n(1-F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\Big \}}{3}\\&\quad =\frac{1+\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-\prod \limits _{j=1}^n(1-I_{_{{\widetilde{A}}_i}}(C_j))^{w_j}+\prod \limits _{j=1}^n(1-F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}}{3} \end{aligned} \end{aligned}$$

  and

  $$\begin{aligned} \begin{aligned} H({\widetilde{R}}_i)=\prod \limits _{j=1}^n(T_{_{{\widetilde{A}}_i}}(C_j))^{w_j}-1+\prod \limits _{j=1}^n(1-F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}. \end{aligned} \end{aligned}$$

• Step 4. According to score and accuracy value, we ranking ${\widetilde{Q}}_i$, i.e., ${\widetilde{A}}_i$, $i=1,2,...,n.$

Neutrosophic decision-making problem for the selection of best hotel

We consider a neutrosophic decision-making problem for choosing the best hotel from four hotels. Let the four hotels be $A_1$, $A_2$, $A_3$, and $A_4$. The decision-maker must decide according to the following four criteria:

• 1. $C_1$ is the customer review.

• 2. $C_2$ is the price.

• 3. $C_3$ is of food quality.

• 4. $C_4$ is the room quality and service.

The weight vector of the criteria is $w=(0.2,~0.3,~0.1,~0.4)$. When an expert gives his/her opinion about choosing hotel $A_1$ under criteria $C_1$, he/she must consider that the possibility in which the report is correct is 0.4, and the report is accurate is 0.2, and he/she is not sure it is 0.3. Therefore, in neutrosophic sense, it can be written as ${\widetilde{a}}_{1,1}=(0.4,~0.3,~0.2)$. If the expert considers the four alternatives $A_1,~A_2,~A_3,~A_4$ concerning four different criteria $C_1,~C_2,~C_3,C_4$, we obtain the neutrosophic decision matrix as follows:

$$\begin{aligned}&{\widetilde{D}}_{m,n} = ({\widetilde{a}}_{i,j})_{m,n}\\&\quad = \begin{pmatrix} (0.4,~0.3,~0.2) &{} (0.4,~0.6,~0.2) &{} (0.2,~0.5,~0.1) &{} (0.1,~0.2,~0.5) \\ (0.8,~0.1,~0.1) &{} (0.6,~0.2,~0.1) &{} (0.7,~0.3,~0.2) &{} (0.5,~0.1,~0.1) \\ (0.9,~0.1,~0.1) &{} (0.6,~0.3,~0.2) &{} (0.8,~0.8,~0.2) &{} (0.4,~0.7,~0.1) \\ (0.7,~0.4,~0.1) &{} (0.5,~0.3,~0.7) &{} (0.8,~0.1,~0.3) &{} (0.8,~0.4,~0.2) \end{pmatrix}. \end{aligned}$$

By aggregating the elements of each row of the decision matrix by using neutrosophic arithmetic average operator, we get:

$$\begin{aligned} \begin{aligned} {\widetilde{R}}_i&=NWA^w({\widetilde{a}}_{i,1}, {\widetilde{a}}_{i,2}, \cdots ,{\widetilde{a}}_{i,n})\\&=\bigg (1-\prod \limits _{j=1}^n(1-T_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-I_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~\prod \limits _{j=1}^n(F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\bigg ). \end{aligned} \end{aligned}$$

Hence:

$$\begin{aligned} \begin{aligned}&{\widetilde{R}}_1=(0.273758,~0.39637,~0.269217)\\&{\widetilde{R}}_2=(0.630066,~0.152807,~0.107177)\\&{\widetilde{R}}_3=(0.667355,~0.537268,~0.131951)\\&{\widetilde{R}}_4=(0.714484,~0.345598,~0.26403). \end{aligned} \end{aligned}$$

Now, we find score value of ${\widetilde{R}}_i$. $S({\widetilde{R}}_1)=0.536057$, $S({\widetilde{R}}_2)=0.790027$, $S({\widetilde{R}}_3)=0.666045$ and $S({\widetilde{R}}_4)=0.701619$. Based on the value of $S({\widetilde{R}}_i)~(i=1,2,3,4)$, we ranking the hotels ${\widetilde{A}}_i~(i=1,2,3,4)$ as follows: ${\widetilde{A}}_2\succ {\widetilde{A}}_4\succ {\widetilde{A}}_3\succ {\widetilde{A}}_1$. Hence, the best hotel is ${\widetilde{A}}_2$. Now, by aggregating the elements of each row of the decision matrix using neutrosophic geometric average operator:

$$\begin{aligned} \begin{aligned}&{\widetilde{Q}}_i=NWG^w({\widetilde{a}}_{i,1}, {\widetilde{a}}_{i,2}, \cdots ,{\widetilde{a}}_{i,n})\\&=\bigg (\prod \limits _{j=1}^n(T_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~\prod \limits _{j=1}^n(I_{_{{\widetilde{A}}_i}}(C_j))^{w_j},~1\\&\quad -\prod \limits _{j=1}^n(1-F_{_{{\widetilde{A}}_i}}(C_j))^{w_j}\bigg ).\\&{\widetilde{Q}}_1=(0.214355,~0.330505,~0.329255)\\&{\widetilde{Q}}_2=(0.600014,~0.137411,~0.110538)\\&{\widetilde{Q}}_3=(0.569412,~0.372807,~0.141419)\\&{\widetilde{Q}}_4=(0.676481,~0.319428,~0.397814). \end{aligned} \end{aligned}$$

Now, we find score and accuracy value of ${\widetilde{R}}_i$. $S({\widetilde{Q}}_1)=0.518198$, $S({\widetilde{R}}_2)=0.784022$, $S({\widetilde{R}}_3)=0.685062$ and $S({\widetilde{R}}_4)=0.65308$. Based on the value of $S({\widetilde{Q}}_i)~(i=1,2,3,4)$, we ranking the hotels ${\widetilde{A}}_i~(i=1,2,3,4)$ as follows: ${\widetilde{A}}_2\succ {\widetilde{A}}_3\succ {\widetilde{A}}_4\succ {\widetilde{A}}_1$. Hence, the best hotel is ${\widetilde{A}}_2$.

Conclusion

Graph theory has many real-life applications to the problems in operations research, computer network, economics, systems analysis, urban traffic planning, and transportation. In real-life scenarios, however, uncertainty may exist in almost every graph theoretic problem. SVNG is a well known and useful graph theory to model uncertain decision-making problem. This paper presents some new operations of SVNG. First, we describe the definition of regular SVNG, complete SVNG, and strong SVNG. Some different operations on SVNG such as rejection, symmetric difference, maximal product, and residue product are presented with appropriate examples, and some of their important theorems are described. We have also described some theorems about the total degree and degree under these operations with proper examples. We have also introduced two new neutrosophic operators (neutrosophic weighted arithmetic average operator and neutrosophic weighted geometric average operator) to solve the neutrosophic decision-making problem. We have modeled a real-life problem for selecting the best hotel of city using SVNG and those two operators are used to solve this problem. In future, we will try to study on single-valued neutrosophic intersection graphs, single-valued neutrosophic interval graphs, single-valued neutrosophic hypergraphs, and so on. The single-valued neutrosophic graph can be utilized to model the social network, image processing, telecommunication, expert systems, and computer networks.