Introduction

Transportation problem is one of the most important engineering problems arises when some products have to be transported from some sources to some sinks of a network. A typical form of transportation problem happens when the amount of products are to be transported from the sources to the sinks via some intermediate points like inventories. This typical form of transportation problem is called transshipment problem which is a two stage problem. This problem has been proposed by Orden [32] for the first time. The transshipment concept can also be applied to determine the shortest route from one node of a network to any other one Kumar et al. [21]. As an application of this problem, simultaneous determination of the flows in a network which connects the processors of products to the market points has been mathematically modeled by King and Logan [20]. A modification of this problem which considers a multi-customer, multi-product and multi-plant combination has been introduced by Judge et al. [13] where a linear programming technique was used. In continue, Hurt and Tramel [12] introduced different model versions for transshipment problem using concepts of general transportation model where the models obtain the solutions of the model of King and Logan [20] where no artificial variable is used. Garg and Prakash [8] focused on time-based transshipment problem where transshipment time had to be minimized. Khurana and Arora [18] proposed a three-dimensional linear transshipment problem. Khurana et al. [19] focused on time-based transshipment problem with given capacities of the commodities to be responded.

The standard (classic) version of transshipment problem is a typical linear minimization cost network flow problem. For such typical optimization problems, a variety of solution methods exists in its old and rich literature. A primal–dual approach hybridized by a cost scaling network simplex method was applied by Goldberg [11]. As another instance, Orlin [33] proposed a polynomial and strongly polynomial dual network simplex pivoting approaches. The above-mentioned approaches act according to capacity scaling methods.

In real-world applications, the parameters may be uncertain. Meaning that the values of parameters may vary in a range of values, may be a fuzzy number, may be determined stochastically, etc. (see [4, 9, 27, 29, 31, 36]). This case may happen for transshipment problem where the time and cost to pass the routes are not certain values. Baskaran et al. [1] considered the transshipment problem with transit points in fuzzy environment. Mohanpriya and Jeyanthi [28] proposed a modified solution approach for solving fuzzy transshipment problem by trapezoidal fuzzy parameters. Ghosh and Mondal [10] introduced a production and distribution planning problem. They used fuzzy transshipment problem for transposing the products between warehouses. A multi-criteria fuzzy transshipment problem for infectious waste management was solved by a new holistic approach by Wichapa and Khokhajaikiat [41]. Pathade et al. [34] developed a systematic approach for solving mixed constraint fuzzy balanced and unbalanced transportation problem. Kaur et al. [17] introduced a new and improved approach for solving the fully fuzzy transshipment problems. In the considered problems of this study the parameters are of the LR flat fuzzy numbers.

This study proposes a new version of two stage transshipment problem. The problem is modified where its all parameters are trapezoidal fuzzy numbers and its objective function is a fractional term which is the ratio of total shipment costs divided by its benefits. The problem is called fuzzy fractional two-stage transshipment problem. In the fuzzy fractional two-stage transshipment problem the obtained solution will have a fuzzy cost. Comparing to the fractional two-stage transshipment problem, the fuzzy fractional two-stage transshipment problem is more complex for solving. This difficulty happens as fuzzy numbers should be compared to obtain the minimal cost. This comparison is much more difficult than comparison between exact values. Optimizing the sum of ratio functions may happen in several real-world social and engineering problems like transportation problems, production engineering problems, government related problems, economical problems, etc. A rich and complete review of generalized fractional mathematical models and its applied area has been prepared by Frenk and Schaible [6] (see also [35, 37, 38]). The proposed fuzzy fractional two-stage transshipment problem needs some techniques to be solved. In this study all necessary techniques is applied. To this aim, an approach dealing with the fuzziness of the problem is constructed based on extension principle (which firstly was introduced in Zadeh [44] and Yager [43]. The extension principle is a popular and effective method that has been used to solve fuzzy combinatorial optimization problems (the works e.g. [22,23,24,25,26, 30] can be referred). Using this principle the problem is modeled as two two-level mathematical formulations to obtain a single lower bound and upper bound for given \(\alpha -\) cut (\(0 \le \alpha \le 1\)) of the fuzzy objective function value and the obtained values construct its membership function. To deal with the ratios of objective function of the problem for converting them to a linear form, a famous approach called Charnes–Cooper transformation is employed. Therefore, the novelties of this paper is summarized as below,

  • The fuzzy fractional two-stage transshipment problem is considered to be solved as a very complex problem which is not tackled in the literature.

  • The extension principle is used to solve the problem, therefore, no ranking function is applied in the solution approach. This is an advantage of the proposed solution approach.

  • The fractional non-linearity of the problem is fully linearized applying a Charnes–Cooper

  • transformation method.

  • Effectiveness of the proposed solution approach is proved by comparing it to the approaches of the literature.

This study is organized as follow. The next section presents some initial concepts of fuzzy sets and fuzzy numbers. The deterministic fractional two-stage transshipment problem and its fuzzy version is formulated in the following section while the next section presents the solution method of the fuzzy version of the problem. The following section highlights some advantages and properties of the proposed solution method. The next section an example is considered to prove the efficiency of the proposed solution method. The paper ends with conclusion.

Some primary concepts of fuzzy theory

Some required basic consepts of fuzzy theory is presented in this section. Below, we give some definitions and notations taken from Kaufmann and Gupta [15] and Kaufmann and Gupta [16].

Basic definitions

Definition 1

Let a set of elements x be denoted by X which is a nonempty set. A fuzzy set \(\tilde{A}\) in X is a set of pairs \((x,\mu_{{\tilde{A}}} (x))\) for \(x \in X\), that \(\mu_{{\tilde{A}}} \left( x \right):X \to \left[ {0,1} \right]\) is its membership function.

Definition 2

Considering \(\tilde{A}\) as a fuzzy subset of X has the support of \(S(\tilde{A})\) which is the crisp subset of X containing the elements having positive membership values in \(\tilde{A}\). The support is represented as \(S(\tilde{A}) = \left\{ {x \in X\left| {\mu_{{_{{\tilde{A}}} }} (x) > 0} \right.} \right\}\).

Definition 3

The subset \(\tilde{A}\) defined on X is a normal subset, if an \(x \in X\) can be found such that \(\mu_{{_{{\tilde{A}}} }} (x) = 1\).

Definition 4

The \(\alpha\)-cut crisp set of the fuzzy set \(\tilde{A}\) shown by the notation \(A_{\alpha }\) and is represented as \(A_{\alpha } = \left\{ {x \in X\left| {\mu_{{\tilde{A}}} (x) \ge \alpha } \right.} \right\}\).

Definition 5

The fuzzy set \(\tilde{A}\) is a convex set, if any \(x_{1} ,x_{2} \in S(\tilde{A})\) and \(\lambda \in [0,1]\) has the following condition.

$$ \mu_{{\tilde{A}}} \left( {\lambda x_{1} + \left( {1 - \lambda } \right)x_{2} } \right) \ge \min \left\{ {\mu_{{\tilde{A}}} \left( {x_{1} } \right),\,\mu_{{\tilde{A}}} \left( {x_{2} } \right)} \right\}. $$
(1)

Definition 6

A normal and convex fuzzy set \(\tilde{A}\) defined on \(X\), can be a fuzzy number where its membership function is of piecewise continuous type.

Definition 7

A fuzzy number \(\,\tilde{A} = \left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right)\) is a trapezoidal type fuzzy number, if it has a membership function as below.

$$ \mu_{{\tilde{A}}} \left( x \right) = \left\{ {\begin{array}{*{20}c} 0 &\quad {x \le a_{1} } \\ {\frac{{x - a_{1} }}{{a_{2} - a_{1} }}} &\quad {a_{1} \le x \le a_{2} } \\ 1 &\quad {a_{2} \le x \le a_{3} } \\ {\frac{{a_{4} - x}}{{a_{4} - a_{3} }}} &\quad {a_{3} \le x \le a_{4} } \\ 0 &\quad {x \ge a_{4} } \\ \end{array} } \right. $$
(2)

In the cases that \(a_{2} = \;a_{3}\) then \(\tilde{A} = \left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right)\) will be converted into \(\tilde{A} = \left( {a_{1} ,\;a_{2} ,\;a_{4} } \right)\) which is named triangular fuzzy number.

Definition 8

Considering \(\tilde{A} = \left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right)\) and \(\tilde{B} = \left( {b_{1} ,\;b_{2} ,\;b_{3} ,\;b_{4} } \right)\) as two positive trapezoidal fuzzy numbers, some mathematical operators of these numbers are defined by the following relationships.

$$ \begin{aligned} & \left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right) \oplus \left( {b_{1} ,\;b_{2} ,\;b_{3} ,\;b_{4} } \right) \\ &\quad= \left( {a_{1} + b_{1} ,\;a_{2} + b_{2} ,\;a_{3} + b_{3} ,\;a_{4} + b_{4} } \right) \end{aligned} $$
(3)
$$ \begin{aligned} & \left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right){ \ominus }\left( {b_{1} ,\;b_{2} ,\;b_{3} ,\;b_{4} } \right) \\ &\quad= \left( {a_{1} - b_{4} ,\;a_{2} - b_{3} ,\;a_{3} - b_{2} ,\;a_{4} - b_{1} } \right) \end{aligned} $$
(4)
$$ k.\left( {a_{1} ,\;a_{2} ,\;a_{3} ,\;a_{4} } \right) = \left\{ \begin{gathered} \left( {ka_{1} ,\;ka_{2} ,\;ka_{3} ,\;ka_{4} } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,k > 0, \hfill \\ \left( {ka_{4} ,\;ka_{3} ,\;ka_{2} ,\;ka_{1} } \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,k < 0, \hfill \\ \end{gathered} \right. $$
(5)

Extension principle

For the first time, the extension principle was introduced by Zadeh [44] and later was developed by Yager [43]. It is an important tool in the theory and application of fuzzy set and numbers. This principle extends a crisp function to a function which accept fuzzy sets as some arguments. The extension principle is described as below.

Let \(f\) be a function of \(X = X_{1} \times \ldots \times X_{n}\) to Y, such that \(f\left( {x_{1} ,\ldots,x_{n} } \right) = y\), and \(\tilde{A}_{i} \,\left( {i = 1,\ldots,n} \right)\) be n fuzzy sets in \(X_{i} \,\left( {i = 1,\ldots,n} \right)\). Then fuzzy set \(\tilde{B}\) in Y is defined as,

$$ \tilde{B} = \left\{ {\left( {y,\mu_{{\tilde{B}}} \left( y \right)} \right)|\,y = f\left( {x_{1} ,\ldots,x_{n} } \right),\,\left( {x_{1} ,\ldots,x_{n} } \right) \in X} \right\} $$
(6)

where,

$$ \mu_{{\tilde{B}}} \left( y \right) = \left\{ \begin{gathered} \mathop {\sup }\limits_{{(x_{1} ,\ldots,x_{n} ) \in f^{ - 1} (y)}} \min \left\{ {\mu_{{\tilde{A}_{1} }} \left( {x_{1} } \right),\ldots,\mu_{{\tilde{A}_{n} }} \left( {x_{n} } \right)} \right\} \hfill \\ 0 \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} \quad{{\text{if}}\,y \in {\text{range}}\,(f)} \\ \quad {{\text{if}}\,y \notin {\text{range}}\,(f)} \\ \end{array} $$
(7)

and \(f^{ - 1} (y) = \{ (x_{1} ,\ldots,x_{n} ) \in X|\,y = f(x_{1} ,\ldots,x_{n} )\}\).

Problem description and mathematical model

This section first introduces a deterministic fractional two-stage transshipment problem and then the problem is converted to a fuzzy one assuming that some of the parameters are fuzzy. The problem focused here, is a new problem, where, for the first time, fractionality of objective function is considered in the transshipment problem.

Consider a single product two-stage transshipment problem with a set of plants I, a set of depots J, and a set of customers K. Plant \(i \in \left\{ {1,2,\ldots,I} \right\}\) has capacity of \(a_{i}\), where, customer \(k \in \left\{ {1,2,\ldots,K} \right\}\) has a demand of \(b_{k}\)(which is also considered as the minimum satisfaction level for the demand of customer k). The total flow into each depot must be equal to the total flow out. The product can be shipped from any plant to any depot and from any depot to any customer, but not between any other ordered pair of locations. Based on the indices introduced above, \(c_{ij}\) is defined for shipping cost of a unit of product from plant i to depot j, while \(e_{ij}\) shows the profit of this shipping. On the other hand, \(d_{jk}\) is defined for shipping cost of a unit of product from depot j to customer k, while \(f_{jk}\) shows the profit of this shipping. As another parameters of the problem, \(g\) and \(h\) denote the total fixed cost and fixed benefit of the shipment. A typical and useful objective function for this problem can be defined by dividing the total shipping costs and total shipping benefits. This objective function is one of the applications of fractional programming which has been suggested by Schaible and Shi [38]. Minimizing this objective function, simultaneously minimizes the total costs and maximizes the total benefits. As variable, \(x_{ij}\) is defined as the amount of the product shipped from plant i to depot j (\(j \in \left\{ {1,2,\ldots,J} \right\}\)) and \(y_{jk}\) denotes the amount of product shipped from depot j to customer k. So, the deterministic mathematical formulation of this fractional two-stage transshipment problem is as follow,

$$ \begin{gathered} \min \,Z\left( {x,y} \right) = \frac{{\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{J} {c_{ij} } x_{ij} + \sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{K} {d_{jk} y_{jk} + g} } } }}{{\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{J} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } }} \hfill \\ {\text{subject to}} \hfill \\ \sum\limits_{j = 1}^{J} {x_{ij} \le } \,\,a_{i} \quad i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \sum\limits_{j = 1}^{J} {y_{jk} \ge b_{k} } \quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{I} {x_{ij} } = \sum\limits_{k = 1}^{K} {y_{jk} } \quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ x_{ij} ,y_{jk} \ge 0\quad i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\}. \hfill \\ \end{gathered} $$
(8)

In order to have feasible solutions in problem (8), the data of the problem should satisfy the equation \(\sum\limits_{i = 1}^{I} {a_{i} } \ge \sum\limits_{k = 1}^{K} {b_{k} }\). Since \(e_{ij}\), \(f_{jk}\) and \(h\) are all positive parameters, so, for any feasible solution of model (8), the equation \(\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {e_{ij} x_{ij} } } + \sum\limits_{j = 1}^{J} {\sum\limits_{k = 1}^{K} {f_{jk} y_{jk} } } + h > 0\) should also be held.

In many real word applications, most of the parameters like demand, capacity, cost, benefit, etc. cannot not have a constant value. The uncertainty of cost and benefit arises from the uncertain prices in market while the uncertainty of demand comes from the uncertain needs of customers. On the other hand, the capacity is considered as an uncertain parameter as a plant cannot always work with its full capacity because of some variations in labor productivity, rate of failure, unexpected work accidents, etc. Therefore, they may be changed in an uncertain environment. In order to consider such uncertainty in the proposed formulation (8), the parameters \(c_{ij} ,\,d_{jk} ,g,e_{ij} ,f_{jk} ,h,a_{i}\) and \(b_{k}\) are considered as fuzzy sets \(\tilde{C}_{ij} ,\,\tilde{D}_{jk} ,\tilde{G},\tilde{E}_{ij} ,\tilde{F}_{jk} ,\tilde{H},\tilde{A}_{i}\) and \(\tilde{B}_{k}\) with membership functions \(\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }}\) and \(\mu_{{\tilde{B}_{k} }}\) respectively. So, the proposed fractional two-stage transshipment problem, considering fuzzy parameters is reformulated as follow,

$$ \begin{gathered} \min \,Z\left( {x,y} \right) = \frac{{\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{J} {\tilde{C}_{ij} } x_{ij} + \sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{K} {\tilde{D}_{jk} y_{jk} + \tilde{G}} } } }}{{\sum\nolimits_{i = 1}^{I} {\sum\nolimits_{j = 1}^{J} {\tilde{E}_{ij} x_{ij} + \sum\nolimits_{j = 1}^{J} {\sum\nolimits_{k = 1}^{K} {\tilde{F}_{jk} y_{jk} + \tilde{H}} } } } }} \hfill \\ {\text{subject to}} \hfill \\ \sum\limits_{j = 1}^{J} {x_{ij} \le } \,\,\tilde{A}_{i} \quad i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \sum\limits_{j = 1}^{J} {y_{jk} \ge \tilde{B}_{k} } \quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{I} {x_{ij} } = \sum\limits_{k = 1}^{K} {y_{jk} } \quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ x_{ij} ,y_{jk} \ge 0\quad i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\}. \hfill \\ \end{gathered} $$
(9)

As crisp values may also be shown by singleton membership functions that include only a single value in their domain, in model (9), the objective function can take fuzzy number.

The proposed solution method

This section presents a solution method to the fuzzy transshipment problem introduced by model (9). The proposed method is a modification of the method of Liu [24] for model (9) and uses the extension principle [44], [43] to tackle the fuzzy fractional two-stage transshipment problem.

Considering \(\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }}\) and \(\mu_{{\tilde{B}_{k} }}\) as the membership functions of the fuzzy parameters \(\tilde{C}_{ij} ,\,\tilde{D}_{jk} ,\tilde{G},\tilde{E}_{ij} ,\tilde{F}_{jk} ,\tilde{H},\tilde{A}_{i}\) and \(\tilde{B}_{k}\) respectively, we will have,

$$ \begin{gathered} \tilde{C}_{ij} = \left\{ {\left( {c_{ij} ,\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right)} \right)|c_{ij} \in S\left( {\tilde{C}_{ij} } \right)} \right\} \hfill \\ \tilde{D}_{jk} = \left\{ {\left( {d_{jk} ,\mu_{{\tilde{D}_{jk} }} \left( {d_{jk} } \right)} \right)|d_{jk} \in S\left( {\tilde{D}_{jk} } \right)} \right\} \hfill \\ \tilde{G} = \left\{ {\left( {g,\mu_{{\tilde{G}}} \left( g \right)} \right)|g \in S\left( {\tilde{G}} \right)} \right\} \hfill \\ \tilde{E}_{ij} = \left\{ {\left( {e_{ij} ,\mu_{{\tilde{E}_{ij} }} \left( {e_{ij} } \right)} \right)|e_{ij} \in S\left( {\tilde{E}_{ij} } \right)} \right\} \hfill \\ \tilde{F}_{jk} = \left\{ {\left( {f_{jk} ,\mu_{{\tilde{F}_{jk} }} \left( {f_{jk} } \right)} \right)|f_{jk} \in S\left( {\tilde{F}_{jk} } \right)} \right\} \hfill \\ \tilde{H} = \left\{ {\left( {h,\mu_{{\tilde{H}}} \left( h \right)} \right)|h \in S\left( {\tilde{H}} \right)} \right\} \hfill \\ \tilde{A}_{i} = \left\{ {\left( {a_{i} ,\mu_{{\tilde{A}_{i} }} \left( {c_{ij} } \right)} \right)|a_{i} \in S\left( {\tilde{A}_{i} } \right)} \right\} \hfill \\ \tilde{B}_{k} = \left\{ {\left( {b_{k} ,\mu_{{\tilde{B}_{k} }} \left( {b_{k} } \right)} \right)|b_{k} \in S\left( {\tilde{B}_{k} } \right)} \right\} \hfill \\ \end{gathered} $$
(10)

where, \(S\left( {\tilde{C}_{ij} } \right),\,S\left( {\tilde{D}_{jk} } \right),S\left( {\tilde{G}} \right),S\left( {\tilde{E}_{ij} } \right),\,S\left( {\tilde{F}_{jk} } \right)\,,S\left( {\tilde{H}} \right),S\left( {\tilde{A}_{i} } \right)\) and \(S\left( {\tilde{B}_{k} } \right)\) denote the support of \(\tilde{C}_{ij} ,\,\tilde{D}_{jk} ,\tilde{G},\tilde{E}_{ij} ,\tilde{F}_{jk} ,\tilde{H},\tilde{A}_{i}\) and \(\tilde{B}_{k}\), respectively. According to definition 4, the \(\alpha\)-cuts of \(\tilde{C}_{ij} ,\,\tilde{D}_{jk} ,\tilde{G},\tilde{E}_{ij} ,\tilde{F}_{jk} ,\tilde{H},\tilde{A}_{i}\) and \(\tilde{B}_{k}\) are defined as follow,

$$ \begin{gathered} \left( {C_{ij} } \right)_{\alpha } = \left\{ {c_{ij} \in S\left( {\tilde{C}_{ij} } \right)|\,\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) \ge \alpha } \right\} \hfill \\ \left( {D_{jk} } \right)_{\alpha } = \left\{ {d_{jk} \in S\left( {\tilde{D}_{jk} } \right)|\,\mu_{{\tilde{D}_{jk} }} \left( {d_{jk} } \right) \ge \alpha } \right\} \hfill \\ \left( G \right)_{\alpha } = \left\{ {g \in S\left( {\tilde{G}} \right)|\,\mu_{{\tilde{G}}} \left( g \right) \ge \alpha } \right\} \hfill \\ \left( {E_{ij} } \right)_{\alpha } = \left\{ {e_{ij} \in S\left( {\tilde{E}_{ij} } \right)|\,\mu_{{\tilde{E}_{ij} }} \left( {e_{ij} } \right) \ge \alpha } \right\} \hfill \\ \left( {F_{jk} } \right)_{\alpha } = \left\{ {f_{jk} \in S\left( {\tilde{F}_{jk} } \right)|\,\mu_{{\tilde{F}_{jk} }} \left( {f_{jk} } \right) \ge \alpha } \right\} \hfill \\ \left( H \right)_{\alpha } = \left\{ {h \in S\left( {\tilde{H}} \right)|\,\mu_{{\tilde{H}}} \left( h \right) \ge \alpha } \right\} \hfill \\ \left( {A_{i} } \right)_{\alpha } = \left\{ {a_{i} \in S\left( {\tilde{A}_{i} } \right)|\,\mu_{{\tilde{A}_{i} }} \left( {a_{i} } \right) \ge \alpha } \right\} \hfill \\ \left( {B_{k} } \right)_{\alpha } = \left\{ {b_{k} \in S\left( {\tilde{B}_{k} } \right)|\,\mu_{{\tilde{B}_{k} }} \left( {b_{k} } \right) \ge \alpha } \right\}. \hfill \\ \end{gathered} $$
(11)

Applying the extension principle, membership function of the fuzzy fractional two-stage transshipment problem can be defined as,

$$ \begin{aligned} \mu_{{\tilde{Z}}} \left( z \right)& = \mathop {\sup \,\min }\limits_{C,D,G,E,F,H,A,B} \,\left\{ {\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }} ,\mu_{{\tilde{B}_{k} }} ,\,}\right.\\&\quad\left.{\forall i,j\,|\,z = Z\left( {C,D,G,E,F,H,A,B} \right)} \vphantom{{\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }} ,\mu_{{\tilde{B}_{k} }} ,\,}}\right\}, \end{aligned} $$
(12)

where \(Z\left( {C,D,G,E,F,H,A,B} \right)\) is the fractional objective function of model (8). Using the definition of \(\alpha\)-cuts, the sets \(\tilde{C}_{ij} ,\,\tilde{D}_{jk} ,\tilde{G},\tilde{E}_{ij} ,\tilde{F}_{jk} ,\tilde{H},\tilde{A}_{i}\) and \(\tilde{B}_{k}\) may be shown by various confidence interval values. Therefore, the fuzzy fractional two-stage transshipment problem is converted to a group of crisp fractional two-stage transshipment problems as \(\left\{ {\left( {C_{ij} } \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( {D_{jk} } \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( G \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( {E_{ij} } \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( {F_{jk} } \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( H \right)_{\alpha } |0 < \alpha \le 1} \right\},\)\(\left\{ {\left( {A_{i} } \right)_{\alpha } |0 < \alpha \le 1} \right\},\) and \(\left\{ {\left( {B_{k} } \right)_{\alpha } |0 < \alpha \le 1} \right\}\). The sets are related to boundaries which can be moved. They give nested structures in order to show the relationships of crisp and fuzzy sets Kaufmann [14].

The \(\alpha\)-cuts defined in Eq. (11) are crisp intervals that also are shown as,

$$ \begin{gathered} \left( {C_{ij} } \right)_{\alpha } = \left[ {\left( {C_{ij} } \right)_{\alpha }^{L} ,\left( {C_{ij} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{c_{ij} }} \left\{ {\,c_{ij} \in S\left( {\tilde{C}_{ij} } \right)\left| {\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{{c_{ij} }} \left\{ {\,c_{ij} \in S\left( {\tilde{C}_{ij} } \right)\left| {\mu_{{\tilde{C}_{ij} }} \left( {c_{ij} } \right) \ge \alpha } \right.} \right\}} \right] \hfill \\ \left( {D_{jk} } \right)_{\alpha } = \left[ {\left( {D_{jk} } \right)_{\alpha }^{L} ,\left( {D_{jk} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{d_{jk} }} \left\{ {d_{jk} \in S\left( {\tilde{D}_{jk} } \right)\left| {\mu_{{\tilde{D}_{jk} }} \left( {d_{jk} } \right)} \right. \ge \alpha } \right\},\,\mathop {\max }\limits_{{d_{jk} }} \left\{ {d_{jk} \in S\left( {\tilde{D}_{jk} } \right)\left| {\mu_{{\tilde{D}_{jk} }} \left( {d_{jk} } \right)} \right. \ge \alpha } \right\}} \right] \hfill \\ \left( G \right)_{\alpha } = \left[ {\left( G \right)_{\alpha }^{L} ,\left( G \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{g} \left\{ {\,g \in S\left( {\tilde{G}} \right)\left| {\mu_{{\tilde{G}}} \left( g \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{g} \left\{ {\,g \in S\left( {\tilde{G}} \right)\left| {\mu_{{\tilde{G}}} \left( g \right)} \right. \ge \alpha } \right\}} \right] \hfill \\ \left( {E_{ij} } \right)_{\alpha } = \left[ {\left( {E_{ij} } \right)_{\alpha }^{L} ,\left( {E_{ij} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{e_{ij} }} \left\{ {\,e_{ij} \in S\left( {\tilde{E}_{ij} } \right)\left| {\mu_{{\tilde{E}_{ij} }} \left( {e_{ij} } \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{{e_{ij} }} \left\{ {\,e_{ij} \in S\left( {\tilde{E}_{ij} } \right)\left| {\mu_{{\tilde{E}_{ij} }} \left( {e_{ij} } \right) \ge \alpha } \right.} \right\}} \right] \hfill \\ \left( {F_{jk} } \right)_{\alpha } = \left[ {\left( {F_{jk} } \right)_{\alpha }^{L} ,\left( {F_{jk} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{f_{jk} }} \left\{ {f_{jk} \in S\left( {\tilde{F}_{jk} } \right)\left| {\mu_{{\tilde{F}_{jk} }} \left( {f_{jk} } \right)} \right. \ge \alpha } \right\},\,\mathop {\max }\limits_{{f_{jk} }} \left\{ {f_{jk} \in S\left( {\tilde{F}_{jk} } \right)\left| {\mu_{{\tilde{F}_{jk} }} \left( {f_{jk} } \right)} \right. \ge \alpha } \right\}} \right] \hfill \\ \left( H \right)_{\alpha } = \left[ {\left( H \right)_{\alpha }^{L} ,\left( H \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{h} \left\{ {\,h \in S\left( {\tilde{H}} \right)\left| {\mu_{{\tilde{H}}} \left( h \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{h} \left\{ {\,h \in S\left( {\tilde{H}} \right)\left| {\mu_{{\tilde{H}}} \left( h \right)} \right. \ge \alpha } \right\}} \right] \hfill \\ \left( {A_{i} } \right)_{\alpha } = \left[ {\left( {A_{i} } \right)_{\alpha }^{L} ,\left( {A_{i} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{a_{i} }} \left\{ {\,a_{i} \in S\left( {\tilde{A}_{i} } \right)\left| {\mu_{{\tilde{A}_{i} }} \left( {a_{i} } \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{{a_{i} }} \left\{ {\,a_{i} \in S\left( {\tilde{A}_{i} } \right)\left| {\mu_{{\tilde{A}_{i} }} \left( {a_{i} } \right) \ge \alpha } \right.} \right\}} \right] \hfill \\ \left( {B_{k} } \right)_{\alpha } = \left[ {\left( {B_{k} } \right)_{\alpha }^{L} ,\left( {B_{k} } \right)_{\alpha }^{U} } \right] = \left[ {\mathop {\min }\limits_{{b_{k} }} \left\{ {\,b_{k} \in S\left( {\tilde{B}_{k} } \right)\left| {\mu_{{\tilde{B}_{k} }} \left( {b_{k} } \right)} \right. \ge \alpha } \right\},\,\mathop {\,\max }\limits_{{b_{k} }} \left\{ {\,b_{k} \in S\left( {\tilde{B}_{k} } \right)\left| {\mu_{{\tilde{B}_{k} }} \left( {b_{k} } \right)} \right. \ge \alpha } \right\}} \right]. \hfill \\ \end{gathered} $$
(13)

Here, the main purpose is to calculate the membership function value of the total fuzzy cost \(\tilde{Z}\), but the varying cost ranges is a core difficulty. To overcome this difficulty, Zadeh’s extension principle is applied. So, based on this principle, the membership function value of \(\tilde{Z}\) is calculated by,

$$ \begin{aligned} \mu_{{\tilde{Z}}} \left( z \right) &= \mathop {\sup \,\min }\limits_{C,D,G,E,F,H,A,B} \,\left\{ {\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }} ,\mu_{{\tilde{B}_{k} }} ,\,}\right.\\&\quad\left.{\forall i,j\,|\,z = Z\left( {C,D,G,E,F,H,A,B} \right)} \vphantom{{\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }} ,\mu_{{\tilde{B}_{k} }} ,\,}}\right\}, \end{aligned} $$
(14)

where \(z = Z\left( {C,D,G,E,F,H,A,B} \right)\) denotes the objective function of model (8). According to Eq. (12), \(\mu_{{\tilde{Z}}} \left( z \right)\) is sup-min of the values \(\mu_{{\tilde{C}_{ij} }} ,\mu_{{\tilde{D}_{jk} }} ,\mu_{{\tilde{G}}} ,\mu_{{\tilde{E}_{ij} }} ,\mu_{{\tilde{F}_{jk} }} ,\mu_{{\tilde{H}}} ,\mu_{{\tilde{A}_{i} }}\) and \(\mu_{{\tilde{B}_{k} }}\). In order to satisfy \(\mu_{{\tilde{Z}}} \left( z \right) = \alpha\), we need to have \(\mu_{{\tilde{C}_{ij} }} (c_{ij} ) \ge \alpha ,\mu_{{\tilde{D}_{jk} }} (d_{jk} ) \ge \alpha ,\mu_{{\tilde{G}}} (g) \ge \alpha ,\mu_{{\tilde{E}_{ij} }} (e_{ij} ) \ge \alpha ,\mu_{{\tilde{F}_{jk} }} (f_{jk} ) \ge \alpha ,\mu_{{\tilde{A}_{i} }} (a_{i} ) \ge \alpha ,\mu_{{\tilde{B}_{k} }} (b_{k} ) \ge \alpha\) and \(\mu_{{\tilde{H}}} (h) \ge \alpha\), where at least one of \(\mu_{{\tilde{C}_{ij} }} (c_{ij} ),\mu_{{\tilde{D}_{jk} }} (d_{jk} ),\mu_{{\tilde{G}}} (g) \ge \alpha ,\mu_{{\tilde{E}_{ij} }} (e_{ij} ),\mu_{{\tilde{F}_{jk} }} (f_{jk} ),\mu_{{\tilde{H}}} (h),\mu_{{\tilde{A}_{i} }} (a_{i} )\) and \(\mu_{{\tilde{B}_{k} }} (b_{k} )\) is equal to \(\,\alpha\). Variables \(c_{ij} ,\,d_{jk} ,g,e_{ij} ,f_{jk} ,h,a_{i}\) and \(b_{k}\) give an objective value that equals to z when they are used in model (8). For all \(\alpha\)-cuts of a nested structure of \(\alpha\) e.g. \(0 < \alpha_{2} < \alpha_{1} \le 1\), the term \(\left[ {\left( {C_{ij} } \right)_{{\alpha_{1} }}^{L} ,\left( {C_{ij} } \right)_{{\alpha_{1} }}^{U} } \right] \subseteq \left[ {\left( {C_{ij} } \right)_{{\alpha_{2} }}^{L} ,\left( {C_{ij} } \right)_{{\alpha_{2} }}^{U} } \right]\) is hold. Thus, \(\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right) \ge \alpha\) and \(\mu_{{_{{\tilde{C}_{ij} }} }} \left( {c_{ij} } \right) = \alpha\) is related to the same \(\alpha\)-cut. This is also hold for \(\mu_{{\tilde{D}_{jk} }} (d_{jk} )\),\(\mu_{{\tilde{G}}} (g),\)\(\mu_{{\tilde{E}_{ij} }} (e_{ij} ),\mu_{{\tilde{F}_{jk} }} (f_{jk} ),\mu_{{\tilde{H}}} (h),\mu_{{\tilde{A}_{i} }} (a_{i} )\) and \(\mu_{{\tilde{B}_{k} }} (b_{k} )\).

In order to calculate the membership function value \(\mu_{{\tilde{Z}}} \left( z \right)\), we need to determine the upper and lower bounds of the \(\alpha\)-cuts of \(\,\tilde{Z}\). The lower bound which is noted by \(Z_{\alpha }^{L}\) is equivalent to \(\min \left\{ {z|\mu_{{\tilde{Z}}} \left( z \right) \ge \alpha } \right\}\) and the upper bound \(Z_{\alpha }^{U}\) is equivalent to \(\max \left\{ {z|\mu_{{\tilde{Z}}} \left( z \right) \ge \alpha } \right\}\). So, the following problems are proposed respectively to calculate the lower and upper bounds.

$$ Z_{\alpha }^{L} = \mathop {\min }\limits_{\begin{gathered} \left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( G \right)_{\alpha }^{L} \le g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( H \right)_{\alpha }^{L} \le h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \hfill \\ \end{gathered} } \,\,\,\,Z\left( {C,D,G,E,F,H,A,B} \right), $$
(15)

and

$$ Z_{\alpha }^{U} = \mathop {\max }\limits_{\begin{gathered} \left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( G \right)_{\alpha }^{L} \le g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( H \right)_{\alpha }^{L} \le h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \hfill \\ \end{gathered} } \,\,\,\,Z\left( {C,D,G,E,F,H,A,B} \right), $$
(16)

where \(Z\left( {C,D,G,E,F,H,A,B} \right)\) shows the objective function term of problem (8). Since \(c_{ij}\), \(d_{jk}\), \(g\), \(e_{ij}\),\(f_{jk}\), \(h\), \(a_{i}\) and \(b_{k}\) are variable type notations, the below mathematical models can be used to find \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\).

$$ Z_{\alpha }^{L} = \mathop {\min \;}\nolimits_{\begin{gathered} \left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( G \right)_{\alpha }^{L} \le g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( H \right)_{\alpha }^{L} \le h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \hfill \\ \end{gathered} } \min \;\,\frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {c_{ij} } x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {d_{jk} y_{jk} + g} } } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } }} $$
(17)

subject to

$$ \sum\limits_{j = 1}^{J} {x_{ij} \le } \,\,a_{i} \;i \in \left\{ {1,\ldots,I} \right\} $$
$$ \sum\limits_{j = 1}^{J} {y_{jk} \ge b_{k} } \;k \in \left\{ {1,\ldots,K} \right\} $$
$$ \sum\limits_{i = 1}^{I} {x_{ij} } = \sum\limits_{k = 1}^{K} {y_{jk} } \;j \in \left\{ {1,\ldots,J} \right\} $$
$$ x_{ij} ,y_{jk} \ge 0\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} $$

and

$$ Z_{\alpha }^{U} = \mathop {\max \;}\nolimits_{\begin{gathered} \left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( G \right)_{\alpha }^{L} \le g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( H \right)_{\alpha }^{L} \le h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \hfill \\ \end{gathered} } \min \;\,\frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {c_{ij} } x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {d_{jk} y_{jk} + g} } } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } }} $$
(18)

subject to

$$ \sum\limits_{j = 1}^{J} {x_{ij} \le } \,\,a_{i} \;i \in \left\{ {1,\ldots,I} \right\} $$
$$ \sum\limits_{j = 1}^{J} {y_{jk} \ge b_{k} } \;k \in \left\{ {1,\ldots,K} \right\} $$
$$ \sum\limits_{i = 1}^{I} {x_{ij} } = \sum\limits_{k = 1}^{K} {y_{jk} } \;j \in \left\{ {1,\ldots,J} \right\} $$
$$ x_{ij} ,y_{jk} \ge 0\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} $$

The problems (17) and (18) are of two-level type models which contain an inner-level and an outer-level. For any set of \(c_{ij}\), \(d_{jk}\), \(g\), \(e_{ij}\),\(f_{jk}\), \(h\), \(a_{i}\) and \(b_{k}\) variables with their respective \(\alpha\)-cuts in the outer-level, the value of objective function is calculated in the inner-level. The set of \(c_{ij}\), \(d_{jk}\), \(g\), \(e_{ij}\),\(f_{jk}\), \(h\), \(a_{i}\) and \(b_{k}\) values generating the minimum and maximum values of the objective function are found in the outer-level of models (17) and (18), respectively. Employing different values for \(\alpha\), the value for membership function of \(\tilde{Z}\) is calculated as an approximate value. As a result, the two-level mathematical model have to be converted to a conventional one-level mathematical model in order to be effectively solvable. This transformation is done in the next sub-sections in order to find efficient upper and lower bounds.

One-level model for lower bound

Model (17) is used for generating lower bound value. Since it is a two-level problem, we convert it to a one-level problem to be easily solvable. Since both levels of the model are of minimization type, it can be replaced by a single-level model according to the constraints of the inner-level problem as follow,

$$ \begin{gathered} Z_{\alpha }^{L} = \min \,\,\frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {c_{ij} } x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {d_{jk} y_{jk} + g} } } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } }} \hfill \\ {\text{subject to}} \hfill \\ \sum\nolimits_{j = 1}^{J} {x_{ij} \le } \,\,a_{i} \;i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \sum\nolimits_{j = 1}^{J} {y_{jk} \ge b_{k} } \;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\nolimits_{i = 1}^{I} {x_{ij} } = \sum\nolimits_{k = 1}^{K} {y_{jk} } \;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {C_{ij} } \right)_{\alpha }^{L} \le \,\,c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le \,\,d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \left( G \right)_{\alpha }^{L} \le \,\,g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le \,\,e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le \,\,f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \left( H \right)_{\alpha }^{L} \le \,\,h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le \,\,a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \;i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le \,\,b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ x_{ij} ,y_{jk} \ge 0\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\}. \hfill \\ \end{gathered} $$
(19)

Since the model (19) is a fractional two-stage transshipment problem the transformation of Charnes and Cooper [3] is used to convert it to a linear model. As the inequality \(\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } > 0\) is true for every \(x_{ij}\) and \(y_{jk}\) in model (19), the transformations \(t = {1 \mathord{\left/ {\vphantom {1 {\left( {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {e_{ij} x_{ij} + \sum\nolimits_{j = 1}^{n} {\sum\nolimits_{k = 1}^{K} {f_{jk} y_{jk} + h} } } } } \right)}}\), \(v_{ij} = t\,x_{ij} \ge 0\) and \(w_{jk} = t\,y_{jk} \ge 0\) is used to convert the model (19) to the following program.

$$ Z_{\alpha }^{L} = \,\,\min \;\,\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {c_{ij} } v_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {d_{jk} w_{jk} + g} } } \,t $$
(20.1)

subject to

$$ \,\sum\limits_{j = 1}^{n} {v_{ij} \le } \,\,a_{i} \quad t\;i \in \left\{ {1,\ldots,I} \right\} $$
(20.2)
$$ \sum\limits_{j = 1}^{n} {w_{jk} \ge b_{k} } \quad t\;k \in \left\{ {1,\ldots,K} \right\} $$
(20.3)
$$ \sum\limits_{i = 1}^{m} {v_{ij} } = \sum\limits_{k = 1}^{K} {w_{jk} } \quad j \in \left\{ {1,\ldots,J} \right\} $$
(20.4)
$$ \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {e_{ij} v_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {f_{jk} w_{jk} + ht} } } } = 1 $$
(20.5)
$$ \left( {C_{ij} } \right)_{\alpha }^{L} \le \,\,c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \quad \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} $$
(20.6)
$$ \left( {D_{jk} } \right)_{\alpha }^{L} \le \,\,d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \quad \;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} $$
(20.7)
$$ \left( G \right)_{\alpha }^{L} \le \,\,g \le \left( G \right)_{\alpha }^{U} $$
(20.8)
$$ \left( {E_{ij} } \right)_{\alpha }^{L} \le \,\,e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \quad \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} $$
(20.9)
$$ \left( {F_{jk} } \right)_{\alpha }^{L} \le \,\,f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \quad \;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} $$
(20.10)
$$ \left( H \right)_{\alpha }^{L} \le \,\,h \le \left( H \right)_{\alpha }^{U} $$
(20.11)
$$ \left( {A_{i} } \right)_{\alpha }^{L} \le \,\,a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \quad \;i \in \left\{ {1,\ldots,I} \right\} $$
(20.12)
$$ \left( {B_{k} } \right)_{\alpha }^{L} \le \,\,b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \quad \;k \in \left\{ {1,\ldots,K} \right\} $$
(20.13)
$$ t > 0,\,\,\,\,\,v_{ij} ,w_{jk} \ge 0\,\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\quad \;k \in \left\{ {1,\ldots,K} \right\}. $$
(20.14)

Since the model (20.1) is of minimization type, thus, the lower bounds of \(c_{ij} ,d_{jk}\) and \(g\) are used as \(\left( {C_{ij} } \right)_{\alpha }^{L} ,\left( {D_{jk} } \right)_{\alpha }^{L}\) and \(\left( G \right)_{\alpha }^{L}\). On the other hand, because of the nonlinear terms of the constraints (20.2), (20.3), and (20.5) the followings are done to convert the model to a linear form.

  • As \(\,v_{ij} = t\,x_{ij}\), \(\,w_{jk} = t\,y_{jk}\), \(\,t\, > 0\) and \(\,x_{ij}\),\(\,y_{jk}\) are non-negative variables, so, \(v_{ij} = t\,x_{ij} \ge 0\) and \(w_{jk} = t\,y_{jk} \ge 0\).

  • The constraints (20.9) and (20.10) are multiplied by \(\,v_{ij} \ge 0\) and \(\,w_{jk} \ge 0\), respectively.

  • The constraints (20.11), (20.12) and (20.13) multiplied by \(t > 0\).

  • Let \(\,a_{i} \,t = p_{i}\), \(b_{k} \,t = q_{k}\), \(e_{ij} v_{ij} = \rho_{ij}\), \(f_{jk} w_{jk} = r_{jk}\) and \(\eta = ht\).

Thus, the following linear model is used instead of model (20.1). This linear model gives lower bound of the objective function value \(Z_{\alpha }^{L}\).

$$ Z_{\alpha }^{L} = \,\,\min \;\,\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\left( {C_{ij} } \right)_{\alpha }^{L} \,} v_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {\left( {D_{jk} } \right)_{\alpha }^{L} \,w_{jk} + \left( G \right)_{\alpha }^{L} } } } \,t $$
(21)

subject to

$$ \,\sum\limits_{j = 1}^{n} {v_{ij} \le } \,\,p_{i} \quad \,\;i \in \left\{ {1,\ldots,I} \right\} $$
$$ \sum\limits_{j = 1}^{n} {w_{jk} \ge q_{k} } \quad \;k \in \left\{ {1,\ldots,K} \right\} $$
$$ \sum\limits_{i = 1}^{m} {v_{ij} } = \sum\limits_{k = 1}^{K} {w_{jk} } \quad \,\;j \in \left\{ {1,\ldots,J} \right\} $$
$$ \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {\rho_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {r_{jk} + \eta } } } } = 1 $$
$$ \left( {E_{ij} } \right)_{\alpha }^{L} v_{ij} \le \,\,\rho_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} v_{ij} \quad \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} $$
$$ \left( {F_{jk} } \right)_{\alpha }^{L} w_{jk} \le \,\,r_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} w_{jk} \quad \;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\} $$
$$ \left( H \right)_{\alpha }^{L} t \le \,\,\eta \le \left( H \right)_{\alpha }^{U} t $$
$$ \left( {A_{i} } \right)_{\alpha }^{L} \,t \le \,\,p_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \quad \,t\;i \in \left\{ {1,\ldots,I} \right\} $$
$$ \left( {B_{k} } \right)_{\alpha }^{L} \,t \le \,\,q_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \quad \,t\;k \in \left\{ {1,\ldots,K} \right\} $$
$$ t > 0,\,\,\,\,\,v_{ij} ,w_{jk} \ge 0\,\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\quad \;k \in \left\{ {1,\ldots,K} \right\}. $$

One-level model for upper bound

In the model (18) the outer-level and inner-level problems have to be maximized and minimized respectively, so, the model is transformed to a one-level problem using a special method which uses the duality principle of linear programming introduced by Bazaraa et al. [2].

Since the inner-level problem of model (18) is the fractional two-stage transshipment problem, the transformation of Charnes and Cooper [3] is applied to transform the fractional two-stage transshipment problem to a linear formulation. Applying the same transformation which used in lower bound generation, the linear inner problem of model (18) is as follow,

$$ \begin{gathered} \min \;\,\sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {c_{ij} } v_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {d_{jk} w_{jk} + g} } } \,t \hfill \\ {\text{subject to}} \hfill \\ \,\sum\limits_{j = 1}^{n} {v_{ij} \le } \,\,a_{i} \,t\;i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \sum\limits_{j = 1}^{n} {w_{jk} \ge b_{k} } \,t\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{m} {v_{ij} } = \sum\limits_{k = 1}^{K} {w_{jk} } \,\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \sum\limits_{i = 1}^{m} {\sum\limits_{j = 1}^{n} {e_{ij} v_{ij} + \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{K} {f_{jk} w_{jk} + h} } } } \,t = 1 \hfill \\ t > 0,\,\,\,\,\,v_{ij} ,w_{jk} \ge 0\,\;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\},\;k \in \left\{ {1,\ldots,K} \right\}. \hfill \\ \end{gathered} $$
(22)

The dual problem of model (22) is as,

$$ \begin{gathered} - \pi_{i} + \mu_{j} + e_{ij} p \le c_{ij} \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \gamma_{k} - \mu_{j} + f_{jk} p \le d_{jk} \;i \in \left\{ {1,\ldots,I} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \max p \hfill \\ {\text{subject to}} \hfill \\ \sum\limits_{i = 1}^{m} {a_{i} \pi_{i} } - \sum\limits_{k = 1}^{K} {b_{k} \,} \gamma_{k} + h\,p \le g \hfill \\ \pi_{i} \ge 0\;,\;\gamma_{k} \ge 0\;i \in \left\{ {1,\ldots,I} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \mu_{j} ,p\;{\text{is unrestricted in sign}}\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \end{gathered} $$
(23)

where \(\pi_{i}\), \(\gamma_{k}\), \(\mu_{j}\) and p are dual variables associated with constraints of the model (22). Therefore, the model (18) is equivalent to the following model

$$ \begin{gathered} Z_{\alpha }^{U} = \mathop {\max }\limits_{\begin{gathered} \left( {C_{ij} } \right)_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( G \right)_{\alpha }^{L} \le \,\,g\, \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \hfill \\ \left( H \right)_{\alpha }^{L} \le \,\,h\, \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \hfill \\ \end{gathered} } \max p \hfill \\ {\text{subject to}} \hfill \\ - \pi_{i} + \mu_{j} + e_{ij} p \le c_{ij} \;i \in \left\{ {1,\ldots,I} \right\},\;j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \gamma_{k} - \mu_{j} + f_{jk} p \le d_{jk} \;i \in \left\{ {1,\ldots,I} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{m} {a_{i} \pi_{i} } - \sum\limits_{k = 1}^{K} {b_{k} \,} \gamma_{k} + h\,p \le g\sum\limits_{i = 1}^{m} {a_{i} \pi_{i} } - \sum\limits_{k = 1}^{K} {b_{k} \,} \gamma_{k} + h\,p \le g \hfill \\ \pi_{i} \ge 0\;,\;\gamma_{k} \ge 0\;i \in \left\{ {1,\ldots,I} \right\},\;k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \mu_{j} ,\;p\;{\text{is unrestricted in sign}}\;j \in \left\{ {1,\ldots,J} \right\}. \hfill \\ \end{gathered} $$
(24)

Here, again the same technique as what was used for lower bound generation problem is applied to convert model (24) to a single-level model as follow,

$$ \begin{gathered} Z_{\alpha }^{U} = \max p \hfill \\ {\text{subject to}} \hfill \\ - \pi_{i} + \mu_{j} + e_{ij} p \le c_{ij} \quad i \in \left\{ {1,\ldots,I} \right\},\quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \gamma_{k} - \mu_{j} + f_{jk} p \le d_{jk} \quad i \in \left\{ {1,\ldots,I} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{m} {a_{i} \pi_{i} } - \sum\limits_{k = 1}^{K} {b_{k} \,} \gamma_{k} + h\,p \le g \hfill \\ \left( {C_{ij} } \right)_{\alpha }^{L} \le \,\,c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} \quad i \in \left\{ {1,\ldots,I} \right\},\quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {D_{jk} } \right)_{\alpha }^{L} \le \,\,d_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \quad j \in \left\{ {1,\ldots,J} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \left( G \right)_{\alpha }^{L} \le \,\,g \le \left( G \right)_{\alpha }^{U} \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \le \,\,e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \quad i \in \left\{ {1,\ldots,I} \right\},\quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \le \,\,f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \quad j \in \left\{ {1,\ldots,J} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \left( H \right)_{\alpha }^{L} \le \,\,h \le \left( H \right)_{\alpha }^{U} \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \le \,\,a_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \quad i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \le \,\,b_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \pi_{i} \ge 0\;,\;\gamma_{k} \ge 0\quad i \in \left\{ {1,\ldots,I} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \mu_{j} ,p\;{\text{is unrestricted in sign}}\quad j \in \left\{ {1,\ldots,J} \right\}. \hfill \\ \end{gathered} $$
(25)

There are some issues to be considered for further simplifying the model (25). These are as follow,

  • In model (25), since \(\left( {C_{ij} } \right)\,_{\alpha }^{L} \le c_{ij} \le \left( {C_{ij} } \right)_{\alpha }^{U} ,\,\left( {D_{jk} } \right)_{\alpha }^{L} \le \,\,d_{jk} \le \,\left( {D_{jk} } \right)_{\alpha }^{U}\) and \(\,\left( G \right)_{\alpha }^{L} \le \,\,g \le \,\left( G \right)_{\alpha }^{U}\), so instead of each \(c_{ij} ,d_{jk}\) and \(g\) its upper limit can be used.

  • The objective function value in model (18) is a positive value, because \(c_{ij} ,d_{jk} ,g,e_{ij} ,f_{jk}\) and \(h\) are positive. According to the theorems of duality, the objective function value of model (25) which is the dual of (18), is positive value too. It implies that in objective function (25), \(p > 0\).

  • Due to the nonlinear terms \(e_{ij} p\), \(f_{jk} p\), \(a_{i} \pi_{i}\), \(b_{k} \gamma_{k}\) and \(h\,p\) the model (25) is a nonlinear problem. Using the transformations \(\,u_{ij} = e_{ij} p\),\(\,\lambda_{jk} = f_{jk} p\), \(\eta_{i} = a_{i} \pi_{i}\), \(\xi_{k} = b_{k} \gamma_{k}\) and \(\omega = h\,p\), also multiplying constraints \(\left( {E_{ij} } \right)_{\alpha }^{L} \le \,\,e_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U}\), \(\left( {F_{jk} } \right)_{\alpha }^{L} \le \,\,f_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U}\) and \(\left( H \right)_{\alpha }^{L} \le \,\,h \le \left( H \right)_{\alpha }^{U}\) by \(p\) the model can be linearized.

Applying the above-mentioned issues in the model (25), we get the following model obtain the upper bound of the objective value, \(Z_{\alpha }^{U}\).

$$ \begin{gathered} Z_{\alpha }^{U} = \max p \hfill \\ {\text{subject to}} \hfill \\ - \pi_{i} + \mu_{j} + u_{ij} \, \le \left( {C_{ij} } \right)_{\alpha }^{U} \quad i \in \left\{ {1,\ldots,I} \right\},\quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \,\,\gamma_{k} - \mu_{j} + \lambda_{jk} \le \left( {D_{jk} } \right)_{\alpha }^{U} \,\quad i \in \left\{ {1,\ldots,I} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \sum\limits_{i = 1}^{m} {\eta_{i} } - \sum\limits_{k = 1}^{K} {\xi_{k} \,} + \omega \le \left( G \right)_{\alpha }^{U} \, \hfill \\ \left( {E_{ij} } \right)_{\alpha }^{L} \,p \le \,\,u_{ij} \le \left( {E_{ij} } \right)_{\alpha }^{U} \,p\quad i \in \left\{ {1,\ldots,I} \right\},\quad j \in \left\{ {1,\ldots,J} \right\} \hfill \\ \left( {F_{jk} } \right)_{\alpha }^{L} \,p \le \,\,\lambda_{jk} \le \left( {F_{jk} } \right)_{\alpha }^{U} \,p\quad j \in \left\{ {1,\ldots,J} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \left( H \right)_{\alpha }^{L} p \le \,\,\omega \le \left( H \right)_{\alpha }^{U} p \hfill \\ \left( {A_{i} } \right)_{\alpha }^{L} \,\pi_{i} \le \,\,\eta_{i} \le \left( {A_{i} } \right)_{\alpha }^{U} \,\pi_{i} \quad i \in \left\{ {1,\ldots,I} \right\} \hfill \\ \left( {B_{k} } \right)_{\alpha }^{L} \,\gamma_{k} \le \,\,\xi_{k} \le \left( {B_{k} } \right)_{\alpha }^{U} \,\,\gamma_{k} \quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \pi_{i} \ge 0\;,\;\gamma_{k} \ge 0\quad i \in \left\{ {1,\ldots,I} \right\},\quad k \in \left\{ {1,\ldots,K} \right\} \hfill \\ \mu_{j} ,p\;{\text{is unrestricted in sign}}\;j \in \left\{ {1,\ldots,J} \right\}. \hfill \\ \end{gathered} $$
(26)

For a given \(\alpha\)-cut, the interval form of the objective function value of the fuzzy fractional two-stage transshipment problem is constructed by its lower and upper bounds obtained from the models (21) and (26).

Considering \(\alpha\)-cuts of \(\alpha_{1}\) and \(\alpha_{2}\) such that \(0 < \alpha_{1} { < }\alpha_{2} \le 1\), using the models (21) and (26), the inequalities \(Z_{{\alpha_{1} }}^{L} \le Z_{{\alpha_{2} }}^{L}\) and \(Z_{{\alpha_{2} }}^{U} \le Z_{{\alpha_{1} }}^{U}\) are obtained. Based on the definition of “convex fuzzy set” [45], and the obtained inequalities \(Z_{{\alpha_{1} }}^{L} \le Z_{{\alpha_{2} }}^{L}\) and \(Z_{{\alpha_{2} }}^{U} \le Z_{{\alpha_{1} }}^{U}\), the objective function \(\,\tilde{Z}\) is convex. Then, the left side function and the right side function of the objective function \(\,\tilde{Z}\) is obtained as \(L\left( Z \right) = \left( {Z_{\alpha }^{L} } \right)^{ - 1}\) and \(R\left( Z \right) = \left( {Z_{\alpha }^{U} } \right)^{ - 1}\), respectively, and \(\mu_{{\tilde{Z}}}\) is defined as follow,

$$ \mu_{{\tilde{Z}}} \left( z \right) = \left\{ \begin{gathered} L\left( Z \right) \hfill \\ 1 \hfill \\ \quad R\left( Z \right) \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} {Z_{\alpha = 0}^{L} \le Z \le Z_{\alpha = 1}^{L} } \\\quad {Z_{\alpha = 1}^{L} \le Z \le Z_{\alpha = 1}^{U} } \\\quad {Z_{\alpha = 1}^{U} \le Z \le Z_{\alpha = 0}^{U} } \\ \end{array} . $$
(27)

Models (21) and (26) are solved for different values of \(\alpha\), and the values of \(Z_{\alpha }^{L}\) and \(Z_{\alpha }^{U}\) together figure out \(L\left( Z \right)\) and \(R\left( Z \right)\) as a fuzzy number.

Summary and advantages of the proposed approach

The summary of the proposed solution approach and its advantages are presented in this section. The proposed solution approach is shown by the flowchart of Fig. 1.

Fig. 1
figure 1

A flowchart showing the summary the proposed approach

Full size image

Considering the similar studies of the literature, the proposed solution approach has some advantages which are pointed below.

  • The proposed solution approach does not apply any ranking function of fuzzy numbers in its procedure.

  • The proposed solution approach is simple and works based on linear models. So, it can be simply implemented by optimization solvers.

  • The proposed solution approach needs just some basic theoretical information of fuzzy sets and numbers.

  • The proposed solution approach can be used to model and solve the real instances of the fuzzy fractional two-stage transshipment problem.

  • In the proposed solution approach, after defuzzifying the fuzzy fractional two-stage transshipment problem, two crisp problems are obtained. In this step any solution approach can be applied to solve these problems.

  • Parametric solution approaches can be used to solve the lower and upper bound problems.

Numerical example and a case study

In this section, to show applicability of the proposed method, we present a numerical example and a case study. To solve the required mathematical models, GAMS 23.5 solver is used to be run on a computer with an Intel Pentium Dual 2 GHz processor and 1024 MB RAM. The results of the proposed approach also is compared to the results of an existing solution procedure of the literature proposed by Chinnadurai and Muthukumar [5].

Numerical example

This example is a network consist of three plants, two depots and four customers that is shown by Fig. 2.

Fig. 2
figure 2

The network of the numerical example

Full size image

The fuzzy parameters of this numerical example are of trapezoidal type. When the example is formulated using formulation (9), the following model is obtained which reflects the data of the example as well.

$$ \tilde{Z}\; = \min \;\frac{{\left[ \begin{gathered} \left( {3,5,8,12} \right)x_{11} + \left( {6,10,14,20} \right)x_{12} + \left( {4,10,15,20} \right)x_{21} + \left( {5,10,15,20} \right)x_{22} + \left( {5,7,12,18} \right)x_{31} \hfill \\ + \,\left( {7,8,13,17} \right)x_{32} + \left( {10,12,15,18} \right)y_{11} + \left( {1,4,8,12} \right)y_{12} + \left( {8,10,12,15} \right)y_{13} + \left( {5,10,15,20} \right)y_{14} \hfill \\ + \,\left( {3,7,10,15} \right)y_{21} + \left( {3,9,15,20} \right)y_{22} + \left( {7,10,13,17} \right)y_{23} + \left( {6,8,10,12} \right)y_{24} + (50,70,100,120) \hfill \\ \end{gathered} \right]}}{{\left[ \begin{gathered} \left( {7,10,15,18} \right)x_{11} + \left( {3,8,10,15} \right)x_{12} + \left( {3,8,10,15} \right)x_{21} + \left( {4,7,8,10} \right)x_{22} + \left( {10,15,20,25} \right)x_{31} \hfill \\ + \,\left( {5,10,12,15} \right)x_{32} + \left( {5,10,15,20} \right)y_{11} + \left( {4,8,15,25} \right)y_{12} + \left( {5,8,10,14} \right)y_{13} + \left( {5,15,20,30} \right)y_{14} \hfill \\ + \left( {7,17,20,25} \right)y_{21} + \left( {3,8,10,17} \right)y_{22} + \left( {2,5,7,11} \right)y_{23} + \left( {10,20,30,40} \right)y_{24} + (100,130,150,180) \hfill \\ \end{gathered} \right]}} $$
(28)

subject to

$$ x_{11} + x_{12} \le \left( {50,70,100,120} \right) $$
$$ x_{21} + x_{22} \le \left( {70,100,150,200} \right) $$
$$ x_{31} + x_{32} \le \left( {75,115,130,150} \right) $$
$$ y_{11} + y_{21} \ge \left( {10,20,30,40} \right) $$
$$ y_{12} + y_{22} \ge \left( {20,30,40,50} \right) $$
$$ y_{13} + y_{23} \ge \left( {25,35,45,60} \right) $$
$$ y_{14} + y_{24} \ge \left( {20,40,60,80} \right) $$
$$ x_{11} + x_{21} + x_{31} - y_{11} - y_{12} - y_{13} - y_{14} = 0 $$
$$ x_{12} + x_{22} + x_{32} - y_{21} - y_{22} - y_{23} - y_{24} = 0 $$
$$ x_{ij} \ge 0,\,\,y_{jk} \ge 0,\,\,i \in \left\{ {1,2,3} \right\},\,\,j \in \left\{ {1,2} \right\},\,\,k \in \left\{ {1,2,3,4} \right\} $$

Applying models (21) and (26), the lower bound and upper bound for the objective function value of the model (28) for various \(\alpha\)-cuts obtained respectively. The results are shown by Table 1.

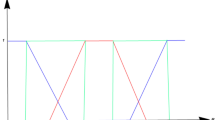
Table 1 The lower and upper bound values of the objective function of the numerical example obtained by the proposed approach
Full size table

The total cost is a trapezoidal fuzzy number as \(\left( {0.13, \, 0.37, \, 0.83, \, 1.98} \right)\) that is illustrated by Fig. 3.

Fig. 3
figure 3

The trapezoidal fuzzy number and its membership function obtained for the objective function value of the numerical example

Full size image

The objective function value obtained by the formulations (21) and (26) are not the same when the values of \(\alpha\)-cuts changed. Here, we report the objective function value and the values obtained for decision variables for smallest and largest \(\alpha\)- cuts.

When \(\alpha = 0\), the value of lower bound is \(Z_{\alpha }^{L*} = 0.13\) while the decision variables with non-zero values are as follow, \(x_{11}^{*} = 120,\) \(x_{21}^{*} = 190,\)\(x_{22}^{*} = 10,\)\(x_{31}^{*} = 150,\)\(y_{12}^{*} = 415,\)\(y_{13}^{*} = 25,\)\(y_{14}^{*} = 20,\)\(y_{21}^{*} = 10\). In this case the upper bound of \(Z_{\alpha }^{U*} = 2.30\) occurs at \(\,x_{11}^{*} = 52,\) \(x_{22}^{*} = 109,\) \(x_{31}^{*} = 75,\) \(y_{11}^{*} = 16,\) \(y_{12}^{*} = 51,\) \(y_{13}^{*} = 62,\) \(y_{21}^{*} = 26,\) \(y_{24}^{*} = 82,\) where all the other variables are 0.

When \(\alpha = 1\), the value of lower bound is \(Z_{\alpha }^{L*} = 0.37\) while the decision variables with non-zero values are as follow, \(x_{11}^{*} = 100,\) \(x_{31}^{*} = 70,\)\(x_{32}^{*} = 60,\)\(y_{12}^{*} = 135,\)\(y_{13}^{*} = 35,\)\(y_{21}^{*} = 20,\)\(y_{24}^{*} = 40\). In this case the upper bound of \(Z_{\alpha }^{U*} = 0.87\) occurs at \(x_{11}^{*} = 75,\) \(x_{31}^{*} = 16,\)\(x_{32}^{*} = 107,\)\(y_{12}^{*} = 43,\)\(y_{13}^{*} = 48,\)\(y_{21}^{*} = 32,\)\(y_{24}^{*} = 75\), where all the other variables are 0.

Applying the approach proposed by Chinnadurai and Muthukumar [5], the results of Table 2 is obtained for the lower and upper bounds of the objective function of the numerical example for different \(\alpha\)-cuts. The total cost is trapezoidal fuzzy number \(\left( {0.13, \, 0.37, \, 0.83, \, 1.98} \right)\) which is exactly the same as what obtained by the proposed approach of this study.

Table 2 The lower and upper bound values of the objective function of the numerical example obtained by the approach of Chinnadurai and Muthukumar [5]
Full size table

A case study

The case study that is focused in this section, is related to a transportation company which give services to an automobile manufacturing company in Iran. The automobile manufacturing company has two production plants (plants), three main inventories (depots) and six main sales agencies (customers) in Iran. They produce the automobiles in the plants, then transport them to the main inventories and the sales agencies consequently. These transportation activities are performed by the transportation company as an outsourcing policy. Because of the uncertain market of Iran, the parameters of this problem is of uncertain type values. For this aim, all the supply and demand values are of fuzzy numbers because of uncertain nature of the production processes and final customer needs. On the other hand the transportation company obtains money per automobile and of course has some transportation costs per automobile too. These costs and income values are also of fuzzy numbers because of the above-mentioned uncertain market. As the transportation costs/incomes are dependent to many uncertain factors like fuel price, fuel consumption value, drivers’ salary, probable accidents, etc., therefore, those should be considered as uncertain values. These uncertainties are some valid reasons showing that the traditional fractional transshipment formulation (model 8) for this case study is not useful and efficient. So, for this case study the fuzzy transshipment formulation (model 9) would be of interest. The data of this case study are shown by Tables 3, 4 and Fig. 4.

Table 3 Income, cost and supply values between plants and depots of the case study
Full size table
Table 4 Income, cost and demand values between depots and customers of the case study
Full size table
Fig. 4
figure 4

Schematic representation of the network of the case of study

Full size image

Applying models (21) and (26), the lower bound and upper bound for the objective function value of the model (9) for various \(\alpha\)-cuts obtained respectively. The results are shown by Table 5.

Table 5 The lower and upper bound values of the objective function of the case study obtained by the proposed approach
Full size table

The objective function value obtained by the formulations (21) and (26) are not the same when the values of \(\alpha\)-cuts changed. Therefore, the trapezoidal fuzzy objective function value is obtained as \(\left( {0.31,0.39,0.54,0.63} \right)\).

Applying the approach proposed by Chinnadurai and Muthukumar [5], the results of Table 6 is obtained for the objective function of the case study for different \(\alpha\)-cuts. The total cost is trapezoidal fuzzy number \(\left( {0.27,0.39,0.53,0.7} \right)\) which is different than what obtained by the proposed approach of this study. The difference is due to solution scheme of two methods. Here we employed the \(\alpha\)-cuts whereas Chinnadurai and Muthukumar [5] uses the \((\alpha ,r)\) acceptable optimal value for linear fractional problem. Indeed, to obtain acceptable \((\alpha ,r)\) optimal values, Chinnadurai and Muthukumar [5], take an \(\alpha\)-cut on the objective function and r-cut on the constraints.

Table 6 The lower and upper bound values of the objective function of the case study obtained by the approach of Chinnadurai and Muthukumar [5]
Full size table

Conclusion

The fractional two-stage transshipment problem is an extension of the two-stage transshipment problem which has a fractional type objective function. This problem has many real-world applications in many fields like production, transportation, finance, engineering, statistics, etc. Its extension to fuzzy environment defines fractional two-stage transshipment problem which has some limitations e.g. fuzziness, fractional type non-linearity, etc. to be solved exactly.

Since there is no significant study in the literature to deal with solution methods of fuzzy fractional two-stage transshipment problem, this study presented a solution method based on the extension principle. The approach applies a decomposition-based algorithm which divides the problem into two different sub-problems which calculate lower bound and upper bound of the main problem. Finally, the fuzzy value of the main objective function is obtained easily. Efficiency of the algorithm is tested over a numerical example as well as a case study and results were compared to those in the literature.

As future study the proposed problem can be considered in other type uncertain environments like Pythagorean fuzzy uncertainty (see [7, 39, 40], or belief degree based uncertainty [42]).