Introduction

Water flowing through open channels often contains sediments. If the channel’s transport capacity is insufficient to transport sediment, solids will deposit. Sediment retention on a riverbed without movement for long periods rises the risk of alteration and the ultimate cementation. During low flow in particular, the permanent deposition on channel beds alters the velocity and the shear stress distribution. Channel pipes are designed based on the concept of self-cleaning. Accordingly, the velocity of the flow passing through a channel must, therefore, be capable of washing the deposited sediments away. Consequently, channel design based on self-cleansing should be done in such manner as to meet the following conditions: first, the channel’s equal or over-the-limit-flow must have the capacity to transport the minimum concentration of small, suspended particles or low-mass particles. Second, the bed load’s flow capacity for transporting rough particles must be at a level that limits the depth of deposition up to a specific pipe diameter.

Among the simplest ways to prevent sediment deposition on channel beds is to use the constant sheer stress [1, 2] or minimum velocity [3, 4] criteria. However, the minimum essential discharge or minimum gradient may be under- or over-predicted when the hydraulic properties of the channel and sediments entering the channel are not considered [5].

Many researchers have undertaken various experimental and empirical studies on sediment transport without sediment [6,7,8,9,10,11,12,13,14]. It can be said that classic methods do not have the capacity to estimate the flow velocity that prevents sediment deposition under different conditions, and there is a need for methods with such capacity. Recently, intelligent learning systems including Neural Networks have been applied extensively in water engineering [15,16,17,18,19,20,21]. Nasseri et al. [22] developed the feed-forward neural network (FNN) to simulate rainfall fields. By combining the Backpropagation (BP) algorithm with the Genetic Algorithm (GA), Nasseri et al. [22] trained and optimized the FNN. This technique led to the prediction of rainfall in different periods using a recorded hyetograph. Nasseri et al.’s study results showed that when combined with the Genetic Algorithm, the neural network with the selected input parameters performed better than in similar works where only the Genetic Algorithm was used. For efficient water supply system design, Montalvo et al. [23] used the PSO algorithm. Altunkaynak [24] predicted sediment load using GA by referring to the flow in different sections. Altunkaynak concluded that GA yields better results than existing regression models. Afshar and Rajabpour [25] used the PSO method to design and operate an irrigation pumping system. Zhang et al. [26] optimized the critical shear stress values for sediment deposition and re-suspension by applying GA method. Tang et al. [27] introduced a method that combines a hydrodynamic model with the intelligent model obtained with GA. Azadnia and Zahraie [28] utilized the PSO algorithm to model the sedimentation problem in reservoirs. Ashraf Vaghefi et al. [29] employed the ICA to estimate the discharge in the Karkheh watershed. Abdollahi et al. [30] utilized the ICA to solve non-linear equation systems. Ebtehaj and Bonakdari [31] used different methods of generating fuzzy inference systems (FIS) and two algorithms for network training and presented various models with ANFIS for predicting the densimetric Froude number. They demonstrated that using the hybrid algorithm for network training and grid partitioning presented the best FIS generation results. The comparison of the ICA and GA [32] and ICA and GA [33] indicates the superior performance of the ICA in optimal training of the feed-forward neural network model for prediction of the bed load sediment transport in sewer pipe network. However, the main limitation of these recent studies is the lack of an explicit expression that can be easily adopted and used by practitioners. Also, the uncertainty of the model predictions in these papers is not clearly presented.

The main objective of this article is to model sediment transport without sedimentation using hybrids of ANN based on the evolutionary algorithms ICA, PSO and GA. The algorithms were combined with ANN to optimally design the layer weights and minimize the objective function to forecast the densimetric Froude number (Fr) parameter. First, the parameters affecting sediment transport were identified and grouped into five categories. Then, six different models were introduced to survey the impact of each parameter. Fr was then estimated using ICA–ANN, PSO–ANN and GA–ANN and the results of evaluating each algorithm were compared with existing laboratory results obtained by Ghani [34]. Afterwards, to assess the flexibility of proposed hybrid models, Ghani’s [34] trained models were evaluated against Vongvisessomjai et al.’s [35] models, which had different hydraulic conditions from the training dataset. Additionally, the obtained results were compared with the ANN results and existing sediment transport equations. Finally, an explicit equation was produced to calculate Fr in practical engineering. In addition, through uncertainty analysis examined the 95% prediction error interval for all hybrid models. Moreover, we employed a sensitivity analysis to study the trend variation of each input variables in the proposed STWS models.

Review of existing equations for STWS

Popular equations for STWS are typically semi-experimental and some are developed through dimensional analysis. Hence, the best semi-experimental relations and two of the newest equations presented using dimensional analysis [36, 37] are used in this study. Consequently, to review the models obtained from existing equations, May et al.’s [38] semi-experimental equation, which is the best among semi-experimental equations [35, 37], is employed along with Azamathulla et al. [36] and Ebtehaj et al.’s [37] equations, which represent the dimensional analysis results.

Using seven different datasets (presented by Ackers et al. [39] in detail), May et al. [38] evaluated seven cases to estimate bed load sediment transport without sediment. The authors found that each equation presented satisfactory results only with certain datasets derived and none provided good results in all hydraulic conditions. Therefore, May et al. [38] presented a new semi-experimental equation by considering the forces affecting a sediment particle in stationary condition as follows:

$$ \begin{aligned} C_{{\text{V}}} & = {3}{\text{.03}} \times {10}^{{ - {2}}} \left( {D^{{2}} {/}A} \right)\left( {d/D} \right)^{{{0}{\text{.6}}}} \\ &\quad \left( {V^{{2}} /g\left( {s - 1} \right)D} \right)^{{{1}{\text{.5}}}} \left( {1 - V_{{\text{t}}} /V} \right)^{{4}} , \end{aligned} $$
(1)
$$ V_{{\text{t}}} = {0}{\text{.125}}\left( {g{(}s - 1{)}d} \right)^{{{0}{\text{.5}}}} \left( {y/d} \right)^{{{0}{\text{.47}}}} , $$
(2)

where CV is the volumetric sediment concentration; A is the flow cross-sectional area; D is the pipe diameter; d is the median particle diameter; V is the flow velocity; Vt is the velocity required for the initial motion of sediment (Eq. 2); s is the specific gravity of sediment; y is the flow depth; and g is the gravitational acceleration.

By considering the different pipe channel diameters that Ghani [34] did not utilize, Azamathulla et al. [36] amended Ghani’s [34] equation coefficient as follows:

$$ {\text{Fr}} = \frac{V}{{\sqrt {g\left( {s - 1} \right)d} }} = {0}{\text{.22}}C_{{\text{V}}}^{{{0}{\text{.16}}}} D_{{{\text{gr}}}}^{{ - {0}{\text{.14}}}} \left( \frac{d}{R} \right)^{{ - {0}{\text{.29}}}} \lambda_{{\text{s}}}^{{ - {0}{\text{.51}}}} , $$
(3)

where Fr is the densimetric Froude number, Dgr (= d(g(s−1)/ν2)1/3) is the dimensionless particle number and λs is the overall sediment friction factor, which is calculated with Nalluri and Kithsiri’s [40] equation below.

$$ \lambda_{{\text{s}}} = {0}{\text{.85}}1\lambda_{{\text{c}}}^{{{0}{\text{.86}}}} C_{{\text{V}}}^{{{0}{\text{.04}}}} D_{{{\text{gr}}}}^{{{0}{\text{.03}}}} , $$
(4)

where λc is the channel’s clear water friction factor.

Ebtehaj et al. [37] evaluated Vongvisessomjai et al.’s [35] equations for bed load sediment transport in channels and found these equations produced ineligible results in diverse hydraulic conditions that were not used for fitting in Vongvisessomjai et al.’s [35] equations. Therefore, Ebtehaj et al. included the volumetric sediment concentration (CV) and relative depth of flow (d/R) as dimensionless parameters in estimating Fr. Ebtehaj et al. [37] presented an equation in the following form:

$$ {\text{Fr}} = \frac{V}{{\sqrt {g\left( {s - 1} \right)d} }} = {4}{\text{.49}}C_{{\text{V}}}^{{{0}{\text{.21}}}} \left( \frac{d}{R} \right)^{{ - {0}{\text{.54}}}} . $$
(5)

Artificial neural networks (ANN)

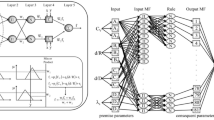
Owing to the ability to model complex problems, the ANN method is used extensively in various engineering fields. In the first step of the training procedure, the initial information is utilized to create a raw MLP structure. The initial information consists of the input variables, number of hidden neurons, number of hidden layers, number of output neurons, and the hidden and output layers’ activation functions. In the second step, according to the learning method considered, the weights and biases of the raw MLP structure formed are determined. Thus, in case of MLP–ANN modeling, the traditional Levenberg–Marquardt learning method is applied, and in case of evolutionary optimization-based ANN method modeling, the algorithm considered is applied in this step. It should be noted that for all MLP modeling applied in the present study, the sigmoid activation function is employed for the hidden neurons and the linear activation function is utilized for the output neurons. The other initial information is presented in the following sections. The MLP weights consist of the input to hidden layer and hidden to output layer weights. The objective function that the evolutionary algorithm attempts to minimize is shown in Eq. (6).

$$ {\text{Objective}}\;{\text{function}} = {\text{Observed}} - {\text{predicted}}{.} $$
(6)

By minimizing the objective function, the simulation performance increases. In each iteration, the evolutionary algorithm runs the MLP neural network with a new set of weight coefficients until it finds the best set. Finally, the results of these hybrid methods are compared with the traditional MLP–ANN. Figure 1 presents the flowchart of the hybrid MLP-evolutionary algorithm (MLP-EA).

Fig. 1
figure 1

Flowchart of hybrid MLP-EA

Full size image

Genetic algorithm (GA)

A genetic algorithm, which is inspired from nature, performs robustly in solving non-linear optimization problems that cannot be solved using classical optimization methods. According to Fig. 2, to optimize the objective function, GA first produces a random initial population of chromosomes. Each chromosome is considered one candidate answer. Next, the objective function is recalled using each chromosome generated and the cost of each is computed. Then, the chromosomes are sorted according to their costs. In the present study, answer reproduction is done using the standard GA in three main steps: elite, crossover and mutation. The best answers of the current generation are saved as elite chromosomes. These answers are transferred directly from the current generation to the next without any changes. In the crossover procedure, two answers from the current generation are selected as parents and two new children are generated and transferred to the next generation. The mutation procedure increases optimization process exploration. Mutation is a random search tool that prevents algorithm entrapment in a locally optimized point. Selecting the genetic mutation probability accurately has great impact on the optimization trend. Thus, the three mentioned processes serve to develop the new generation of answers. This generation produced is run until convergence occurs and no more precision enhancement takes place. Details of the GA procedure are shown in Fig. 2.

Fig. 2
figure 2

GA flowchart

Full size image

Particle swarm optimization (PSO)

The PSO algorithm is an evolutionary algorithm which is inspired from creatives’ social intelligence. With this method, each creative is like a bird or fish in a group and is called a particle. Particles are answers to the problem. Each particle moves at a speed that can be regulated in the search space and retains the best previous position in its memory. In the total space searched by PSO, the best position obtained by the group is also shared with all other components. Suppose there is a space with X-dimension, the ith particle in the population is denoted as a position and velocity vector. Change in the velocity and position structure of each particle result in alteration in the position of the particle in the next iteration.

The position of each particle is achieved by comparison between the current position of particle xi and the best value it has attained (pbest). Furthermore, the best response that each particle has achieved so far by the swarm from pbest is known as gbest. The velocity and position of each particle (Eqs. 7 and 8, respectively) are updated after finding gbest and pbest using the following equations.

$$ v_{i} = w*v_{i} + R_{{1}} \left( {{\text{pbest}}_{i} - x_{i} } \right) + R_{{2}} \left( {{\text{gbes,t}}_{i} - x_{i} } \right), $$
(7)
$$ x_{i} = x_{i} + v_{i} , $$
(8)

where xi denotes the position of the particle i; vi is the velocity of particle i; and R1 and R2 are learning parameters. The basic steps in PSO are summarized in the flowchart given in Fig. 3.

Fig. 3
figure 3

PSO flowchart

Full size image

Imperialist competitive algorithm (ICA)

The ICA algorithm introduced by Atashpaz-Gargari and Lucas [41] is one of the most effective evolutionary optimization algorithms inspired from the human political/social evolution concepts. The initial countries population of the ICA algorithm is randomly generated. In the first generation, the existing countries are randomly categorized as the imperialists and colonies and based on the power of each colony, they are distributed between the imperialists.

The countries’ costs are calculated using the fitness function of the considered problem. After that, countries are sorted according to their costs. Countries with the most strength are chosen as imperialist and the rest of them are considered as the colonies of imperialists. The imperialists use the absorption policy to increase their colonies. The main theme of ICA optimization technique is the attraction policy, which is based on the evolution of the countries towards efficiency. The main ICA procedure for finding the optimum answer is the imperialist competition for attracting colonies. Throughout this process, weaker empires lose colonies and their power decreases. At the final optimization process, all colonies fall under the strongest empire’s control and the other ones are vanished. Thus, the algorithm proceeds until only one empire remains. Figure 4 presents the details of the ICA procedure.

Fig. 4
figure 4

ICA flowchart

Full size image

Data collection

In this study, Ghani [34] and Vongvisessomjai et al.’s [35] data were used in the model training and validation processes. Ghani [34] conducted experiments in two cases: non-deposition and loosely deposited beds. The author used 20.5-m-long pipes with three diameters of 154, 305 and 450 mm for the rigid bed tests. In addition, the author used 305-mm- and 405-mm-diameter pipes for the rough and loose bed tests, respectively. The pipe with the larger diameter was made of concrete while the others were PVC. The maximum slope and discharge were 0.006 and 40 l/s, respectively. To supply sediment to the flow and measure the flow depth, different openings were located at the top of the pipes. The velocity profile was achieved at the center line of the pipe channel. The number of data employed from Ghani’s [34] study was 120 and categorized in 2 groups: training (96 samples) and validation (24 samples).

The data ranges used in Ghani’s [34] tests for non-deposition state were as follows: 0.153 < y/D < 0.8, 0.033 < R (m) < 0.136, 0.24 < V (m/s) < 1.216, 0 < k (mm) < 1.34, 38 < CV (ppm) < 1450 and 0.93 < d (mm) < 8.3.

Vongvisessomjai et al. [35] conducted a laboratory study with 16-m-long PVC pipes with 2 diameters: 100 and 150 mm. The top of the pipes was removed for open channel condition. The channel slope was adjusted mechanically. Sediment was supplied to the flow using a vibrating screw feeder attached downstream. The downstream end of the channel operated as a sediment trap. The water level and flow velocity in each pipe were measured by a point gauge and an electronic current meter, respectively. Using a sluice gate, the tail water was adjusted to provide uniform flow, which was constant with time. The downstream gate was regulated by trial and error until the water level in each section became equal. Vongvisessomjai et al. [35] also conducted laboratory experiments at limit of deposition. The data ranges in Vongvisessomjai et al.’s [35] experiments were as follows: 0.2 < y/D < 0.4, 0.24 < V (m/s) < 0.63, 0.012 < R (m) < 0.032, 4 < CV (ppm) < 90 and 0.2 < d (mm) < 0.43. Vongvisessomjai et al.’s [35] dataset utilized in this study including 27 samples was employed to survey and appraise the performance of the proposed methods using a dataset that was not used in the training phase.

Methodology

Based on previous laboratory studies conducted [32, 33, 36], the most significant parameters used in equations of sediment transports can be presented as follows:

$$ V =\Phi \left( {g{,}\;C_{{\text{V}}} {,}\;d{,}\;D{,}\;y{,}\;R{,}\;A{,}\;\lambda_{{\text{s}}} ,\;s{,}\;\upsilon } \right), $$
(9)

where Φ is an operator and CV and λs are dimensionless parameters. The flow velocity to prevent sedimentation in pipes (limiting velocity, V) is given as the densimetric Froude number (Fr = V/(g(s−1)d)0.5). In a two-phase flow condition including water–sediment interaction, a dimensionless variable, dimensionless particle number (Dgr = d(g(s−1)/ν2)1/3) is defined.[16, 32, 34]. To identify the dimensionless parameters affecting sediment transport in pipe channels and when d is selected as a basic parameter, the Buckingham ∏-theorem [42] is used. Therefore, all dimensionless parameters are presented as follows:

$$ {\text{Fr}} = \frac{V}{{\sqrt {g\left( {s - {1}} \right)d} }} = \Phi \left( {C_{{\text{V}}} {,}\lambda_{{\text{s}}} {,}\;D_{{{\text{gr}}}} {,}\frac{\;d}{D}{,} \;\frac{{D^{2} }}{A}{,}\;\frac{y}{D}{,}\;\frac{d}{R}} \right). $$
(10)

By considering the nature of the dimensionless parameters obtained from dimensional analysis, that parameters can be placed in different groups [31]: movement, transport, sediment, transport form and flow resistance.

Accordingly, the main objective of the modeling is to predict the limiting velocity (V) using Fr as a dimensionless parameter. In previous studies [32, 33], densimetric Froude number, Fr (= V/√gd(s−1)), is estimated based on six different dimensionless models, Model 1: Φ(CV, Dgr, d/R, λs), Model 2: Φ(CV, Dgr, D2/A, λs), Model 3: Φ(CV, Dgr, y/D, λs), Model 4: Φ(CV, d/D, d/R, λs), Model 5 Φ(CV, d/D, D2/A, λs), Model 6: Φ(CV, d/D, y/D, λs).

The k-fold cross validation method is employed to obtain a more reliable estimation of prediction accuracy. The k value in this work is 10. With this method, all data are fragmented into ten subsets. In each subset, a single sub-sample is preserved to test the models and the remaining sub-samples are for model training. This trend is repeated 10 times, where one from each of the ten subsets is utilized exactly once as validation data. The number of training and validation data is 96 and 24, respectively. To evaluate the models’ flexibility, their accuracy is validated using Vongvisessomjai et al.’s [35] data.

The ANN analysis results, whereby ANN is trained using evolutionary algorithms, are established on the criteria of Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), Index of Agreement (IOA) and Efficiency (EFF), as defined below. The method of evaluating the models based on these indicators is in the form: the more the IOA and EFF indicators approach 1, and RMSE and MAPE approach 0, the greater the model’s desirability is.

$$ {\text{RMSE}} = \sqrt {\left( \frac{1}{n} \right)\sum\limits_{i = 1}^{n} {\left( {{\text{Fr}}_{{{\text{EXP}}_{i} }} - {\text{Fr}}_{{{\text{ANN}}_{i} }} } \right)^{{2}} } } , $$
(11)
$$ {\text{MAPE}} = \left( \frac{1}{n} \right)\sum\limits_{i = 1}^{n} {\left( {\frac{{\left| {{\text{Fr}}_{{{\text{EXP}}_{i} }} - {\text{Fr}}_{{{\text{ANN}}_{i} }} } \right|}}{{{\text{Fr}}_{{{\text{EXP}}_{i} }} }}} \right)} \times {100,} $$
(12)
$$ {\text{IOA}} = {1} - \frac{{\sum\nolimits_{i = 1}^{n} {\left( {{\text{Fr}}_{{{\text{EXP}}_{i} }} - {\text{Fr}}_{{{\text{ANN}}_{i} }} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{n} {\left( {\left| {{\text{Fr}}_{{{\text{EXP}}_{i} }} - \overline{{{\text{Fr}}_{{{\text{EXP}}_{i} }} }} } \right| + \left| {{\text{Fr}}_{{{\text{ANN}}_{i} }} - \overline{{{\text{Fr}}_{{{\text{EXP}}_{i} }} }} } \right|} \right)^{2} } }}, $$
(13)
$$ {\text{EFF}} = \left[ {\frac{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {{\text{Fr}}_{{{\text{EXP}}_{i} }} - \overline{{{\text{Fr}}_{{{\text{EXP}}_{i} }} }} } \right)^{2} } } }}{{\sqrt {\sum\nolimits_{i = 1}^{n} {\left( {{\text{Fr}}_{{{\text{ANN}}_{i} }} - \overline{{{\text{Fr}}_{{{\text{EXP}}_{i} }} }} } \right)^{2} } } }}} \right]^{2} . $$
(14)

Results and discussion

Comparison of MLP–GA, MLP–PSO and MLP–ICA in sediment transport prediction

The results from training the ANN models using GA, PSO and ICA are presented in this section. All models contain a typical ANN. In addition, a one-hidden layer network is considered for each model. To make a reasonable comparison between GA, PSO and ICA, the same population size (300) and iteration number (1000) are considered for all models. Figures 5, 6 and 7 display the densimetric Froude number (Fr) prediction results using GA, PSO and ICA, respectively, for the 6 models presented in this study. The prediction accuracy results are similar for all models in training and testing modes. Model 4 estimated Fr with less than 10% relative error with GA and PSO in both testing and training modes. GA sometimes made overestimated and underestimated predictions with Models 2 and 5 (respectively) and had a higher relative error than the other models, which can lead to uneconomical designs, sediment deposition on the pipe channel bed and eventually problems caused by deposition such as blockage. Models 1 and 4 that contain GA produced relative errors of approximately 13% and 9% (respectively), which indicates that GA predicted Fr relatively accurately. Models 2 and 5 were not as accurate as the other models with PSO and GA, because most predictions were overestimated in this state. This can result in uneconomic designs. The dimensionless parameters in model 4 (CV, d/D, d/R, λs) produced less than 10% relative error with PSO, and this model, thus, made the best predictions. With most models, ICA estimated Fr with less than 10% relative error, which indicates this algorithm’s superiority over the other two algorithms.

Fig. 5
figure 5

Evaluation of Fr estimation by six models with GA in training and testing

Full size image
Fig. 6
figure 6

Evaluation of Fr estimation by six models with PSO in training and testing

Full size image
Fig. 7
figure 7

Evaluation of Fr estimation by six models with ICA in training and testing

Full size image

Statistical indices were employed to quantitatively survey the accuracy of each evolutionary algorithm (GA, PSO and ICA) in predicting Fr with models 1–6. The results of these statistical indices are shown in Table 1 for testing and training modes. This table indicates that the MAPE value was below 10% for all models and for all three algorithms except GA in testing mode with models 5 (MAPE = 11.2%) and 6 (MAPE = 11.9%) and PSO (MAPE = 10.5%) in training mode with model 2. Besides, the values of the remaining indices for the three algorithms prove the evolutionary algorithms’ performance in optimizing the weights of different neural network layers to minimize the target function. The table also signifies that using the data with no role in model training (testing) did not have a noticeable effect on the models’ performance, because not much difference was noted between the indices in the training and testing modes. The maximum mean relative error (of nearly 12%) was for model 6 (GA) in testing mode. Moreover, model 4 with ICA (model 4-ICA) seemed to perform the best amongst all models and algorithms. Although GA and PSO also presented good prediction results with model 4, model 4-ICA was still selected as the best model.

Table 1 Evaluation of the accuracy of Fr estimation by GA, PSO and ICA with all models in training and testing
Full size table

Performance evaluation of proposed hybrid methods with MLP using validation dataset [35]

Figure 8 compares the abilities of the evolutionary algorithms (GA, PSO and ICA) and MLP neural network in Fr prediction. The experimental dataset in this figure was produced by Vongvisessomjai et al. [35]. The aim of selecting this dataset was to examine the flexibility of the proposed models under different conditions. ICA and PSO made better predictions than GA and MLP. It is clear that MLP made forecasts with a relative error of approximately 10% in most cases. This method mostly overestimated, which can lead to uneconomic designs. In general, it can be stated that using evolutionary algorithms increases the prediction accuracy more than using gradient algorithms in MLP.

Fig. 8
figure 8

Comparison of evolutionary algorithms (ICA, PSO and GA) and MLP neural network in estimating Fr using Vongvisessomjai et al.’s [35] dataset

Full size image

Because ICA (Model 4) produced the best results, we can calculate Fr with the following equation:

$$ Fr = {\text{purelin}}\,\,\left( {\left( {{\text{tansig}}\left( {{\text{input}} \times iw + b_{1} } \right)} \right) \times lw + b_{2} } \right), $$
(15)
$$ {\text{input}} = \left[ {C_{{\text{V}}} ,d/D{,}d/R,\lambda_{{\text{s}}} } \right], $$
(16)
$$ {\text{purelin}}\left( x \right) = x, $$
(17)
$$ transig(x)=\frac{2}{1+e^{-2x}}-1 $$
(18)
$$ iw = \left[ {\begin{array}{*{20}l} { - \;{1}{\text{.1643}}} \hfill & { - \;{7}{\text{.3668}}} \hfill & {{2}{\text{.1575}}} \hfill \\ {{0}{\text{.0866}}} \hfill & {{7}{\text{.5079}}} \hfill & { - \;{6}{\text{.4150}}} \hfill \\ {{2}{\text{.8735}}} \hfill & {{4}{\text{.4912}}} \hfill & { - \;{13}{\text{.8707}}} \hfill \\ { - \;{0}{\text{.0806}}} \hfill & { - \;{1}{\text{.7714}}} \hfill & { - \;{0}{\text{.5592}}} \hfill \\ \end{array} } \right], $$
(19)
$$ lw = \left[ \begin{gathered} - \;{3}{\text{.1226}} \hfill \\ { 6}{\text{.8832}} \hfill \\ { 6}{\text{.0567}} \hfill \\ \end{gathered} \right], $$
(20)
$$ b_{1} = \left[ {\begin{array}{*{20}c} {{3}{\text{.1621}}} & {{10}{\text{.0650}}} & { - {19}{\text{.7723}}} \\ \end{array} } \right], $$
(21)
$$ b_{2} = \left[ {{1}{\text{.3657}}} \right]. $$
(22)

Comparison of the best hybrid ANN with existing sediment transport equations

With respect to the explanations provided, it is evident that ICA was more accurate than the two other evolutionary algorithms (GA and PSO) and the MLP neural network. Figure 9 compares the Fr values predicted using ICA with the results of the sediment transport equations. ICA produced a relative error below 10% in all states, whereas none of the sediment transfer equations presented did so. May et al.’s [38] equation results were in the forms of under- and over-design, whereby the predicted values had low quantitative accuracy in both states because the relative error reached 30% in some cases. Azamathulla et al.’s [36] equation often underestimated Fr. Since the relative error was lower than May et al.’s [38], it can lead to sediment deposition on channel beds. This will result in diminished transport capacity due to the reduced transverse flow cross section and increased bed roughness. Ebtehaj et al.’s [37] equation was more accurate than the two other equations, but it also predicted Fr with approximately 11% relative error, which is less accurate than ICA.

Fig. 9
figure 9

Comparison of ICA and existing sediment transport equations in estimating Fr

Full size image

Table 2 compares the results of ICA, PSO and GA, and the MLP neural network with existing sediment transport algorithms according to different statistical indices and Vongvisessomjai et al.’s [35] dataset. It is clear that the soft computing methods presented in this study (ICA, GA, PSO and MLP) are more accurate than the regression equations. The best regression equation was that proposed by Ebtehaj et al. [37], which is less capable of predicting Fr than the evolutionary algorithms proposed in this study. It should be mentioned that despite the higher accuracy of the evolutionary optimization-based MLP neural network models over the classical MLP and other regression models, these models have some disadvantages. One downfall is with training speed and another is that neural network modeling using evolutionary algorithms is much more time consuming than MLP, which is trained by classical learning algorithms such as Levenberg–Marquardt and other simple regression models.

Table 2 Comparison of evolutionary algorithms (ICA, PSO and GA) and the MLP neural network with existing sediment transport equations according to statistical indices
Full size table

Uncertainty analysis for hybrid ANN model predictions

In this sub-section, we present the quantitative appraisal of the uncertainty [43, 44] in the non-deposition sediment transport model forecast for three different hybrid ANN methods, including PSO–ANN, GA–ANN, ICA–ANN. The difference between the predicted values (Pi) and the actual values (Ai) is known as the error (ei = Pi−Ai). Using the ei as the value of predicted error, the mean \((\overline{e} = \sum\nolimits_{i = 1}^{n} {e_{i} } )\) and standard deviation \(S_{e} = \sqrt {\sum\nolimits_{i = 1}^{n} {\left( {e_{i} - \overline{e}} \right)^{2} /n - 1} }\) of the prediction errors are computed. The standard deviation of prediction error (SDPE) and MPE as well as Wilson score technique are employed to defined a 95% confidence band around forecasted values of Fr. The results of MPE, SDPE, 95% prediction error interval (95PEI) and width of uncertainty band (WUB) for 18 different models (six models for each hybrid ANN models) are presented in Table 3. It is clear that the lowest value of MPE, SDPE and WUB belong to Model 4 for entire hybrid methods (PSO–ANN, GA–ANN, ICA–ANN). The WUB for Model 4 of PSO–ANN, GA–ANN, ICA–ANN are ± 0.026, ± 0.032 and ± 0.024, respectively. The MPE for ICA–ANN is computed as 0.16 compared to 0.209 and 0.223 for PSO–ANN and GA–ANN. The results of MPE for all models including ICA, GA, PSO indicate the overestimation performance of all 18 models. The MPE were ranged from 0.162 to 0.396 which are related to ICA 4 and PSO 2, respectively. The model PSO 5 had the highest WUB of 0.06, while ICA 4 had the lowest WUB of 0.024. Similarity, the lowest 95PEI was shown for the ICA 4 model. Generally, the results of this table demonstrate the lowest MPE and the smallest WUB and 95PEI compared to other hybrid models.

Table 3 Uncertainty analysis for ICA, PSO and GA models
Full size table

Partial derivative sensitivity analysis (PDSA) for proposed equation

In this sub-section, we studied the sensitivity of an equation by partial deference of this equation related to each input variable, also known as the partial derivative sensitivity analysis (PDSA), and the trend variation of ICA–ANN due to different samples of each input parameters [45,46,47,48,49]. The highest value of sensitivity indicates the higher impact of each input parameter in calculation of target value by the proposed equation. The negative (or positive) value of PDSA demonstrates that a reduction in parameter xi leads to an increase (or decrease) of target value calculated by proposed equation. Figure 10 presents the results of partial derivative sensitivity analysis (PDSA) for all input parameters of ICA (Mode 4). The result of PDSA demonstrated the direct relation of CV and λS and the indirect relation of d/D and d/R with the variation trend of densimetric Froude number (Fr).

Fig. 10
figure 10

The results of partial derivative sensitivity analysis (PDSA) for all input parameters of ICA (Mode 4)

Full size image

Conclusions

An omnipresent factor affecting channel pipes is sediment deposition on channel beds. In this study, Fr was estimated using ANN with the GA, PSO and ICA algorithms to optimize the layer design and minimize the target functions. To obtain an equation for predicting Fr, the effective parameters were categorized into 5 groups, and 6 models were presented to survey the impact of each parameter on Fr prediction using ICA–ANN, GA–ANN and PSO–ANN. The model generated by all algorithms that includes the volumetric sediment concentration (CV), median relative particle size (d/D), relative flow depth (d/R) and overall sediment friction factor (λs) parameters to estimate Fr returned the best results. Moreover, to validate the flexibility of the models generated by the evolutionary algorithms in different hydraulic conditions, their results were compared with Vongvisessomjai et al.’s [35] laboratory test results. The outcome demonstrated that these algorithms also produced good results under different conditions that were not applied in network training. A comparison of the predictions made by the used evolutionary algorithms with the ANN indicated that using these algorithms raises Fr prediction accuracy. Moreover, the evolutionary algorithms’ prediction accuracy was compared with existing equations. The results indicated that ICA (MAPE = 3.29%, RMSE = 0.024, IOA = 0.997 and EFF = 1.029) predicted Fr more accurately than other equations. Furthermore, an explicit equation was presented that can be easily applied in practical situations.