Critical ranking of steam handling unit using integrated cloud model and extended PROMETHEE for maintenance purpose

Abstract

To determine the critical component in an industry is one of the most important tasks performed by maintenance personnel to choose the best maintenance policy. Therefore, the purpose of the current paper is to develop a methodology based on integrated cloud model and extended preference ranking organization method for enrichment evaluation (PROMETHEE) method for finding the most critical component of the framework by ranking the failure causes of the system from multiple decision maker perspective. For this purpose, ranking of failure causes is performed by taking into account five factors namely chances of occurrence of failure (F₀), non-detection probability (N_d), downtime duration (D_d), spare part criticality (S_pc) and safety risk (S_r). In this paper, first the primary and secondary weight of decision makers are calculated based on the uncertainty degree and divergence degree, respectively, to determine overall weight using cloud model theory by converting the uncertain linguistic evaluation matrix into interval cloud matrix, and then ranking of the steam handling subunit of paper making unit in a paper mill using extended PROMETHEE. The effectiveness of the proposed methodology is explained by considering steam handling subunit of paper making unit to find the critical component.

Introduction

In today’s world as the competition is increasing day by day, it is necessary for industries to meet the order regularly and to supply quality items as with time, disintegration and break down of framework occurs which result in sudden breakdown of the framework and safety risks. To evade such circumstances, it is must to adopt an appropriate maintenance policy which is imperative with a particular conclusion to repair/reinstate the disintegrated framework before total failure. Kaplan and Garrick [1] measured the risk in terms of probability of disappointment event, in this way firms perform maintenance procedures as a strategy for directing the risks. Grievink et al. [2] detailed that within start-up phase, servicing expenses are expected to be 2–6% of investment expenses and Bevilacqua and Braglia [3] stated due to need of maintenance exercises, its cost may expend up to 70% of total manufacturing expenses based upon the industry, above 15% for heavy process industries [4]. Also doing corrective maintenance will diminish the expenditure cost, but may result in failure of the machine which ultimately results in excessive loss to the firm [5]. It causes according to Moore and Starr [6] inherent misfortunes to the organization due to unsatisfied clients and Zaim et al. [7] augmentation in the production cost, shipment delay, benefit reduction, loss of future growth chances. To overcome these situations, it is must to adopt an appropriate maintenance strategy [8]. For this to achieve, the primary goal is to perform the critical ranking of failure causes of the system so that appropriate maintenance policy can be adopted.

Literature review

To select a suitable maintenance policy, it is must to perform the failure mode and effect analysis (FMEA) [9] as through FMEA it is possible to assess and eliminate root causes of system/process failure. It is considered as an obvious tool to perform the criticality analysis for process industry through Risk Priority Number (RPN) that is defined as a product of probability of failure occurrence, severity and chance of non-detection and adopted by Xu et al. [10] in diesel engine turbocharger, Panchal and Kumar [11] in coal handling system and by many more researchers. The limitation of the tradition FMEA, i.e. considering only three attributes which are of equal importance, sometimes combination of these three factors results in a same RPN but in actual, reality may be different and ignorance of dependence among the factors and performed the assessment of risk factors using Dempster’s combination rule [12]. Many researchers highlighted that FMEA is not concerned to individuals but it is a group oriented task which includes experts of multidisciplinary field. This makes the traditional FMEA inappropriate and to overcome these drawbacks, researchers have used numerous Multi-Criteria Decision Making (MCDM) approaches in their research work.

Analytic hierarchy process (AHP) as explained by Saaty [13] is an approach where priority weights of the alternatives being used to rank the considered alternatives. Various researchers applied AHP method for various problems such as Sachdeva et al. [14] in a process industry, Cascales and Lamata [15] for diesel engine cleaning system part selection maintenance, Bahadir and Bahadir [16] in textile structure industry. Hwang and Yoon [17] proposed Technique for order preference by similarity to ideal solution (TOPSIS) method. Song et al. [18] performed FMEA to evaluate the risk of failure modes in steam valve system using TOPSIS. Various researchers applied TOPSIS technique for various problems such as (Sachdeva et al. [19], Zhou and Lu [20]) for risk assessment; in a process industry and of dynamic alliance, respectively. Aktas and Kabak [21], Ahmed et al. [22] used AHP-TOPSIS to evaluate the location site for solar energy plant, selection of material in the construction industry, respectively. Singh and Singh [23] used fuzzy AHP-TOPSIS to find the ranking of alternative routes in multicriteria decision situation. Chatterjee et al. [24] applied Vlse Kriterijumska Optimizacija Kompromisno Resenje (VIKOR) and ELimination and Et Choice Translating Reality (ELECTRE) an outranking method for supplier selection. Panwar et al. [25] applied AHP-VIKOR for ranking the various failure causes in pulping unit. Mohsen and Fereshteh [26] applied fuzzy VIKOR to rank and prioritize the failure causes of geothermal power plant. Preference Ranking Organization Method for Enrichment of Evaluations (PROMETHEE) is an outranking method in multi-criteria analysis [27]. Cavalcante and Almeida [28] used PROMETHEE for preventive maintenance equipment breakdown. Abdelhadi [29] used PROMETHEE for maintenance scheduling. Sen et al. [30] applied PROMETHEE II for selection of robot for industrial purpose. PROMETHEE method has been widely used widely to solve various MCDM problems such as airport location selection [31], service quality evaluation [32], and emergency response assessment [33].

Lo and Liu [34] proposed a novel approach for FMEA-based risk assessment using best worse method and grey relation analysis (GRA) in an electronics company. According to Li et al. [35], Cloud model is an approach incorporating randomness with fuzziness. Due to its distinguished capability of handling uncertainty, various researchers have used this approach in various applications. Liu et al. [36] performed ranking of failure modes of C-arm of X-ray machine using combination of cloud model and GRA. Wang et al. [37] solved MCDM problems using cloud model. Zhao and Li [38] developed a model that integrates cloud computing and fuzzy method to perform the risk analysis in power construction sector. Shi et al. [39] performed an integrated cloud model and multi-attributive border approximation area comparison method for selecting best healthcare waste treatment advances by considering three decision makers. Wang et al. [40] developed an integrated cloud model and qualitative flexible multiple criteria method to an auto manufacturer industry. Using integrating cloud model theory and PROMETHEE II approach, Liu et al. [41] performed the FMEA of healthcare delivery system by incorporating eight failure causes and Liu [42] performed FMEA of emergency department. Wang et al. [43] performed robot selection for automobile industry using cloud TODIM approach. Liu et al. [44] performed risk analysis of scraper arm control system and Lei et al. [45] performed risk analysis using of metro vehicle by integrating cloud model and TOPSIS approach. Failure causes of a steam valve system is identified using Cloud model and extended TOPSIS [46]. Hu et al. [47] performed risk analysis of health care department by ranking the failure causes using cloud model and GRA-TOPSIS approach. Huang et al. [48] performed the risk analysis of enterprise architecture and information system using probabilistic linguistic term sets to handle the intrinsic ambiguity and TODIM approach to rank the failure modes. Li et al. [49] performed risk assessment of CNC machine using cloud model and best–worst method. Liu et al. [50] performed risk ranking of identified failure causes in a process industry using cloud model and extended GRA to overcome the limitation of traditional FMEA. Zhu et al. [51] obtained the risk priority of failure modes in water gasification system using modified PROMETHEE under linguistic neutrosophic context.

With reference to the above literature analysis, efforts have been made to overcome the limitations of traditional FMEA but still little attention has been paid to the vagueness and randomness inherent in the group-based FMEA decision makers. For this reason, we define an integrated approach based on cloud model and extended PROMETHEE in which firstly using cloud model, the failure causes are defined in terms of linguistic evaluators which are transformed into interval cloud matrix and then to group cloud matrix by taking into account the overall weights of the decision maker. To calculate the overall weights of the decision makers, first, primary weights are calculated using uncertainty degree and then secondary weights using divergence degree. By doing this, we can avoid the imprecise subjective assigning of weights to the decision maker. Second, an extended PROMETHEE is used to rank the failure causes using the concept of net outranking flow calculated based on leaving and entering flow. Finally, the proposed methodology is applied to rank the failure causes of Steam handling subunit to illustrate its effectiveness and also it will allow the maintenance personnel to select the best maintenance policy.

Cloud model methodology

According to Li et al. [35], cloud model is a modern cognition demonstrates of vulnerability proposed based on likelihood hypothesis and fuzzy set hypothesis, which permits a stochastic unsettling influence of the membership degree encompassing a decided central esteem.

Definition 1:

[35, 37]. Given a subjective concept $N$ characterized on a universe of talk $V,P \subseteq V$, let $p\left( {p \in P} \right)$ be an arbitrary instantiation of the concept $N$ and $F_{N} \left( P \right) \in \left[ {0,1} \right]$ be the membership degree of $p$ belonging to $F$, which corresponds to an arbitrary number with steady inclination. Then, the dispersion of the membership over the space is called a membership cloud, or basically, a cloud.

Definition 2:

[35, 37]. The characteristics of a cloud $z$ are delineated by three numerical parameters, specially expectation $E_{p}$, entropy $S_{n}$ and hyper entropy $S_{e}$. Here, $E_{p}$ is the middle value of the subjective concept space, $S_{n}$ measures the uncertainty of the subjective concept, and $S_{e}$ reflects the scattering degree of a cloud’s beads and the irregular changes of the membership. The cloud can be written as $\tilde{z} = \left( {E_{p} ,S_{n} ,S_{e} } \right)$.

Note that the cloud $\tilde{z} = \left. {\left( {\left[ {\underline{Ep} } \right.} \right.,\left. {\overline{Ep} } \right],Sn,Se} \right)$ is called an interval integrated cloud when the anticipated value is an interval range $\left[ {\underline{{E_{p} }} ,\overline{{E_{p} }} } \right]$.

Definition 3:

Consider any two interval integrated clouds $\tilde{z}_{1} = \left. {\left( {\left[ {\underline{{Ep_{1} }} } \right.} \right.,\left. {\overline{{Ep_{1} }} } \right],Sn_{1} ,Se_{1} } \right)$ and $\tilde{z}_{2} = \left. {\left( {\left[ {\underline{{Ep_{2} }} } \right.} \right.,\left. {\overline{{Ep_{2} }} } \right],Sn_{2} ,Se_{2} } \right)$, then

$$ \begin{aligned} \tilde{z}_{1} \times \tilde{z}_{2} & = \left(\left[ {\underline{{Ep_{1} Ep_{2} }}} , {\overline{{Ep_{1} Ep_{2} }} } \right],\sqrt {\left( {Sn_{1} Ep_{2} } \right)^{2} + \left( {Sn_{2} Ep_{1} } \right)^{2} } , \right. \\ &\quad \left. \sqrt {\left( {Se_{1} Ep_{2} } \right)^{2} + \left( {Se_{2} Ep_{1} } \right)^{2} } \right)\end{aligned} $$

(1)

$$ \lambda \tilde{z}_{1} = \left( {\left[ {\lambda \underline{{Ep_{1} }} } \right.} \right.,\left. {\lambda \overline{{Ep_{2} }} } \right],\sqrt \lambda Sn_{1} ,\left. {\sqrt \lambda Se_{1} } \right),\lambda > 0 $$

(2)

$$ \tilde{z}_{1}^{\lambda } = \left( {\left[ {\underline{{Ep_{1}^{\lambda } }} } \right.} \right.,\left. {\overline{{Ep_{1}^{\lambda } }} } \right],\sqrt \lambda \left( {Ep_{1} } \right)^{\lambda - 1} Sn_{1,} \left. {\sqrt \lambda \left( {Ep_{1} } \right)^{\lambda - 1} Se_{1} } \right),\lambda > 0 $$

(3)

where $Ep_{1} = \frac{{\underline{{Ep_{1} }} + \overline{{Ep_{1} }} }}{2}$ and $Ep_{2} = \frac{{\underline{{Ep_{2} }} + \overline{{Ep_{2} }} }}{2}.$

Using Eq. 1, we can find multiplication of two interval clouds and with Eq. 2, we can find out weighted interval cloud.

Definition 4:

Let $\tilde{z}_{i} = \left. {\left( {\left[ {\underline{{Ep_{i} }} } \right.} \right.,\left. {\overline{{Ep_{i} }} } \right],Sn_{i} ,Se_{i} } \right)$ $\left( {i = 1,2,.....n} \right)$ be $n$ interval integrated clouds in the space $V,$ and $w = \left( {w_{1} ,w_{2} ,....,w_{n} } \right)^{N}$ be their associated weights with $w_{i} \in \left[ {0,1} \right]$ and $\sum\limits_{i = 1}^{n} {w_{i} } = 1,$ then the floating interval cloud $\tilde{z} = \left. {\left( {\left[ {\underline{Ep} } \right.} \right.,\left. {\overline{Ep} } \right],Sn,Se} \right)$ is generated as follows:

$$ \begin{gathered} \tilde{z} = \sum\limits_{i = 1}^{n} {w_{i} \tilde{z}_{i} } = \sum\limits_{i = 1}^{n} {w_{i} } \left( {\left[ {\underline{{Ep_{i} }} } \right.} \right.,\left. {\overline{{Ep_{i} }} } \right],Sn_{i} ,\left. {Se_{i} } \right) \hfill \\ \tilde{z} = \left( {\sum\limits_{i = 1}^{n} {w_{i} \left[ {\underline{{Ep_{i} }} } \right.} } \right.,\left. {\overline{{Ep_{i} }} } \right],\sqrt {\sum\limits_{i = 1}^{n} {w_{i} Sn_{i}^{2} } } ,\sqrt {\sum\limits_{i = 1}^{n} {w_{i} Se_{i}^{2} } } . \hfill \\ \end{gathered} $$

(4)

Definition 5:

[37]. Let $\tilde{z}_{1} = \left. {\left( {\left[ {\underline{{Ep_{1} }} } \right.} \right.,\left. {\overline{{Ep_{1} }} } \right],Sn_{1} ,Se_{1} } \right)$ and $\tilde{z}_{2} = \left. {\left( {\left[ {\underline{{Ep_{2} }} } \right.} \right.,\left. {\overline{{Ep_{2} }} } \right],Sn_{2} ,Se_{2} } \right)$ be two self-assertive interval integrated clouds, then the distance between the two is characterized as

$$ \begin{aligned} d\left( {\tilde{z}_{1} ,\tilde{z}_{2} } \right) &= \frac{1}{2}\left( {\left| {\left( {1 - \left. {\frac{{Sn_{1} + Se_{1} }}{{Sn_{1} }}} \right)} \right.} \right.} \right.\underline{{Ep_{1} }} - \left. {\left. {\left( {1 - \frac{{Sn_{2} + Se_{2} }}{{Sn_{2} }}} \right.} \right)\underline{{Ep_{2} }} } \right| \nonumber\\ &\quad + \left| {\left( {1 - \left. {\frac{{Sn_{1} + Se_{1} }}{{Sn_{1} }}} \right)} \right.\overline{{Ep_{1} }} } \right. - \left. {\left. {\left. {\left( {1 - \frac{{Sn_{1} + Se_{2} }}{{Sn_{2} }}} \right.} \right)\overline{{Ep_{2} }} } \right|} \right).\end{aligned} $$

(5)

If $Sn_{1} = Se_{1} = Sn_{2} = Se_{2} = 0,$ then the interval integrated clouds changes to interval numbers and $d(\tilde{z}_{1} ,\tilde{z}_{2} ) = \frac{1}{2}\left( {\left| {\underline{{Ep_{1} }} } \right.} \right. - \left. {\underline{{Ep_{2} }} } \right| + \left| {\overline{{Ep_{1} }} } \right. - \left. {\left. {\overline{{Ep_{2} }} } \right|} \right).$

Definition 6:

$S = \left\{ {s_{0} ,s_{1} .......s_{m} } \right\}$ be linguistic term set, then m + 1 essential clouds corresponding to the expression of linguistic values can be produced and denoted as $z_{0} = \left( {Ep_{0} ,Sn_{0} ,Se_{0} } \right),$$z_{1} = \left( {Ep_{1} ,Sn_{1} ,Se_{1} } \right),........,z_{m} = \left( {Ep_{g} ,Sn_{g} ,Se_{g} } \right)$.

By golden section method [37, 39] based on a seven label linguistic term set $S = \left\{ \begin{gathered} s_{0} = {\text{Verylow}}\left( {V_{L} } \right),s_{1} = {\text{Low}}\left( L \right),s_{2} = {\text{Mediumlow}}\\ \left( {M_{L} } \right), s_{3} = {\text{Medium}}\left( M \right),s_{4} = {\text{Mediumhigh}}\left( {M_{H} } \right), \hfill \\ s_{5} = {\text{High}}\left( H \right),s_{6} = {\text{Veryhigh}}\left( {V_{H} } \right) \hfill \\ \end{gathered} \right\},$ and the corresponding expressions are shown below:

$$ \begin{gathered} Ep_{i} = \frac{i}{m},i = 0,2,.....,g, \hfill \\ Sn_{2} = Sn_{4} = 0.382(Y_{\max } - Y_{\min } )/6,Sn_{3} = 0.618Sn_{2} , \hfill \\ Sn_{1} = Sn_{5} = Sn_{2} /0.618,Sn_{0} = Sn_{6} = Sn_{1} /0.618, \hfill \\ Se_{2} = Se_{4} = Se_{3} /0.618,Se_{1} = Se_{5} = Se_{2} /0.618, \hfill \\ Se_{0} = Se_{6} = Se_{1} /0.618 \hfill \\ \end{gathered} $$

The effective domain $V = \left[ {Y_{\min } ,Y_{\max } } \right] = \left[ {0,1} \right]$ and $Se_{3}$ is designated in advance. The basic idea of the golden section is that the closer to the centre of the valid universe, the smaller the Sn and Se of the cloud, and the further from the centre of the valid universe, the larger the S_n and S_e of the cloud. The larger one of the Sn and Se of the adjacent cloud is 1/0.618 times the smaller one.

Example 1:

Assuming Se = 0.1, seven basic clouds can be generated as z₀ = (0, 0.167, 0.424), z₁ = (0.167, 0.103, 0.267), z₂ = (0.333, 0.064, 0.162), z₃ = (0.5, 0.039, 0.1), z₄ = (0.667, 0.064, 0.162), z₅ = (0.833, 0.103, 0.262), z₆ = (1, 0.167, 0.424).

Definition 7:

Let $S = \left\{ {s_{0} ,s_{1} .......s_{m} } \right\}$ be a linguistic term set and $\left[ {s_{i} ,s_{j} } \right]$ be an interval linguistic value, and then its equivalent interval cloud $\tilde{z} = \left. {\left( {\left[ {\underline{Ep} } \right.} \right.,\left. {\overline{Ep} } \right],Sn,Se} \right)$ is acquired by

$$ \begin{gathered} \underline{Ep} = \min \left\{ {Ep_{i} ,Ep_{j} } \right\},\overline{Ep} = \max \left\{ {Ep_{i} ,Ep_{j} } \right\} \hfill \\ Sn = \sqrt {\frac{{Sn_{i}^{2} + Sn_{j}^{2} }}{2}} ,Se = \sqrt {\frac{{Se_{i}^{2} + Se_{j}^{2} }}{2},} \hfill \\ \end{gathered} $$

(6)

where $z_{i} = (Ep_{i} ,Sn_{i} ,Se_{i} )$ and $z_{j} = (Ep_{j} ,Sn_{j} ,Se_{j} )$ are the clouds formed from the linguistic term set S.

Example 2:

Let the domain V be [0, 1] and [s₁ and s₂] be the interval linguistic value. First, convert linguistic term s₁ and s₂ into two clouds z₁ = (0.167, 0.103, 0.267) and z₂ = (0.333, 0.064, 0.162), respectively, and then, $Ep$= min {0.167, 0.333} = 0.167, $\stackrel{-}{Ep}$= max {0.167, 0.333} = 0.333.

$Sn=\sqrt{\frac{{0.103}^{2}+{0.064}^{2}}{2}}$=0.086, $Se=\sqrt{\frac{{0.267}^{2}+{0.162}^{2}}{2}}$= 0.218.

Proposed cloud model and extended PROMETHEE

In the succeeding section, we build up a new risk assessment ranking model using cloud and extended PROMETHEE method. The proposed methodology consists of three phases:

• (1) Risk assessment of failure causes through cloud model.

• (2) Determining the weights of decision makers through cloud model, and

• (3) Using PROMETHEE II method to obtain the ranking of failure causes.

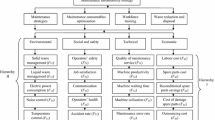
Figure 1 shows the schematic representation of the proposed methodology.

Fig. 1

The framework of ranking failure causes

Phase 1. Failure causes risk assessment

Suppose there are $p$ failure causes $D_{i}$ $\left( {i = 1,2,......p} \right),$ and $q$ risk factors $C_{j} \left( {j = 1,2,.....q} \right)$ with the weight vector $w = \left( {w_{1} ,w_{2} ,....w_{q} } \right)$, where $w_{j} \in \left[ {0,1} \right]$ and $\sum\nolimits_{j = 1}^{q} {w_{j} } = 1$. Assume that $h$ decision makers $DM_{k} \left( {k = 1,2,....h} \right)$ are included in the risk assessment process whose relative weights are obscure. Let $T^{k} = \left( {t_{ij}^{k} } \right)_{p \times q}$ be the linguistic assessment matrix of the $k^{th}$ decision maker, where $d_{ij}^{k}$ is the linguistic rating of $D_{i}$ on $CF_{j}$ inferred from the linguistic term set $S^{{^{k} }} = \left\{ {s_{0}^{k} ,s_{1}^{k} ,.....s_{m}^{k} } \right\}.$

Step 1: Construct risk assessment normalized linguistic evaluation matrix using definition 6.

Step 2: Convert the linguistic evaluation matrix into interval cloud matrix using definition 7.

Phase 2. Computing weights of FMEA decision makers

Step 3: Determine the weights of FMEA decision makers based on uncertainty degree.

For finding weightage of decision makers, the uncertainty degree has been used in MCDM [37, 39] by the expression

$$ H\left( {\tilde{R}^{k} } \right) = \sum\limits_{i = 1}^{p} {\sum\limits_{j = 1}^{q} {\frac{{\overline{{Ep_{ij}^{k} }} - \underline{{Ep_{ij}^{k} }} }}{m + 1}} } , $$

(7)

where $H({\stackrel{\sim }{R}}^{k})$ is Uncertainty degree of the risk assessment matrix $({\stackrel{\sim }{R}}^{k})$

Lower the uncertainty degree, the more exact the assessment information will be, which recommends that higher weight should be given to the decision maker. Hence, the primary weight vector of decision maker $\lambda^{\left( 1 \right)} = \left( {\lambda_{1}^{\left( 1 \right)} ,\lambda_{2}^{\left( 1 \right)} ,...,\lambda_{h}^{\left( 1 \right)} } \right)$ is derived by

$$ \lambda_{k}^{(1)} = \frac{{1/H(\tilde{R}^{k} )}}{{\sum\nolimits_{k = 1}^{l} {1/H(\tilde{R}^{k} )} }} $$

(8)

Step 4: Determine the weights of FMEA decision makers based on divergence degree.

While making a group decision, the risk rating of the individual team member should be consistent with the others to the maximum extent. Therefore, according to [39], the divergence degree between the risk assessment matrix $\tilde{R}^{k}$ and the risk assessment matrices of other FMEA decision makers is derived by

$$ G\left( {\tilde{R}^{k} } \right) = \frac{1}{{\sum\nolimits_{u = 1,u \ne \kappa }^{l} {\sum\nolimits_{i = 1}^{p} {\sum\nolimits_{j = 1}^{q} {d\left( {\tilde{z}_{ij}^{k} ,\tilde{z}_{ij}^{u} } \right)} } } }}, $$

(9)

where $G({\stackrel{\sim }{R}}^{k})$ is divergence degree of the risk assessment matrix $({\stackrel{\sim }{R}}^{k})$ and $d\left( {\tilde{z}_{ij}^{k} ,\tilde{z}_{ij}^{u} } \right)$ is the distance between two interval clouds and can be calculated by (5).

If the risk evaluation given by the $k^{th}$ decision maker $DM_{k}$ is consistent with other decision makers, then it can be seen that $DM_{k}$ plays a moderately greater part and ought to be given a greater weight. Thus, the secondary weight vector of decision maker $\lambda^{\left( 2 \right)} = \left( {\lambda_{1}^{\left( 2 \right)} ,\lambda_{2}^{\left( 2 \right)} ,...,\lambda_{h}^{\left( 2 \right)} } \right)$ is calculated by

$$ \lambda_{k}^{2} = \frac{{G(\tilde{R}^{k} )}}{{\sum\nolimits_{k = 1}^{l} {G(\tilde{R}^{k} )} }}. $$

(10)

Step 5: Determine the overall weights of decision makers.

To calculate overall weight of the decision maker the primary and secondary weight are combined using the following equation:

$$ \lambda^{k} = \sigma \lambda_{k}^{(1)} + (1 - \sigma )\lambda_{k}^{2} , $$

(11)

where $\sigma$ shows characteristics of risk examiners and satisfies $0 \le \sigma \le 1$.

Phase 3. Determine the ranking of failure causes

In PROMETHEE, first normalisation of decision matrix is performed, then alternative pair wise comparison to calculate the preference function, and then computes leaving and entering outranking flows to find out the overall outranking flow to rank the alternatives. In this paper, PROMETHEE II approach is suggested to rank the failure causes taken under consideration, whose description is shown as below.

Step 6: Using the overall weights calculated, construct group interval cloud matrix.

The individual interval cloud matrices $\tilde{Z}^{k} \left( {k = 1,2,...,h} \right)$ are aggregated using the overall weights derived for decision maker $\lambda = \left( {\lambda_{1} ,\lambda_{2} ,...,\lambda_{h} } \right),$ from uncertainty $H\left( {\tilde{R}^{k} } \right)$ and divergence $G\left( {\tilde{R}^{k} } \right)$ degree to develop a group interval cloud matrix $\tilde{Z} = \left( {\tilde{z}_{ij} } \right)_{p \times q}$ using the Interval cloud weighted averaging (ICWA) operator [37]. $\tilde{z}_{ij} = \left( {\left[ {\underline{{Ep_{ij} ,}} } \right.} \right.\left. {\overline{{Ep_{ij} }} } \right],Sn_{ij} ,\left. {Se_{ij} } \right)$ of failure cause $D_{i}$ against risk factor $C_{j}$ is computed by

$$ \begin{aligned} \tilde{z}_{ij} & = {\text{ICWA}}_{\lambda } (\tilde{z}^{1}_{ij} ,\tilde{z}^{2}_{ij} ,......\tilde{z}^{h}_{ij} ) \\ &\quad = \sum\limits_{k = 1}^{h} \lambda_{k} \tilde{z}^{1}_{ij} = \left( {\sum\limits_{k = 1}^{h} {\lambda_{k} \left[ {\underline{{Ep_{ij}^{k} }} } \right.} } \right.,\left. {\overline{{Ep_{ij}^{k} }} } \right],\\ &\quad \sqrt {\sum\limits_{k = 1}^{h} {\lambda_{k} \left( {Sn_{ij}^{k} } \right)^{2} } } ,\left. {\sqrt {\sum\limits_{k = 1}^{h} {\lambda_{k} \left( {Se_{ij}^{k} } \right)^{2} } } } \right) \end{aligned} $$

(12)

The ICWA operator accomplishes the usual properties of weighted average operators.

Step 7: Develop the risk index $C_{{_{j} }} (D_{r} ,D_{s} )$.

According to [30], the risk index for each pair of failure cause $(D_{r} ,D_{s} )$ $\left( {r,s = 1,2,....,p,r \ne s} \right)$ is designed as

$$ \begin{array}{*{20}c} {C_{{_{j} }} (D_{r} ,D_{s} ) = 0} & {{\text{if}}\,\tilde{z}_{rj} \le \tilde{z}_{sj} } \\ {C_{{_{j} }} (D_{r} ,D_{s} ) = d(\tilde{z}_{rj} ,\tilde{z}_{sj} )} & {{\text{if}}\,\tilde{z}_{rj} > \tilde{z}_{sj} } \\ \end{array} , $$

(13)

where $j = 1,2, \ldots n$ and $d\left( {\tilde{z}_{rj} ,\tilde{z}_{sj} } \right)$ is the distance between two interval clouds $\tilde{z}_{rj}$ and $\tilde{z}_{sj} .$ The risk index $C_{j} (D_{r} ,D_{s} )$ is the measure to back the theory that $D_{r}$ has a higher risk than $D_{s}$ concerning the risk factor${C}_{j}$.

Step 8: Determine overall risk index $C(D_{r} ,D_{s} )$ using weights of each failure causes.

Considering risk factor weights, the overall risk index of $D_{r}$ over $D_{s}$ across q risk factors can be determined by

$$ \begin{gathered} C(D_{r} ,D_{s} ) = \sum\limits_{j = 1}^{q} {w_{j} C_{j} \left( {D_{r} ,D_{s} } \right)} , \hfill \\ r,s = 1,2,..........p,r \ne s \hfill \\ \end{gathered} $$

(14)

where $w_{j}$ shows the priority weight of the $j^{th}$ risk factor.

Step 9: Determine the leaving and the entering outranking flows.

The leaving outranking flow of failure cause $D_{r}$, a measure of the risk of failure cause $D_{r}$ over the other failure causes, is denoted by

$$ \beta^{ + } \left( {D_{r} } \right) = \frac{1}{p - 1}\sum\limits_{r = 1,r \ne s}^{p} {C(D_{r} ,D_{s} ),} $$

(15)

In the same way, the entering outranking flow of failure cause $D_{r}$, a measure of the risk of failure cause $D_{r}$ over the other failure causes, is denoted by

$$ \beta^{ - } \left( {D_{r} } \right) = \frac{1}{p - 1}\sum\limits_{r = 1,r \ne s}^{p} {C(D_{s} ,D_{r} ),} $$

(16)

Step 10: Obtain the net outranking flow for each failure cause.

The net outranking flows can be obtained by

$$ \beta \left( {D_{r} } \right) = \beta^{ + } \left( {D_{r} } \right) - \beta^{ - } \left( {D_{r} } \right),\,r = 1,2, \ldots p $$

(17)

Case study

In the current paper, an actual case study of northern region of Indian paper mill is considered. There are numerous functional units in a paper plant (feeding, pulping, screening, bleaching and paper production unit). The current study is done to perform risk analysis of steam handling subsystem in a paper production unit. The objective of the steam handling subunit is to heat the dryer’s rolls with the superheated steam to remove the moisture content of the paper rolled over the dryer rolls. To find the failure cause of steam handling subunit, a team is constructed which consist of graduate engineer trainee, maintenance assistant engineer and maintenance head denoted as $DM_{k} \left( {k = 1,2,3)} \right)$. After that root cause failures of steam handling subunit is identified and root cause analysis diagram is drawn (Fig. 2), which shows that there are eight causes of failure. The entire three decision maker $DM_{1} ,DM_{2} ,DM_{3}$ assesses the failure causes risks using definition 6 in terms of seven label linguistic term.

Fig. 2

Root cause analysis of Steam handling subunit

Illustration of proposed model

In the present paper, as discussed in the preceding sections, we use the integrated cloud model and extended PROMETHEE approach to find out the risk ranking of eight failure causes of steam handling subunit. To begin with in phase 1st, the different sorts of linguistic evaluations given in Table 1 are represented as linguistic intervals to develop the interval linguistic assessment evaluation matrices $\tilde{C}^{k} = \left( {\tilde{c}_{ij}^{k} } \right)_{8 \times 5} \left( {k = 1,2,3} \right)$. Then, the interval cloud matrices $\tilde{Z}^{k} = \left( {\tilde{z}_{ij}^{k} } \right)_{8 \times 5} \left( {k = 1,2,3} \right)$ are determined in line with the conversion method between linguistic ratings and interval clouds. The interval linguistic evaluation matrix and the interval cloud matrix are obtained for 1st decision maker ${\text{DM}}_{1}$ as shown in Tables 2 and 3, 2nd decision maker ${\text{DM}}_{2}$ as shown in Tables 4 and 5 and 3rd decision maker ${\text{DM}}_{{3}}$ as shown in Tables 6 and 7, respectively.

Table 1 Linguistic evaluation on the eight failure causes by the three FMEA decision makers

Table 2 Interval linguistic evaluation matrix for 1st FMEA decision maker

Table 3 Interval cloud matrix for 1st FMEA decision maker

Table 4 Interval linguistic evaluation matrix for 2nd FMEA decision maker

Table 5 Interval cloud matrix for 2nd FMEA decision maker

Table 6 Interval linguistic evaluation matrix for 3rd FMEA decision maker

Table 7 Interval cloud matrix for 3rd FMEA decision maker

In the 2nd phase, with the interval cloud matrices $\tilde{Z}^{k} \left( {k = 1,2,3} \right),$ as shown in Tables 3, 5, 7, the uncertainty degree of each FMEA decision maker are determined by (7), and the primary weights $\lambda_{k}^{\left( 1 \right)} \left( {k = 1,2,3} \right)$ are determined based on (8). Similarly, the divergence degree of each decision maker is find out using (9), the secondary weights $\lambda_{k}^{\left( 2 \right)} \left( {k = 1,2,3} \right)$ are obtained using (10). Lastly, the overall weight related with the three decision makers $\lambda = \left( {\lambda_{1} ,\lambda_{2} ,\lambda_{3} } \right)$ can be obtained with (11). The results obtained are shown in Table 8.

Table 8 Objective weights of the FMEA decision makers

In the third phase of our approach, risk ranking of failure causes of steam handling unit is determined. To begin with individual interval cloud matrix of three decision makers considered are aggregated using ICWA operator to set up the group interval cloud matrix $\tilde{Z} = \left( {\tilde{z}_{ij} } \right)_{8 \times 5}$ as shown in Table 9. Then, using (13) and (14), the risk indices $C_{j} \left( {D_{r} ,D_{s} } \right)\left( {r,s = 1,2,......8,r \ne s} \right)$ related to the risk factors F_o, N_d, D_l, S_pc, S_r and the overall risk indices $C\left( {D_{r} ,D_{s} } \right)\left( {r,s = 1,2,......8,r \ne s} \right)$ are calculated. Table 10 shows the overall risk indices for each eight pair of failure causes. The weights of the considered five risk factors are taken as 0.427, 0.208, 0.191, 0.111 and 0.2, respectively using AHP. Subsequently, using (15) and (16), the leaving outranking flows $\beta^{ + } \left( {D_{r} } \right)\left( {r = 1,2,...,8} \right)$ and the entering outranking flows $\beta^{ - } \left( {D_{r} } \right)\left( {r = 1,2,...,8} \right)$ of the eight failure causes are determined and shown in Table 11. At last, the net outranking flow for each failure causes $\beta \left( {D_{r} } \right)\left( {r = 1,2,...,8} \right)$ is derived using (17), as shown in Table 11. From Table 11, it can be concluded that the order of eight failure causes are $SH_{1} \succ SH_{6} \succ SH_{5} \succ SH_{3} \succ SH_{4} \succ SH_{7} \succ SH_{8} \succ SH_{2}$, in short failure cause electric failure in moisture controller is most critical and steam valve malfunctioning is least critical.

Table 9 Group interval cloud matrix

Table 10 Results of overall risk indices

Table 11 Ranking of failure causes by the proposed methodology

Comparisons and discussion

In this section, a comparative analysis is carried with two other alternative approaches fuzzy VIKOR and fuzzy TOPSIS to illustrate the effectiveness of the proposed approach. The critical ranking of the failure causes acquired by the alternative approaches with the proposed approach is shown in Table 12.

Table 12 Comparison analysis against alternative approaches

From Table 12, it can be seen that the critical ranking of failure causes by the proposed model agrees almost completely with those obtained by the fuzzy VIKOR and the fuzzy TOPSIS methods except in failure causes; SH₃, SH₄ between proposed approach and alternative Fuzzy TOPSIS approach and SH₅, SH₆ between proposed approach and alternative Fuzzy VIKOR approach. The main reason behind that is (1) the proposed method uses cloud model to describe the fuzziness and randomness of linguistic assessment information and deal with uncertainty and multi-granularity linguistic scale to assess the risk of failure causes. (2) The proposed model determines the weights of the decision makers objectively based on uncertainty degree and divergence degree which avoids the imprecise subjective randomness of assigning weights to the decision maker. Furthermore, in the proposed model, ranking of the failure causes is performed using PROMETHEE II which is a simple and easily comprehensible approach in comparison to other multi-criteria decision making approaches and produces complete ranking of alternatives.

The comparison analysis above manifests that the proposed model has ability to derive more accurate and practical risk ranking of failure causes which will be useful for practical risk management decision making.

Conclusion

In current research work, for ranking the failure causes in a process industry, an integrated approach based on cloud theory and PROMETHEE II was developed in which failure causes are evaluated by means of linguistic evaluations, then the interval linguistic evaluation are converted to interval cloud matrix, then using uncertainty degree and divergence degree weights of the decision makers are calculated which are used to obtain the group interval cloud matrix. Then, extended PROMETHEE approach was applied to rank the failure causes and determine the most critical one for risk reduction measures. An actual case study of steam handling subunit of paper production unit in a paper mill was proposed to illustrate the effectiveness of the proposed model and from which it was found that failure cause SH₁ is the most critical and SH₂ is the least critical. Ranking orders as inferred through proposed methodology have shown almost same result as obtained by other researcher through various multi-criteria decision making approaches. The finding of the paper will allow the maintenance personal to select the best maintenance policy for the critical component to minimize the risk and cheapest corrective maintenance policy for the least critical component.

For future research, the proposed model can be further improved: First, many calculations are contained in the implementation of the proposed model to derive the critical ranking of failure causes. Therefore, a specialised software tool should be developed for the execution of the proposed risk evaluation approach in real applications. Second, in the proposed model, we used fixed weight of decision maker’s member for all the failure causes therefore in future research, it would be interesting to develop a method for assigning diverse weights to decision makers according to the failure cause to obtain more reliable risk ranking results.