Introduction

During recent years, advanced automation techniques have been applied to assembly systems to improve flexibility and productivity. One of the most successful applications is the robotic assembly line, which uses robots to replace human labors. Compared to manual assembly line, the robotic assembly line can speed up the assembly process and reduce the work stress of workers [1]. Moreover, it provides more favorable conditions for decision-makers to design and manage the assembly line.

Assembly line balancing (ALB) problem is a typical problem in the design and management of assembly lines. It aims to balance the workload among different workstations by appropriately determining the task assignments subject to operational constraints. The ALB problem can be classified into four types according to the objectives, i.e. ALB-1, ALB-2, ALB-E and ALB-F [2, 3]. The objective of ALB-1 is to minimize the number of workstations with a given cycle time, while ALB-2 minimizes the cycle time with a predetermined workstation number. ALB-E attempts to maximize the line efficiency by minimizing the cycle time and workstation number simultaneously. ALB-F is a feasibility problem to figure out whether a feasible solution exists with a given combination of cycle time and workstation number. The most basic version of ALB is known as simple assembly line balancing (SALB) problem [2], which considers straight manual assembly lines with deterministic task time. The robotic assembly line balancing (RALB) problem can be regarded as the extension of SALB. Different from SALB, the decisions of RALB include not only the task assignment but also the robot assignment, which makes the problem more challenging.

So far, some mathematical models and model-based optimization algorithms have been proposed for RALB with different objectives and problem assumptions. In Rubinovitz and Bukchin [4], the RALB was considered as a RALB-1 to minimize the workstation number with a given cycle time. They proposed a frontier-search based branch-and-bound (B&B) algorithm to solve the problem. Although some heuristic rules were incorporated to reduce the search space, the storage space and computation time of the B&B based method are still too large to solve large scale problems. Bukchin and Tzur [5] considered a flexible assembly line designing problem to minimize total equipment costs with a given cycle time. They developed a B&B algorithm to solve small scale problems and proposed a B&B based heuristic to solve large scale problems. However, the performance of the heuristic is sensitive to the algorithm parameter, which is hard to calibrate when solving practical problems with different scales. Tsai and Yao [6] developed a line-balance-based capacity planning heuristic, which determines the type and number of robots required in each workstation to minimize the deviation of the workstation output rate. In the heuristic, an integer programming model is developed to generate an initial solution. Then, special heuristic rules are designed to identify the bottleneck workstation and improve the initial solution by making task adjustments to the bottleneck workstation. However, the proposed heuristic was only tested on ten small scale instances. Kim and Park [7] developed an integer programming model for a special type of RALB and solved it using a cutting plane algorithm. However, the assignment of robots was considered to be fixed for each workstation instead of decision variables in the model.

Due to the NP-hardness of RALB problem [8], it is difficult to obtain satisfied solutions by using the traditional model-based methods for large scale problem in acceptable time. So many researchers attempt to design efficient data-driven metaheuristics to solve large scale problems. Levitin et al. [9] proposed a genetic algorithm (GA) for RALB to minimize the cycle time with given workstation number. Two different decoding procedures were developed for task and robot assignments, including a recursive procedure and a consecutive procedure. The algorithm was tested on randomly generated instances, the results showed that the consecutive procedure is better than the recursive procedure. Gao et al. [10] proposed a hybrid GA for RALB-2. However, the problem assumptions in the two papers are different. In [9], one type of robot can be assigned to different workstations. But in [10], each robot can only be assigned to one workstation. Recently, a particle swarm optimization (PSO) and a hybrid of cuckoo search and PSO (CS-PSO) were proposed by Nilakantan et al. [11]. The problem assumptions in [11] are the same as [9]. The consecutive procedure is adopted to determine the task and robot assignment. The computational results show that the PSO and the CS-PSO are better than the hybrid GA. Following [10], Li et al. [12] developed four mixed-integer linear programming models to find optimal solutions of small scale problems and proposed two simulated annealing (SA) algorithms to solve large scale problems. The experiments showed that the SAs are superior to other algorithms under the same problem assumptions. In addition to the study of one-sided straight assembly line, Li et al. proposed a discrete cuckoo search algorithm [13] and a migrating birds optimization [14] to solve the two-sided and U-type RALB problems, respectively. Moreover, there are also some papers considering the reduction of energy consumption brought by robots in robotic assembly lines [15,16,17].

From the literature review, it can be seen that the existing RALB algorithms are either model-based approaches or data-driven metaheuristics. Both of them have their own merits and limitations. Model-based approaches can obtain the optimal solution for small scale problems, but it is hard to tackle large scale problems. Data-driven metaheuristics are able to solve large scale problems with satisfactory results, while their random nature makes it difficult to guarantee the robustness. In this paper, we propose a hybrid algorithm fusing these two kinds of approaches together to solve the RALB-2 following the assumptions in [9, 11]. It employs the estimation of distribution algorithm (EDA) [18] as the search framework due to its successful applications in many optimization problems [19,20,21,22,23] and fuses B&B strategy as knowledge into the sampling process of EDA to enhance search efficiency. With the reasonable integration, the proposed EDA with B&B based knowledge (EDA-BB) outperforms other existing metaheuristics in solving the RALB-2 with different scales.

The remaining of the paper is organized as follows. The next section provides the description and formulation of the RALB-2. The following section presents the details and analysis of the proposed EDA-BB. Computational results and comparisons are reported in the next section. Finally, the paper is ended with some conclusions and future work in the last section.

Problem description

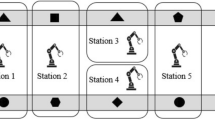
An assembly line consists of a conveyer belt and a sequence of workstations as shown in Fig. 1. The components are consecutively launched down the assembly line through the conveyer belt and move from workstation to workstation until they reach the end of the line [2]. When a component passes through a workstation, a certain amount of tasks will be performed by a robot. The processing time of a task is called the task time, the sum of the task time in a workstation is called the workstation time. The workstation time needs to be smaller than the duration of a component passing through the workstation, which is referred as the cycle time. The tasks need to be executed in a specified order given by the precedence constraints. The precedence constraints can be illustrated as a directed acyclic graph (DAG), where the nodes represent the tasks and the arcs represent the precedence relationships between the tasks. An example with 9 tasks is shown in Fig. 2.

Fig. 1
figure 1

The layout of the robotic assembly line

Full size image
Fig. 2
figure 2

The illustration of precedence constraints

Full size image

The objective of the RALB-2 is to minimize the cycle time by determining the task and robot assignment of each workstation under the precedence constraints. The basic assumptions of the RALB-2 are given as follows.

  • A single type of product is assembled on the assembly line.

  • The assembly line is paced, i.e. the cycle time of all workstations equals to the same value.

  • The task time is deterministic and depends on the type of operating robot.

  • A task can only be operated in one workstation and all tasks should be performed without violating the precedence constraints.

  • Only one robot can be assigned to a workstation. Any task can be operated by any robot.

  • Different workstations can use the same type of robot. There is no number limit for each type of robot.

  • The setup time and tool changing time are included in the task time.

According to the same assumptions as [11], the 0–1 integer programming model is presented with the following notations.


Parameters:

\(N\): number of tasks.

\(i,j\): indexes of tasks, \(i,j = 1,2, \ldots ,N\).

\(M\): number of workstations.

\(k\): index of workstations, \(k = 1,2, \ldots ,M\).

\(R\): number of robot types.

\(r\): index of robot types, \(r = 1,2, \ldots ,R\).

\(t_{i,r}\): processing time of task \(i\) by robot \(r\).

\(P_{i}\): the set of predecessors of task \(i\).


Decision variables:

\(c\): cycle time.

\(x_{i,k}\): 1, if task \(i\) is assigned to station \(k\); 0, otherwise.

\(y_{r,k}\): 1, if robot \(r\) is assigned to station \(k\); 0, otherwise.

$$ \min c = \mathop {\max }\limits_{1 \le k \le M} \mathop \sum \limits_{i = 1}^{N} \mathop \sum \limits_{r = 1}^{R} t_{i,r} \cdot x_{i,k} \cdot y_{r,k} $$
(1)
$$ {\text{s}}.{\text{t}}.\quad \mathop \sum \limits_{k = 1}^{M} k \cdot x_{i,k} - \mathop \sum \limits_{k = 1}^{M} k \cdot x_{j,k} \le 0, \forall i \in P_{j} , \forall j $$
(2)
$$ \mathop \sum \limits_{k = 1}^{M} x_{i,k} = 1, \forall i $$
(3)
$$ \mathop \sum \limits_{r = 1}^{R} y_{r,k} = 1, \forall k $$
(4)
$$ x_{i,k} \in \left\{ {0,1} \right\}, \forall i,k $$
(5)
$$ y_{r,k} \in \left\{ {0,1} \right\}, \forall r,k $$
(6)

The objective function (1) is to minimize the cycle time, which is defined as the maximum workstation time. Constraints (2) ensure the precedence relationships cannot be violated. Constraints (3) and (4) imply that each task must be assigned to one single workstation and each workstation must be assigned a robot, respectively. Constraints (5) and (6) indicate the type of the decision variables.

EDA-BB for RALB-2

Owing to the NP-hard nature of RALB-2, only small scale problems can be solved using mathematical programming in acceptable time [11]. Therefore, it is important and necessary to develop efficient metaheuristics to solve large scale problems. In this section, an estimation of distribution algorithm with B&B based knowledge will be presented for RALB-2.

Outline of the EDA-BB

EDA [18] is a typical population-based metaheuristic with good performances in solving complex optimization problems. The major difference between EDA and other metaheuristics like GA is the means of generating new solutions. EDA builds a probability model to estimate the distribution of elite solutions and generates new solutions by sampling the probability model. The advantage of the probability model is that it can adapt itself towards superior structural elements during the evolution [24]. Hence, the exploration ability of EDA is usually stronger than other metaheuristics. However, owing to the lack of problem-specific design, the exploitation ability of EDA needs to be enhanced. In this paper, the B&B strategy is fused as knowledge into the sampling of the EDA to improve the search efficiency and a problem-specific local search is developed to improve the quality of elite solutions. The flowchart of the proposed EDA-BB is illustrated in Fig. 3.

Fig. 3
figure 3

Flowchart of EDA-BB

Full size image

In the initialization phase, the probability model is initialized uniformly and the upper bound of cycle time is initialized using simple heuristic rules. Then, the probability model is sampled to generate a population of candidate solutions. The B&B based knowledge and the upper bound of cycle time are used in the sampling process to guarantee the quality of generated solutions. After that, the candidate solutions are sorted according to their objective values and some better solutions are selected as elite solutions. Then, the problem-specific local search is performed to further improve the elite solutions, which are used to update the probability model and the upper bound. Finally, the algorithm outputs the best solution when the stopping criteria are met.

More details of the proposed EDA-BB will be presented in the following sections.

Probability model

The probability model plays an important role in the design of EDA since it is used to describe the distribution of the solution space and generate new solutions. A good probability model should be able to reflect the characteristics of the problem and also easy to implement.

There are two classes of decision variables in the RALB-2: the assignment of tasks and the assignment of robots. Since the number of robots is not limited, we can first determine the assignment of tasks and then choose the best-fit robot for each workstation. So the probability model can be designed to describe the distribution of tasks assigned to different workstations. We use a matrix \(P\left( g \right)\) to represent the probability model in generation \(g\) as follows:

$$ \begin{array}{*{20}c} {P\left( g \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\rho_{11} \left( g \right)} & {\rho_{12} \left( g \right)} \\ {\rho_{21} \left( g \right)} & {\rho_{22} \left( g \right)} \\ \end{array} } & {\begin{array}{*{20}c} \ldots & {\rho_{1N} \left( g \right)} \\ \ldots & {\rho_{2N} \left( g \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots & \vdots \\ {\rho_{M1} \left( g \right)} & {\rho_{M2} \left( g \right)} \\ \end{array} } & {\begin{array}{*{20}c} \ddots & \vdots \\ \ldots & {\rho_{MN} \left( g \right)} \\ \end{array} } \\ \end{array} } \right]} \\ \end{array} , $$

where element \(\rho_{ki} \left( g \right)\) denotes the probability that task \(i\) is assigned to workstation \(k\) in the \(g\)th generation. Since a task must be assigned to one workstation, it is clear that \(\mathop \sum \nolimits_{k = 1}^{M} \rho_{ki} \left( g \right) = 1,{ }\forall i,g\).

Initialization

The initialization of the EDA-BB includes two parts: the initialization of the probability model and the initialization of the upper bound of cycle time. As there is no prior knowledge of the elite solution distribution, the probability model is initialized uniformly, i.e. \(\rho_{ki} \left( g \right) = 1/M, \forall k,i,g\).

The upper bound of cycle time is important for the sampling of EDA-BB. A common way to obtain an upper bound of a problem is to calculate the objective value of a feasible solution. Hence, we develop a heuristic to construct good initial solutions and use the best objective of the initial solutions as the initial upper bound.

The heuristic includes into two steps. The first step is to generate task sequences and the second step is to decode the task sequences into feasible solutions. There have been a lot of priority rules proposed in the literature to construct task sequences. The most widely-used priority values are computed based on the task time and the precedence relations [8]. In this paper, we select two rules (maximum task time and maximum immediate follower number) from [8] to generate the task sequences. The second step is to decode the task sequences into feasible solutions. The consecutive procedure proposed in [9] is used due to its superiority to other methods according to [9]. Then, the cycle time of each feasible solution is calculated and the lower one is used to initialize the upper bound.

Sampling mechanism with B&B based knowledge

The population of EDA is generated by sampling the probability model. Due to the fuse of the B&B based knowledge, the sampling process of EDA-BB is divided into \(M\) stages, where \(M\) is the number of workstations. The procedure of each sampling stage is explained as follows.

In the first stage, \(PS\) partial solutions are generated. Each partial solution contains the task and robot assignments of the first workstation. The tasks are assigned by selecting from the task list using the Roulette Wheel Method [25] iteratively. The task list records the tasks which can be assigned to workstation \(m\) without violating the precedence constraints, and the proportions in the Roulette Wheel Method are taken from the probability model. Once a task is selected from the task list, the best-fit robot that performs the assigned tasks in the least time is assigned to the workstation and the related workstation time is calculated. The assigning procedure continues until the workstation time reaches the upper bound of the cycle time. Specific procedures are given in Algorithm 1.

figure a

In each stage \(m \in \left[ {2,{\text{M}} - 1} \right]\), it first calculates the lower bounds of the \(PS\) partial solutions from the previous stage by (7), where \(A_{k}\) denotes the set of tasks assigned in workstation \(k\) and \(U\) denotes the set of unassigned tasks. Then, the \(PS\) partial solutions are sorted according to their lower bounds, and the \({\text{PS}}/2\) partial solutions with larger lower bounds are deleted from the population. After that, each of the remaining partial solutions is expanded into two new branches by generating the task and robot assignments for workstation \(m\) using Algorithm 1. Each branch is a new partial solution with the task and robot assignments of the first \(m\) workstations. To guarantee the diversity of the two branches, their task assignments of workstation \(m\) are compared with each other. If the task assignments of the two branches are the same, a replace or delete operator will be performed on one of them. Specific procedures of the sampling process in stage \(m \in \left[ {2,{\text{M}} - 1} \right]\) are given in Algorithm 2.

$$ LB = \mathop \sum \limits_{k = 1}^{m} \mathop {\min }\limits_{1 \le r \le R} \mathop \sum \limits_{{i \in A_{k} }} t_{i,r} + \mathop \sum \limits_{i \in U} \mathop {\min }\limits_{1 \le r \le R} t_{i,r} $$
(7)
figure b

In the last stage, each of the \(PS\) partial solutions from stage \(M - 1\) is expanded into a complete solution by assigning all the unassigned tasks into the last workstation and allocating the robot with the shortest workstation time.

In this way, \(PS\) complete solutions are generated. The whole procedures of the sampling mechanism are given in Algorithm 3.

figure c

For clarity, an illustration of the whole sampling process is shown in Fig. 4. The grey circles represent the partial solutions which are dismissed in the sampling process and the white ones represent the partial solutions to be expanded in the next stage. From the figure, it can be seen that the sampling process is guided by the B&B based knowledge. The promising partial solutions with better lower bounds are expanded to generate more branches and the inferior ones are dismissed to avoid wasting much computation. In this way, the search space of the sampling is reduced and the search is concentrated on the promising area to generate more high-quality solutions.

Fig. 4
figure 4

An illustration of sampling process with B&B based knowledge

Full size image

Elite selection and local search

After a population is generated by sampling the probability model, we rank the solutions in the population in the ascending order of their cycle time. The first \(\left\lfloor {PS \cdot \alpha } \right\rfloor\) solutions are selected as elite solutions, where \(\alpha\) is a user-determined parameter. Then, a problem-specific local search is performed on the elite solutions to further reduce their cycle time.

The local search is an iterative process with neighborhood structure. It is clear that the solution can be improved only if the workload of the fullest workstation is reduced and the workloads of other workstations do not exceed the original cycle time. Thus, we select the workstation with the maximum workload as the critical workstation. Then it uses two operators on the tasks assigned to the critical workstation and its adjacent workstations.

The first one is the insert operator, which attempts to move one task from the fullest workstation to its left or right neighbor workstation (if any). Owing to the precedence constraints, one task can be inserted to the left (right) workstation only if it has no predecessors (followers) in the selected workstation.

The second one is the swap operator, which attempts to exchange one task in the fullest workstation with another task in its left or right neighbor workstation (if any). Similar to the insert operator, task A in the selected workstation can be exchanged with task B in the left (right) workstation only if the following conditions hold: (1) task A has no predecessors (followers) in the selected workstation; (2) task B has no followers (predecessors) in the left (right) workstation; (3) task A is not the follower (predecessor) of task B.

Figure 5 shows an illustration of the insert and swap operator. In Fig. 5, there are nine tasks assigned to four workstations. The task assignments and the workstation time (WT) are given in the figure and the precedence relations are supposed to be the same as in Fig. 2. It can be seen from the figure that the WT of workstation 3 is the biggest among all workstations, so it is selected as the critical workstation. According to Fig. 2, task 7 is the predecessor of task 8, so task 7 can be inserted to workstation 2, however, it cannot be inserted to workstation 4 or exchanged with the tasks assigned in workstation 4. Moreover, as task 7 is the follower of task 2, they are not allowed to be exchanged by the swap operator. While task 7 and task 5 can be exchanged since they do not have precedence relations.

Fig. 5
figure 5

Illustration of insert and swap operator

Full size image

At each iteration of the local search, it first selects the critical workstation. Then the tasks assigned to the critical workstation are explored by the insert and swap operators sequentially. The variation of the objective value is calculated for each possible move. Once the solution is improved, the operator is implemented and the algorithm goes to the next iteration. The algorithm terminates if no improvements are made throughout the iteration. The procedure of the above local search is given in Algorithm 4.

figure d

Update probability model and upper bound

After the problem-specific local search, the elite solutions are used to update the probability model and the upper bound. The probability model is updated based on the population-based incremental learning (PBIL) method [26]. The basic idea is to increase the probability of using construction steps that are contained in high quality solutions via positive feedback [24, 27]. The specific update rule in EDA-BB is given as follows:

$$ \rho_{ki} \left( {g + 1} \right) = \left( {1 - \beta } \right) \cdot \rho_{ki} \left( g \right) + \beta \cdot \frac{1}{{\left\lfloor {PS \cdot \alpha } \right\rfloor }} \cdot \mathop \sum \limits_{h = 1}^{{\left\lfloor {PS \cdot \alpha } \right\rfloor }} I_{ki}^{h} \left( g \right), \forall i,k, $$
(8)

where \(\beta \in \left( {0,1} \right)\) represents the learning rate and \(I_{ki}^{h} \left( g \right)\) is the following indicator function corresponding to the \(h\)th elite solution:

$$ I_{ki}^{h} \left( g \right) = \left\{ {\begin{array}{*{20}l} {1, \quad {\text{ if task }}i{\text{ is assigned to workstation }}k{\text{ in the }}h{\text{th elite solution}}} \\ {0, \quad {\text{ otherwise}}} \\ \end{array} } \right.. $$
(9)

The upper bound is updated using the objective value of the best solution found in each generation as (11). In this way, the best-so-far objective value is recorded as the upper bound and will be used as a reference value when generating new solutions in the following generation:

$$ UB\left( {g + 1} \right) = \min \left\{ {UB\left( g \right), C_{{{\text{best}}}} } \right\}, $$
(10)

where \(UB\left( g \right)\) is the upper bound in generation \(g\), \(C_{{{\text{best}}}}\) is the cycle time of the best solution.

Complexity analysis

The time complexity of EDA-BB is analyzed as follows. According to the flowchart in Fig. 3, the time is mainly spent in running the searching loop in the proposed EDA-BB. In each generation of the loop, the algorithm needs to execute sampling, elite selecting, local search and update. The time complexities of elite selecting and update are easily derived as \(O\left( {PS \cdot \log PS} \right)\) and \(O\left( {PS \cdot N + M \cdot N} \right)\), respectively. The time complexity of the sampling can be calculated by Algorithms 1–3. In Algorithm 1, there are at most \(N\) tasks assigned to workstation \(m\) and for each task assignment, the time complexity is \(O\left( N \right)\). So the time complexity of the task assignment is \(O\left( {N^{2} } \right)\). Additionally, by introducing the time list \(WT_{r}\), the time complexity of assigning the best-fit robot is \(O\left( {N \cdot R} \right)\). Thus, the time complexity of generating the assignment for a workstation is \(O\left( {N^{2} + N \cdot R} \right)\). In Algorithm 2, the time complexity of selecting \(PS/2\) partial solutions is \(O\left( {PS \cdot \log PS} \right)\) and the time complexity of expanding \(PS/2\) partial solutions into \(PS\) branches in the next stage is \(O\left( {PS \cdot N^{2} + PS \cdot N \cdot R} \right)\). Based on the analysis of Algorithm 1 and 2, the total time complexity of the sampling procedures in Algorithm 3 can be derived as \(O\left( {M \cdot PS \cdot \log PS + PS \cdot N^{2} + PS \cdot N \cdot R} \right)\). For the local search, the time complexity of one iteration is \(O\left( {N^{2} + N \cdot R} \right)\). As the local search terminates until no improvements can be made in one iteration, the number of iterations is at most \({\Delta }C = \left( {UB - LB} \right)\), where \(UB\) and \(LB\) are the upper bound and lower bound of the cycle time, respectively. Therefore, the total time complexity of the local search is \(O\left( {PS \cdot {\Delta }C \cdot \left( {N^{2} + N \cdot R} \right)} \right)\). Accordingly, the time complexity of the EDA-BB is \(O\left( {Gen \cdot \left( {PS \cdot \left( {{\Delta }C \cdot \left( {N^{2} + N \cdot R} \right) + M \cdot \log PS} \right) + M \cdot N} \right)} \right)\).

The space complexity of the EDA-BB can be analyzed as follows. In EDA-BB, each solution needs an array of size \(\left( {N + M} \right)\) to store the task assignment and an array of size \(M\) to store the robot assignment. Moreover, for each solution, the size of the time list and task list is \(R\) and at most \(N\), respectively. Thus, the space complexity of the EDA-BB is \(O\left( {PS \cdot \left( {N + M + R} \right)} \right)\).

Computational results

Experimental settings

To test the performance of the proposed EDA-BB, we carry out numerical experiments on the RALB-2 dataset with 32 benchmark instances which were used in [10, 11]. The instances are generated by adding the robot task times to the widely-used SALB dataset prepared by Scholl [28], where the precedence graphs can be found at https://www.assemblyline-balancin.de/. There are 8 problem scales in the dataset varying from 25 to 297 tasks. For each scale, there are four instances with different workstation and robot numbers. While for each instance, the numbers of workstations and robots are supposed to be the same.

The EDA-BB is coded in C++ and tested on a PC with an Intel Core i5-6500 CPU @ 3.2-GHz. As our comparative algorithms, the PSO and CS-PSO proposed in [11] are also coded in C++ but tested on Intel Core i5 CPU @ 2.3 GHz. For fair comparisons with PSO and CS-PSO, we use Passmark Performance Test on https://www.cpubenchmark.net to test the performance of both processors. The test results show that both processors are comparable. So our experimental results are compared with the results reported in [11] directly in the following comparisons.

Parameter settings

The EDA-BB has three key parameters: the population size \(PS\), the rate of elite solutions \(\alpha\), and the learning rate \(\beta\). The population size is a parameter determining the number of solutions generated in each generation. A small value will result in insufficient search in each generation, while a large value will result in long convergence time. We carry out a large amount of preliminary experiments to determine a moderate value of \(PS\) and a suitable stopping criterion of the algorithm. Through the preliminary experiments, the population size is set as 500, and the stopping criterion of the algorithm is set as 300 generations.

In order to investigate the effect of the other two parameters, the Taguchi method of design-of-experiments [29] is used. Four factor levels are considered for each parameter, as listed in Table 1. Accordingly, an orthogonal array \(L_{16} \left( {4^{2} } \right)\) is selected, which includes 16 different \(\left( {\alpha ,\beta } \right)\) combinations. The 32 instances are used for the investigation. For each instance, the EDA-BB with each combination \(n\) is run ten times independently to obtain the average objective value \(\overline{C}_{n}\). Then the best average objective value \(\overline{C}_{{{\text{best}}}}\) among 16 combinations is derived as the reference objective value and the relative percentage deviation (RPD) of each combination \(n\) is calculated as \({\text{RPD}}_{n} = \left( {\overline{C}_{n} - \overline{C}_{{{\text{best}}}} } \right)/\overline{C}_{{{\text{best}}}} \times 100\). Finally, the average of \({\text{RPD}}_{n}\)s in 32 instances is calculated as the average response value (ARV) for combination \(n\). The orthogonal array and the ARVs are listed in Table 2.

Table 1 Parameter values
Full size table
Table 2 Orthogonal array and ARVs
Full size table

Furthermore, the trend of each factor is shown in Fig. 6. It can be seen that \(\beta\) is more significant than \(\alpha\). The value of \(\beta\) controls the learning speed of the probability model. The bigger the value, the larger the learning speed. However, too big value will result in the premature convergence of the algorithm. The value of \(\alpha\) determines the size of elite solution set in each generation. A small value leads the algorithm to learn from a small number of best solutions, while a large value allows more solutions to be learned. According to the results of DOE, moderate values are recommended for the two parameters: \(\alpha = 0.28,\; \beta = 0.08\). These values are used for the following tests and comparisons.

Fig. 6
figure 6

Factor level trend

Full size image

Effect of B&B based knowledge and local search

To demonstrate the effectiveness of the B&B based knowledge and the problem-specific local search, we compare the EDA-BB with the EDA without B&B based knowledge (EDAnBB) and the EDA without local search (EDAnLS). In EDAnBB, the lower bound will not be used to evaluate the partial solutions in each stage of the sampling process. Thus, all the partial solutions will enter the next stage without selecting and branching. In EDAnLS, the elite solutions will be directly used to update the probability model without further improvement by the problem-specific local search. Because of the random factors in the EDA-based algorithms, each instance is run 20 times. For each run, the RPD of objective value obtained by each algorithm is calculated as \({\text{RPD}}_{{\text{a}}} = \left( {C_{{\text{a}}} - C_{{{\text{best}}}} } \right)/C_{{{\text{best}}}} \times 100\), where \(C_{{\text{a}}}\) is the cycle time obtained by algorithm \(a\), and \(C_{{{\text{best}}}}\) is the best cycle time among the three algorithms. The average RPD values of 20 runs are summarized in Table 3.

Table 3 Comparisons of EDA-BB with EDAnBB and EDAnLS
Full size table

From Table 3, it can be seen that the average RPD obtained by EDA-BB is smaller than those obtained by the other two algorithms on most instances. Regarding the only exception, the small-scale instance with 35 tasks and 12 workstations, the EDAnBB performs better than EDA-BB. However, as the problem scale increases, the advantage of the EDA-BB becomes more apparently. This implies the effectiveness of the B&B based knowledge to reduce the search space for large scale problems. To analyze whether the advantages of the EDA-BB over the other two algorithms are significant, we carry out the nonparametric Mann–Whitney test with 95% confidence level. The p values are listed in Table 3, where “–” means the objective values obtained by the two tested algorithms are all same. The p values show that the EDA-BB is significantly better than EDAnBB on all large scale instances (\(N > 89\)). The advantage of EDA-BB over EDAnLS is also testified according to their average RPD and p values.

Figure 7 shows the boxplots of all RPD values obtained by the three algorithms. From Fig. 7, it can be seen that the box sizes of EDA-BB and EDAnLS are smaller than EDAnBB. This implies that the B&B based knowledge fused in the EDA is able to enhance the algorithm’s stability in solving different scales of problems. Compared with EDAnLS, the objective values achieved by EDA-BB are smaller, which demonstrates the effectiveness of the local search in improving the elite solutions. From the above investigation, it can be concluded that the B&B based knowledge and the problem-specific local search are both effective in improving the performance of EDA.

Fig. 7
figure 7

Boxplot of RPD with or without B&B based knowledge and local search

Full size image

Comparisons with other algorithms

Next, we compare EDA-BB with the PSO and CS-PSO which showed good performances in solving RALB-2 [11]. The results of PSO and CS-PSO are taken from [11] directly, and the results of EDA-BB are obtained by running each instance 20 times. Comparative results are reported in Table 4.

Table 4 Comparisons between EDA-BB and other algorithms
Full size table

In Table 4, the RPD values of each algorithm are calculated as \({\text{RPD}}^{b} = \left( {C^{*} - C_{{{\text{best}}}}^{*} } \right)/C_{{{\text{best}}}}^{*} \times 100\), where \(C^{*}\) denotes the best cycle time found by the certain algorithm and \(C_{{{\text{best}}}}^{*}\) denotes the best cycle time found by the three tested algorithms. In addition, another two RPD values are calculated for the proposed EDA-BB: \({\text{RPD}}^{w} = \left( {C^{w} - C_{{{\text{best}}}}^{*} } \right)/C_{{{\text{best}}}}^{*} \times 100 \) and \({\text{RPD}}^{m} = \left( {C^{m} - C_{{{\text{best}}}}^{*} } \right)/C_{{{\text{best}}}}^{*} \times 100\), where \(C^{w}\) and \(C^{m}\) denote the worst and mean cycle time found by EDA-BB among 20 runs, respectively. In Table 4, the best results are displayed in bold font.

It can be seen that EDA-BB obtains the best objective values among the three algorithms for all instances. By contrast, PSO and CS-PSO only obtain four best objective values on small scale instances. Furthermore, the \({\text{RPD}}^{w}\) of EDA-BB is smaller than the \({\text{RPD}}^{b}\) of PSO and CS-PSO. This implies the worst solutions obtained by EDA-BB are even better than the best solutions obtained by the other two algorithms. In addition, EDA-BB achieves \({\text{RPD}}^{w} = 0\) on nine small scale instances, which shows the stability of EDA-BB in solving small scale problems.

Moreover, the average CPU time of the three algorithms is also reported in Table 4. It can be seen that the CPU time cost of EDA-BB is much shorter than PSO and CS-PSO. To further investigate the relationship between the computational time and the problem scale, the trend of CPU time with the increase of task number is plotted in Fig. 8. It is clear that the CPU time of PSO and CS-PSO grows dramatically when the task number is larger than 89, while the CPU time of EDA-BB grows slightly.

Fig. 8
figure 8

Comparison of average CPU time

Full size image

From the computational results, it can be concluded that EDA-BB is of better performances than the existing algorithms in solving the RALB-2 in terms of both the solution quality and computational time.

Conclusion

In this paper, we propose a hybrid algorithm by fusing the B&B strategy as knowledge into the estimation of distribution algorithm to solve the RALB-2. The computational complexity of the proposed algorithm is analyzed and the performances are tested. Numerical comparison shows that the proposed EDA-BB performs more effective and efficient than the existing algorithms. The B&B based knowledge employs the lower bound with mathematical model analysis, while the EDA employs the data-driven search via probability model sampling. EDA-BB is the fuse of the model-based analysis and data-driven metaheuristics. The effectiveness of the proposed hybrid algorithm mainly owes to the probability model based exploration, the problem-specific local search based exploitation, and the B&B knowledge based sampling. Therefore, exploration and exploitation are well balanced in EDA-BB, and promising search area can be focused in sampling process.

The future work is to study the multi-objective RALBs by considering several objectives simultaneously like the cycle time, equipment cost, and energy consumption. It is also important to study the mixed-model RALBs by considering different product assembly line. In addition, adaptive swarm intelligence algorithms will be studied in the future research.