Introduction

The SPP among the specified starting vertex and a target vertex is a popular combinatorial optimization problem in operation research and graph theory. We emerge graph/network as a mathematical model of many optimization problems, e.g., traffic scheduling, transportation system, telecommunication system, computer wireless network, texture mapping, supply demand management, computer wireless network, etc. Many real-life problems can be remodeled as a path finding problem between one node and an another node in a network/graph. The optimal path is calculated based on total number of predetermined measure. We evaluate the optimality measure in terms of arc lengths which are real numbers, and each and every arc is associated with those real values of the network. In any real-life network, an arc/link is related with a specific direction and with an evaluate of impedance, computing the several parameters, such as traveling cost, traveling time, traffic condition, capacity, demand, etc., along the graph. In most of real-world applications, such as transportation, communication, vehicle green scheduling, routing, etc., which are very much associated with several environmental matters, the edge costs may be changeable. Since it depends on the variation with traffic issues or weather issues, however, the length between two location is always constant. Therefore, ticketing the accurate path cost in such real-world networks/graphs always be very hard. We can use the idea of fuzziness into a graph to handle this uncertain environment.

In any metro city, there are many route and different paths between two cities. It is very useful information to determine minimum cost and time of transportation, the least traffic issues, the reliable path, etc. This type of problem can be modeled as network/graph and the shortest path is needed to make a decision of this problem. For e.g., in the ambulance service stations, the main object is to visit the ambulance to patient home within the specific network in the minimum possible time. For any disaster management term, the purpose is to search for the least destructed route for evacuation. For any online cab booking system, it also needs to determine a route in the city with the minimum time/lowest cost. The SPP is said to CSPP [1,2,3,4]. If and only if the time limit is considered into account. For example, the main objective of a online cab booking system is to decide a path with the lowest traveling cost, so that cars could arrive to destination locations in the minimum possible time. These types of transportation companies are new establish throughout the world; however, nowadays, these companies are very much popular in India. Online cab booking system was first established in 2010 in India. Uber Cab service is an online based cab company in India. It has introduced itself easily and cheapest available online cab service. This company has begun with their own website, and now, this company has established their own app. This cab company has many cab drivers in China, India, and many other major metro cities. The arrival time of the online cab into the transportation network minimizes the transportation cost of passenger. Uber Cab service has their own technique to find and prepare a fair amount of the cab. From the data of the starting and destination locations of each and every passenger in different clock time, weather condition and traffic scenarios are gradually gathered by their algorithms. Their algorithms provide the cab drivers to have a host of fare amount at various specific clock times that increase their avidity to do in this system. Routing of cab service is not efficient based on past traffic information. This is the main reason that there would sometimes be varied in the traffic condition due to route repairs or accidents. That is why, the application of uncertain data such as fuzzy numbers, as the parameters of the CSPP, is much more useful than crisp numbers.

The SPP with real values as edge weights has been researched by some great researchers, and they have introduced several efficient algorithms to solve the SPP. These algorithmic methods are considered as precise shortest path algorithms. However, in real life, there are frequently several types of uncertainty encountered in arc lengths of a network due to incomplete information, imperfect information, failure, or some unexpected reasons. In such cases, algorithms of determining the shortest paths of network are considered as approximate shortest algorithms. In uncertain environments, it is more naturalistic and authentic to use SPP with fuzzy arc lengths. While introducing an algorithmic method for working FSPP, we need ranking and addition methods between two fuzzy number. SPP with different types fuzzy number as arc lengths has received attention of several researchers over the last 2 decades. This type of problem in fuzzy environment is called fuzzy SPP (FSPP). There are several studies in FSPP [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. An algorithmic technique for FSPP was developed for the first time by Dubois and Prade [5]. They have extended the standard Ford–Moore–Bellman algorithm to solve the FSPP. They have described the concept of criticality of any path. Let \(D_{x,y}\) be a fuzzy number, which describes the length of shortest path between the vertex x and vertex y, and the criticality value of any path possible p is described the possibility value that the path will be the shortest path. They have assumed the fuzzy membership value of p of the shortest paths between the vertex x and vertex y. \(D_{x,y}\) is used as a possibility of being the shortest path among the vertex x and vertex y. However, the main disadvantage of the algorithmic technique is unable to determine the length of the shortest path. Chanas and Kamburowski [9] described a fuzzy relationship to chose a specific path and applied it in their introduced algorithm for solving FSPP. The main drawback of their algorithm is that they have not considered the fuzzy membership function as discussed in [5]. Yager [14] introduced a method for solving FSPP using the concept of possibility measurement. He considered a possibility of visiting among two nodes and determined the total possibility of any path between a starting vertex and destination vertex utilizing the T-norm. Their technique determines the path with highest possibility. They presented a searching method to eliminate the combinatorial increasing of paths which reduces the required time of the introduced algorithm. In [15], the authors described each edge with a significant value in the graph. The most significant arc eliminates from the graph enhances the length of the shortest path maximum. The edge weight of their fuzzy graph is presented using fuzzy number. The authors have introduced a fuzzy membership degree of the FSPP by modeling this problem as a linear programming model. Using this idea, they have developed an algorithmic approach for finding the one most significant edge in a fuzzy graph. Okada and Soper [16] used triangular fuzzy number to represent edge weight of the fuzzy graph. The authors developed an order relationship between the different fuzzy numbers using the idea of “fuzzy min” and “fuzzy max” which used to generate all nondominated paths of the graph. Their proposed method determines each and every nondominated paths within the starting vertex and all other vertices. They have used the multiple labeling [28] approach for figuring out the multicriteria SPP. The main disadvantage of their proposed method is that all the possible paths within starting vertex and goal vertex cannot be determined by the expert. For any big graph, the total number of paths can be very high. In such case, they suggested the concept of h-nondominated paths. The lower number of h-nondominated path always has maximum the possibility value of h. In [11], the author has also considered fuzzy numbers to represent the edge weight of a directed fuzzy graph. They have used the fuzzy addition operation to determine cost of the path. Every path within starting node and another node is assumed to be dependent, because the two different paths may be shared some common edges. Each and every edge has a specific possibility grade to present in a shortest path. They have considered \(\alpha \)-cut of triangular fuzzy number the multiple labeling approach in their algorithm. In [12], Takahashi et al. presented the FSPP and extended the method introduced by Okada [11]. They have presented a genetic algorithm to find the solution of FSPP for large graph. Nayeem and Pal [17] denoted the edge weights of a fuzzy graph by imprecise numbers. Those imprecise numbers are represented by triangular fuzzy number and interval number. Their proposed algorithm determines the shortest path and their algorithm can work with two different types of uncertain numbers. They have proposed the concept of index of acceptability for describing a grading method between the different fuzzy numbers. The degree of satisfaction of the expert is calculated based on value of acceptability index. However, the drawback of their proposed method is that it can provide several different shortest paths for a specific index value of acceptability [29, 30]. Moazeni [18] used a positive fuzzy quantity to represent the each edge weight of the fuzzy graph. They described a lexicographic-order relationship between the edges. Using the extension principle of fuzzy set, they introduced a method for computing all non-dominated paths between a source vertices and every other vertices on a fuzzy network. In their method, they used the idea of Dijkstra’s algorithm [31] and Hansen’s labeling algorithm [28]. In [19], the authors presented a generic method for solving SPP in fuzzy environment. They have assumed the triangular fuzzy numbers to represent the edge weights. They have applied a generic ranking method in their algorithm for comparing the fuzzy edges. This algorithmic method is modification of Bellman Ford technique. In [13], Mahdavi et al. developed an algorithm based on dynamic programming to find the shortest path in fuzzy environment. Their proposed ranking technique can able to eliminate to generate the Pareto shortest paths, because there may exist high number of possible Pareto shortest paths in a large fuzzy network. In such scenarios, it will be difficult for an expert to chose a specific path. Deng et al. [20] have modified the simple Dijkstra’s method to find the solution of shortest path problem with fuzzy edge weight. They have used the idea of graded mean method of triangular fuzzy numbers in their proposed algorithm to determine the fuzzy shortest path length and fuzzy shortest path among the all possible paths. Hassanzadeh et al. [7] presented a method to determine the fuzzy shortest path in a fuzzy graph. They introduced an addition of fuzzy number applying \(\alpha \) cut to determine the length of path. They have developed a least square method to determine an approximation membership grade for any addition operation in their proposed addition operation. A genetic algorithm is developed to solve the FSPP. This algorithm can deal with FSPP for a large fuzzy graph.

The CSPP determines the shortest path between a specific starting vertex and a specific goal vertex with in a directed graph under some predetermined constraint, e.g., time, cost, distance, etc. The value of the constraint must not be greater than upper limit. CSPP is NP-hard problem and it is studied as a special type of shortest path problem. Several real-world problems can be modeled as CSPP, e.g., aircraft scheduling [32,33,34], communications networks [35, 36], etc.

Generally, methods of determining the solutions of CSPP by optimization algorithms are classified into three categories: path ranking algorithms, lagrangian relaxation algorithms, and dynamic programming approach. The lagrangian relaxation algorithm for CSPP first determines some specific Lagrangian dual of CSPP and different techniques are used to minimize the lagrangian duality gap. In [1], the authors proposed a Lagrangian relaxation method to find the solutions of the Lagrangian dual problem. They have used the shortest path algorithm to minimize the duality gap, stopping with the starting path meeting the constraint. An algorithm is introduced which looked for in this way. Their algorithm is applied to find a shortest path between the starting vertex and goal vertex in a graph, subject to constraint. Carlyle et al. [3] introduced an algorithmic technique for CSPP.

The main motivation of this manuscript is to introduce a special type of fuzzy shortest path problem which will be very efficient for real-life problems. As far as this author’s knowledge, most of the studies made on FSPP focused on fuzzy graphs with several types of fuzzy numbers as the edge weights, and there exists no study on the CSPP with fuzzy numbers as edge weights in the literature. We need to formulate the time and cost for solving the CSPP problem. It is impossible to prediction the exact traveling time and traveling cost of a path due to traffic jam and weather scenarios. In this paper, we present the constrained shortest path problem with edge weights as trapezoidal fuzzy numbers. We call this problem as fuzzy constrained shortest path problem. Here, the edge weights are used to represent the cost and time. In this study, we present a mathematical formulation for a CSPP with fuzzy arc lengths. LINGO software is applied to find the solution the FCSPP. An algorithm is also introduced to solve this CSPP in fuzzy environment. We have also modified the Disktra’s algorithm and a genetic algorithm to find the solution of this problem. Finally, we present an application of the proposed model on online-based cab service.

Preliminaries

In this section, some significant and basic concepts of fuzzy set, fuzzy graph, triangular fuzzy number, and ranking and addition operation on fuzzy numbers are described.

Definition 1

There are many types in which a network can be fuzzy network. Below we have described the different ways of fuzziness possible in networks.

Type 1: A fuzzy graph/network makes up with a fuzzy collection of crisp networks.

Type 2: A fuzzy graph/network makes up with a collection of crisp nodes and fuzzy arcs.

Type 3: A fuzzy graph/network makes up with a collection of crisp nodes and fuzzy arcs with connectivity.

Type 4: A fuzzy graph/network makes up with a collection of fuzzy nodes and crisp arcs.

Type 5: A fuzzy graph/network makes up with a crisp graph with fuzzy arc lengths.

Definition 2

A fuzzy number is a special type of fuzzy set which satisfies the following four conditions.

  1. (a)

    This fuzzy set must be convex.

  2. (b)

    This fuzzy set must be normalized.

  3. (c)

    The membership grade of this fuzzy set must be exactly continuous.

  4. (d)

    The membership grade must be in the real number.

    There are various different types of fuzzy number in the literature, e.g., bell shape, triangular, trapezoidal, and L–R.

Definition 3

Let \(\widetilde{N}=\{\underline{n},n_{0}, \overline{n}\}\) be a triangular fuzzy number (TFN). The fuzzy number \(\widetilde{N}\) is described by a membership function \(\mu _{\widetilde{N}}(y)\) and it is defined by the following equations:

$$\begin{aligned} \mu _{\widetilde{N}}(y)=\left\{ \begin{array}{lr} \frac{y-\underline{n}}{n_{0}-\underline{n}} &{} \quad \mathrm{if}\, n_{0} \ge y \ge \underline{n} \\ \frac{\overline{n}-y}{\overline{n}-n_{0}} &{} \quad \mathrm{if} \, \overline{n} \ge y \ge n_{0}\\ 0 &{} \quad \mathrm{otherwise} \end{array}\right. \end{aligned}$$
(1)

Here, \(\underline{n}\) is the lowest possible value, \(n_{0}\) is the primary possible value, and \(\overline{n}\) is the maximum possible value. Figure 1 is used to represent the graph of a TFN.

Fig. 1
figure 1

A TFN

Full size image

Definition 4

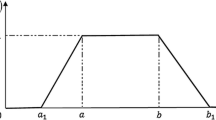
Let \(\widetilde{M}\)= \(\left\{ \underline{m}, m_{1}, m_{2}, \overline{m}\right\} \) be a trapezoidal fuzzy number (TrFN). \(\widetilde{M}\) always has a trapezoidal shaped membership function. The membership function \(\mu _{\widetilde{M}}\) satisfies the following equations:

$$\begin{aligned} \mu _{\widetilde{M}}(y)=\left\{ \begin{array}{ll} \frac{y-m_{1}}{m_{1}-\underline{m}} &{} \quad \mathrm{if}\ m_{1} \ge y \ge \underline{m}\\ 1 &{} \quad \mathrm{if}\ m_{1} \ge y \ge m_{2}\\ \frac{\overline{m}-y}{\overline{m}-m_{2}} &{} \quad \mathrm{if}\ \overline{m} \ge y \ge m_{2}\\ 0 &{} \quad \mathrm{if} \ y < \underline{m}\ \mathrm{or} \ y > \overline{m} \end{array}\right. \end{aligned}$$
(2)

Here, the values of \(m_{1}\) and \(m_{2}\) are two main possible values, \(\underline{m}\) is the least possible value, and \(\overline{m}\) is the maximum possible value. We have shown a TrFN in Fig. 2.

Fig. 2
figure 2

A TrFN

Full size image

Ranking of operations on fuzzy numbers

Ranking is the most significant part in any decision-making in fuzzy optimization problem. The ranking operation of fuzzy number is done by defuzzification technique which transfers the fuzzy set into a real number. This real value is used to find the rank of n number of fuzzy numbers. In the literature, there exists several ranking methods, but the most well-known and efficient defuzzification techniques are center of area, first of maximal, last of maximal, and middle of maximal. In this manuscript, we use the canonical form of TrFNs [37] in our proposed algorithm.

Definition 5

Let \(\widetilde{N} = \left\{ \underline{n}, n_{0}, \overline{n}\right\} \) is a TFN; the graded mean of \(\widetilde{N}\) is calculated as:

$$\begin{aligned} P(\widetilde{N})=\frac{1}{6}(\underline{n}+4n_{0}+\overline{n}). \end{aligned}$$
(3)

Definition 6

Let \(\widetilde{N} = \left\{ \underline{n}, n_{0}, \overline{n}\right\} \) and \(\widetilde{M} = \left\{ \underline{m}, m_{0}, \overline{m}\right\} \) be two TFNs. The graded mean values of two TFNs can be calculated by the following equations:

$$\begin{aligned} P(\widetilde{N})&=\frac{1}{6}(\underline{n}+4n_{0}+\overline{n}) \end{aligned}$$
(4)
$$\begin{aligned} P(\widetilde{M})&=\frac{1}{6}(\underline{m}+4m_{0}+\overline{m}). \end{aligned}$$
(5)

The comparison between two number \(\widetilde{N}\) and \(\widetilde{M}\) can be described as follows:

  1. (a)

    The value of \(\widetilde{N}\) is equal to the value of \(\widetilde{M}\) if \(P(\widetilde{N})\) \(=\) \(P(\widetilde{M})\).

  2. (b)

    The value of \(\widetilde{N}\) is greater than the value of \(\widetilde{M}\) if \(P(\widetilde{N})\) > \(P(\widetilde{M})\).

  3. (c)

    The value of \(\widetilde{N}\) is less than the value of \(\widetilde{M}\) if \(P(\widetilde{N})\) < \(P(\widetilde{M})\).

Definition 7

Let \(\widetilde{N} = \left\{ \underline{n}, n_{0}, \overline{n}\right\} \) and \(\widetilde{M} = \left\{ \underline{m}, m_{0}, \overline{m}\right\} \) be two TFNs. The formula of addition method is described as:

$$\begin{aligned} P(\widetilde{N}\oplus \widetilde{M})=\frac{1}{6}(\underline{n}+4n_{0} +\overline{n})+\frac{1}{6}(\underline{m}+4m_{0}+\overline{m}). \end{aligned}$$
(6)

Definition 8

Let \(\widetilde{N} = \left\{ \underline{n}, n_{1}, n_{2}, \overline{n}\right\} \) be a TrFN. The graded mean value of \(\widetilde{N}\) can be determined as:

$$\begin{aligned} P(\widetilde{N})=\frac{1}{6}(\underline{n}+ 2n_{1}+2n_{2}+\overline{n}). \end{aligned}$$
(7)

Definition 9

Let \(\widetilde{N} = \left\{ \underline{n}, n_{1}, n_{2}, \overline{n}\right\} \) and \(\widetilde{M}\) = \(\left\{ \underline{m}, m_{1}, m_{2}, \overline{m}\right\} \) be two TrFNs. The addition \(\oplus \) between \(\widetilde{N}\) and \(\widetilde{M}\) can be calculated by:

$$\begin{aligned} P(\widetilde{N}\oplus \widetilde{M})=\frac{1}{6}(\underline{n} +2n_{1}+2n_{2}+\overline{n})+\frac{1}{6}(\underline{m}+ 2m_{1}+2m_{2}+\overline{m}). \end{aligned}$$
(8)

Mathematical formulation for FCSPP

In this section, we describe the FCSPP and a fuzzy mathematical programming method is also introduced to model the FCSPP.

Let \(G = (X,\tilde{Y})\) be an acyclic discrete directed fuzzy network consisting of n number of vertices symbolized as \(X=\{1,2,\ldots ,n\}\) and of m number of directed edges \(\tilde{Y}\subseteq X \times X\). Each edge is represented by a simple ordered pair (a, b); here, \(a \ne b\) and \(a, b\in X\). We have considered in this network that there exists only one directed edge (a, b) among the two vertices a and b. A path is a consequence of finite of alternating vertices and edges between the two nodes in which the starting vertex of each edge is same as the ending vertex of preceding edge in the sequence. The source vertex of this fuzzy network is s and ending vertex is t. Here, we consider two non negative trapezoidal fuzzy numbers \(\tilde{t}_{a,b}\) and \(\tilde{c}_{a,b}\) which are associated with the edge (a, b). Here, \(\tilde{T}_{a,b}\) is used to represent the fuzzy traversal time between the nodes u and v. The another fuzzy number \(\tilde{c}_{a,b}\) is used to represent the fuzzy cost between the nodes a and b.

In this FCSPP, we have to select a shortest path within the source vertex and other vertices with a specific constraint that the fuzzy traveling time of the selected path does not more than a fuzzy predetermined waiting time \(\widetilde{T}_\text {delay}\). Here, \(\widetilde{T}_\text {delay}\) represents the highest possible travel time to transverse a specific path. In another sentence, we can say that the additional constraint demonstrates the a maximum time limit on the sum of fuzzy travel time of edges in the path.

The fuzzy mathematical programming of FCSPP is described as follows:

$$\begin{aligned} \text {Minimize} \sum _{a=1}^{n}\sum _{b=1}^{n}\tilde{c}_{ab}x_{ab} \end{aligned}$$

subject to:

$$\begin{aligned}&\sum _{a=1}^{n}x_{ab}-\sum _{a=1}^{n}x_{ba}\nonumber \\&\quad = {\left\{ \begin{array}{ll} 1 ~~ \qquad { if} ~~ a=s,\\ 0 ~~ \qquad { if} ~~ a \ne s,\quad d(a=1,2,\ldots ,n)\\ -1 ~~\quad { if} ~~ a=t,\\ \end{array}\right. }\nonumber \\&\sum _{a=1}^{n}\sum _{b=1}^{n}\tilde{t}_{ab}x_{ab} \le \widetilde{T}_\text {delay}\nonumber \\&x_{ij} \in \left\{ 0,1\right\} , \forall (u,v) \in \widetilde{Y}. \end{aligned}$$
(9)

Here, \(x_{ab}\) is variable associated with each edge (a, b). If edge (a, b) belongs to the set of edges admitted in the fuzzy constrained shortest path, then \(x_{ab}\) =1, otherwise \(x_{ab}\) =0.

The collection of all possible paths between the vertex s to vertex d is represented by \(P_{sd}\). Let \(T(p)=\sum _{{u,v}\in p} \tilde{t}_{u,v}\) be fuzzy travel time of the path p and \(L(p)=\sum _{{u,v}\in p} \tilde{c}_{u,v}\) be fuzzy traveling cost of the path p. Given \(\tilde{T} > 0\) and \(P_{sd} (\tilde{T}) =\{p_{sd} :T( p_{st})\le \tilde{T}\}\) is the set of all possible paths between two nodes s and d which satisfies the condition \(T( p_{sd})\ne \tilde{T}\). Each and every path belongs to the set \(P_{sd} (\tilde{T})\) is said to be a fuzzy feasible path. In this FCSPP, our main objective to select a fuzzy feasible path with minimum fuzzy cost.

Definition 10

Let \(p^*_{sd}\) be a fuzzy feasible path. \(p^*_{sd}\) is called as fuzzy optimal constrain path in a FCSPP if and only if \(P \left( {\tilde{L}\left( {p_{sd}^* } \right) } \right) \le P \left( {\tilde{L}\left( {p_{sd} } \right) } \right) \) for any fuzzy feasible path \(p_{sd}\). Here, \(\tilde{L}(p_{sd})\) is trapezoidal fuzzy number and the value of \(P(\tilde{L} (p_{sd}))\) is calculated using (7).

Let \(\tilde{d}_j \left( {\tilde{\omega }} \right) \) denotes the fuzzy shortest path length between the source point/node s and destination point/node j subject to a specific criteria that the traversing time of the path does not more than \(\tilde{\omega }\). Let \(\tilde{p}_j \left( {\tilde{\omega }} \right) \) is the last edge of this path. We consider that \(P \left( {\tilde{d}_j \left( {\tilde{\omega }} \right) } \right) = \infty \) for \(\tilde{\omega }\prec \tilde{0}\). In this case, the dynamic formulation is given as follows:

$$\begin{aligned}&\tilde{d}_j \left( {\tilde{0}} \right) = \tilde{0}\\&\tilde{d}_j \left( {\tilde{\omega }} \right) = \min \left\{ {\tilde{d}_j \left( {\tilde{\omega }\ominus \tilde{1}} \right) , \mathop {\min }\limits _k \left\{ {\tilde{d}_k \left( {\tilde{\omega }\ominus \tilde{t}_{kj} } \right) \oplus \tilde{c}_{kj} } \right\} } \right\} . \end{aligned}$$

Proposed algorithm for FCSPP

In Sect. 4, we present an algorithmic approach to determine the fuzzy constrained optimal paths within a source node s and every other nodes in the fuzzy network. The proposed algorithm is presented in Algorithm 1.

figure a

Case study

In this section, we present an application of the proposed model on a location-based online cab service.

People visit from one city to another cities due to several purposes, e.g., jobs, business, few for holidays and vacations, education, etc. It is not to take their own a car in each and every cities or countries which they visit. Travelers always choose other alternatives like cabs, trains, public transports, rent cars, buses, and bikes. It is very much popular to take a car on rent due to the traveling cost of a car is very much cheaper than taking a car/cab/taxi for a total day. To solve this transportation problem, some entrepreneurs have developed an app-based car rental service and users can book the car using online car rental system. The affordable mobile app-based cab services have provided the senior citizens, working women, students, and the party goers to visit alone to the place at any time of the day. For this reason, recently, it becomes an efficient tool when a person wants to hire a cab. These mobile app-based cab services were first time established in the UK, but it has now very much popular all over the world. It becomes very much comfortable to find a cab in the minimum possible waiting time rather of waiting to find a cab on a busy road. Each app-based cab service has always their own advantages and they provide several services to the user. Each user needs a mobile app to determine the proper location of the traveler.

Uber is the most popular and largest mobile app-based cab service in India. It is very simple for citizenry to arrive to their possible destination place easily and safely with Uber cab wherever users are in a specific city or even send their parcels. To find a cab for ride via Uber, the user has to choose the source location and the destination location. Then, the passenger watches the traveling cost beforehand, and finally, he finds the traveling time in the mobile app. Their mobile app system connects with the specific passenger to the closest Uber driver and it sends the a message of passenger’s location to the driver. The Uber driver can accept or even refuse the request of the passenger. If he accepts the request of the passenger, the driver will must pick up that passenger.

Fig. 3
figure 3

A network

Full size image
Table 1 Fuzzy traveling costs and fuzzy traveling time of the network
Full size table
Table 2 Solutions of our proposed algorithm
Full size table

In this manuscript, we have examined our proposed model in the Uber cab service system in China. Here, we have used the Fig. 3 to demonstrate the proposed algorithmic technique for Uber. The main objective of this case study is to find the FCSP for the online cabs. This graph describes a network among several locations of China. This graph consists of 23 vertices and lines (arcs). Table 1 shows the fuzzy cost value and the fuzzy travel time from each line. This table includes the triangular fuzzy numbers which have been figured out based on the average daily traffic.

Algorithm 1 is used to determine the fuzzy constrained shortest path from source vertex 1 to several destination vertices. In Table 2, we have shown the values of fuzzy traveling cost and the fuzzy traveling time of the FCSP from the source vertex 1 to several target vertices. The shortest path between the source vertex 1 and the target vertex 23 path is \(1 \rightarrow 5 \rightarrow 11 \rightarrow 17 \rightarrow 21 \rightarrow 23\), as long as the maximum waiting time is [33, 52, 60, 70]. The fuzzy traveling cost of this path is [1260, 1370, 1450, 1610]. If the maximum waiting time allowed is decreased to [32, 49, 56, 74], then there exists no path between vertex 1 and vertex 23 meeting this additional criterion of the FCSPP. The fuzzy shortest path from the vertex 1 to vertex 18 is \(1 \rightarrow 5 \rightarrow 12 \rightarrow 15 \rightarrow 18\) if the maximum waiting time allowed is [34, 45, 55, 67] and the fuzzy traveling cost of this specific path is [840, 860, 925, 1070]. In this path, if the maximum waiting time permitted is to increase to [40, 50, 65, 70], the fuzzy shortest path will be \(1 \rightarrow 3 \rightarrow 8 \rightarrow 13 \rightarrow 15 \rightarrow 18\) with fuzzy cost [510, 720, 820, 900]. There exists no possible path from the vertex 1 to vertex 18 if the maximum waiting time is reduced to [31, 42, 48, 64]. We have shown the FCSP from the starting vertex 1 to several other destination vertices.

Table 3 Comparison of our proposed algorithm with fuzzy linear programming
Full size table

In this manuscript, we have also solved this FCSPP using fuzzy linear programming approach. The fuzzy mathematical model, the FCSPP, is described in (9). The LINGO software is used to solve the fuzzy mathematical model, the FCSPP. We have shown the results of our proposed method and fuzzy linear programming approach in Table 3. In Table 3, the calculated shortest paths between the source vertex and all the other target vertices using proposed algorithm are exactly the same to the results of the fuzzy linear programming approach. However, our proposed algorithm needs less time then fuzzy Dijkstra’s algorithm and fuzzy linear programming approach. It is shown in Table 3.

Conclusion

The FSPP is one of most popular combinatorial optimization problems in the area of fuzzy operation research. There exists many different types of FSPPs. CSPP is a special type of SPP which determines the shortest paths between a predetermined starting point and all other target points in a directed graph under an additional constraint of being not more than the sum of traveling time for the shortest path. Two import transportation parameters (traveling time and traveling cost) are related to each and every arc in a CSPP. It is not always possible to predicate the exact traveling cost and traveling time of a path due to the fluctuation of weather conditions and traffic frequency of the path. The fuzzy set is an useful method to deal those uncertainties in the information. In this manuscript, we investigate the constrained shortest path problem, where edge weights are presented by trapezoidal fuzzy numbers. We define this type of FSPP as FCSPP. The significance of using trapezoidal fuzzy numbers as edge weights in FCSPP is described in this study. This paper introduces a mathematical model for a constrained shortest path problem with fuzzy edge weights. The LINGO software is used to solve this problem. Here, we present an algorithmic technique for solving this problem. In our proposed method, we incorporate the uncertainties in dynamic programming algorithm for FCSPP using trapezoidal fuzzy number as edge weight. Finally, we describe a real-life application of our proposed model on an app-based taxi service in China. In future, the proposed algorithm can be utilized to real-life problems in supply chain management, transportation, and other relevant fields.