Downsizing and enhancing broad learning systems by feature augmentation and residuals boosting

Abstract

Recently, a broad learning system (BLS) has been theoretically and experimentally confirmed to be an efficient incremental learning system. To get rid of deep architecture, BLS shares the same architecture and learning mechanism of the well-known functional link neural networks (FLNN), but works in broad learning way on both the randomly mapped features of original features of data and their randomly generated enhancement nodes. As such, BLS often requires a huge heap of hidden nodes to achieve the prescribed or satisfactory performance, which may inevitably cause both overwhelming storage requirement and overfitting phenomenon. In this study, a stacked architecture of broad learning systems called D&BLS is proposed to achieve enhanced performance and simultaneously downsize the system architecture. By boosting the residuals between previous and current layers and simultaneously augmenting the original input space with the outputs of the previous layer as the inputs of current layer, D&BLS stacks several lightweight BLS sub-systems to guarantee stronger feature representation capability and better classification/regression performance. Three fast incremental learning algorithms of D&BLS are also developed, without the need for the whole re-training. Experimental results on some popular datasets demonstrate the effectiveness of D&BLS in the sense of both enhanced performance and reduced system architecture.

Introduction

As everyone may know well, over the past decade, deep learning systems have earned great success in many application fields [1, 2] and have been drawing more and more attentions in today’s academic and industrial communities. Typical deep learning systems include deep restricted Boltzmann machines (RBM) [3], deep belief networks (DBN) [4, 5] and deep convolutional neural networks (CNN) [6]. Deep learning systems exhibit their overwhelming performance by taking their complicated deep structures and deep learning methods. However, they often suffer from very time-consuming training because a huge number of hyperparameters in the corresponding complicated deep structures are involved. Besides, updating their deep structure becomes an extraordinarily tedious task, due to the need for the whole re-training. To get rid of complicated deep architecture and effectively avoid very time-consuming training (and even re-training), as an alternative to deep learning systems, broad learning system (BLS in brevity) [7] has been recently invented to organize the well-known functional link neural networks (FLNN) [8, 9] in broad learning way. Up to date, several variants of BLS have been developed. A typical example is fuzzy BLS [10] which is based on Takagi–Sugeno–Kang fuzzy systems [11,12,13]. Theoretical and experimental evidences have revealed BLS’s excellent classification/regression performance, with fast wide learning capability.

Since FLNN has both its simple structure of single-layer feedforward neural networks and its fast learning which can be realized quickly using its analytical solution, BLS takes FLNN as its basic structure and then expands it in broad learning way. In contrast to FLNN, BLS has two distinctive discrepancies in the structure sense: (1) BLS transforms the set of the original input features of data into randomly mapped features and then take sparse autoencoders (SAE) to optimize them into sparse mapped features [14] so as to capture the intrinsic correlations of the input features. (2) BLS generates the enhancement nodes using nonlinear activation functions with randomly generated weights on all the sparse mapped features. All the sparse mapped features and the enhancement nodes are linked to the output layer, where the weights between the hidden nodes and the output layer are determined analytically by ridge regression [15], without the need for iterative updates of the weights. More importantly, without the need for re-training the whole network, BLS can train its structure in broad learning way for the incremental increase of randomly mapped features, enhancement nodes and input data, thereby avoiding very time-consuming training especially for big data. BLS has been theoretically proved to be a universal approximator [16]. A large amount of experimental evidences has indicated that BLS indeed has at least comparably and even much more satisfactory classification/regression performance and strong generalization capability, in contrast to the corresponding deep learning system. However, because the mapped features and enhancement nodes are randomly generated, BLS often needs a huge heap of enhancement nodes to achieve the prescribed performance, which may inevitably cause both overwhelming storage requirement and overfitting phenomenon, therefore, how to downsize a BLS system and simultaneously keep the strong capability of the whole system is becoming an urgent demand.

In this study, we attempt to tackle with this issue by stacking several lightweight BLS sub-systems with both feature augmentation and residuals boosting into its stacked structure called D&BLS. The basic idea can be clearly stated as follows.

• 1. To avoid overfitting phenomenon of the general BLS and simultaneously downsize its structure, D&BLS is proposed to stack several lightweight BLS sub-systems. As a deep classifier, the whole stacked structure and learning of D&BLS has its novelty in the sense of two joint stacking ways: feature augmentation and residuals boosting, which indeed guarantees enhanced performance of D&BLS.

• 2. Using the bootstrap strategy on feature nodes of each lightweight BLS sub-system, enhancement nodes are generated and hence each lightweight BLS sub-system is built to maintain powerful capability in both fast training and good generalization.

• 3. When D&BLS has its fixed depth, three incremental learning algorithms are designed for three incremental cases to endow D&BLS with the ability of fast learning in broad expansion of each layer without the whole re-training process.

• 4. Experimental results on six classification datasets demonstrate that D&BLS can reduce the number of enhancement nodes of BLS to about 76% or less with the same or better performance. On ten regression datasets, D&BLS can achieve smaller error with comparable number of enhancement nodes. On the MNIST dataset, three incremental algorithms of D&BLS can reach the performance comparable to that of D&BLS with one-shot construction and the training time of three incremental algorithms is much less than that of D&BLS with the one-shot construction, In addition, D&BLS only needs much less running time than BLS when they both share the same sizes. In general, D&BLS with some (i.e., from 2 to 4) lightweight sub-systems can obtain promising learning ability.

The rest of this paper is organized as follows. Section “On BLS” reviews BLS in brevity. Section “On D&BLS” proposes the structure of D&BLS, gives the learning algorithm of D&BLS, and discusses its computational complexity. Besides, three incremental algorithms of D&BLS are also designed in this section. Experimental results about image/non-image dataset classification, regression and incremental learning are presented in section “Experimental results”. And the last section concludes this paper.

On BLS

In this section, we give a brief review about BLS’s structure and three incremental learning algorithms.

Framework of BLS

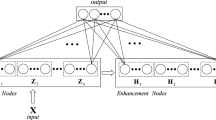
In [7], BLS is conceptually composed of four basic parts: (1) original input; (2) feature nodes; (3) enhancement nodes; and (4) output layer. BLS begins with the original input as the input to certain feature mapping algorithms [7], which then generates the feature nodes by taking the sparse autoencoder to slightly fine-tune the random features. As such, all the mapped feature nodes actually form an efficient representation way of the original data. Accordingly, BLS generates a series of enhancement nodes by consecutively acting certain activation function with random parameters on all the mapped feature nodes, then all mapped features generated an enhancement node. Finally, BLS links both feature nodes and enhancement nodes to the output layer with each output weight. As one of the most famous merits, all the output weights can be trained analytically by the well-known ridge regression method [15].

Figure 1 gives an illustrative structure of BLS. According to Fig. 1, we can concretely state how to construct a BLS as follows.

Fig. 1

An illustrative structure of BLS

Without loss of generality, here we only consider the multi-input and single-output case. Suppose the training dataset X contains the total T original input samples with D dimensions and its output vector Y corresponds the total T target outputs, i.e., $\varvec{X} \in {\mathbb{R}}^{T \times D} ,\;\varvec{Y} \in {\mathbb{R}}^{T \times 1}$. We assume BLS has the total n groups of feature nodes in which the ith group of feature nodes takes the mapping function $\phi_{i} ,\;i = 1,2, \ldots ,n$ and contains the total $d_{i}$ feature nodes and the total m groups of enhancement nodes in which the jth group of enhancement nodes takes the activation function $\xi_{j} ,\;j = 1,2, \ldots ,m$ and contains the total $q_{j}$ enhancement nodes. As such, the ith group of feature nodes may be expressed as:

$$ \varvec{M}_{i} = \phi_{i} (\varvec{XW}_{ei} +\varvec{\beta}_{ei} ),\quad \;i = 1,2, \ldots ,n $$

(1)

where the weight matrix ${\mathbf{W}}_{ei} \in {\mathbb{R}}^{{D \times d_{i} }}$ and the bias matrix $\varvec{\beta}_{ei} \in {\mathbb{R}}^{{T \times d_{i} }}$ are randomly generated according to a certain distribution, such as normal distribution. According to [7], sparse autoencoder is taken to slightly fine-tune the random feature matrix $\varvec{M}_{i}$ into sparse and compact feature matrix. Using alternating direction method of multiplier (ADMM), the weight matrix tuned by sparse autoencoder can be solved by the following iterative steps:

$$ \left\{ \begin{aligned} & \hat{\varvec{W}}_{k + 1} = \left( {\hat{\varvec{M}}_{i}^{T} \hat{\varvec{M}}_{i} + r\varvec{I}} \right)^{ - 1} \left( {\hat{\varvec{M}}_{i}^{T} \varvec{X} + r\left( {\varvec{o}_{k} - \varvec{u}_{k} } \right)} \right) \hfill \\ & \varvec{o}_{k + 1} = \text{S}_{{{\lambda \mathord{\left/ {\vphantom {\lambda r}} \right. \kern-0pt} r}}} \left( {\hat{\varvec{W}}_{k + 1} + \varvec{u}_{k} } \right) \hfill \\ & \varvec{u}_{k + 1} = \varvec{u}_{k} + \left( {\hat{\varvec{W}}_{k + 1} - \varvec{o}_{k + 1} } \right) \hfill \\ \end{aligned} \right. $$

(2)

where $\hat{\varvec{M}}_{i}$ is the desired sparse feature matrix, $\hat{\varvec{W}}$ is the sparse autoencoder solution, $\hat{\varvec{W}}_{0}$, $\varvec{o}_{0}$ and $\varvec{u}_{0}$ are zero matrices, $\lambda$ is the given regularization parameter. In addition, r > 0 and S is the soft thresholding operator which is defined as:

$$ \text{S}_{t} \left( a \right) = \left\{ {\begin{array}{*{20}c} {a - t,} \\ {0,} \\ {a + t,} \\ \end{array} } \right.\begin{array}{*{20}c} {\quad a > t} \\ {\quad \left| a \right| \le t} \\ {\quad a < - t} \\ \end{array} $$

(3)

After a certain number of iterations, the sparse feature matrix can be obtained by:

$$ \varvec{M}_{i} = \varvec{X\hat{W}} $$

(4)

We collect all the groups of feature nodes to form the group $\varvec{M}^{n} \triangleq \left[ {\varvec{M}_{1} ,\varvec{M}_{2} , \ldots ,\varvec{M}_{n} } \right]$, which will be used to generate the enhancement nodes. Similarly, the jth group of enhancement nodes may be expressed as:

$$ \varvec{E}_{j} = \xi_{j} (\varvec{M}^{n} \varvec{W}_{hj} +\varvec{\beta}_{hj} ),\;j = 1,2, \ldots ,m $$

(5)

where the weight matrix $\varvec{W}_{hj} \in {\mathbb{R}}^{{\left( {\sum\nolimits_{i = 1}^{n} {d_{i} } } \right) \times q_{j} }}$ and the bias matrix $\varvec{\beta}_{hj} \in {\mathbb{R}}^{{T \times q_{j} }}$ are also randomly generated according to a certain distribution. We collect all the groups of enhancement nodes $\varvec{E}_{j}$ to form the group $\varvec{E}^{m} \triangleq \left[ {\varvec{E}_{1} ,\varvec{E}_{2} , \ldots ,\varvec{E}_{m} } \right]$. In this way, the output vector of such a BLS becomes:

$$ \varvec{Y} = \left[ {\varvec{M}_{1} ,\varvec{M}_{2} , \ldots ,\varvec{M}_{n} |\varvec{E}_{1} ,\varvec{E}_{2} , \ldots ,\varvec{E}_{m} } \right]\varvec{W}_{n}^{m} = \left[ {\varvec{M}^{n} |\varvec{E}^{m} } \right]\varvec{W}_{n}^{m} $$

(6)

where $\varvec{W}_{n}^{m} \in {\mathbb{R}}^{{\left( {\sum\nolimits_{i = 1}^{n} {d_{i} } + \sum\nolimits_{j = 1}^{m} {q_{j} } } \right)\, \times \,1}}$ are the output weight vector that can be solved analytically by ridge regression method. That is to say, after denoting $\varvec{U}_{n}^{m} = \left[ {\varvec{M}^{n} |\varvec{E}^{m} } \right]$, with the Moore–Penrose inverse of $\varvec{U}_{n}^{m}$, we have the analytical solution of $\varvec{W}_{n}^{m}$.

$$ \varvec{W}_{n}^{m} = \left[ {\varvec{U}_{n}^{m} } \right]^{\dag } \varvec{Y} $$

(7)

Using ridge regression [15], the pseudoinverse of $\varvec{U}_{n}^{m}$ can be solved as follows:

$$ \left[ {\varvec{U}_{n}^{m} } \right]^{\dag } = \left\{ {\begin{array}{*{20}c} {\left( {\lambda \varvec{I} + \left( {\varvec{U}_{n}^{m} } \right)^{T} \varvec{U}_{n}^{m} } \right)^{ - 1} \left( {\varvec{U}_{n}^{m} } \right)^{T} ,} &\quad {\text{if}\,\;T \ge h} \\ {\left( {\varvec{U}_{n}^{m} } \right)^{T} \left( {\lambda \varvec{I} + \varvec{U}_{n}^{m} \left( {\varvec{U}_{n}^{m} } \right)^{T} } \right)^{ - 1} ,} &\quad {\text{if}\,\;T < h} \\ \end{array} } \right. $$

(8)

where $\lambda$ is the given regularization parameter, $h = \sum\nolimits_{i = 1}^{n} {d_{i} } + \sum\nolimits_{j = 1}^{m} {q_{j} }$ is the total number of hidden nodes of BLS.

As a result, such a BLS is built quickly, without the need for iterative updates at a very slow learning speed, likewise in BP neural network learning [18].

Incremental learning of BLS

Except for fast training of BLS, another famous merit exists in its simple yet fast incremental learning methods, which indeed reveals its very applicability in online scenarios and/or practical situations where the more promising performance is expected. According to [7], without re-training the whole network structure, incremental learning of BLS can be realized from three cases.

Increment of enhancement nodes

In this case, BLS is expanded by adding the (m + 1)th group of enhancement nodes. That is to say, we have

$$ \varvec{E}_{m + 1} = \xi_{m + 1} \left( {\varvec{M}^{n} {\kern 1pt} \varvec{W}_{h(m + 1)} +\varvec{\beta}_{h(m + 1)} } \right) $$

(9)

$$ \varvec{U}_{n}^{m + 1} = \left[ {\varvec{U}_{n}^{m} |\varvec{E}_{m + 1} } \right] $$

(10)

After denoting $\varvec{U}^{ex} = \varvec{E}_{m + 1}$, we can decompose the pseudoinverse of $\varvec{U}_{n}^{m + 1}$ as,

$$ \left[ {\varvec{U}_{n}^{m + 1} } \right]^{\dag } = \left[ {\begin{array}{*{20}c} {\left[ {\varvec{U}_{n}^{m} } \right]^{\dag } - \varvec{AB}^{T} } \\ {\varvec{B}^{T} } \\ \end{array} } \right] $$

(11)

where

$$ \begin{aligned} & {\kern 1pt} \varvec{A} = \left[ {\varvec{U}_{n}^{m} } \right]^{\dag } \varvec{U}^{ex} \\ & \varvec{B}^{T} \; = \left\{ \begin{aligned} \,& \varvec{C}^{\dag } ,{\text{ if }}\varvec{C} \ne 0, \hfill \\ & \left( {{\mathbf{1}} + \varvec{A}^{T} \varvec{A}} \right)^{ - 1} \varvec{A}^{T} \left[ {\varvec{U}_{n}^{m} } \right]^{ + } {\text{ if }}\varvec{C}{ = 0} . { } \hfill \\ \end{aligned} \right. \\ & {\kern 1pt} \varvec{C}\;{\kern 1pt} = \;\;\varvec{U}^{ex} - \varvec{U}_{n}^{m} \varvec{A} \\ \end{aligned} $$

(12)

Therefore, the new output weight vector $\varvec{W}_{n}^{m + 1}$ becomes

$$ \varvec{W}_{n}^{m + 1} = \left[ {\begin{array}{*{20}c} {\varvec{W}_{n}^{m} - \varvec{AB}^{T} \varvec{Y}} \\ {\varvec{B}^{T} \varvec{Y}} \\ \end{array} } \right] $$

(13)

Since $\varvec{W}_{n}^{m}$, $\varvec{U}_{n}^{m}$ and $\left[ {\varvec{U}_{n}^{m} } \right]^{\dag }$ have been obtained in advance, $\varvec{W}_{n}^{m + 1}$ can be quickly obtained according to Eqs. (12) and (13).

Increment of feature nodes

In this case, BLS is expanded by adding the (n + 1)th group of feature nodes. As such, we have,

$$ \varvec{M}_{n + 1} = \phi_{n + 1} \left( {\varvec{XW}_{e(n + 1)} +\varvec{\beta}_{e(n + 1)} } \right) $$

(14)

$$ \varvec{U}_{{n{ + }1}}^{m} = \left[ {\varvec{U}_{n}^{m} |\varvec{M}_{n + 1} |\varvec{E}_{1}^{ex} |\varvec{E}_{2}^{ex} | \cdots |\varvec{E}_{m}^{ex} } \right] $$

(15)

where $\varvec{E}_{1}^{ex} |\varvec{E}_{2}^{ex} | \cdots |\varvec{E}_{m}^{ex}$ are the additional outputs of the enhancement nodes corresponding to the (n + 1)th group of feature nodes. After denoting $\varvec{U}^{ex} = \left[ {\varvec{M}_{n + 1} |\varvec{E}_{1}^{ex} |\varvec{E}_{2}^{ex} | \cdots |\varvec{E}_{m}^{ex} } \right]$, we can decompose the pseudoinverse of $\left[ {\varvec{U}_{{n{ + }1}}^{m} } \right]$ as,

$$ \left[ {\varvec{U}_{{n{ + }1}}^{m} } \right]^{\dag } = \left[ {\begin{array}{*{20}c} {\left[ {\varvec{U}_{n}^{m} } \right]^{\dag } - \varvec{AB}^{T} } \\ {\varvec{B}^{T} } \\ \end{array} } \right] $$

(16)

where A and B can be obtained according to Eq. (12). Therefore, the new output weight vector $\varvec{W}_{{n{ + }1}}^{m}$ is,

$$ \varvec{W}_{{n{ + }1}}^{m} = \left[ {\begin{array}{*{20}c} {\varvec{W}_{n}^{m} - \varvec{AB}^{T} \varvec{Y}} \\ {\varvec{B}^{T} \varvec{Y}} \\ \end{array} } \right] $$

(17)

Obviously, since $\varvec{W}_{n}^{m}$, $\varvec{U}_{n}^{m}$ and $\left[ {\varvec{U}_{n}^{m} } \right]^{\dag }$ have been obtained in advance, $\varvec{W}_{{n{ + }1}}^{m}$ can be quickly obtained according to Eqs. (12) and (17).

Increment of input data

In this case, BLS is fed with the additional training data ${\text{\{ }}\varvec{X}^{ex} ,\varvec{Y}^{ex} {\text{\} }}$. The additional feature node $\varvec{M}^{ex}$ generated from $\varvec{X}^{ex}$ is

$$ \varvec{M}^{ex} = \left[ {\phi_{1} \left( {\varvec{X}^{ex} \varvec{W}_{e1} +\varvec{\beta}_{e1} } \right), \ldots ,\phi_{n} \left( {\varvec{X}^{ex} \varvec{W}_{en} +\varvec{\beta}_{en} } \right)} \right] $$

(18)

The output of enhancement nodes corresponding to $\varvec{M}^{ex}$ is

$$ \varvec{E}^{ex} = \left[ {\xi_{1} \left( {\varvec{M}^{ex} \varvec{W}_{h1} +\varvec{\beta}_{h1} } \right), \ldots ,\xi_{m} \left( {\varvec{M}^{ex} \varvec{W}_{hm} +\varvec{\beta}_{hm} } \right)} \right] $$

(19)

Please note, both $\varvec{W}_{ei}$, $\varvec{\beta}_{ei}$ (i = 1,…,n) and $\varvec{W}_{hj}$, $\varvec{\beta}_{hj}$ (j = 1,…,m) are initialized by taking their corresponding values in Eqs. (1) and (5). Let

$$ \left( {\varvec{U}_{n}^{m} } \right)^{ex} = \left[ {\begin{array}{*{20}c} {\varvec{U}_{n}^{m} } \\ {\varvec{U}^{ex} } \\ \end{array} } \right] $$

(20)

and $\varvec{U}^{ex} = \left[ {\varvec{M}^{ex} |\varvec{E}^{ex} } \right]$, the pseudoinverse of $\left( {\varvec{U}_{n}^{m} } \right)^{ex}$ can be decomposed as,

$$ \left( {\left( {\varvec{U}_{n}^{m} } \right)^{ex} } \right)^{\dag } = \left[ {\left( {\varvec{U}_{n}^{m} } \right)^{\dag } - \varvec{BA}^{T} |\varvec{B}} \right] $$

(21)

where

$$ \begin{aligned} & {\kern 1pt} \,\varvec{A} = \left( {\left( {\varvec{U}_{n}^{m} } \right)^{T} } \right)^{\dag } \left( {\varvec{U}^{ex} } \right)^{T} \\ & \varvec{B}^{T} \; = \left\{ \begin{aligned} & \varvec{C}^{\dag } ,{\text{ if }}\varvec{C} \ne 0, \hfill \\ & \left( {{\mathbf{1}} + \varvec{A}^{T} \varvec{A}} \right)^{ - 1} \varvec{A}^{T} \left( {\left( {\varvec{U}_{n}^{m} } \right)^{T} } \right)^{\dag } ,{\text{ if }}\varvec{C}{ = 0} . { } \hfill \\ \end{aligned} \right. \\ & {\kern 1pt} \varvec{C}\;{\kern 1pt} = \;\left( {\varvec{U}^{ex} } \right)^{T} - \left( {\varvec{U}_{n}^{m} } \right)^{T} \varvec{A} \\ \end{aligned} $$

(22)

Therefore, the new output weight vector $\left( {\varvec{W}_{n}^{m} } \right)^{ex}$ is

$$ \left( {\varvec{W}_{n}^{m} } \right)^{ex} = \varvec{W}_{n}^{m} + \varvec{B}\left( {\varvec{Y}^{ex} - \varvec{U}^{ex} \varvec{W}_{n}^{m} } \right) $$

(23)

Obviously, since $\varvec{W}_{n}^{m}$, $\varvec{U}_{n}^{m}$ and $\left[ {\varvec{U}_{n}^{m} } \right]^{\dag }$ have been obtained in advance, $\left( {\varvec{W}_{n}^{m} } \right)^{ex}$ can be quickly obtained according to Eqs. (22) and (23).

While BLS shares the fast training originating from the flexible yet random construction of both feature nodes and enhancement nodes, it indeed requires a large amount of feature nodes and especially enhancement nodes to achieve satisfactory performance, which may cause an overwhelming storage requirement and overfitting phenomenon. For example, for MNIST dataset, according to [7], the built BLS needs 11,000 enhancement nodes. Therefore, in the next section, we will deepen BLS by stacking its structures into the proposed classifier so as to downsize the structure of BLS and simultaneously share the promising advantages of BLS.

On D&BLS

In this section, by means of feature augmentation, we first state the deep structure of D&BLS and its learning algorithm and then derive three incremental learning algorithms of D&BLS for three incremental cases. Their computational complexities are also discussed.

Structure and learning of D&BLS

Given D&BLS with L layers, the original training dataset $\varvec{X} \in {\mathbb{R}}^{T \times D}$ and its target output vector $\varvec{Y} \in {\mathbb{R}}^{T \times 1}$. The parameters of the ith lightweight sub-system include the total $n_{i}$ groups of feature nodes in which each group contains the total $d_{i}$ feature nodes, the number of the selected feature nodes $p_{i}$ that are chosen to generate enhancement nodes, and the total $m_{i}$ groups of enhancement nodes in which each group contains the total $q_{i}$ enhancement nodes. For convenience, we use $\left( {d_{1} \times n_{{{\kern 1pt} 1}} ,p_{1} ,q_{1} \times m_{1} } \right) - \cdots - \left( {d_{L} \times n_{{{\kern 1pt} L}} ,p_{L} ,q_{L} \times m_{L} } \right)$ to represent the parameters setting of this D&BLS and $\left( {\sum\nolimits_{i = 1}^{L} {\sum\limits_{{}}^{{}} {d_{i} \times n_{{{\kern 1pt} i}} } ,\;\sum\nolimits_{i = 1}^{L} {q_{i} \times m_{{{\kern 1pt} i}} } } } \right)$ to denote its whole structure.

Figure 2 illustrates its deep structure. According to Fig. 2, D&BLS essentially stacks several lightweight BLS sub-systems into its deep structure simultaneously by two ways: (1) augmenting the original input space with the outputs of previous layer as the inputs of current layer; (2) boosting the residual outputs between the original outputs and the outputs of all the previous layers as the target outputs of current layer. According to stacked generalization principle [17], the use of feature augmentation guarantees enhanced performance of D&BLS, whereas the use of residual outputs maintains good local approximation of current BLS sub-system for subtle output differences remaining in current layer. In general, a lightweight BLS sub-system takes not so many feature nodes and enhancement nodes, in contrast to the BLS system for the same training dataset. To stack lightweight BLS sub-systems well, the deep structure of D&BLS embodies our three reliable considerations as follows.

Fig. 2

Structure of D&BLS

(1) According to the adopted feature augmentation, the ith lightweight sub-system has its augmented training dataset $\varvec{X}_{i}$, i.e.,

$$ \varvec{X}_{\varvec{i}} { = }\left\{ \begin{aligned} & \varvec{X},\,\;i = 1 \hfill \\ & \left[ {\varvec{X}|\varvec{Y^{\prime}}_{i - 1} \,\,} \right],\quad i = 2,3, \ldots ,L \hfill \\ \end{aligned} \right. $$

(24)

where $\varvec{Y^{\prime}}_{i - 1}$ corresponds to the augmented feature and denotes the output vector of the (i − 1)th sub-system. In other words, the augmented training dataset $\varvec{X}_{i}$ contains the output information of previous sub-system. Please note, each system always has only one augmented feature whose values are the outputs of previous layer in D&BLS.

(2) Inspired by the idea of residuals boosting [19,20,21], each target output of sub-system in current layer is taken to be the residual value between the corresponding target output and the corresponding outputs of the sub-systems of all the previous layers. As such, the ith sub-system has its target output vector $\varvec{Y}_{i}$:

$$ \varvec{Y}_{i} = \left\{ \begin{aligned} & \varvec{Y},\quad i = 1 \hfill \\ & \varvec{Y}_{i - 1} - \varvec{Y^{\prime}}_{i - 1} ,\quad i = 2,3, \ldots ,L \hfill \\ \end{aligned} \right. $$

(25)

Obviously, according to stacked generalization principle, the above stacking way of both feature augmentation and residuals boosting can surely enhance the performance of D&BLS with the increase of the number of sub-systems. In other words, with the prescribed performance, a downsized structure can be expected in the sense of the total number of hidden nodes, in contrast to the general BLS.

(3) When combining all the lightweight sub-systems together, diversity between them should be emphasized to achieve an effective ensemble. To do so, D&BLS only randomly boostraps [22] some feature nodes to generate an enhancement node. Suppose the ith sub-system selects $p_{i}$ feature nodes to generate an enhancement node. After denoting $\varvec{M}^{{p_{i} }} \triangleq \left[ {\varvec{M}_{{c_{1} }} ,\varvec{M}_{{c_{2} }} , \ldots ,\varvec{M}_{{c_{{p_{i} }} }} } \right]$ as the random selected feature nodes, where $c_{1} ,c_{2} , \ldots ,c_{{p_{i} }} \in \left[ {1,n_{i} } \right]$ denote random integers, then an enhancement node $\varvec{E}_{j}$ can be generated as,

$$ \varvec{E}_{j} = \xi_{j} (\varvec{M}^{{p_{i} }} \varvec{W}_{hj} +\varvec{\beta}_{hj} ),\quad j = 1,2, \ldots ,m $$

(26)

Once feature nodes and enhancement nodes of each lightweight BLS system are fixed according to the above strategy, this sub-system can be quickly constructed by the same learning algorithm of BLS as in the last section.

D&BLS begins with the construction of the first lightweight. BLS sub-system on the original training dataset X and its target output vector Y. And then D&BLS obtains the output vector $\varvec{Y^{\prime}}_{1}$ of the first lightweight BLS sub-system. After generating $\varvec{X}_{2} = \left[ {\varvec{X}|\varvec{Y^{\prime}}_{1} } \right]$ and $\varvec{Y}_{2} = \varvec{Y} - \varvec{Y^{\prime}}_{1}$, respectively, as the inputs and target outputs of the second lightweight BLS sub-system, the second sub-system is built in the same way as in the above. This procedure is repeated until the maximum number of sub-systems (i.e., layers) or the prescribed performance of D&BLS is achieved. As a result, the final output vector of D&BLS on the original training dataset can be expressed as,

$$ \varvec{Y}^{\prime } = \sum\limits_{{i{\kern 1pt} = {\kern 1pt} 1}}^{L} {\varvec{Y}_{i}^{{{\kern 1pt} \prime }} } $$

(27)

In summary, the learning algorithm is given in Algorithm 1. To visualize the effectiveness of Algorithm 1, a simple two-class classification dataset contained 200 training samples (100 positive samples) is taken for didactic experimentation. The dataset is generated from the model make_moons of Scikit-learn [29] package with 0 noise, as shown in Fig. 3a. Four D&BLSs with different number of sub-systems are taken and the deeper one is deepened from the shallower one. The deepest one is a four-layer D&BLS: (6 × 6, 9, 1 × 3)–(5 × 6, 9, 1 × 2)–(5 × 6, 9, 1 × 2)–(5 × 6, 9, 1 × 2), its whole structure becomes (126, 9). Here the average results of the ten runs are reported. Figure 3b–e shows the decision boundary of all D&BLSs.

Fig. 3

The moon dataset and corresponding decision boundary of four D&BLSs with different number of sub-systems

From Fig. 3, the decision boundary of D&BLS becomes more complex to match the distribution of training samples as D&BLS becomes deeper. It indicates that Algorithm 1 is effective and the learning ability of D&BLS can be enhanced by adding more sub-systems with appropriate parameters.

The computational complexity of Algorithm 1 can be analyzed in terms of D&BLS with L sub-systems. Without loss of generality, according to the same strategy of BLS in [7], here we suppose $\xi$ in step 12 is a sigmoid activation function [23] and the number of iterations of sparse autoencoder taken in step 6 is K.

Thus the computational complexity of step 2 and 3 can be calculated to be $O\left( {2T} \right) \approx O\left( T \right)$. The computational burden from step 4 to step 7 about the generation of feature nodes takes,

$$ \begin{aligned} & O\left( {n_{i} \left( \begin{aligned} & d_{i} \left( {D + 1} \right) + 2Td_{i} \left( {D + 1} \right) + 3Td_{i} + \hfill \\ & K\left( {Td_{i}^{2} + 2d_{i} + d_{i}^{3} + Td_{i} \left( {D + 1} \right) + 7d_{i} \left( {D{ + }1} \right){ + }d_{i}^{2} \left( {D + 1} \right)} \right) \hfill \\ \end{aligned} \right)} \right) \\ & \quad \approx O\left( {2TDn_{i} d_{i} + Kn_{i} \left( {Td_{i}^{2} + d_{i}^{3} + TDd_{i} + Dd_{i}^{2} } \right)} \right) \\ \end{aligned} $$

In general, $d_{i} < T$, $d_{i} < D$ and $2 < K$ can be assured, so the computational complexity mentioned above will be reduced to $O\left( {KTDn_{i} d_{i} } \right)$. Then step 8 requires $O\left( {Tn_{i} d_{i} } \right)$. The computational burden of the generation of enhancement nodes from step 9 to step 13 takes

$$ O\left( {m_{i} \left( {Tp_{i} + p_{i} q_{i} + Tq_{i} p_{i} + 3Tq_{i} } \right)} \right) \approx O\left( {Tm_{i} q_{i} p_{i} } \right) $$

Then steps 14 and 15 require $O\left( {2Tm_{i} q_{i} } \right) \approx O\left( {Tm_{i} q_{i} } \right)$. The calculation of the pseudoinverse of $\left( {U_{{n_{i} }}^{{m_{i} }} } \right)_{i}$ in step 16 requires

$$ \left\{ \begin{aligned} & O\left( {\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{3} + 2T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} + 2\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) \approx O\left( {T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} } \right),\quad {\text{if }}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \le T \hfill \\ & O\left( {T^{3} + 2T^{2} \left( {n_{i} d_{i} + m_{i} q_{i} } \right) + 2T} \right) \approx O\left( {T^{2} \left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right),{\text{ if }}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) > T \hfill \\ \end{aligned} \right. $$

while step 17 and step 18 require

$$ O\left( {2T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) \approx O\left( {T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) $$

Hence, with the total L sub-systems, the computational complexity of Algorithm 1 becomes

$$ \left\{ \begin{aligned}& O\left( {\left( {L - 1} \right)T + \sum\nolimits_{i = 1}^{L} {\left( \begin{aligned} KTDn_{i} d_{i} + Tn_{i} d_{i} + Tm_{i} q_{i} p_{i} + Tm_{i} q_{i} + \hfill \\ T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \hfill \\ \end{aligned} \right)} } \right)\\ &\approx O\left( {\sum\nolimits_{i = 1}^{L} {\left( {KTDn_{i} d_{i} + Tm_{i} q_{i} p_{i} + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} } \right)} } \right),\\ & {\text{ if }}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \le T \\ &O\left( {\left( {L - 1} \right)T + \sum\nolimits_{i = 1}^{L} {\left( \begin{aligned} KTDn_{i} d_{i} + Tn_{i} d_{i} + Tm_{i} q_{i} p_{i} + Tm_{i} q_{i} + \hfill \\ T^{2} \left( {n_{i} d_{i} + m_{i} q_{i} } \right) + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \hfill \\ \end{aligned} \right)} } \right) \\ &\approx O\left( {\sum\nolimits_{i = 1}^{L} {\left( {KTDn_{i} d_{i} + Tm_{i} q_{i} p_{i} + T^{2} \left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)} } \right),\\ & {\text{ if }}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) > T \, \hfill \\ \end{aligned} \right. $$

As we can see, the most time-consuming parts for each sub-system in D&BLS are the generation of feature nodes, the generation of enhancement nodes and the calculation of pseudoinverse. Similarly, we can calculate the computational complexity of BLS for comparison. Suppose BLS contains d × n feature nodes and q × m enhancement nodes, its computational complexity is

$$ \left\{ \begin{aligned} O\left( {KTDnd + Tmqnd + T\left( {nd + mq} \right)^{2} } \right),\quad {\text{if }}\left( {nd + mq} \right) \le T \hfill \\ O\left( {KTDnd + Tmqnd + T^{2} \left( {nd + mq} \right)} \right),\quad {\text{if }}\left( {nd + mq} \right) > T \hfill \\ \end{aligned} \right. $$

For easy comparison, here we suppose each sub-system of D&BLS has the total $\left\lceil {n/L} \right\rceil \times d$ feature nodes and $\left\lceil {m/L} \right\rceil \times q$ enhancement nodes. As such, the computational complexity of Algorithm 1 becomes

$$ \left\{ \begin{aligned} O\left( {KTDnd + \frac{Tmq}{L}\sum\nolimits_{i = 1}^{L} {p_{i} } + \frac{T}{L}\left( {nd + mq} \right)^{2} } \right), \, \quad {\text{ if }}\frac{{\left( {nd + mq} \right)}}{L} \le T, \hfill \\ O\left( {KTDnd + \frac{Tmq}{L}\sum\nolimits_{i = 1}^{L} {p_{i} } + T^{2} \left( {nd + mq} \right)} \right), \, \quad {\text{ if }}\frac{{\left( {nd + mq} \right)}}{L} > T \, \hfill \\ \end{aligned} \right. $$

In general, $\frac{1}{L}\sum\nolimits_{i = 1}^{L} {p_{i} } < nd$ and $\left( {nd + mq} \right) \le T$ can be assured. Thus the computational complexity is obviously less than that of BLS.

Incremental learning for D&BLS

To achieve enhanced performance, it seems that we may expand D&BLS by increasing a lightweight BLS sub-system successively. However, too many lightweight BLS sub-systems often cause overfitting phenomenon. Our experimental evidences demonstrate that the total number of layers (i.e., sub-systems) should generally take a small integer (i.e., from 2 to 4). Therefore, a feasible strategy is to develop its incremental algorithms with the fixed number of layers. What is more, we should still consider how to expand D&BLS for the case of incremental input data. Here we develop three incremental algorithms of D&BLS for three incremental cases, without the need of re-training the whole classifier.

Increment of enhancement nodes

In this case, each sub-system in D&BLS is expanded by adding $\bar{m}$ (i.e., a small integer) groups of enhancement nodes in which each group contains $\bar{q}$ enhancement nodes.

The additional enhancement nodes $\varvec{E}_{1}^{ex} ,\varvec{E}_{2}^{ex} , \cdots ,\varvec{E}_{{\bar{m}}}^{ex}$ are generated from a portion of the original feature nodes. After denoting $\varvec{U}^{ex} = \left[ {\varvec{E}_{1}^{ex} ,\varvec{E}_{2}^{ex} , \cdots ,\varvec{E}_{{\bar{m}}}^{ex} } \right]$, the pseudoinverse of $\varvec{U}_{{n_{i} }}^{{m_{i} + \bar{m}}} = \left[ {\varvec{U}_{{n_{i} }}^{{m_{i} }} |\varvec{U}^{ex} } \right]$ can be calculated by Eqs. (11) and (12). Then the output weight vector can be determined by $\left( {\varvec{W}_{{n_{i} }}^{{m_{i} + \bar{m}}} } \right)_{i} = \left( {\varvec{U}_{{n_{i} }}^{{m_{i} + \bar{m}}} } \right)^{\dag } \varvec{Y}_{i}$, and hence the output of this sub-system after expansion becomes $\varvec{Y}_{i}^{\prime } { = }\varvec{U}_{{n_{i} }}^{{m_{i} + \bar{m}}} \left( {\varvec{W}_{{n_{i} }}^{{m_{i} + \bar{m}}} } \right)_{i}$. The incremental algorithm for this case is summarized in Algorithm 2.

Below let us analyze the computational complexity of Algorithm 2 in terms of L sub-systems. Because the training of each sub-system in this incremental case only deals with both the generation of the incremental enhancement nodes and the calculation of the corresponding pseudoinverse, we mainly observe the corresponding steps in Algorithm 2.

That is to say, the computational complexity from step 3 to step 7 takes $O\left( {T\bar{m}\bar{q}p_{i} } \right)$, while steps 8 and 9 require $O\left( {2T\bar{m}\bar{q}} \right) \approx O\left( {T\bar{m}\bar{q}} \right)$. What is more, because the number of the additional enhancement nodes is generally a small integer, i.e., $\bar{m}\bar{q} < \left( {n_{i} d_{i} + m_{i} q_{i} } \right)$ and $\bar{m}\bar{q} < T$, the calculation of the pseudoinverse $\left( {U_{{n_{i} }}^{{m_{i} + \bar{m}}} } \right)^{\dag }$ in step 10 requires

$$ O\left( {3T\bar{m}\bar{q}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + T\left( {\bar{m}\bar{q}} \right)^{2} + 2T\bar{m}\bar{q}} \right) \approx O\left( {T\bar{m}\bar{q}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) $$

Obviously, step 11 and step 12 require $O\left( {2T\left( {n_{i} d_{i} + m_{i} q_{i} + \bar{m}\bar{q}} \right)} \right) \approx O\left( {T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)$. Hence, with the total L iterations, the computational complexity of Algorithm 2 becomes

$$ \begin{aligned} & O\left( {LT\bar{m}\bar{q} + \sum\limits_{i = 1}^{L} {\left( {T\bar{m}\bar{q}p_{i} + T\bar{m}\bar{q}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)} } \right) \\ & \quad \approx O\left( {\sum\limits_{i = 1}^{L} {\left( {T\bar{m}\bar{q}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)} } \right) \\ \end{aligned} $$

If we re-train the whole model based on Algorithm 1 and assume $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < T$ is assured, its computation complexity will become

$$ O\left( {\sum\limits_{i = 1}^{L} {\left( {KTDn_{i} d_{i} + T\left( {m_{i} q_{i} + \bar{m}\bar{q}} \right)p_{i} + T\left( {n_{i} d_{i} + m_{i} q_{i} + \bar{m}\bar{q}} \right)^{2} } \right)} } \right) $$

Obviously, increment of enhancement nodes can save much training time.

Increment of feature nodes

In this case, after $\bar{n}$ (i.e., a small integer) groups of feature nodes with $\bar{d}$ feature nodes are added, each sub-system in D&BLS is further expanded by the corresponding additional $\bar{m}$ (i.e., a small integer) groups of enhancement nodes with $\bar{q}$ enhancement nodes.

After the total $\bar{n}$ groups of the additional feature nodes $\varvec{M}^{ex}$ are generated from $\varvec{X}_{i}$, the total $\bar{m}$ groups of the additional enhancement nodes $\varvec{E}^{ex}$ are accordingly generated from a portion of the additional feature nodes $\varvec{M}^{ex}$. After denoting $\varvec{U}^{ex} = \left[ {\varvec{M}^{ex} |\varvec{E}^{ex} } \right]$, the pseudoinverse of $\varvec{U}_{{n_{i} { + }\bar{n}}}^{{m_{i} }} = \left[ {\varvec{U}_{{n_{i} }}^{{m_{i} }} |\varvec{U}^{ex} } \right]$ can be calculated by Eqs. (12) and (16). As such, the output weight vector can be obtained by $\left( {\varvec{W}_{{n_{i} + \bar{n}}}^{{m_{i} }} } \right)_{i} = \left( {\varvec{U}_{{n_{i} { + }\bar{n}}}^{{m_{i} }} } \right)^{\dag } \varvec{Y}_{i}$ and the output of this sub-system accordingly becomes $\varvec{Y}_{i}^{\prime } { = }\varvec{U}_{{n_{i} + \bar{n}}}^{{m_{i} }} \left( {\varvec{W}_{{n_{i} + \bar{n}}}^{{m_{i} }} } \right)_{i}$. The incremental algorithm for this case is summarized in following Algorithm 3.

The computational complexity of Algorithm 3 can be analyzed in terms of L sub-systems. Obviously, the training of each sub-system in this incremental case mainly has three stages, namely, the generation of the additional feature nodes and the corresponding additional enhancement nodes and the calculation of the pseudoinverse. According to Algorithm 3, the computational burden from step 4 to step 7 about the generation of feature nodes takes $O\left( {KTD\bar{n}\bar{d}} \right)$. Step 8 requires $O\left( {T\bar{n}\bar{d}} \right)$. The computational complexity from step 9 to step 13 about the generation of enhancement nodes is $O\left( {T\bar{m}\bar{q}p_{i} } \right)$. Then steps 14 and 15 require $O\left( {2T\bar{m}\bar{q}} \right) \approx O\left( {T\bar{m}\bar{q}} \right)$, step 16 requires $O\left( {T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)} \right)$. Because the number of both the additional feature nodes and the additional enhancement nodes is generally a small integer, i.e., $\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right) < \left( {n_{i} d_{i} + m_{i} q_{i} } \right)$ and $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < T$, and the calculation of the pseudoinverse $\left( {U_{{n_{i} { + }\bar{n}}}^{{m_{i} }} } \right)^{ + }$ in step 17 requires

$$ \begin{aligned} & O\left( 3T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)\right.\\ &\quad\left. + T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)^{2} + 2T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)\right) \\ & \qquad \approx O\left( {T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right). \\ \end{aligned} $$

What is more, step 18 and step 19 require $O\left( {2T\left( {n_{i} d_{i} + m_{i} q_{i} + \bar{n}\bar{d} + \bar{m}\bar{q}} \right)} \right) \approx O\left( {T\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)$. In summary, with the totalL iterations, the computational complexity of Algorithm 3 becomes

$$ \begin{aligned} & O\Bigg( LKTD\bar{n}\bar{d} + 2LT\bar{m}\bar{q} + 2LT\bar{n}\bar{d}\\ &\qquad + \sum\nolimits_{i = 1}^{L} \left( T\bar{m}\bar{q}p_{i} + T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)\right. \\ &\qquad \left. + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \right) \Bigg)\hfill \\ & \approx O\left( {\sum\nolimits_{i = 1}^{L} {\left( {T\left( {\bar{n}\bar{d} + \bar{m}\bar{q}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)} } \right) \hfill \\ \end{aligned} $$

If we re-train the whole structure based on Algorithm 1 and suppose $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < T$ is assured, its computation complexity will become

$$ \begin{aligned} & O\left( \sum\nolimits_{i = 1}^{L} \left( KTD\left( {n_{i} d_{i} + \bar{n}\bar{d}} \right) + T\left( {m_{i} q_{i} + \bar{m}\bar{q}} \right)p_{i} \right.\right.\\ & \quad \left.\left. + T\left( {n_{i} d_{i} + m_{i} q_{i} + \bar{n}\bar{d} + \bar{m}\bar{q}} \right)^{2} \right) \right) \end{aligned} $$

Obviously, increment of feature nodes can save much training time.

Increment of input data

In this case, D&BLS is expanded by adding $\bar{T}$ input data $\{ \varvec{X}_{{\bar{T}}} ,\varvec{Y}_{{\bar{T}}} \} ,\varvec{X}_{{\bar{T}}} \in {\mathbb{R}}^{{\bar{T} \times D}} ,\varvec{Y}_{{\bar{T}}} \in {\mathbb{R}}^{{\bar{T} \times 1}}$. Suppose that $\{ \varvec{X}_{{T + \bar{T}}} ,\varvec{Y}_{{T + \bar{T}}} \}$ denotes the all input data after incremental operation. After the total $n_{i}$ groups of the additional feature nodes $\varvec{M}^{ex}$ with $d_{i}$ feature nodes are generated from $\varvec{X}_{{\bar{T}}}$, the total $m_{i}$ groups of the additional enhancement nodes $\varvec{E}^{ex}$ with $q_{i}$ enhancement nodes are generated from a portion of the additional feature nodes $\varvec{M}^{ex}$. After denoting $\varvec{U}^{ex} = \left[ {\varvec{M}^{ex} |\varvec{E}^{ex} } \right]$, the pseudoinverse of $\left( {\varvec{U}_{{n\,_{i} }}^{{m_{i} }} } \right)^{ex} = \left[ {\begin{array}{*{20}c} {\varvec{U}_{{n_{\,i} }}^{{m_{i} }} } \\ {\varvec{U}^{ex} } \\ \end{array} } \right]$ can be calculated by Eqs. (21) and (22). As a result, the output weight vector can be obtained by $\left( {\varvec{W}_{{n_{i} }}^{{m_{i} }} } \right)_{i}^{ez} { = }\left( {\left( {\varvec{U}_{{n\,_{i} }}^{{m_{i} }} } \right)^{ex} } \right)^{\dag } \varvec{Y}_{i}$ and the output of this sub-system becomes $\varvec{Y}_{\varvec{i}}^{\prime } { = }\left( {\varvec{U}_{{n\,_{i} }}^{{m_{i} }} } \right)^{ex} \left( {\varvec{W}_{{n_{i} }}^{{m_{i} }} } \right)_{i}^{ex}$. The incremental algorithm for this case is summarized in Algorithm 4.

The computational complexity of Algorithm 4 can also be analyzed in terms of L sub-systems. The computational complexity of each sub-system in this incremental case mainly contains three stages: the generation of the additional feature nodes and the additional enhancement nodes and the calculation of pseudoinverse. According to Algorithm 4, the computational complexity from step 4 to step 7 about the generation of feature nodes takes $O\left( {K\bar{T}Dn_{i} d_{i} } \right)$. Step 8 requires $O\left( {\bar{T}n_{i} d_{i} } \right)$. Then the computational burden from step 9 to step 13 about the generation of enhancement nodes is $O\left( {\bar{T}m_{i} q_{i} p_{i} } \right)$. Step 14 and 15 require $O\left( {2\bar{T}m_{i} q_{i} } \right) \approx O\left( {\bar{T}m_{i} q_{i} } \right)$, then step 16 requires $O\left( {\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)$. Suppose $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < \bar{T}$ and $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < T$ are assured, the calculation of $\left( {\left( {U_{{n\,_{i} }}^{{m_{i} }} } \right)^{ex} } \right)^{ + }$ in step 17 requires

$$ \begin{aligned} & O\left( \bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} + 2\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)\right.\\ & \quad \left. + T\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + 3T\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \right)\\ & \qquad \approx O\left( {T\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) \end{aligned} $$

What is more, steps 18 and 19 require $O\left( {2\left( {T + \bar{T}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right) \approx O\left( {\left( {T + \bar{T}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)$. Suppose $\bar{T} < T$ and $KD < T$ are assure, with the total L iterations, the total computational complexity of Algorithm 4 can be described as

$$ \begin{aligned} & O\left( \sum\nolimits_{i = 1}^{L} \left( K\bar{T}Dn_{i} d_{i} + 2\bar{T}n_{i} d_{i} + \bar{T}m_{i} q_{i} p_{i} + 2\bar{T}m_{i} q_{i}\right.\right.\\ & \qquad \left.\left. + T\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right) + \left( {T + \bar{T}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right) \right) \right) \\ & \quad \approx O\left( {\sum\nolimits_{i = 1}^{L} {\left( {T\bar{T}\left( {n_{i} d_{i} + m_{i} q_{i} } \right)} \right)} } \right) \\ \end{aligned} $$

If we re-train the whole structure based on Algorithm 1 and suppose $\left( {n_{i} d_{i} + m_{i} q_{i} } \right) < T + \bar{T}$ is assured, its computation complexity will become

$$ O\left( {\sum\nolimits_{i = 1}^{L} {\left( {K\left( {T + \bar{T}} \right)Dn_{i} d_{i} + \left( {T + \bar{T}} \right)m_{i} q_{i} p_{i} + \left( {T + \bar{T}} \right)\left( {n_{i} d_{i} + m_{i} q_{i} } \right)^{2} } \right)} } \right) $$

Obviously, increment of input data can save training time.

Finally, let us state how to set appropriate parameters in the above algorithms. As pointed out in the above, the total number of layers generally take a small integer (i.e., from 2 to 4). Besides, according to our extensive experiments, the weight matrix $\varvec{W}$ and the bias matrix $\varvec{\beta}$ involved in hidden nodes generally are drawn from standard normal distributions, respectively. Since the number $p_{i}$ of selected feature nodes should generally be much less than the total of feature nodes, it is set to be at most 75% of the total number of feature nodes. As for the regularization parameters $\lambda$ and $r$ involved in sparse autoencoder, they are simply set to be 0.001 and 1, respectively. The regularization parameter $\lambda$ involved in ridge regression is simply set to be 2⁻³⁰. In our experiments, the number of additional hidden nodes for each sub-system is simply taken to be 10 and the number of additional input data is simply set to be 3000.

Experimental results

In this section, to evaluate the performance of D&BLS, we organize four groups of experiments. The first group about classification is carried out on both five image datasets and 1 UCI [24] classification datasets, the second about regression on ten UCI regression datasets, the third about incremental learning on popular datasets MNIST [25], and the last about running time is compared between BLS and D&BLS. All the experiments are carried out under a computer that equips Intel-i3 3.40 GHz CPU, 4 GB memory. The experiments of LSSVM are carried out in MATLAB environment and the other experiments are carried out in Python environment. Before the experiments, all the datasets are divided into training and testing set.

The comparative methods include BLS [7], support vector machine (SVM) [26], least squared SVM (LSSVM) [27]. Because the regularization parameter $C$ and the kernel parameter $\gamma$ of SVM play an essential role in performance, they need to be chosen appropriately for a fair comparison. In our experiments, we determine them by taking a grid search from $\{ 2^{ - 24} ,2^{ - 23} , \ldots ,2^{24} ,2^{25} \}$ for the parameters $\left( {C,\gamma } \right)$ in SVM, while the parameters $\left( {C,\gamma } \right)$ of LSSVM are decided using LS-SVMlab Toolbox.

In our experiments, the original codes of BLS in [7] (classification version) and in [16] (regression version) are taken. As for SVM, its classification version SVC and its regression version SVR are taken from Scikit-learn [29] package.

As for BLS and D&BLS, to make a fair comparison between them, the weight matrix $\varvec{W}$ and the bias matrix $\varvec{\beta}$ are drawn from standard normal distributions and the tansig functions are taken as the activation functions of enhancement nodes. All other parameters involved in BLS and D&BLS keep the same and their settings have been stated in the last section.

Classification

This group of experiments consists of two parts. The first part is to observe the performance of D&BLS and the comparative methods on image data, while the second part deals with the 1 UCI non-image classification datasets. Five popular image datasets are MNIST [25] and USPS [29] about handwritten digits, COIL20 [30] and COIL100 [31] about 3-D objects, and extended YaleB [32] about human faces. A UCI classification dataset is isolet [33] about spoken letter recognition. To obtain good performance, we use “one vs. one” strategy for LSSVM when faced with multi-class problems and thus omit its parameters setting here.

According to the accuracies obtained by BLS on the adopted datasets, we determine D&BLS by the trial and error strategy. This involves the number of lightweight BLS sub-systems in D&BLS. To make our comparison fair, here we report average results (i.e., mean and standard deviations) for ten trials on each dataset.

MNIST

MNIST contains 70,000 handwritten digits of ten classes. Every digit is represented by an image with the size of 28 × 28 gray-scaled pixels. 60,000 out of all the handwritten digits are partitioned into the training dataset and the remaining 10,000 handwritten digits into the testing dataset. Here a subset of MNIST is chosen for our experiment with the first 10,000 training images and all the 10,000 testing images. In our experiments, we perform a grid search for the optimal parameters of BLS, including the size of feature node groups, the number of feature node groups and the number of enhancement nodes from [10, 30] × [10, 20] × [100, 5000] with the steps being 1, 1 and 100 due to the large searching range of enhancement nodes. The parameters setting can be checked in Table 1 and the classification accuracies of all the adopted methods are given in Table 2.

Table 1 Parameters setting of the adopted methods on the classification datasets

Table 2 Accuracies (%) of the adopted methods on the classification datasets

Obviously, D&BLS reaches better accuracy (97.37%) than that (97.19%) of BLS, while D&BLS only needs 3490 enhancement nodes, which is about 72.71% number of enhancement nodes (i.e., 4800 nodes) in BLS. In addition, D&BLS exhibits its superiority of classification performance over other comparative methods: SVM (94.32%) and LSSVM (91.40%).

USPS

US Postal Service (USPS) handwritten digits recognition corpus is another well know dataset, which contains 9298 gray images of size 16 × 16 pixels, with ten class digit 0–9. We randomly select 7500 images for training and the rest 1798 images for testing. In our experiment, the search range for BLS is [10, 30] × [10, 20] × [100, 5000] with the steps being 1, 1 and 100. The parameters setting is shown in Table 1 and the classification accuracies are listed in Table 2.

We can see that D&BLS exceeds the accuracy of BLS (i.e. 95.90% vs. 95.77%) with much less enhancement nodes (i.e., only 1877 nodes), which is about half the number of enhancement nodes (i.e., 3700 nodes) in BLS. Compared to SVM (93.44%) and LSSVM (95.27%), D&BLS also achieves the best performance.

COIL20

COIL20 contains 1440 gray images of 20 different 3-D objects with 128 × 128 pixels. The images of each object were taken 5 degrees apart as the object is rotated on a turntable and each object has 72 images. There are 36 images of each object for training and the remaining 720 images for testing. In our experiment, the search range for BLS is [10, 30] × [10, 20] × [100, 3000] with the steps being 1, 1 and 100. The parameters setting are given in Table 1 and the classification accuracies can be checked in Table 2.

In contrast to BLS, D&BLS has higher accuracy (99.78%) with much less enhancement nodes (i.e., only 1357 nodes), which is about 61.68% of the number of enhancement nodes (i.e., 2200 nodes) in BLS. D&BLS also achieves best performance compared to SVM (83.19%) and LSSVM (89.86%).

COIL100

COIL100 contains 7200 color images of 100 different 3-D objects with 128 × 128 pixels. The images of each object were taken 5 degrees apart as the object is rotated on a turntable and each object has 72 images. In this experiment, each image was resized into 32 × 32 and converted into gray image. We randomly select 5000 images for training and the rest 2200 images for testing.

In our experiment, the search range for BLS is [10, 30] × [10, 20] × [100, 5000] with the steps being 1, 1 and 100. The parameters setting are listed in Table 1 and the classification accuracies are shown in Table 2.

As we can see, D&BLS exceeds the accuracies of all the adopted methods with much less enhancement nodes (i.e., only 2710 nodes), which is about 61.59% of the number of enhancement nodes in BLS.

Extended YaleB

Extended YaleB face consists of 2414 cropped images of 38 objects with the size of 32 × 32 pixels. The images contain large variations in terms of illumination conditions and expressions for each subject. There are 30 images of each person for training and the remaining 1274 images for testing. Following [16], BLS contains 60 × 30 feature nodes and 1 × 6000 enhancement nodes. The parameters setting of other models are shown in Table 1 and the classification accuracies of all the adopted methods are listed in Table 2.

From Tables 1 and 2, D&BLS matches the accuracy (97.92%) of BLS with only 232 enhancement nodes, which is about 3.87% of the number of enhancement nodes in BLS. D&BLS also exceeds the accuracy of SVM (89.32%) and LSSVM (89.95%).

UCI

To verify the effectiveness of D&BLS for non-image data, we choose the isolet dataset here, which contains 1560 spoken letter recognition samples of 26 classes with 617 features in each sample. We randomly choose 1092 samples for training and the rest 468 samples for testing. In our experiment, the search range for BLS is [10, 30] × [10, 20] × [100, 3000] with the steps being 1, 1 and 100. The parameter details are shown in Table 1 and the classification performance are given in Table 2.

D&BLS indeed gets the best result (95.49%) among all the adopted methods and only needs about 76% of the number of enhancement nodes in BLS, which actually demonstrates the effectiveness of D&BLS for non-image samples.

Regression

In this subsection, we attempt to verify that D&BLS can achieve smaller regression errors than BLS when they both have comparable number of enhancement nodes. We take ten UCI regression datasets, whose details are listed in Table 3

Table 3 Details of the UCI regression datasets

Following [16], the same parameters setting of BLS are taken by a grid search from [1, 10] × [1, 30] × [1, 200] with step being 1 and the best experimental results about the root-mean-square errors (RMSE) from ten trials are taken to make a fair comparison. The detailed parameter settings and the experimental results by SVM, LSSVM, BLS and D&BLS on these datasets are given in Tables 4 and 5, respectively.

Table 4 Parameters setting of the adopted methods (1) on the UCI regression datasets and (2) on the UCI datasets for regression

Table 5 RMSEs of the adopted methods on the UCI datasets for regression

Clearly, D&BLS performs comparably to BLS on the datasets Bodyfat and Weather Izmir and better than BLS with comparable number of enhancement nodes in the remaining eight datasets. It can be concluded that with almost the same sizes of the architectures, D&BLS attractively outperforms BLS in the sense of testing accuracy on these datasets, which actually hints that D&BLS may take smaller sizes of the architectures to achieve comparable regression performance to BLS. Compared to SVM and LSSVM, the D&BLS also achieves the best performance.

Incremental algorithms

In this section, we divide it into three cases to observe the average performances (with their standard deviations) of incremental learning algorithms of D&BLS for ten runs on the dataset MNIST: (1) increment of enhancement nodes (corresponding to Algorithm 2); (2) feature nodes (corresponding to Algorithm 3); and (3) input data (corresponding to Algorithm 4).

Our experiments begin with a three-layer D&BLS, whose whole structure is (696,275) consisting of (30 × 8, 10, 1 × 100)–(29 × 8, 10, 1 × 95)–(28 × 8, 10, 1 × 80) on the MNIST dataset where the first 10,000 samples from the total 60,000 training samples are taken as the initial training samples, and the same 10,000 testing samples are still kept. The parameter $p_{i}$ of the additional enhancement nodes is also set to be 10. Besides, the testing accuracy, training time and testing time of D&BLS with one-shot construction are also provided to highlight the advantage of the proposed three incremental algorithms.

Increment of enhancement nodes

Two groups of experiments are arranged to observe Algorithm 2 for this case. The first group considers the total 4 times of incremental operations. That is, it takes the addition of ten enhancement nodes in an incremental way. The second group keeps the same except 12 rather 10 enhancement nodes. Thus, the whole network with three sub-systems has 30 or 36 more enhancement nodes after enhancement nodes are increased in a step-by-step way. The results are given in Table 6.

Table 6 Experimental results of the MNIST dataset using increment of enhancement nodes

As we can see, the testing accuracy continues to be improved as the additional enhancement nodes are inserted into D&BLS in an incremental way and finally reaches the performance comparable to that of D&BLS with the one-shot construction (see the last row in Table 6). Obviously, the training time of Algorithm 2 is much less than that of D&BLS with the one-shot construction, e.g., 1.8399 s vs. 5.5217 s.

Increment of feature nodes

Two groups of experiments are arranged to observe Algorithm 3 for this case. The first group considers the total 4 times of incremental operations. That is, it takes the addition of ten feature nodes and ten corresponding enhancement nodes in an incremental way. The second group keeps the same except 12 rather 10 feature nodes and enhancement nodes. All the results can be checked in Table 7.

Table 7 Experimental results of the MNIST dataset using increment of feature nodes

It can be seen that the testing accuracy continues to go up as the additional feature nodes are inserted into D&BLS in an incremental way and finally reaches the performance comparable to that of D&BLS with the one-shot construction (see the last row in Table 7). Obviously, the training time of Algorithm 3 is much less than that of D&BLS with the one-shot construction, e.g., 3.3657 s vs. 6.4858 s.

Increment of input data

Two groups of experiments are arranged to observe Algorithm 4 for this case. The first group considers the total 4 times of incremental operations. That is, it takes the addition of 3000 training samples each time in an incremental way from all the remaining training samples. The second group keeps the same except 8000 rather than 3000 training samples. The incremental results are shown in Table 8.

Table 8 Experimental results of the MNIST dataset using increment of input data

It can be observed that the testing accuracy has a slight decline (e.g., from 94.18 to 93.54%) when the additional input data are fed in the first time into D&BLS, while the testing accuracy begins to go steadily up as more input data are fed in an incremental way and finally reaches the performance comparable to that of D&BLS with the one-shot construction (see the last row in Table 8). Obviously, the training time of Algorithm 4 is much less than that of D&BLS with the one-shot construction, e.g., 3.6203 s vs. 10.4513 s.

Running time comparison

In this subsection, we will show D&BLS’s another attractive property—it only needs much less running time (i.e., training time and testing time) than BLS when they both share the same sizes (i.e., feature nodes and enhancement nodes). The COIL-100 and the USPS datasets are taken for experiments. For a fair comparison, here we report average results and standard deviations for ten trials on each dataset.

D&BLS takes a three-layer structure and each sub-system keeps the same parameters setting, especially the number of selected feature nodes is 1. In other words, if a BLS has 30 × 10 feature nodes and 1 × 2100 enhancement nodes, each sub-system in the corresponding D&BLS will contain 10 × 10 feature nodes, 1 selected feature node, and 1 × 700 enhancement nodes. The obtained experimental results are given in Table 9.

Table 9 Running time of BLS and D&BLS (1) on the COIL-100 dataset (s) and (2) on the USPS dataset (s)

According to Table 9, D&BLS indeed needs much less running time than BLS. What is more, D&BLS runs much more quickly than BLS with the increasing number of enhancement nodes. This tendency becomes considerably surprising in the case of 3600 enhancement nodes for the USPS dataset. That is, BLS occupies 27.2773 s while D&BLS occupies only 9.8075 s for the USPS dataset.

Conclusion

While the recently developed broad learning system BLS has been exhibiting its promising performance without the need of deep structure, it often requires a huge heap of hidden nodes, which may perhaps inevitably cause both overwhelming storage requirement and overfitting phenomenon. In this paper, D&BLS is proposed to synthesize both deep and broad learning so as to guarantee enhance performance, downsize the structure and reduce the running time of the general BLS. D&BLS consists of several lightweight BLS sub-systems. D&BLS has its structure novelty in its joint stacking way of feature augmentation and residuals boosting. The whole learning algorithm and three incremental algorithms of D&BLS are proposed and then verified by our experiments about image datasets and UCI datasets.

Since the parameter settings of each sub-system in D&BLS are given only by the trial and error strategy, a deeper D&BLS sometimes cannot assure better performance than a shallower D&BLS. As a result, how to determine the structure of D&BLS in a moderate time and how to design a deeper D&BLS with desirable ability for practical application scenarios are our research works in near future.