Circuit design and simulation for the fractional-order chaotic behavior in a new dynamical system

Abstract

This paper presents a novel 3D fractional-ordered chaotic system. The dynamical behavior of this system is investigated. An analog circuit diagram is designed for generating strange attractors. Results have been observed using Electronic Workbench Multisim software, they demonstrate that the fractional-ordered nonlinear chaotic attractors exist in this new system. Moreover, they agree very well with those obtained by numerical simulations.

Introduction

Recently, the study of fractional calculus have become a focus of interest [1,2,3,4,5,6,7,8,9,10,11,12]. Because the applications of fractional calculus were found in many scientific fields, such as rheology, diffusive transport, electrical networks, electromagnetic theory, quantum evolution of complex systems, colored noise, etc. Compared with the classical well-known models, it was found that fractional derivatives provide a better tool for modeling memory and heredity properties of various phenomena. Various types of fractional derivatives and their applications can be found in the literature, for instance, the Caputo derivative [13], the recently introduced fractional derivative without singular kernel (Caputo–Fabrizio derivative) [14] and the Atangana–Baleanu derivative which is based upon the well-known generalized Mittag–Leffler function [15, 16].

Besides, many scientists and engineers have been attracted to the theory of chaos since the discovery of the Lorenz attractor [17]. It was found that fractional-order chaos has useful application in many field of science like engineering, physics, mathematical biology, psychological, and life sciences [18,19,20,21,22,23]. On the other hand, chaotic signal is a key issue for future applications of chaos-based information systems, and can be applied to secure communication and control processing, e.g., the transmitted signals can be masked by chaotic signals in secure communications and the image messages can be covered by chaotic signals in image encryption. In addition, the circuit implementation can verify the chaotic characteristics of the chaotic systems physically, provide support for the application of chaos, and promote their technological application in the future. Therefore, the circuit implementation of the chaotic systems has also attracted more and more attention for engineering applications. Especially, for those fractional-order attractors, the circuit implementations for them are more important [24,25,26,27,28,29,30].

In this work, we construct a new 3D fractional-order chaotic system. Through studying its dynamical behavior by numerical simulation based on the improved Adams–Bashforth–Moulton method [31] and designs chain ship fractional-order chaotic circuit based on frequency-domain approximation method [28]. Besides, we realize the fractional-order chaotic system through Multisim software 13.0 circuit simulation platform.

Preliminaries

In what follows, Caputo derivatives are considered, taking the advantage that this allows for traditional initial and boundary conditions to be included in the formulation of the considered problem.

Definition 1

A real function $f(x),\,x>0,$ is said to be in the space $C_{\mu },\,\mu \in {\mathbb {R}}$ if there exits a real number $\lambda > \mu$, such that $f(x)=x^{\lambda }g(x)$, where $g(x)\in C[0,\infty )$ and it is said to be in the space $C^{m}_{\mu }$ if and only if $f^{(m)}\in C_{\mu }$ for $m\in \mathbb {N}$.

Definition 2

The Riemann–Liouville fractional integral operator of order $\alpha$ of a real function $f(x)\in C_{\mu },\ \mu \ge -1$, is defined as

$$\begin{aligned}&J^{\alpha }f(x)= \frac{1}{\varGamma (\alpha )}\int ^{x}_{0}(x-t)^{\alpha -1}f(t)\mathrm{d}t,\nonumber \\&\alpha> 0, x>0 \quad \mathrm{and} \quad J^{0}f(x)=f(x). \end{aligned}$$

(1)

The operators $J^{\alpha }$ has some properties, for $\alpha ,\beta \ge 0$ and $\xi \ge -1$:

• $J^{\alpha }J^{\beta }f(x)=J^{\alpha +\beta }f(x),$

• $J^{\alpha }J^{\beta }f(x)=J^{\beta }J^{\alpha }f(x),$

• $J^{\alpha }x^{\xi }= \frac{\varGamma (\xi +1)}{\varGamma (\alpha + \xi +1)}x^{\alpha + \xi }$.

Definition 3

The Caputo fractional derivative $D^{\alpha }$ of a function f(x) of any real number $\alpha$ such that $m-1<\alpha \le m$, $m\in \mathbb {N}$, for $x > 0$ and $f \in C_{-1}^{m}$ in the terms of $J^{\alpha }$ is

$$\begin{aligned} D^{\alpha }f(x)= & {} J^{m-\alpha } D^{m}f(x)\nonumber \\= & {} \frac{1}{\varGamma (m-\alpha )}\int ^{x}_{0}(x-t)^{m-\alpha -1}f^{(m)}(t)\mathrm{d}t \end{aligned}$$

(2)

and has the following properties for $m-1<\alpha \le m$, $m\in \mathbb {N}$, $\mu \ge -1$ and $f \in C_{\mu }^{m}:$

• $D^{\alpha }J^{\alpha } f(x)= f(x),$

• $J^{\alpha }D^{\alpha } f(x)= f(x)-\displaystyle \sum \limits _{k=0}^{m-1} f^{(k)}(0^{+})\frac{x^{k}}{k!},$ for $x > 0,$

Stability criterion

To investigate the dynamics and to control the chaotic behavior of a fractional-order dynamic system:

$$\begin{aligned} \displaystyle D^\alpha _t x(t) = f(x(t)), \end{aligned}$$

(3)

we need the following indispensable stability theorem (Fig. 1).

Theorem 1

(See [32, 33]) For a given commensurate fractional-order system (3), the equilibria can be obtained by calculating $f(x) = 0$. These equilibrium points are locally asymptotically stable if all the eigenvalues $\lambda$ of the Jacobian matrix $\displaystyle J = \frac{\partial f}{\partial x}$ at the equilibrium points satisfy

$$\begin{aligned} \displaystyle |\mathrm{arg}(\lambda )| > \frac{\pi }{2} \alpha . \end{aligned}$$

(4)

Fig. 1

Stability region of the fractional-order system (3)

Circuit implementation and numerical simulations

Adams–Bashforth (PECE) algorithm

We recall here the improved version of Adams–Bashforth–Moulton algorithm [31, 34] for the fractional-order systems. Consider the fractional-order initial value problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle D_t^{\alpha }{x}= f(x(t)) \quad 0\le t \le T,\\ \\ \displaystyle x^{(k)}(0) = x_0^{(k)}, \quad k= 0,1,\ldots ,m-1. \end{array}\right. \end{aligned}$$

(5)

It is equivalent to the Volterra integral equation:

$$\begin{aligned} \displaystyle {x(t)}= \sum _{k=0}^{[\alpha ]-1} x_0^{(k)}\frac{t^k}{k!}+\frac{1}{\varGamma (\alpha )}\int _{0}^{t}(t-s)^{\alpha -1}f(s,x(s)) \mathrm{d}s. \end{aligned}$$

(6)

Diethelm et al. have given a predictor–corrector scheme (see [34]), based on the Adams–Bashforth–Moulton algorithm to integrate Eq. (6). By applying this scheme to the fractional-order system (5), and setting

$$\begin{aligned} \displaystyle h = \frac{T}{N}, \quad t_n = nh, \quad n=0,1,\ldots ,N. \end{aligned}$$

Equation (6) can be discretized as follows:

$$\begin{aligned} \displaystyle {x_h(t_{n+1})}= & {} \sum _{k=0}^{[\alpha ]-1} x_0^{(k)}\frac{t^k}{k!} + \frac{h^\alpha }{\varGamma (\alpha + 2)}f(t_{n+1},x_h^p(t_{n+1})) \nonumber \\&+ \frac{h^\alpha }{\varGamma (\alpha + 2)} \sum _{j=0}^{n} a_{j, n+1}f(t_{j},x_h(t_{j})), \end{aligned}$$

(7)

where

Fig. 2

Chain ship unit of: a $\displaystyle \frac{1}{s^{0.98}}$ and b $\displaystyle \frac{1}{s^{0.9}}$

Table 1 Equilibrium points and corresponding eigenvalues

Fig. 3

Chaotic attractors of the fractional-order system (16) obtained by numerical simulations: a $x-y$, b $y-z$, c $x-z$, for $\alpha = 0.98$

Fig. 4

Asymptotically stable orbits of the fractional-order system (16) by numerical simulations: a $x-y$, b $x-z$, c $y-z$, for $\alpha = 0.9$

$$\begin{aligned} a_{j, n + 1} = \left\{ \begin{array}{ll} \displaystyle n^{\alpha +1} - (n-\alpha )(n+1)^\alpha , \, j = 0,\\ \\ \displaystyle (n - j + 2)^{\alpha +1} + (n-j)^{\alpha +1} - 2(n- j + 1)^{\alpha +1}, \quad 1\le j \le n\\ \\ \displaystyle 1, \quad j=n+1, \end{array}\right. \end{aligned}$$

(8)

and the predictor is given by

$$\begin{aligned} \displaystyle x_h^p(t_{n+1}) = \sum _{k=0}^{[\alpha ]-1} x_0^{(k)}\frac{t^k}{k!}+\frac{1}{\varGamma (\alpha )} \sum _{j=0}^{n} b_{j, n+1}f(t_{j},x_h(t_{j})), \end{aligned}$$

(9)

where $\displaystyle b_{j,n+1} = \frac{h^\alpha }{\alpha }((n+1) - j)^\alpha - (n-j)^\alpha .$

Fig. 5

Time series of the fractional-order system (16) by numerical simulations: a x, b y, c z for $\alpha = 0.9$

The error estimate of the above scheme is

$$\begin{aligned} \displaystyle {\max }_{j=0,1,\ldots ,N}\left\{ |x(t_j)-x_h(t_j)|\right\} = O(h^p), \end{aligned}$$

in which $p = \mathrm{min}(2, 1+\alpha )$.

The fractional frequency-domain approximation

The standard definition of fractional differintegral does not allow the direct implementation of the fractional operators in time-domain simulations. To study such systems, it is necessary to develop approximations to the fractional operators using the standard integer order operators. According to circuit theory, the approximation formulation of $\alpha$, from 0.1 to 0.9, in reference [30], bode plot approximation chart, can be realized by the complex-frequency domain of the chain ship equivalent circuit. When $\alpha = 0.98$, it can be worked out that the approximation formula of $\displaystyle \frac{1}{s^{0.98}}$ is

$$\begin{aligned} \displaystyle \frac{1}{s^{0.98}} = \frac{1.2974(s+1125)}{(s+1423)(s+0.01125)}. \end{aligned}$$

(10)

In formula (10), $s= j\omega$, its complex frequency and the chain ship circuit unit is described in Fig. 2a. The transfer function between A and B can be obtained as follows:

$$\begin{aligned} \displaystyle H_{0.98}(s)= & {} \frac{R_1}{sR_1C_1+1}+\frac{R_2}{sR_2C_2+1}\nonumber \\= & {} \frac{1}{C_0}\frac{\left( \frac{C_0}{C_1}+\frac{C_0}{C_2} \right) \left[ s+ \frac{\frac{1}{R_1}+\frac{1}{R_2}}{C_1+C_2}\right] }{\left( s+\frac{1}{R_1C_1}\right) \left( s+\frac{1}{R_2C_2}\right) }. \end{aligned}$$

(11)

Taking $C_0 = 1\nu \text{ F }$. Since $\displaystyle H(s)C_0 =\frac{1}{s^{0.98}}$, we can reach

$$\begin{aligned} \displaystyle R_1= & {} 91.1873\,\text{ M }\varOmega , \quad R_2= 190.933\,\omega ,\nonumber \\ C_1= & {} 975.32\,\mathrm{n}\text{ F },\quad \text{ and } \quad C_2= 3.6806\,\upmu \text{ F }. \end{aligned}$$

(12)

Similarly, for $\alpha = 0.9$, we can reach that the approximation formula of $\displaystyle \frac{1}{s^{0.9}}$ is

$$\begin{aligned} \displaystyle \frac{1}{s^{0.9}} = \frac{2.2675(s+1.292)(s+215.4)}{(s+0.01292)(s+2.154)(s+359.4)}. \end{aligned}$$

(13)

Fig. 6

Circuit diagram for the realization of the fractional-order chaotic system (16) for $\alpha = 0.98$

Fig. 7

Circuit diagram for the realization of the fractional-order chaotic system (16) for $\alpha = 0.9$

Fig. 8

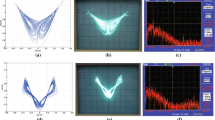
Chaotic attractors of the fractional-order system (16) observed by the oscilloscope 1V/Div: a $x-y$, b $y-z$, c $x-z$ with $\alpha = 0.98$

Fig. 9

Circuit simulation asymptotically stable orbits of the fractional-order system (16) observed by the oscilloscope 1V/Div: a $x-y$, b $x-z$, c $y-z$, for $\alpha = 0.9$

The chain ship circuit unit for this case is shown in Fig. 2b. The transfer function between A and B is

$$\begin{aligned} \displaystyle H_{0.9}(s) = \frac{\frac{1}{C_1}}{s+\frac{1}{R_1C_1}}+\frac{\frac{1}{C_2}}{s+\frac{1}{R_2C_2}}+ \frac{\frac{1}{C_3}}{s+\frac{1}{R_3C_3}}, \end{aligned}$$

(14)

we can reach

$$\begin{aligned} \displaystyle R_1= & {} 62.84\, \text{ M }\varOmega , \,\,R_2= 250\,\text{ k }\varOmega ,\,\, R_3= 2.5\,\text{ k }\varOmega ,\nonumber \\ C_1= & {} 1.23\,\upmu \text{ F },\,\, C_2= 1.83\,\upmu \text{ F },\,\, \text{ and } \,\, C_3= 1.1\,\upmu \text{ F }. \end{aligned}$$

(15)

Fig. 10

Time series of the fractional-order system (16) observed by the oscilloscope 1V/Div: a x, b y, c z, for $\alpha = 0.9$

A new 3D fractional-order chaotic system

We introduce the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle D^{\alpha } x = -2x - y^2, \\ \\ \displaystyle D^{\alpha } y = -4xz + 3y - {z}^{2},\\ \\ \displaystyle D^{\alpha } z = 4xy - 7z + yz, \end{array}\right. \end{aligned}$$

(16)

where the fractional-order $\alpha \in (0,1]$.

Dynamical analysis

To reveal dynamical properties of the nonlinear system (16), the equilibria should be considered at first

$$\begin{aligned} \left\{ \begin{array}{ll} \displaystyle -2x - y^2 = 0, \\ \\ \displaystyle -4xz + 3y - {z}^{2} = 0,\\ \\ \displaystyle 4xy - 7z + yz =0. \end{array}\right. \end{aligned}$$

(17)

The obtained equilibrium points from (17) and the corresponding eigenvalues are given in Table 1.

Hence, $E_{0}$ is unstable, and $E_1$ is a saddle point of index 2. With the aid of Theorem 1, a necessary condition for the fractional-order systems (16) to remain chaotic is keeping at least one eigenvalue $\lambda _i$ in the unstable region, i.e., $\displaystyle |\mathrm{arg}(\lambda _i)| > \frac{\alpha \pi }{2},$ It means that when $\alpha > 0.949318$ system (16) exhibits a chaotic behavior.

Circuit designs and numerical simulations

Applying the improved version of Adams–Bashforth–Moulton numerical algorithm described above with a step size $h=0.01$, system (16) can be discretized. It is found that chaos exists in the fractional-order system (16) when $\alpha > 0.94$ with the initial condition $(x_0,y_0,z_0) = (0.7,0.1,0)$. Figure 3a–c demonstrate that the systems has chaotic behavior for $\alpha =0.98$. On the other hand, when we take some values of $\alpha \le 0.94$, the fractional system (16) can display the periodic attractors, and asymptotically stable orbits (see Figs. 4, 5). Moreover, using Multisim software 13 to conduct simulations on the 3D fractional-order system (16), analog circuits are designed to realize the behavior of (16). Three state variables x, y and z are implemented by three channels, respectively. The implementations use resistors, capacitors, analog multipliers, and analog operational amplifiers, as shown in Figs. 6 and 7. A comparison of Figs. 3, 4, 5, 6, 7, and 8 (resp. 4–9 and 5–10) proves that analog circuit for system (16) is well coincident with numerical simulations. A conclusion can be made that the chaotic and non-chaotic behaviors exist in the fractional-order system (16), which verifies its existence and validity (Figs. 9, 10).

Conclusion

In this paper, we introduce a new three-dimensional fractional-order chaotic system and its existence and stability. By adopting a chain ship circuit form , the circuit experimental simulation of this fractional-order system is presented. The derived results between numerical simulation and circuit experimental simulation are in agreement with each other.