Abstract
This paper presents a hybrid decision support model aimed to help the travelers in selecting best route among multiple alternatives. The proposed model consists of three parts: (i) analytic hierarchy process (AHP) to determine relative importance of route attributes, (ii) axiomatic fuzzy set (AFS) theory for description of alternative routes, and (iii) technique for order preference by similarity to ideal solution (TOPSIS)-based final selection. TOPSIS methodology is used to determine ranking order of alternative routes in multicriteria decision situations. In TOPSIS, the alternative routes are described using AFS theory to normalize the decision matrix for consistent rating of routes over attributes. The main advantage of the developed model is that it copes inconsistency caused by both, different types of fuzzy numbers and normalization methods. An illustrative example of route selection is presented to better understand the hybrid methodological process. A comparative analysis with an established multicriteria decision-making technique shows the effectiveness and validity of the hybrid model for route selection.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The individuals need information to make decisions, particularly for complex decisions. Although the need for information applies to various types of decisions, it is very important when it comes to making decisions about travel. In real world, transit passengers choose the best path by considering not only the usual link-based shortest criteria but also other attributes, which could affect their path choice, such as avoid highway toll, good scenery along the path, and avoid difficult roads. It is important for travelers to be able to gather information before starting their trips to reach their destinations as safely and efficiently as possible. An efficient travel plan can increase the efficiency of trip, and reduce energy consumption, traffic congestion and air pollution, which are growing problems in many urban areas.
In a transport network, represented in the form of nodes (junctions) and links (roads), there could be multiple routes between a given source and destination. It might be difficult for travelers to determine the optimal route because of complex and multiple criteria evaluation process involved in route choice. The optimal route among multiple alternatives can be defined as the alternative with high performance on its associated attributes (selection criteria).
In general, the route selection is a multicriteria decision-making (MCDM) problem which involves both quantitative and qualitative aspects in decision-making process. The quantitative aspects are generally assessed by means of precise numerical values, but qualitative aspects are complex to assess with precise and exact values. It is not possible to model such imprecise situations using traditional MCDM approaches and requires combining these with fuzzy logic and other techniques in a hybrid manner to deal with the qualitative aspects and uncertainty in decision-making process. However, the fuzzy set theory deals with fuzzy numbers and the use of different shapes of fuzzy numbers leads to different results.
In practice, the decision matrix of a MCDM problem involves the criteria values having different dimensions or units of measurement. It may be difficult to select an appropriate method for normalizing the decision matrix (converting the criteria values into the dimensionless form) since a lot of normalization methods have been developed and the choice of different methods might change the final selection and ranking for a specific problem [13].
This paper focuses on the development of a hybrid decision support model aimed to help the travelers in selecting optimal route based on their personalized preferences or constraints. The integration of AFS theory, AHP and TOPSIS methodology pave a new way for evaluating routes under multicriteria decision environment. The main advantage of the developed hybrid model is that it processes the linguistic values using axiomatic fuzzy logic that overcomes the ambiguity in human decision-making process and copes the inconsistency caused by different types of fuzzy numbers. Moreover, the route selection model also copes the inconsistency due to choice of different normalization methods since it performs the normalization process under AHP calculation framework.
The remainder of this paper is organized as follows: “Mathematical background” section presents the mathematical background of AHP, AFS theory and TOPSIS methodology. “The proposed model” section outlines the development phases of hybrid methodology. “Illustrative example” section illustrates a hypothetical example of route selection to better understand the hybrid methodological process. In “Comparative analysis and model validation” section, a comparative analysis and model validation is reported. Sensitivity analysis is reported in “Sensitivity analysis” section and finally, “Conclusion” section of this paper.
Mathematical background
Analytic hierarchy process (AHP)
AHP, developed by Saaty [35], is a mathematical technique to model subjective decision-making processes based on multiple criteria in a hierarchical system. The ability to incorporate judgments on intangible qualitative criteria alongside tangible quantitative criteria makes AHP an ideal methodology to solve multiple criteria decision problems. The method of AHP is based on three principles: first, structure of the model; second, comparative judgment of alternatives and decision-making criteria; third, synthesis of the priorities [35,36,37]. In recent research, the AHP methodology has been applied to solve many complex multiple criteria decision problems [1, 23, 26, 30, 31, 39, 40, 43, 44]. The process starts with organizing the decision problem in a hierarchical structure of decision elements (criteria and alternatives). The decision maker is asked to subjectively evaluate each pair of criteria using Saaty’s [35] 9-point standardized scale. The pair-wise comparisons allow to compute a relative importance value (also known as weight) for each criterion using eigenvalue calculation framework.
The result of the pairwise comparison on n criteria can be summarized in an \((n \times n)\) algebraic matrix P, as shown:
where \(p_{ij}\) is the relative importance for i to j, \(p_{ji}=1/p_{ij}\) and \(p_{ij}=1\) if \(i=j\).
The process commences to normalize the pairwise comparison matrix and obtains the relative weights. The relative weights are given by right eigenvector (w) corresponding to the largest eigenvalue \((\lambda _\mathrm{max})\), as:
To ensure the consistency of subjective perception in pairwise comparisons, two indices, consistency index (CI) and consistency ratio (CR) are suggested. The CI of a matrix of order n is expressed as:
CR is calculated as the ratio of CI and random index (RI), as indicated:
where RI refers to a random consistency index derived from a randomly generated pairwise comparison matrix. The random indices with respect to different size matrices are shown in Table 1. If the calculated CR of a pairwise comparison is less than 0.1, the decision maker’s judgment is consistent and acceptable; otherwise, the evaluation procedure is considered inconsistent and needs revision to improve consistency.
Axiomatic fuzzy set (AFS) theory
The AFS theory, proposed by Liu [18], is a mathematical framework that aims to explore how fuzzy set theory and probability can be made to work in concert, so that the uncertainty of randomness and of imprecision can be treated in a unified and coherent manner. It provides an effective tool to convert the information in observed data into the membership functions and logic operations of fuzzy concepts. The recent research literature on AFS studies and their applications [14,15,16,17, 21, 22, 33, 42] reveals that it has become a flexible and powerful framework for representing human knowledge and studying intelligent systems in real-world applications.
The AFS theory is based on the AFS algebra—a kind of semantic methodology of fuzzy concepts, and AFS structure—a kind of mathematical description of data structures.
AFS algebra
Liu [18] defined a family of completely distributive lattices, referred to as AFS algebras and applied them to study the semantics of expressions and representations of fuzzy concepts. For a multicriteria decision problem, Let \(X=\{x_{1}, x_{2}, \ldots , x_{5}\}\) be a set of decision alternatives, \(M=\{m_{1}, m_{1}^{\prime }, \ldots , m_{5}, m_{5}^{\prime }\}\) be a set of fuzzy attributes on X, where \(m_{1}\): “attribute 1 is good”, \(m_{1}^{\prime }\): “attribute 1 is not good”, ..., \(m_{5}\): “attribute 5 is good”, \(m_{5}^{\prime }\): “attribute 5 is not good”. For each set of concepts \(A \subseteq M, \prod _{m \in A}m\) represents conjunction of the concepts in A; for instance, \(A=\{m_{1}, m_{5}\} \subseteq M, \prod _{m \in A}m=m_{1}m_{5}\) represents a new fuzzy concept “attribute 1 is good and attribute 5 is good”. \(\sum _{i \in I}(\prod _{m \in A_{i}})m\), a formal sum of \(\prod _{m \in A_{i}}m, A_{i} \subseteq M, i \in I\), is the disjunction of the conjunctions represented by \(\prod _{m \in A_{i}}m\)’s (i.e., the disjunctive normal form of a formula representing a concept). For instance, we may have \(m_{1}m_{5}+m_{2}m_{3}\) which translates as “attribute 1 is good and attribute 5 is good” or “attribute 2 is good and attribute 3 is good” (the “+” sign represents disjunction of concepts). For \(A_{i} \subseteq M\) and \(i \in I\), \(\sum _{i \in I}(\prod _{m \in A_{i}}m)\) has a well-defined meaning as discussed above. The semantics of the logic expressions such as “equivalent to”, “or”, and “and” as expressed by \(\sum _{i \in I}(\prod _{m \in A_{i}}m)\), \(A_{i} \subseteq M\), \(i \in I\) can be formulated in terms of the AFS algebra \((\mathrm{EM}^{*})\), defined as:
Definition 1
[18] Let M be a non-empty set. A binary relation R on \(EM^{*}\) is defined as follows: \(\forall \sum _{i \in I}(\prod _{m \in A_{i}}m)\) and \(\sum _{j \in J}(\prod _{m \in B_{j}}m) \in \mathrm{EM}^{*}\), \(\left[ \sum _{i \in I}(\prod _{m \in A_{i}}m)\, R \right. \)\(\left. \sum _{j \in J}(\prod _{m \in B_{j}}m)\right] \Leftrightarrow \) (i) \(\forall A_{i}(i \in I)\), \(\exists B_{h}(h \in J)\) such that \(B_{h} \subseteq A_{i}\), and (ii) \(\forall B_{j}(j \in J)\), \(\exists A_{k} (k \in I)\) such that \(A_{k} \subseteq B_{j}\). It is obvious that R is an equivalence relation and the quotient set \(\mathrm{EM}^{*}/R\) is denoted by EM. The notation \(\sum _{i \in I}(\prod _{m \in A_{i}}m)=\sum _{j \in J}(\prod _{m \in B_{j}}m)\) means that \(\sum _{i \in I}(\prod _{m \in A_{i}}m)\) and \(\sum _{j \in J}(\prod _{m \in B_{j}}m)\) are equivalent under relation R. Thus, the semantics they represent are equivalent.
Theorem 1
[18] Let M be a non-empty set, then \((EM, \wedge , \vee )\) forms a completely distributive lattice under the binary compositions \(\wedge \) and \(\vee \), defined as follows: \(\forall \sum _{i \in I}(\prod _{m \in A_{i}}m)\) and \(\sum _{j \in J}(\prod _{m \in B_{j}}m) \in EM^{*}\),
\(k \in I \sqcup J\) (the disjoint union of I and J, i.e., every element in I and every element in J are always regarded as different elements in \(I \sqcup J\)); \(C_{k}=A_{k}\) if \(k \in I\) and \(C_{k}=B_{k}\) if \(k \in J\). \((EM, \wedge , \vee )\) is called the EI (expending on M) algebra over M.
AFS structure
An AFS structure represented by a triple \((M,\tau ,X)\) gives rise to membership functions and fuzzy logic operations of the concepts in EM.
Definition 2
[18, 19] Let X and M be sets, \(2^{M}\) be the power set of M, and \(\tau : X \times X \rightarrow 2^{M}\). \((M,\tau ,X)\) is called an AFS structure if \(\tau \) satisfies the following axioms: (a). \(\forall (x_{1}, x_{2}) \in X \times X, \tau (x_{1}, x_{2}) \subseteq \tau (x_{1},x_{1})\), and (b). \(\forall (x_{1}, x_{2}), (x_{2}, x_{3}) \in X \times X, \tau (x_{1}, x_{2}) \bigcap \tau (x_{2}, x_{3}) \subseteq \tau (x_{1}, x_{3})\). X is called the universe of discourse, M is called the concept set and \(\tau \) is called the structure. In real-world applications, \(\tau \) can be constructed from a linearly ordered relation \(\ge _{m}\) as follows:
where \(x\ge _{m}y\) implies that the degree of x belonging to concept m is greater than or equal to y.
Definition 3
[19] Let X and M be sets, \((M,\tau ,X)\) be an AFS structure and \((M,\sigma ,m)\) be a measure space, where m is a finite and positive measure, \(m(X)\ne 0, A_{i}^{\tau }(x) \in \sigma , x \in X,i \in I\). For the fuzzy concept \(\eta =\sum _{i \in I}(\prod _{m \in A_{i}}m) \in EM\), the membership function of \(\eta \) is defined as follows:
where \(A_{i}^{\tau }(x)=\{y \in X \mid x \ge _{m}y\), for any \(m \in A_{i}\), \(A_{i}\subseteq M\}\). In other words, \(A_{i}^{\tau }\) is the set of all elements in X whose degrees of belonging to concept \(\prod _{m \in A_{i}}\) are less than or equal to that of x.
Technique for order preference by similarity to ideal solution (TOPSIS)
TOPSIS, developed by Hwang and Yoon [12], is one of the most popular multiple criteria decision analysis techniques for evaluating a finite set of decision alternatives in terms of a set of potentially conflicting criteria. The basic principle of TOPSIS is that the best alternative would be one that is nearest to the positive-ideal solution and farthest from the negative ideal solution [8]. The positive-ideal solution is a solution that maximizes the benefit criteria and minimizes the cost criteria, whereas the negative-ideal solution maximizes the cost criteria and minimizes the benefit criteria [45]. In literature, there have been a large number of studies using TOPSIS for the solution of complex decision-making problems ([2,3,4, 24, 25, 41, 48, 49]). For this present study, the procedure of TOPSIS can be expressed in following steps:
-
Step 1.
Establish a normalized decision matrix \([r_{ij}]_{m \times n}\), where \(r_{ij} (i=1, \ldots , m\) and \(; j=1, \ldots , n)\) represents the performance score of ith alternative over jth criterion. The values of \(r_{ij}\) are obtained by performing pairwise comparisons (using 9-point scale of AHP) between each pair of decision alternatives according to benefit and cost criterion in their best fuzzy descriptions. Since the performance scores \(r_{ij}\) are obtained using AHP, these are considered as normalized under AHP calculation framework and therefore there is no need to further normalize them explicitly.
-
Step 2.
Calculate the weighted normalized decision matrix \([v_{ij}]_{m \times n}\), where \(v_{ij} (i=1, \ldots , m; j=1, \ldots , n)\) is calculated as \(v_{ij}=r_{ij} \times w_{j}\), \(w_{j}\) is the weight of criterion \(m_{j}\) and \(\sum _{j=1}^{n}w_{j}=1\).
-
Step 3.
Determine the positive ideal solution and the negative ideal solution as follows:
$$\begin{aligned} A^+= & {} \{v_{1}^{+}, v_{2}^{+}, \ldots , v_{n}^{+}\}\nonumber \\= & {} \{(\max _{j}v_{ij}: i \in I), (\min _{j}v_{ij}: i \in J)\} \end{aligned}$$(9)$$\begin{aligned} A^-= & {} \{v_{1}^{-}, v_{2}^{-}, \ldots , v_{n}^{-}\}\nonumber \\= & {} \{(\min _{j}v_{ij}: i \in I), (\max _{j}v_{ij}: i \in J)\} \end{aligned}$$(10)where I is associated with benefit criteria, and J is associated with cost criteria.
-
Step 4.
Calculate the separation measures using the n-dimensional Euclidean distance. The separation of each alternative from the positive-ideal solution and negative ideal solution is given as:
$$\begin{aligned} D_{i}^{+}= & {} \sqrt{\sum _{j=1}^n(v_{ij}-v_{j}^{+})^{2}},\quad i=1, \ldots , m, j=1, \ldots , n\nonumber \\ \end{aligned}$$(11)$$\begin{aligned} D_{i}^{-}= & {} \sqrt{\sum _{j=1}^n(v_{ij}-v_{j}^{-})^{2}}, \quad i=1, \ldots , m, j=1, \ldots , n\nonumber \\ \end{aligned}$$(12) -
Step 5.
Calculate the relative closeness to the ideal solution. The relative closeness of the alternative \(A_{i}\) is defined as:
$$\begin{aligned} C_{i}=\dfrac{D_{i}^{-}}{D_{i}^{+}+D_{i}^{-}} \end{aligned}$$(13)where the value of \(C_{i}\) lies between 0 and 1.
-
Step 6.
Rank the alternatives according to the preference value and select the maximal ration in Step 5.
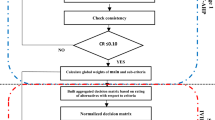
The proposed model
This section documents the methodological steps of a hybrid decision support model for ranking the decision alternatives under MCDA environment. The ranking process utilizes the axiomatic fuzzy logic into the MCDA techniques to model the fuzziness in human knowledge representation and reasoning process. It can evaluate and rank the decision alternatives based on qualitative and quantitative (mixed data sets) aspects. The proposed model is composed of AHP, AFS theory and TOPSIS methodology. It consists of five basic phases:
Phase 1: Identification of decision alternatives and decision criteria, and linguistic assessment of alternatives with respect to criteria.
-
(a)
Identify all possible decision alternatives \(a_{i}\) \((i=1,2,\ldots , m)\) and decision criteria \(c_{j}\) \((j=1,2,\ldots , n)\).
-
(b)
Establish a matrix \([l_{ij}]_{m \times n}\) for linguistic assessment of alternatives in terms of decision criteria. The matrix element \(l_{ij}\) represents assessment of ith alternative in terms of jth criterion using linguistic term.
-
(c)
Establish a hierarchy such that the objective is in the first level, criteria are in second level and alternatives are on the third level.
Phase 2: Computation of relative weights (\(w_{j}\)) of decision criteria.
-
(a)
Establish a matrix \([p_{ij}]_{n \times n}\) by performing pairwise comparisons (using 9-point scale) between each pair of criterion.
-
(b)
Compute the criteria weights \((w_{j}, j = 1, 2, \ldots , n )\) using AHP calculation framework.
Phase 3: Determine the best fuzzy descriptions (\(\zeta _{A_{i}}\)) of each decision alternative using AFS theory. Let \(A=(a_1, a_2, , a_5)\) be a set of decision alternatives and \(C=\{c_{1}, c_{1}^{\prime }, \ldots , c_{5}, c_{5}^{\prime }\}\) be a set of fuzzy criteria on A, then the fuzzy description for each alternative is determined by running following steps [20]:
-
(a)
Find the set of fuzzy criteria in C, defined as:
$$\begin{aligned} B_{a_{i}}^{\epsilon }=\left\{ c_{k} \in C | \mu _{c_{k}}(a_{i}) \ge \mu _{v}(a_{i})-\epsilon \right\} \end{aligned}$$(14)\(B_{a_{i}}^{\epsilon }\) is the set of fuzzy attributes in C such that the degrees of \(a_{i}\) belonging to them are larger than or equal to \(\mu _{v}(a_{i})-\epsilon \).
-
(b)
Find the set \(\bar{B}_{a_{i}}^{\epsilon }\), defined as follows:
$$\begin{aligned} \bar{B}_{a_{i}}^{\epsilon }=\left\{ \prod _{c \in X}c | \mu _{\prod _{c \in X}c}(a_{i}) \ge \mu _{v}(a_{i})-\epsilon , X \subseteq B_{A_{i}}^{\epsilon }\right\} \end{aligned}$$(15)\(\bar{B}_{a_{i}}^{\epsilon }\) is the set of the conjunctions of the attributes in \(B_{A_{i}}^{\epsilon }\) such that the degrees of \(a_i\) belonging to the conjunctions are larger than or equal to \(\mu _{v}(a_{i})-\epsilon \).
-
(c)
Select the best fuzzy description \(\zeta _{a_{i}} \in \bar{B}_{a_{i}}^{\epsilon }\) for the alternative \(a_{i}\), as follows:
$$\begin{aligned} \zeta _{a_{i}}=\mathrm{arg min}_{\zeta \in \bar{B}_{a_{i}}^{\epsilon }}\left\{ \sum _{a \in A, a \ne a_{i}}\mu _{\zeta }(a)\right\} \end{aligned}$$(16)Thus, \(a_i\) can be distinguished by \(\zeta _{a_{i}}\) from other objects in A at maximum extent.
Phase 4: Establish a normalized weighted decision matrix by rating each alternative \(a_i\) over each decision criterion \(c_j\).
-
(a)
Perform pairwise comparisons (using 9-point scale) between each pair of decision alternatives according to benefit and cost criterion in their best fuzzy descriptions (\(\zeta _{a_{i}}\)). For benefit criterion, the alternatives are compared based on \(c_j\) (criterion \(c_j\) is positive) and for cost criterion, the comparison process is carried out based on \(c_{j}^{\prime }\) (criterion \(c_j\) is negative).
-
(b)
Compute the performance scores of alternatives over decision criteria using AHP and establish a normalized decision matrix \([r_{ij}]_{m \times n}\), where each element \(r_{ij}\) represents the performance score of ith alternative over jth criteria. Since the performance scores \(r_{ij}\) are obtained by performing pairwise comparisons under AHP, these are considered as normalized under AHP calculation framework and therefore there is no need to further normalize them explicitly.
Phase 5: Establish a weighted normalized decision matrix \([v_{ij}]_{m \times n}\) by calculating \(v_{ij}=r_{ij} \times w_{j}\) and then process this matrix using TOPSIS approach, as described in “Technique for order preference by similarity to ideal solution (TOPSIS)” section, to obtain ranking.
Illustrative example
It is important for travelers to be able to gather route information in advance to make their trip safe and efficient. The route information before starting the trip can also help to reduce energy consumption, traffic congestion and air pollution, which are growing problems in many urban areas. The selection of optimal route among the multiple alternatives is very complex where the alternatives dominate each other in different qualitative and quantitative characteristics, and, therefore, requires an integrated approach to deal with complexities in multicriteria route selection. In following section, a real-life application of multicriteria route selection is conducted to illustrate the utilization of the proposed model. The presented application is based on the phases explained in previous section.
Phase 1: This phase begins with forming a team of experts responsible for identifying a set of route attributes important to determine best route. A list of route attributes was prepared based on expert’s opinion and extensive literature survey [7, 9, 10, 28, 29, 34, 38, 47, 50]. A calibration process was applied to narrow down the list to include only those attributes the travelers’ feel relevant to select best route. This process results in a set of six main attributes \((m_{1}, m_{2}, \ldots , m_{6})\), as shown in Table 2. From Table 2, it can be noticed that \(m_{1}\), \(m_{2}\), \(m_{3}\), \(m_{4}\), and \(m_{6}\) are negative (cost) attributes because their minimum values will be preferred and \(m_{5}\) is a positive attribute which is preferred to be maximized. Next, a set of five hypothetical alternative routes \((A_{1}, A_{2}, \ldots , A_{5})\) is considered between a source and destination. These routes together with their attribute values are presented in Table 3 and a three-level decision hierarchy is structured in Fig. 1, where the first level represents the goal “selection of best route”, second level represents route selection criteria and the alternative routes are on the third level of hierarchy.
The attributes’ values in Table 3 are measured in two different forms: quantitative and linguistic, which need to be uniform. The fusion method, given by Herrera and Martinez [11], is used for transforming the numeric values to linguistic values. The transformation process results in a linguistic judgment matrix \([a_{ij}]_{m \times n}\), as given in Table 4.
The linguistic ratings of different route attributes in Table 4 can be defined as: NA = Not at All, VL = Very Low, B.VL&L = Between Very Low and Low, L = Low, B.L&M = Between Low and Medium, M = Medium, B.M&H = Between Medium and High, H = High, B.H&VH = Between High and Very High, and VH = Very High.
Phase 2: In this phase, the prioritization procedure is applied to calculate the relative weights of route selection criteria. The traveler’s preferences for criteria are reflected in a pairwise comparison matrix \([p_{ij}]_{n \times n}\) (Table 5) by using Saaty’s [35] standardized comparison scale of nine levels. The criteria weights \(w_{j}\) are determined using AHP calculation framework with consistency ratio (CR = 0.047) representing consistency in comparison matrix.
Phase 3: This phase determines the best fuzzy description of each alternative route \((\zeta _{A_{i}})\) using axiomatic fuzzy logic. Let \(X=\{A_{1}, A_{2}, A_{3}, A_{4}, A_{5}\}\) be the set of five alternative routes, \(M=\{m_{1}, m_{1}^{\prime }, m_{2}, m_{2}^{\prime }, \ldots , m_{6}, m_{6}^{\prime }\}\) be the set of selection criteria on X, \(v=m_{1}+m_{1}^{\prime }+m_{2}+m_{2}^{\prime }+ \ldots m_{6}+m_{6}^{\prime }\), and \(\epsilon =0\). Using the linguistic judgment matrix given in Table 4 and the semantic meanings of the selection criteria in M, we have following linearly ordered relations:
The best fuzzy description of each route \((\zeta _{A_{i}})\) is obtained as follows:
Using Eq. (8),
Therefore, the best fuzzy description of route \(A_{1}\) is such that “distance, time and difficulty level are strong attributes”.
Similarly,
Phase 4: In this phase, a normalized decision matrix \([r_{ij}]_{m \times n}\) is established by performing pairwise comparisons between each pair of routes according to attributes in their fuzzy descriptions. In this comparison process, \(m_{5}\) is considered as positive (benefit) attribute while \(m_{1}\), \(m_{2}\), \(m_{3}\), \(m_{4}\), and \(m_{6}\) are considered as negative (cost) attributes.
For illustration, the comparison process of alternative routes over \(m_{1}^{\prime }\) (since \(m_{1}\): travel distance is negative attribute) is presented in Table 6 with explanation as: since \(m_{1}^{\prime }\) appears in \(\zeta _{A_{5}}\), hence \(A_{5}\) is extremely preferred over \(A_{1}\), \(A_{2}\), \(A_{3}\), and \(A_{4}\).
For \(m_{2}^{\prime }\), \(m_{3}^{\prime }\), \(m_{4}^{\prime }\), \(m_{5}\) and \(m_{6}^{\prime }\), the same process is repeated and a normalized decision matrix \([r_{ij}]_{m \times n}\) is obtained in Table 7.
Phase 5: In this last phase, a weighted normalized decision matrix \([v_{ij}]_{m \times n}\) (Table 8) is established by calculating \(v_{ij}=r_{ij}\times w_{j}\).
The fuzzy positive-ideal solution and fuzzy negative-ideal solution are calculated using the data as given in Table 8. The separation of each alternative route from fuzzy positive-ideal solution \((D_{i}^{+})\) and fuzzy negative-ideal solution \((D_{i}^{-})\) are determined in Table 9 which also summarizes the TOPSIS analysis. Based on \(C_{i}\) values as given in Table 9, the ranking of routes in descending order is \(A_{2}, A_{3}, A_{5}, A_{4}\) and \(A_{1}\), which indicates that \(A_{2}\) is the best route.
Comparative analysis and model validation
To test the validity of the developed model, it is applied to four existing case studies, with already known results, taken from [5, 6, 32, 46]. For these case studies, AFS theory is used to find the best fuzzy descriptions of decision alternatives and rankings are obtained using TOPSIS approach. The comparative analysis presented in Tables 10, 11, 12 and 13 reveals that the top ranking results obtained using developed model are same as with the existing studies. These results ensure the acceptability and validity of the developed model.
Sensitivity analysis
The solution to a decision problem (ranking of alternatives) may not provide enough information to the decision maker to make a final decision because the parameter values in decision-making problems are often imprecise and changeable. Sensitivity analysis (SA) is the investigation of changes in parameter values and their impacts on results drawn from the model. In this analysis, criteria weights are slightly modified to observe the impact on the ranking. Hence, performing sensitivity analysis on the results of a decision problem may provide valuable information to the decision maker to be able to make more informed decision.
According to the results obtained in Table 9 of Phase 5, the best route alternative is \(A_{2}\) based on traveler’s personalized criteria weights. To analyze the alternative routes using different criteria weights, a sensitivity analysis is conducted. For this study, the purpose of sensitivity analysis is to increase/decrease each criterion’s weight and decrease/increase the weights of other criteria evenly; thus, 6 cases for 6 criteria are analyzed by means of simulation with equal weights of criteria. The closeness coefficients (\(C_{i}\)) are calculated with each case.
Case 1: If the traveler (decision maker) increases distance criterion weight to 26%, no change in result/ranking is observed. However, the increment of 27% in distance criterion and decrement of other criteria’ weights evenly alters the outranking as shown in Table 14. On the contrary, no alternation in outranking is seen when this criterion weight is decreased up to 100% and the weights of other criteria are increased evenly. The reason for distance criterion is not altering results while decreasing its weight to 100% is that the best alternative has powerful value. In this way, simulations are performed to carry out the sensitivity analysis for other criteria
Case 2: The increment of time criterion weight up to 100% and decrement in other criteria’s weight evenly does not alter the outranking. However, the decrement of time criterion weight to 10% and increment in the weights of other criteria evenly results in change in ranking as given in Table 15. The reason of no change in the ranking even after increasing the distance criterion weight to 100% is that the best alternative has powerful value.
Case 3: An increment of 8% in ‘level of congestion’ criterion weight results in ranking alteration as shown in Table 16. Further, 51% decrement in weight also changes the outranking.
Case 4: When ‘level of difficulty’ criterion weight is incremented up to 100% and other criteria weights are decremented evenly, no alteration in outranking is seen (Table 17). This is due to powerful value of best alternative. However, decrementing the weight by 10% causes outranking changes.
Case 5: An increment in the weight of scenery criterion by 8% and then decrement in other criteria’s weights evenly results in outranking alteration, as shown in Table 18. This is due to powerful value of best alternative. However, decrementing the weight by 10% causes outranking changes.
Case 6: If the traveler increases toll criterion weight to 85% and decreases the weights of other criteria evenly, the outranking alters as shown in Table 19. However, no alternation in outranking is seen when this criterion weight is decreased up to 100% and the weights of other criteria are increased evenly. This is due to best alternative has powerful value
Conclusion
This paper presents the development of a hybrid decision support model to solve multicriteria route selection problem. The developed model integrates AHP as a multiple criteria decision-making method to determine priorities among route selection criteria, and TOPSIS method to obtain the ranking of all possible alternative routes between a source and destination. The best fuzzy description of each alternative route is obtained using AFS theory and the performance scores of all route are determined by performing pairwise comparisons between each pair of routes over cost or benefit criteria as described in routes’ best fuzzy description. Finally, the resulting scores (decision matrix) are used to rank the routes using TOPSIS methodology. The AFS theory is incorporated into the model to overcome the uncertainty and ambiguity in linguistic knowledge representation. The main advantage of the developed hybrid model is that it processes the linguistic values using AFS theory that copes the inconsistency caused by different types of fuzzy numbers. The hybrid method also copes the inconsistency due to choice of different normalization methods. A hypothetical application of best route selection is presented to illustrate the utilization of hybrid model. Finally, a sensitivity analysis is performed. As a result of comparative analysis and model validation carried out for the developed model, it is found that the developed model is practical for selecting best route under multicriteria environment.
References
Ahmad S, Tahar RM (2014) Selection of renewable energy sources for sustainable development of electricity generation system using analytic hierarchy process: a case of Malaysia. Renew Energy 63:458–466
Ameri AA, Pourghasemi HR, Cerdac A (2018) Erodibility prioritization of sub-watersheds using morphometric parameters analysis and its mapping: a comparison among TOPSIS, VIKOR, SAW, and CF multi-criteria decision making models. Sci Total Environ 613–614:1385–1400
Azadeh A, Salehi V, Jokar M, Asgari A (2016) An integrated multi-criteria computer simulation-AHP-TOPSIS approach for optimum maintenance planning by incorporating operator error and learning effects. Intell Ind Syst 2(1):35–53
Beg I, Rashid T (2014) Multi-criteria trapezoidal valued intuitionistic fuzzy decision making with Choquet integral based TOPSIS. OPSEARCH 51(1):98–129
Buyukozkan G, Feyzioglu O, Nebol E (2008) Selection of the strategic alliance partner in the logistic value chain. Int J Prod Econ 113(1):148–158
Cables E, Garcia-Cascales MS, Lamata MT (2012) The LTOPSIS: an alternative to TOPSIS decision-making approach for linguistic variables. Expert Syst Appl 39(2):2119–2126
Delavar MR (2011) Multi-criteria, personalized route planning using quantifier-guided ordered weighted averaging operators. Int J Appl Earth Obs Geoinf 13:322–335
Ertugrul I, Karakasoglu N (2007) Performance evaluation of Turkish cement firms with fuzzy analytic hierarchy process and TOPSIS methods. Expert Syst Appl 36(1):702–715
Hartman JL (2012) Special issue on transport infrastructure: a route choice experiment with an efficient toll. Netw Spatial Econ 12(2):205–222
Hasan MK, Al-Qaheri H (2013) Optimization and GIS-based intelligent decision support system for urban transportation systems analysis. World Acad Sci Eng Technol 75:03–23
Herrera F, Martinez L (2000) An approach for combining linguistic and numerical information based on the 2-tuple fuzzy linguistic representation model in decision-making. Int J Uncertain Fuzzy Knowl Based Syst 8(5):539–562
Hwang CL, Yoon K (1981) Multiple attribute decision making: methods and applications, a state of the art survey. Springer, NY
Jahan A, Edwards KL (2015) A state-of-the-art survey on the influence of normalization techniques in ranking: improving the materials selection process in engineering design. Mater Des 65:335–342
Li Y, Liu X, Chen Y (2011) Selection of logistics center location using axiomatic fuzzy set and TOPSIS methodology in logistics management. Expert Syst Appl 38(6):7901–7908
Li Y, Liu X, Chen Y (2012) Supplier evaluation and selection using axiomatic fuzzy set and DEA methodology in supply chain management. Int J Fuzzy Syst 14(2):215–225
Li Z, Duan X, Zhang Q, Wang C, Wang Y, Liu W (2017) Multi-ethnic facial features extraction based on axiomatic fuzzy set theory. Neurocomputing 242:161–177
Li Z, Zhang Q, Duan X, Wang Y (2018) A novel semantic approach for multi-ethnic face recognition. Int J Pattern Recognit Artif Intell 32(4):1856005
Liu XD (1998a) The fuzzy theory based on AFS algebras and AFS structure. J Math Anal Appl 217(2):459–478
Liu X (1998b) The fuzzy sets and systems based on AFS structure, EI algebra and EII algebra. Fuzzy Sets Syst 95(2):179–188
Liu XD, Pedrycz W (2009) AFS fuzzy clustering analysis. In: Kacprzyk J (ed) Studies in fuzziness and soft computing: axiomatic fuzzy set theory and its applications, 244th edn. Springer, Germany, pp 351–421
Liu X, Feng X, Pedrycz W (2013) Extraction of fuzzy rules from fuzzy decision trees: an axiomatic fuzzy sets (AFS) approach. Data Knowl Eng 84:1–25
Liu X, Wang X, Pedrycz W (2015) Fuzzy clustering with semantic interpretation. Appl Soft Comput 26:21–30
Nagar B, Raj T (2012) An AHP-based approach for the selection of HFMS: an Indian perspective. Int J Oper Res 13(3):338–358
Nazari-Shirkouhi S, Miri-Nargesi S, Ansarinejad A (2017) A fuzzy decision making methodology based on fuzzy AHP and fuzzy TOPSIS with a case study for information systems outsourcing decisions. J Intell Fuzzy Syst 32(6):3921–3943
Nooramin AS, Sayareh J, Moghadam MK, Alizmini HR (2012) TOPSIS and AHP techniques for selecting the most efficient marine container yard gantry crane. OPSEARCH 49(2):116–132
Pakkar MS (2016) Multiple attribute grey relational analysis using DEA and AHP. Complex Intell Syst 2(4):243–250
Pannell DJ (1997) Sensitivity analysis of normative economic models: theoretical framework and practical strategies. Agric Econ 16:139–152
Park D, Kim H, Lee C, Lee K (2010) Location-based dynamic route guidance system of Korea: system design, algorithms and initial results. KSCE J Civ Eng 14(1):51–59
Peeta S, Yu JW (2005) A hybrid model for driver route choice incorporating en-route attributes and real-time information effects. Netw Spatial Econ 5:21–40
Raikov A (2015) Convergent networked decision-making using group insights. Complex Intell Syst 1(1–4):57–68
Ramanathan R, Karpuzcu H (2011) Comparing perceived and expected service using an AHP model: an application to measure service quality of a company engaged in pharmaceutical distribution. OPSEARCH 48(2):136–152
Rao RV (2007) Evaluation of flexible manufacturing systems. In: Decision making in the manufacturing environment. springer series in advanced manufacturing. Springer, London
Ren Y, Li Q, Liu W, Li L (2016) Semantic facial descriptor extraction via axiomatic fuzzy set. Neurocomputing 171:1462–1474
Russo F, Vitetta A, Quattrone A (2006) Route choice modelling for freight transport at national level. In: Proceeding of the European transport conference, France
Saaty T (1980) The analytic hierarchy process. McGraw-Hill, New York
Saaty T (1982) Decision making for leaders: the analytic hierarchy process for decisions in a complex world. Wadsworth Publishing, Belmont, CA
Saaty T (2008) Decision making with the analytic hierarchy process. Int J Serv Sci 1(1):83–98
Santos L, Coutinho-Rodrigues J, Antunes CR (2011) A web spatial decision support system for vehicle routing using Google Maps. Decis Support Syst 51:1–9
Sharma MJ, Yu SJ (2013) Selecting critical suppliers for supplier development to improve supply management. OPSEARCH 50(1):42–59
Singh SP, Chauhan MK, Singh P (2015) Using multicriteria futuristic fuzzy decision hierarchy in SWOT analysis: an application in tourism industry. Int J Oper Res Inf Syst 6(4):38–56
Soltani A, Marandi EZ, Ivaki YE (2013) Bus route evaluation using a two-stage hybrid model of Fuzzy AHP and TOPSIS. J Transp Lit 7(3):34–58
Tian X, Liu X, Wang L (2014) An improved PROMETHEE II method based on axiomatic fuzzy sets. Neural Comput Appl 25(7–8):1675–1683
Tuysuz F, Simsek B (2017) A hesitant fuzzy linguistic term sets-based AHP approach for analyzing the performance evaluation factors: an application to cargo sector. Complex Intell Syst 3(3):167–175
Veisi H, Liaghati H, Alipour A (2016) Developing an ethics-based approach to indicators of sustainable agriculture using analytic hierarchy process (AHP). Ecol Ind 60:644–654
Wang YM, Elhag TMS (2006) Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Exp Syst Appl 31(2):309–313
Wei J (2010) TOPSIS method for multiple attribute decision making with incomplete weight information in linguistic setting. J Conver Inf Technol 5(10):181–187
Younas I, Ilyas M, Ali R (2008) A traffic advisory system for Islamabad. Communications of the IBIMA 3:56–61
Zangeneh M, Akram A, Nielsen P, Keyhani A, Banaeian N (2015) A solution approach for agricultural service center location problem using TOPSIS, DEA and SAW techniques. In: Golinska P, Kawa A (eds) Technology management for sustainable production and logistics, Springer, Berlin, pp 25–56
Zhang H, Gu CL, Gu LW, Zhang Y (2011) The evaluation of tourism destination competitiveness by TOPSIS & information entropy—a case in the Yangtze river delta of China. Tour Manag 32(2):443–451
Zheng J (2015) Grey relational analysis for route choice decision-making under uncertain information. Int J Secur Appl 9(4):1–8
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Singh, S.P., Singh, P. A hybrid decision support model using axiomatic fuzzy set theory in AHP and TOPSIS for multicriteria route selection. Complex Intell. Syst. 4, 133–143 (2018). https://doi.org/10.1007/s40747-018-0067-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-018-0067-y