Abstract
Feature selection methods have been used in various applications of machine learning, bioinformatics, pattern recognition and network traffic analysis. In high dimensional datasets, due to redundant features and curse of dimensionality, a learning method takes significant amount of time and performance of the model decreases. To overcome these problems, we use feature selection technique to select a subset of relevant and non-redundant features. But, most feature selection methods are unstable in nature, i.e., for different training datasets, a feature selection method selects different subsets of features that yields different classification accuracy. In this paper, we provide an ensemble feature selection method using feature–class and feature-feature mutual information to select an optimal subset of features by combining multiple subsets of features. The method is validated using four classifiers viz., decision trees, random forests, KNN and SVM on fourteen UCI, five gene expression and two network datasets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Feature selection is used to select a subset of relevant and non-redundant features from a large feature space. In many applications of machine learning and pattern recognition, feature selection is used to select an optimal feature subset to train the learning model. While dealing with large datasets, it is often the case that information available is somehow redundant for the learning process. The process of identifying and removing the irrelevant features from the original feature space, so that the learning algorithms can mainly focus on the relevant data which are useful for analysis and future predictions, is called feature or variable or attribute selection. The main objectives of feature selection are: (i) to improve predictive accuracy (ii) to remove redundant features and (iii) to reduce time consumption during analysis. Rodriguez et al. [23] state that performance of classification models improves when irrelevant and redundant features are eliminated from the original dataset. Moreover, a single feature selection method may generate local optimal or sub-optimal feature subset for which a learning method compromises its performance. In ensemble-based feature selection method, multiple feature subsets are combined to select an optimal subset of features using combination of feature ranking that improves classification accuracy. In the first step of ensemble method, a set of different feature selectors are chosen and each selector provides a sorted order of features. The second step aggregates the selected subsets of features using different aggregation techniques [28].
In the last two decades, a significant number of feature selection methods have been proposed that work differently using various metrics (like probability distribution, entropy, correlation etc) [1, 3, 11, 12, 15, 22, 26, 29]. Feature selection methods are used to reduce dimensionality of data for big data analytics [8, 16], gene expression data analysis and network traffic traffic analysis [7, 13, 19]. For a given dataset, different feature selection algorithms may select different subset of features and hence the result obtained may have different accuracy. So, people use ensemble-based feature selection method to select a stable feature set which improves classification accuracy. But, the main problem which needs to be considered in designing an ensemble-based feature selection is diversity [27]. Diversity may be achieved through using different datasets, feature subsets, or classifiers.
Types of feature selection
Filter approach [9] is used to select a subset of features from high dimensional datasets without using a learning algorithm. Filter-based feature selection methods are typically faster but the classifier accuracy is not ensured. Whereas, wrapper approach [4] uses a learning algorithm to evaluate the accuracy of a selected subset of features during classification. Wrapper methods can give high classification accuracy than filter method for particular classifiers but they are less cost effective. Embedded approach [9] performs feature selection during the process of training and is specific to the applied learning algorithms. Hybrid approach [14] is basically a combination of both filter and wrapper-based methods. Here, a filter approach selects a candidate feature set from the original feature set and the candidate feature set is refined by the wrapper approach. It exploits the advantages of both these approaches.
Discussion
As the dimensionality of the data is increasing day-by-day, difficulty in analyzing the data is also increasing with the same pace. In that context, feature selection is becoming an essential requirement in many data mining applications. From our empirical study, it has been observed that use of a single filter often fails to provide consistent performance on multiple datasets. So different filters can be ensembled to overcome the biasness or limitations of the identical classifiers and to provide consistent performance over a wide range of applications.
Motivation and problem definition
In literature, we found a large number of filter-based feature selection methods such as cfs, gain ratio, info gain and reliefF. The main problems of filter-based feature selection are (i) most of them do not consider the redundancy among the selected features, (ii) a single filter-based method may have biasness on selected feature subset and (iii) inconsistent prediction accuracy during classification. To overcome these problems, an ensemble of feature selection methods is introduced to select an optimal subset of non-redundant and relevant features which improves prediction accuracy during classification. However, most ensemble-based feature selection methods do not consider redundancy among the selected features during feature selection. For example, Canedo et al. [5] tested an ensemble-based feature selection method where the combiner simply takes the union of different subsets of features generated by multiple filter methods. After the experimental analysis on 5–15 datasets, they claim that the accuracy of their ensemble method was degraded. We are motivated to improve the classification accuracies of classifiers using an ensemble method that uses feature-class and feature-feature mutual information to combine different subsets of features. Feature-class mutual information is used to select relevant features whereas feature-feature mutual information is used to select non-redundant features. The union operation simply selects unique features from different subsets of features but it does not consider the redundant features in terms of prediction information or irrelevant features. Hence, we propose an ensemble feature-selection method that selects only a subset of relevant and non-redundant features. We formulate our problem as follows:
For a given dataset D, it is aimed to select initially different subsets of features, say \(S_1, S_2, \ldots , S_n\) using n filter-based feature-selection methods. Next, is to combine these feature subsets using feature-class and feature-feature mutual information to generate an optimal feature subset, say F which contains only non-redundant, yet relevant features. The appropriateness of the feature subset is to be validated using unbiased classifiers on benchmark datasets.
Paper organization
The rest of the paper is organized as follows: In the section, “Related work”, we report related work in brief. In the section, “EFS-MI: the proposed MI-based ensemble feature selection”, we explain our proposed method and related concepts. The experimental results are analyzed in the section, “Experimental results” followed by conclusions and future work in the section, “Conclusion and future work”.
Related work
In the past two decades, a good number of ensemble feature selection methods have been proposed. Bagging [6] and boosting [25] are two most popular examples, which work on bootstrap samples of the training set. A bootstrap sample is a replica of dataset created by randomly selecting k instances, with replacement from the training set. Each of the replica is fed to a filter. Prediction of each classifier is combined using simple voting. On the other hand, the boosting approach samples the instances in proportion to their weights. An instance is weighed heavily if the previous model misclassified it. Olsson et al. [20] combines three commonly used ranker documents such as frequency threshold, information gain and chi-square for text classification problems. Wang et al. [28] present the ensemble of six commonly used filter-based rankers whereas Optiz [21] studies the ensemble feature selection for neural networks called genetic ensemble feature selection. Lee [18] and Rokachetal [24] combine outcomes of various non ranker filter-based feature subset selection techniques.
Moreover, feature selection methods have been applied in the classification problems such as bioinformatics and signal processing [33]. Generally, a cost-based feature selection method is used to maximize the classification performance and minimize the classification cost associated with the features, which is a multi-objective optimization problem. Zhang et al. [32] propose a cost-based feature selection method using multi-objective particle swarm optimization (PSO). The method generates a Pareto front of nondominated solutions, that is, feature subsets, to meet different requirements of decision-makers in real-world applications. In order to enhance the search capability of the proposed algorithm, a probability-based encoding technology and an effective hybrid operator, together with the ideas of the crowding distance, the external archive, and the Pareto domination relationship, are applied to PSO. A binary bare bones particle swarm optimization (BPSO) method is proposed to select an optimal subset of features [31]. In this method, a reinforced memory strategy is designed to update the local leaders of particles for avoiding the degradation of outstanding genes in the particles, and a uniform combination is proposed to balance the local exploitation and the global exploration of algorithm. The experiments show that the proposed algorithm is competitive in terms of both classification accuracy and computational performance. Canedo et al. [5] propose an ensemble of filters and classifiers for microarray data classification. Yu et al. [30] propose an ensemble based on GA wrapper feature selection, wherein they use three real-world data sets to show that the proposed method outperforms a single classifier employing all the features and a best individual classifier is obtained from GA based feature subset selection. Stephen Bay claims that ensemble of multiple classifiers is an effective technique for improving classification accuracy [2] and propose a combining algorithm for nearest neighbor classifiers using multiple feature subsets. Our study reveals that none of the existing ensemble methods are totally free from those limitations, as reported initially in section “Motivation and problem definition”.
EFS-MI: the proposed MI based ensemble feature selection
To overcome the limitations, we introduced an ensemble feature selection method uses mutual information to select an optimal subset of features. In information theory, mutual information I(X; Y) is the amount of uncertainty in X due to the knowledge of Y [17]. Mathematically, mutual information is defined as
where P(x, y) is the joint probability distribution function of X and Y, and P(x) and P(y) are the marginal probability distribution functions for X and Y. We can also say
where, H(X) is the marginal entropy, H(X|Y) is the conditional entropy, and H(X; Y) is the joint entropy of X and Y. Here, if H(X) represents the measure of uncertainty about a random variable, then H(X|Y) measures what Y does not say about X. This is the amount of uncertainty in X after knowing Y and this substantiates the intuitive meaning of mutual information as the amount of information that knowing either variable provides about the other. In our method, a mutual information measure is used to calculate the information gain among features as well as between feature and class attributes. We define the marginal entropy and conditional entropy as follows.
Definition 1
Marginal Entropy For a random variable X, if the marginal distribution is P(X) then the distribution has an associated marginal entropy which is defined as follows:
Definition 2
Conditional Entropy If X and Y are two discrete random variables; P(x, y) and P(y|x) are joint and conditional probability distributions respectively, then the conditional entropy associated with these distributions is defined as
For better understanding let us take an example, assume a language with the following letters and associated probabilities as given in Table 1:
X | p | t | k | a | i | u |
|---|---|---|---|---|---|---|
p(X) | \(\frac{1}{8}\) | \(\frac{1}{4}\) | \(\frac{1}{8}\) | \(\frac{1}{4}\) | \(\frac{1}{8}\) | \(\frac{1}{8}\) |
Here, marginal entropy of X is:
The joint probability of a vowel and a consonant occurring together is given in Table 2:
P(x,y) | p | t | k | P(y) |
|---|---|---|---|---|
a | \(\frac{1}{16}\) | \(\frac{3}{8}\) | \(\frac{1}{16}\) | \(\frac{1}{2}\) |
i | \(\frac{1}{16}\) | \(\frac{3}{16}\) | 0 | \(\frac{1}{4}\) |
u | 0 | \(\frac{3}{16}\) | \(\frac{1}{16}\) | \(\frac{1}{4}\) |
P(x) | \(\frac{1}{8}\) | \(\frac{3}{4}\) | \(\frac{1}{8}\) |
Now, the conditional entropy of a vowel and a consonant can be computed as follows:
EFS-MI: Algorithm
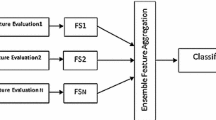
Our proposal is an ensemble approach that combines the subsets obtained from various filters using feature-class and feature-feature mutual information as shown in Fig. 1. The method combines the subsets of features selected by different feature selection methods using greedy search approach. For a particular rank, if a common feature is chosen by all the selectors, then that feature is selected without using greedy search technique and put into the optimal subset. Otherwise, the method computes feature–class and feature-feature mutual information and selects a feature that has maximum feature–class mutual information but minimum feature-feature mutual information. It removes redundancy among the selected features using feature-feature mutual information and selects relevant features using the feature–class mutual information and hence removes the biasness induced by the individual feature-selection methods. The steps of the algorithm are shown in Algorithm 1.
Function of a combiner
The combiner combines the selected subset of features based on feature–class and feature-feature mutual information. First, the combiner considers the first raked features from all the selected subsets and if all the first-ranked features are same then without computing feature–class and feature-feature mutual information, we pick up that common feature as an optimal feature. But, if the features are different then first we compute feature–class mutual information for every feature and consider the feature that has the highest feature–class mutual information. Now, for this feature we compute feature-feature mutual information with all the features that are already been selected as optimal features and if the feature-feature mutual information of that feature with all other selected features is less than a user defined threshold say, \(\alpha \) then the feature will be selected. The feature-feature mutual information is used to measure the feature-relevance of a non-selected feature with selected features. We introduce an effective value for \(\alpha \) (\(\alpha =0.75\)) based on our exhaustive experimental study. In ensemble approach, a ’combiner’ plays an important role in ensembling various feature selection methods. People use different methods such as majority voting, weighted voting, sum rule, mean rule, product rule, maximum rule, minimum rule, correlation and mutual information to build the combiner. However, the combiner for the proposed ensemble feature selection method emphasizes on reducing the redundancy among the selected subset of features by incorporating feature–class as well as feature-feature mutual information. To explain our method, following definitions are useful.
Definition 3
Feature–class relevance: It is defined as the degree of feature–class mutual information between a feature f and a class label C.
Definition 4
Feature-feature relevance: It is defined as the degree of feature-feature mutual information between any two features, say \(f_i\) and \(f_j\) where \(f_i, f_j \in F\).
Definition 5
Redundant feature: Two non-selected features say \(f_i\) and \(f_j\) are defined as redundant with respect to a given selected feature say \(f_k, if \, feature\_feature\_MI(f_i,f_k)=feature\_feature\_MI(f_j,f_k)\).
Lemma The subset of features identified by EFS-MI is non-redundant and relevant.
Proof
The proposed EFS-MI selects a feature \(f_i\) as relevant only when the feature–class relevance between \(f_i\) and a given class, say C is high (as per Definition 1). Again, for a given selected feature \(f_k\), EFS-MI considers any two features say \(f_i\) and \(f_j\) as redundant, if \(feature\_feature\_MI(f_i,f_k)=feature\_feature\_MI(f_j,f_k)\) and exclude from further consideration. Hence the proof. \(\square \)
A feature \(f_i \in F\) identified by EFS-MI, if \(f_i\) has a high feature–class relevance based on mutual information with the class label C (as per Definition 1). Further, for any two given features, \(f_j\) and \(f_k\), our method EFS-MI shall include only \(f_i\) in the final subset of features if the feature-feature mutual information of \(f_i\) is smaller than both \(f_j\) and \(f_k\) , i.e., shall discard both the redundant features \(f_j\) and \(f_k\) (as per Definition 3).
Lemma EFS-MI removes biasness of individual feature selection method during ensemble.
Proof
The proposed method considers the following two situations to remove biasness of each individual feature selection method.
-
(i)
if a feature \(f_i\) is selected by all the individual feature selection methods say \(M_j\), for rank \(R_k\), the feature is intuitively placed in the optimal subset at rank \(R_k\).
-
(ii)
if the features \(f_i\) is not same for all the individual feature selection methods \(M_j\), for a particular rank \(R_k\), the biasness of a feature selection methods is removed using \(feature\_feature\_MI()\) and \(feature\_class\_MI()\). EFS-MI selects a feature \(f_i\) if its feature-class mutual information is comparatively high but the feature-feature mutual information with all other features selected already are comapratively low. \(\square \)

In algorithm 1, the value of K is an user input that represents the number of selected features in the optimal set. The value of K is decided heuristically based on empirical study. The proposed method first considers the highest ranked feature and computes the classification accuracy using a classifier. In the next iteration, it considers a subset of features that includes both the first-ranked feature as well as the second-ranked feature, and then the first-, second- and third-ranked features and so on. For each subset of features, the method computes classification accuracy. If a subset of features that includes K high ranked features gives the highest classification accuracy compared to another subset that includes K + 1 high ranked features, then the subset of K high ranked features is considered as an optimal subset of features. From the empirical analysis, we found that the number of selected features is in the range 3–5.
Complexity analysis
Let size of each feature subset is K and the number of subsets obtained is n, then for the outer loop complexity is \(O(K \times n)\). If at any time total number of features included in F is m, the function \(feature\_feature\_MI()\) loop iterates for O(m) times. Thus, the overall complexity of the above algorithm is \(O(K\times n)\) + O(m) approximately. If K is very large then complexity will be almost linear because the number of filters employed will be less as compared to the value of K. If the value of K and m are also very large, overall complexity will be linear.
Experimental results
The proposed EFS-MI feature selection method is implemented in MATLAB 2008 software. We carried out the experiment on a workstation having 12 GB main memory, 2.26 Intel(R) Xeon processor and 64-bit Windows 7 operating system. Also, we use a freely available toolbox called Weka [10] where many feature-selection algorithms are available.
Result analysis
The proposed EFS-MI feature selection method is evaluated on three different applications, viz., network security, UCI and gene expression datasets. A brief description of the datasets and the selected features are given in Table 1. We consider five different rank-based feature-selection methods, viz., Symmetric Uncertainty (SU), Gain Ratio (GR), Info Gain (IG), ReliefF (RF) and Chi Square (CS) and four different classifiers to find classification accuracy. We compare classification accuracies found on the selected subset of features by the proposed method, i.e., EFS-MI with all other subsets of selected features for each feature selection method using decision trees, random forest, KNN and SVM. To establish the effectiveness of our method, we also consider average classification accuracy (ACA) found for a given dataset for each of the classifiers. The value of \(\alpha \) is considered as 0.75 and the value of K depends on accuracy obtained from the features set.
Analysis on network intrusion datasets
We use NSL-KDD and TUIDS dataset to validate classification accuracy of our method using three classifiers, namely decision trees, random forest and KNN. We have chosen these three classifiers because of their (i) performance and (ii) diverse nature. On NSL-KDD, the proposed ensemble feature selection method gives 92–98% classification accuracy. As shown in Table 2, the EFS-MI gives higher classification accuracy than all other competing feature selection methods with KNN and decision trees classifiers. However, the classification accuracy given by the proposed method with random forest classifier is almost similar to other compared feature selection methods. Similarly, on TUIDS dataset, classification accuracy of our method is higher than all the competing feature selection methods with decision trees, random forest and KNN classifiers.
Analysis on gene expression datasets
As shown in Table 3, in the breast cancer and colon cancer datasets, the proposed method yields high classification accuracy with decision trees, random forest, KNN and SVM classifiers than all the compared feature-selection methods in both the datasets. In the colon cancer dataset, all the classifiers give 65–88% classification accuracy, whereas EFS-MI yields high classification accuracy with decision trees classifier for all the compared individual feature selection methods. But, in case random forests and KNN, the EFS-MI gives high classification accuracy. However, the method gives a bit of poor classification accuracy with SVM classifier.
In the lung cancer dataset, our method gives better classification accuracy with decision trees than other competing methods except reliefF. However, with random forest, the method yields almost equivalent classification accuracy, whereas KNN yields better accuracy than all other competing methods. But, we found a bit low classification accuracy with SVM classifier for our method.
We observed a wide range of classification accuracy i.e, 49–97% on different classifiers using various feature selection methods on Lymphoma dataset. From the average classification accuracy found on different feature selection methods using different classifiers, we observed that decision tree, random forest, KNN and SVM yield high classification accuracy than other feature selection methods.
On SRBCT dataset, all the classifiers give excellent classification accuracy in the range between 76 and 100%. Accuracy with decision trees is found better on the proposed algorithm compared to other feature selection algorithms except reliefF. However, Random forest gives highest classification accuracy than all other compared feature selection methods. Similarly, KNN and SVM give higher accuracy for all the competing feature selection methods except chisquare.
The proposed EFS-MI gives high classification accuracy on high dimensional datasets like TUIDS, NSL-KDD, SRBCT, Lymphoma, Lung Cancer and Colon Cancer datasets. We plot the maximum accuracy found against number of features for various datasets as shown in Fig. 2. From the plotted graph, we observe that the maximum accuracy is obtained for a subset of features that contains 3–7 features.
Analysis on UCI datasets
The proposed EFS-MI is compared with five filter-based feature selection methods as shown in Table 4. In case of Accute1, Accute2 and Abalone datasets classification accuracy of EFS-MI is 100% for features numbered 4, 4 and 5, respectively for the classifiers viz. decision trees, random forests, KNN and SVM. For Accute1 and Accute2, we get similar classification accuracy in comparison to all the feature selection methods for decision trees, random forest, KNN and SVM. The SVM gives 100% classification accuracy for all the feature selection methods. In case of Glass dataset, our method yields around 60–70% classification accuracy for decision trees, random forest and KNN classifiers whereas classification accuracy with SVM is only 22–24%.
In Wine dataset, EFS-MI gives better classification accuracy with decision trees, KNN and SVM. However, the random forest yields a slightly low classification accuracy on the proposed method. In the iris dataset, classification accuracy for the proposed method is slightly low with decision trees, random forest, KNN and SVM classifiers. Similarly, on Monk1 dataset, we observe that the proposed method yields higher accuracy than info gain and reliefF only with decision trees and random forest, whereas KNN gives a slightly low classification accuracy on the proposed method. However, the SVM classifier gives better accuracy on the proposed method than all other competing feature-selection methods. Moving onto the Monk2 dataset, the proposed method achieves 67% accuracy with decision trees, random forests and SVM classifiers which is higher that the accuracy produced by other feature-selection methods. However, KNN yields a slightly low classification accuracy for the proposed method. In case of Monk3 dataset, classification accuracy is around 78% for decision trees and random forests whereas accuracy found with KNN and SVM is 66–72% which is lower than the accuracy achieved using other employed methods. The EFS-MI gives lower classification accuracy on Iris, Monk1, Monk2 and Monk3 datasets because the dimensionality of the dataset is only 4, i.e, relatively lower, hence produces less scope to established the effectiveness of an ensemble approach.
As shown in Table 6, on the Tic-Tac-Toe dataset, experimental result establishes that the performance of the proposed method is almost similar with other feature selection methods using SVM classifier. But, decision trees, random forest and KNN show low classification accuracy on the proposed method. In the similar fashion, on Zoo dataset, decision trees yield around 87% accuracy which is almost same to the accuracy found on other feature selection methods. Similarly, SVM approximately yields 95% accuracy, which is better than the results obtained by other feature selection methods employed in ensemble. Random forests and KNN yield a slightly lower classification accuracy on our proposed method.
Moving onto the diabetes dataset, we see that decision trees and KNN yield almost equivalent classification accuracy for the proposed method compared to other feature selection methods. However, the proposed method shows a slightly low classification accuracy with random forest and SVM classifiers. With the Car dataset, decision tree achieves 95% classification accuracy which is equivalent to the results obtained for other feature selection methods. Similarly, with random forest our method gives around 96% accuracy which is almost similar to the accuracy found on other feature selection methods. Moreover, KNN and SVM give higher classification accuracy on the proposed method compared to other feature selection methods. On Heart dataset, classification accuracy found on the proposed method is comparatively low with random forest, KNN and SVM classifier. However, decision tree gives better result on the proposed method compared to chisquare feature selection method only.
Analysis based on average accuracy
From the analysis of average accuracy as plotted in Figs. 3 and 4, we found that on Accute1 and Accute2, our method gives similar classification accuracy for the competing feature selection methods with all the four applied classifiers. On Abalone dataset, EFS-MI yields better average classification accuracy than other feature selection methods with decision trees, random forest and SVM. However, KNN gives lower average accuracy than other methods. In Wine dataset, the average classification accuracy found on EFS-MI with decision trees, random forest and SVM is better than all the compared feature selection methods except for chisqure. However, the KNN classifier shows higher accuracy than other methods. Similarly, in case of Iris, Monk1, Monk2, Monk3, Tic-Tac-Toe and Zoo datasets, average accuracy found on the proposed method with different classifiers is lower than other compared feature selection methods. However, on Monk1, Monk2, Tic-Tac-Toe and Zoo, only the SVM classifier gives comparatively better accuracy on EFS-MI.
On gene expression and network datasets, all the four classifiers show better average classification accuracy than the competing feature selection methods. But, the random forest classifier shows a slightly low classification accuracy on NSL-KDD dataset. Similarly, on Lung Cancer dataset, the SVM classifier yields lower classification than other feature selection methods.
Although the average classification accuracy on EFS-MI is better than other feature selection methods, however as shown in the Figs. 3 and 4, the advantage of EFS-MI is not obvious. This is because if the selected subset of features contains a single redundant feature then the accuracy of the classifier may decrease. However, average classification accuracy is computed from the accuracy obtained from each individual feature. Therefore, there is a gap between average classification accuracy obtained from each individual feature and the accuracy obtained from the selected subset of features together.
Conclusion and future work
In this paper, we have introduced an ensemble of feature selection methods called Ensemble Feature Selection using Mutual Information (EFS-MI), which combines subsets of features selected by different filters, viz., InfoGain, GainRatio, ReliefF, Chi-square and SymmetricUncertainity and yields an optimal subset of features. To evaluate the performance of the ensemble method, we have used different classifiers, viz., Decision Trees, Random Forests, KNN and SVM on the UCI, network and gene expression datasets. The overall performance has been found to be excellent for all these datasets. From our average classification accuracy (ACA) analysis, it can be observed that the proposed EFS-MI mostly overcomes the local optimal problem of the individual filters especially for high dimensional datasets. The quality of features identified by EFS-MI in terms of relevance and non-redundancy also has been established theoretically. To remove the biasness induced by a single classifier, an ensemble of classifiers using soft computing approach is underway.
References
Abdullah S, Sabar NR, Nazri MZA, Ayob M (2014) An exponential monte-carlo algorithm for feature selection problems. Comput Ind Eng 67:160–167
Bay SD (1998) Combining nearest neighbor classifiers through multiple feature subsets. In: ICML, vol. 98, pp 37–45. Citeseer
Bhattacharyya DK, Kalita JK (2013) Network anomaly detection: a machine learning perspective. CRC Press, Boca Raton
Blum AL, Langley P (1997) Selection of relevant features and examples in machine learning. Artif Intell 97(1):245–271
Bolón-Canedo V, Sánchez-Maroño N, Alonso-Betanzos A (2012) An ensemble of filters and classifiers for microarray data classification. Pattern Recogn 45(1):531–539
Breiman L (1996) Bagging predictors. Mach Learn 24(2):123–140
Das D, Bhattacharyya DK (2012) Decomposition+: Improving-diversity for multiple sensitive attributes. In: Advances in computer science and information technology. Computer science and engineering, vol 131, pp 403–412
Fernández A, del Río S, Chawla NV, Herrera F (2017) An insight into imbalanced big data classification: outcomes and challenges. Complex Intell Syst 3(2):105–120
Guyon I, Elisseeff A (2003) An introduction to variable and feature selection. J Mach Learn Res 3:1157–1182
Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH (2009) The weka data mining software: an update. ACM SIGKDD Explor Newslett 11(1):10–18
Hoque N, Bhattacharyya D, Kalita J (2014) Mifs-nd: a mutual information-based feature selection method. Expert Syst Appl 41(14):6371–6385
Hoque N, Ahmed H, Bhattacharyya D, Kalita J (2016) A fuzzy mutual information-based feature selection method for classification. Fuzzy Inf Eng 8(3):355–384
Hoque N, Bhattacharyya DK, Kalita JK (2016) Ffsc: a novel measure for low-rate and high-rate ddos attack detection using multivariate data analysis. Secur Commun Netw 9(13):2032–2041
Hsu HH, Hsieh CW, Lu MD (2011) Hybrid feature selection by combining filters and wrappers. Expert Syst Appl 38(7):8144–8150
Hu W, Choi KS, Gu Y, Wang S (2013) Minimum–maximum local structure information for feature selection. Pattern Recogn Lett 34(5):527–535
Kashyap H, Ahmed HA, Hoque N, Roy S, Bhattacharyya DK (2015) Big data analytics in bioinformatics: a machine learning perspective. arXiv preprint arXiv:1506.05101
Kraskov A, Stögbauer H, Grassberger P (2004) Estimating mutual information. Phys Rev E 69(6):066138
Lee K (2002) Combining multiple feature selection methods. In: Proceedings of MASPLAS’02 The Mid-Atlantic Student Workshop on Programming Languages and Systems Pace University, April 19
Mira A, Bhattacharyya DK, Saharia S (2012) Rodha: robust outlier detection using hybrid approach. Am J Intell Syst 2(5):129–140
Olsson J, Oard DW (2006) Combining feature selectors for text classification. In: Proceedings of the 15th ACM international conference on information and knowledge management, pp 798–799
Opitz DW (1999) Feature selection for ensembles. In: AAAI/IAAI, pp 379–384
Pudil P, Novovičová J, Kittler J (1994) Floating search methods in feature selection. Pattern Recogn Lett 15(11):1119–1125
Rodríguez D, Ruiz R, Cuadrado-Gallego J, Aguilar-Ruiz J (2007) Detecting fault modules applying feature selection to classifiers. In: IEEE international conference on information reuse and integration, 2007, pp 667–672
Rokach L, Chizi B, Maimon O (2006) Feature selection by combining multiple methods. Springer, New York
Schapire RE (1999) A brief introduction to boosting. IJCAI 99:1401–1406
Swiniarski RW, Skowron A (2003) Rough set methods in feature selection and recognition. Pattern Recogn Lett 24(6):833–849
Wang H, Khoshgoftaar TM, Napolitano A (2012) Software measurement data reduction using ensemble techniques. Neurocomputing 92:124–132
Wang H, Khoshgoftaar TM, Napolitano A (2010) A comparative study of ensemble feature selection techniques for software defect prediction. In: 2010 Ninth International Conference on Machine Learning and Applications (ICMLA), pp 135–140
Xuhua Y, Furuhashi T, Obata K, Uchikawa Y (1996) Selection of features for signature verification using the genetic algorithm. Comput Ind Eng 30(4):1037–1045
Yu E, Cho S (2006) Ensemble based on ga wrapper feature selection. Comput Ind Eng 51(1):111–116
Zhang Y, Gong D, Hu Y, Zhang W (2015) Feature selection algorithm based on bare bones particle swarm optimization. Neurocomputing 148:150–157
Zhang Y, Gong DW, Cheng J (2017) Multi-objective particle swarm optimization approach for cost-based feature selection in classification. IEEE/ACM Trans Comput Biol Bioinf 14(1):64–75
Zhang L, Shan L, Wang J Optimal feature selection using distance-based discrete firefly algorithm with mutual information criterion. Neural Comput Appl 28(9):2795–2808
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hoque, N., Singh, M. & Bhattacharyya, D.K. EFS-MI: an ensemble feature selection method for classification. Complex Intell. Syst. 4, 105–118 (2018). https://doi.org/10.1007/s40747-017-0060-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-017-0060-x