Abstract
Many-objective optimization problems (MaOPs) are vital and challenging in real-world applications. Existing evolutionary algorithms mostly produce an approximate Pareto-optimal set using new dominance relations, dimensionality reduction, objective decomposition, and set-based evolution. In this paper, we propose a mutation operator guided by preferred regions to improve an existing set-based evolutionary many-objective optimization algorithm that integrates preferences. In the proposed mutation operator, optimal solutions in a preferred region are first chosen to form a reference set; then for each solution within the individual to be mutated, an optimal solution from the reference set is specified as its reference point; finally, the solution is mutated towards the preferred region via an adaptive Gaussian disturbance to accelerate the evolution, and thus an approximate Pareto-optimal set with high performances is obtained. We apply the proposed method to 21 instances of seven benchmark MaOPs, and the experimental results empirically demonstrate its superiority.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Various optimization problems involving multiple objectives exist in real-world situations, such as the automated design of analog and mixed-signal circuits [1] and power system dispatch [2]. Farina et al. termed problems with more than three objectives as many-objective optimization problems (MaOPs) [3]. We focus on the following minimization problem in this paper:
where x is an n-dimensional decision vector, and its feasible set is S; \({f_i}(\mathbf x ),i = 1,2, \ldots ,m\) is the ith objective, and m is larger than three.
The objectives of MaOPs usually conflict with each other, and more objectives may result in a dramatic increase of the computational complexity; additionally, other factors, such as the high-dimensional objective space, Pareto resistance and visualization, make MaOPs difficult to be solved as well. As a result, MaOPs are very challenging and have received a lot of attention in the evolutionary optimization community in recent years [4,5,6,7,8,9,10]. At present, approaches for solving MaOPs can be grouped into the following four categories: (1) increasing the selection pressure via novel Pareto dominance relations [5,6,7,8,9]; (2) deleting redundant objectives according to certain principles [11,12,13,14]; (3) transforming an MaOP into one or several single-objective optimization problems by weighting or decomposing objectives [15,16,17,18,19,20]; (4) utilizing a certain performance indicator to evaluate individuals [21, 22]; (5) taking a set of solutions and performance indicators as the variable and objectives of a new optimization problem, respectively, and utilizing set-based evolutionary operators to solve the new problem [23,24,25,26]. The fifth approach is called set-based many-objective evolutionary optimization, where an individual contains a set of solutions of problem (1) and is called a set-based individual. The above approaches improve the efficiency of solving MaOPs in various ways. However, they seldom enhance their performances from the perspective of evolutionary operators.
In the context of evolutionary optimization, evolutionary operators, including crossover and mutation, are indispensable for solving a problem. The performances of evolutionary algorithms (EAs), such as convergence, diversity, and exploration capability, depend on them to a large extent. Gong et al. have put forward an effective crossover operator guided by preferred regions in [27]. Many researches have indicated that mutation operators play an important role in EAs [28, 29]; however, they are less well understood in many-objective evolutionary optimization, and in particular, effective mutation operators guided by preferences are rather lacking in EAs that integrate preferences. As a result, it is essential to investigate and develop mutation operators guided by preferences.
Following the above motivation, in this paper we develop a new mutation operator guided by preferred regions based on the study of Gong et al. [27]. To be specific, a preferred-region-based adaptive Gaussian mutation operator is designed to guide the set-based individuals to evolve towards the preferred region, thus accelerating the evolution and enhancing the performances of Pareto-optimal solutions.
The main contribution of this paper is that evolutionary information of a population is fully utilized to develop a mutation operator to guide its evolution towards its preferred region. On one hand, the proposed adaptive Gaussian mutation operator is related to a reference point in the decision space, which makes the individual mutate towards the preferred region; on the other hand, the random number in the operator is connected with the achievement function value in the objective space, suggesting that the operator is closer to the preferred region. Both of the above techniques guarantee the quality of the individual after mutation, which undoubtedly accelerates the evolution and makes the proposed adaptive Gaussian mutation operator distinct from existing mutation operators.
The remainder of this paper is organized as follows. The following section reviews related work. The framework of set-based evolutionary optimization integrating preferences is illustrated in “PSEA-m”. A preferred region-based adaptive Gaussian mutation operator for set-based evolution is expounded in “Adaptive Gaussian mutation guided by preferred regions”. The proposed mutation operator is applied to seven benchmark MaOPs to evaluate its effectiveness in “Applications to benchmark MaOPs”. The final section concludes the main work of this paper and highlights several topics to be researched in the future.
Related work
EAs for MaOPs
Most solutions are non-dominated by each other in the context of many-objective optimization. In this circumstance, it is necessary to employ new dominance relations to distinguish them so as to increase the selection pressure of Pareto-optimal solutions. Sato et al. [4] used a predefined parameter to control the degree of expansion or contraction of the dominance area of solutions, and thus change their dominance relation. In the method presented by Yang et al. [6], the objective space of an optimization problem is divided into several grids, and individuals are compared via their grid coordinates. Yuan et al. [7] proposed a \(\theta \) dominance-based EA. The \(\theta \) dominance relation is a strict partial order in a population. The algorithm enhances the convergence of NSGA-III by developing an efficient fitness evaluation strategy in MOEA/D and inherits the capabilities of NSGA-III. Zhang et al. [8] suggested an approximate non-dominated sorting algorithm for MaOPs, where the dominance relationship between solutions is determined by comparing at most three objectives. He et al. [9] adopted the concept of fuzzy logic to propose a fuzzy Pareto dominance relation. Zhu et al. [10] generalized conventional Pareto dominance both symmetrically and asymmetrically by expanding the dominance area of solutions.
Saxena et al. [11] presented a framework based on principal component analysis and maximum variance unfolding for reducing linear or nonlinear objectives. Bandyopadhyay and Mukherjee [12] developed an algorithm for MaOPs that periodically orders objectives based on the correlation and selects a subset of conflicting objectives. In the method proposed by He and Yen [13], a scheme of reducing the objective space and a strategy of improving the diversity of a population are employed to address the following two issues: a large search space and an ineffective Pareto-optimal set. Cheung et al. [14] proposed a method of extracting objectives that minimizes the correlation between reduced objectives using a linear combination of the original objectives.
Zhang and Li [15] decomposed a multi-objective optimization problem (MOP) into several scalar optimization sub-problems and simultaneously optimized them. Li et al. [17] suggested a unified framework that combines the merits of both dominance- and decomposition-based methodologies to balance the convergence and diversity of the algorithm. Cheng et al. [18] proposed a reference vector guided EA for many-objective optimization, in which the reference vector can not only be adopted to decompose the original optimization problem into a number of single-objective sub-problems, but also be used to guide the search towards a preferred region. Jiang and Yang [19] improved a early proposed strength Pareto-based EA by developing three techniques, i.e., a novel reference direction-based density estimator, a brand-new fitness function and a new environmental selection strategy. In the method proposed by Wang et al. [20], the weighted sum method is adopted in a local manner, and for each search direction, the optimal solution is chosen only from its neighborhood, which is defined by a hyper-cone.
Hyper-volume is one of the most important performance indicators in the context of both multi- and many-objective optimization. Bader and Zitzler [21] analyzed the hyper-volume indicator and put forward a hyper-volume estimation algorithm, which can fast calculate the value of the hyper-volume, to rank individuals. Jiang et al. [22] suggested a simple and fast hyper-volume indicator-based MOEA to update the exact hyper-volume contributions of different individuals quickly via partial individuals.
Set-based many-objective optimization
The goal of a multi-objective evolutionary algorithm (MOEA) is to produce an approximate Pareto-optimal set that is well converged, evenly distributed, and well extended. If a set of solutions and its performance indicators are taken as the decision variable and objectives of a new optimization problem, respectively, it is more likely that a Pareto-optimal set that satisfies the performance indicators will be obtained. Based on this consideration, an MaOP can be transformed into an MOP with two or three objectives, and then a series of set-based evolutionary operators are employed to solve the transformed MOP. A big difference between set-based EAs and indicator-based EAs lies in their individuals. An individual of the former is a set of solutions of problem (1), while an individual of the latter is one solution of problem (1). As a result, their evolutionary operators are totally different.
A variety of researches on set-based MOEAs have been carried out so far, including the frameworks, the methods of transforming objectives, and the approaches for comparing set-based individuals, to mention but a few. The first set-based MOEA was proposed by Zitzler et al. [23]. In their work, the preference relation between a pair of set-based individuals is defined. Furthermore, the representation of preferences, the design of the algorithm, and the performance evaluation are incorporated into a framework. Bader et al. [24] first divided solutions in a population into a number of sets of the same size, and then transformed the problem into a single-objective optimization problem whose objective is hyper-volume. In addition, they developed a scheme for recombining sets based on the hyper-volume. The empirical results show that the proposed method is very effective.
Gong et al. [25] proposed a set-based EA based on hyper-volume and distribution. Besides, they [26] also presented a set-based genetic algorithm for interval MaOPs based on hyper-volume and imprecision.
Many-objective evolutionary optimization integrating preferences
Auger et al. [30] incorporated preferences into an evolutionary many-objective optimization algorithm via weighted hyper-volume, and defined a preferred region of the objective space through a weighted function. Wang et al. [31] utilized co-evolution of double populations to solve MaOPs on the basis of the preference priority. Gong et al. developed two methods of incorporating preferences into the framework of set-based many-objective evolutionary optimization [25, 32]. One of these methods builds a preference function through integrating preferences into objectives before optimization and employing the function to steer a population to seek a satisfactory solution set during the set-based evolution. The other constructs a new function by weighting all the objectives on the basis of preferences to the performance indicators to further distinguish non-dominated solutions. Reynoso-Meza et al. [33] integrated the technique of handling preferences into the optimization process in order to improve the pertinence of the Pareto front for tuning a multi-variable PI controller.
There are now numerous methods of representing a preference, such as reference points [34], reference directions [35], reference vectors [18, 36], relative importance between objectives [37], and preferred regions [38]. An achievement scalarizing function is a special one based on reference points and can mirror preferences to some degree. On the basis of reference points [39], Gong et al. proposed an approach of determining the preferred region of a population by an achievement scalarizing function in the framework of set-based evolution [27]. In addition, they developed preferred-regions-based selection and crossover schemes as well.
Genetic operators based on evolutionary directions
Crossover and mutation operators are pivotal to the performances of an algorithm and are one of the hot topics in the evolutionary optimization community [40,41,42,43]. There have been a variety of studies on genetic operators based on evolutionary directions. Tan et al. [44] proposed a dual-population differential EA based on crossover and mutation operators to enhance the exploration capability of the algorithm. Zhu et al. [45] improved crossover and mutation operators to avoid premature convergence of genetic algorithms. In the method presented by Liu et al. [46], a crossover operator is designed to increase the diversity of a part of the Pareto front with a small density, and a mutation operator is developed to steer individuals far from the front towards the front. Qu and He [47] presented an algorithm based on adaptive Gaussian mutation to obtain the global extremum and to improve the quality of optimal solutions as well as the efficiency of the algorithm. Yen et al. [48] utilized the simplex method to conduct a crossover operation among individuals so as to produce new ones along the evolutionary direction. Bi et al. [49] suggested an adaptive differential EA based on a new mutation operator, which employs Pareto-optimal solutions to guide the evolution of a population and provides more information for producing new individuals directionally. All of the above methods employ directional genetic operators. The empirical results show that the desired goals are achieved and the proposed algorithms have a significant improvement in efficiency.
The above genetic operators based on evolutionary directions are special for MOPs. However, directional mutation operators for solving MaOPs are scarce. In this paper, we propose an adaptive Gaussian mutation operator guided by preferred regions for set-based many-objective evolutionary optimization that can steer individuals to mutate towards the preferred region. The set-based EA that integrates preferences combined with the proposed mutation operator guided by preferred regions is called PSEA-m.
PSEA-m
This section elaborates the framework of PSEA-m. The main idea is that in the framework of set-based evolution, problem (1) is first transformed into a bi-objective one, whose objectives are the hyper-volume and average crowding distance. Then, a set-based population is initialized. After that, the preferred region of the population is determined by the method presented in [27] and utilized to guide the evolution. In particular, we focus on the mutation operator guided by preferred regions, which will be expounded in “Adaptive Gaussian mutation guided by preferred regions” section. The steps of PSEA-m are as follows:
-
Step 1:
Transform problem (1) into a bi-objective one employing the method presented in “Objective transformation of MaOPs” section;
-
Step 2:
Initialize a population, P(0), and let \(t = 0\);
-
Step 3:
Determine the preferred region using the method presented in “Preferred regions” section;
-
Step 4:
Execute the selection and crossover operators on sets and the adaptive Gaussian mutation operator proposed in “Adaptive Gaussian mutation guided by preferred regions” section by the methods given in “Set-based evolutionary scheme guided by preferred regions” section to produce a temporary population of the same size;
-
Step 5
: Produce the next population \(P(t + 1)\) by executing the \(\mu + \mu \) replacement scheme presented in “Set-based evolutionary scheme guided by preferred regions” section;
-
Step 6:
Judge whether the termination condition is met. If yes, output the Pareto-optimal solutions; otherwise, let \(t = t + 1\), and go to Step 3.
Objective transformation of MaOPs
Considering that the hyper-volume can reflect convergence and distribution and also mirror extension to some degree, we choose the hyper-volume and average crowding distance to transform problem (1) into the following bi-objective one in this paper, where the average crowding distance is employed to further describe the distribution.
where P(S) is the power set of S, \(X= \{ {\mathbf{{x}}^1},{\mathbf{{x}}^2}, \ldots ,{\mathbf{{x}}^M}\}\) represents a set composed of M solutions of problem (1), i.e., \(|X|=M\), \(\lambda \) means the Lebesgue measure, \(\mathbf x _\mathrm{{ref}}\) is the reference point, \(d(\mathbf{{x}}^j) = {\mathop {\mathop {\min }\nolimits _{\scriptstyle l \in \{ 1,2, \ldots , M\}}}\limits _{\scriptstyle l \ne j}} \sum \nolimits _{i = 1}^m \left| {f_i}({\mathbf{{x}}^j}) -\right. \left. {f_i}({\mathbf{{x}}^l}) \right| \), \(j = 1,2, \ldots ,M\), represents the crowding distance of \(\mathbf x _j\) in the objective space, and \({f_i}(\mathbf{{x}}^j)\) refers to the ith objective value of \(\mathbf x ^j\), \({d^*}({X}) = {1 \over M}\sum \nolimits _{j = 1}^M {d({\mathbf{{x}}^j})} \) indicates the average crowding distance of X, and \(F_\mathrm{{1}}(X)\) and \(F_\mathrm{{2}}(X)\) measure convergence and distribution of X, respectively.
Additionally, some other effective performance indicators, such as the shift-based density [50], proximity and crowding degree estimations [51], can be used to transform problem (1) and may be more beneficial to enhancing the distribution and diversity of an algorithm, which will be our future research topics.
The following Pareto dominance relation on sets special for set-based evolution was proposed in [25].
Pareto dominance on sets For two set-based individuals, \({X_i}\) and \({X_j}\), where \({X_i} \ne {X_j}\), and the set of indicators is \(F = \{ {F_1},{F_2}, \ldots ,{F_I}\} \). If \({F_k}({X_i}) \ge {F_k}({X_j})\) is held for \(\forall k \in \left\{ {1,2, \ldots ,I} \right\} \), and there exists \(k' \in \left\{ {1,2, \ldots ,I} \right\} \) such that \({F_{{k'}}}({X_i}) > {F_{{k'}}}({X_j})\), set \(X_i\) is said to dominate \(X_j\), denoted as \({X_i}{ \succ _\mathrm{spar}}{X_j}\).
If there exists at least one \(k' \in \left\{ {1,2, \ldots ,I} \right\} \), such that \({F_{{k'}}}({X_i}) \ge {F_{{k'}}}({X_j})\), and at least one \(k'' \in \left\{ {1,2, \ldots ,I} \right\} \), such that \({F_{{k''}}}({X_i}) \le {F_{{k''}}}({X_j})\), sets \({X_i}\) and \({X_j}\) are said to be mutually non-dominated, denoted as \({X_i}\left\| {_\mathrm{spar}{X_j}} \right. \).
Preferred regions
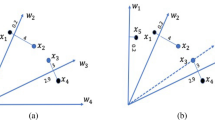
Figure 1 illustrates a preferred region based on a reference point \(Z^{ \mathrm {ref}}=(z_1^{\mathrm{{ref}}},z_\mathrm{{2}}^{\mathrm{{ref}}},\) \(\ldots ,z_m^{\mathrm{{ref}}})\), which can be specified by a decision-maker’s preference or derived according to a given ruler. In the context of set-based evolution, \(z_i^{\mathrm{{ref}}} = \mathop {\min }\nolimits _{{X_k} \in P(t)} \) \(\mathop {\min }\nolimits _{\mathbf{{x}}_k^j \in {X_k}} \{ {f_i}(\mathbf{{x}}_k^j)\} ,\;i = 1,2, \ldots ,m \), where \({X_k} = \{ \mathbf{{x}}_k^1,\mathbf{{x}}_k^2, \ldots ,\mathbf{{x}}_k^M\} \), \(k = 1,2, \ldots ,\) N, is the kth set-based individual in the tth population, P(t), and \({f_i}(\mathbf x _k^j)\), \(i = 1,2, \ldots m\), \(j = 1,2, \ldots ,M\), is the value of the ith objective function of \(\mathbf x _k^j\). The achievement function can be expressed as \({s_\infty }({z}|{{z}^{\mathrm{{ref}}}}) = \mathop {\max }\nolimits _{i = 1,2,\ldots ,m}\) \( \{ {{\lambda _i}( {{z_i} - z_i^{\mathrm{{ref}}}} )}\} + \rho \sum \nolimits _{i = 1}^m {{\lambda _i}} ( {{z_i} - z_i^{\mathrm{{ref}}}} )\) on the basis of the reference point, where \(z=({z_1},{z_2}, \ldots ,{z_m})\) is a point in the objective space, \(\lambda = ({\lambda _1},{\lambda _2}, \ldots ,{\lambda _m})\) is a vector of weight, and \(\lambda _i=1/(z_i^{\max } - z_i^{\min })\), where \({z}_i^{\max }\) and \({z}_i^{\min }\) are the maximum and minimum values of the ith objective function in the current population, \(\rho > 0\) is a sufficiently small augmentation coefficient, and set to \({10^{ - 6}}\) in this paper.
The preferred region is \(R(P(t),{z^{\mathrm{{ref}}}})= \{ z|{s_\infty }(z|z^\mathrm{{ref}}) \le s_\infty ^{\min }(P(t)) + \delta \}\), where \(s_\infty ^{\min } (P(t)) = \mathop {\min }\nolimits _{{\mathbf{{X}}_k} \in P(t)} \mathop {\min }\nolimits _{x_k^j \in \mathbf{{X}_k}} \{ {s_\infty }(z_k^j|z^\mathrm{{ref}})\}\). \(\delta \) is a threshold to determine the size of the preferred region, and \(\delta = \tau \cdot (s_\infty ^{\max }(P(t)) - s_\infty ^{\min }(P(t)))\). The value of \(\tau \) in [27] is determined by the formula, \(\tau = \mathrm{e}^{ - s_\infty ^\mathrm{avg}P(t)\cdot s_\infty ^\mathrm{std}P(t)}\), where \(s_\infty ^\mathrm{avg}(P(t))\) and \(s_\infty ^\mathrm{std}(P(t))\) measure the distance of the population to the reference point and reflect distribution of individuals, respectively.
A preferred region in the bi-dimensional objective space [39]
Comparing set-based individuals using preferred regions
We employ the method based on the above preferred regions to distinguish all the set-based individuals in a population. In this method, Pareto dominance on sets is first employed to compare two set-based individuals. If they are non-dominated, the numbers of solutions they have inside the preferred region are compared, and the larger the number, the better performance of the individual. If they have the same number, the one with a smaller achievement function wins.
Set-based evolutionary scheme guided by preferred regions
We adopt the crossover operator guided by preferred regions proposed in [27], which utilizes the guidance of individuals inside the preferred region to individuals outside the preferred region. Also, the \(\mu +\mu \) replacement scheme is adopted. To fulfill this task, the parent and temporary populations after executing set-based evolutionary operators are first combined. Then, the method of comparing individuals proposed in “Comparing set-based individuals using preferred regions” section is utilized to obtain the total order of the combined population. Finally, the first \(\mu \) set-based individuals are chosen to form the next population.
Adaptive Gaussian mutation guided by preferred regions
Gong et al. utilized evolutionary information of the current population to determine its preferred region, based on which a crossover operator is developed to produce individuals with high performances [27]. In fact, the preferred region indicates the evolutionary direction of the population as well. If individuals after crossover can be further mutated towards the preferred region, those after mutation will have better performances, thus accelerating the convergence of the algorithm. Motivated by the above consideration, we develop an adaptive Gaussian mutation operator guided by preferred regions to enhance the exploitation capability of the algorithm. The steps of the proposed mutation operator are as follows:
-
Step 1:
Form a mutation reference set based on several high-performance individuals;
-
Step 2:
Choose set-based individuals to be mutated according to a probability;
-
Step 3:
Specify an appropriate reference point for each solution within an individual to be mutated;
-
Step 4:
Conduct directional mutation of each solution;
-
Step 5:
Repeat Steps 3 and 4 for each individual to be mutated.
To finish the proposed mutation operation, the following three issues should be considered: (1) how to select a mutation reference set, (2) how to determine a mutation reference point, and (3) how to conduct directional mutation.
Forming a mutation reference set
As stated before, the preferred region indicates the evolutionary direction of a population. We should select a number of appropriate solutions to form a mutation reference set so that set-based individuals mutate along with the above direction. In addition, MOEAs aim to seek an approximate Pareto-optimal set that is well converged and evenly distributed. As a result, the mutation reference set should also be well converged and evenly distributed so as to generate high-performance individuals. To this end, we propose the following scheme for forming the mutation reference set, shown as Algorithm 1.
The size of the mutation reference set is first set to M, which is the same as that of solutions in a set-based individual. Then, solutions inside the preferred region are picked out from the Pareto-optimal set of the current population, shown as Line 2. Finally, a number of solutions are chosen from the above ones to form the mutation reference set. Lines 13–21 show that those with a large crowding distance are preferred to maintain the diversity of mutated individuals until the number of reference points is M. If the number of solutions inside the preferred region and lying on the Pareto front is less than M, additional solutions are selected from those lying on the Pareto front but outside the preferred region. Under this circumstance, we prefer those with a small value of the achievement function, indicating that they are close to the preferred region, shown as Lines 3–12.

Determining the mutation reference points
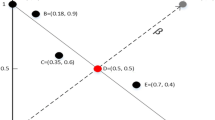
Reference points in the mutation reference set can guide the individuals to directionally mutate. This subsection addresses the issue of how to choose an appropriate mutation reference point for each solution within the individual to be mutated, since it is critical for the distribution of solutions in the individual after mutation. To this end, for each solution in an individual to be mutated, its nearest point is chosen from the mutation reference set in order to produce a set-based individual with good performances in terms of distribution and diversity. If the nearest point has not been chosen as the reference point of other solutions, it is just the mutation reference point of the solution; otherwise, the second-nearest one is chosen as its mutation reference point. In this way, the distribution and diversity of solutions in the set-based individual after mutation can be guaranteed to a large extent. Figure 2 illustrates the approach of determining mutation reference points in the bi-objective space, where \(\mathbf{z ^{\mathrm{{ref}}}}\) is a reference point in the preferred region, the rectangle indicates the preferred region of the population, the square points refer to the mutation reference points, and the dotted ones represent solutions to be mutated. As shown in Fig. 2, the nearest point to \(\mathbf{x ^1}\) is \(\mathbf x _1^{\mathrm{{ref}}}\) in the reference set, and \(\mathbf x _1^{\mathrm{{ref}}}\) is thus chosen as the mutation reference point of \(\mathbf{x ^1}\). The nearest point to \(\mathbf{x ^2}\) is also \(\mathbf x _1^{\mathrm{{ref}}}\) in the reference set; however, \(\mathbf x _1^{\mathrm{{ref}}}\) has been chosen as the mutation reference point of \(\mathbf{x ^1}\), and the second-nearest point, \(\mathbf x _2^{\mathrm{{ref}}}\), is thus chosen as the mutation reference point of \(\mathbf{x ^2}\).
An adaptive Gaussian mutation operator
For each solution in a set-based individual to be mutated, once its mutation reference point has been specified, its mutation direction is determined accordingly, and then the directional mutation can be performed according to the direction.
Gaussian mutation, which adds a stochastic disturbance with Gaussian distribution to a solution, is an important type of mutation. Considering that the mutation step is related not only to the distance between the reference point and the solution in the decision space, but also to the distance between the reference point and the solution in the objective space, we propose the following adaptive Gaussian mutation operator. Let the set-based individual to be mutated be X, let one of its solutions be \(\mathbf{x _p}, p=1,2,\ldots , M\), and let the mutation reference point of \(\mathbf{x _p}\) be \(\mathbf{x _{R1}}\); then the proposed mutation operator is as follows:
where \(x_p^d\) and \(x_{p'}^d\) are the dth components of \(\mathbf{x _p}\) before and after mutation, respectively, \(d = 1,2,\ldots n\), \(x_{R1}^d\) represents the dth component of \(\mathbf{x _{R1}}\), and \({s_\infty }{{(}}{{\mathbf{x }}_{R1}})\) and \({s_\infty }{{(}}{{\mathbf{x }}_{p}})\) indicate the values of the achievement function of \(\mathbf{x _{R1}}\) and \(\mathbf{x _p}\), respectively. In addition, \(N(0,|{s_\infty }{{(}}{{\mathbf{x }}_{R1}}) - {s_\infty }(\mathbf{x _p})|)\) is a stochastic value obeying a Gaussian distribution with a mean of 0 and a variance of \(|{s_\infty }{{(}}{{\mathbf{x }}_{R1}}) - {s_\infty }(\mathbf{x _p})|\).
Each component of the solution adds an adaptive Gaussian disturbance of Formula (3). The disturbance is composed of a mutation step and a factor, which are determined by the differences between the solution and the mutation reference point in the decision space and the objective space, respectively. On one hand, when the difference between their dth components is large in the decision space, the mutation step will be large; otherwise, the mutation step will be small. On the other hand, when the difference between the values of their achievement functions in the objective space is small, the value of the Gaussian stochastic value, \(N(0,|{s_\infty }{{(}}{{\mathbf{x }}_{R1}}) - {s_\infty }(\mathbf{x _p})|)\), will be large. In this case, the factor will be small and the dth component of the solution will be subjected to a small disturbance; otherwise, the factor will be large and the dth component of the solution to be mutated will be subjected to a big disturbance. It can be seen that Formula (3) guides individuals to directionally mutate by using the preferred region. As a result, individuals will be superior after mutation and the exploitation efficiency of the algorithm will be enhanced.
Applications to benchmark MaOPs
To evaluate the proposed mutation operator, we compare the algorithm proposed in “PSEA-m” section, PSEA-m, with several state-of-the-art EAs. The first one, in the framework of the algorithm proposed in [25] and called SEA, converts an MaOP into a bi-objective optimization problem based on the hyper-volume and average crowding distance. It conducts simulated binary crossover within a set-based individual, and stochastic crossover between individuals. Then, polynomial mutation is conducted on solutions belonging to an individual. The second one, called PSEA and proposed in [27], carries out set-based selection and crossover guided by preferred regions as well as polynomial mutation. The third one is MOEA/D, proposed by Zhang and Li [15]; it employs the Tchebychev function to decompose objectives and its genetic operators are simulated binary crossover and polynomial mutation. The fourth one is KnEA, proposed by Zhang et al. [52], and its genetic operators are simulated binary crossover and polynomial mutation as well. The fifth one is NSGA-III, proposed by Deb and Jain [53], and is implemented by a Python experimental platform [54].
All the methods are employed to solve the DTLZ test suite [55], and the hyper-volume (H indicator, for short) and distribution (D indicator, for short) are adopted to compare their performances. In addition, for each optimization problem, each algorithm is run independently 20 times and the average of the experimental results corresponding to an indicator is calculated. The environment in which these algorithms were implemented was as follows: an Intel(R) Core\(^\mathrm{{TM}}\) i3-2100 CPU @ 3.10 GH with 2.00 GB of RAM, Windows XP, and Matlab2013(a).
Parameter settings
The population size is set to 10 and the number of solutions contained in a set-based individual is set to 20 for the three set-based methods, that is, SEA, PSEA, and PSEA-m. The population size of MOEA/D and KnEA is set to 200. The probabilities of the crossover and mutation operators are 0.9 and 0.1, respectively, and their distribution coefficients both take value of 20, these parameter setting are the same as those used in [27]. The largest number of generations is set to 100. The parameters and weight vectors of NSGA-III are defaults in the experimental platform [54]. The neighborhood size of the weight vectors in MOEA/D is set to 10. In addition, the Monte Carlo approximate method proposed in [21] is employed to estimate the value of hyper-volume, and the number of sampling points is 10,000.
Experimental results and analysis
The experiments include the following three groups. The first one verifies the effectiveness of the proposed mutation operator via distribution of a set-based individual before and after mutation in the objective space; the second one compares the values of the H indicator of Pareto fronts produced by different mutation operators with respect to the number of generations in order to demonstrate that the proposed mutation operator can accelerate the convergence of the algorithm; the last one contrasts the statistical results of the H and D indicators obtained by different methods to validate the superiority of PSEA-m.
Distribution of a set-based individual before and after mutation
To verify and intuitively inspect the effectiveness of the proposed directional mutation operator, we apply PSEA-m to solve a bi-objective benchmark optimization problem, that is, DTLZ2, and observe the distribution of a set-based individual before and after mutation in the objective space at the 1st, 10th, 30th, and 70th generations. The experimental results are depicted in Fig. 3, where the rectangular area is the preferred region and points and circles represent solutions in a set-based individual before and after mutation, respectively.
The following conclusions can be drawn from Fig. 3: (1) solutions contained in the set-based individual after mutation are mostly located in the preferred region, indicating that the proposed mutation operator can guide the individuals to evolve towards the preferred region, which is consistent with the intended purpose; (2) the set-based individual after mutation is closer to the true Pareto front in the same generation, suggesting that the proposed mutation operator is purposeful and directional. Compared with the ordinary mutation operator, it can accelerate the convergence of the algorithm to some degree.
The above analysis indicates that the proposed directional mutation operator can guide the algorithm to evolve towards the preferred region, and thus steer the population towards the true Pareto front.
The convergence rate of the algorithm
We compare the values of the H indicator obtained by PSEA and PSEA-m with respect to the number of generations in this subsection. The difference between these methods lies in the mutation operator, where the former adopts polynomial mutation, whereas the latter applies adaptive Gaussian mutation guided by preferred regions. For DTLZ test suites, the values of the H indicator obtained by PSEA and PSEA-m with respect to the number of generations have the same tendency of changes. Due to space limitations, we only show the curves of the H indicator of DTLZ1 and DTLZ3 in Fig. 4.
From Fig. 4, it can be seen that, (1) the values of the H indicator obtained by PSEA-m are mostly larger than those obtained by PSEA after the same number of generations, suggesting that the proposed directional mutation operator can produce set-based individuals with high performances, and PSEA-m has a more rapid convergence rate than PSEA; (2) PSEA-m can produce a better Pareto-optimal set than PSEA.
Performances of Pareto fronts obtained by different methods
Tables 1 and 2 list the values of the H and D indicators obtained by different methods when tackling DTLZ test suites, respectively, where the data shown in bold typeface are the best. Table 3 lists the results of the Mann–Whitney U distribution test on these values, where the results are obtained by the statistical software package SPSS V.19.0 and the significance level is 0.05. In Table 3, ‘\(+\)’ (‘−’) indicates that PSEA-m is significantly superior (inferior) to the compared method and ‘0’ indicates that there are no significant differences between them.
From Tables 1, 2 and 3, the following conclusions can be drawn: (1) for most optimization problems, the values of the H indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by SEA except for 10-objective DTLZ2 and 5-objective DTLZ4. For most optimization problems, the values of the D indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by SEA except for 5-objective DTLZ3, 10-objective DTLZ5, and 20-objective DTLZ6. (2) For most optimization problems, the values of the H indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by the two methods except for 5-objective DTLZ4, 5-objective DTLZ6, 10-objective DTLZ2, and 10-objective DTLZ4. For all of the optimization problems, the values of the D indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by PSEA. (3) For most optimization problems, the values of the H indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by MOEA/D except for 10-objective DTLZ2. For the other optimization problems, the values of the D indicator obtained by the proposed method are larger than those obtained by MOEA/D except for 5-objective DTLZ5. A possible reason for this is that MOEA/D decomposes the original MaOP into a number of single-objective sub-problems based on a uniform weight vector, which guarantees a uniform distribution of solutions to a large extent. (4) For most optimization problems, the values of the H indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by KnEA except for 10-objective DTLZ2. For 72.7% of optimization problems, the values of the D indicator obtained by PSEA-m are larger than those obtained by KnEA, suggesting that PSEA-m has inferior performance on the D indicator compared to KnEA. The most likely reason is that KnEA is good at maintaining the distribution of solutions. (5) For most optimization problems, the values of the H indicator obtained by PSEA-m are larger than or have no significant difference from those obtained by NSGA-III except for 5-objective DTLZ6. For 52.4% of optimization problems, the values of the D indicator obtained by PSEA-m are larger than those obtained by NSGA-III, which implies that PSEA-m has a similar performance to NSGA-III with regard to the D indicator.
Figure 5 shows the final solutions of all the algorithms in a single run on the 10-objective DTLZ4 by parallel coordinates. It indicates that KnEA has a good performance with regard to distribution.
From the above analysis, it is clear that PSEA-m is superior to the other set-based EAs with regard to convergence and distribution, and compared with the other three state-of-the-art many-objective EAs, PSEA-m has a good performance with regard to convergence and a competitive performance with regard to distribution, possibly due to ineffective performance indicators of transforming objectives. Additionally, compared with the traditional mutation operator, the proposed directional mutation operator is beneficial for improving the performances of a Pareto-optimal set in the context of set-based evolution.
The above experimental results and analyses reveal that PSEA-m utilizes evolutionary information to guide directional mutation of set-based individuals, which can accelerate the convergence of the algorithm and improve the performances of a Pareto-optimal set to some degree.
Conclusions
MaOPs are important and challenging in real-world applications, and the increase in the number of objectives makes them difficult to solve. Although there are a variety of methods of tackling these problems, the performances of these methods should be further improved. In the framework of set-based evolution integrating preferences, we have proposed another set-based EA that integrates preferences, PSEA-m, by developing an adaptive Gaussian mutation operator guided by preferred regions in this paper, which effectively and fully uses the evolutionary information of a population. We have applied PSEA-m to seven benchmark MaOPs and compared it with several state-of-the-art methods. The empirical results demonstrate that the proposed mutation operator guided by preferred regions can accelerate the evolution of the population and improve the performances of the Pareto-optimal set.
It can be found from the experimental results that evolutionary information is beneficial for improving the performances of an algorithm, and effective performance indicators can enhance the competitiveness of the algorithm. In view of this, utilizing other directional crossover and mutation operators to accelerate the evolution of a population and developing new performance indicators to enhance distribution of set-based EAs will be our research topics.
References
Kammara A, Palanichamy L, Konig A (2016) Multi-objective optimization and visualization for analog design automation. Complex Intell Syst 2:251–267
Ghasemi A, Gheydi M, Golkar M, Esiami M (2016) Modeling of wind/environment/economic dispatch in power system and solving via an online learning meta-heuristic method. Appl Soft Comput 43(6):454–468
Farina M, Amato P (2002) On the optimal solution definition for many-criteria optimization problems. In: Annual meeting on fuzzy information processing society, pp 232–238
Sato H, Aguirre HE, Tanaka K (2007) Controlling dominance area of solutions and its impact on the performance of MOEAs. In: Evolutionary multi-criterion optimization (EMO), pp 690–702
Zou X, Chen Y, Liu M, Kang L (2008) A new evolutionary algorithm for solving many-objective optimization problems. IEEE Trans Syst Man Cybern Part B Cybern 38(5):1402–1412
Yang S, Li M, Liu X, Zheng JH (2013) A grid-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 17(5):721–736
Yuan Y, Xu H, Wang B, Yao X (2016) A new domiance relation-based evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 20(1):16–37
Zhang X, Tian Y, Jin Y (2016) Approximate non-dominated sorting for evolutionary many-objective optimization. Inf Sci 369(10):14–33
He Z, Yen GG, Zhang J (2014) Fuzzy-based pareto optimality for many-objective evolutionary algorithms. IEEE Trans Evol Comput 18(2):269–285
Zhu C, Xu L, Goodman ED (2016) Generalization of pareto-optimality for many-objective evolutionary optimization. IEEE Trans Evol Comput 20(2):299–315
Saxena D, Duro J, Tiwari A, Deb K, Zhang Q (2013) Objective reduction in many-objective optimization: linear and nonlinear algorithms. IEEE Trans Evol Comput 17(1):77–99
Bandyopadhyay S, Mukherjee A (2015) An algorithm for many-objective optimization with reduced objective computations: a study in differential evolution. IEEE Trans Evol Comput 19(3):400–413
He Z, Yen G (2016) Many-objective evolutionary algorithm: objective space reduction and diversity improvement. IEEE Trans Evol Comput 20(1):145–160
Cheung Y, Gu F, Liu H (2016) Objective extraction for many-objective optimization problems: algorithm and test problems. IEEE Trans Evol Comput 20(5):755–772
Zhang Q, Li H (2007) MOEA/D: a multi-objective evolutionary algorithm based on decomposition. IEEE Trans Evol Comput 11(6):712–731
Gong D, Liu Y, Sun X, Han Y (2015) Parallel many-objective evolutionary optimization using objectives decomposition. Acta Auto Sin 41(8):1438–1457
Li K, Deb K, Zhang Q, Kwong S (2015) An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans Evol Comput 19(5):694–716
Cheng R, Jin Y, Olhofer M, Sendhoff B (2016) A reference vector guided evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 20(5):773–791
Jiang S, Yang S (2017) A strength pareto evolutionary algorithm based on reference direction for multi-objective and many-objective optimization. IEEE Trans Evol Comput 21(3):329–346
Wang R, Zhou Z, Ishibuchi H, Liao T, Zhang T (2016) Localized weighted sum method for many-objective optimization. IEEE Trans Evol Comput. doi:10.1109/TEVC.2016.2611642
Bader J, Zitzler E (2011) HypE: an algorithm for fast hypervolume-based many-objective optimization. Evol Comput 19(1):45–76
Jiang S, Zhang J, Ong Y, Zhang A, Tan P (2015) A simple and fast hypervolume indicator-based multiobjective evolutionary algorithm. IEEE Trans Cybern 45(10):2202–2213
Zitzler E, Thiele L, Bader J (2010) On set-based multi-objective optimization. IEEE Trans Evol Comput 14(1):58–79
Bader J, Brockhoff D, Welten S, Zitzler E (2009) On using populations of sets in multiobjective optimization. In: Evolutionary multi-criterion optimization (MEO), pp 140–154
Gong D, Ji X, Sun X (2014) Solving many-objective optimization problems using set-based evolutionary algorithms. Acta Electron Sin 42(1):77–83
Gong D, Sun J, Miao Z (2016) A set-based genetic algorithm for interval many-objective optimization problems. IEEE Trans Evol Comput. doi:10.1109/TEVC.2016.2634625
Gong D, Sun F, Sun J, Sun X (2017) Set-based many-objective optimization guided by a preferred region. Neurocomputing 228(3):241–255
Falco I, Cioppa A, Tarantino E (2002) Mutation-based genetic algorithm: performance evaluation. Appl Soft Comput 2:285–299
Eiben A, Schoenauer M (2002) Evolutionary computing. Inf Process Lett 82(1):1–6
Auger A, Bader J, Brockhoff D (2009) Articulating user preferences in many-objective problems by sampling the weighted hypervolume. In: Conference on genetic and evolutionary computation (GECCO), pp 555–562
Wang R, Purshouse R, Fleming P (2013) Preference-inspired co-evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 17(4):474–494
Gong D, Wang G, Sun X (2014) Set-based evolutionary optimization algorithms integrating decision-maker’s preferences for many-objective optimization problems. Acta Electron Sin 42(5):933–939
Reynoso-Meza G, Sanchis J, Blasco X, Freire R (2016) Evolutionary multi-objective optimisation with preferences for multivariable PI controller tuning. Expert Syst Appl 51(6):120–133
Goulart F, Campelo F (2016) Preference-guided evolutionary algorithms for many-objective optimization. Inf Sci 329:236–255
Deb K, Kumar A (2007) Interactive evolutionary multi-objective optimization and decision-making using reference direction method. In: Conference on genetic and evolutionary computation (GECCO), pp 781–788
Cheng R, Rodemann T, Fischer M, Olhofer M, Jin Y (2017) Evolutionary many-objective optimization of hybrid electric vehicle control: from general optimization to preference articulation. IEEE Trans Emerg Top Comput Intell 1(2):97–111
Gong D, Ji X, Sun J, Sun X (2014) Interactive evolutionary algorithms with decision-maker’s preferences for solving interval multi-objective optimization problems. Neurocomputing 137(4):241–251
Sato H, Tomita K, Miyakawa M (2015) Preferred region based evolutionary multi-objective optimization using parallel coordinates interface. In: International symposium on computational and business intelligence, pp 33–38
López J, Coello C (2014) Including preferences into a multi-objective evolutionary algorithm to deal with many-objective engineering optimization problems. Inf Sci 277(2):1–20
Casjens S, Schwender H, Brning T (2014) A novel crossover operator based on variable importance for evolutionary multi-objective optimization with tree representation. J Heuristics 21(1):1–24
Guo W, Wang L, Ge SS (2014) Drift analysis of mutation operations for biogeography-based optimization. Soft Comput 19(7):1–12
Suresh S, Huang H, Kim H (2014) Hybrid real-coded genetic algorithm for data partitioning in multi-round load distribution and scheduling in heterogeneous systems. Appl Soft Comput 24:500–510
Vannucci M, Colla V (2015) Fuzzy adaptation of crossover and mutation rates in genetic algorithms based on population performance. J Intell Fuzzy Syst 28:1805–1818
Tan Y, Tan G, Wu D (2010) Dual population differential evolution algorithm based on crossover and mutation strategy. Comput Eng Appl 46(18):9–12
Zhu F, Deng H, Li F, Cheng S (2010) Improved crossover operators and mutation operators to prevent premature convergence. Sci Technol Eng 10(6):1540–1542
Liu Y, Niu B, Zhao Q (2011) Multi-objective particle swarm optimization based on crossover and mutation. J Comput Appl 31(1):82–84
Qu L, He D (2009) Artificial fish-school algorithm based on adaptive gauss mutation. Comput Eng 35(15):182–189
Yen J, Liao JC, Lee B, Randolph D (1998) A hybrid approach to modeling metabolic systems using a genetic algorithm and simplex method. IEEE Trans Syst Man Cybern Part B Cybern 28(2):173–191
Bi X, Liu G, Xiao J (2012) Dynamic adaptive differential evolution based on novel mutation strategy. J Comput Res Dev 49(6):1288–1297
Li M, Yang S, Liu X (2014) Shift-based density estimation for pareto-based algorithms in many-objective optimization. IEEE Trans Evol Comput 18(3):348–365
Li M, Yang S, Liu X (2015) Bi-goal evolution for many-objective optimization problems. Artif Intell 228:45–65
Zhang X, Tian Y, Jin Y (2015) A knee point driven evolutionary algorithm for many-objective optimization. IEEE Trans Evol Comput 19(6):761–776
Deb K, Jain H (2014) An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach. Part I: Solving problems with box constraints. IEEE Trans Evol Comput 18(4):577–601
PyOptimization (2015). https://github.com/O-T-L
Deb K, Thiele L, Laumanns M, Zitzler E (2005) Scalable test problems for evolutionary multiobjective optimization. In: Evolutionary multi-criterion optimization (EMO), pp 105–145
Acknowledgements
This work is jointly supported by National Natural Science Foundation of China with Grant Nos. 61403155, 61375067 and 61773384, National Basic Research Program of China (973 Program) with Grant No. 2014CB046306-2, and Jiangsu Overseas Research & Training Program for University Prominent Young & Middle-aged Teachers and Presidents.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sun, J., Sun, F., Gong, D. et al. A mutation operator guided by preferred regions for set-based many-objective evolutionary optimization. Complex Intell. Syst. 3, 265–278 (2017). https://doi.org/10.1007/s40747-017-0058-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-017-0058-4