Abstract
First, this paper investigates the effect of good and bad news on volatility in the BUX return time series using asymmetric ARCH models. Then, the accuracy of forecasting models based on statistical (stochastic), machine learning methods, and soft/granular RBF network is investigated. To forecast the high-frequency financial data, we apply statistical ARMA and asymmetric GARCH-class models. A novel RBF network architecture is proposed based on incorporation of an error-correction mechanism, which improves forecasting ability of feed-forward neural networks. These proposed modelling approaches and SVM models are applied to predict the high-frequency time series of the BUX stock index. We found that it is possible to enhance forecast accuracy and achieve significant risk reduction in managerial decision making by applying intelligent forecasting models based on latest information technologies. On the other hand, we showed that statistical GARCH-class models can identify the presence of leverage effects, and react to the good and bad news.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
Introduction
To investigate effects of good and bad news on volatility in the BUX return time series as well as predict the high-frequency time series of the BUX stock index, we used quantitative approaches based on time series models which can be derived from the linear filter model. Box and Jenkins [4] integrated all the knowledge about autoregressive and moving average (ARIMA) models. From that time, ARIMA models have been very popular in time series modelling for long time. tof non-linearity in the financial data. Financial markets behave like complex, random, or chaotic non-linear systems. In this context, asymmetric GARCH models introduced by Bollerslev [3] arose as an appropriate framework for studying these problems.
Artificial neural networks (ANNs) which are the mathematical models inspired by biological neural system are regarded as universal approximators. They are able to perform tasks like pattern recognition, classification, or predictions [1, 8, 11]. They also have the biggest potential in predicting time series, which are applied very often in financial risk management. The big potential in applying ANN in finance was also confirmed by Hill et al. [13], where the authors showed that ANNs work best in connection with high-frequency financial data. According to Orr [22], Marcek [18], the most used model of regression neural network type is the RBF neural network. A very important concept, which was put forward in scientific field, is Fuzzy cognitive maps (FCM). According to Magalhães et al. [17], FCMs are originated from the theories of neural networks, fuzzy logic, and evolutionary computing. Miao [20] FCM extended to dynamic cognitive network (DCN), taking in the account dynamic nature of the cause with uncertainties. Using historical data, these tools are capable to identify a pattern assuming that the identified pattern will continue into the future.
The first objective of this paper is to investigate the effect of good and bad news on volatility in the Hungary stock market. The second objective is to find any functional relation in the behaviour of the BUX time series and, in turn, forecast future vales of the series. Firstly, the paper investigates volatility in the BUX return time series using specified non-linear asymmetric models EGARCH, PGARCH which allow identify the presence of leverage effects. Then, the paper proposes three forecasting modelling approaches [statistical, neural networks and support vector machines (SVM)] that generate forecasts on the BUX stock time series. The aim is to examine whether potentially non-linear neural networks outperform latest statistical methods or generate results which are at least comparable with those of statistical models.
This paper is organized in following manner. “Theoretical Background section” deals with the theoretical background of ARMA/GARCH-family models, multilayer feed-forward networks and some basic concepts of SVM theory are refreshed for this paper. “Data and volatility modelling” section examines asymmetric response of volatility to return in the Hungary stock market using asymmetric ARCH-types models. In “Building a prediction model for BUX stock time series and results” section, the resulting statistical models with heteroscedastic noise, the neural networks, and SVMs are applied on 1-day prediction of the BUX stocks index. Here, a novel RBF neural network model is introduced based on error-correction concept. The empirical analysis and findings are presented in “Empirical comparison and discussion” section. “Conclusion” section concludes this paper.
Theoretical background
ARIMA and asymmetric GARCH-type models
Time series models have been initially introduced either for descriptive purposes like prediction or dynamic control. ARIMA models belong to the group of Box-Jenkins methods [4], which are well-established for time series prediction. They combine autoregressive (AR) process, and moving average (MA) process, ‘I’ is an operator for differencing a time series. An ARMA(p, q) model of orders p and q is defined as
where \(\left\{ {\phi _i } \right\} \) and \(\left\{ {\theta _i } \right\} \) are the parameters of autoregressive and moving average parts, respectively, and \(\varepsilon _t \) is white noise with mean zero and variance \(\sigma ^{2}\). We assume that \(\varepsilon _t \) is normally distributed, that is, \(\varepsilon _t \sim N(0,\sigma ^{2})\). Then, the ARIMA (p, d, q) model represents the d-th difference of original time series as a process containing p autoregressive and q moving average parameters. The method of building an appropriate time series forecast model is an iterative procedure that consists of the implementation of several steps. The main four steps are as follows: identification, estimation, diagnostic checking, and forecasting. For details, see [4].
To model the effect of good and bad news on volatility in the Hungary stock market, we will also investigate response of equity volatility to stock return shock. The first model that provides a systematic framework for volatility modelling is the ARCH model proposed by Engle [7]. Bollerslev [3] proposed a useful extension of Engle’s ARCH model known as generalized ARCH (GARCH) model for time sequence \(\left\{ {\varepsilon _t } \right\} \) in the following form:
where \(\left\{ {\nu _t } \right\} \) is a sequence of Independent Identical Distribution (IID) random variables with zero mean and unit variance. \(\alpha _i \), \(\beta _j \) are the ARCH and GARCH parameters, and \(h_t \) represents the conditional variance of time series. One of the primary restrictions of the GARCH models is that it forces a symmetric response of volatility to positive and negative news. The asymmetric response of good and bad news to future volatility, or leverage effect is such that bad news should increase future volatility while good news should decrease future volatility. In the basic GARCH model (2), if only squared residual \(\varepsilon _{t-i} \) enter the equation, the signs of the residuals or shocks have no effects on conditional volatility. Nelson [21] proposed the following exponential GARCH model abbreviated as EGARCH to allow for leverage effect in the form:
Note if \(\varepsilon _{t-i} \) is positive or there is “good news”, the total effect of \(\varepsilon _{t-i} \) is \(\left( {1+ \gamma _i } \right) \varepsilon _{t-i} \). However, contrary to the “good news”, i.e., if \(\varepsilon _{t-i} \) is negative or there is “bad news”, the total effect of \(\varepsilon _{t-i} \) is \(\left( {1-\gamma _i } \right) \left| {\varepsilon _{t-i} } \right| \). Bad news can have a large impact on the volatility. As stated in the work by Zivot and Wang [24], the value of \(\gamma _i \) would be expected to be negative.
The basic GARCH model can also be extended to allow for the leverage effect. This is performed by treating of the GARCH-type model as a special case of the power GARCH (PGARCH) model proposed by Ding et al. [6]:
where d is a positive exponent, and \(\gamma _i \) denotes the coefficient of leverage effects.
Neural networks
Neural networks can be understood as systems which produce output based on inputs the user has defined. It is important to say that user has no knowledge about internal working of the system of ANN. Examples are brought forward the network and then the network tries to get as close as possible to the given output by adapting its parameters (weights). Neural network model has a large number of internal variables which are supposed to set up well to optimize the outputs.
Mathematical model of the neuron is constructed on the basis of functional neuron as a central element of human nervous system, whose task is to transform information from one neuron to the others. The goal of mathematical neuron is the process identification. In other words, we try to find input–output functions, so that the output would have desired parameters and the predicted error would be minimal.
Let \(F: x_t \in R^{k}\rightarrow y_t \in R^{1}\) is a projection assigning k-dimensional vector of inputs, \(x_t^T =(x_{1t} ,x_{2t},\ldots ,x_{kt} )\) in one-dimensional output \(y_{t}\) in specific time t.
Let \(G:\,G(x_t ,w_t ):x_t \in R_\mathrm{train}^k \rightarrow y_t \in R_\mathrm{train}^1 \) is a restriction of F. The task is then to find the values of the weights \(w_{t }\), so that functional values of G would be so close to known sample as it is possible. Let E(w) is a function defined as
This function represents the squares of the deviations of function G from the expecting values of function F. If a minimum is found, G is adapted for approximation of F. Training or adaption of the network weights \(w_{t}\) is performed on training data set. The validation data set is used for validation of learned network.
According to Anderson [1], the most common used neural network for prediction tasks is the feed-forward network that has at least one hidden layer of neurons. In this network, each layer comprises neurons that receive weighted inputs from the preceding layer and send weighted outputs to the neurons in the succeeding layer. There is no feedback connections. The most known representatives of feed-forward networks are perceptrons and their modified version called RBF neural network (RBFNN) [10].
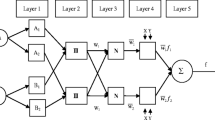
The RBFNN architecture illustrated in Fig. 1a is quite similar to the perceptron type network; however, there are some differences which include: calculation of the potential and different activation functions in the hidden layer neurons.
Architecture and learning scheme of classic RBF neural network for time series prediction with lagged error term \(e_{t-1} \) feedback. Dashed arrow indicated that weights adaption depends on the error \(e_t \). CAF means the cloud activation function, \(o_j^N , j = 1, 2,{\ldots },s\) the normalized outputs from neurons in the hidden layer
The RBFNN defines the potential of the jth neuron in the layer as a difference of the Euclidean distance given by the vector:
where x is a k-dimensional neural input vector, and \(w^{j}\) represents the weights in the hidden layer. The RBFNN also uses different types of the activation functions known as Gaussian or radial basis function. The activation function for jth hidden neuron is defined as
where \(\sigma _j^2 \) is the variance of input data sets. If the data in the input vectors are not orthogonal, then the activation function looks like this
where \(\sum ^{-1}\) is the inverse of the variance–covariance matrix of input data.
The activation function of the output neuron is also different; the output neuron is always activated by the linear function \(y~=~u\), where u is the potential of the output neuron calculated as the scalar product of the weight vector v and the output vector o.
To find the weights \(\mathbf{w}_{{\varvec{j}}}\) or centres of activation functions for the neurons in the hidden layer, we used the following adaptive (learning) version of K-means clustering algorithm for s clusters, which uses the Kohonen’s adaptive rule [15]
Step 1. Randomly initialize the centres of RBF neurons \(c_j^{(t)} , j~=~1, 2, {\ldots },s\) where s represents the number of chosen RFB neurons (clusters). |
Step 2. Apply the new training vector \(x^{\left( t \right) }=\left( {x_1 , x_2 , \ldots ,x_k } \right) \). |
Step 3. Find the nearest centre to \(x^{\left( t \right) }\) and replace its position as follows: \(c_j^{\left( {t+1} \right) } = c_j^{\left( t \right) } +\lambda \left( t \right) (x^{\left( t \right) }-c_j^{\left( t \right) } )\), where \(\lambda \left( t \right) \) is the learning coefficient selected as a linearly decreasing function of t by \(\lambda \left( t \right) =\lambda _0 \left( t \right) \left( {1-\frac{t}{N}} \right) \) where \(\lambda _0 \left( t \right) \) is the initial value, t is the presented learning cycle, and N is the number of learning cycle. |
Step 4. After chosen epochs number, terminate learning. Otherwise go to Step 2. |
The RBFNN computes the output data set as
where N is the size of data samples, and s denotes the number of hidden layer neurons. Hidden layer neurons receive the Euclidian distances \(\left( \Vert {\mathbf{x}- \mathbf{c}_\mathbf{j} }\Vert \right) \) and computes the scalar values \(o_{j,t} \) of the Gaussian function \(\psi _2 \left( {\mathbf{x}_\mathbf{t} , \mathbf{c}_j } \right) \) that form the hidden layer output vector \(\mathbf{o}_\mathbf{t} \). Finally, the single linear output layer neuron computes the weighed sum of the Gaussian functions that form the output value of \(\hat{y}_{t}\) .
If the output values \(o_{j,t} \) from the hidden layer will be normalized, where the normalisation means that the sum of the outputs from the hidden layer is equal to 1, then the RBF neural network will compute the output data set \(\hat{{y}}_t\) as follows:
The network with one hidden layer and normalized output values \(o_{j,t}^N \), according to Kecman [14], is called the fuzzy logic model or soft RBF neural network, see Fig. 2. The learning scheme uses the first-order gradient procedure. In our case, the subjects of learning are the weights \(v_{j,t} \) only. These weights can be adapted by error Back-propagation algorithm. In this case, the weight update is particularly simple. If the estimated output for the single output neuron is \(\hat{{y}}_t \), and the correct output should be \(y_t \), then the error term \(e_t \) is given by \(e_t=y_t -\hat{{y}}_t \) and the learning rule has the form:
where the term, \(\eta \in (0, 1>\), is a constant called the learning rate parameter, and \(o_{j,t}^N \) is the normalized output signal from the hidden layer. Typically, the updating process is divided into epochs. Each epoch involves updating all the weights for all the examples.
Neuron in the hidden layer of RBF neural network can also be described from granular computing perspective, see Fig. 1b. Granules as basic components of granular computing are used to represent these neurons. Granules are extracted from data in the form of clusters. Clustering is performed via competitive learning using Kohonen’s adaptive rule as the above K-mean clustering method. Thus, granules are extracted from data in the form of clusters, i.e., entities embracing collections of numerical data that exhibit some functional or descriptive commonalities. The centres of clusters are regarded as the means of granules. Above-mentioned competitive learning algorithm is regarded as one of the granular methods presenting bottom–up granulation, i.e., input data are combined into large granules. The standard deviation of a granule can be calculated as follows:
where \(x_m \) is the mth input vector with input patterns which belongs to the cluster with centre \(c_j . \, M_{j}\) is the number of input vectors which belong to the cluster with the centre \(c_{j}\). To improve the abstraction ability of soft RBF neural networks with architecture depicted in Fig. 1b, we replace the standard Gaussian activation (membership) function of RBF neurons with functions based on the normal cloud concept [16]. Cloud models are described by three numerical characteristics: expectation (Ex) as the most typical sample which represents the qualitative concept, entropy (En) as the uncertainty measurement of the qualitative concept and hyper entropy (He) which represents the uncertain degree of entropy, see Fig. 1c. Then, in case of soft RBF neural network, the Gaussian activation \(\psi _2 \left( {./.} \right) \) in Eq. (9) or (10) has the form [19]:
where is a normally distributed random number with mean and standard deviation is the expectation operator. We call this neural network as granular RBF neural network (GRBFNN).
Novel RBF neural network model based on error-correction mechanism
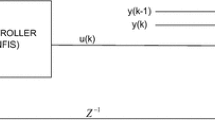
We show a new approach for economic (financial) time series forecasting by means of RBF neural networks based on Gaussian activation function modelled by cloud concept. Most of the existing learning approaches do not take in account the feedback of error terms identified in the output neuron as
In economic modelling, the feedback of error term was proposed by Banerjee et al. [2]. According to stationary and equilibrium relationship concept, the feedback of error terms (14) plays an explicit role in economic modelling. The thought of this proposal is based on the economic theory of the co-integrated variables which are related to an error-correction model. The simple mean equation (1) can be interpreted as long-run relationship that hold among the k = p + q input variables to y when the system is in equilibrium. The phrase ‘long-run equilibrium’ is used to denote the equilibrium relationship to which a system converges over time. Thus, long-run relationship will often hold “on average” over time [2]. If we denote the equilibrium by \(y_t =\mathop \sum \nolimits _{i=1}^{s+1} v_{i,t} o_{i, t} \), then the previous discrepancy \(\left\{ {y_{t-1} - \mathop \sum \nolimits _{i=1}^{s+1} v_{i,t} o_{i, t} } \right\} \) represents the previous disequilibrium. This previous disequilibrium or error should be useful explanatory variable for the next direction of movement of output variable \({\hat{y}}_t \). For example, when \(\left\{ {y_t - \mathop \sum \nolimits _{i=1}^{s+1} v_{i,t} o_{i, t} } \right\} \) is positive, \(y_t \) is too high relatively to \({\hat{y}} _t \), and on average, we might expect an increment in \({\hat{y}}_t \) in future periods relatively to its trend growth. The formula \(\left\{ {y_t -{\hat{y}}_t } \right\} =\left( {y_t -\mathop \sum \nolimits _{i=1}^{s+1} v_{i,t} o_{i, t} } \right) , t = 1, 2, {\ldots }, N\), is also called an error-correction mechanism and is also denoted as ’short-run relationship’, because in comparison with long-run relationships, those holding over a relatively short period.
The true parameters (weights) \(v_i \) characterizing the relationships expressed by Eq. (14) are not known, but they can be estimated in the course of modelling and learning the variable of interest. The network architecture with new learning scheme taking in account the feedback of error term for BUX time series predictions is shown in Fig. 2.
Support vector regression model
Despite the fact that RBF neural networks possess a number of attractive properties such as universal approximation ability and parallel structure, they still suffer from problems like the existence of many local minima and the fact that it is unclear how one should choose the number of hidden units. The SVM method is comparatively new learning system that is used in both forecasting and classification problems. This machine uses the hypothesis space of the linear functions in a high-dimensional feature space, and it is trained with a learning algorithm based on optimization theory. The SVM has been recently, introduced by Vapnik [23]. Support vector regression (SVR) is an extension of the support vector machine algorithm for numeric prediction. Its decision boundary can create complex non-linear decision boundaries while reducing the computational complexity.
Non-linear SVR is frequently interpreted by using the training data set \(\left\{ {y_k , \mathbf{x}_k } \right\} _{k=1}^N \) with input data \(\mathbf{x}_k \in \mathfrak {R}^{N}\) and output data \(\mathbf{x}_k \in \mathfrak {R}\) as follows:
where \(\varphi _i \left( \mathbf{x} \right) \) are called features (the input data are projected to a higher dimensional feature space). To perform SVM regression one optimizes the cost (empirical risk) function
containing Vapnik’s \(\varepsilon \)-insensitive loss function with \(\varepsilon \)-insensitivity zone which is defined as follows [23]:
This leads to the optimization problem:
subject to
where \(\xi _i , \xi _i^*\) are positive slack variables and C is regularization parameter which influences a trade-off between an approximation error and weights vector norm.
Finally, the SVM non-linear function estimation takes the form:
where so-called kernel trick was applied \(K\left( {\mathbf{x}_i , \mathbf{x}_j } \right) = {\varvec{\upvarphi } }^{T}\left( {\mathbf{x}_i } \right) \mathbf{\varvec{\upvarphi } }\left( {\mathbf{x}_j } \right) \) (so-called Kernel function) within the formulation of this quadratic programming problem. Note that in the case of RBF kernels, the parameters \(C, \sigma , \varepsilon \) have to be considered as additional tuning parameters.
Data and volatility modelling
Our goal is to examine and compare the behaviour of asymmetric response of equity volatility on return shocks in the Hungary stock market before, during and after financial crisis for the period January 7, 2004 to December 21, 2012, which provided of 2256 daily observations. We have 9 year long time series of the closing prices of BUX stocks data. To access the BUX time series data, see [5]. The return \(r_t \) at time t is defined in the logarithm of BUX indices \(y_{t}\) values that is, \(r_t =\log \left( {y_t } \right) -\hbox {log}\left( {y_{t-1} } \right) \). Time series of daily BUX values which is depicted in Fig. 3 on the left exhibits non-stationary behaviour. However, after its first differencing becomes stationary. As can be seen from Fig. 3 on the right, returns fluctuate around mean value that is closed to zero and also shows volatility clustering where large returns tend to be followed by small returns. Since the volatility is highest in 2008 when the values of BUX stocks reached the minimum in investigated period, we divided the basic period into two periods. First period (as the training data set) was defined from January 2004 to the end of June 2007, i.e. the time before the global financial crisis, and the second one so-called crisis and post-crisis period (validation data set or ex post period) started at the beginning of July 2007 and finished by the end of 2012.
The summary statistics (mean, standard deviation, skewness, and kurtosis) for the daily BUX returns in both investigated periods are given in Table 1. From Table 1 can be seen that the skewness coefficient is negative, suggesting that the BUX return series have a long tail while kurtosis is high what means that the distribution is leptokurtic. Jacques–Bare test is significant at 0.05.
We estimated appropriate GARCH, EGARCH, and PGARCH models for BUX returns series using the maximum likelihood method assuming the Gaussian standard normal distribution. The estimation results for BUX returns are given in Table 2. The asymmetric effect captured by the parameter estimate \(\gamma \) was positive and significant in the PGARCH(1,1) model suggesting the presence of leverage effect in both periods. For instance, in crisis period, it is clear that the good news has an impact of 0.30564 magnitude and the bad news has an impact of 0.30564 + 0.89006 = 1.19570. The estimation results of EGARCH(1,1) model captured by the parameter estimate \(\gamma \) was insignificant for both periods.
In many cases, the basic GARCH-family models (2), (3), (4) which are modelled with normal Gaussian error distribution provides a reasonably good model for analysing financial time series and estimating conditional volatility. However, there are some aspects of the model which can be improved, so that it can better capture the characteristics and dynamics. Furthermore, we re-estimated asymmetric GARCH models after having eliminated the restrictive assumption that their error terms follow a normal distribution. Table 3 presents Akaike Information Criteria (AIC) and Log-Likelihood functions (LL) based on assumptions that residuals follow successively a Student’s distribution or Generalized Errors Distribution (GED). From Table 3, it is shown that the assumption of Student’s errors is the best.
Building a prediction model for BUX stock time series and results
We illustrate the ARIMA/GARCH methodology on the developing a forecast model for BUX stocks using the data sets as for each GARCH-type model above.
Statistical approach
The relevant lag structure of potential inputs was analysed using traditional statistical tools, i.e., the autocorrelation function (ACF), partial autocorrelation function (PACF), and the Akaike information criterion. We look to determine maximum lag for which PACF coefficient was statistically significant and the lag gives the minimum AIC. According to these criterions the ARIMA(1, 1, 0) model was specified as follows:
where \(\Delta \) is the difference operator defined as \(\Delta y_t =y_t -y_{t-1} , e_t \) are the residuals. The estimated parameters of specified ARIMA(1, 1, 0) model are reported in Table 4.
As we mentioned early, high-frequency financial data, like our BUX stock time series, reflect a stylized fact of changing variance over time. An appropriate model that would account for conditional heteroscedasticity should be able to remove possible non-linear pattern in the data. Various procedures are available to test an existence of ARCH-type model. A commonly used test is the LM (Lagrange Multiplier) test [7]. The LM test assumes the null hypothesis \(H_0 : \alpha _1 =\alpha _2 =\cdots =\alpha _p =0\) that there is no ARCH. The LM statistics has an asymptotic \(\chi ^{2}\) distribution with p degrees of freedom under the null hypothesis. The ARCH-LM test up to 10 lags was statistically significant of the mean equation (21).
For estimation the parameters of an ARCH or GARCH model the maximum likelihood procedure was used and resulted into the following variance equation:
Furthermore, the variance model given by Eq. (22) was re-estimated considering that the residual follow Student’s distribution, and after GED. The model with the lowest value of AIC fits the data best. Table 5 presents AIC, log-likelihood (LL) functions in all cases. As can be seen in Table 5 the smallest AIC has just the EGARCH(1,1) with GED distribution. After these findings we re-estimated the mean Eq. (21) assuming that the random component \(e_t \) follows EGARCH(1,1) GED. Re-estimated parameters are given in Table 6.
Neuronal and SVM approach
The GRBFNN according to the architecture depicted in Fig. 2 was trained using the variables and data sets as the statistical ARIMA(1,1,0)/EGARCH(1,1) model above. In the GRBFNN, the non-linear forecasting function \(f\left( \mathbf{x} \right) \) was estimated according to the expression (10) with radial basic function \(\psi _2 \left( {./.} \right) \) given by Eq. (13). We used own application of the feed-forward neural network of RBF type with one hidden layer. For standard neural network, we tested three-to-ten hidden neurons to achieve the best results of the network. For every model, only the result with the best configuration was stated. We used linear function as an activation function for the output layer too. The weights of investigated networks were initiated randomly-generated from the uniform distribution \({<}0, 1)\). The learning rate of back-propagation algorithm was set to 0.005 to avoid the easy imprisonment in the local minimum. Final results were taken from the best of 5000 epochs and not from the last epoch to avoid overfitting of the neural network.
The prediction of BUX stock values for the ex post period was also done by SVR model using software developed by Gunn [9] which is the implementation of Vapnik’s Super Vector Machine for the problem of pattern recognition, regression, and ranking function [23]. To achieve high testing accuracy, a suitable kernel function, its parameters, and the regularization parameter C should be properly selected. Hua and Sun [12] have proved that the Gaussian kernel provide superior performance in the generalization ability and convergence speed. To set the standard deviation \(\sigma \) of Gaussian kernel function, and the magnitude of insensitivity zone \(\varepsilon \), we examined various combination of \(\varepsilon ,\sigma \) and searched which combination provides the lowest prediction error. The regularization parameter C which control the trade-off between complexity and misclassified training example was set to \(10^{5}\). The best parameter settings \(\varepsilon , \sigma \) on estimated SVR function (20) are 0.2, 0.52 respectively.
Empirical comparison and discussion
Table 7 presents two statistical measures of model’s forecast accuracy based on the Mean Absolute Percentage Error (MAPE) and the root mean square error (RMSE) calculated over the validation data set and shows the results of the methods used for comparison. The best performing method is GRBFNN with error-correction mechanism followed SVR and soft GRBFNN. A comparison between latest statistical and intelligent methods shows that intelligent prediction methods outperformed the latest statistical forecasting method. Practical advantage of the error-correction mechanism is that the extent of adjustment in a given period to deviations from long-run equilibrium is given by the estimated input–output equation directly from neural network without any further calculation. Further, from Table 7 it is shown that all forecasting models used are very accurate. The development of the error rates on validation data set showed a high inherent deterministic relationship of the underlying variables. Though promising results were achieved with all approaches, for the chaotic financial markets a purely linear (statistical) approach for modelling relationships does not reflect the reality. For example if investors do not react to a small change in the BUX stock values at the first instance, but after crossing certain interval of threshold react all the more, then a non-linear relationship between \(\Delta y_t \) and \(\Delta y_{t-1} \) exists in model (20).
RBFNNs have such attributes as computational efficiency, simplicity, and easy adjusting to changes in the process being forecast. Thus, neural networks are usually used in the complicated problems of prediction, because they minimize the analysis and modelling stages and the resolution time.
Conclusion
We investigated the volatility of the BUX stock return using two non-linear asymmetric models: PGARCH (1,1) and EGARCH(1,1). We found that the BUX stock return series exhibits leverage effects. In addition to leverage effect, it exhibits other stylized facts such as volatility clustering and leptokurtosis associated with return on developed market. In case of the BUX returns we found that PGARCH(1,1) model with Student’s errors can be appropriate representative of the asymmetric conditional volatility process in both pre-crisis and crisis or post-crisis periods.
In case of construction forecasting models for BUX stock time series, we proposed four approaches. The first one was based on latest statistical ARMA/GARCH methodologies, the second one on soft GRBFNN, the third on novel GRBFNN based on incorporation of an error-correction mechanism. The fourth approach was forecasting model based on SVR method, which is comparatively new learning method that uses hypothesis space of linear function in a high-dimensional feature space and it is trained with a learning algorithm based on the optimization theory.
After performed experiments it was established that forecasting model based on SVR is better than ARMA/GARCH one to predict high-frequency financial data for the BUX stock time series. The direct comparison of forecast accuracies between the statistical ARMA/GARCH forecasting model and its neural representation shows that both investigated methodologies yield very little MAPE values. Moreover, our experiments show that neural forecasting systems are economical and computational very efficient, well suited for high-frequency data forecasting. In future also more ways of combining prediction techniques will also be tested to see if hybrid network architectures are better than single one.
References
Anderson JA, Rosenfeld E (1988) A collection of articles summarizing the state-of-the-art as of 1988. Neurocomputing: foundations of research. MIT Press, Cambridge
Banerjee AJ, Dolado J, Galbrait JW, Hendry DF (1999) Co-integration, error correction, and the econometric analysis of non-stationary data. Oxford University Press, Oxford. http://www.oxfordscholarship.com/view/10.1093/0198288107.001.0001/acprof-9780198288107
Bollerslev D (1986) Generalized autoregressive conditional heteroscedasticity. J Econ 31:307–327. http://www.sciencedirect.com/science/article/pii/0304407686900631
Box GEP, Jenkins GM (1970) Time series analysis, forecasting and control. Holden-Day, San Francisco. http://garfield.library.upenn.edu/classics1989/A1989AV48500001.pdf
BUX time series data. http://www.bse.hu. Accessed 21 Sep 2014
Ding Z, Granger CW, Engle RF (1993) A long memory property of stock market returns and a new model. J Empir Finance 1: 83–106. http://www.sciencedirect.com/science/article/pii/0927-5398(93)90006-D
Engle RF (1982) Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 50(4): 987–1007. http://links.jstor.org/sici?sici=0012-9682%2819820...O%3B2-3&origin=repec
Gooijer JG, Hyndman RJ (2006) 25 years of time series forecasting. Int J Forecast 22:443-473. http://www.robjhyndman.com/papers/ijf25.pdf
Gunn SR (1997) Support vector machines for classification and regression. Technical report, image speech and intelligent systems research group. University of Southampton, Southampton. http://www.isis.ecs.soton.ac.uk/isystems/kernel
Hecht-Nielsen R (1990) Neuro-computing. Addison-Wesley, Reading
Hertz H, Krogh A, Palmer RG (1991) Introduction to the theory of neural computation. Westview Press, USA
Hill TL, Marquez M, O’Connor, Remus W (1994) Neural networks models for forecasting and decision making. Int J Forecast 10. http://www.sciencedirect.com/science/article/pii/0169207094900450
Hua S, Sun Z (2001) A method of protein secondary structure prediction with high segment overlap measure: support vector machine approach. J Mol Biol 308:397–407. https://www.ncbi.nlm.nih.gov/pubmed/11327775
Kecman V (2001) Learning and soft computing—support vector machines, neural networks and fuzzy logic models. Massachusetts Institute of Technology. http://dl.acm.org/citation.cfm?id=559026&preflayout=flat
Kohonen T (2012) Self-organization and associative memory. Springer, Berlin. http://scholar.google.cz/scholar?q=Kohonen+T+2012+Self-Organization+and+Associative+Memory.+Berlin:+Springer-Verlag&hl=cs&as_sdt=0&as_vis=1&oi=scholart&sa=X&ved=0ahUKEwjh0rzL4c_PAhUMCcAKHZViDw8QgQMIGTAA
Li D, Du Y (2008) Artificial intelligence with uncertainty. Chapman & Hall/CRC, Taylor & Francis Group, Boca Raton. http://dlia.ir/Scientific/e_book/Science/Cybernetics/006280.pdf
Magalhães MH, Ballini R, Gomide FAC (2008) Granular models for time-series forecasting. In: Pedrycz W, Skowron A, Kreinovich V (eds) Handbook of granular computing. Wiley, Chichester, pp 949–967
Marcek D (2004) Some intelligent approaches to stock price modelling and forecasting. J Inf Control Manag Syst 2(1). http://jicms.fri.uniza.sk/index.php/jicms/article/view/742
Marcek M, Marcek D (2008) Granular RBF neural network implementation of fuzzy systems: application to time series modeling. J Mult.-Valued Logic Soft Comput 14(3–5):401–414. http://dblp2.uni-trier.de/db/journals/mvl/mvl14
Miao Y, Liu Z, Siew C, Miao C (2001) Dynamical cognitive network an extension of fuzzy cognitive map. IEEE Trans Fuzzy Syst 9(5):760–770. http://dl.acm.org/citation.cfm?id=2234978
Nelson DB (1991) Conditional heteroskedasticity in asset returns: a new approach. Econometrica 59(2): 347–370. http://scholar.google.sk/scholar?q=Nelson+DB+1991+Conditional+Heteroskedasticity+in+Asset+Returns:+A+New+Approach,+Econometrica+59+(2),+pp+347-370&hl=sk&as_sdt=0&as_vis=1&oi=scholart&sa=X&ved=0ahUKEwjx48mF08bPAhUDSBQKHekaCb8QgQMIGDAA
Orr MJL (1986) Introduction to radial basis function networks. http://www.anc.ed.ac.uk/rbf/intro/intro.html
Vapnik V (1990) Statistical learning theory. Wiley, New-York. http://eu.wiley.com/WileyCDA/WileyTitle/productCd-0471030031.html
Zivot E, Wang EF (2005) Modeling financial time series with S-PLUS. Springer, New York. http://www.springer.com/la/book/9780387279657
Acknowledgements
This work was supported within Operational Programme Education for Competitiveness—Project No. CZ.1.07./2.3.00./20.0296.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Marcek, D. Forecasting of financial data: a novel fuzzy logic neural network based on error-correction concept and statistics. Complex Intell. Syst. 4, 95–104 (2018). https://doi.org/10.1007/s40747-017-0056-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-017-0056-6