Abstract
Coronary artery disease (CAD) is one of the leading causes of death globally. Angiography is one of the benchmarked diagnoses for detection of CAD; however, it is costly, invasive, and requires a high level of technical expertise. This paper discusses a data mining technique that uses noninvasive clinical data to identify CAD cases. The clinical data of 335 subjects were collected at the cardiology department, Indira Gandhi Medical College, Shimla, India, over the period of 2012–2013. Only 48.9% subjects showed coronary stenosis in coronary angiography and were confirmed cases of CAD. A large number of cases (171 out of 335) were found normal after invasive diagnosis. Hence, a requirement of noninvasive technique was felt that could identify CAD cases without going for invasive diagnosis. We applied data mining classification techniques on noninvasive clinical data. The data set is analyzed using a hybrid and novel k-means cluster centroid-based method for missing value imputation and C4.5, NB Tree and multilayer perceptron for modeling to predict CAD patients. The proposed hybrid method increases the accuracy achieved by the basic techniques of classification. This framework is a promising tool for screening CAD and its severity with high probability and low cost.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
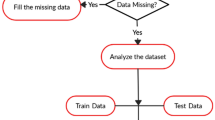
Cardiovascular diseases (CVD) are due to disorders of the heart and blood vessels [1]. It is one of the leading causes of death and disability. Early diagnosis and treatment of the disease can reduce the threat of having a further severity of the disease. It is necessary to gain clear understanding of risk and prevention factors as well as to improve the accuracy of diagnosis [2]. CAD is a cardiovascular disease in which presence of atherosclerotic plaques in arteries can restrict blood flow to the heart muscle by physically clogging the artery, leads to cardiac death or myocardial infraction [3]. CAD can be diagnosed using noninvasive and invasive methods. These tests help in evaluating the severity of disease and its effect on the function of the heart and possible form of treatment to be given to a patient. Noninvasive diagnostic methods are echocardiogram, exercise stress testing, magnetic resonance imaging, single photon emission computer tomography, but the result of these methods are inconclusive and not reliable as angiography [4,5,6,7,8]. Angiography is an invasive, costly and highly technical procedure. It cannot be utilized for screening of large population or close follow-up of treatments [9]. Moreover, these methods utilize enormous amount of resources such as time, require expensive laboratory setup, specialized tools and techniques. Limitations of diagnostic methods encourage researchers to seek other less expensive and noninvasive methods for diagnosis of CAD such as data mining that can lead to easy detection of CAD without going through angiography. Various epidemiological studies have been done in the past including Framingham Heart study [10, 11], Nippon–Honolulu–San Francisco study [12, 13], Monitoring Trends and Determinants in Cardiovascular Disease [14, 15], INTERHEART study [16, 17] for understanding the patterns, cause and risk factors for the disease. Data mining methods have been used to find patterns and models from clinical data [18, 19]. During the past few decades statistical and machine learning techniques have been increasingly applied to assist medical diagnosis. It includes both predictive and descriptive data mining techniques. Predictive data mining is widely used for generating models that can be used for prediction and classification. Descriptive data mining uses associations, clustering and subgrouping for finding interesting patterns in data [20]. If mined properly, the information hidden in these records is a huge resource bank for medical research. These data often contain hidden patterns and relationships which can lead to improved diagnosis and treatment, and provides a platform to better understand the mechanisms governing almost all aspects of the medical domain [21]. Various data mining techniques, namely, decision tree [22,23,24,25,26,27,28], support vector machine (SVM) [24, 25, 27], artificial neural networks (ANN) [24, 25, 27, 28], Naïve Bayes [28], Bayesian Networks [25], have been used for CVD diagnosis as black box and models generated were not clinically interpretable. On the other hand, the rules generated by decision trees are clinically interpretable, which is highly desirable in clinical applications [29]. Decision trees can be constructed relatively fast and their results are clinically interpretable. They do not require complex parameter adjustment from a user’s point of view [30]. In most of the studies, instances with missing values were eliminated before applying learning processes or use of machine learning technique for handling missing values. The presence of missing values in a data set can affect the performance of a model constructed. Instance deletion is practical only when the data include lesser cases of missing values and when analysis of the rest of the cases will not lead to any serious bias in clinical decisions. 1% of missing data is usually considered trivial, 1–5% as manageable. But, 5–15% require sophisticated methods to handle, and more than 15% may severely impact any kind of interpretation [31]. One may use missing value imputation to increase accuracy of predictive models. K-means is an unsupervised learning algorithm that can be used for missing value imputation [32]. In this paper, we propose an intelligent machine learning framework for CAD prediction (Fig. 1). The framework also handles missing values through data imputation.
Data set description
Clinical data of 335 consecutive patients were collected from Department of Cardiology, Indira Gandhi Medical College, Shimla, India. All the subjects had been suspected for CAD and enrolled for angiography. 27 features were recorded for each patient including demographic, historic and laboratory features namely age, sex, smoking history, hypertension, diabetes mellitus, dyslipidemia, chest pain type, random blood sugar, cholesterol, low density lipoprotein, high density lipoprotein, triglycerides, systolic blood pressure, diastolic blood pressure, height, weight, body mass index, waist circumference, central obesity, ankle–brachial index, exercise duration, METS achieved, rate pressure product, duration of recovery with persistent ST changes, duke treadmill test and result of angiography (significant CAD and severity of the disease) (Table 1).
Machine learning framework
Data were preprocessed using data encoding for leveling of qualitative attributes (indicated in Table 1) before the cluster formation and further imputed the missing value with centroid value of the features of the clusters. To predict CAD cases, we prepared CAD data set (we call it CDS) using CAD class as predict and severity data set (we call it SDS) using severity class as predictant. Then, models were constructed using supervised learning algorithms: C4.5, NB Tree and MLP for diagnosis of CAD and its severity The models are trained and validated using k-fold cross-validation method, where all the samples are eventually used for both training and testing. In this method, data set is divided into k equal size subsets where \(k=10\) and \(k-1\) data subsets are used to train the model and remaining subset is used to test the model. This procedure is repeated k-times to allow every sample to act as training and testing samples. The average result across all k trials is computed to produce final estimation.
K-means clustering
Various missing value imputation techniques have been employed by researchers, such as case-wise deletion, mean value imputation, maximum likelihood, machine learning algorithms including decision tree and MLP. Statistical methods were also explored in the medical domain [33]. Many researchers have used K-means clustering algorithm (KMCA) to impute missing values in medical data [34] and financial data [35]. K-means clustering algorithm takes input parameter k (number of clusters) and partition data into k clusters with high inter-cluster similarity based on distance function. It allocates membership to each data point for different k clusters. The remaining objects are assigned to another cluster whose center is nearest to the object. Then, centroid of the cluster is computed as new cluster center. This process iterates until the criterion function is met.
Model construction using learning schemes
In this study, we explored two classification techniques, namely, decision tree and neural network, for diagnosis of CAD and its severity.
Decision tree (C4.5, NB Tree)
A decision tree is a tree in which each non-leaf node denotes a test on an attribute of cases, each branch is a resultant of the test, and each leaf node denotes a class extrapolation. It selects the most discriminant set of attributes based on the outcome of statistical measures [36]. It is an iterative process helpful in splitting the data set into partitions.
C4.5 is the extension of ID3 algorithm developed by the Ross Quinlan [37]. It uses divide-and-conquer approach to build decision tree and uses information gain as splitting criteria. It works with top-down approach, looking at each stage an attribute of relevance to split the features that distinguish the classes in the best possible way and then recursively processing the sub problems that result from the split [11].
NB Tree The Naive Bayes Classifier is based on Bayesian concept, generates decision tree with Naive Bayes classifiers at the leaves which works with the assumption that the features in a data set are mutually independent. Being relatively robust, easy to implement, fast, and accurate, it is used widely. Some of the key areas include the diagnosis of diseases and decision support systems for different medical diagnosis [38], in taxonomic studies for the classification of RNA sequences [39] and spam filtering in e-mail clients [40]
Multilayer perceptron
An artificial neural network is a mathematical model consisting of a number of highly interconnected elements organized into layers inspired by nature. It is suitable for training large amounts of data with very few inputs. It requires less formal statistical training and have the ability to implicitly detect complex nonlinear relationships between dependent and independent variables. Multilayer perceptron is a popular ANN architecture with back propagation, a class of supervised neural network and can be used to model complex relationship between inputs and outputs [36, 41].
Performance measures
The performance of a classification model is measured in terms of accuracy, sensitivity, specificity and error rate [11].
Accuracy—accuracy is a measure of the percent of correctly classified objects by the classification method:
Error rate—the percentage of incorrectly classified object by the classification method:
Sensitivity (true positive rate)—the percentage of positive examples predicted correctly:
Specificity (true negative rate)—the percentage of negative examples predicted correctly:
where TP is true positive, TN is true negative, FP is false positive and FN is false negative
Results
The models were constructed using CDS data set with algorithms C4.5, NB Tree and MLP. The performance of the models were evaluated for accuracy, misclassification error rate, sensitivity and specificity. Other statistical measures such as kappa statistics, mean absolute error and root mean square error have been calculated. The results are presented in Table 2. It is found that C4.5 achieves the prediction accuracy of 97.6% for detection of CAD and lowest misclassification error rate of 2.38% and highest sensitivity and specificity of 97.5% and 97.6% It achieves the higher value of Cohen’s Kappa, i.e., 0.952 lowest value of RMSE 0.154.
For prediction of severity of the disease, SDS data set was used. Results (Table 3) show that C4.5 has the highest prediction accuracy among the three methods and lowest misclassification error rate and highest value of Kappa statistics (KS) and lowest value of mean absolute error (MAE) and root mean square error (RMSE).
We, therefore, consider C4.5 for rule extraction. Some of the rules extracted are shown in Fig. 2.
We also compared C4.5, NB Tree and MLP with missing data toleration techniques [33, 42] for presence and absence of stenosis in the arteries (CAD) and severity of disease. The results are shown in Tables 4 and 5 (Figs. 3, 4, 5, 6, 7, 8).
The optimized model constructed using C4.5 for disease severity has the highest prediction accuracy, lowest misclassification error rate of 80.8 and 19.1%, respectively. For CAD diagnostic model cluster-based missing value imputation does not improve the performance of the C4.5 classifier because the features used to construct the CAD model do not contain missing values, but in case of NB Tree and MLP there is significant improvement in accuracy.
Discussion and conclusion
Literature review suggested that models with the best classification performance may differ from one problem to another; they rely on data preprocessing techniques, feature selection methods, selection of algorithms for model construction and validation. The study examines the two predictive data mining approaches: decision tree and MLP with cluster-based missing value imputation method in search for an optimal model capable of performing more accurate and sensitive disease diagnosis. The experiments are conducted using Waikato Environment for knowledge analysis toolkit. MLP ignores missing values, C4.5 uses distribution-based imputation.
Model constructed with C4.5 for prediction of coronary artery disease with 25 features with predictor (presence and absence of coronary artery disease) reaches highest accuracy, of 97.6 as compared to other predictive models. Proposed method improves the prediction accuracy by 0.9%, sensitivity and specificity of 0.4 and 1.7%. Other statistical measures are also calculated such as Cohen’s Kappa, mean absolute error and root mean square error. Increase of 0.08 value of KS, reduction of 0.015 in MAE and 0.023 in RMSE for NB Tree. In case of MLP there is also improvement of 1.2% for accuracy 0.6% for sensitivity and 1.7% for specificity, increment of 0.024 in KS 0.024 and reduction of 0.018 and 0.047 for MAE and RMSE. Further, to predict the severity of disease, the models were constructed with 25 features with class severity using the decision tree and MLP algorithms. Proposed method improves the prediction accuracy by 3.2% in case of C4.5 and 4.77, 3.56% for NB Tree and MLP. Significant reduction of misclassification error rate, i.e., by 3.28% in case of C4.5 and 4.77, 3.65% for NB Tree and MLP. Significant improvement of statistical measures such as KS, MAS and RMSE. Significant rules (Fig. 2) extracted from optimized C4.5 show that chest pain type [43, 44] is the major predictor of CAD. Angina chest pain has the highest probability of CAD. High density lipoprotein >48 shows the healthy attribute of the subjects [45, 46] (rules 3–6). In rules 1 and 2 angina chest pain, Duke score, METS are same, but weight and waist circumference can affect the probability of single vessel and multi-vessel disease, higher value of weight and higher value of WC can lead to multi-vessel disease. The rules extracted are clinically interpretable and aid in the decision-making process. The study showed that decision tree, based on intelligent diagnostic model using noninvasive and clinical features, was capable of disease diagnosis and its severity with high accuracy, with low cost. However, the rules extracted from the decision tree are crisp and its performance could be improved by fuzzy rule-based approach. The results are reproducible. Parameters used to construct models were recorded as routine clinical examination (noninvasive) of symptomatic patients. The proposed model gives the high pretest probability of CAD and its severity without using an invasive diagnosis technique.
References
Wong ND (2014) Epidemiological studies of CHD and the evolution of preventive cardiology. Nat Rev Cardiol 11(5):276–289
Delen D, Walker G, Kadam A (2005) Predicting breast cancer survivability: a comparison of three data mining methods. Artif Intell Med 34(2):113–127
Tsipouras MG, Exarchos TP, Fotiadis DI, Kotsia AP, Vakalis KV, Naka KK, Michalis LK (2008) Automated diagnosis of coronary artery disease based on data mining and fuzzy modeling. IEEE Trans Inf Technol Biomed 12(4):447–458
http://www.nhlbi.nih.gov/health/health-topics/topics/cad Acces-sed Jan 2016
Montalescot G, Sechtem U, Achenbach S, Andreotti F, Arden C, Budaj A, Bugiardini R, Crea F, Cuisset T, Di Mario C, Ferreira JR (2013) 2013 ESC guidelines on the management of stable coronary artery disease. Eur Heart J 34(38):2949–3003
Acharya UR, Sree SV, Krishnan MM, Krishnananda N, Ranjan S, Umesh P, Suri JS (2013) Automated classification of patients with coronary artery disease using grayscale features from left ventricle echocardiographic images. Comput Methods Progr Biomed 112(3):624–632
Alizadehsani R, Habibi J, Hosseini MJ, Mashayekhi H, Boghrati R, Ghandeharioun A, Bahadorian B, Sani ZA (2013) A data mining approach for diagnosis of coronary artery disease. Comput Methods Progr Biomed 111(1):52–61
Kahramanli H, Allahverdi N (2008) Design of a hybrid system for the diabetes and heart diseases. Expert Syst Appl 35(1):82–89
Escolar E, Weigold G, Fuisz A, Weissman NJ (2006) New imaging techniques for diagnosing coronary artery disease. Can Med Assoc J 174(4):487–495
Wong ND, Levy D (2013) Legacy of the Framingham Heart Study: rationale, design, initial findings, and implications. Glob Heart 8(1):3–9
Dawber TR et al (1957) Coronary heart disease in the Framingham Study. Am J Public Health Nations Health 47:4–24
Worth RM, Kato H, Rhoads GG, Kagan A, Syme SL (1975) Epidemiologic studies of coronary heart disease and stroke in Japanese men living in Japan, Hawaii and California: mortality. Am J Epidemiol 102(6):481–490
Sekikawa A et al (2003) Natural experiment in cardiovascular epidemiology in the early 21st century. Heart 89:255–257
Tunstall-Pedoe H, Kuulasmaa K, Mähönen M, Tolonen H, Ruokokoski E, Amouyel P (1999) Contribution of trends in survival and coronary-event rates to changes in coronary heart disease mortality: 10-year results from 37 WHO MONICA Project populations. Lancet 353(9164):1547–1557
Evans A, Tolonen H, Hense HW, Ferrario M, Sans S, Kuulasmaa K (2001) Trends in coronary risk factors in the WHO MONICA project. Int J Epidemiol 30(suppl 1):S35
Yusuf S, Hawken S, Ôunpuu S, Dans T, Avezum A, Lanas F, McQueen M, Budaj A, Pais P, Varigos J, Lisheng L (2004) Effect of potentially modifiable risk factors associated with myocardial infarction in 52 countries (the INTERHEART study): case–control study. Lancet 364(9438):937–952
Rosengren A, Hawken S, Ôunpuu S, Sliwa K, Zubaid M, Almahmeed WA, Blackett KN, Sitthi-amorn C, Sato H, Yusuf S, INTERHEART investigators (2004) Association of psychosocial risk factors with risk of acute myocardial infarction in 11 119 cases and 13 648 controls from 52 countries (the INTERHEART study): case–control study. Lancet 364(9438):953–962
Austin PC, Tu JV, Ho JE, Levy D, Lee DS (2013) Using methods from the data-mining and machine-learning literature for disease classification and prediction: a case study examining classification of heart failure subtypes. J Clin Epidemiol 66(4):398–407
Gamberger D, Lavrač N, Krstačić G (2003) Active subgroup mining: a case study in coronary heart disease risk group detection. Artif Intell Med 28(1):27–57
Han J, Kamber M, Pei J (2011) Data mining: concepts and techniques. The morgan kaufmann series in data management systems, 3rd edn. Elsevier
Isola R, Carvalho R, Tripathy AK (2012) Knowledge discovery in medical systems using differential diagnosis, LAMSTAR, and-NN. IEEE Trans Inf Technol Biomed 16(6):1287–1295
Karaolis MA, Moutiris JA, Hadjipanayi D, Pattichis CS (2010) Assessment of the risk factors of coronary heart events based on data mining with decision trees. IEEE Trans Inf Technol Biomed 14(3):559–566
Tu MC, Shin D, Shin D (2009) Effective diagnosis of heart disease through bagging approach. In: 2nd International conference on biomedical engineering and informatics, 2009. BMEI’09, 17 Oct 2009. IEEE, pp 1–4
Xing Y, Wang J, Zhao Z, Gao Y (2007) Combination data mining methods with new medical data to predicting outcome of coronary heart disease. In: International conference on convergence information technology, 2007, 21 Nov 2007. IEEE, pp 868–872
Bouali H, Akaichi J (2014) Comparative study of different classification techniques: heart disease use case. In: 13th International conference on machine learning and applications (ICMLA), 2014, 3 Dec 2014. IEEE, pp 482–486
Srinivas K, Rao GR, Govardhan A (2010) Analysis of coronary heart disease and prediction of heart attack in coal mining regions using data mining techniques. In: 5th International conference on computer science and education (ICCSE), 2010, 24 Aug 2010. IEEE, pp 1344–1349
Melillo P, Izzo R, Orrico A, Scala P, Attanasio M, Mirra M, De Luca N, Pecchia L (2015) Automatic prediction of cardiovascular and cerebrovascular events using heart rate variability analysis. PLoS One 10(3):e0118504
Palaniappan S, Awang R (2008) Intelligent heart disease prediction system using data mining techniques. In: IEEE/ACS international conference on computer systems and applications, 2008. AICCSA 2008, 31 Mar 2008. IEEE, pp 108–115
Marateb HR, Goudarzi S (2015) A noninvasive method for coronary artery diseases diagnosis using a clinically-interpretable fuzzy rule-based system. J Res Med Sci 20(3):214
Jain R (2004) Rough set based decision tree induction for data mining, Ph.D Thesis, Jawaharlal Nehru University, New Delhi, India
Acuna E, Rodriguez C (2004) The treatment of missing values and its effect on classifier accuracy. In: Classification, clustering, and data mining applications. Springer, Berlin, pp 639–647
Sulthana AR, Subburaj R (2016) An improvised ontology based K-means clustering approach for classification of customer reviews. Indian J Sci Technol 9(15). doi:10.17485/ijst/2016/v9i15/87328
Rahman MM, Davis DN (2013) Machine learning-based missing value imputation method for clinical datasets. In: IAENG transactions on engineering technologies. Springer, Netherlands, pp 245–257
Patil BM, Joshi RC, Toshniwal D (2010) Missing value imputation based on K-mean clustering with weighted distance. In: Contemporary computing. Springer, Berlin, pp 600–609
Purwar A, Singh SK (2014) Empirical evaluation of algorithms to impute missing values for financial dataset. In: 2014 International conference on issues and challenges in intelligent computing techniques (ICICT). IEEE, pp 652–656
Eom JH, Kim SC, Zhang BT (2008) AptaCDSS-E: a classifier ensemble-based clinical decision support system for cardiovascular disease level prediction. Expert Syst Appl 34(4):2465–2479
Quinlan JR (1993) C4.5: programs for machine learning. Morgan Kaufmann, Los Altos
Kazmierska J, Malicki J (2008) Application of the Naive Bayesian classifier to optimize treatment decisions. Radiother Oncol 86(2):211–216
Wang Q, Garrity GM, Tiedje JM, Cole JR (2007) Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl Environ Microbiol 73(16):5261–5267
Sahami M, Dumais S, Heckerman D, Horvitz E. A Bayesian approach to filtering junk e-mail. In: Learning for text categorization: papers from the 1998 workshop, 26 Jul 1998, vol 62, pp 98–105
Yeh DY, Cheng CH, Chen YW (2011) A predictive model for cerebrovascular disease using data mining. Expert Syst Appl 38(7):8970–8977
Purwar A, Singh SK (2015) Hybrid prediction model with missing value imputation for medical data. Expert Syst Appl 42(13):5621–5631
Nahar J, Imam T, Tickle KS, Chen YP (2013) Association rule mining to detect factors which contribute to heart disease in males and females. Expert Syst Appl 40(4):1086–1093
Diamond GA, Staniloff HM, Forrester JS, Pollock BH, Swan HJ (1983) Computer-assisted diagnosis in the noninvasive evaluation of patients with suspected coronary artery disease. J Am Coll Cardiol 1(2):444–455
Gordon T, Castelli WP, Hjortland MC, Kannel WB, Dawber TR (1977) High density lipoprotein as a protective factor against coronary heart disease: the Framingham Study. Am J Med 62(5):707–714
McGrowder D, Riley C, Morrison EY, Gordon L (2010) The role of high-density lipoproteins in reducing the risk of vascular diseases, neurogenerative disorders, and cancer. Cholesterol 2011: 496925. doi:10.1155/2011/496925
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Verma, L., Srivastava, S. & Negi, P.C. An intelligent noninvasive model for coronary artery disease detection. Complex Intell. Syst. 4, 11–18 (2018). https://doi.org/10.1007/s40747-017-0048-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-017-0048-6