Abstract
The automated design of analog and mixed-signal circuits is a well-known subject of increasing technical and economical significance, e.g., sensory circuits for internet of things, cyber-physical systems, and Industry 4.0.The demand for rapid solution achievement under constraints, as, e.g., robustness, in established and emerging technologies as well as the migration between technologies gives incentive to automation activities. Existing approaches and tools still show improvement potential with regard to multi-variate modeling, efficient and multi-objective optimization, as well as transparence and user interaction options during the design. This paper presents new approaches applied within an emerging design environment, denoted as ABSYNTH, with an evolving self-learning architecture for efficient hierarchical optimization in a cascade, which includes function approximators and simulators trained by proven evolutionary optimization algorithms, as well as a novel domain-specific visualization of the optimization space and the trajectory of the design process. Nominal schematic-level sizing of the commonly used Miller, buffer, and folded-cascode amplifier circuits has been studied with our approach. For Miller, buffer, and folded-cascode, a cascade of harmony search and particle swarm optimization on SVR, ngspice, and cadence simulators was found to be roughly 4 times, 2.5 times, and 2.5 times faster, respectively, than the flat approach with equal or better results. In future work, we will improve the approach by including more demanding circuits, statistical deviations, circuit breeding, advanced optimization, and layout generation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The design of integrated circuits and systems, in particular, with analog and mixed-signal units, is a well-known subject of increasing technical and economical significance. The underlying optimization of the design parameters, from device sizing for established circuits to creation or synthesis of customized or novel circuits, traditionally is executed by experienced human designers, but the issue of analog design automation has been pursued in academia and industry for more than two decades now. The advance of Moore’s law and the increasing complexity and heterogeneity of established and leading edge processes along with increasing robustness and dependability requirements further kindle the interest in efficient analog electronics design automation. In addition to circuit sizing/creation for a new task, also the migration of existing circuit libraries to a new technology is a rewarding task for automation. Adding of statistical, drift, and aging considerations for design centering and yield optimization, including layout synthesis and post-layout simulation results in the loop, can be witnessed from concept to commercial tool level, e.g., in Muneda’s WickED framework [1]. Predominantly, uni-variate statistical approaches are used, the employed optimization methods are computationally costly, and the design process is rather opaque and lacks interactivity options for the user during the design process.
In our work, we pursue the conception of a modular, multi-platform, and open-access python system for analog design automation, denoted as Analog Block and system Sizing and sYNTHesis (ABSYNTH) framework. The research goals are the design of an evolving, self-learning architecture for incremental inclusion of cells and knowledge with efficient reuse, to employ well-performing hierarchical optimization by cascading methods, e.g., SVR and proven work-horses like PSO, and Harmony Search algorithms, during the automated design process, and adding transparence and improved user interaction by domain-specific visualization techniques. The self-learning approach promises to create a perfect balance between speed and low accuracy of function approximation techniques and high accuracy and low speed of the simulation-based techniques, additionally removing the need for massive set of examples required to train the function approximators.
In this paper, well will focus on a three-level optimization cascade and novel visualization techniques, which are demonstrated for commonly used circuits [2–5] nominal sizing on schematic level.
In Sect. 2, the state-of-the-art is briefly rehearsed. Section 3 describes the baseline of our research and investigation, referring to the previously outlined state-of-the-art. Section 4 presents the architecture of the design environment, and Sect. 5 introduces our custom dynamic optimization space visualization. Before concluding, Sect. 7 presents and discusses our experiments and obtained results.
State-of-the-art
Automated analog design automation has been subject of intensive research for the last three decades starting with works like IDAC [6] and OASYS [7]. There are four major approaches to tackle this problem: (1) knowledge-based [6, 8], (2) equation-based [9, 10], (3) simulation-based [11, 12], and (4) model-based approaches [13, 14] as surveyed in [15]. Each approach has its advantages and disadvantages. The first two approaches require considerable preparatory work for each circuit individually. The substantial time and expertise required for this preparatory work is not alleviating the introduction of more circuits, the growth of the design database, and the corresponding increase in productivity [16]. Simulation-based approaches can be very effective in this regard, however, they consume a lot of computational resources and time, if applied in straight or flat form. With the increase in the speed of computing machinery, this problem is not as significant as it has been a decade ago, but the complexity of the design tasks is also increasing. The fourth approach deals with using regression methods like support vector regression (SVR) and neural networks to create a model-based equivalent representation as a replacement for simulators and costly detailed simulation runs. Though the model-based computations are extremely fast, they require careful training and a significant amount of samples selected in a time-consuming and sensitive process for each circuit and process technology pair to reach an acceptable prediction accuracy [17].
Optimization algorithms are an essential part of the last three approaches. While, older equation-based approaches used simulated annealing [12] genetic algorithms [18] etc., approaches with posynomial equations and geometric programming are becoming more predominant in the last decade [19–21]. From our survey, we found that genetic algorithms (GA), genetic programming and simulated annealing have been predominantly used in simulator- and model-based approaches. Other evolutionary algorithms such as Particle swarm optimization (PSO) [22], differential evolution (DE), harmony search (HS) [23], and artificial bee colony optimization (ABC) which have become popular in other fields have also been used to a lesser degree in these approaches. Some notable works are [2–5]. In the first work [5], ultra-low-power Miller OTA and a three-stage Miller op-amp were sized using PSO, GA, and a modified PSO called HPSO and found that HPSO converges better than the alternatives. In [2] OTA Miller has been optimized using DE, PSO and ABC they are compared. They found that DE performs better than PSO, while ABC does not reach the targets in this scenario. In the third work [3], nth order filters were optimized by PSO, ABC, HS, and DE. They found that, while HS is the fastest algorithm, it has the highest error while the other algorithms converged better. In [4], comparing DE and HS, the authors also came to a similar conclusion. In our experiments, comparing standard PSO (SPSO) 2007, SPSO 1995, harmony search, and cuckoo search, we found that PSO (SPSO95) and HS are able to provide fast solutions reaching our desired target values. We will be employing PSO and HS in our work in a more involved way, both individually for reference purpose as well as in a dedicated hierarchy. We will also show that our approach produces effective results even with default parameter settings.
Baseline of investigation
In general, analog sizing and synthesis has been applied to a rich variety of practical circuits, e.g., filters, oscillators, PLLs, amplifiers and comparators, and in part new circuits have been created or evolved by the algorithms. However, in most of the work we refer to, the focus has been on amplifier circuits. Thus, we considered three typical single-ended op amp circuits of increasing complexity as a research vehicle for this work. These are a two-stage Miller amplifier (MA) [24], three-stage buffer amplifier (BA) [24], and a folded-cascode amplifier (FCA). For all these circuits, for each transistor the length was fixed as 1 \(\upmu \)m and the width was chosen as a design parameter. Narrowing down the degrees of freedom by choosing a unit length of all transistors, the number of devices corresponds to the number of optimization parameters. These variables are the parameters that shall be used for the optimization process inside the framework. There is one restriction in the investigations: the passive components are fixed to a typical value and are not yet subject to optimization themselves. The knowledge-based information such as matching information or symmetry constraints for transistor pairs were obtained from the schematic and provided to the systems optimization engine, further reducing the number of parameters.
Circuits
The MA shown in Fig. 1 is taken from [24]. It consists of ten transistors. After symmetry considerations, we optimize eight design parameters, while pursuing ten objectives in the multi-objective approach, as shown in Table 4.
The second amplifier is a BA shown in the Fig. 2. It is taken from [24]. It consists of twenty-four transistors. After symmetry considerations we optimize nine parameters, while pursuing ten objectives in the multi-objective approach, as shown in Table 4.
The third amplifier is an FCA [24] as shown in the Fig. 3. The circuit consists of twenty-nine transistors. After symmetry considerations, we optimize 18 parameters, while again pursuing ten objectives in the multi-objective approach, as shown in Table 4. The vast number of transistors is attributed to the type of bias circuit used, while constructing this circuit. This FCA was created in a practical activity of our group as a part of a voltage-controlled voltage-source for impedance spectroscopy.
Meta-heuristic algorithms
In this work, we focus on two algorithms mentioned in Sect. 2. The first one is PSO which has been used in analog design automation before in [2, 3, 5]. In our work, we will use the PSO as presented in [22]. The parameters of PSO are described below.
-
w: Inertia. typ.range: [0, 1].
-
c1: Cognitive scaling factor. typ. range: [0, 2].
-
c2: Social scaling factor. typ. range: [0, 2].
-
r1, r2: Random values between 0 and 1.
-
Velocity: Particle’s velocity.
-
Local: Particle’s local best known position.
-
Global: Swarm’s best known position.
-
Current: Current position of the particle.
The second algorithm is harmony search (HS). It is a music-inspired algorithm, which has been studied for analog design automation in a few papers [3, 4]. In this work, we use harmony search as described by the algorithm [23].
The parameters of the HS algorithm are provided below:
-
HMS (harmony memory size): problem dependent.
-
HMCR (harmony memory considering rate): typ.range: [0.7, 0.99].
-
PAR (pitch adjusting rate): typ range: [0.1, 0.5].
Multi-objective optimization approach
We employ an agglomerative approach for fitness function computation in multi-objective optimization, which makes use of the weighted sum of normalized fitness values of each parameter. A thresholded normalized difference between the target specifications and the simulator outputs are used to obtain the individual specifications as described in Eq. (1).
where ov is the obtained value from function approximators or simulators. Due to this advantageous normalization, for the regarded moderate complexity circuits, unity weights could be successfully employed unlike in previous works [25], where the finding of appropriate weights for unnormalized cost function represented a major challenge. We have found by moderate sensitivity investigations that other than unity weights will not have perceivable advantages in result quality. Only if one of several objectives are esteemed considerably higher in value than the others, then the application of non-unity weights will be meaningful.
Time measurement
In our work, we deal with two simulators, the open source ngspice simulator (NGS) and cadence virtuoso OCeaN (OCN). We use AMS hitkit 4.1 with 350 nm technology. All the experiments were performed on a Core2 Duo PC with 2 GHz frequency and 4 GB memory. We have used the linux time command to measure the time taken for the simulations. This provided three time values, real time, which is the same as wall clock time, user time, which is the time when the simulation was using the CPU resources, and system time, when the program was accessing the kernel. The sum of user time and system time would provide information independent of the other processes running in the system. In all cases, the time values mentioned are the mean of five or more runs.
ABSYNTH concept and architecture
Hybrid multi-objective optimization approach
ABSYNTH concept is shown in Fig. 4. As we have mentioned in Sect. 2, the accuracy vs. speed properties of model-based and simulator-based approaches are substantially different, which is illustrated in Fig. 5. The time comparison in running simulations with these methods is provided in Tables 1 and 2. Further, the BSIM3v3 version employed by cadence and ams hitkit is 3.24, while ngspice uses the newer BSIM3v3 version 3.3. This leads to subtle discrepancies in the results, which are not harmful in our hierarchical approach (Fig. 5).
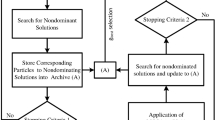
From the information above, we can come to a conclusion that seeding the more accurate simulators with the results of less accurate ones will provide a nice balance. This is exploited in our work by cascading the methods as shown in Fig. 1. The mixture of random seeds and seeds from the simulators help in maintaining the diversity. This approach has shown to be very robust to problems with the insufficiently trained SVR model during the start-up phase of the self-learning system explained in Sect. 4.2, as it will only increase the time consumed to reach the results, but will not affect their quality.

Incrementally evolving self-learning capability
In standard model-based approaches using function approximators, usually neural networks [26] or support vector regression [13, 17] methods, etc., are employed together with sufficient and suitable training data for each investigated circuit to predict the simulator results [17]. Acquiring these data and performing the training of the named methods take substantial time until acceptable results are achieved. This implies, that for every new circuit the designer has to cope with this overhead, even for sophisticated methods, like the active training described in [17]. In our work, in contrast, we try to incrementally obtain the initial SVR training data for a new circuit from the results generated by the meta-heuristic algorithms on NGS and cadence OCN simulators from previous runs. Thus, we have a high initial simulation effort for a new circuit, which decreases with the number of conducted circuit simulations in our evolving self-learning architecture. The procedure is transparent to the user, i.e., there is no workload overhead imposed on the user. This is illustrated in Fig. 6. The parameters of the SVR \(\gamma \), \(\varepsilon \) and K are found automatically using the same meta-heuristic algorithms again, e.g., PSO or HS, as an efficient alternative to the commonly used grid search. This search is done only during the first training phase for each new circuit. Here, the percentage of random seeds, as shown in Algorithm 1, can be controlled based on the number of iterations in NGS for effective learning in SVR.
Status of the ABSYNTH architecture’s implementation
Figure 7 shows a block diagram with all the current elements and the building blocks planned in the immediate future of this work.
TRAVISOS: optimization space visualization
The monitoring of the optimization process by visualization means adds transparency to the design process and allows for assessing the quality of the obtained solution [27, 28]. In addition to the conventional cost function over time-based visualizations, as shown in Fig. 8, the optimization space itself and the evolution of the regarded population of optimization solutions can be elucidated by suitable visualization techniques. The underlying problem of optimization space visualization is quite related to the well-known task of feature space visualization in pattern recognition and intelligent system design [29, 30]. As in these related fields, the high-dimensional data, comprised here by the design or sizing parameters in analog circuit and system design automation, have to be subject to a dimensionality reducing mapping, as, e.g., multi-dimensional-scaling (MDS) and, in particular, non-linear-mapping (NLM) methods, like Sammon’s mapping and its extension to data recall (NLMR) [27, 29, 31]. The application of these methods allow the generation of a lower dimensional, e.g., three-dimensional, similarity preserving scatter plot, which will show solution quality and relative location of the solutions. For instance, the latter information allows to understand which regions of the solution space have been explored and what level of diversity is currently maintained by the optimization algorithm. This can naturally be extended from single snapshot monitoring of the optimization process to a complete solution swarm trajectory visualization. As will be shown in the following experimental section, our suggested visualization approach can give numerous salient insights not to be obtained from the conventional cost or progress curve plots. In addition, the approach opens the door to interactive visualization and optimization [28] by allowing selective user manipulations from one population to the next. The proposed new heuristic method for solution swarm trajectory visualization in the regarded optimization space is illustrated in Fig. 2. First, a standard NLM is computed based on the initialization data of the optimization problem. Then, the projections of all swarm elements for the next and all following populations will be computed by the NLMR, which uses the previously obtained results as anchor points. Thus, at low cost successive mappings with smooth transitions of solution locations for the trajectory visualization can be computed. However, it is a well-known fact that all dimensionality reducing mappings have their problems in terms of displaying an unavoidable mapping error related to the intrinsic dimensionality of the data to be mapped as well as to the employed mapping method itself. This means that solutions with unchanged location in the original design parameter space could see unjustified and disturbing location fluctuations in successive projections.
To avoid this problem, in our work, the previous position in the projection space of solutions with unchanged location in the design space will be just copied to the new projection space of the next optimization iteration, only the solutions with changes will be subject to NLMR projection.

Summarizing, the TRAVISOS heuristic mapping approach given in Fig. 2 allows the creation of solution swarm trajectory visualization in the regarded optimization space and problem at low to moderate computational cost. This can be employed for transparent analysis and user-centered interactive optimization or designer-in-the-loop optimization, e.g., [27]. The suggested TRAVISOS algorithm and the overall approach are salient for but not limited to the analog sizing and synthesis activities regarded in this work.
Experiments and results
Circuit sizing methods results
As prepared in the previous sections, here we study two different optimization cascades embedded in our hybrid self-learning architecture. The first optimization cascade will employ PSO algorithm for all three steps in the cascade. This will be referred to as PPP. The second approach employs Harmony Search algorithm on the model-based (SVR) and NGS levels, while PSO is the choice for OCN simulation level. Table 4 shows the results for mean of a minimum of five runs of the algorithm. The target specifications, which are composed of 10 objectives in the multi-objective approach, have been taken from the respective references mentioned above with the circuits. We have also added the resulting specifications manually reached in our group, by students with moderate experience in analog design. A flat reference run of PSO OCN combination is additionally added for comparison. All the transistor sizes are in integer steps in this work; however, resolution can be changed as desired. The experiment parameters can be found in Table 3. The minimum and maximum values shown in Table 3 are the soft boundary conditions for the algorithms. These are also the transistor size limits. At present, area has not been included as an optimization parameter in the algorithm (Fig. 9).
From these results we can see that both the algorithm cascades work at least competitively and are able to reach their targets much faster than the corresponding manual and flat approaches. We can also see that using Harmony search for providing the seeds is faster than using PSO without any reduction in the quality of results. In Fig. 10, we can see the progress of the fitness function over each iteration for one example per type. In the case of the MA, we can see how the fitness improves ideally for both PPP and HHP approaches (HHP reaches the target in lesser number of iterations.). In the second scenario with BA, we can observe that the SVR model fitness and the ngspice fitness varies, this is because of the models training and the scale of the Y-axis, which is much smaller for this example. In the FCA example, the SVR is unable to reach a meaningful fitness value; however, the NGS and OCN are able to reach the targets. These examples underpin the robustness of such a hybrid approach. From Fig. 10a and Fig. 12, we can observe the evolution of MA as described in Fig. 6. Even though the latter takes more iterations than the former, the computational effort is much less. Further, it is possible to stop the SVR much earlier, when it reaches saturation with little or no error reduction (see Fig. 12).
Comparison of conventional visualization and TRAVISOS 5: TRAVISOS NGS generation 1 (1954 in Fig. 12)
Visualization methods results
In this section, we would like to demonstrate the advantages of the suggested TRAVISOS method in giving additional insight into crucial steps of the optimization processes by selected examples and visualization snapshots from our investigations reported above. However, the main advantage of TRAVISOS method and tool will only be fully be visible, when it is interactively employed in the ABSYNTH design framework. We have attached a complementary video (online) [32] generated from visualizations of all optimization iterations for one example of PSO with Miller amplifier. Each point in the video represents one solution. One has be to reminded about the fact that in the given form of visualization, reducing from ten or more dimensions down to three, the values given on the three axes only express similarity or closeness of design parameter sets, but have no explicit physical meaning.
First, we regard here the example of the FCA discussed above. Though the conventional visualization given in Fig. 10c is salient, more relevant information can be provided. In Fig. 11, we have visualized snapshots of one particular, tentatively trained SVR results for PPP by TRAVISOS approach. Additionally, we have run a complete simulation using ngspice, merged the two data sets, and visualized the resulting solution space.
From Fig. 10c, we cannot understand the issue, as information on solution diversity, clogging, clustering, or coverage in the optimization space cannot explicitly be extracted. In contrast, TRAVISOS allows this, showing that the SVR model here has not been trained with sufficient data and it is compelled to move towards one, obviously not too fortunate region in the optimization space, while the ngspice results, which have achieved good fitness, are more diverse and spread out into more fortunate regions of the optimization space. The visualization helps to understand the optimization space, as well as the current aptness of SVR training for new cells, and opens the door for interactive optimization.
In Figs. 12, 13, 14, 15, 16 and 17, the entire cascade of the optimization process is visualized by the TRAVISOS method, limiting to a series of representative snapshots here. A complementary video showing the process can be found in [32].
These clearly show the movement of the PSO particles for the SVR model in the optimization space and the evolution of the solution quality. Then, it can be monitored, how these are translated into solutions in the NGS simulations. In the end, we see the final solutions achieved by the OCN.
While the training of the SVR model in general can be understood as a continuing process without a definite termination, the visualization can help to assess whether a sufficient training quality has been achieved. In the investigated case, SVR seems to have been satisfactorily trained, as can be understood from the unchanged solution space for the final result.
This is confirmed by the following simulations steps, since the NGS simulations finish in one generation and OCN reach the target in just three generations.
Summarizing, the TRAVISOS method complements conventional graphical monitoring and assessment techniques of optimization processes. Even the simple examples of the first realization step given here show that salient additional information to better understand and in the future guide the optimization and the underlying design process are provided.
Conclusions
In this paper, we have introduced three novel contributions to the vivid field of electronic design automation for analog and mixed-signal circuits and systems. Inspired by concepts from computational intelligence, we introduced an evolving self-learning architecture that alleviates the introduction of new circuits into the supported cell spectrum, and we introduced and demonstrated a hierarchical multi-objective optimization cascade from SVR, PSO, and HS in the context of this architecture that saves effort in general and is flexible with regard to existing a priori knowledge vs. required computational effort. This approach was demonstrated as part of our emerging ABSYNTH environment together with cadence tools, ngspice and ams AG 0.35 \(\upmu \)m CMOS technology on schematic level for amplifier structures commonly used in related work, but with a more comprehensive set of specification values as optimization goals in an agglomerative approach. Results compared to conventional flat optimization approaches and comparison to manual design activities showed the viability and salience of our approach, e.g., for the best case of the Miller amplifier and HHP as the best variant of our approach, consumed only 26% time of the flat approach, while fully meeting the specifications. A final comparison between the properties and advantages of ABSYNTH to other ADA methods is shown in Table 5.
Further, we introduced a novel visualization method of the optimization space and trajectory (TRAVISOS) that allows more efficient and transparent human supervision of optimization process properties, e.g., diversity and neighborhood relations of solution qualities.
In future work, we will extend the palette of pursued specifications values also to area, etc., take our work to higher level circuits, e.g., instrumentation amplifiers, filters, phase-locked loops, and voltage-controlled current sources, or even non-linear circuits, and add statistical, yield-related optimization, circuit breeding, as well as physical layout generation, extraction, and inclusion in the optimization loop. In particular, we will also extend our work on the TRAVISOS method moving it from an analysis to an interactive tool, achieving designer-in-the-loop functionality, i.e., letting the designer observe, potentially interfere, and guide the optimization by existing expert knowledge or intuition to faster explore better locations in the optimization space.
References
Muneda (2014) EDA tools for design migration, modelling, verification and optimization of custom IC design and OLED simulation. http://www.muneda.com
Sabat S, Kumar K, Udgata S (2009) Differential evolution and swarm intelligence techniques for analog circuit synthesis. In: World congress on nature biologically inspired computing, 2009. NaBIC 2009, pp 469–474. doi:10.1109/NABIC.2009.5393356
Vural R, Ayten U (2012) Optimized analog filter approximation via evolutionary algorithms. In: 2012 12th international conference on intelligent systems design and applications (ISDA), pp 485–490. doi:10.1109/ISDA.2012.6416586
Kudikala S, Sabat S, Udgata S (2011) Performance study of harmony search algorithm for analog circuit sizing. In: 2011 international symposium on electronic system design (ISED), pp 12–17. doi:10.1109/ISED.2011.42
Thakker R, Baghini M, Patil M (2009) Low-power low-voltage analog circuit design using hierarchical particle swarm optimization. In: 2009 22nd international conference on VLSI design, pp 427–432. doi:10.1109/VLSI.Design.2009.14
Degrauwe MGR, Nys O, Dijkstra E, Rijmenants J, Bitz S, Goffart BLAG, Vittoz E, Cserveny S, Meixenberger C, Van Der Stappen G, Oguey H (1987) IDAC: an interactive design tool for analog CMOS circuits. IEEE J Solid State Circuits 22(6):1106–1116. doi:10.1109/JSSC.1987.1052861
Maulik P, Carley L, Allstot D (1993) Sizing of cell-level analog circuits using constrained optimization techniques. IEEE J Solid State Circuits 28(3):233–241. doi:10.1109/4.209989
El-Turky F, Perry E (1989) Blades: an artificial intelligence approach to analog circuit design. IEEE Trans Comput Aided Design Integr Circuits Syst 8(6):680–692. doi:10.1109/43.31523
Koh HY, Sequin C, Gray P (1990) OPASYN: a compiler for CMOS operational amplifiers. IEEE Trans Comput Aided Design Integr Circuits Syst 9(2):113–125. doi:10.1109/43.46777
Gielen GGE, Walscharts H, Sansen W (1989) ISAAC: a symbolic simulator for analog integrated circuits. IEEE J Solid State Circuits 24(6):1587–1597. doi:10.1109/4.44994
Nye W, Riley D, Sangiovanni-Vincentelli A, Tits A (1988) Delight.spice: an optimization-based system for the design of integrated circuits. IEEE Trans Comput Aided Design Integr Circuits Syst 7(4):501–519. doi:10.1109/43.3185
Medeiro F, Perez-Verdu B, Rodriguez-Vazquez A, Huertas J (1995) A vertically integrated tool for automated design of sigma; delta; modulators. IEEE J Solid State Circuits 30(7):762–772. doi:10.1109/4.391115
Bernardinis FD, Jordan MI, Sangiovanni-Vincentelli A (2003) Support vector machines for analog circuit performance representation. In: Proceedings of DAC, pp 964–969
Barros M, Guilherme J, Horta N (2007) An evolutionary optimization kernel using a dynamic GA-SVM model applied to analog IC design. In: 18th European conference on circuit theory and design, 2007. ECCTD 2007, pp 32–35. doi:10.1109/ECCTD.2007.4529529
Barros MFM, Guilherme JMC, Horta NCG (2010) Analog circuits and systems optimization based on evolutionary computation techniques. Springer, Berlin
Ochotta E, Rutenbar R, Carley L (1996) Synthesis of high-performance analog circuits in ASTRX/OBLX. IEEE Trans Comput Aided Design Integr Circuits Syst 15(3):273–294. doi:10.1109/43.489099
Ding M, Vemuri R (2005) An active learning scheme using support vector machines for analog circuit feasibility classification. In: 18th international conference on VLSI design, 2005, pp 528–534. doi:10.1109/ICVD.2005.47
Wim Kruiskamp DL (1995) Darwin: CMOS OPAMP synthesis by means of a genetic algorithm. In: 32nd conference on design automation, 1995. DAC ’95, pp 433–438. doi:10.1109/DAC.1995.249986
Zhang Y, Liu B, Yang B, Li J, Nakatake S (2012) CMOS op-amp circuit synthesis with geometric programming models for layout-dependent effects. In: 2012 13th international symposium on quality electronic design (ISQED), pp 464–469. doi:10.1109/ISQED.2012.6187534
del Mar Hershenson M (2002) Design of pipeline analog-to-digital converters via geometric programming. In: IEEE/ACM international conference on computer aided design, 2002. ICCAD 2002, pp 317–324. doi:10.1109/ICCAD.2002.1167553
DasGupta S, Mandal P (2010) An improvised MOS transistor model suitable for geometric program based analog circuit sizing in sub-micron technology. In: 23rd international conference on VLSI design, 2010. VLSID ’10, pp 294–299. doi:10.1109/VLSI.Design.2010.31
Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings., IEEE international conference on neural networks, 1995, vol 4, pp 1942–1948. doi:10.1109/ICNN.1995.488968
Geem ZW, Kim JH, Loganathan G (2001) A new heuristic optimization algorithm: harmony search. Simulation 76(2):60–68. doi:10.1177/003754970107600201
Allen PE, Holberg DR (2002) CMOS analog circuit design. Oxford University Press, Oxford
Tawdross PMM (2007) Bio-inspired circuit sizing and trimming methods for dynamically reconfigurable sensor electronics in industrial embedded systems. Ph.D. thesis, Institute of Integrated Sensory Systems (ISE), Dept. EIT, University of Kaiserslautern, Kaiserslautern
Alpaydin G, Balkir S, Dundar G (2003) An evolutionary approach to automatic synthesis of high-performance analog integrated circuits. IEEE Trans Evolut Comput 7(3):240–252. doi:10.1109/TEVC.2003.808914
Hayashida N, Takagi H Visualized IEC: interactive evolutionary computation with multidimensional data visualization. In: 26th annual conference of the IEEE industrial electronics society, 2000. IECON 2000, vol 4, pp 2738–2743 (2000). doi:10.1109/IECON.2000.972431
König A, Blutner FE, Eberhardt M, Wenzel R (1998) An acoustic data base navigator for the interactive analysis of psycho-acoustic sound archives. In: Proceedings of the 5th international conference on soft computing and information/intelligent systems IIZUKA’98, 16–20 October 1998, Iizuka, Fukuoka, Japan. World Scientific, pp 60–63
König A (2001) Dimensionality reduction techniques for interactive visualization, exploratory data analysis, and classification. In: Pattern recognition in soft computing paradigm. World Scientific Publishing Co., Inc., River Edge, pp 1–37. http://dl.acm.org/citation.cfm?id=375278.375282
König A, Eberhardt M, Wenzel R (1999) Quickcog self-learning recognition system—exploiting machine learning techniques for transparent and fast industrial recognition system design. In: Image processing Europe, pp 10–19
Pohlheim H (2006) Multidimensional scaling for evolutionary algorithms 8212; visualization of the path through search space and solution space using sammon mapping. Artif Life 12(2):203–209. doi:10.1162/artl.2006.12.2.203
(2015) Travisos (supplementary video). https://www.youtube.com/watch?v=I8qFMB9Xtss
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kammara, A.C., Palanichamy, L. & König, A. Multi-objective optimization and visualization for analog design automation. Complex Intell. Syst. 2, 251–267 (2016). https://doi.org/10.1007/s40747-016-0027-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40747-016-0027-3