Estimating Reliability Characteristics of the Log-Logistic Distribution Under Progressive Censoring with Two Applications

Abstract

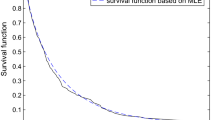
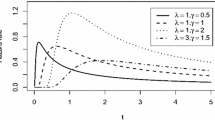
Let a progressively type-II (PT-II) censored sample of size m is available. Under this set-up, we consider the problem of estimating unknown model parameters and two reliability characteristics of the log-logistic distribution. Maximum likelihood estimates (MLEs) are obtained. We use expectation–maximization (EM) algorithm. The observed Fisher information matrix is computed. We propose Bayes estimates with respect to various loss functions. In this purpose, we adopt Lindley’s approximation and importance sampling methods. Asymptotic and bootstrap confidence intervals are derived. Asymptotic intervals are obtained using two approaches: normal approximation to MLEs and log-transformed MLEs. The bootstrap intervals are computed using boot-t and boot-p algorithms. Further, highest posterior density (HPD) credible intervals are constructed. Two sets of practical data are analyzed for the illustration purpose. Finally, detailed simulation study is carried out to observe the performance of the proposed methods.

Appendix A

For the present problem, we have $(\eta _1,\eta _2)=(\alpha ,\beta )$. Denote $\varpi (t_i; \alpha , \beta )=\frac{( \beta ^{\alpha } \ln \beta + t_i^{\alpha } \ln t_i)}{\beta ^{\alpha }+t_i^{\alpha }}$ and $\varsigma (t_i; \alpha , \beta )=\frac{\alpha \beta ^{\alpha }}{\beta ^{\alpha }+t_i^{\alpha }}$. We obtain the following expressions, which are required to compute the desired Bayes estimates.

$$\begin{aligned} l_{03}= & {} \frac{2 m}{\alpha ^3}-\sum _{i=1}^m \left( U_i+2\right) \bigg ( 2\varpi ^3(t_i; \alpha , \beta )-\frac{3\varpi (t_i; \alpha , \beta )(\beta ^\alpha (\ln \beta )^2+t_i^\alpha (\ln t_i)^2)}{\beta ^\alpha +t_i^\alpha }\nonumber \\&+\frac{(\beta ^\alpha (\ln \beta )^3+t_i^\alpha (\ln t_i)^3)}{\beta ^\alpha +t_i^\alpha }\bigg ), \end{aligned}$$

(A.1)

$$\begin{aligned} l_{30}= & {} \frac{1}{\beta ^3}\left[ 2 \alpha \left( \sum _{i=1}^m U_i+m\right) -\sum _{i=1}^m \left( U_i+2\right) \varsigma (t_i; \alpha , \beta ) \bigg ((\alpha -2) (\alpha -1)+2\varsigma ^2(t_i; \alpha , \beta )\right. \nonumber \\&\left. -3(\alpha -1)\varsigma (t_i; \alpha , \beta ) \bigg )\right] , \end{aligned}$$

(A.2)

$$\begin{aligned} l_{12}= & {} -\frac{1}{\beta ^2}\left[ \left( \sum _{i=1}^m U_i+m\right) -\sum _{i=1}^m \frac{\left( U_i+2\right) \varsigma (t_i; \alpha , \beta )}{\alpha } \bigg (2 \alpha \varsigma (t_i; \alpha , \beta ) \varpi (t_i; \alpha , \beta )\right. \nonumber \\&\left. -2 \varsigma (t_i; \alpha , \beta ) (1+\alpha \ln \beta )- (\alpha -1) \alpha \varpi (t_i; \alpha , \beta ) +(\alpha -1) \alpha \ln \beta +2\alpha -1\bigg )\right] , \end{aligned}$$

(A.3)

$$\begin{aligned} l_{21}= & {} -\sum _{i=1}^m \frac{\left( U_i+2\right) \varsigma (t_i; \alpha , \beta ) }{\alpha \beta }\left[ 2\ln \beta +\alpha (\ln \beta )^2 - 2(1+\alpha \ln \beta ) \varpi (t_i; \alpha , \beta )\right. \nonumber \\&\left. +\alpha (2\varpi ^2(t_i; \alpha , \beta )-\frac{\beta ^\alpha (\ln \beta )^2+t_i^\alpha (\ln t_i)^2}{\beta ^\alpha +t_i^\alpha }) \right] . \end{aligned}$$

(A.4)

The following derivatives are useful for the computation of the Bayes estimates of r(t) and h(t) as discussed in Sect. 4.1.2. Under the LINEX loss function, $\vartheta (\alpha ,\beta )=\exp \{-dr(t)\}$. Denote $\iota (t; \alpha , \beta )=\frac{d \beta ^{\alpha } t^{\alpha } \exp \{-d r(t)\}}{\left( \beta ^{\alpha }+t^{\alpha }\right) ^2}$. Thus,

$$\begin{aligned} u_1= & {} \ln \left( \frac{t}{\beta }\right) \iota (t; \alpha , \beta ) , \end{aligned}$$

(A.5)

$$\begin{aligned} u_2= & {} -\frac{\alpha \iota (t; \alpha , \beta )}{\beta } , \end{aligned}$$

(A.6)

$$\begin{aligned} u_{11}= & {} \frac{ (\ln (\frac{t}{\beta }))^2 \left( \beta ^{2 \alpha }+d\beta ^{\alpha } t^{\alpha }-t^{2 \alpha }\right) \iota (t; \alpha , \beta ) }{\left( \beta ^{\alpha }+t^{\alpha }\right) ^2}, \end{aligned}$$

(A.7)

$$\begin{aligned} u_{22}= & {} \frac{\alpha \left( (\alpha +1) \beta ^{2 \alpha }+\beta ^{\alpha } (\alpha d+2) t^{\alpha }-(\alpha -1) t^{2 \alpha }\right) \iota (t; \alpha , \beta )}{(\beta \left( \beta ^{\alpha }+t^{\alpha }\right) )^2}, \end{aligned}$$

(A.8)

$$\begin{aligned} u_{21}= & {} u_{12}=\frac{ \left( \alpha \left( -\beta ^{2 \alpha }-d \beta ^{\alpha } t^{\alpha }+t^{2 \alpha }\right) \ln (\frac{t}{ \beta })-\left( \beta ^{\alpha }+t^{\alpha }\right) ^2\right) \iota (t; \alpha , \beta ) }{\beta \left( \beta ^{\alpha }+t^{\alpha }\right) ^2}. \end{aligned}$$

(A.9)

When the loss function is taken to be the entropy loss function, then $\vartheta (\alpha ,\beta )=r(t)^{-c}$. Denote $\Omega (t; \alpha , \beta )=t^\alpha r(t)^{-c}$. We compute the following derivatives:

$$\begin{aligned} u_1= & {} c \beta ^{-\alpha } \ln \left( \frac{t}{\beta }\right) r(t) \Omega (t; \alpha , \beta ) , \end{aligned}$$

(A.10)

$$\begin{aligned} u_2= & {} -\alpha c \beta ^{-(\alpha +1)} r(t)\Omega (t; \alpha , \beta ), \end{aligned}$$

(A.11)

$$\begin{aligned} u_{11}= & {} \frac{c (\ln (\frac{t}{\beta }))^2 \left( \beta ^{\alpha }+c t^{\alpha }\right) \Omega (t; \alpha , \beta )}{\left( \beta ^{\alpha }+t^{\alpha }\right) ^2}, \end{aligned}$$

(A.12)

$$\begin{aligned} u_{22}= & {} \frac{\alpha c \left( (\alpha +1) \beta ^{\alpha }+(\alpha c+1)t^{\alpha }\right) \Omega (t; \alpha , \beta )}{\beta ^2 \left( \beta ^{\alpha }+t^{\alpha }\right) ^2}, \end{aligned}$$

(A.13)

$$\begin{aligned} u_{21}= & {} u_{12}=\frac{c \left( -\beta ^{\alpha }-\alpha \ln (\frac{t}{\beta })\left( \beta ^{\alpha }+c t^{\alpha }\right) -t^{\alpha }\right) \Omega (t; \alpha , \beta )}{\beta \left( \beta ^{\alpha }+t^{\alpha }\right) ^2}. \end{aligned}$$

(A.14)