1 Introduction

Volatility of exchange rate can be defined as the variation of price at which two different countries’ currencies are traded [1]. Exchange rate volatility is a major source of concern for macroeconomic policy makers because it is synonymous with risk and uncertainty. It is well-documented that internationally-oriented countries are particularly sensitive to foreign exchange rate volatility [2]. Understanding the dynamics of volatility is therefore crucial for the design of a well-informed policy that seeks to minimize the deleterious impact of uncertainty on the national welfare.

From a microeconomic perspective, corporate strategists and business analysts make wide use of exchange rate volatility models in financial risk management and portfolio construction. Forecasting the volatility of foreign exchange rate has a great importance for international traders’ export and import decisions. Exchange rate volatility causes risk-averse traders to reduce their transaction because of the high unpredictability of their profits. By contrast, risk-takers could benefit from seeking out hedging opportunities. Furthermore, accurate volatility forecasting is crucial for international investors who require portfolio diversification beyond their national border.

In light of the preceding discussion, we conduct a rigorous research on volatility forecasting using weekly Euro-ETB exchange rate as a case study. In particular we seek to evaluate the forecasting performance of GARCH-type models with a view to analyzing their ability to capture stylized features of volatility clustering, persistence, and leverage effects.

The current exchange rate system classified as a (defacto) crawling peg to the USA, i.e. a managed (or dirty) float. In this sense, officially determined USD-ETB exchange rate variation does not fully capture the extent of currency volatility. This has motivated our choice of using Euro-ETB, not least because Euro-area countries are major trading partners of Ethiopia. Furthermore by using high frequency (i.e. weekly) data, we avoid the danger of averaging-out volatility episodes that characterizes studies based on yearly data. It is also worth noting that using weekly data obviates the need to construct real exchange rate which relies on having accurate domestic and foreign prices deflators.

As explained earlier, volatility of exchange rate affects policy makers as well as investors. Hence, the importance of exchange rate volatility studies cannot be overestimated. Many researchers including [3,4,5] modeled exchange rate volatility using GARCH type models, but without offering insight on their models. de Dieu Ntawihebasenga et al. [6] modeled volatility of exchange rate in Rwandese markets using symmetric GARCH models neglecting asymmetric models. To the best of my knowledge, no research has been done on forecasting volatility of weeklely Euro—ETB exchange rate using a variety of GARCH type models, and robust forecast evaluation techniques. Hence, the present study contributes to the literature by bridging existing knowledge gap on volatility forecasting in Ethiopia.

The general objective of the study is to forecast volatility of Ethiopian Birr/Euro exchange rate using GARCH-type models. Specifically assess the patterns of ETB/Euro exchange rate volatility, explore GARCH type models that capture the volatility of Euro-ETB exchange rate behavior, and evaluate the volatility forecasting power of various GARCH-type models.

2 Research Methodology

2.1 Data Source

To achieve the objectives of the study, weekly Euro-ETB exchange rate data were collected from the National Bank of Ethiopia. In the literature, statistical test of model’s forecast performance are commonly conducted by splitting a given data set into an in-sample period which are used for initial parameter estimation and model selection; and out–sample period which are used to evaluate forecast performance. In this study, the in-sample period runs from January 3, 2000 to December 31, 2014 (780 observations), whereas the out-of-sample period runs from January 1, 2015 to December 2, 2015 (48 observations).

2.2 Model Specification and Econometric Tests

2.2.1 Unit Root Test of the Variables

There are many tests for determining whether a time series is stationary or non stationary. The ones used in the present study are Augmented Dickey–Fuller (ADF) test and the Phillips–Perron (PP) test.

2.2.1.1 Augmented Dickey–Fuller test

The Augmented Dickey Fuller (ADF) test, originally developed by [7]. The ADF test constructs a parametric correction for higher order correction by assuming that the series \( y_{t} \) follows an AR (P) process and adding P lagged difference terms of the dependent variable to the right hand side of the test regression. The ADF test equation is specified as:

$$ \Delta y_{t} = \omega + \beta \,t + (\rho - 1)\,y_{t - 1} + \sum\limits_{i = 1}^{p} {\alpha_{i} } \Delta y_{t - i} + \varepsilon_{t} $$
(2.1)

where \( \varepsilon_{t} \) is the error term,\( \omega \) the intercept and, \( \beta \,t \) shows that the time series has a trend. The test statistic is given below:

$$ Z_{t} = \frac{{\hat{\rho }^{*}}}{{SE(\hat{\rho }^{*})}} $$

where \( SE(\rho ^{*}) \) standard error of \( \rho ^{*} \). The test is carried out by testing the joint effect hypothesis:\( Ho:\,\beta = \rho^{*} = 0 \) where \( \rho^{*} = \rho - 1 \) using the conventional F test but comparing the test statistic with the critical F values developed by Dicky and Fuller.

2.2.1.2 Phillips–Perron (PP) Test

Phillips and Perron [8] developed a number of unit root tests that have become popular in the analysis of financial time series. The Pillips–Perron (PP) unit root tests differ from ADF test mainly in how they deal with serial correlation and heteroscedasticity in the errors. The test regression for the PP test is:

$$ \Delta y_{t} = \,\,\,\alpha_{o} + \beta \,t + \pi \,y_{t - 1} + u_{t} $$
(2.2)

where is \( \alpha_{o} \) intercept, \( \beta \,t \) shows that the time series has a trend and \( u_{t} \) is the disturbance term. The tests correct for any serial correlation and heteroscedasticity in the error term \( u_{t} \) of the test regression by directly modifying the test statistics \( t_{\pi = 0} \) and \( T_{{\hat{\pi }}} \). These modified statistics, denoted \( Z_{t} \) and \( Z_{\pi } \), are given by:

$$ Z_{t} = \left( {\frac{{\hat{\sigma }^{2} }}{{\hat{\lambda }^{2} }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} t_{\pi = 0} - \frac{1}{2}\left( {\frac{{\hat{\lambda }^{2} - \hat{\sigma }^{2} }}{{\hat{\lambda }^{2} }}} \right)\left( {\frac{{TSE(\hat{\pi })}}{{\hat{\sigma }^{2} }}} \right) $$
$$ Z_{\pi } = T_{{\hat{\pi }}} - \frac{1}{2}\left( {\frac{{T^{2} \cdot SE(\hat{\pi })}}{{\hat{\sigma }^{2} }}} \right)\left( {\hat{\lambda }^{2} - \hat{\sigma }^{2} } \right) $$

The terms \( \hat{\sigma }^{2} \) and \( \hat{\lambda }^{2} \) are consistent estimates of the variance parameters.

$$ \sigma^{2} = \mathop {\lim }\limits_{T \to \infty } T^{ - 3} \mathop \sum \limits_{t = 1}^{T} E\left( {u_{t}^{2} } \right) $$
$$ \mathop {\lim }\limits_{ \to \infty } \mathop \sum \limits_{t = 1}^{T} E\left( {T^{ - 1} \cdot S_{T}^{2} } \right) $$

where \( S_{T} = \sum\nolimits_{t = 1}^{T} {u_{t} } \). The sample variance of the least squares residual \( \hat{u}_{t} \) is a consistent estimate of \( \sigma^{2} \), and the Newey–West long run variance estimate of \( u_{t} \) using \( \hat{u}_{t} \) is consistent estimate of \( \lambda^{2} \). Under the null hypothesis that \( \pi = 0 \) the PP Zt and \( Z_{\pi } \) statistics is used the conventional F test but comparing the test statistic with the critical F values developed by Dicky and Fuller.

2.2.2 Autoregressive Integrated Moving Average (ARIMA) Model

Prior to analyzing conditional variance model, estimating adequate conditional mean models is important. This paper was used ARIMA (p, d, q) process which is given as below:

$$ \alpha \,(Z)\nabla^{d} r_{t} = \omega + \theta (Z)\varepsilon_{t} $$
(2.3)

where \( \alpha (Z) = \,1 - \alpha_{1} Z - \cdots - \alpha_{p} Z^{p} \), \( \theta (Z) = 1 + \theta_{1} Z + \cdots + \theta_{q} Z^{q} \), d is the order of differencing, Z is the backward shift operator (\( Z^{p} r_{t} = r_{t - p} ,\quad Z^{q} \varepsilon_{t} = \varepsilon_{t - q} \) p, q = 1,2,3,…), \( \varepsilon_{t} \) is the disturbance term,\( \omega \), \( \alpha = \,\alpha_{1} ,\alpha_{2} , \ldots ,\alpha_{p} \) and \( \theta_{{}} = \theta_{1} ,\theta_{2} , \ldots ,\theta_{q} \) are parameters and \( r_{t} \) is returns of weekly Euro-ETB exchange rate.

2.2.2.1 Testing for ARCH Effects

The presence of conditional heteroscedasticity is referred to as the ARCH effects. Ljung–Box statistics Q (m) and Lagrange Multiplier (LM)tests are the appropriate ARCH effects tests and were used in this study. Ljung–Box test statistic (Q) was used to assess the independency among the residuals.

$$ Q = n\left( {n + 2} \right)\mathop \sum \limits_{k = 1}^{h} \frac{{\hat{\rho }_{k} }}{n - K}^{2} $$
(2.4)

where n is the sample size, \( \hat{\rho }_{k} \) is the sample correlation of the residuals at a lag k and h is the number of lags being tested. Q is asymptotically distributed as Chi-square with (h-p-q) degree of freedom, where h is the maximum lag considered, p and q are order of AR and MA respectively.

$$ LM = TR^{2} \sim x^{2} \left( q \right) $$
(2.5)

where q is degree of freedom, T denotes the number of total observations, and R2 coefficient of determination computed from the regression equation of \( \hat{\varepsilon }^{2}_{t} \) specified as:

$$ \hat{\varepsilon }_{t}^{2} = \gamma_{o} + \gamma_{1} \hat{\varepsilon }_{t - 1}^{2} + \gamma_{2} \hat{\varepsilon }_{t - 2}^{2} + \cdots + \gamma_{q} \hat{\varepsilon }_{t - q}^{2} $$
(2.6)

The hypothesis of LM test is:\( H_{O} :\gamma_{q} = 0 \) \(\; versus \,H_{1} :\gamma_{q} \ne 0 \). The rejection of the null hypothesis indicates the presence of ARCH (q) effect. It is important to apply the LM test on the residuals from the mean equation (ARIMA) model not ARCH/GARCH-type model.

2.2.2.2 Test of Normality

When dealing with ARCH/GARCH-type models, we first examine the characteristics of the unconditional distribution of the exchange rate. This will enable us to explore and explain some stylized facts exist in the financial time series. In statistics, the Bera and Jarque [9] test is a test of departure from normality based on the sample skewness and kurtosis. The test statistics is:

$$ JB = \frac{{nS^{2} }}{6} + \frac{{n(K - 3)^{2} }}{24} $$

where n is number of observations, S is the sample skewness and K is the sample kurtosis. Under the null hypothesis, the Jarque–Bera statistic is distributed as Chi-square with two degree of freedom.

2.2.3 ARCH Models

The ARCH (Autoregressive Conditionally Heteroscedasticity) model, introduced by [10], is one of the main methods used to analyze financial time series data. The basic idea of ARCH model is that the mean corrected exchange rate return \( \varepsilon_{t} \) is serially uncorrelated, but dependent. The dependency of \( \varepsilon_{t} \) can be described by a simple quadratic function of its lagged values. Specifically, an ARCH (q) model is specified as:

$$ \begin{aligned} \varepsilon_{t} & = \eta_{t} \sigma_{t} \\ \sigma_{t}^{2} & = \alpha_{o} + \alpha_{1} \varepsilon_{t - 1}^{2} + \alpha_{2} \varepsilon_{t - 2}^{2} + \cdots + \alpha_{q} \varepsilon_{t - q}^{2} \\ \end{aligned} $$
(2.7)

where \( \varepsilon_{t - i}^{2} ,\;\;i = 1,2, \ldots ,q \) are the lagged squared residuals from the conditional mean equation of the series exchange rate \( \eta_{t} \) is a white noise process with zero mean and unit variance. Here we impose the non negativity constraints: \( \alpha_{o} > 0,\;\alpha_{i} \ge 0,\;\;i = 1,2, \ldots ,q \)

2.2.4 Generalized Autoregressive Conditional Heteroscedasticity (GARCH) Models

There are some short comings of ARCH models. First of all, ARCH models assume that positive and negative shocks have the same effects on volatility because it depends on the square of previous shocks, which is not the case in practice. Also the ARCH formulation can lead to complexity as the order of the model gets higher. GARCH model used as alternative ARCH model. This model has been introduced by Bollerslev [11]. A typical GARCH (p, q) model is specified as:

$$ \varepsilon_{t} = \eta_{t} \sigma_{t} $$
$$ \sigma_{t}^{2} = \alpha_{o} + \alpha_{1} \varepsilon_{t - 1}^{2} + \alpha_{2} \varepsilon_{t - 2}^{2} + \cdots + \alpha_{q} \varepsilon_{t - q}^{2} + \beta_{1} \sigma_{t - 1}^{2} + \beta_{2} \sigma_{t - 2}^{2} + \cdots + \beta_{p} \sigma_{t - p}^{2} $$
(2.8)

where \( \eta_{t} \) is sequence of independent and identically distributed random variables with zero mean and unit variance, \( \alpha_{i} ,\quad i = 0,1,2, \ldots ,q \) and \( \beta_{j} ,\quad j = 1,2, \ldots ,p \) are parameters of the model. \( \alpha_{i} \ge 0,\,\,\,\,\beta_{j} \ge 0 \) given the non negativity restriction, \( \alpha_{1} + \alpha_{2} + \cdots + \alpha_{q} + \beta_{1} + \beta_{2} + \cdots + \beta_{p} \) < 1 is the condition for stationary. \( \beta_{1} ,\beta_{2} , \ldots ,\beta_{p} \) measure the extent to which volatility shock today feed through into the next period’s volatility.

2.2.5 GARCH Model Extensions

In most cases, the basic GARCH model provides a reasonably good model for analyzing financial time series and estimating conditional volatility. However, there are some aspects of the model which can be improved so that it can better capture characteristics and dynamics of a particular time series. Since bad news (negative shocks) tends to have a larger impact on volatility than good news (positive shocks) [12], we explore various asymmetric volatility models such as EGARCH and GJR-GARCH.

2.2.5.1 E-GARCH Model

E-GARCH model was proposed by [13] allows for asymmetric and leverage effects. The model has the following representation:

$$ \varepsilon_{t} = \eta_{t} \delta_{t} $$
$$ \log \,\sigma^{2}_{t} = \alpha_{o}^{{}} + \sum\limits_{i = 1}^{q} {\alpha_{i} \frac{{\left| {\varepsilon_{t - i} } \right| + \gamma_{i} \varepsilon_{t - i} }}{{\sigma_{t - i}^{{}} }}} + \sum\limits_{j = 1}^{p} {b_{j} \log \,\sigma^{2}_{t - j} } $$
(2.9)

where the coefficients \( \gamma_{i} \) capture the asymmetric impact of news. If \( \gamma_{i} \) = 0, then a positive surprise (\( \varepsilon_{t - 1} \) > 0) has the same effect on volatility as a negative surprise of the same magnitude. If − 1 < \( \gamma_{i} \) < 0, a positive surprise increases volatility less than a negative surprise. If \( \gamma_{i} \) < − 1, a positive surprise actually reduces volatility while a negative surprise increases volatility

2.2.5.2 GJR-GARCH Model

Asymmetric consequences of positive and negative innovations can also be captured with simple modification of the linear GARCH framework. This was introduced by Glosten et al. [14]. The general specification of this model is as follows:

$$ \varepsilon_{t} = \eta_{t} \sigma_{t} $$
$$ \sigma^{2}_{t} = \omega + \sum\limits_{i = 1}^{q} {(\alpha_{i} } \varepsilon^{2}_{t - i} + \gamma_{i} s_{t - i} \varepsilon^{2}_{t - i} ) + \sum\limits_{j = 1}^{p} {\beta_{j} } \sigma^{2}_{t - j} $$
(2.10)

where \( s_{t - i} \) is a dummy variable which takes the value of 1 when \( \varepsilon_{t - i} < 0 \) and otherwise zero. This extra term allows for the asymmetric effect (impact of negative shocks: \( (\alpha_{i} + \,\gamma_{i} )\varepsilon_{t - i}^{2} \) and impact of positive shocks: \( \alpha_{i} \varepsilon_{t - i}^{2} \)). In this GJR-GARCH model, it is supposed that the impact of \( \varepsilon^{2}_{t - i} \) on \( \delta_{t}^{2} \) depends on whether the shock is negative or positive. A nice aspect of GJR-GARCH model is that it is easy to test the null hypothesis of no leverage effect. The parameter \( \gamma \), which captures the asymmetric effect, is expected to be positive. In fact, \( \gamma_{1} = \gamma_{2} = \cdots = \gamma_{q} = 0,\, \) means that the news impact curve is symmetric, i.e. past positive shocks have the same impact on today’s volatility as negative shocks

2.2.6 Choosing the Optimal Lag Length and Model Selection Criterion

The optimal lag length of the ARIMA and ARCH/GARCH type’s model was chosen using ACF, PACF plot and information criteria. The PACF of a time series is a function of its ACF and is a useful tool for determining the order p of an AR model, because PACF cuts off at lag p for an AR (P) process. For MA models, ACF is useful in specifying the order because ACF cuts off at lag q for an MA (q) [15]. Some of the more popular information criterion includes AIC and BIC are also used to select the appropriate models.

2.2.7 Parameter Estimation

Ordinary least squares (OLS) works great (assuming we meet some preliminary conditions), but one assumptions that must be made for OLS to work is that the disturbance term \( \varepsilon_{t} \) are homoscedastic, that is, the variance of each disturbance term is the same. However, this is not always a very realistic assumption in real life, since variance is not always constant. Under the presence of ARCH effects, OLS estimation is not efficient. Therefore, the study employed maximum likelihood estimation (MLE) for estimating unknown parameters in GARCH type models.

2.2.7.1 The Distribution of Error Term (\( \varepsilon_{t} \))

To explore the effect of changing the distributional assumptions, this study explores the use of the normal distribution, student t-distribution and GED.

2.2.7.2 Gaussian Distribution

If a random variable \( \varepsilon_{t} \) is assumed to follow a normal distribution with mean zero and conditional variance \( \delta_{t}^{2} \), the probability density function is given by:

$$ f\left( {{\raise0.7ex\hbox{${\varepsilon_{t} }$} \!\mathord{\left/ {\vphantom {{\varepsilon_{t} } ,}}\right.\kern-0pt} \!\lower0.7ex\hbox{$,$}}\;\varepsilon_{t - 1} , \ldots ,\varepsilon_{o} } \right) = \frac{1}{{\sqrt {2\pi \sigma_{t}^{2} } }}e^{{\frac{{ - 1\varepsilon_{t}^{2} }}{{2\sigma_{t}^{2} }}}} $$
(2.11)

where \( \varepsilon_{t}^{2} \) is the residual square and \( \sigma_{t}^{2} \) conditional variance.

2.2.7.3 Student’s t-Distribution

The unconditional distribution of many financial time series seems to have fatter tails than allowed by the Gaussian family. Some of this can be explained by the presence of ARCH; that is, even if error term has a Gaussian distribution, the unconditional distribution of \( \varepsilon_{t} \) is non Gaussian with heavier tails than the Gaussian distribution. Even so, there is a fair amount of evidence that the conditional distribution of \( \varepsilon_{t} \) is often non Gaussian as well. The same basic approach can be used with non Gaussian distributions. For example, [11] proposed that \( u_{t} \) might be drawn from a t-distribution with v degree of freedom, where v is regarded as a parameter to be estimated by maximum likelihood method. If \( \varepsilon_{t} \) has a t-distribution with v degree of freedom and a scale parameter \( s_{t} \), then its probability density function(PDF) is given by:

$$ f(\varepsilon_{t} ) = \frac{{\varGamma \left( {\frac{v + 1}{2}} \right)}}{{\sqrt {\pi v} \,\varGamma (v/2)}}\,\,s_{t}^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left[ {1 + \frac{{\varepsilon_{t}^{2} }}{{s_{t} v}}} \right]^{{\left( {\frac{v + 1}{2}} \right)}} $$
(2.12)

where \( \varGamma (.) \) is the Gamma function. This density can be used in place of Gaussian specification along with the same specification of the conditional mean and conditional variance [16]. For v = 2, the expression (3.15) is just the standard normal distribution. If v < 2, the density has thicker tails than normal, were as for v > 2 it has thinner tails. If v > 2, then \( \varepsilon_{t} \) has mean zero and variance:

$$ E(\varepsilon_{t}^{2} ) = \frac{{s_{t} v}}{v - 2} $$

hence a t-variable with v degrees of freedom and variance \( \sigma_{t}^{2} \) obtained by taking

$$ s_{t} = \frac{{\sigma_{t}^{2} (v - 2)}}{v} $$
2.2.7.4 Generalized Error Distribution (GED)

The GED is a symmetric distribution than can be both leptokurtic and platykurtic depending on the degree of freedom v (v > 1). The GED has the following density function:

$$ f(\varepsilon_{t} ) = \frac{{v\exp \left[ { - 1/2\left| {{\raise0.7ex\hbox{${\varepsilon_{t} }$} \!\mathord{\left/ {\vphantom {{\varepsilon_{t} } \lambda }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\lambda $}}} \right|^{v} } \right]}}{{\lambda 2^{{\left( {{\raise0.7ex\hbox{${v + 1)}$} \!\mathord{\left/ {\vphantom {{v + 1)} v}}\right.\kern-0pt} \!\lower0.7ex\hbox{$v$}}} \right)}} \varGamma (1/v)}},\quad \lambda = \left[ {\frac{{2^{ - 2/v} \varGamma \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 v}}\right.\kern-0pt} \!\lower0.7ex\hbox{$v$}}} \right)^{{}} }}{\varGamma (3/v)}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} $$
(2.13)

For v = 2, the GED is a standardized normal distribution whereas the tails are thicker than in the normal case when v < 2, and thinner when v > 2.

2.2.8 Model Adequacy Checking

The model diagnostic checks are performed to determine adequacy or goodness of fit of a chosen model. The model diagnostic checks are performed on residuals and more specifically on standardized residuals. Jarque–Bera normality test and plot of residuals such as the histogram normal probability plot were used. If the model fits the data well, the histogram of the residuals should be approximately symmetric. Lagrange Multipliers and Ljung–Box Q-test were used to check the presence of the remaining ARCH effects as well as test for autocorrelation.

2.2.9 Forecasting

The out- of- sample optimal l-step ahead forecast of \( Y_{t + 1} \) given all information up to a time t is the conditional expectation E(Yt+l). The associated l-step ahead forecast error is \( \varepsilon_{t + l} = Y_{t + l} - E(Y_{t + l} ) \). Forecast of ARCH model in Eq. (2.7) can be obtained recursively as those of an AR model. Consider an ARCH (q) model at forecast origin h. The 1-step ahead forecast of \( \sigma^{2}_{h + 1} \) is:

$$ \delta_{h(1)}^{2} = \hat{\alpha }_{o} + \hat{\alpha }_{1} \varepsilon_{h}^{2} + \cdots + \hat{\alpha }_{q} \varepsilon_{h + 1 - q}^{2} $$
(2.14)

GARCH model forecast can be obtained using the methods similar to those of an ARMA model [15]. Consider the GARCH (p, q) in Eq. (3.9) and assume that the forecast origin is h. A 1-step ahead forecast of \( \sigma^{2}_{h + 1} \) is:

$$ \sigma_{h(1)}^{2} = \hat{\alpha }_{o} + \hat{\alpha }_{1} \varepsilon_{h}^{2} + \cdots + \hat{\alpha }_{q} \varepsilon_{h + 1 - q}^{2} + \hat{\beta }_{1} \sigma_{h}^{2} + \cdots + \hat{\beta }_{p} \sigma_{h + 1 - p}^{2} $$
(2.15)

Once we had picked the best model that fit data, then a one step-ahead forecast was computed. The objective is to evaluate the forecasting ability of those selected models. In particular we will explore the role of the forecasting evaluation criteria and the importance of the measure of “realized volatility”.

2.2.9.1 Realized Volatility Measures

Realized volatility is defined as the sum of squared high frequency returns (such as intraday returns) and is a popular measure of volatility in empirical finance [17, 18]. The realized volatility models are calculated from high frequency data, intraday data. The measure of this realized volatility can be expressed as:

$$ R_{V} = \sum\limits_{i = 1}^{m} {r_{t}^{2} } $$

where \( r_{t}^{2} \) the intra daily return square in the mth interval. Similarly, in the case of this study, since we have no intra daily data, the realized variance of the weekly data set was computed using the daily data as follows:

$$ \delta_{Rvt}^{2} = \frac{{\sum\nolimits_{i = 1}^{m} {(r_{t} - \bar{r}_{t} )^{2} } }}{m - 1} $$

where \( r_{t} \) is the daily returns of Euro-ETB exchange rate (\( r_{t} = \log (y_{t} ) - \log (y_{t - 1} ) \) of the mth days interval (m = 5) and \( \bar{r}_{t} \) is the average of return daily of Euro-ETB exchange rate and m is the number of intervals of days.

2.2.9.2 Volatility Forecast Comparisons

There are many ways to evaluate the forecasting performance of a model and there is no widely accepted single measure to compare models [15]. In this study, two types of methods were employed (magnitude measured and distributional measures). It is common to use the out-of-sample forecast to aid the selection of which model is best suited for the series under the study. Typically one divides the data into subsets, one in which the model parameters are fitted (estimation subsample) and another subset used to evaluate the forecasting performance of the models (forecasting subsamples). An out-of sample comparison involves using first part of a sample to estimate the parameters of the models and saving the latter part of the sample against which to gauge its forecasting ability. In this study 1-step-ahead forecast horizon was considered. Throughout two proxies of true volatility which is a latent variable (the squared return and realized variance) was used. The relative performance of the models used to generate exchange rate volatility forecasts is determined according to the following two criteria:

2.2.9.3 Mean Square Error (MSE)

Mean square error is one of the statistically most widely measures forecasting accuracy of the models. The MSE for a sample size T is given as below:

$$ MSE = \frac{1}{T}\sum\limits_{t = 1}^{T} {\left( {r_{t}^{2} - \hat{\sigma }_{t}^{2} } \right)} )^{2} $$

where \( \hat{\sigma }_{t}^{2} \), t = 1, 2,…,T is the estimated conditional variance obtained from the fitted the ARCH/GARCH type models and \( r^{2} \) is the proxy variables (squared returns and realized variance). The model with smallest value of MSE indicates that the most powerful forecasting ability out of the other models under consideration.

2.2.9.4 Mean Absolute Error (MAE)

The mean absolute error (MAE) is defined as:

$$ MAE = \frac{1}{T}\sum\limits_{t = 1}^{T} {\left| {r_{t}^{2} - \hat{\delta }_{t}^{2} } \right|^{{}} } $$

If we compute MAE of the various forecasting models, then we would prefer the model with the smallest value of MAE.

3 Results and Discussions

The plot of weekly Euro-ETB exchange rate for the period of January 2000–December 2015 is shown in Fig. 1. From this figure, it is evident that unconditional mean and variance are changing over time and the series has an increasing trend over time. The changing mean and variance of Euro-ETB exchange rate over time is an indication of the non stationarity of the level series. This implies that it is difficult to model ARIMA and ARCH/GARCH-type models for non stationary series. Therefore, in order to achieve stationary, logarithmic and differencing transformation were applied on the level series.

Fig. 1
figure 1

Euro-ETB exchange rate at level

Full size image

Table 1 presents the findings of the ADF test and PP test and formally confirms that the first difference of natural logarithms of Euro-ETB exchange rate is stationary.

Table 1 ADF and PP unit root test of first differenced logarithm of weekly Euro-ETB Exchange rate
Full size table

3.1 Test for ARCH Effect

Table 2 portrays the ARCH effect tests on the residuals of ARIMA (5, 1, 2) model. These results show the presence of ARCH effects in the Euro-ETB exchange rate. This suggests that modeling ARCH/GARCH types is appropriate for the data set.

Table 2 ARCH effect tests
Full size table

3.2 Fitting GARCH (1, 1) Model

Table 3 shows that in the mean equation ARIMA (5, 1, 2) with students-t distribution, except at lag 4 and 5, all the coefficients are significant at 5% significance level. In the variance equation, except for the constant term (\( \alpha_{o} \)), ARCH term (\( \alpha_{1} \)) and GARCH term (\( \beta_{1} \)) for GARCH (1, 1) with the assumption of students-t distribution are significant at 5 percent significance level. The sum of two estimated ARCH and GARCH coefficients suggest that shocks to the conditional variance are highly persistent.

Table 3 GARCH models with different distributional assumptions
Full size table

3.3 Fitting EGARCH (1, 1) Model

Table 4 presents the EGARCH (1, 1) estimation results. The result of EGARCH (1, 1) with students t-distribution reveals in the variance equation, except for the constant term and \( \alpha_{1} \), the other coefficients are statistically significant at 5% significance level. The coefficient \( \gamma_{1} \) for leverage effects in the output is 0.1778 and significantly different from zero at 5% level, indicating that there exist asymmetric effects.

Table 4 EGARCH (1, 1) model with student-t distribution and GED
Full size table

3.4 Fitting GJR-GARCH (2, 2) Model

Table 5 shows the output of GJR-GARCH with different error distributional assumptions. Results reveal that the variance equation of GJR-GARCH with student’s-t distribution are more significant at 5% level of significance than the normal distribution and GED. The variance equation of GJR-GARCH (2, 2) with student’s-t distribution model shows that except the constant (\( \alpha_{o} \)), all the coefficients are statistically significant at 5 percent significance level. As it is observed from the results of GJR-GARCH with student’s-t distribution in Table 5, the both coefficients (\( \gamma_{1} \) and \( \gamma_{2} \)) that represent the asymmetric feature of conditional variance is significant, implying that there are asymmetric volatility in the series. Furthermore, the sign of \( \gamma \) is negative, indicating the presence of opposite leverage effect (anti-leverage effects) in the exchange rate. The possible explanation is that when there is a bad news (the lagged error is negative) the variance decreases.

Table 5 GJR-GARCH with different error distributions
Full size table

3.5 Model Adequacy Checking

Model diagnosis for ARCH (8), GARCH (1, 1), EGARCH (1, 1) and GJR-GARCH (2, 2) reveal that the remaining serial correlation and ARCH effect test of the standardized squared residuals of the series. The null hypotheses of the series stating that there is no serially correlated and ARCH effects respectively can not be rejected at 5 percent significance level. This implies that there is no serial correlation and no remaining ARCH effect. Jarque–Bera normality test confirms the null hyphothesis of normal distribution. Therefore, the model is correctly specified and used for forecasting the volatility of the series.

3.6 Volatility Forecast Comparison of Models

Tables 6 and 7 present forecast performance results through MSEs and MAEs for all models. Table 6 shows that GJR-GARCH (2, 2) with normal and students t-distribution has the smallest values MSE 6.04e−08 and MAE 0.0001902 respectively by taking the squared returns of Euro-ETB exchange rate as a proxy variable. This implies that GJR-GARCH (2, 2) with normal distribution and students t-distribution has the highest forecasting power of volatility of Euro-ETB exchange rate. Table 7 reveals that the GARCH (1, 1) with students t-distribution had the smallest values of MSE 2.24e−08 and MAE 0.0001409 by considering the realized variance as a proxy variable. This indicates that GARCH (1, 1) with students t-distribution have high forecasting ability of the volatility of Euro-ETB exchange rate. Table 7 also shows that the MSE and MAE values associated with realized variance as the proxy for against which to measure forecasts is higher than when squared returns of weekly Euro/ETB exchange rate are utilized (Table 6). This indicates that realized variance increases the measure of forecasting ability of the models.

Table 6 Model comparisons of forecasting ability using squared return of weekly ETB/Euro exchange rate as a proxy variable
Full size table
Table 7 Model comparisons of forecasting ability using realized variance as a proxy variable
Full size table

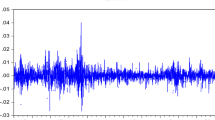
Figure 2 Shows a one-step-ahead forecasted conditional variance of the first difference of weekly logarithm of Euro-ETB exchange rate by using GARCH type models. From this figure it is evident that the variance forecasted has one large spike around 2010 by using ARCH/GARCH models and have two large spikes before 2010 and after 2010 by using EGARCH and GJR-GARCH models. This large spike indicates that devaluation of Ethiopian birr against the Euro. Before and after a period of relatively high conditional variances around 2010, the variances stabilize and enter a phase of clustering behavior. In this forecast, we are looking at a series of rolling one-step-ahead forecasts for the conditional variance. The result of EGARCH and GRJ-GARCH models shows an existence of a relatively high volatility of Euro-ETB exchange rate.

Fig. 2
figure 2

A one-step-ahead forecasted conditional variance of Euro-ETB exchange rate by using GARCH type models

Full size image

4 Summary and Conclusions

This paper provides analysis of volatility forecasting of Euro-ETB exchange rate using weekly data spanning the period January 3, 2000 to December 2, 2015. The forecasting performance of various GARCH-type models is investigated based on forecasting performance criteria such as MAE and MSE based tests, and alternative measures of realized volatility.

The empirical results have implied that the Euro-ETB exchange rate series exhibits persistent volatility clustering over the study period. We document evidence that ARCH (8), GARCH (1, 1), EGARCH (1, 1) and GJR-GARCH (2, 2) with normal distribution, students-t distribution and GED are found to be the best in-sample estimation models in terms of the volatility behavior of the series. Amongst these models, GJR-GARCH (2, 2)and GARCH (1,1) models with students t-distribution appeared to perform best in terms of one step-ahead forecasting based on realized variance calculated from the underlying daily data and squared return of the series, respectively. Realized variance as the proxy for against which to measure forecasts is higher than when squared returns of weekly Euro/ETB exchange rate are utilized. This indicates that realized variance increases the measure of forecasting. A one-step-ahead forecasted conditional variance of Euro-ETB exchange rate portrays one large spike around 2010. This large spike indicates that devaluation of Ethiopian birr against the Euro. From the forecasted conditional variance, it is evident that Euro-ETB exchange rate are volatile. The current validity of weekly Euro-ETB exchange rate followed by the past volatility. This volatility behavior may affects International Foreign Investment and the trade balance of the country.

Therefore, GJR-GARCH (2, 2) with student’s t-distribution is the best model both interms of fit the stylized facts and forecasting performance of the volatility of weekly Euro-ETB exchange rate among others.