1 Introduction

Massive exploitation of offshore wind energy is planned worldwide and much of this is in depths greater than 50 m requiring floating platforms. Various concepts are being developed with spar-type and semi-sub platforms already deployed successfully, e.g. Hywind and Windfloat, respectively. Tension leg platforms (TLPs) and barge-type platforms are also being considered. Present turbine capacities of around 5 MW are being extended to 12–15 MW and platforms for 20 MW are being designed (De Souza and Bachynski-Polić 2022). However, significant wind power requires speeds greater than about 5 m/s which has only 30–40% availability, e.g. Arinaga and Cheung (2012), which means that substantial storage is required for continuity of supply. On the other hand, swell wave power greater than 20 kW/m has availability typically of 90%, also Arinaga and Cheung (2012). Combining wave energy devices in wind farms has been assessed (Kluger et al. 2023) and shown to reduce the storage required. Wave energy devices may also be incorporated on wind semi-sub platforms directly, both to provide additional power output and potentially to reduce platform pitch motion. The wind turbine nacelle acceleration should be below about 0.3 g for drive train operation, e.g. Carbon Trust (2015). Platform motion is also a concern for on/off loading of equipment and personnel and is a general concern for human wellbeing.

Heaving point absorbers have been incorporated on a three-float semi-sub of Windfloat type (Roddier et al. 2010) between the upper and lower connecting beams (Hu et al. 2020). Analysis indicates average power of 300 kW is possible in regular waves with height 2 m. 6–15 wave floats were tested and the smaller number was optimal. In addition, the wave floats reduced pitch motion. Si et al. (2021) considered the three-float DeepCwind semi-sub (Robertson et al. 2017) with an additional hinged wave float outer to each float. In irregular waves with significant wave height \({H}_{{\text{s}}}\) = 2.5 m and peak period \({T}_{{\text{p}}}\) = 10 s, 180 kW mean wave power was generated with reactive control, although this increased platform motion while spring-damper control halved wave power, but slightly decreased platform motion. Kamarlouei et al. (2022) investigated experimentally a six-float semi-sub in a hexagonal formation and added three and six outer wave floats on three sides of the hexagon. The results are quite complex showing that wave floats affect platform motion, but optimisation is necessary to be effective. Michailides et al. (2016) investigated flap wave energy on a three-column semi-sub and estimated average power of 60 kW with \({H}_{{\text{s}}}\) = 3 m and \({T}_{{\text{p}}}\) in the range 7–12 s. A further concept with torus wave floats on the columns of a braceless three-float 5 MW wind platform was investigated numerically by Tian et al. (2023). In regular waves with height 2 m, four torus generated nearly 400 kW of mean wave power. However, pitch motions may be increased in swell waves and decreased in smaller wave periods. Li et al. (2018) investigated torus wave energy generation on a spar platform estimating 100 kW average power with \({H}_{{\text{s}}}\) = 2.3 m and \({T}_{{\text{p}}}\) = 10 s. Ren et al. (2020) also investigated torus wave energy generation on a TLP giving 800 kW with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 11 s.

Platform motion may be reduced directly in semi-subs by allowing water to oscillate internally between floats as tuned mass dampers in resonance, e.g. Fath et al. (2020), or by actively pumping between floats (Stansby 2021). The latter reduces motion by 30–50% by balancing heave-induced forces in floats with relatively small power requirements as the pumps can also operate as turbines, so the net power required has only to overcome friction losses in the connecting pipes.

In this paper, we consider further the addition of hinged wave floats to generate power from swell waves which are generally present even when the regional wind speed is small, below the cut-in value for a wind turbine. When wind speed is above rated, wave power will be small relative to wind and not necessary. The wave floats are integrated with the wind floats to be aligned and of the same size. Wave power should be significant for a wide range of headings. The fore-aft spacing of wind to wave floats should enable forcing to be roughly in anti-phase to generate moment due to surge forcing about the hinges above the deck level. A further aim is to reduce pitch and roll on the wind floats and hence acceleration at the hub. The analysis is by time domain linear diffraction–radiation modelling, validated previously for multi-float wave energy configurations (Stansby et al. 2017; Stansby and Carpintero Moreno 2020), shown experimentally to be remarkably linear even in large waves (Santo et al. 2017; Stansby and Carpintero Moreno 2020).

The paper is organised as follows. The next section describes the idealised platform to support an NREL 5 MW turbine, e.g. Robertson et al. (2017). The hydrodynamic modelling Sect. 3 follows, based on a time domain linear wave–platform interaction model of Cummins form including the actuator torques and float drag. This is developed from an in-house code applied to the multi-float wave energy converter M4 showing good agreement with experiment, as reviewed in Stansby and Draycott (2024). Section 4 describes the results for various wave and wind conditions. Waves with headings between 0° and 360° are analysed. The results are discussed in Sect. 5 and conclusions follow.

2 Platform design

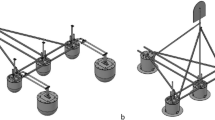
We consider a three float wind platform similar to WindFloat (Fig. 1) except the angle between the floats outer to the float supporting the turbine is 90°. This is so that two additional floats may be located opposite the outer floats with hinges on the central supporting float as shown in Fig. 2. These float positions rotate principally in vertical planes and damping torque is applied at the hinges to absorb mechanical energy.

Fig. 1
figure 1

Windfloat platform, photo of the Kincardine Offshore Wind Farm project courtesy of Principle Power

Full size image
Fig. 2
figure 2

Diagrammatic sketch of hybrid wind–wave platform. The yellow floats are rigidly connected to support the wind turbine. The blue floats are connected to the wind floats by green beams which rotate the power take-off (PTO) on hinges. On the mid-float hinges, PTO boxes are incorporated for wave energy conversion, shown enlarged in the inset

Full size image

To test this concept, we use the well-known 5 MW NREL turbine (Robertson et al. 2017) and all floats are of 15 m diameter and 15.7 m draft. This provides sufficient buoyancy to support the turbine. The hinged floats are effectively free floating with axes vertical in still water. The effective mass distribution is given in Table 1 incorporating the masses of cross beams. The buoyancy of each float is 2774e3 kg. This is an idealised platform specified to demonstrate the concept. The hinge point for floats 4 and 5 is 10 m above SWL and freeboard is 9 m. Higher hinge points were not found to increase power. The spacing between outer floats and mid float 2 is 40 m. These dimensions are similar to those of DeepCwind.

Table 1 BEM mode notation
Full size table

Float number

Float

Ballast

Turbine + column (OC5)

Mass (kg)

Position relative to SWL (m)

Mass (kg)

Position relative to SWL (m)

Mass (kg)

position relative to SWL (m)

1

1500e3

− 2.85

1274e3

− 12.56

  

2

1500e3

− 2.85

236e3

− 14.13

1038e3

67.5

3

1500e3

− 2.85

1274e3

− 12.56

  

4

1500e3

− 2.85

1274e3

− 12.56

  

5

1500e3

− 2.85

1274e3

− 12.56

 

–

  1. The centre of mass of combined floats A (123) is 0.15 m above SWL, while the centre of buoyancy is − 7.85 m

3 Mathematical formulation and model

In the multi-float time-domain formulation, hydrodynamic forces are due to linear wave excitation including diffraction, added mass, radiation damping, restoring, drag and wind forces. Their definitions are based on hydrodynamic frequency-domain potential-flow coefficients from the BEM OREGEN code (Li and Stansby 2023) in Cummins method for irregular waves. The standard form of the JONSWAP wave spectrum will be used with a high spectral peakedness \(\gamma \) = 3.3 representative of swell waves. Five degrees of freedom are included with yaw assumed to be negligible due to mooring constraint.

Angular rotations about the \(y\) axis \({\theta }_{y}\) and the \(x\) axis \({\theta }_{x}\) through O are clockwise positive, \(h\) is the horizontal longitudinal distance from O to a float mid-point, \(t\) is the transverse distance from O, and \(v\) is the vertical distance from O, positive downwards. \(H\), \(V\) and \(T\) are total hydrodynamic forces in conventional \(x,z,y\) directions, \({M}_{y}\) is pitch moment and \({M}_{x}\) is roll moment about O.

Although there are three A floats, these may be considered as a single body (\({n}_{A}=3\) floats) with hinged float B (\({n}_{B}=1\)) and float C (\({n}_{{\text{c}}}=1\)) acting individually in Fig. 3. The total number of floats \(N={n}_{A}+{n}_{B}+{n}_{C}=5.\) Note the mooring constraint will be applied as a small horizontal stiffness forces in two directions to prevent drift.

Fig. 3
figure 3

Plan view of configuration with wind support body A (in red) and stabilising hinged wave floats B and C (in black) with hinges/PTO at right angles at O shown as thick solid lines. Principal beams are shown as thick lines and secondary beams as thin lines. The turbine column on A is solid orange. \(\beta \) is the heading angle.

Full size image

Bodies A and C are effectively combined in pitch and \({\Sigma }^{{n}_{AC}}\) denotes summation for bodies A and C. Taking moments about the \(y\) axis at O for pitch accounting for masses (turbine, floats, ballast),

$$-\sum_{i=1}^{{n}_{AC}} {m}_{i }{v}_{i} {\ddot{x}}_{i}-\sum_{i=1}^{{n}_{AC}}{m}_{i} {h}_{i} {\ddot{z}}_{i }+ {I}_{AC}{\ddot{\theta }}_{y}={M}_{{\text{mech}},y}+{M}_{{\text{wind}},y}+\sum_{i=1}^{{n}_{AC}}{M}_{y,i}-\sum_{i=1}^{{n}_{AC}}{h}_{i}{V}_{i}-\sum_{i=1}^{{n}_{AC}}{v}_{i}{H}_{i}.$$
(1)

\(I\) is moment of inertia about the centre of mass for A and C and \({I}_{AC}={I}_{A}+{I}_{C}\), \({M}_{{\text{mech}},y}\) is moment due to mechanical damping (PTO) about the \(y\) axis at O and \({M}_{{\text{wind}},y}\) is the moment due to wind thrust \({H}_{{\text{wind}}, x}\) defined below.

For B, with \(i\) = 1, taking moments about O as the float responds individually:

$${- m}_{i }{v}_{i}{\ddot{x}}_{i}- {m}_{i} {h}_{i}{\ddot{z}}_{i }+ {I}_{i}{\ddot{\theta }}_{y,i} = -{M}_{{\text{mech}},y}+{M}_{y,i }-{h}_{i}{V}_{i} - {v}_{i}{H}_{i}$$
(2)

where \({M}_{{\text{mech}},y}= {- B}_{{\text{mech}}} {\dot{\theta }}_{r,y}\), and \({\theta }_{r,y}= {\theta }_{y,AC}- {\theta }_{y,i}\).

Bodies A and B are effectively combined in roll. Taking moments about \(x\) axis at O:

$$\sum_{i=1}^{{n}_{AB}}{m}_{i}{v}_{i} {\ddot{y}}_{i}+ \sum_{i=1}^{{n}_{AB}}{m}_{i} {t}_{i} {\ddot{z}}_{i } + {I}_{AB}{\ddot{\theta }}_{x} = {M}_{{\text{mech}},x}+\sum_{i=1}^{{n}_{AB}}{M}_{x,i}+ \sum_{i=1}^{{n}_{AB}}{t}_{i} {V}_{i} + \sum_{i=1}^{{n}_{AB}}{v}_{i} {T}_{i} , $$
(3)

where \({I}_{AB}={I}_{A}+{I}_{B}\), and \({M}_{{\text{mech}},x}\) is moment due to mechanical damping about the \(x\) axis at O. Wind thrust in this direction is not considered here.

For C, with \(i=1\), taking moments about O as the float responds individually:

$${m}_{i }{v}_{i}{\ddot{y}}_{i}+ {m}_{i} {t}_{i} {\ddot{z}}_{i }+ {I}_{i}{\ddot{\theta }}_{x,i} = -{M}_{{\text{mech}}, x }+{M}_{x,i }+{t}_{i}{V}_{i}+ {v}_{i} {H}_{i },$$
(4)

where \({M}_{{\text{mech}}, x }= {- B}_{{\text{mech}}} {\dot{\theta }}_{r,x}\), and \({\theta }_{r,x}= {\theta }_{x,AB}- {\theta }_{x,i}\),

for the whole system as there is no net force or net moment on a hinge.

In the longitudinal horizontal direction (for all masses),

$$\sum_{i=1}^{N}{m}_{i} {\ddot{x}}_{i} = \sum_{i=1}^{N}{H}_{i}+{H}_{{\text{wind}}, x}+{H}_{{\text{stiff}}},$$
(5)

where stiffness force \({H}_{{\text{stiff}}}=-{k}_{{\text{s}}}{x}_{{\text{O}}}\) and \({k}_{{\text{s}}}\) is the elastic constant.

In the transverse horizontal direction,

$$\sum_{i=1}^{N}{m}_{i} {\ddot{y}}_{i} = \sum_{i=1}^{N}{T}_{i} +{T}_{{\text{stiff}}},$$
(6)

where stiffness force \({T}_{{\text{stiff}}}=-{k}_{{\text{s}}}{y}_{{\text{O}}}\).

In the vertical direction,

$$\sum_{i=1}^{N}{m}_{i} {\ddot{z}}_{i} = \sum_{i=1}^{N}{{V}_{i}. }$$
(7)

The positions of the centres of gravity of each float \({x}_{i}, {z}_{i}, {y}_{i}\) in relation to O, linearised for small angles, are defined by:

For all floats, \(i=1, N\)

$${x}_{i}= {x}_{{\text{O}}}+{h}_{i}- {v}_{i} {\theta }_{y,}$$
(8a)
$${z}_{i}= {z}_{{\text{O}}}-{v}_{i}- {h}_{i} {\theta }_{y}+{t}_{i} {\theta }_{x},$$
(8b)
$${y}_{i}= {y}_{{\text{O}}}+{t}_{i}+ {v}_{i} {\theta }_{x}.$$
(8c)

We thus have seven equations for seven unknowns \({x}_{{\text{O}}}\), \({y}_{{\text{O}}}, {z}_{{\text{O}}}, {\theta }_{y,A} , {\theta }_{y,B}, {\theta }_{x,A}, {\theta }_{x,C}\).

For AC in pitch:

$$-\sum_{i=1}^{{n}_{AC}} {m}_{i }{v}_{i} \left({\ddot{x}}_{{\text{O}}}-{v}_{i}{\ddot{\theta }}_{y}\right) -\sum_{i=1}^{{n}_{AC}}{m}_{i} {h}_{i} \left({\ddot{z}}_{{\text{O}}}-{h}_{i} {\ddot{\theta }}_{yA}+{t}_{i}{\ddot{\theta }}_{x}\right)+ {I}_{AC}{\ddot{\theta }}_{y} = {M}_{{\text{mech}},y}+{M}_{{\text{wind}}, y}+\sum_{i=1}^{{n}_{AB}}{M}_{y, i}-\sum_{i=1}^{{n}_{AB}}{h}_{i} {V}_{i}-\sum_{i=1}^{{n}_{AB}}{v}_{i} {H}_{i},$$
(9)

giving

$${\ddot{\theta }}_{y}\left(\sum_{i=1}^{{n}_{AC}}{m}_{i }{v}_{i}^{2} +\sum_{i=1}^{{n}_{AC}}{m}_{i} {h}_{i}^{2} + {I}_{AC} \right)= \sum_{i=1}^{{n}_{AC}} {m}_{i }{v}_{i} {\ddot{x}}_{{\text{O}}}+\sum_{i=1}^{{n}_{AC}}{m}_{i} {h}_{i}{\ddot{z}}_{{\text{O}}}+ {M}_{{\text{mech}},y}+{M}_{{\text{wind}}, y}+\sum_{i=1}^{{n}_{AC}}{M}_{y,i}-\sum_{i=1}^{{n}_{AC}}{h}_{i} {V}_{i}-\sum_{i=1}^{{n}_{AC}}{v}_{i} {H}_{i}+\sum_{i=1}^{{n}_{AC}}{m}_{i}{h}_{i} {t}_{i}{\ddot{\theta }}_{x},$$
(10)

and for B float i \(=1,\)

$$-{m}_{i }{v}_{i} \left({\ddot{x}}_{{\text{O}}}-{v}_{i}{\ddot{\theta }}_{y,i}\right)- {m}_{i} {h}_{i}\left({\ddot{z}}_{{\text{O}}}-{h}_{i} {\ddot{\theta }}_{y, i}+{t}_{i} {\ddot{\theta }}_{x}\right) +{I}_{y,i}{\ddot{\theta }}_{y,i}={-M}_{{\text{mech}} y} + {M}_{y,i}- {h}_{i} {V}_{i}-{v}_{i}{H}_{i},$$
(11)

giving

$$ {\ddot{\theta }}_{y,i}\left({m}_{i} {v}_{i}^{2}+ {m}_{i} {h}_{i}^{2}+ {I}_{y,i}\right) = {m}_{i }{v}_{i} {\ddot{x}}_{{\text{O}}}+{m}_{i} {h}_{i} {\ddot{z}}_{{\text{O}}}+{m}_{i}{h}_{i}{t}_{i}{\ddot{\theta }}_{x,i} - {M}_{{\text{mech}} y}+ {M}_{y,i}- {h}_{i} {V}_{i} - {v}_{i} {H}_{i}.$$
(12)

For AB in roll:

$$\sum_{i=1}^{{n}_{AB}} {m}_{i }{v}_{i} \left({\ddot{y}}_{{\text{O}}}+{v}_{i}{\ddot{\theta }}_{x}\right) +\sum_{i=1}^{{n}_{AB}}{m}_{i} {t}_{i} \left({\ddot{z}}_{{\text{O}}}-{h}_{i} {\ddot{\theta }}_{y}+{t}_{i}{\ddot{\theta }}_{x}\right)+ {I}_{AB}{\ddot{\theta }}_{x} = {M}_{{\text{mech}},x}+\sum_{i=1}^{{n}_{AB}}{M}_{x, i}+ \sum_{i=1}^{{n}_{AB}}{t}_{i} {V}_{i} + \sum_{i=1}^{{n}_{A}B}{v}_{i} {T}_{i} , $$
(13)

giving

$${\ddot{\theta }}_{x}\left(\sum_{i=1}^{{n}_{AB}}{m}_{i }{v}_{i}^{2} +\sum_{i=1}^{{n}_{AB}}{m}_{i} {t}_{i}^{2} + {I}_{AB} \right)= -\sum_{i=1}^{{n}_{AB}} {m}_{i }{v}_{i} {\ddot{y}}_{\rm O}-\sum_{i=1}^{{n}_{AB}}{m}_{i} {t}_{i}{\ddot{z}}_{\rm O}+ {M}_{{\text{mech}},x}+\sum_{i=1}^{{n}_{AB}}{M}_{x,i}+\sum_{i=1}^{{n}_{AB}}{t}_{i} {V}_{i}+\sum_{i=1}^{{n}_{AB}}{v}_{i} {T}_{i} +\sum_{i=1}^{{n}_{AB}}{m}_{i}{h}_{i} {t}_{i}{\ddot{\theta }}_{y}.$$
(14)

For C float \(i=1\),

$${m}_{i }{v}_{i} \left({\ddot{y}}_{\rm O}+{v}_{i}{\ddot{\theta }}_{x,i}\right)+ {m}_{i} {t}_{i} \left({\ddot{z}}_{\rm O}-{h}_{i} {\ddot{\theta }}_{x,i}+{t}_{i} {\ddot{\theta }}_{x}\right) +{I}_{x,i}{\ddot{\theta }}_{x,i}={-M}_{{\text{mech}},x}+{M}_{x,i}+ {t}_{i} {V}_{i}+ {v}_{i}{H}_{i},$$
(15)

giving

$${\ddot{\theta }}_{x,i}\left({m}_{i }{v}_{i}^{2}+ {m}_{i} {t}_{i}^{2}+ {I}_{x,i}\right) = {-m}_{i }{v}_{i} {\ddot{y}}_{\rm O}-{m}_{i} {t}_{i} {\ddot{z}}_{\rm O}+{m}_{i}{h}_{i}{t}_{i}{\ddot{\theta }}_{x,i}- {M}_{{\text{mech}},x}+ {M}_{x,i}+ {t}_{i} {V}_{i}+ {v}_{i} {H}_{i}.$$
(16)

For the whole system in the horizontal longitudinal direction,

$$\sum_{i=1}^{N}{m}_{i}\left({\ddot{x}}_{\rm O}-{v}_{i}{\ddot{\theta }}_{y,i}\right) = \sum_{i=1}^{N}{H}_{i}+{H}_{{\text{wind}}, x }+{H}_{{\text{stiff}} },$$
(17)

giving

$${\ddot{x}}_{{\text{O}}}\sum_{i=1}^{N}{m}_{i} = \sum_{i=1}^{N}{H}_{i }+{H}_{{\text{wind}}, x }+{H}_{{\text{stiff}} }+\sum_{i=1}^{N}{m}_{i}{v}_{i}{\ddot{\theta }}_{y, i};$$
(18)

in the transverse direction,

$$\sum_{i=1}^{N}{m}_{i}\left({\ddot{y}}_{{\text{O}}}+{v}_{i}{\ddot{\theta }}_{x,i}\right) = \sum_{i=1}^{N}{T}_{i}+{T}_{{\text{stiff}} },$$
(19)

giving

$${\ddot{y}}_{{\text{O}}}\sum_{i=1}^{N}{m}_{i} = \sum_{i=1}^{N}{T}_{i }+{T}_{{\text{stiff}} }-\sum_{i=1}^{N}{m}_{i}{v}_{i}{\ddot{\theta }}_{x,i}$$
(20)

and in the vertical

$$\sum_{i=1}^{N}{m}_{i}\left({\ddot{z}}_{{\text{O}}}-{h}_{i}{\ddot{\theta }}_{y, i}+ {t}_{i} {\ddot{\theta }}_{x,i}\right) = \sum_{i=1}^{N}{V}_{i },$$
(21)

giving

$${\ddot{z}}_{{\text{O}}}\sum_{i=1}^{N}{m}_{i} = \sum_{i=1}^{N}{V}_{i }+\sum_{i=1}^{N}{m}_{i}{h}_{i}{\ddot{\theta }}_{y,i}-{m}_{i}{t}_{i} {\ddot{\theta }}_{x,i}.$$
(22)

We thus have equations for \({\ddot{\theta }}_{y,AC}, {\ddot{\theta }}_{x,AB}, {\ddot{\theta }}_{y,B} , {\ddot{\theta }}_{y,C}, {\ddot{x}}_{{\text{O}}}, {\ddot{y}}_{{\text{O}}}, {\ddot{z}}_{{\text{O}}}\) which are further complicated by \({H}_{i},{T}_{i}, {V}_{i}, {M}_{y,i}, {M}_{x,i}\) defined below also being a function of these variables and hydrodynamic (BEM) coefficients.

We are concerned with irregular waves with surface elevation \(\eta (t)\), which will be defined by linear superimposition of \(K\) components of amplitude \({a}_{k}\), frequency \(f=k\Delta f\), and random phase \({\varphi }_{r,k}\),where \(k=1,K\) and \(\Delta f\) is frequency increment, such that

$$\eta \left(t\right)= \sum_{k=1}^{K}{a}_{k}{\text{cos}}(-k 2\pi \Delta f t+{\varphi }_{r,k}),$$
(23)

specified in Sect. 5.

Hydrodynamic moments and forces are defined using conventional notation as shown in Table 1.

Linear diffraction forces and moments for each float are defined by frequency-dependent BEM coefficients for force/moment amplitude \(F\) and phase \(\varphi \), or real and imaginary parts, but the former is more convenient as there is already a random phase for each frequency component. For each float \(i=1,N\)-Pitch moment:

$${M}_{y,D\ 5+6(i-1)}= \sum\limits_{k=1}^{K}{a}_{k} {F}_{5+6\left(i-1\right), k }{\text{cos}}\left(-k 2\pi \Delta f t+{\varphi }_{5+6\left(i-1\right), k}+{\varphi }_{r,k}\right).\\ $$
(24a)

Roll moment:

$${M}_{x,D\ 4+6(i-1)}= \sum_{k=1}^{K}{a}_{k} {F}_{4+6\left(i-1\right), k }{\text{cos}}\left(-k 2\pi \Delta f t+{\varphi }_{4+6\left(i-1\right), k}+{\varphi }_{r,k}\right).\\ $$
(24b)

Vertical force:

$${V}_{D\ 3+6(i-1)}= \sum_{k=1}^{K}{a}_{k} {F}_{3+6\left(i-1\right), k }{\text{cos}}\left(-k 2\pi \Delta f t+{\varphi }_{3+6\left(i-1\right), k}+{\varphi }_{r,k}\right).$$
(24c)

Longitudinal horizontal force:

$${H}_{D\ 1+6(i-1)}= \sum_{k=1}^{K}{a}_{k} {F}_{1+6\left(i-1\right), k }{\text{cos}}\left(-k 2\pi \Delta f t+{\varphi }_{1+6\left(i-1\right), k}+{\varphi }_{r,k}\right).$$
(24d)

Transverse horizontal force:

$${T}_{D\ 2+6(i-1)}= \sum_{k=1}^{K}{a}_{k} {F}_{2+6\left(i-1\right), k }{\text{cos}}\left(-k 2\pi \Delta f t+{\varphi }_{2+6\left(i-1\right), k}+{\varphi }_{r,k}\right).$$
(24e)

Added mass and radiation damping forces and moments are defined by frequency-dependent coefficients \(A\) and \(B\), respectively, using the Cummins method. With a single body and one degree of freedom \(x\) we have

$$m\ddot{x}\left(t\right)=f\left(t\right)-{A}^{\infty }\ddot{x}\left(t\right)-{\int }_{-\infty }^{t}L\left(t-\tau \right) \dot{x}\left(\tau \right){\text{d}}\tau ,$$
(25)

where \(f\) includes forces due to excitation, restoring and PTO; \({A}^{\infty }\) is added mass for infinite frequency and the impulse response function for radiation damping is given by

$$L\left(t\right)= \frac{2}{\pi } {\int }_{0}^{\infty }B\left(\omega \right){\text{cos}}\left(\omega t\right){\text{d}}\omega .$$
(26)

In discrete form with time step \(\Delta t\), time \(t=n \Delta t\) and \(\omega =2 \pi f=k \Delta \omega ,\)

$${L}^{m}= \frac{2}{\pi } \sum_{k=0}^{K}{B}_{k}{\text{cos}}\left(k \Delta \omega n \Delta t\right) \Delta \omega ,$$
(27)

which is precomputed and in discrete form

$$-{\int }_{-\infty }^{t}L\left(t-\tau \right) \dot{x}(\tau ) {\text{d}}\tau = - \sum_{l=n-2\mathcal{M}}^{n}{L}^{n-l}{\dot{x}}^{l} \Delta \tau ,$$
(28)

where \(\Delta \tau = \Delta t\) and \(\mathcal{M}={T}_{{\text{p}}}/\Delta t\). The lower limit \((m-2\mathcal{M})\) is generally used to represent \(-\infty \) with almost identical results given by \((m-4\mathcal{M})\).

The RHS is generalised for each float with six modes.

For each float \(i=1, N\) pitch moments are defined by:

$${M}_{y, i}={M}_{D\ 5+6(i-1)}-\sum_{j=1}^{n}{{A}^{\infty }}_{5+6\left(i-1\right), 5+6\left(j-1\right)} \cdot {\ddot{\theta }}_{j}-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 5+6\left(j-1\right)}\left(t-\tau \right) {\dot{\theta }}_{j}(\tau )\mathrm{ d}\tau $$
$$-\sum_{j=1}^{n}{{A}^{\infty }}_{5+6\left(i-1\right), 4+6\left(j-1\right)} \cdot {\ddot{\theta }}_{R j}-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 4+6\left(j-1\right)}\left(t-\tau \right) {\dot{\theta }}_{R j}(\tau )\mathrm{ d}\tau $$
$$-\sum_{j=1}^{n}{{A}^{\infty }}_{5+6\left(i-1\right), 1+6\left(j-1\right)} \cdot {\ddot{x}}_{j}-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 1+6(j-1)}\left(t-\tau \right) {\dot{x}}_{j}\left(\tau \right) {\text{d}}\tau $$
$$- \sum_{j=1}^{n}{{A}^{\infty }}_{5+6\left(i-1\right), 3+6\left(j-1\right)} \cdot {\ddot{z}}_{j}-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 3+6\left(j-1\right)}\left(t-\tau \right) {\dot{z}}_{j} {\text{d}}\tau $$
$$- \sum_{j=1}^{n}{{A}^{\infty }}_{5+6\left(i-1\right), 2+6\left(j-1\right)} \cdot {y}_{j}-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 2+6\left(j-1\right)}\left(t-\tau \right) {\dot{y}}_{j} {\text{d}}\tau $$
$$+ {M}_{y, {\text{rest}} i},$$
(29)

where the subscripts \({\text{rest}}\) indicate restoring moments to be described below.

As an example, the discrete form of the term

$$-\sum_{j=1}^{n}{\int }_{-\infty }^{t}{L}_{5+6\left(i-1\right), 5+6\left(j-1\right)}\left(t-\tau \right){\dot{\theta }}_{j}(\tau ) {\text{d}}\tau = - \sum_{j=1}^{n}\sum_{l=m-2\mathcal{M}}^{m}{L}_{5+6\left(i-1\right), 5+6\left(j-1\right)}^{m-l} {\dot{\theta }}_{j}^{l}\Delta t.$$

There are equivalent terms for roll, heave, surge and sway; for heave, surge and sway there are additional terms for drag: \({V}_{{\text{drag }} i}\), \({H}_{{\text{drag }} i}\), \({T}_{{\text{drag }} i}\), defined below, e.g. Stansby et al. (2017).

The restoring heave force for a single float \({V}_{{\text{rest}}, i}=-\rho g\pi {r}^{2}{z}_{i}\). The restoring pitch and roll moments for floats are given by \({M}_{y,{\text{rest}},1235}=7.48e8 {\theta }_{y}\), \({M}_{x,{\text{rest}},1234}=7.48e8 {\theta }_{x}\), (both acting on 4 floats) \({M}_{y,{\text{rest}},4}=-\rho g\pi \frac{{r}^{4}}{4}{\theta }_{y}\), \({M}_{x, {\text{rest}}, 5}=-\rho g\pi \frac{{r}^{4}}{4}{\theta }_{x}\), where r is float radius (\({H}_{{\text{rest}} }={T}_{{\text{rest}}}=0\)). The hydrostatic rotation effect is included for all floats. For floats 4 and 5, this is the only effect as centre of buoyancy and mass are assumed coincident, but they are not for 1235 and 1234 causing positive values. The drag forces are given by \({H}_{{\text{drag }} i}=-0.5 \rho {{A}_{i}C}_{D } \left|\dot{{x}_{i}}\right| \dot{{x}_{i}}\), \({T}_{{\text{drag }} i}=-0.5 \rho {A}_{i } \left|\dot{{y}_{1}}\right| \dot{{y}_{1}}, {V}_{{\text{drag}} i}=-0.5 \rho \pi {r}_{i}^{2} {C}_{D } \left|\dot{{z}_{1}}\right| \dot{{z}_{1}}\). \({A}_{i}\) is the vertical submerged frontal area for a float. Note float velocity relative to flow velocity is not considered and drag coefficient \({C}_{D}\) is generally unity in this study.

The equations were advanced in time using the explicit Beeman’s method for \({\theta }_{y, AC}\), \({\theta }_{y, B}\), \({\theta }_{x, AB}\), \({\theta }_{x, C}\), \({x}_{{\text{O}}}\), \({y}_{{\text{O}}}\), \({z}_{{\text{O}}}\) with time step \(\Delta t\) for general variable \(f\)

$${f}^{n+1}={f}^{n}+{\dot{f}}^{n}\Delta t+{\ddot{f}}^{n}{\Delta t}^{2}/2,$$
(30a)
$${\dot{f}}^{n+1}={\dot{f}}^{n}+{\ddot{f}}^{n}\Delta t.$$
(30b)

The BEM coefficients are for all cross coupled terms between floats as well as for the directly coupled (diagonal) terms which have the greatest magnitude. There are thus \({(5N)}^{2}\) non-zero coefficients for \(N\) floats with five modes here (heave, surge, sway, pitch and roll) for radiation damping and added mass and with \(5N\) coefficients for diffraction forces. Forming a direct formulation for each term with all cross coupled terms would be tedious to generalise.

However, the dominant diagonal terms in added mass for each of \({\ddot{\theta }}_{y, AC}\), \({\ddot{\theta }}_{y, B}\), \({\ddot{\theta }}_{x, AB}\), \({\ddot{\theta }}_{x, C}\), \({\ddot{x}}_{{\text{O}}}\), \({\ddot{y}}_{{\text{O}}}\), \({\ddot{z}}_{{\text{O}}}\) may be removed from the RHS of each of \({H}_{i},{T}_{i} {V}_{i}, {M}_{x,i}, {M}_{y,i}\) and added to the LHS of Eqs. (10), (12), (14), and (16). This proved desirable for numerical stability. An iteration is required with updated values of accelerations \({\ddot{\theta }}_{A}, {\ddot{\theta }}_{B}, {{\ddot{\theta }}_{R}, \ddot{x}}_{{\text{O}}}, {\ddot{z}}_{{\text{O}}}\) for terms on the RHS, but this showed fast convergence with less than ten iterations (default value). The radiation damping and diffraction force terms were not modified in the iteration. A time step size of \({T}_{{\text{p}}}\)/200 was sufficiently small to give converged results (to plotting accuracy).

The equation set with numerical solution is thus complete and proved stable and convergent.

4 Linear damper and wind thrust

For wave energy conversion, the torques are passive linear dampers such that

$${M}_{{\text{mech}},y}=-{B}_{{\text{mech}}} {\dot{\theta }}_{y,r},$$
(31a)
$${M}_{{\text{mech}},x}=-{B}_{{\text{mech}}} {\dot{\theta }}_{x,r},$$
(31b)

where \({B}_{{\text{mech}}}\) is the linear damping constant, \({\dot{\theta }}_{y,r}={\dot{\theta }}_{y, AC}-{\dot{\theta }}_{y,B}\) and \({\dot{\theta }}_{x,r}={\dot{\theta }}_{x, AB}-{\dot{\theta }}_{y,C}\).

Mechanical power is given by

$${P}_{{\text{mech}}}={B}_{{\text{mech}}} {{\dot{\theta }}_{y,r}}^{2}+{B}_{{\text{mech}}} {{\dot{\theta }}_{x,r}}^{2}.$$
(32)

The unsteady wind thrust in the x direction is given by

$${H}_{{\text{wind}}, x}=0.5 {\rho }_{{\text{air}} }{A}_{{\text{turb}}} {C}_{{\text{T}}} {\left({U}_{{\text{hub}}}-{\dot{x}}_{{\text{hub}}}\right)}^{2},$$
(33)

where \({U}_{{\text{hub}}}\) is the uniform wind speed at the hub, \({\dot{x}}_{{\text{hub}}}\) is the hub velocity, \({\rho }_{{\text{air}}}\) is the air density (1.2 kg/m3) and \({A}_{{\text{turb}}}\) is the swept area for the rotor of radius \({r}_{{\text{turb}}}\) , \(\pi {r}_{{\text{turb}}}^{2}\). The thrust coefficient \({C}_{{\text{T}}}\) is dependent on the wind speed and is determined from blade element momentum theory (BEMT) using the NREL 5 MW turbine characteristics. The force is assumed to be quasi steady and defined by the relative velocity \(\left({U}_{{\text{hub}}}-{\dot{x}}_{{\text{hub}}}\right)\). The quasi-steady behaviour has been shown to be a close approximation to CFD modelling using the actuator line model (Apsley and Stansby 2020). The moment \({M}_{{\text{wind}}, y}={{v}_{{\text{hub}}}H}_{{\text{wind}},x}\) where \({v}_{{\text{hub}}}\) is the height of the hub above hinge O.

5 Wave conditions

We specify irregular waves by the standard JONSWAP spectrum \(S(f)\) defined by a significant wave height \({H}_{{\text{s}}}\) and a peak frequency \({f}_{{\text{p}}}=1/{T}_{{\text{p}}}\), where \({T}_{{\text{p}}}\) is the peak period; a spectral peakedness factor \(\gamma \) =3.3 was applied. The surface elevation \(\eta \) at O may be defined by linear superposition of the discretised wave amplitude components as given by Eq. 23. The lower limit on frequency was 0.032 Hz (0.2 rad/s) and the upper limit 0.318 Hz (2.0 rad/s), between two and four times \({f}_{{\text{p}}}\), \(\Delta f=\) 0.00159 Hz (0.01 rad/s) giving 181 frequency components with amplitude \({a}_{k}=\sqrt{2 S\left(f\right)\Delta f}\), and \({\varphi }_{{\text{r}}}\) is the phase from a uniform random distribution between 0 and \(2\pi \). This defines the frequencies for which the BEM coefficients are computed. The frequency increment, however, determines the repeat times which would be 629 s (approximately 10 min) while run times are required to be typically 3600 s (1 h). A frequency increment \(\Delta f_{{{\text{rt}}}} = {1 \mathord{\left/ {\vphantom {1 {t_{{{\text{rt}}}} }}} \right. \kern-0pt} {t_{{{\text{rt}}}} }}\) would give the run time \({t}_{{\text{rt}}}\) as a repeat time and the associated spectrum is obtained by interpolation within a frequency increment \(\Delta f\) at \(\Delta f/{\Delta f}_{{\text{rt}}}\) (to nearest integer) intervals. Uni directional irregular waves are thus defined and we now consider spread waves.

There are various options for generating directional waves, e.g. Latheef et al. (2017). The directional wave spectrum is usually defined by \(S\left(f,\beta \right)=S\left(f\right)\cdot G(\beta )\) where the spreading function

$$G\left(\beta \right)=\alpha {\left(\cos\frac{\beta }{2}\right)}^{2s}$$
(34)

with the mean wave direction (heading) given by \(\beta =0\), for \(-\pi <\beta <\pi \), and \(s\) is the spreading parameter. \(\alpha \) is defined by the requirement \({\int }_{-\pi }^{\pi }G\left(\beta \right) {\text{d}}\beta =1\). One approach for generating directional waves is to split each frequency component into directions defined by \(G(\beta )\) known as the double summation method. However, this means that a specific frequency has several directional components and partial standing waves result; the wave field is non-ergodic (Jefferys 1987). To avoid this, each frequency component may be subdivided into a number of smaller components with different frequencies which together satisfy the spreading across the original frequency band, known as the single summation method. An equivalent more efficient approach, often employed experimentally, is known as the random directional method (Latheef et al. 2017). The direction of propagation of any one frequency component is chosen randomly, subject to a weighting function based upon the desired directional spread. This approach also avoids components of the same frequency co-existing and results in ergodic wave fields. The appropriate weighting for choosing the direction of the components is based upon a normal distribution with a standard deviation of \({\sigma }_{\beta }\) in accordance with the directional distribution

$$G\left(\beta \right)=\frac{\alpha }{{\sigma }_{\beta }\sqrt{2\pi }} {\text{exp}}\left[- \frac{{\beta }^{2}}{2 {{\sigma }_{\beta }}^{2}}\right],$$
(35)

where \({{\sigma }_{\beta }}^{2}=\frac{2}{1+s}\) as a close approximation to Eq. (38) above. This is applied to each frequency component in the spectrum, as defined by the run time. The random angle is determined by the Box–Muller method where two random number numbers (\({u}_{1},{u}_{2}\)) are first generated from a uniform distribution between 0 and 1 and then converted to a random number:

$${u}_{3}=\sqrt{-2 {\text{ln}}({u}_{1})} {\text{cos}}(2\pi {u}_{2})$$

with unit standard deviation and mean zero, giving a random angle \({u}_{3}{\sigma }_{\beta }\). This is the approach adopted here to represent the effect of directional spread waves defined by the measured spectrum and a spread factor \(s\).

The excitation forces and moments are affected by the heading angle and hydrodynamic (BEM) coefficients are determined at 2° intervals. The excitation forces and moments are as defined by Eq. (24) except that each frequency component \(k\) has a random heading from the normal distribution defined above, defining the excitation coefficients. This follows Stansby et al. (2022a)

6 Results

We assess the power capture and platform response in swell waves and choose a heading angle of zero for preliminary assessment. The hub acceleration is vital for reliable wind turbine operation, although wind speeds may be small in swell waves. With zero heading, the x acceleration is in line with the wave direction and greater than the y acceleration.

Passive dampers with \({B}_{{\text{mech}}}\) = 2 × 109 Nms/rad were found to give close to optimum average power and have been used throughout, although power is only slightly sensitive to this value. The dependence of average power on a wide range of \({B}_{{\text{mech}}}\) is shown in Fig. 4 for swell waves with \({T}_{{\text{p}}}\) = 12 s and \({H}_{{\text{s}}}\) = 2 m at zero heading. The small horizontal stiffness constant \({k}_{{\text{s}}}\) for station keeping was generally 5 × 105 N/m, although the results were insensitive to increasing by factor 10.

Fig. 4
figure 4

Variation of average power with mechanical damping \({B}_{{\text{mech}}}\) for \({T}_{{\text{p}}}\) = 12 s and \({H}_{{\text{s}}}\) = 2 m at zero heading

Full size image

The floats have circular cross section but flat bases, which will generate some wake effects. The effect of drag coefficient \({C}_{{\text{d}}}\) on mean power is shown in Fig. 5. With \({C}_{{\text{d}}}\) = 1, the average power is about 17% smaller than with the inviscid value \({C}_{{\text{d}}}\) = 0. \({C}_{{\text{d}}}\) = 1 is used as a representative value.

Fig. 5
figure 5

Variation of average power with \({C}_{{\text{d}}}\) for \({T}_{{\text{p}}}\) = 12 s and \({H}_{{\text{s}}}\) = 2 m at zero heading

Full size image

Figure 6 shows the hub x acceleration dependence on \({T}_{{\text{p}}}\) for \({H}_{{\text{s}}}\) = 2 m with uni directional waves.

Fig. 6
figure 6

Variation of hub acceleration in x direction with \({T}_{{\text{p}}}\) for \({H}_{{\text{s}}}\) = 2 m with uni directional waves at zero heading

Full size image

For swell waves (\({T}_{{\text{p}}}\) > 10 s), the hub acceleration is greatest with a maximum of about 1.3 m/s2 around \({T}_{{\text{p}}}\) = 12 s. This is well below the operational limit of 3 m/s2 and rms values are generally about a factor of 4 below the maxima. We next show the average power variation with \({T}_{{\text{p}}}\) for the same conditions in Fig. 7. The maximum of about 270 kW occurs with \({T}_{{\text{p}}}\) = 12 and 13 s where the energy wavelength (based on the energy period) is about 160 m, so the bow and stern floats with spacing of 80 m experience surge forces predominantly in anti-phase. The peak to mean power ratio is generally around 10. We have not considered the effect of wind as we only consider swell waves in low wind.

Fig. 7
figure 7

Variation of average power with \({T}_{{\text{p}}}\) for \({H}_{{\text{s}}}\) = 2 m with uni directional waves

Full size image

Uni directional waves rarely occur outside the laboratory and Fig. 8 shows the variation of average power with standard deviation \(\sigma \) of spread angle for \({H}_{{\text{s}}}\) = 2 m and \({T}_{{\text{p}}}\) = 12 s at zero heading.

Fig. 8
figure 8

Variation of average power with standard deviation \(\sigma \) of spread angle for \({H}_{{\text{s}}}\) = 2 m and \({T}_{{\text{p}}}\) = 12 s at zero heading

Full size image

There is a small drop in power due to spread which is only slightly dependent on spread angle. The variation of hub accelerations in the x and y directions with heading are shown in Fig. 9 for uni directional waves. The results show anti-symmetry as expected, e.g. for 0° and 90° and − 90° and 180° where values for x and y directions swap.

Fig. 9
figure 9

Variation of rms and maximum hub accelerations in the x and y directions with heading for uni directional waves with \({H}_{{\text{s}}}\) = 2 m and \({T}_{{\text{p}}}\) = 12 s with power take off

Full size image

Finally, we show the average power variation with heading in Fig. 10 for \({T}_{{\text{p}}}\) = 10 and 12 s.

Fig. 10
figure 10

Variation of average power with heading for \({T}_{{\text{p}}}\) = 10 and 12 s with \({H}_{{\text{s}}}\) = 2 m for uni directional waves

Full size image

It can be seen that power is greatest between headings of 0° and 100°. Since swell waves come from a prevalent range of directions, usually around westerly, moorings can be arranged so that the platform is suitably oriented. The pitch angular motion of the supporting wind platform is of interest for access and maintenance purposes and Fig. 11 shows rotations \(\theta \) about the y and x axes. The rms angles are about 0.8° while the maxima are about 2.7°. The relative pitch angles between the wave floats and the wind platform which generate power are shown in Fig. 12 to be somewhat larger with maxima over 4° corresponding with headings for maximum power, while the maximum rms values are 1.2°.

Fig. 11
figure 11

Variation of wind platform pitch angle \(\theta \) about the x and y axes variation with heading for uni directional waves with \({H}_{{\text{s}}}\) = 2 m and \({T}_{{\text{p}}}\) = 12 s with PTO

Full size image
Fig. 12
figure 12

Variation of the relative pitch angle \(\theta \) between the wind platform and wave floats about the x and y axes with heading for uni directional waves with \({H}_{{\text{s}}}\) = 2 m and \({T}_{{\text{p}}}\) = 12 s with PTO

Full size image

With the hinge almost rigid the hub accelerations are increased, the rms and maximum by 36%. This is counterintuitive, as one might expect larger rigid bodies to respond less.

Results for different heading with a large \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s are shown without mechanical damping: in Fig. 13 for wind platform pitch angle, in Fig. 14 for relative pitch angle \(\theta \) between wind platform and wave float, and in Fig. 15 for the rms and maximum hub accelerations. For these wave conditions, wind speed is likely to be above rated, but wind effect is not included as this will be seen to slightly reduce motion. The wind platform angles are small, with maxima of about 4½° and rms of 1½°. In contrast, the relative angles are quite large with the largest maxima of 22° and rms of about 8°. The greatest hub accelerations are just less than 3 m/s2 and rms are about 1 m/s2. With the wave float connection made effectively rigid, the rms is increased by 64% and the maximum by 87% with zero heading. This is consistent with the result for \({H}_{{\text{s}}}\) = 2 m with PTO engaged where a smaller increase resulted. It should be noted that in extreme steep waves, the wave floats will be intermittently overtopped and partially submerged based on experience for the multi-float wave energy converter M4, limiting the pitch motion and providing a passive end stop to rotation, e.g. Stansby et al. (2022b), and this is obviously not captured in a linear wave diffraction–radiation model.

Fig. 13
figure 13

Variation of wind platform pitch angle \(\theta \) about the x and y axes variation with heading for uni directional waves with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s with no PTO

Full size image
Fig. 14
figure 14

Variation of the relative pitch angle \(\theta \) between the wind platform and wave floats about the x and y axes with heading for uni directional waves with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s with no PTO

Full size image
Fig. 15
figure 15

Variation of rms and maximum hub accelerations in the x and y directions with heading for uni directional waves with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s with no PTO and no wind

Full size image

The effect of spread on hub acceleration is shown in Fig. 16 for the x direction only. In general, spread slightly reduces rms acceleration, but can slightly increase maximum values which is unexpected.

Fig. 16
figure 16

Variation of rms and maximum hub accelerations in the x direction with heading for uni directional and spread waves (s = 20, \(\sigma \) = 17.7°) with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s with no PTO and no wind

Full size image

Finally, we consider the effect of wind in line with zero heading. The effect on hub acceleration with speeds up to 25 m/s was small with maximum 6% reduction at about 10 m/s, close to rated, tested with \({H}_{{\text{s}}}\) = 6 m (without PTO). There was a maximum 13% reduction in wave power with \({H}_{{\text{s}}}\) = 2 m at this wind speed. Some reduction is to be expected as an oscillating turbine provides damping.

7 Discussion

The model is based on linear diffraction–radiation theory which is strictly limited to small wave heights and response. Similar multi-float configurations have been compared with experiment for both M4 wave energy generation (Stansby and Carpintero Moreno 2020; Stansby and Draycott 2024) and a floating wind platform with damping plates (Stansby et al. 2019) using a single point mooring buoy and have shown good agreement for response in operational and also in steep waves. Experimental analysis for M4 in focussed waves has also shown response to be remarkably linear in large waves with weak higher-order effects (Santo et al. 2017). Measured mooring forces were, however, highly nonlinear (Stansby et al. 2019, 2022b), but not considered here where a small spring stiffness is added in the horizontal directions for station keeping. In large steep waves, the float decks were intermittently overtopped and partially submerged causing sloshing and energy dissipation, capping the pitch motion, acting as an end stop (Stansby et al. 2022b). In these cases, the wave PTO is disengaged. This will also occur for the hybrid wind–wave platform considered here. The angular response was effectively decoupled from the mooring forces, but this may be affected by moorings if attached directly to the wind floats. The results for response and power are thus expected to be realistic while nonlinear analysis and experimentation will eventually be desirable particularly in relation to drag effects with sharp corners. A representative drag coefficient is used here and results have been shown to be relatively insensitive to its value for this configuration between 0 and 2.

The aim is to generate power from swell waves when wind power is negligible while preferably reducing platform pitch and hence hub acceleration in larger waves. Swell has periods larger than about 10 s and heave resonance would require impractically large drafts where wave excitation on the base would be small. However, with distance between wind floats (with 3 floats forming an effectively rigid body) and wave floats of about half a wavelength, the excitation forces are approximately in anti-phase generating an oscillatory moment about the hinge points. Significant swell wave power is generated between 10 and 14 s with headings over a 100° range. The effect of wave spread is relatively small. Also with insensitivity to drag coefficient, there is little advantage in having hemi-spherical or rounded bases to reduce drag as found desirable for wave energy converters in wind waves of smaller periods (Stansby et al. 2017). For this application, wind power exceeds swell wave power with wind speeds above about 5 m/s. A flat float base is desirable for ease of fabrication.

The response between wave floats is strongly coupled, e.g. with zero heading and PTO engaged, the relative angular motion in roll is 25% of that for pitch, although the corresponding wave power due to roll is 8% of that due to pitch. Without the PTO engaged for the wind floats, the roll motion is 63% of the pitch motion, while the relative roll motion is still 25% of pitch motion. This complex cross coupling must cause the rotational wind platform motions in both directions to be relatively small, which is desirable. The relative rotation with the wave floats is larger and power generation requires very high torques at low rotational speeds. This raises the question of when to disengage the power take-off. Clearly, there is no point in generating wave power when wind power is far greater. When to disengage depends on the combination of swell wave height and wind speed and is site specific; this is not analysed here.

The three-float wind platform pitch response without the PTO engaged in large waves is quite small, with rms of 1.5° and maxima of about 4.5° with \({H}_{{\text{s}}}\) = 6 m and \({T}_{{\text{p}}}\) = 12 s. Importantly, this causes the hub accelerations to be less than 3 m/s2 and this will be reduced slightly with wind damping. The maximum relative angular response, however, is about 22°. With the five floats acting almost as a rigid body, the wind pitch is increased markedly by about 120% and the maximum hub acceleration by 87%. This is counterintuitive, as one generally expects larger bodies to respond less. It does mean that the wave floats have a beneficial effect on the wind floats in large waves with the PTO disengaged, although this will be modified by intermittent float overtopping and submergence which requires experimental investigation. Damping plates may be added to the wind floats to reduce motion further, but this may reduce wave power generation in low wind conditions. Control of motion by pumping water between wind floats to reduce pitch may also be beneficial in large waves while switched off for swell wave generation.

The dimensions and spacing of the floats were chosen to be similar to Windfloat with sufficient buoyancy to support the wind turbine and column and WEC PTOs. The spacing between fore and aft floats is close to half the energy wavelength with \({T}_{{\text{p}}}\) = 12 s, but the length of wave float beam may be adjusted to suit most likely swell wave conditions. Clearly, there is scope for optimisation of dimensions, which will be site specific. There is also scope for the torque control to optimise swell wave power generation which would be expected to increase the average power by up to 100% for long wave periods (Liao et al. 2020, 2021). Control to minimise response in combination with maximising power is probably not necessary, as response is small in swell waves and power is disengaged in large waves.

It is possible to make some comparison with other hybrid systems. The system with torus absorbers on four columns gave 400 kW mean power in regular waves with 2 m height (Tian et al. 2023), which is approximately equivalent to 200 kW in irregular waves with \({H}_{{\text{s}}}\) = 2 m, similar to that produced here; however, this increased pitch motion in swell waves. The addition of three outer floats to the three-float DeepCwind platform generated 180 kW with \({H}_{{\text{s}}}\) = 2.5 m and \({T}_{{\text{p}}}\) = 10 s and reactive control (Si et al. 2021) which is equivalent to 115 kW with \({H}_{{\text{s}}}\) = 2 m. Adding heaving point absorbers between the upper and lower connecting beams of a Windfloat-type platform gave an average power of 300 kW in regular waves with height of 2 m (Hu et al. 2020), equivalent to 150 kW in irregular waves with \({H}_{{\text{s}}}\) = 2 m. The magnitudes of wave power generated are thus generally similar in the range 100–200 kW, although the effect on pitch angle is quite uncertain. In the present configuration, the magnitudes of power in swell are slightly larger and would be increased further by control. There is the advantage that wind platform pitch is reduced in large waves, but with quite large relative pitch motions, e.g. 22° with \({H}_{{\text{s}}}\) = 6 m. In practice, the extent of pitch motion is limited by overtopping of the wave floats, to about 40° for a wave energy converter (Stansby and Carpintero Moreno 2020; Stansby et al. 2022b).

It is apparent that the economic benefit of such a wind–wave platform is dependent on many factors, including the wind and wave climate for a potential site. The wave PTOs will be an additional cost; the storage required for continuity of supply will be reduced; wave PTO control will increase wave energy capture; the upper wind speed limit for wind power generation will be increased as disengaged wave floats reduce wind float pitch and hence hub acceleration. The platform cost is thus effectively increased by the two wave PTOs with hinges and the question is whether there is a cost benefit from the additional wave and wind energy generation. There is the additional consideration that the spot price of electricity is higher in low wind conditions when the ever-present swell wave energy would have an above average value.

Finally, it is useful to compare with a platform used only for wave energy conversion. The three-float M4 device was designed with a hydraulic PTO for Leixoes, Portugal, with a most likely wave condition of \({H}_{{\text{s}}}\) = 2.3 m and \({T}_{{\text{p}}}\) = 13 s giving an average power of 840 kW (Gaspar et al. 2021). With four PTOs, power is approximately quadrupled to 3.4 MW (Liao et al. 2021) with capacity of say 10 MW. In due course, this may be a viable alternative to wind or hybrid wind–wave platforms.

8 Conclusions

The aim of the hybrid concept is to generate wave energy on a semi-sub wind platform from the almost ever present swell waves, important when wind speed is too low to generate wind power. This naturally improves uniformity of supply and reduces the need for storage of wind energy. With swell periods over 10 s, heave resonance is difficult to achieve, but pitch resonance may be achieved with the fore and aft floats about half a wavelength apart with anti-phase forcing causing pitch moment on hinges above water level. Importantly significant wave power occurs for omnidirectional headings over a range of about 100°. With \({H}_{{\text{s}}}\) = 2 m, the average power is over 200 kW with an optimised passive damper and this may be improved by control. In large waves and generally strong winds, with wave power disengaged, wind float pitch and hence hub accelerations are reduced potentially enabling longer times before shutdown due to the hub acceleration limit, typically 3 m/s2. The intention here is to demonstrate the platform concept for swell waves. Designs would need to be optimised for a given ocean wind and wave climate, taking account of materials, fabrication and moorings.