Tidal turbine array modelling using goal-oriented mesh adaptation

Abstract

To examine the accuracy and sensitivity of tidal array performance assessment by numerical techniques applying goal-oriented mesh adaptation. The goal-oriented framework is designed to give rise to adaptive meshes upon which a given diagnostic quantity of interest (QoI) can be accurately captured, whilst maintaining a low overall computational cost. We seek to improve the accuracy of the discontinuous Galerkin method applied to a depth-averaged shallow water model of a tidal energy farm, where turbines are represented using a drag parametrisation and the energy output is specified as the QoI. Two goal-oriented adaptation strategies are considered, which give rise to meshes with isotropic and anisotropic elements. We present both fixed mesh and goal-oriented adaptive mesh simulations for an established test case involving an idealised tidal turbine array positioned in a channel. With both the fixed meshes and the goal-oriented methodologies, we reproduce results from the literature which demonstrate how a staggered array configuration extracts more energy than an aligned array. We also make detailed qualitative and quantitative comparisons between the fixed mesh and adaptive outputs. The proposed goal-oriented mesh adaptation strategies are validated for the purposes of tidal energy resource assessment. Using only a tenth of the number of degrees of freedom as a high-resolution fixed mesh benchmark and lower overall runtime, they are shown to enable energy output differences smaller than 2% for a tidal array test case with aligned rows of turbines and less than 10% for a staggered array configuration.

1 Introduction

The tides represent a promising renewable energy source that benefits significantly from their high predictability. This paper focuses on the numerical modelling of a tidal farm comprised of an array of turbines and aims to find a discretisation method which allows for an accurate tidal energy resource assessment with a low overall computational cost. Our approach to arriving at such a discretisation method is to apply mesh adaptation, whereby the spatial resolution is varied over the spatial domain and time period of interest.

We consider idealised test cases in localised domains in this work. However, it should be noted that the domains of interest for a realistic tidal array typically extend over a much larger scale, containing physical features and processes that exist on multiple spatial scales. Whilst capturing the evolution of tides often requires models to extend hundreds of kilometres away from a site of interest, specific modelling for tidal stream energy extraction by turbines and arrays must resolve smaller-scale features that relate to local blockage and turbine wake effects within a single array. Subject to the research objectives, robust modelling must account for the device scale ($10^{-3}$–10$^2\,\mathrm m$), the array scale ($10^{0}$–10$^3\,\mathrm m$) and the regional scale ($10^2$–10$^5\,\mathrm m$) (Adcock et al. 2021). For an example, see Jordan et al. (2022), which features mesh element sizes ranging from $10^{0}$ to 10$^5\,\mathrm m$.

The proposed approach to guide the mesh adaptation process is goal-oriented mesh adaptation, which is formulated in terms of accurately estimating the value of a diagnostic quantity of interest (QoI). There are a number of candidate QoIs that would be relevant to the application at hand, including power/energy output or financial performance, as well as undesirable outcomes such as the impact on ecological habitats (du Feu et al. 2019). For a given QoI, we make use of goal-oriented error estimation techniques, which interpret QoI evaluation errors in terms of PDE residuals and adjoint sensitivity information. By restricting the error estimates to individual mesh elements/timesteps, we are able to indicate the associated local contributions to the overall QoI error. These so-called ‘error indicators’ can then be used to guide a mesh adaptation algorithm as to the resolution required at a given time and location.

In traditional ‘h-adaptive’ methods, mesh elements or patches thereof are ‘tagged’ for refinement or coarsening, based on local error indicator values, and the adaptation is performed in a hierarchical manner. This approach is advantageous because its mesh-to-mesh data transfers induce relatively little interpolation error and because there exist efficient implementations, such as the space-filling curve approach presented in Behrens and Zimmermann (2000).

An alternative approach is given by the Riemannian metric framework, which was first introduced in George et al. (1991). It encodes the desired mesh resolution across the domain using a Riemannian metric space based on error indicator data and updates the mesh so that its elements are ‘unit’ when viewed in that space. That is, they have edges of (near) uniform length and consequently are appropriately multi-scale in physical space. The metric-based approach differs from traditional h-adaptive approaches because it allows for the control of element orientation and shape, as well as size. This can be particularly beneficial for strongly direction-dependent flows, or applications with anisotropic features, as demonstrated for steady-state ‘flow past turbines’ scenarios in Wallwork et al. (2020), see also Piggott et al. (2009) for wider oceanographic applications. The capability to construct truly multi-scale meshes is provided by (for example) Loseille and Alauzet (2011a, 2011b).

Mesh adaptation—in the traditional h-adaptive form mentioned above—has already been applied to tidal farm modelling test cases before, notably in Divett et al. (2013). The authors of that work assess the impact of different configurations of an idealised tidal array on energy output, with the finite volume mesh adapted based on the magnitude of vorticity. Further investigation on the impact of the number of array columns is made in Divett et al. (2016). In those papers, the turbines comprising a tidal farm are parametrised as patches of increased bottom friction in a depth-averaged 2D shallow water model (Draper et al. 2010). Such a model is advantageous because it allows large, multi-scale coastal ocean modelling problems to be solved with higher computational efficiency than a 3D model with the same horizontal resolution. The use of a shallow water-based model implies a number of assumptions, such as limited vertical accelerations, well-mixed water column and relatively negligible vertical dimensions compared to the horizontal.

Metric-based mesh adaptation was first applied to transient tidal farm modelling in Abolghasemi et al. (2016), although in that work metrics are not normalised in time. That is, the mesh adaptation process is applied on an instantaneous basis, rather than as a fixed point iteration with a total ‘vertex count budget’ over all timesteps (Alauzet and Olivier 2010). Metric-based, goal-oriented mesh adaptation was applied to tidal array modelling for the first time in Wallwork et al. (2020), albeit in the steady-state case. In that paper, it was found to lead to a reduction in error accrued when estimating array power output, for an equivalent number of DoFs. This was later extended to the time-dependent case in Wallwork et al. (2022), which revisited the test case introduced in Divett et al. (2013), but with a different (metric-based) mesh adaptation method and a more advanced (goal-oriented) method for identifying where refinement should occur. Qualitative comparisons were made between a high-resolution fixed mesh run and an adaptive simulation, both in terms of the adapted meshes’ structure and in terms of power output curves. In that work, only one tidal array configuration was used, wherein the turbines were aligned into three rows and five columns. This paper supersedes the work of Wallwork et al. (2022), through additional quantitative comparisons related to energy outputs and providing in-depth discussion, as well as considering both aligned and staggered array configurations. Whilst Divett et al. (2013, 2016) and Wallwork et al. (2020, 2022) use different mesh adaptation approaches (hierarchical vs. metric-based; adaptation on vorticity vs. goal-oriented error metrics), the underlying model remains the same, i.e. all of them approximate tidal hydrodynamics using the shallow water equations (although nonlinear terms are dropped in the earlier works).

The organisation of this paper is as follows. Section 2 is the methodology section. Within it, Sect. 2.1 describes the depth-averaged tidal turbine modelling framework, including details on the model parameters and discretisation used. Section 2.2 then goes on to describe a goal-oriented metric-based mesh adaptation method, which is framed around minimising the error accrued when evaluating the energy output of a tidal farm. Section 3 is the numerical experimentation section, documenting results and providing discussion thereof. Simulations focus on an idealised tidal array test case, with two different configurations for its turbine positions. This mesh adaptation method of Sect. 2.2 is applied and compared against equivalent outputs from high-resolution fixed mesh runs. Detailed power/energy output and performance comparisons are made both between the aligned and staggered configurations and between the fixed and adaptive mesh runs. From these, conclusions are drawn and future work is proposed in Sect. 4. Appendices 1 and 2 provide details on the derivative recovery procedure and software used to conduct the numerical experiments in this study.

Table 1 A list of all physical quantities and acronyms used in this paper

2 Methods

2.1 Tidal farm modelling

2.1.1 Shallow water equations

As mentioned in Sect. 1, this paper uses the shallow water equations to model coastal hydrodynamics. In particular, we use the time-dependent, non-linear and non-conservative form,

$$\begin{aligned} \frac{\partial {\textbf{u}}}{\partial t} +{\textbf{u}}\cdot \nabla {\textbf{u}} +g\nabla \eta +\frac{c_{{\mathcal {B}}}+c_{{\mathcal {F}}}}{H}\Vert \textbf{u}\Vert {\textbf{u}} -\nabla \cdot (\nu \nabla {\textbf{u}})&={{\textbf{F}}_{{\textbf{u}}}},\nonumber \\ \frac{\partial \eta }{\partial t} +\nabla \cdot (H{\textbf{u}})&={F_\eta }, \end{aligned}$$

(1)

the nomenclature for which is provided in Table 1.

The shallow water equations are defined on a two-dimensional spatial domain, $\Omega \subset {\mathbb {R}}^2$, and some time interval. They are solved for the (depth-averaged) fluid velocity, ${\textbf{u}}$, and free surface elevation, $\eta$, which we often collect as ${\textbf{q}}:=({\textbf{u}},\eta )$. Without a subscript, the norm notation denotes fluid speed: $\Vert \textbf{u}\Vert \equiv \sqrt{{\textbf{u}}\cdot {\textbf{u}}}$. Given a temporally fixed bathymetry field, b, the total water depth is given by $H=\eta +b$. A quadratic drag representation is used to represent bottom friction. This involves dimensionless coefficients $c_{{\mathcal {B}}}$ and $c_{{\mathcal {F}}}$, which convey the (global) background drag and (local) resistance due to the turbines in the tidal farm. The turbine drag contribution is described in detail later in this subsection. We use a kinematic viscosity $\nu$ which includes turbulent effects, i.e. eddy turbulent viscosity. This is also described later in this subsection.

The symbol ${\textbf{F}}_{{\textbf{u}}}$ on the right-hand side of the momentum equation denotes any additional forces to be included in the model, such as the Coriolis force and wind shear stress. However, we do not consider such forces in this work and therefore can assume ${\textbf{F}}_{{\textbf{u}}}\equiv {\varvec{0}}$ and drop this term henceforth. Similarly, we do not include additional forcings on the continuity equation and so drop the $F_\eta$ term.

2.1.2 Discretisation

Shallow water dynamics are modelled using the Thetis coastal ocean model (Kärnä et al. 2018). Thetis is an unstructured mesh DG code, based on the Firedrake finite element library (Rathgeber et al. 2016). We make use of its default 2D setting, whereby fluid velocity and free surface elevation are approximated in an equal order ${\mathbb {P}}1_{DG}-{\mathbb {P}}1_{DG}$ space defined on a given mesh. Whilst Thetis can be run on either triangular or quadrilateral meshes, we use the former in this paper, since they are well suited to representing irregular domains such as those bounded by coastlines and because the applied mesh adaptation toolkit assumes simplicial meshes. We also use the default time integration scheme for Thetis 2D: Crank–Nicolson method with implicitness $\theta =\frac{1}{2}$.

Throughout this paper, we denote meshes using the symbol $\mathcal H$ and interpret them as finite collections of elements, $K\subset \Omega$.

2.1.3 Viscosity

Molecular viscosity is a physical property of a fluid. However, the viscosity term can be treated according to the eddy viscosity approximation, whereby it becomes associated with turbulence-based momentum diffusion. It, thus, becomes a tool for controlling turbulent effects in a fluids simulation and for improving the stability of the associated numerical scheme. In particular, artificially increasing viscosity dissipates turbulent effects, whereby the flow becomes increasingly well-mixed. This is undesirable in applications which aim to capture vortices in the wake of tidal turbines, since such features are inherently turbulent and therefore cannot be resolved without an appropriately small viscosity. On the other hand, the multi-scale nature of meshes sought in this work mean that using a globally small (eddy) viscosity value leads to systems of equations which are challenging to solve over coarser regions of the mesh.

The above concerns are addressed by adopting a mesh-dependent viscosity coefficient that is small enough to allow vortices to develop in the wake of turbines, yet large enough elsewhere to ensure stability of the spatial discretisation and capture the large scale tidal dynamics. The adoption of a mesh-dependent viscosity provides a route to vary the importance of different scales of motion by artificially controlling the eddy diffusivity based on the resolution. This idea is not new; a similar rationale is applied in the context of Large Eddy Simulations (LES) (Pope 2000). LES approaches typically adopt subgrid-scale models to resolve the motion that cannot be resolved by a given domain discretisation (Rodi et al. 2013). Given that mesh adaptation often leads to significantly variable resolution, it is instructive to connect the flow scales resolved to a characteristic length-scale associated with the local discretisation.

Given a characteristic fluid speed U and the circumradius $h_K$ of an isotropic mesh element $K\in {\mathcal {H}}$, the mesh Reynolds number associated with viscosity coefficient $\nu$ is defined by,

$$\begin{aligned} \textrm{Re}_K:=\frac{h_KU}{\nu }. \end{aligned}$$

(2)

Ideally, we would like to impose a sufficiently small viscosity value $\nu _{\textrm{target}}$ such that vortices can be accurately captured. However, we are bound by the maximum mesh Reynolds number $\textrm{Re}_{\max }$ that the model can tolerate. By not exceeding this value, we ensure that the discrete problem remains stable. Together, these considerations lead us to the mesh-dependent viscosity,

$$\begin{aligned} \nu _K:=\left\{ \begin{array}{ll} \nu _{\textrm{target}} &{} \textrm{Re}_K\le \textrm{Re}_{\max }\\ \frac{h_K\,U}{\textrm{Re}_{\max }} &{} \textrm{Re}_K>\textrm{Re}_{\max } \end{array} \right. , \qquad K\in {\mathcal {H}}. \end{aligned}$$

(3)

For simplicity, the characteristic speed is set to the constant value of $4\,\mathrm {m\,s}^{-1}$, which provides an upper bound for all velocity magnitudes observed in the numerical experiments presented in Sect. 3. Consequently, the mesh Reynolds number is overestimated. This is preferable to underestimation because it puts more emphasis on stability, rather than vortex capture. In practice, the element-wise quantity (3) is projected into (vertex-wise) ${\mathbb {P}}1$ space, which has an additional smoothing effect that can be beneficial for the shallow water solver. Thetis applies additional stabilisation by treating the viscosity term using the SIPG method described in Hillewaert (2013).

2.1.4 Tidal forcing

Coastal ocean dynamics are driven by tidal forcings, which are comprised of a multitude of tidal constituents related to the celestial bodies, the principal lunar and solar semi-diurnal constituents being the most significant. It is a common practice to include tidal forcings in shallow water coastal ocean models as boundary conditions for the free surface elevation on open ocean (i.e. non-coastal) boundary segments. That is, the choice of tidal constituents is encapsulated in the definition of the prescribed elevation field $\eta _F(x,t)$.

On coastal boundaries, we opt for free-slip conditions for simplicity, amounting to treating the coasts as infinitely tall and frictionless cliffs. Decomposing the boundary into the disjoint union, $\partial \Omega =\Gamma _F\cap \Gamma _{\textrm{freeslip}}$, of forced and free-slip boundary segments, our boundary condition choice is given by

$$\begin{aligned} \eta =\eta _F\quad \text {on}\quad \Gamma _F,\qquad \textbf{u}\cdot \widehat{\textbf{n}}=0\quad \text {on}\quad \Gamma _{\textrm{freeslip}}. \end{aligned}$$

(4)

Note that these values are only weakly enforced in Thetis, as is common practice in DG methods. The normal component of the velocity is treated using a linear Riemann solver, making the formulation consistent with so-called Flather boundary conditions.

2.1.5 Tidal turbine parametrisation

Consider a tidal farm, ${\mathcal {F}}$, as a collection of turbines, ${\mathcal {T}}\in {\mathcal {F}}$. Each turbine is identified with its ‘footprint’ region, so that ${\mathcal {T}}\subset \Omega$. Moreover, each turbine is meshed explicitly, so that $\mathcal T\subset {\mathcal {H}}$. For example, the initial meshes used in Sect. 3 use $5\,\mathrm m$ fine resolution to capture the turbine footprints.

We focus on horizontal axis tidal turbines, which extract energy from the flow based on the area they sweep out in the horizontal, $A^{\textrm{swept}}$, or, more precisely, according to the force

$$\begin{aligned} F_{{\mathcal {T}}}({\textbf{u}}) =\frac{1}{2}\rho \,C_{\mathcal T}A^{\textrm{swept}}\Vert {\textbf{u}}\Vert {\textbf{u}}. \end{aligned}$$

(5)

In practice, the thrust coefficient, $C_{{\mathcal {T}}}=C_{\mathcal T}({\textbf{u}})$, of turbine ${\mathcal {T}}$ is a function of fluid velocity, which may depend on a cut-in speed, for example. However, we assume it to be constant across all turbines for the purposes of this paper. Note that we do not include turbine support structures in this model, so the parametrisation is based on the turbine footprints and their thrust coefficients alone.

We are not able to evaluate (5) in the shallow water framework because area swept in the vertical has no meaning in a depth-averaged model. As such, it must be scaled so that it applies over the turbine footprint instead:

$$\begin{aligned} c_{{\mathcal {T}}}:=\frac{1}{2}\frac{A^{\textrm{swept}}}{A^{\textrm{footprint}}}\,C_{\mathcal T}\,\mathbbm {1}_{{\mathcal {T}}}, \end{aligned}$$

(6)

giving the drag coefficient for turbine ${\mathcal {T}}$. Here $\mathbbm {1}_{{\mathcal {T}}}$ is an indicator function which is unity within the footprint of turbine ${\mathcal {T}}$ and zero elsewhere. To obtain the drag coefficient $c_{{\mathcal {F}}}$ associated with the farm, we simply sum the turbine drag coefficients:

$$\begin{aligned} c_{{\mathcal {F}}}:=\sum _{{\mathcal {T}}\in {\mathcal {F}}}c_{{\mathcal {T}}}. \end{aligned}$$

(7)

Note that the thrust coefficients as described are based on an upstream velocity, but the shallow water model makes use of the depth-averaged velocity at a turbine. This can be accounted for by applying the thrust correction recommended in Kramer and Piggott (2016).

Given that the turbines are deployed in water of (assumed constant) density $\rho$, a proxy for the power output of tidal farm $\mathcal F$ based on (5)–(7) is given by

$$\begin{aligned} P_{{\mathcal {F}}}({\textbf{q}}):=\int _\Omega \rho \,c_{\mathcal F}\,\Vert {\textbf{u}}({\textbf{x}},t)\Vert ^3\;\mathrm dx. \end{aligned}$$

(8)

Further, a proxy for the energy output of the tidal farm generated over a time interval $[t_{\textrm{start}},t_{\textrm{end}}]$ is given by

$$\begin{aligned} E_{{\mathcal {F}}}({\textbf{q}}):=\int _{t_{\textrm{start}}}^{t_{\textrm{end}}}P_{{\mathcal {F}}}(\textbf{q})\;\mathrm dt. \end{aligned}$$

(9)

2.2 The goal-oriented framework

Mesh adaptation involves three components. First, the objective of the adaptation must be identified and either quantified or estimated. In our case, the objective is to minimise the error in the QoI, which we evaluate using goal-oriented error estimation. The second step is to use this information to form an ‘optimal mesh concept’, i.e. provide a blueprint for a mesh that would (approximately) satisfy the objective. For this, we use the Riemannian metric framework. Finally comes the adaptation step itself, where modifications are made to obtain a new mesh. The three steps are described in more detail in the following.

2.2.1 Goal-oriented error estimation

Recall that ${\textbf{q}}=({\textbf{u}},\eta )$ stands for the exact solution of the shallow water problem. In addition, the DG discretisation mentioned in Sect. 2.1 gives rise to the approximating weak solution, ${\textbf{q}}_h=({\textbf{u}}_h,\eta _h)$, which lives in a ${\mathbb {P}}1_{DG}-{\mathbb {P}}1_{DG}$ space, $V_h$. Given QoI (9) and a tidal farm $\mathcal F$, goal-oriented error estimation enables us to approximate the error

$$\begin{aligned} \delta E_{{\mathcal {F}}}:=E_{{\mathcal {F}}}({\textbf{q}})-E_{\mathcal F}({\textbf{q}}_h). \end{aligned}$$

(10)

This is achieved by solving an adjoint problem associated with the shallow water equations (1). The adjoint problem depends on the QoI—in this case the energy output—and conveys how its sensitivities propagate across the space–time domain. We refer to Funke et al. (2014) for a presentation of the continuous formulation of the adjoint equation associated with the shallow water system. This can be derived using a Lagrange multiplier approach, for example. Although a continuous adjoint shallow water model has already been derived, it must be modified or re-derived if any terms of the PDE or the QoI are changed. In order to avoid such error-prone manual calculations, we opt to use a discrete adjoint formulation instead in this work. The discrete adjoint method amounts to differentiating through the discretised model—a process that can be more readily automated. See Wallwork (2021)[Chapter 3] for an in-depth comparison of continuous and discrete adjoint methods.

Let us temporarily restrict attention to the finite element problem associated with a single timestep of the shallow water model; the time-dependent case is treated subsequently. The associated weak form may be expressed as a ‘weak residual’,

$$\begin{aligned} r({\textbf{q}}_h,\,{\textbf{w}})=0,\quad \forall {\textbf{w}}\in V_h. \end{aligned}$$

(11)

In line with the notation above, let ${\textbf{q}}^*$ denote the exact adjoint solution and ${\textbf{q}}^*_h\in V_h$ denote the solution of the adjoint of the discrete shallow water model. The first-order dual-weighted residual (DWR) Becker and Rannacher (2001) uses these ingredients to provide the following error estimate for the energy output:

$$\begin{aligned} \delta E_{{\mathcal {F}}}\approx |r({\textbf{q}}_h,\,{\textbf{q}}^*-\textbf{q}^*_h)|. \end{aligned}$$

(12)

This means that the accuracy of the QoI evaluation on a given mesh can be computed in terms of the weak residual of the corresponding forward problem, but with the test function replaced by the error in the corresponding adjoint solution.

Note that (12) is not computable in general, due to its dependency on the exact adjoint solution.

Error indicator

Error estimate (12) is a global quantity, but mesh adaptation is an inherently local process, which modifies the discretisation such that it has higher resolution in some regions than others. As such, we must deduce local contributions from (12) to obtain information related to error distribution. The localisation approach used in this work is to split the estimate into its contributions from each element:

$$\begin{aligned} |r({\textbf{q}}_h,\,{\textbf{q}}^*-{\textbf{q}}^*_h)| =\sum _{K\in \mathcal H}|r({\textbf{q}}_h,\,{\textbf{q}}^*-{\textbf{q}}^*_h)|\mathbbm {1}_K, \end{aligned}$$

(13)

where $\mathbbm {1}_K$ is the indicator function for element K. We refer to the associated piece-wise constant field as an error indicator.

It is common practice to split the error indicator into strong residual and flux term components on each element. That is, a component conveying how well the shallow water equations are solved locally and a component conveying how smooth the solution field is. The details of this treatment are omitted for brevity; we refer to Wallwork et al. (2020) for details. For the shallow water problem, this gives rise to three strong residual components, $(\Psi _u,\Psi _v,\Psi _\eta )$, and three flux term components, $(\psi _u,\psi _v,\psi _\eta )$. The flux terms include contributions due to integrating by parts, weak enforcement of boundary conditions and the fluxes used in the DG discretisation.

It remains to find an approximation that does not involve the exact adjoint solution, ${\textbf{q}}^*$. There are a number of ways of doing this, such as substituting it with a higher order approximation (e.g. from a globally or locally enriched finite element space), or by applying superconvergent patch recovery (see Zienkiewicz and Zhu (1992) and Dolejší and Solin (2016), for example). In this work, we instead use the so-called difference quotient method proposed in Becker and Rannacher (2001), which has a much lower computational cost in general. It was found to be effective when applied to time-dependent tracer transport problems in Wallwork et al. (2021). Applied to the shallow water problem at hand, it gives (Wallwork et al. 2022),

$$\begin{aligned} {\mathcal {E}}_K&:=\left( \Vert \Psi _u(u_h)\Vert _{L^2(K)} +h_K^{-\frac{1}{2}}\Vert \psi _u(u_h)\Vert _{L^2(\partial K)} \right) \,\Vert \nabla ^2u^*_h\Vert _{L^2(K)}\nonumber \\&\quad +\left( \Vert \Psi _v(v_h)\Vert _{L^2(K)} +h_K^{-\frac{1}{2}}\Vert \psi _v(v_h)\Vert _{L^2(\partial K)} \right) \,\Vert \nabla ^2v^*_h\Vert _{L^2(K)}\nonumber \\&\quad +\left( \Vert \Psi _\eta (\eta _h)\Vert _{L^2(K)} +h_K^{-\frac{1}{2}}\Vert \psi _\eta (\eta _h)\Vert _{L^2(\partial K)} \right) \,\Vert \nabla ^2\eta ^*_h\Vert _{L^2(K)}, \end{aligned}$$

(14)

where ${\textbf{u}}_h=(u_h,v_h)$ and with norms evaluated in the $L^2$ sense, over K or its edge set $\partial K$. In practice, the Laplacians of the adjoint solution components are constructed using a recovery method (see Appendix 1 for details).

The formulation in (14) comes with a number of caveats, as follows. First, it is not useful as an error estimator because its sum over all elements consistently overestimates the true QoI error, with the overestimation increasing with mesh size. Nevertheless, its local contributions may still be used to guide mesh adaptation because global scale factors are not important. Second, (14) is not derived using rigorous error analysis techniques; to the best of the authors’ knowledge, such estimators have only currently been proved for elliptic problems. Finally, an expression of this form (with adjoint solutions appearing only in the weighting terms) cannot be arrived at from the ${\mathbb {P}}1_{DG}-{\mathbb {P}}1_{DG}$ formulation using integration by parts alone. In particular, two terms which act to symmetrise the viscosity operator in the SIPG method must be dropped (see Wallwork (2021)[Subsection 7.2.2] for details), meaning that we are not able to fully account for errors introduced by the stabilisation approach. Despite these drawbacks, the experiments in Sect. 3 show that it is possible to use the difference quotient approach described here to drive goal-oriented mesh adaptation methods, with promising results.

2.2.2 Riemannian metrics

Given an error indicator field, the next step is to form the optimal mesh concept, which will guide the mesh adaptation algorithm. As mentioned above, we use the Riemannian metric framework, the key ingredient of which is a Riemannian metric field, or ‘metric’, ${\mathcal {M}}=\{\underline{{\textbf{M}}}({\textbf{x}})\}_{\textbf{x}\in \Omega }$. In 2D, this is a tensor field, whose value at each point in the domain is a $2\times 2$ SPD matrix.

The way that the metric guides the mesh adaptation process is that mesh modifications are made inside the mesher until a quasi-unit mesh is obtained w.r.t. the associated Riemannian metric space. This means that each mesh element is close to equilateral and has edges close to unit length (Loseille and Alauzet 2011b). Consequently, an adapted mesh will be rather regular when viewed in the Riemannian metric space, but may be highly irregular and distorted in (Euclidean) physical space.

One of the key tunable parameters for metric-based mesh adaptation is the metric complexity. For steady-state problems, it is the analogue of the (inherently discrete) mesh vertex count in (continuous) metric space, given by

$$\begin{aligned} {\mathcal {C}}({\mathcal {M}})=\int _\Omega \sqrt{\underline{\textbf{M}}({\textbf{x}})}\;\mathrm dx. \end{aligned}$$

(15)

As such, by increasing the target metric complexity, we allow for heightened overall mesh resolution. Whilst this typically implies a heightened computational cost, it should also imply a reduction in QoI error (provided the metric is chosen appropriately). In the time-dependent case, (15) becomes

$$\begin{aligned} {\mathcal {C}}(\mathcal M)=\int _{t_{\textrm{start}}}^{t_{\textrm{end}}}\int _\Omega \sqrt{\underline{\textbf{M}}({\textbf{x}})}\;\mathrm dx\;\mathrm dt \end{aligned}$$

(16)

and is the continuous analogue of the sum of all mesh vertex counts over all timesteps. In this way, the target metric complexity can be likened to a ‘vertex count budget’ for the simulation.

See Loseille and Alauzet (2011a, 2011b) for further details on the Riemannian metric framework and the duality it shares with the computational mesh.

Isotropic goal-oriented metric

When goal-oriented mesh adaptation was first applied to time-dependent tidal array modelling in the preliminary work of Wallwork et al. (2022), it was done using an isotropic metric. In particular, an element-wise metric was obtained by scaling the $2\times 2$ identity matrix $\underline{{\textbf{I}}}$ by a scalar-valued function, m, involving fractional powers of the error indicator (14) (see Carpio et al. (2013) for details):

$$\begin{aligned} \widetilde{\underline{{\textbf{M}}}}_K^{\textrm{isotropic}} =m(\mathcal E_K)\;\underline{{\textbf{I}}}, \qquad K\in {\mathcal {H}}. \end{aligned}$$

(17)

Most metric-based mesh adaptation toolkits—including the one used herein—assume ${\mathbb {P}}1$ metric approximations, i.e. vertex-wise data. As such, an element-wise formulation such as (17) requires an additional projection step.

Anisotropic goal-oriented metric

One of the great advantages of metric-based mesh adaptation is that it allows for control of element shape and orientation, as well as size. For example, the a posteriori anisotropic metric due to Carpio et al. (2013) was applied to a steady-state tidal farm modelling problem in Wallwork et al. (2020) and is redeployed here. Again, it uses an element-wise formulation, which is then projected to obtain a vertex-wise metric. On element K we have,

$$\begin{aligned} \widetilde{\underline{{\textbf{M}}}}_K^{\textrm{anisotropic}} =m({\mathcal {E}}_K)\;\underline{{\textbf{V}}_K}\;\underline{\textbf{S}_K}\;\underline{{\textbf{V}}_K}^\textrm{T}, \qquad K\in {\mathcal {H}}, \end{aligned}$$

(18)

where $\underline{{\textbf{V}}_K}$ and $\underline{{\textbf{S}}_K}$ are matrix-valued functions. The details of each component are omitted here, but the essence of the approach is that the identity matrix in (17) is replaced by the matrix product, within which $\underline{{\textbf{V}}_K}$ controls element orientation and $\underline{{\textbf{S}}_K}$ controls element shape. These components are normalised in such a way that $m({\mathcal {E}}_K)$ then controls element size.

Whilst the information in the sizing term is derived from the error indicator, the information in the orientation and shape terms come from the curvature of the forward solution. That is, the QoI and the associated adjoint solution influence the local element size, but elemental anisotropy is inherited from features of the forward solution alone.

2.2.3 Adaptation

Given an isotropic or anisotropic metric defined upon some mesh, a new mesh is constructed by applying local transformations. In the 2D case considered in this work, we make use of four operations: vertex insertion, vertex removal, edge swapping and local Laplacian smoothing. The first three modify the mesh topology, whilst the fourth does not.

2.2.4 Time-dependent case

So far in this subsection, we have described an approach to goal-oriented mesh adaptation in the steady-state case. Moving to the time-dependent case typically involves the added complication of solving the PDE and its adjoint across a sequence of ‘adapted meshes’, which we often refer to collectively as an ‘adaptive mesh’.

We begin by partitioning the simulated time period into N subintervals,

$$\begin{aligned}{}[t_{\textrm{start}},t_{\textrm{end}}]=\cup _{i=1}^N[t^{(i-1)},t^{(i)}],\nonumber \\ t_{\textrm{start}}=t^{(0)}<t^{(1)}<\cdots<t^{(N-1)}<t^{(N)}=t_{\textrm{end}}, \end{aligned}$$

(19)

each of which is associated with a different mesh, i.e. there are N meshes in the sequence. We adopt a fixed point iteration approach inspired by that presented in Belme et al. (2012), where the forward and adjoint problems are solved on each mesh in reverse, metrics are constructed for each subinterval and solution fields are transferred between subintervals using mesh-to-mesh interpolation. The metrics are post-processed using a space–time normalisation procedure, which controls the space–time complexity (16)—i.e. vertex count budget—as well as allowing the discretisation to be multi-scale in space and distributing its DoFs appropriately over the temporal domain so as to improve the QoI accuracy. This implies that some subintervals may be associated with meshes that are much finer or coarser than others.

The fixed point iteration continues until either the QoI value converges to within a pre-specified relative tolerance, or the same occurs for the element counts of the adapted meshes on each subinterval.

We refer to Belme et al. (2012) for details on the fixed point iteration algorithm and note that the main difference here is the use of goal-oriented metrics derived from an a posteriori error result (12) rather than an a priori one. For details on how metrics (17) and (18) in particular extend to the time-dependent case, we refer to (Wallwork et al. 2021, Section 5).

2.3 Problem specification

Numerical experiments presented in Wallwork et al. (2020) involve an idealised array of two turbines. The shallow water problem was solved to steady state, meaning there was no tidal forcing and dynamic turbulent effects could not manifest (the latter of which implying laminar flow). However, the setup is useful for illustrating the impact that the locations of the turbines within the array can have upon the total power output. In that paper, the power output was found to be 15% lower when turbines were aligned in the flow, compared with when they were offset by one turbine diameter in opposite directions, orthogonal to the background flow. In addition, it was illustrated that the application of goal-oriented metric-based mesh adaptation can lead to more accurate approximations of array power output for similar numbers of DoFs.

In this paper, we consider the extension to a time-dependent case of a larger tidal farm scale. The test case was originally proposed in Divett et al. (2013) and consists of an array of fifteen turbines arranged in three rows and five columns. That work also demonstrated the importance of array configuration in tidal farm design; a staggered turbine layout was found to extract 54% more energy from the flow than a centred, aligned configuration.¹ This is because a staggered array gives the turbine wakes more opportunity to recover before interacting with downstream turbines, as well as turbines being able to exploit accelerated bypass flow. Tidal turbines act to extract energy from the flow, so their wakes are effectively momentum deficits. The investigation in Divett et al. (2013) also considered an array which is offset so that the turbines are closer to the channel boundary, as well as an array with wider spacing between turbines. For the purpose of the numerical experiments presented in this paper, we just consider the (centred) aligned and (centred) staggered configurations.

Initial meshes of the rectangular domain $\Omega =[-1500\,\mathrm m,$$1500\,\mathrm m]\times [-500\,\mathrm m,500\,\mathrm m]$ were generated using gmsh (Geuzaine and Remacle 2009). Figure 1 shows the spatial domain for each configuration, including the forced and free-slip boundary segments, the five columns of turbines and a grey box indicating the ‘farm region’, $\Omega _{{\mathcal {F}}}\subset \Omega$. In addition to the mesh-dependent viscosity treatment summarised by (3), we apply additional stabilisation by increasing the viscosity outside of the grey rectangle shown in the plots. That is, we set

$$\begin{aligned} \nu ({\textbf{x}})=\left\{ \begin{array}{ll} \nu _K &{}\quad {\textbf{x}}\in \Omega _{{\mathcal {F}}}\\ \nu _{\textrm{base}} &{}\quad {\textbf{x}}\not \in \Omega _{{\mathcal {F}}} \end{array} \right. , \end{aligned}$$

(20)

recalling that $\nu _K$ stands for the mesh-dependent viscosity in (3). A linear ‘viscosity sponge’ is used to smoothen out the transition between the two values in (20). The farm region is also used for zooms in subsequent plots.

Fig. 1

Diagrams showing the domain for each configuration of the tidal array test case, including its (forced and free-slip) boundary segments, five columns of turbines and zoom region

A simple sinusoidal tidal forcing at the western and eastern boundaries is used to drive the hydrodynamics. The two forcings are exactly out of phase:

$$\begin{aligned} \eta _F(x,t):=\left\{ \begin{array}{ll} 0.5\,\cos \left( \omega t\right) &{} x{=}-1500\\ 0.5\,\cos \left( \omega t+\pi \right) &{} x{=}1500 \end{array}\right. , \omega =\frac{2\pi }{T_{\textrm{tide}}}{.} \end{aligned}$$

(21)

The tidal period $T_{\textrm{tide}}$ is specified in Table 2, along with all the values used for parametrising the shallow water model and representing tidal turbines within it. The resulting boundary conditions are given by substitution of (21) in (4). Note that the tidal period is 10% of the commonly dominant semi-diurnal ($\mathrm M_2$) tidal constituent; it was reduced in (Divett et al. 2013) to emphasise vorticity and accelerate the simulation. We retain this value for consistency with that work.

The turbine thrust value $c_{{\mathcal {T}}}=2.985$ shown in Table 2 was chosen so that the corresponding (corrected) turbine drag coefficient is $C_{{\mathcal {T}}}=12$, to again be consistent with what was used in Divett et al. (2013). It is worth noting that the thrust coefficient is ordinarily in the range (0, 1), so it is likely that power and energy output values reported in this paper are unrealistically large.

3 Results

3.1 Spinning up the tidal dynamics

Figure 2 shows the total power output from both array configurations, as computed on coarse fixed meshes with increased mesh resolution in the farm region. On these meshes, we observe that the total energy output fluctuates between each flood and ebb tide. Whilst it continues to do so, it appears to stabilise slightly after three or four tidal periods to $11\,\mathrm {MW\,h}$ and $19\,\mathrm {MW\,h}$, respectively. These preliminary coarse mesh runs suggest that the tidal hydrodynamics eventually stabilise. They also confirm that the staggered array is able to extract more energy than the aligned array—something we will return to in more detail.

Table 2 Parameter values used in the shallow water model and its tidal turbine parametrisation for all numerical experiments in this paper

Fig. 2

Total power output from the aligned and staggered arrays over four tidal cycles, as computed on coarse meshes with 35,784 and 33,314 elements, respectively. Text annotations indicate the total energy output over the corresponding half-period. The first vertical line indicates the end of the spin-up period and the second indicates the end of the half-period of interest

For the subsequent numerical experiments in this paper, we use finer meshes to generate the spun-up hydrodynamics so that they are more reliable and can be used as benchmarks. The meshes are very close to uniform over the whole domain, except for some minor adjustments to ensure that the turbines are explicitly meshed. These adjustments occur outside the farm region and are where most of the deviations in element area and aspect ratio occur. Both meshes have low overall aspect ratio and therefore can be said to be isotropic. Henceforth, we refer to these meshes as the ‘high-resolution aligned mesh’ and ‘high-resolution staggered mesh’. Whilst we could choose a spin-up period of three or four periods so that the hydrodynamics have stabilised, this would be expensive to perform on such high resolution meshes. Given that one of the motivations of this paper is to improve computational efficiency, we opt for the shorter spin-up, noting that the power/energy output of the third half-cycle is already a reasonable approximation of the later ones.

3.2 Velocity and vorticity comparisons on fixed meshes

Figure 3 shows snapshots of the fluid velocity field for both the aligned configuration (left hand panels) and staggered configuration (right-hand panels), as computed on the high-resolution fixed meshes. A range of time levels from the half tidal cycle $[T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$ following spin-up are shown. The snapshots at $t=T_{\textrm{tide}}$ show an initial state of low magnitude velocity, with a number of vortex features left over from the spin-up phase, both to the west of and surrounding the tidal farm. In subsequent snapshots, the flow speed accelerates westward for the first quarter cycle, before decelerating so that the velocity returns to a similar low magnitude state, except with vortices to the east of and surrounding the tidal farm. At intermediate time levels $1.125\,T_{\textrm{tide}}$, $1.25\,T_{\textrm{tide}}$ and $1.375\,T_{\textrm{tide}}$ for the aligned configuration, the west-most column of turbines experiences relatively laminar flow, whilst the flow around the other turbines is much more turbulent. In the right-hand panels, the array staggering means that the west-most two columns experience quasi-laminar flow at these time levels.

Fig. 3

Snapshots of fluid velocity for high-resolution fixed mesh simulations of the tidal array test case over the time interval $[\,T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$. Left-hand panels show the aligned configuration, whilst right-hand panels show the staggered configuration. Turbine footprints are indicated by grey rectangles

In addition, Fig. 4 shows plots of the corresponding (2D interpretation of) fluid horizontal vorticity,

$$\begin{aligned} \zeta :=\nabla \cdot {\textbf{u}}^\perp =-\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}, \end{aligned}$$

(22)

at $t=1.25\,T_{\textrm{tide}}$. That is, the top row of plots in Fig. 4 corresponds to the middle row in Fig. 3. In practice, we approximate this quantity in ${\mathbb {P}}1$ space using the derivative recovery method described in Appendix 1. The corresponding outputs from adaptive simulations are also shown in Fig. 4, for ease of comparison with the fixed mesh results when they are discussed later in Sects. 3.4.1 and 3.4.2.

Fig. 4

Snapshots of fluid vorticity in the staggered configuration at $t=1.25\,T_{\textrm{tide}}$, as computed on a high-resolution fixed mesh and under different mesh adaptation techniques. Turbine footprints are indicated by grey rectangles

In the aligned case, we observe that vortices do not form until after the second column of turbines. These vortices hold their structure within the turbine farm region and only begin to disintegrate towards the end of the plot. Within the farm region, there are fairly distinct gaps of low vorticity between the rows of turbines. In the top right plot, the array staggering means that there are no clear gaps with low vorticity and there appears to be greater vorticity overall.

3.3 Power contributions by column

Before considering the application of mesh adaptation, we first analyse the power output curves of each array column over high-resolution fixed mesh runs, as shown by the top row of plots in Fig. 5. These outputs come from the same high-resolution fixed mesh runs as the velocity plots in Fig. 3. Moreover, the x-axis bounds and the vertical grey lines correspond to the timesteps where the snapshots were taken. The corresponding outputs from adaptive simulations are also shown in Fig. 5. Again, this is for ease of comparison with the fixed mesh results when they are discussed later in Sects. 3.4.1 and 3.4.2.

Fig. 5

Power output as a function of time in both farm configurations, separated by turbine column in the array. The values in the top row were computed using the same high-resolution fixed meshes as in Sect. 2.3, whereas the middle and bottom rows use isotropic and anisotropic goal-oriented mesh adaptation, respectively

3.3.1 Aligned configuration

The nonlinear interactions between turbines and the fact that turbines act to remove momentum from the flow means that the first (i.e. west-most) column of turbines (indicated by the bright blue curve) extracts the most energy when the flow is eastward. Turbine columns downstream do occasionally extract similar amounts of energy, but they typically extract less and the levels fluctuate more due to wake-induced turbulence. For example, there is a spike in the final column’s power output (indicated by the dark green curve) around $t=1.15\,T_{\textrm{tide}}$, when the meandering bypass (i.e. accelerated) flow from columns 2 and 4 first reaches it around $t=1.125\,T_{\textrm{tide}}$. (See the patch of high magnitude velocity near column 4 in the left-hand plot of Fig. 3).

In this study, the instantaneous power output values are not of primary interest, but rather the sum of the integrated areas under the curves—the total energy extracted over a half-cycle. The largest area corresponds to the leading column of turbines, meaning it contributes most to the energy output. Columns 2–4 have smaller contributions to the overall energy output. In particular, turbines in the second column generate the least power. This is because the wakes of the first column are quasi-steady and only become unstable upon reaching the second column, implying a significant momentum deficit for those turbines for much of the simulation. The fact that the first column generates the most power and the second column generates the least power is consistent with results reported in Divett et al. (2013). This steady wake is a clear limitation of the actuator disk approach to tidal turbine modelling, as dynamic wake meandering due to the moving blades would be expected even from the first column.

3.3.2 Staggered configuration

Interestingly, the column-wise power output curves take rather different forms in the staggered configuration shown in the top right panel of Fig. 5. In the following, we discuss some of the key differences.

First, the power output curve associated with the second column is relatively smooth—like for the first column—because the flow it experiences is close to laminar. This is not the case for the three downstream columns, where there is much more turbulence. These observations are consistent with those for Fig. 3.

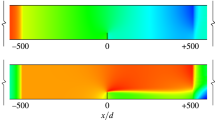
Second, all columns are reported to have higher power output in the staggered case. Where in the aligned case the second column generates the lowest power output—due to being fully obstructed—it generates the most power in the staggered configuration. One explanation is that this is due to accelerated bypass flow, as a result of the ‘funnelling’ effect of the first column. However, the first column also experiences a small increase in power output, so this cannot be the full explanation. An alternative explanation is that more energy is extracted by the staggered configuration during the spin-up cycle and so a greater flow rate is required through the boundary to satisfy the pressure wave that has been imposed. To investigate whether this is the case, Fig. 6 examines cross sections of both the velocity normal to the inflow boundary ($x=0$) at a selection of timesteps, as well as the corresponding theoretical ambient power output due to turbines experiencing the full inflow velocity and no drag effects. The left-hand plot confirms that the tidal influx is indeed greater at the start of the time period of interest in the staggered case. Due to the cube term, this is exaggerated in the right-hand plot of theoretical power output. The increased tidal influx observed here is notable because it contradicts the common assumption that upstream flow remains unaffected for CFD studies on tidal arrays positioned within confined domains.

Fig. 6

Cross sections of the normal inflow velocity component (left) and theoretical ambient power output (right) at a range of timesteps, for the high-resolution fixed mesh runs. Both plots consider slices along the y-axis (at $x=0$)

Interestingly, the inflow velocity appears to become rather asymmetric at $t=1.25\,T_{\textrm{tide}}$ for both configurations. In the staggered configuration, there is a significantly lower inflow velocity to the south than the north. This can also be observed in the right-hand $t=1.25\,T_{\textrm{tide}}$ panel of Fig. 3.

3.4 Mesh adaptation based on farm energy output

Let us now consider the adaptive mesh case. Goal-oriented metrics are applied, with the aim of minimising the error in energy output. The simulated interval $[T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$ is divided into 40 subintervals of equal length and we construct a different Riemannian metric for each subinterval.

Once the sequence of metrics has been constructed, they are post-processed in two ways. First, a target value for the space–time metric complexity (16) is imposed, to control the overall DoF count of the simulation. The target complexity is increased from a base value of 400,000 up to the target value of 2,000,000 over the first three fixed point iterations. Doing so does not usually hamper the effectiveness of the adaptation algorithm, but can significantly improve its computational efficiency in the early iterations (see Wallwork et al. (2021), for example). The second post-processing step is to impose minimum and maximum metric magnitudes, to ensure that adapted mesh elements are not too small or too large. Minimum and maximum values of $1\,\textrm{cm}$ and $100\,\mathrm m$ are imposed across most of the domain, but the metric is treated differently inside the turbine footprint regions (where the momentum sink is applied). There, a maximum magnitude of $2\,\mathrm m$ is used to ensure that the footprints are not under-resolved, whilst a minimum magnitude of $10\,\textrm{cm}$ ensures that they are correctly defined when few DoFs are used overall.

3.4.1 Isotropic metric

First, consider the application of isotropic goal-oriented mesh adaptation. Figure 7 shows snapshots of both fluid velocity and the underlying isotropic adapted mesh for the staggered configuration at a selection of time levels. We do not show the corresponding plots for the aligned configuration because they follow a similar pattern. Similar mesh and velocity snapshots have also already been presented in Wallwork et al. (2022).

Fig. 7

Snapshots of fluid velocity and the underlying mesh for an adaptive simulation of the staggered configuration of the tidal array test case over the time interval $[T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$. Mesh adaptation is driven by an isotropic metric of the form (17). Turbine footprints are indicated by grey rectangles

A first observation is that all of the presented meshes have low maximum aspect ratios across their elements. This confirms that the isotropic metric formulation has indeed given rise to isotropic meshes. Another is that all of the turbine footprints are captured at all time levels, thanks to the increased mesh resolution due to the spatially varying maximum metric magnitude.

At $t=T_{\textrm{tide}}$, there do not appear to be any regions of notably high mesh resolution, except around the turbine footprints. Zooming out, the left-hand plot in Fig. 8 shows that there is also increased mesh resolution near to the domain boundaries, particularly surrounding the western boundary. This enables the weakly imposed inflow conditions to be correctly treated.

Fig. 8

Adapted meshes used at $t=T_{\textrm{tide}}$ in the staggered configuration (no zoom)

At $t=1.125\,T_{\textrm{tide}}$ and $t=1.25\,T_{\textrm{tide}}$, significant resolution is deployed upstream of the first column, especially its middle turbine. One explanation for this is that the top two turbines in the second columns experience greater accelerated bypass flow than the bottom one, due to the ‘funnelling’ effect of the first column. Another is that accuracy of the hydrodynamics in the centre of the array are more important overall, since their wakes encounter more turbines during the simulation. Interestingly, little mesh resolution is deployed for the purposes of capturing vortices. As a consequence, turbulent effects are largely smoothed out, especially in the regions with coarser meshing. This effect is also visible in the bottom left plot in Fig. 4, where vortices do not take on anything close to the complex structures resolved in the fixed mesh case and vanish sooner after passing through the array.

The ‘arrow of time’ implies that dynamics at a particular instant are only important from then onwards. At the start of the simulation, the dynamics can potentially impact the entire solution trajectory, whereas towards the end of the simulation the impact is much more limited. This explains why slightly more resolution is deployed at $t=T_{\textrm{tide}}$ than at $t=1.5\,T_{\textrm{tide}}$, despite the low magnitude velocity (and hence the low energy output contribution) in both cases. This highlights the strong dependence of the adapted mesh sequence upon the simulation period length in the goal-oriented framework; if the time period were extended then these effects would likely have a different manifestation.

Figure 5 suggests that the power curve is slightly out of phase with the tidal forcing, with the outputs of all columns becoming near-zero before the slack tide. This is likely due to the significant drag forces inherent in the tidal farm. As a consequence, the power outputs of all columns are significantly larger at $t=1.125\,T_{\textrm{tide}}$ than at $t=1.375\,T_{\textrm{tide}}$. Combined with the above argument about the arrow of time, this explains why the mesh used at time $t=1.375\,T_{\textrm{tide}}$ is so much coarser than that at $t=1.125\,T_{\textrm{tide}}$. At $t=1.375\,T_{\textrm{tide}}$ and $t=1.5\,T_{\textrm{tide}}$, the pre-specified maximum metric magnitude is being imposed within the turbine footprints.

One possible suggestion for much of the mesh resolution being concentrated upstream of the first two columns of turbines is that they may form the highest contributions to the QoI, $E_{\mathcal F}$. However, we tested adaptation with respect to $E_{\mathcal C^3}$ and $E_{{\mathcal {C}}^5}$ (i.e. the third and fifth columns being the only ones that contribute to the QoI) and found the mesh patterns to be similar to those of Fig. 7. (Results not shown due to their similarity.) As such, the first two columns having the highest contributions cannot be the main explanation for why resolution is distributed this way. A better explanation is that we have a strongly advection-dominated problem, whereby the accurate capture of upstream hydrodynamics evolution is required to represent the operation of the entire farm.

3.4.2 Anisotropic metric

Now consider the application of anisotropic goal-oriented mesh adaptation. Figure 9 shows the corresponding velocity and adapted mesh snapshots. Again, we do not show the plots for the aligned configuration because they follow a similar pattern.

Fig. 9

Snapshots of fluid velocity and the underlying mesh for an adaptive simulation of the staggered configuration of the tidal array test case over the time interval $[T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$. Mesh adaptation is driven by anisotropic metric of the form (18). Turbine footprints are indicated by grey rectangles

Some of the features observed under isotropic adaptation appear again under the anisotropic metric. For example, significant resolution is focused upstream of the first two columns at $t=1.125\,T_{\textrm{tide}}$. In addition, the metric appears to be controlled purely by the minimum imposed magnitude at $t=1.5\,T_{\textrm{tide}}$. Further, the bottom right plot in Fig. 4 shows that the anisotropic approach does not dedicate resolution for the purpose of capturing the vortex structures that are apparent in the fixed mesh simulation of the staggered configuration. It is not surprising that the anisotropic adapted meshes have some similarities to the isotropic ones, since the metrics that they are constructed from are scaled by the same error indicator. However, there are also some notable differences, as described in the following.

At $t=T_{\textrm{tide}}$, the spun-up hydrodynamics are interpolated as an ‘initial condition’. Accordingly, the mesh associated with the first subinterval is adapted so that these hydrodynamics may be accurately captured. Moderate mesh resolution is also deployed over the domain at other timesteps, such as at $t=1.375\,T_{\textrm{tide}}$, where there is more downstream resolution than in the isotropic case. These features are inherited from the curvature of the forward solution, which does not contribute to the isotropic metric.

Another key difference is that the meshes are more anisotropic, as expected. Where high mesh resolution is deployed, it typically comes with moderately anisotropic elements. In particular, anisotropic elements are used in alignment with the wakes of the first and second turbines. The maximum aspect ratio is typically an order of magnitude greater than observed in the isotropic case.

Finally, whilst the isotropic mesh at $t=1.375\,T_{\textrm{tide}}$ is effectively defined by the minimum imposed magnitude, the corresponding anisotropic mesh retains much of the structure from previous meshes. Again, this is likely due to the inclusion of the Hessian of the forward solution in the metric formulation. As discussed in Appendix 1, the Hessian is normalised in space. This means that minor variations in the curvature of the velocity and free surface elevation fields get picked up and in some cases result in structures within the adapted meshes.

3.4.3 Computational cost comparison

There are a number of ways to measure the computational cost of an adaptive simulation. Here, we focus on one that is directly related to the sequence of adapted meshes (DoF count statistics) and one related to a given simulation (runtime).

DoF count

Figures 7 and 9 only provide a sample of snapshots and do not show the aligned array case at all. To give a sense of what the missing meshes are like, Fig. 10 presents DoF counts for the meshes associated with each subinterval in both configurations.

Fig. 10

Adaptive mesh DoF counts as a function of time, separated by configuration

Interestingly, the left-hand plot shows how the DoF counts of an isotropic adaptive simulation mimic the total power output, to some extent, in the aligned configuration (c.f. Fig. 2). That is, the DoF count starts relatively low, increases to a peak around $t=1.15\,T_{\textrm{tide}}$ and then decreases. The staggered case is similar, but has a later peak, at around $t=1.2\,T_{\textrm{tide}}$. The plot highlights that the coarse meshes used towards the end of the isotropic adaptive simulation arise from metrics that are effectively defined by the minimum tolerated magnitudes (c.f. Fig. 7). These meshes reach a plateau of around 74,000 DoFs for both configurations.

The right-hand plot shows that the DoF counts in the anisotropic adaptive simulation take a rather different form; there is no clear pattern, except that the adaptive meshes start off with around 300,000 DoFs and lose overall resolution at some point in the following eighth-cycle. DoFs are more evenly distributed in time for the anisotropic metric because resolution is dedicated to capturing flow features of the forward solution, as well as prescribing element sizing according to the goal-oriented error estimate.

Table 3 summarises some key statistics associated with the DoF count patterns presented in Fig. 10, reiterating that the isotropic adapted meshes have both wider ranges and variance in DoF count. Given that all of the simulations use the same target space–time metric complexity, we would expect the total DoF counts to be comparable. The values stated in the table are indeed comparable across configurations, but the isotropic runs have significantly more DoFs overall than the anisotropic ones. The reason for this is that the minimum and maximum metric magnitudes are applied after space–time normalisation, so the last twelve or so isotropic meshes in the sequences have more DoFs than would otherwise be the case. The equivalent DoF counts for the fixed mesh simulations are also included in Table 3, for reference.

Table 3 DoF count statistics for each run. ‘Std.’ stands for ‘standard deviation’

Runtime

Whilst the above DoF count statistics allow us to compare the different ways in which the adaptive methods distribute resolution in time and space, they do not account for any of the fixed point iterations before convergence, nor do they account for additional costs such as solving the adjoint equation or recovering derivatives. In practice, application scientists are often much more interested in the time taken to run the adaptive simulation.

The mesh adaptation toolkit used in this work does not support parallelism for 2D problems. As such, all of the results presented in this work come from experiments run in serial. A typical uniform mesh simulation was found to take 15 h to complete on a Intel$^{\circledR }$ Core$^{\text {TM}}$ i7-10750 H CPU @ 2.60GHz. With isotropic adaptation, convergence was achieved after five fixed point iterations in around 11 h for the staggered configuration. Note that each iteration involves solving the shallow water equations over 40 subintervals and then solving the equations and their adjoint over the subintervals in reverse, plus the timing includes a final forward run on the converged adapted meshes. As such, the isotropic adaptive run contains a total of 11 forward solves and five adjoint solves. The same is true under the anisotropic approach, which also converges after five fixed point iterations. In that case, the total runtime was around 13 h. Of course, the main reason that the adaptive simulations are able to complete sooner than the fixed mesh approach is because the dimensions of the underlying linear systems are typically significantly smaller and are therefore amenable to rapid numerical solution.

In terms of the relative costs of each component of one typical fixed point iteration of the mesh adaptation routines, we find that solving forward in time to generate checkpoints takes around 28.6% and then the forward solves on each subinterval to record the associated operations takes around 31.7% in total. The small increase is because the former skips the final subinterval and there are some minor costs associated with the annotation for the latter. The adjoint solves are found to take 33.6% altogether. Finally, the metric construction takes 2.6% and the calls to the mesh adaptation toolkit around 0.8%. As such, we find that the cost of the goal-oriented mesh adaptation routine is dominated by the forward and adjoint solves and the contributions from metric construction and adaptation are minor. The costs associated with forward and adjoint solves can be straightforwardly reduced by introducing parallelism.

Note that the cost of the metric construction step would not necessarily be so small if a different method were used to evaluate error indicator (12) than the difference quotient formulation (14). If the indicator were instead represented by approximating the adjoint solution in an enriched finite element space, for example, then it is likely that the metric construction step would take a significant proportion of the runtime, due to the computationally expensive nature of solving auxiliary PDEs and using enriched spaces.

Table 4 Relative discretisation “errors” in power output over a single flood tide for both aligned and staggered configurations, separated by array column

3.4.4 Power contribution comparison

Recall the columnar power output curves shown in Fig. 5. Below the row of fixed mesh results, there are curves due to isotropic adaptation in the middle row and those due to anisotropic adaptation in the bottom row.

First, consider the aligned configuration (middle left and bottom left). Despite the fact that even the adapted meshes with highest overall size have less than a third of the high-resolution fixed mesh element count, the power output curve for the first column agrees well with the high-resolution fixed mesh benchmark. The general trend of the second column’s power output curve is also well represented, even though it contributes the least. This is partly because its upstream conditions are well resolved and partly because its variability is fairly small. The anisotropic metric appears to capture the power output timeseries for column 2 slightly better than the isotropic one, as the latter contains more variability. The power curves for columns 3–5 do not appear to be well captured for either metric. This is for a number of reasons. First, the power curves of these columns are much more difficult to capture than the first two columns because of the turbulent conditions there, of which the high variability in those curves is a symptom. Second, the target complexity is relatively small for a problem of this size; if it were increased, then it is likely that the mesh adaptation algorithm would deploy more DoFs for the purpose of capturing columns 3–5.

Now consider the staggered configuration (middle right and bottom right). Again, the timeseries are well represented for the first two columns, despite the fact that even the finest adaptive mesh instance has fewer than a third as many elements as the mesh used throughout the fixed mesh, high-resolution run. In this configuration, the second column is accurately modelled because of the close to laminar flow which it experiences, meaning that the timeseries has little variability. For the target metric complexity used in this work, the timeseries associated with the downstream turbines are less well captured. Like in the aligned case, there are a number of reasons, including the smaller contribution to the total energy output and the difficulty of representing turbulent phenomena numerically.

Table 5 Energy output by array column over a single flood tide, for both aligned and staggered configurations. High-resolution (fixed mesh) results are shown, alongside both isotropic and anisotropic goal-oriented adaptive runs.

Table 6 Differences in energy output over a single flood tide for both aligned and staggered configurations, separated by array column

Table 4 provides quantitative evidence to support the claim that the trends of the first and second columns are better captured by mesh adaptation than the downstream ones. It also confirms that the anisotropic approach does a better job of capturing the second column in the aligned configuration. In the table, this is measured by the relative $L^1$ “error” for the power output of each column, where the output of the high-resolution fixed mesh run is held to be “truth”. That is,

$$\begin{aligned}{} & {} \left\| P_{{\mathcal {C}}^k}(\textbf{q}^{\textrm{adapt}})\right\| _{L^1([t_{\textrm{start}},t_{\textrm{end}}])}\nonumber \\{} & {} \quad :=\frac{ \int _{t_{\textrm{start}}}^{t_{\textrm{end}}}|P_{\mathcal C^k}({\textbf{q}}^{\textrm{adapt}})-P_{{\mathcal {C}}^k}(\textbf{q}^{\textrm{fixed}})|\;\mathrm dt }{ \int _{t_{\textrm{start}}}^{t_{\textrm{end}}}|P_{\mathcal C^k}({\textbf{q}}^{\textrm{fixed}})|\;\mathrm dt }, \end{aligned}$$

(23)

where $P_{{\mathcal {C}}^k}({\textbf{q}}^{\textrm{adapt}})$ and $P_{{\mathcal {C}}^k}({\textbf{q}}^{\textrm{fixed}})$ are the power outputs of column ${\mathcal {C}}^k\subset {\mathcal {F}}$ generated in a given adaptive run and in the corresponding fixed mesh benchmark, according to formula (8). We use the $L^1$ norm because of its close relation to energy output—the QoI—for strictly positive quantities.

The errors for the two array configurations follow a similar pattern, in that the error is lowest in the first two columns and increases downstream. It should be noted that the energy outputs being higher in the staggered case means that the $L^1$ norms on the denominators will be larger. This is at least part of the reason why the errors over the whole farm are smaller for that configuration.

3.4.5 Energy contribution comparison

The above assessment of the ability of adaptive methods to accurately evaluate power output is interesting, but this is not actually the goal of the adaptation approach. For the purposes of this paper, it is the time integral—energy output—which is of primary interest. Table 5 breaks down the contributions to the energy output from each run column-wise. In this format, the contributions from each column are clearer. Different aspects of the comparison are discussed in the following.

Before comparing the adaptive methods, we note that the final column of Table 5 shows clearly that array staggering yields a significantly higher overall energy output than an array whose rows are aligned both internally and with the direction of flow. This occurs because the staggered array blocks the flow more and—because the channel is relatively narrow—there is more artificial blockage than with the aligned array, leading to a heightened energy output. Staggering leads to increases of 81%, 68% and 65% in the fixed mesh, isotropic and anisotropic runs, respectively. This increase is consistent with studies in the literature, such as Draper and Nishino (2014). However, the proportions reported here are higher than the 54% increase reported in Divett et al. (2013). There are a number of possible reasons for this. First, the increase is computed over $[T_{\textrm{tide}},1.5\,T_{\textrm{tide}}]$ here (not including spin-up), whereas it was computed over $[0,2\,T_{\textrm{tide}}]$ in that paper. Second, there are a number of differences in the model configuration and discretisation between that work and the present one. For example, in the previous work, the linearised shallow water equations are solved numerically using a finite volume method with an adaptive timestep, whilst here we solve the nonlinear shallow water equations using a DG finite element method with a fixed timestep.

The adaptive mesh energy output values appear to be fairly consistent with those due to the fixed mesh, at least for the first two columns. The differences are made clearer in Table 6, which makes a number of comparisons. The ‘$\text {Iso.}-\text {Fixed}$’ and ‘$\text {Aniso.}-\text {Fixed}$’ rows comparing adaptive mesh energy outputs with the high-resolution fixed mesh runs can be interpreted as “discretisation errors”, in the sense that the fixed mesh runs can be viewed as benchmarks. These rows reveal that, from the standpoint of accurately evaluating energy output, both adaptive methods give consistent results to using fixed meshes in both configurations. In particular, despite having much lower DoF budgets, they are able to give “errors” as low as 8.8–9.0% in the staggered case and 0.0–1.7% in the aligned case. Remarkably, the anisotropic metric is able to match the aligned array energy output calculation using only a tenth of the DoFs overall (c.f. Table 3) and in less CPU time.

The fact that both adaptive approaches are more consistent with the benchmark run in the aligned case can be gleaned from Fig. 5; in the left-hand plots, at least the magnitudes of the downstream power timeseries are well captured, whereas in the right-hand plots they are largely underestimated. It is not entirely surprising that the performance is worse for the staggered array because the flow is more turbulent overall (c.f. Fig. 4) and, therefore, more difficult to model numerically.

Negative signs in the table indicate underestimates, whilst positive signs indicate overestimates. Therefore, it appears that the adaptive methods have a tendency to underestimate the QoI. This is not surprising, because each adaptive mesh simulation involves 40 mesh-to-mesh interpolation steps and the method we use for this is known to have a diffusive effect (Farrell et al. 2009).

It should be noted that all of the relative differences in energy output presented in Table 6 are smaller in magnitude than the relative $L^1$ errors in power output presented in Table 4. This is to be expected, because the former measures errors between two integrated quantities, whereas the latter measures errors between two timeseries in an integral norm. The upshot is that—as has been observed—the power output curves may not always be well matched by the goal-oriented adaptation method, but the resulting energy output approximations are still good. Under a different (hypothetical) adaptation scheme, highly accurate power output approximations would imply accurate energy output estimates. However, achieving this would likely require the deployment of many more DoFs, increasing the computational cost significantly. Goal-oriented mesh adaptation has one objective: evaluate the energy output accurately at low cost; we argue that this objective is achieved and that it would be unreasonable to expect it to provide equally accurate power output estimates as a by-product.

Table 6 also contains ‘$\text {Iso.}-\text {Aniso.}$’ rows, which show the difference between the two adaptive runs, normalised by the corresponding fixed mesh value. The final column shows that, even though the two adaptive meshes distribute resolution very differently across the space–time domain, they are remarkably consistent in their energy output prediction, especially for the staggered configuration. There are some columns where they differ, but these differences are offset so that the overall value is similar. Again, this highlights the fact that the goal-oriented approach seeks to accurately estimate the energy output of the whole farm, not some subset of it.

Recall Fig. 6, which shows differences in inflow velocities between the aligned and staggered configurations. Table 7 accounts for these differences by normalising the power output at each timestep by the ambient theoretical power that would be generated by a single tidal turbine (using formulae from Kramer and Piggott (2016)). The normalised energy outputs for the first column are now more consistent. Lower values are reported than the combined output of three individual turbines. This is because the ambient theoretical values do not include the drag effects of the turbines, which are of course significant. The overall agreement between fixed mesh and adaptive runs remains similar after normalisation, although the influence on individual columns varies.

Table 7 Normalised energy output by array column over a single flood tide, for both aligned and staggered configurations

After applying normalisation, the increases in energy output going from the aligned configuration to the staggered configuration become 23%, 15% and 21% for the fixed mesh, isotropic and anisotropic runs, respectively—much smaller than the 81%, 68% and 65% reported before normalisation. Given that the increased tidal influx shown in Fig. 6 is largely due to the constrained nature of the channel domain, we expect that the effect of array staggering be less significant in more open domains.

3.5 Potential extensions for the tidal array test case

The numerical experiments in this paper provide some key extensions to the preliminary work in Wallwork et al. (2022), which applied goal-oriented mesh adaptation techniques to the idealised tidal array test case introduced in Divett et al. (2013). These extensions include the consideration of array staggering, the use of anisotropic metrics and the effect of choosing QoIs based on individual columns, as opposed to the whole array. However, there are still a number of avenues of investigation that would be beneficial for future research, as detailed in the following.

Convergence analysis experiments would also be extremely useful. By gaining an understanding of the relationship between the accuracy of mesh adaptive methods and the associated computational cost, we would be able to quantify the improvement that is to be obtained by moving from the fixed mesh case. We would hope to see improved accuracy, for a similar computational cost.

So far, goal-oriented mesh adaptation has only been applied over a single flood tide. It would also be interesting to see how the adaptation algorithms act to deploy mesh resolution over a sequence of flood and ebb tides. In particular, would the DoF count become periodic in the same way that the power output is?

4 Conclusion

This paper provides important extensions to Wallwork et al. (2022), which was the first published work to use goal-oriented mesh adaptation to simulate time-dependent hydrodynamics within a tidal array. In particular, we consider the effects of array staggering on power and energy output, compare the isotropic adaptation approach from that paper with an alternative anisotropic one and make detailed investigations on the different ways in which mesh resolution is used to capture important features of the flow.

4.1 Effects of array staggering

We focus on the same idealised fifteen turbine array test case introduced in Divett et al. (2013), where four different configurations of the turbines were considered. In addition to the ‘aligned’ configuration considered in Wallwork et al. (2022), we examine another configuration where the columns of turbines are ‘staggered’. The results of our numerical experiments indicate that this staggering is beneficial in terms of yielding increased energy output, which is in agreement with the literature (Divett et al. 2013; Draper and Nishino 2014). Within our investigation, we observe that this is at least in part due to there being increased velocity across the inflow boundary in the staggered configuration. We argue that the constrained nature of the channel domain exacerbates the amount of energy that the staggered array is able to extract from the flow, leading to there being a greater tidal influx, so that the boundary conditions may be satisfied. If the power output values are normalised by the theoretical ambient power that would be generated by turbines experiencing the full inflow velocity then the increased output due to array staggering is less significant. As such, we expect the increased energy output due to array staggering to be smaller for arrays positioned in more open domains.

4.2 Comparison of goal-oriented approaches

Section 2.2 describes a framework for goal-oriented error estimation and mesh adaptation, including two approaches that give rise to isotropic and anisotropic adapted meshes. These methods are applied to the idealised tidal array scenario in Sect. 3.4, with the aim of accurately assessing its energy output. We investigate how each approach deploys mesh resolution across space and time in order for this aim to be achieved. We find that there is a tendency for the adaptive methods to place resolution surrounding and upstream of the first two out of the five columns of turbines. This is believed to be due to the advection-dominated nature of the problem, meaning that accurate capture of downstream hydrodynamics is predicated by that of the upstream conditions.

Using the high-resolution fixed mesh runs as benchmarks, we make detailed comparisons between the power and energy output estimates due to the adaptive methods, both over the whole array and column-wise. Despite the fact that the adaptive simulations we present have only a tenth of the DoFs overall compared with the fixed mesh benchmarks and terminate in shorter overall runtime, they are found to give rise to energy output errors smaller than 10% in the staggered configuration and smaller than 2% in the aligned configuration. The larger errors in the staggered configuration are believed to be due to the difficulty of numerically modelling its more turbulent dynamics. In addition, we find that, whilst the isotropic and anisotropic goal-oriented mesh adaptation methods often distribute resolution quite differently and the latter uses elements with aspect ratios an order of magnitude higher, the energy output estimates over the whole array are highly consistent.

4.3 Outlook

A number of potential extensions for the specific test case considered in this paper are suggested in Sect. 3.5. More generally, we plan to apply the goal-oriented metric-based mesh adaptation framework to more complex problems. In particular, it would be beneficial to investigate to what extent the results obtained in this work extend to real-world scenarios with spatially varying bathymetry and realistic tidal forcings. For example, it would be beneficial to apply adaptive methods to seek accurate energy output comparisons for proposed tidal power infrastructure projects. In realistic applications, additional physics will come into play such as the Coriolis force, wind shear stress and vertical variations in fluid motion (e.g. due to turbine rotation). Additional terms were omitted in this study due to the confined nature of the domain and the idealised structure of the case studies that aimed to showcase the value of mesh adaptation.

Whilst the metric-based mesh adaptation approach is motivated by its ability to produce truly multi-scale discretisations, this feature is not used to its full extent in this work due to the localised nature of the tidal array test case. For realistic scenarios with tidal arrays positioned within greater coastal ocean domains, there would be a more opportunity to benefit from the generation of multi-scale adaptive meshes.

Finally, it is plausible that the integration of mesh adaptation techniques such as those described in this paper could be used to accelerate design optimisation calculations for tidal turbine arrays (Funke et al. 2014; Culley et al. 2016; Piggott et al. 2022). Moreover, in the case of goal-oriented mesh adaptation methods and adjoint/gradient-based optimisation methods, it is possible to improve computational efficiency by only solving the adjoint equation once and then using the result to compute both the error indicator (for mesh adaptation) and QoI gradient (for optimisation).

Appendices

Appendix A Derivative recovery

The goal-oriented error estimator (14) and anisotropic metric (18) used in this work make use of second derivatives of fields that are approximated in ${\mathbb {P}}1_{DG}$ space, i.e. are not twice continuously differentiable. As such, this information must be obtained in an approximate sense using a recovery method.

We opt to use two applications of $L^2$ projection, first projecting the finite element gradient into vector-valued $L^2$ space and then projecting the gradient of the result into matrix-valued $L^2$ space. In detail, let $f\in {\mathbb {P}}1_{DG}$ denote the scalar field which we seek to recover second derivatives for. Taking one finite element gradient gives a (vector-valued) ${\mathbb {P}}0$ field. We apply $L^2$ projection such that we recover a (vector-valued) ${\mathbb {P}}1$ approximation to the gradient of f. Taking another finite element gradient gives a (matrix-valued) ${\mathbb {P}}0$ field. A final application of $L^2$ projection then recovers a (matrix-valued) ${\mathbb {P}}1$ approximation to the Hessian of f, as required. In practice, we perform the two projection steps simultaneously using a mixed finite element method. Recovering the Laplacian of f amounts to taking the trace of the recovered Hessian.

Note that the Hessians of u, v and $\eta$ computed using this method do not necessarily have the same orders of magnitude. As such, we apply $L^\infty$ normalisation (see Loseille and Alauzet (2011a)) to each of them before combining them using metric intersection (see Pain et al. (2001)) to obtain a single Hessian for the forward solution tuple.

For the purpose of recovering the first derivative required for calculating fluid vorticity (22), we apply a single $L^2$ projection.

Appendix B Software

As mentioned in Sect. 2.1, the shallow water equations are solved using the Thetis coastal ocean model (Kärnä et al. 2018) in this work—a discontinuous Galerkin package, built using the Firedrake finite element library (Rathgeber et al. 2016). Whilst Firedrake is a Python package, it automatically generates C code and uses PETSc (Balay et al. 2019, 2021) to solve linear and nonlinear systems. It also enables the solution of adjoint problems in the discrete sense using dolfin-adjoint (Farrell et al. 2013). Support for mesh-to-mesh solution transfer by conservative interpolation is provided by libsupermesh (Farrell and Maddison 2011). The Pyroteus goal-oriented mesh adaptation toolkit (Wallwork 2022) is used to handle the mesh adaptation fixed point iteration loop, including the solution of forward and adjoint problems across multiple meshes, with the mesh adaptation step itself done using Mmg (Dobrzynski and Frey 2008; Wallwork et al. 2022).