Abstract
Interaction of linear and nonlinear, long-crested waves with currents in deep and finite water depths is studied by use of the computational fluid dynamics approach. Various wave conditions are considered by systematically changing the wave height and the wavelength. Several current profiles are studied as polynomial functions of water depth following the profiles and magnitudes of the available ocean current data. Both following and opposing currents are considered, and in total, 26 wave–current configurations are investigated. The two-dimensional study is carried out computationally by solving the Navier–Stokes equations for a laminar flow. The governing equations are solved by use of the finite volume approach in an open-source computational fluid dynamics package, namely OpenFOAM. Modifications are made to an existing wave-making toolbox, waves2Foam, to generate combined nonlinear waves and currents in deep and finite waters. Results of the numerical wave–current tank are compared with the existing laboratory measurements and overall very good agreement is observed. Discussion is provided on the effect of these currents on the change of the wave field, including quantitative change of the surface elevation, wave profile, pressure distribution, and fluid particle velocity of waves. Overall, it is observed that opposing current has a remarkable impact on the wave field, and the particle velocity and wave height are affected the most from the presence of the current.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Ocean waves and currents coexist often simultaneously in nature and their interaction affects the properties of waves. The way in which ocean currents modify the waves is of high importance to coastal engineering applications as well as deep-water operations. Toffoli et al. (2013) have pointed out that the presence of opposing currents (wave and current propagating in the opposite direction) can cause stable wave packets to become unstable and break. Studying the process of wave–current interaction provides insight into predicting the behaviour of waves as they interact with currents, which could help mitigate dangerous effects of wave propagation. Markus et al. (2013) have pointed out that the wave–current interaction also affects the wave loads created in a wave field, which in turn influences the wave–structure interaction as the drag forces resulting from the current begin to have a significant impact, in addition to the wave-induced loads on the structure.
Several experimental studies have investigated the interaction between waves and currents. These studies generally include a current profile that is (i) uniform across the water depth or (ii) a non-uniform shear current, varying as a linear or quadratic function over the water depth. A theoretical assessment of the wave–current interaction between waves propagating in the same direction as a shear current was carried out by Dalrymple (1975). Their theory was initially used for small amplitude waves and then modified using numerical perturbation technique for higher order waves. It was found that large disparities exist in the maximum horizontal particle velocity and the wavelength for the same wave interacting with different currents. Brevik and Aas (1979) studied the interaction of waves with following (wave and current propagating in the same direction) as well as opposing currents propagating over a rippled bed and later over a smooth bed in Brevik (1980). They observed that wavelength increases in case of following current, while wave height decreases, whereas wavelength reduced and wave height increased in case of opposing current. Experimental and numerical study of wave–current interaction carried out by Thomas (1981) for linear waves interacting with various non-uniform opposing current profiles showed that the wave height increases and wavelength decreases as the wave interacts with currents of increasing velocities.
Kemp and Simons (1982) conducted an experimental study in a laboratory channel with rough and smooth beds, to investigate the interaction between gravity waves and currents with a uniform profile. The wave period was fixed in the study, and parameters, such as mean velocity profile, wave attenuation, and bed shear stress, were observed for waves with varying wave heights interacting with a non-uniform current. The mean velocity profile was found to generally differ from those proposed by a linear superposition of wave and current velocities. Thomas (1990) conducted an experimental and numerical assessment of nonlinear waves interacting with non-uniform currents. It was found that as the velocity of the current opposing the wave direction increases, the wave height increases and the wavelength decreases. The studies conducted by Thomas (1981) and Thomas (1990) indicate that the change in wavelength and wave height of linear and nonlinear waves shows a similar trend when interacting with currents of increasing velocities; however, the effect of the current profile was not studied.
The method to incorporate theoretically the change in wave period of a wave due to its interaction with a uniform current, also called Doppler-shifted period, was investigated by Swan (1991) for the case of a uniform current interacting with a nonlinear wave, through a series of laboratory experiments. It was found that the use of the Doppler-shift method predicts the horizontal particle velocity and surface elevation in case of uniform currents; however, depth-dependent currents required an alternate approach. The study by Swan (1991) also considered the effect of current profile on waves along with the effect of its velocity; and currents with a uniform profile and linearly sheared following and opposing profiles were considered.
An experimental study of two-dimensional surface water waves propagating on depth-varying currents was carried out by Swan et al. (2001). Current profiles considered in the experiments were: a uniform current, and a following and opposing mixed profile current that maintains a uniform profile up to a certain depth, and then, a linear profile thereafter. Swan et al. (2001) is one of the only studies where a mixed current profile, often observed in oceanographic data, is utilized. Swan et al. (2001) assessed the changes in wave height and wavelength as a function of wave period, due to the presence of following and opposing currents. It was found that the wavelength increased linearly with increasing wave period for following and opposing currents, whereas wave height largely remained constant as the wave period increased for both current directions. The study focused on the effect of current on waves due to the interaction of several waves with one current, but the effect of different currents on one wave case was not explored.
An experimental study of the waves interacting with following and opposing uniform currents was carried out by Umeyama (2009). The horizontal, lateral, and vertical velocity components were measured to study the changes in turbulent intensity, Reynolds stress, and velocity distributions due to the wave–current interaction. It was observed that in case of a following current, the mean horizontal velocity increases further away from the seabed until mid-depth and then decreases gradually till the free surface with an increase in wave height. Umeyama (2011) conducted another experimental study of waves interacting with a uniform current focusing on particle velocities and trajectories, and found that the wave height in case of a wave-only condition is 13%-17% larger than a wave–current interaction condition for the same wave-paddle motion. Additionally, Umeyama (2011) also showed that a linear superposition of the current velocity and the water particle velocity due to waves is unlikely to predict correctly the horizontal particle velocity distribution.
Several numerical studies have been carried out to assess the interaction of waves and currents. Choi (2003) has investigated the interaction of strongly nonlinear solitary waves and a linear shear current by deriving an asymptotic model for long surface gravity waves of large amplitude in shallow water. It was observed that a solitary wave interacting with a following current narrows down, while it widens when the current is opposing the wave propagation. The effect of current direction on the mean velocity distribution was observed by Umeyama (2005) by studying the interaction of a nonlinear wave with following and opposing uniform currents experimentally, and then comparing the results with the theoretical data obtained using third-order Stokes wave theory and phase-averaged Prandtl momentum transfer theory. They found that the velocity distribution in case of waves interacting with a following current exhibited a higher velocity close to the tank floor and lower velocity beyond a certain water depth; the reverse was found to be true in case of an opposing current interacting with the wave.
The interaction of nonlinear water waves with a uniform current was presented by Hsu et al. (2009) based on the analytical solutions of periodic waves propagating over a uniform current. They studied the variations in the wave profile and the water particle orbits resulting from the interaction with a steady uniform current of different magnitudes. It was observed that the following current increased the relative horizontal distance traveled by a water particle, while the reverse occurs in the case of an opposing current. The effect of following and opposing uniform currents on a solitary wave was investigated by Zhang et al. (2014) using a numerical model based on solving the Reynolds-Averaged Navier-Stokes (RANS) equations. They observed that an increase in current velocity led to an increase in the wavelength, but the effect of change in current profile was not investigated. Zhang et al. (2014) also observed that following currents increased the wavelength of a solitary wave while reducing its wave height and had an opposite effect in case of opposing currents. Guyenne (2017) studied the interaction of a linear shear current with nonlinear water waves using a two-dimensional direct numerical simulation method for solving the time-dependent equations describing nonlinear water waves over uniform depth with non-zero constant vorticity. They observed that a following currents aided in stabilising the wave dynamics while opposing current-assisted wave growth.
The steady solution of a solitary wave propagating in the presence of a linear shear background current was investigated using the Green–Naghdi equations in the study conducted by Duan et al. (2018). The results of Duan et al. (2018) were compared with the results of Choi (2003) and it was found that their assessments were similar to those obtained by Choi (2003). The steady solutions of solitary waves in the presence of non-uniform shear currents were obtained by use of the high-level Green–Naghdi (HLGN) model by Wang et al. (2020). They found that the vorticity field and the velocity field of the solitary wave were modified by the non-uniform shear current. The effect of following and opposing currents with a vertically sheared profile on a nonlinear wave was studied numerically using a Navier–Stokes (NS) solver in the computational fluid dynamics package, OpenFOAM, by Chen and Zou (2019) and the results were compared with the experimental work carried out by Swan (1991). They observed that the wave profile was modified due to the presence of following and opposing currents.
Ocean current data are seldom used in previous investigations of wave–current interactions. A numerical study using ocean current data obtained from oceanographic studies was conducted by Liang et al. (2017), wherein the wave-energy under wave–current interaction in the Qingdao coast of China was estimated. Their study showed that the wave–current interactions should be assessed when analyzing the wave-energy resources.
While the present numerical study is carried out in two dimensions where only following and opposing current directions are considered, orthogonal wave–current interactions, where the wave and current approach each other at angles other than \(0^{\circ }\) or \(180^{\circ }\), are studied in three dimensions by Lim and Madsen (2016), Faraci et al. (2018), Faraci et al. (2021).
From the assessment of the experimental and numerical studies conducted on wave–current interaction, it is observed that the current implementation seldom follows a profile similar to that observed in oceanographic data. Therefore, a study of the current profiles and velocities commonly observed in ocean currents is conducted, and accordingly, the currents are chosen to be implemented in the numerical simulation. Our goal in this study is to assess the change in the behaviour of nonlinear waves in deep and finite water depths, as they interact with currents with different profiles, velocities, and directions. Specifically, the effect of these currents on wave height, wavelength, surface elevation, pressure, and horizontal particle velocity is studied, for waves of various wave heights and wavelengths.
The theory pertaining to the numerical approach used in this study and the computational process involved in solving the problems posed by the theory is outlined in Sect. 2, while the setup of the numerical wave tank is discussed in Sect. 3. Discussion on the selection of various waves and current profiles being considered is presented in Sect. 4. Finally, the comparison of the numerical wave tank results with experimental studies, the results of the wave–current study, and their implications are discussed in Sect. 5, followed by concluding remarks.
2 Theory and numerical solution
The numerical field is setup within the Cartesian coordinate system, with the wave propagating along the positive \(x-\)direction (to the right), and z is the vertical axis, positive pointing up. The origin of the coordinate system is at the still water level (SWL). The fluid is assumed to be Newtonian, homogeneous, incompressible continuous substance for the scale at which it is observed. The fields of interest pertaining to the flow, including pressure and velocity, are considered differentiable, and the flow is considered laminar. The flow is governed by the NS equations, namely the mass and momentum conservation equations
where \({{{\textbf {V}}}} = {{{\textbf {U}}}_X} + {{{\textbf {U}}}_Z}\) is the velocity vector, t is the time, \(\rho \) is the density of the fluid which can be air or water in this study, p is the pressure, \({\nu }\) is the kinematic viscosity, and \({{\textbf {g}}}\) represents the body force vector due to gravity. \(\nabla \) and \(\nabla ^2\) in Eqs. (1) and (2) refer to the divergence and the Laplacian vector, respectively. Unless otherwise specified, all physical parameters in the study are presented dimensionless using water depth (h), acceleration due to gravity (g), and density of water (\(\rho \)), as the dimensionally independent set. Therefore, \({\overline{\lambda }} = \lambda /h\), \({\overline{H}} = H/h\), \({\overline{T}} = T/\sqrt{h/g}\), \({\overline{P}} = P/\rho g z\) and \({\overline{U}} = U/\sqrt{gh}\). For simplicity, the bar over the variables is removed from all dimensionless quantities.
The free surface between water and air is captured by the use of Volume of Fluid method (Hirt et al. 1975; Hirt and Nichols 1981). A function \(\alpha \) is defined, such that its value can be between 0 and 1: 0 signifying that there is no water present in the cell and 1 implying that the cell is filled with water. Two wave theories are utilized to generate nonlinear deep and finite water depth waves in this study, namely Stokes Second-Order wave theory and the Stokes Function wave theory; the former has a closed-form analytical equation, whereas the latter is solved, iteratively. In the numerical wave–current tank, the horizontal particle velocity is achieved by linear superposition of the wave and the current velocities. Hence, the wave–current horizontal velocity (\(U_{WC}\)) for Stokes Second-Order wave theory reads
The current velocity (\(U_{C}\)), which evolves as a function of the water depth, is defined as
where z is the vertical coordinate and it varies from 0 to -1 (SWL to sea floor), U is the uniform current velocity, \(U_F\) is the current velocity at the free surface, and \(Z_C\) is the depth (measured from the SWL) at which the current profile changes from uniform to linear. Unless otherwise specified, U is kept fixed at 0.001 in all cases. \(U_F\) and \(Z_C\) are given three values each, which are shown in Table 3. The superposition of the velocities modifies the wave field and this will be discussed in the following sections.
The governing equations are discretized by use of the finite volume approach and the equations of motion for both water and air above are solved simultaneously. The computations are carried out using an open-source computational fluid dynamics package, OpenFOAM. The numerical wave–current tank is created by modifying the existing wave2Foam toolbox (Jacobsen et al. 2012) of OpenFOAM. The numerical wave–current tank consists of three sections: (i) the wave–current generation zone or the inlet relaxation zone, where the wave theory is used to generate the required wave–current system by calculating the surface elevation, pressure, and velocity, which is obtained by the linear superposition of wave and current velocities [Eqs. (3) and (4)], (ii) the middle zone, where the N–S equations are solved, and (iii) the wave–current absorption zone or the outlet relaxation zone at the opposite end, where the wave–current system is allowed to gradually dissipate and die out over the length of the outlet zone (Jacobsen et al. 2012). The outlet zone is used to limit the size of the computational tank and hence reduce the computational cost. Alternate methods of wave generation and absorption available in OpenFOAM include the use of static boundary conditions, where the surface elevation and particle velocities are defined as Dirichlet boundary conditions at the wave generation and absorption boundaries, and the use of dynamic boundary conditions, where a moving wall and dynamic mesh motion is used to mimic the physical wave maker geometry (Windt et al. 2019). Wave generation and absorption toolboxes, such as IHFoam and olaFlow, have utilized these techniques (Higuera et al. 2013). Newer versions of OpenFOAM, OF v7 and above, include a static boundary wavemaker implemented with the interFoam solver (Schmitt et al. 2020).
In this study, a numerical wave–current tank is created to study the wave–current interaction problems. The tank bottom is flat and stationary with a prescribed no-slip boundary condition, i.e., the fluid velocity at this fixed boundary is set to 0. The front and back are kept empty [i.e., the aforementioned Eqs. (1) and (2) are only solved in the x and z directions] in this two-dimensional simulation. The velocities, pressure, and surface elevation at the inlet are set up by the respective wave theories. The pressure–velocity coupling problem is solved iteratively using the PIMPLE algorithm, which is a combination of PISO (Pressure Implicit with Splitting of Operator) and SIMPLE (Semi-Implicit Method for Pressure-Linked Equations) algorithms (Ferziger et al. 2002).
3 Numerical tank setup
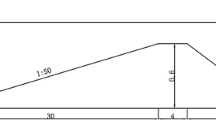
In this section, the efficiency of the numerical wave domain in generating the required wave, while keeping reflections from the boundaries to a minimum, is discussed. A convergence study is performed in the numerical wave tank to determine the optimum size of the mesh.
A nonlinear wave with H = 0.12 and T = 2.81 propagating over a water depth of 0.7 m is studied using different mesh configurations given in Table 1. Figure 1 shows the time series of surface elevation recorded at a gauge at the middle of the wave domain for the three mesh configurations and Fig. 2 shows a snapshot of surface elevation in the wave domain for the three mesh configurations. The relative difference between the results of each mesh is determined by assessing the effect of the mesh on the peak of surface elevation. The peak of surface elevation is obtained by observing all waves, excluding the ramp wave, and discarding the maximum and minimum peak values before calculating the arithmetic mean of the remaining peaks in the time signal of surface elevation. The relative difference is then calculated as \(E_{rel} = [(\eta _m-\eta _B)/\eta _B]\times 100\), where \(\eta _m\) is the peak of surface elevation obtained from the computations using meshes A and C, and \(\eta _B\) is the peak of surface elevation obtained from the computations carried out using mesh B. It is observed that the relative difference between meshes B and C is very small. Based on these results, the mesh configuration B is found to be the optimum mesh with a feasible computational time.
An assessment of wave reflection from the outlet relaxation zone is carried out to determine the efficiency of the wave absorption zone. The length of the outlet relaxation zone is varied as: (i) \(0.5\lambda \), (ii) \(0.75\lambda \), and (iii) \(\lambda \). The wave reflection at the centre of the domain is studied using the two-gauge method outlined by Grue (1992). In this method, the time series of surface elevation is obtained from two wave gauges placed at the centre of the domain separated by an arbitrary distance of 0.2857. Then, the Fourier transform of the two signals is used to separate the incident and reflected wave amplitudes. The ratio of the reflected wave amplitude to the incident wave amplitude is called the reflection coefficient (\(C_R\)). This method was used successfully by Hayatdavoodi et al. (2017) to investigate the reflection and transmission of strongly nonlinear waves. The variation of \(C_R\) with time for different outlet relaxation zones is presented in Fig. 3. Here, the results indicate that an outlet relaxation zone of length \(0.75\lambda \) is appropriate. Therefore, a wave domain with an inlet relaxation zone (wave generation zone) of length \(\lambda \) and an outlet relaxation zone of length \(0.75\lambda \) is chosen. The total length of the numerical wave tank is \(7\lambda \). This is done, so that there would be at least five waves outside the relaxation zones which can be used to assess the deformation of the wave profile in the presence of current. This is in agreement with the previous investigations of Hayatdavoodi et al. (2015) on the computational domain length for nonlinear waves. The schematic of the numerical wave tank, along with the location of the wave gauges, pressure, and velocity sensors, is shown in Fig. 4.
4 Wave–current conditions
The various waves and currents chosen in this study are discussed in this section. This study focuses on waves in deep and finite water depths. In the numerical wave–current tank, the water depth is fixed at 0.7 m and the wave parameters are altered to consider five linear and nonlinear waves in deep and finite water depths, given in Table 2. For cases W1, W2, and W3, the wavelength is kept constant, while the wave height is reduced by a factor of 2.5. For cases W2, W4, and W5, the wave height is kept constant, while the wavelength is increased by a factor of 2.
To obtain the current profiles, available oceanographic data of Sheikh and Brown (2010), Jeans et al. (2003), Jeans et al. (2012), and Carollo et al. (2005) are considered and the current profiles that are observed most commonly in oceans were selected. These provide insightful data on the vertical current velocity profiles observed in deep-water conditions in South China sea, Faroe-Shetland channel, offshore Brazil, and the Iceland–Scotland Ridge, respectively. The behaviour of current profiles showed that currents generally maintain a uniform profile from the seafloor up to a certain water depth, and then exhibit changes near the surface. The details of all the selected current profiles are provided in Table 3. Here, a positive current velocity indicates a following current and a negative current velocity indicates an opposing current.
In this study, 18 current configurations are considered by changing the current velocity on the free surface (three velocities), the depth at which the current profile changes (three depths), and the current direction relative to the wave propagation direction (following or opposing). These current configurations along with the ocean current data are shown in Fig. 5.
First, a set of wave–current interaction cases are considered involving the wave condition W2 (H = 0.036 and \(\lambda \) = 1.429), for the 18 current configurations mentioned above. Then, the current with \(U_F\) = ±0.004 and \(Z_C\) = \(-\)0.5 is considered with both following and opposing current directions, for all five wave conditions. Table 4 outlines all the 26 wave–current cases being considered in the study. The results of these wave–current cases are then assessed to determine (i) the effect of current velocity, (ii) current profile, and (iii) current direction on the wave parameters, namely surface elevation, wavelength, wave height, horizontal particle velocity, and pressure.
5 Results and discussion
The results obtained from assessing the numerical wave–current tank are discussed in this section. First, the results of numerical wave–current tank are compared with the existing laboratory experiments and computational studies. Then, the physical parameters pertaining to the incoming wave are studied and the change in their behaviour, as the waves interacts with different currents, is observed. A study of surface elevation, wavelength, wave height, horizontal particle velocity, and pressure is carried out and their evolution is assessed quantitatively.
5.1 Comparison with laboratory experiments
The numerical wave–current tank is used to generate a coexisting wave–current field and the results are compared with laboratory measurements of Umeyama (2011) and computations of Zhang et al. (2014), who used a computational fluid dynamics model for solving the RANS equations. The current implementation is carried out in two ways: using the Stream Function wave theory and using the Stokes Second-Order wave theory that are modified to include a uniform current. The reason behind this implementation is that the linear superposition of current and wave velocities can be achieved with either wave theories, but the Stokes Second-Order wave theory may not be valid for all nonlinear wave cases chosen for the study. Therefore, the Stream Function wave theory has been included to ensure that it can be used to generate the required wave–current interactions accurately.
The wave case considered in this comparison is a nonlinear wave with H = 0.0343, T = 5.72, and h = 0.3 m interacting with a uniform current across the water depth, U = 0.0466. Figures 6 and 7 show the variation of horizontal particle velocity with water depth under the wave crest and wave trough, respectively. Here, it can be observed that due to the no-slip boundary condition, the horizontal particle velocity at the tank floor is zero. In Fig. 6, it is seen that under the wave trough, the horizontal particle velocity is less than the uniform current velocity in the domain, whereas the opposite is observed under the wave crest in Fig. 7. This behaviour of the horizontal particle velocity is as expected, because the water particle velocity due to the wave is negative under the wave trough and positive under the wave crest. Additionally, the results obtained using Stream Function wave theory show very good agreement with those obtained using Stokes Second-Order wave theory. This provides confidence in the use of Stream Function wave theory for numerically simulating wave–current interactions in the tank. All the wave-only cases as well as the wave–current interaction cases considered in this study are implemented using Stream Function wave theory. Figure 8 shows time series of surface elevation in the presence of current, and it is observed that the surface elevation of the wave in the presence of the current is accurately predicted by both wave theories. Finally, it is also observed that the results from the numerical simulations agree well with the laboratory measurements and previous computations.
The results obtained from the laboratory measurements conducted by Swan et al. (2001) are also used to assess the performance of the numerical wave–current tank while generating a current consisting of a uniform profile from the seabed to a certain water depth and then followed by a linear profile thereafter until the free surface, similar to that considered in this study. The wave case considered in this comparison is a nonlinear wave with H = 0.12, T = 2.81, and h = 0.7 m interacting with a depth-varying following current. Table 5 shows the modified wavelength and wave height obtained using the NS model, along with those obtained from the experiments and computations of Swan et al. (2001). Additionally, the percentage change in wavelength and wave height, \(\lambda ^\prime = (\lambda _{WC}-\lambda )/\lambda \) and \(H^\prime = (H_{WC}-H)/H\), where \(\lambda _{WC}\) and \(H_{WC}\) are the wavelength and wave height under the influence of the current, respectively, are given in Table 5. The results from the preliminary assessment of the numerical wave–current domain show good agreement when compared with the experimental and numerical data.
Next, the results of the wave–current study are presented and discussed in four subsections, namely change in surface elevation, change in wavelength and wave height, change in horizontal particle velocity, and change in pressure.
5.2 Change in surface elevation
In this subsection, the evolution of surface elevation of the incoming waves as they interact with different currents is investigated. First, the stability of the numerical wave–current tank while generating waves \(W1-W5\) is assessed. This is depicted in Fig. 9, which shows the surface elevation of the waves generated in the numerical tank, recorded by the three wave gauges, in the absence of current, and compares their profiles with Stokes Second-Order wave theory. Good agreement is observed between the numerical results and the analytical solution. Next, the interaction of these waves with the current with \(U_F\) = ±0.004 and \(Z_C\) = \(-\)0.5 (cases WC5, WC10, WC11, WC12 and WC13) is studied. Figure 10 shows the surface elevation of the waves under the presence of the current, recorded at gauge GI. An enlarged view of the wave crest is also presented for all five wave cases along with an enlarged view of the wave trough for wave case W3. It is observed that under the influence of current, the wave trough changes in similar way as the wave crest. Subsequently, quantitative discussion about only the wave crest is carried out from here on. In all five waves, it is seen that a following current causes an increase in surface elevation, whereas an opposing current causes a decrease in the same. This indicates that the current direction plays a significant role in modifying the surface elevation of the wave.
The change in surface elevation is obtained using the surface elevation value at the peak of the wave crest and is given by \(\eta ^\prime \) = (\(\eta _{WC}-\eta )/\eta \), where \(\eta _{WC}\) is the surface elevation under the influence of the current. It is the percentage increase or decrease in surface elevation for following or opposing wave–current cases when compared with wave-only cases. Waves W1–W3 have the same wavelength, while their wave height reduces by a factor of 2.5. By observing the \(\eta ^\prime \) values corresponding to these cases in Fig. 11a, it is inferred that currents have a diminishing effect on the surface elevation of a wave as its wave height increases. As the wave height increases by a factor of 2.5, \(\eta ^\prime \) also roughly changes by 2.5 for both following and opposing current cases. Waves W2, W4, and W5 have the same wave height, while their wavelength increases by a factor of 2. Figure 11b shows a similar diminishing effect of current on surface elevation as observed in case of increasing wave height.
The interaction of wave W2 with following and opposing currents with varying velocities and \(Z_C\) = \(-\)0.5 is shown in Fig. 12. The effect of changing current velocity on surface elevation can be observed from this assessment. It is observed that an opposing current has a more pronounced effect on the surface elevation when compared to a following current. Similar results are observed when the current profile varies while maintaining a constant current velocity of \(U_F\) =±0.004, as shown in Fig. 13. Figure 14 shows the evolution of \(\eta ^\prime \) as a function of current velocity and current profile. It is observed that opposing current reduces the surface elevation by up to 30%, while following current increases the surface elevation by at most 6%, for the currents chosen in this study. Additionally, it is observed that \(\eta ^\prime \) varies linearly with increasing current velocity but not with increasing current profile. An increasing current velocity presents a more substantial change in the surface elevation than an increasing current profile. As shown in Fig. 14, the surface elevation, in general, shows remarkable changes due to an opposing current as compared to a following current.
5.3 Change in wavelength and wave height
In this subsection, the effect of currents on the wave profile is assessed by observing the change in wave height and wavelength. The interaction of the wave W2 with varying current velocities and current profiles is analyzed in Figs. 16, 17, 1819. The change in wave height and wavelength is observed while systematically varying one current parameter (velocity or profile) and keeping the other parameter constant. The change in wave height and wavelength is obtained by analyzing the waves outside the inlet and outlet relaxation zones. From the five waves within the domain, as shown in Fig. 15 for wave W5, the maximum and minimum wave height and wavelength values are removed from the analysis, and the arithmetic mean of the remaining waves is taken to obtain the wave height and wavelength. This is done to rectify minor numerical errors in the individual waves and to obtain a statistically sound data set. In case of wave–current interaction, the modified wave height and wavelength are obtained similarly and compared with the original wave height and wavelength from the wave-only cases. The changes are given in percentages by \(H^\prime \) and \(\lambda ^\prime \).
First, the effect of current profile, with the current velocity fixed at \(U_F\) = ±0.004, on the wavelength and wave height is shown in Figs. 16 and 17. Figure 16 shows that the wavelength increases by up to 2% as the wave interacts with a following current and it decreases by up to 4% when the wave interacts with an opposing current, indicating a stronger influence of opposing current on wavelength as compared to a following current. Additionally, it is observed that increasing the current profile generally leads to an increase in wavelength by about 1%, irrespective of current direction. Similar trends are observed while assessing the change in wave height in Fig. 17, where the wave height reduces by up to 4% as the wave interacts with an opposing current, and it increases by up to 4% as the wave interacts with a following current. Here, however, it is observed that increasing the current profile generally leads to an increase in wave height only in case of an opposing current interaction. Increasing current profile does not seem to affect \(H^\prime \) if the wave interacts with a following current.
Next, the effect of increasing current velocity, with the current profile fixed at \(Z_C\) = \(-\)0.5, on wavelength and wave height is shown in Figs. 18 and 19. Figure 18 shows that increasing the current velocity leads to an almost linear change in \(\lambda ^\prime \), in most cases. For the currents considered in this study, the wavelength decreases by up to 4% in case of an opposing current and it increases by up to 2% in case of a following current. The effect of current velocity on wave height is shown in Fig. 19 and it is observed that increasing the current velocity causes the wave height to decrease nonlinearly in case of opposing current and increase nonlinearly in cases of following current. The maximum change in wave height was observed to be ±4%.
Finally, an assessment is made to evaluate the effect an incident wave has on change in its wavelength and wave height when interacting with a given current. The parameters \(\lambda ^\prime \) and \(H^\prime \) are presented as functions of H and \(\lambda \) in Figs. 20 and 21. Figure 20 shows that for the waves and currents chosen in this study, the change in wavelength remains at about ±1%, irrespective of the wave height, whereas it goes down from about ±1.5% to ±0.3% as the wavelength increases. This implies that the effect of current on change in wavelength is sensitive to the incident wavelength and almost invariant with wave height. The change in wave height is presented Fig. 21, which shows that wave height changes from about 4% to 1% with an increase of wave height as well as wavelength. This observation implies that the effect of current on change in wave height varies with both wavelength and wave height of the incident wave.
5.4 Change in horizontal particle velocity
The effect of currents on horizontal particle velocity of a wave field is studied in this subsection. The horizontal particle velocity is recorded by numerical velocity sensors at depths z = \(-\)0.33, \(-\)0.66 and \(-\)1.0, as shown in Fig. 4. Figure 22 shows the effect of following and opposing currents with \(U_F = \pm \)0.004 and \(Z_C\) = \(-\)0.5, on the horizontal particle velocity of the wave W2. It is observed that the velocity increases for following currents and decreases for opposing currents. The change in horizontal particle velocity is obtained using the horizontal particle velocity at the peak of the wave crest and is given by \(U_X^\prime \) = (\(U_{X(WC)}-U_X)/U_X\), where \(U_{X(WC)}\) corresponds to the horizontal particle velocity under the influence of the current. It is the percentage increase or decrease in horizontal particle velocity for following or opposing wave–current cases when compared with wave-only cases. Figure 23 shows that at z = \(-\)0.33, the horizontal particle velocity reduces by about 40% as the wave interacts with a opposing current, while it registers an increase of about 20% as the wave interacts with a following current. This indicates that an opposing current has a stronger effect on the horizontal particle velocity than a following current.
The effect of current velocity on horizontal particle velocity is shown in Fig. 24, and its evolution is quantified using \(U_X^\prime \) in Fig. 25. From Fig. 24, it is observed that the current velocity has a stronger effect on the horizontal particle velocity in case of opposing currents. Figure 25 shows that for the currents considered in this study, increasing current velocity decreases the horizontal particle velocity from − 10% to three times smaller, in case of opposing current interaction. In case of following current, increasing current velocity does not seem to strongly influence \(U_X^\prime \), which mostly fluctuates around 50%.
The effect of changing current profile on horizontal particle velocity is shown in Fig. 26 and its evolution is quantified using \(U_X^\prime \) in Fig. 27. Figure 27 shows that an opposing current has a more pronounced effect on the horizontal particle velocity, for the currents selected in this study. From Fig. 27b, it is observed that current profile changes \(U_X^\prime \) from − 150% to − 50%, in case of opposing current, whereas in case of following current, the current profile does not seem to strongly influence \(U_X^\prime \), which fluctuates around 50%.
5.5 Change in pressure
The effect of currents on the pressure is studied in this subsection. The pressure is recorded by numerical pressure sensors at depths, z = \(-\)0.33, \(-\)0.66, \(-\)1.0. The total pressure at these points is normalized by the respective hydrostatic pressure at the given depths (from the SWL) to obtain the hydrodynamic pressure. The interaction of wave W2 with following and opposing current with \(U_F = \pm 0.004\) and \(Z_C = -0.5\) is shown in Fig. 28. A following current increases the pressure, while an opposing current reduces it. It is observed that the pressure change is larger in case of an opposing current interaction. The change in pressure is obtained using the pressure at the peak of the wave crest and is given by \(P^\prime \) = (\(P_{WC}-P)/P\), where \(P_{WC}\) corresponds to the pressure under the influence of the current. It is the percentage increase or decrease in pressure for following or opposing wave–current cases when compared with wave-only cases. Figure 29 shows that for the currents considered in this study, the pressure decreases by about 1% in case of opposing current while increasing by only about 0.25% in case of following current.
The effect of current velocity on pressure is shown in Fig. 30, and its evolution is quantified using \(P^\prime \) in Fig. 31. Figure 30 shows that changing current velocity has very little effect on pressure in case of following current compared to the opposing current. Figure 31 shows that in case of following current, there is no change in pressure, whereas in case of opposing current, the pressure decreases by up to 1.7%. As the current velocity increases, \(P^\prime \) increases nonlinearly for following current and decreases nonlinearly in case of opposing current.
The effect of current profile on pressure is shown in Fig. 32, and its evolution is quantified using \(P^\prime \) in Fig. 33. Figure 32 shows that changing current profile has very little effect on pressure in case of following current compared to the opposing current. Figure 33 shows that pressure registers a maximum change between \(-\)1.5% and 0.5%, for the currents selected in this study.
6 Conclusions
A numerical wave–current tank is created to assess the effect of current velocity, current profile, and current direction on the deep and intermediate water wave fields. Various parameters, including surface elevation, wavelength, wave height, horizontal particle velocity, and pressure, are considered and analyzed. An assessment of the effect of the type of wave interacting with a current is also carried out to understand the effect of wave height and wavelength on wave–current interactions. Five waves and 18 current configurations are considered in the study. Based on the results obtained, it is observed that the wave field significantly changes as it interacts with the following and opposing currents.
The evolution of surface elevation as the wave interacts with currents is studied and it is observed that a following current causes an increase in surface elevation, whereas an opposing current causes a decrease in the same. It is also observed that increasing wavelength and wave height leads to a diminishing effect of currents on the surface elevation. For the current conditions considered in this study, an opposing current reduces the surface elevation by up to 30%, while a following current increases the surface elevation by at most 6%. Changing current velocity results in a linear increase in surface elevation, but changing current profile does not.
Based on the results obtained for the current velocities and profiles chosen here, an assessment of the effect of current on the wave profile shows that wavelength increases by up to 2% and decreases by up to 4% under following and opposing currents, respectively. Increasing current profile changes the wavelength by ±1%, irrespective of current direction. For the currents chosen in this study, an assessment of the effect of current on the wave profile shows that wave height increases by up to 2% and decreases by up to 4% under following and opposing currents, respectively. Increasing current profile changes the wave height by up to ±4%. It is also observed that the effect of current on change in wavelength is sensitive to the incident wavelength and almost invariant with wave height. The effect of current on change in wave height, however, varies with both wavelength and wave height of the incident wave.
A study of the effect of currents on horizontal particle velocity shows that an opposing current has a stronger effect than a following current. The horizontal particle velocity reduces by more than twice in cases of opposing currents, whereas it increases by about 50% in case of following currents. For the current conditions considered in this study, changing current velocity and current profile influences the change in horizontal particle velocity only in case of opposing current. The current, in general, has significant effect on the horizontal particle velocity, when compared to the other wave parameters considered in this study.
A study of the effect of currents on pressure shows that an opposing current has a stronger effect than a following current. The change in pressure due to presence of current is relatively small and it varies between -1% and 0.25%. Based on the results obtained for the current velocities and profiles chosen here, change in current velocity and current profile weakly affects the pressure in case of following currents (close to 0.1%), but shows slightly stronger effect on pressure in case of opposing currents (up to 1.5%). The current, in general, has little effect on the pressure field.
It is also observed that an opposing current has a more significant effect on most of the wave parameters for various wave cases, than a following current.
References
Brevik I (1980) Flume experiment on waves and currents II. Smooth bed. Coastal Engineering 4:89–110
Brevik I, Aas B (1979) Flume experiment on waves and currents. I. Rippled bed. Coastal Engineering 3:149–177
Carollo, C., Astin, I., Graff, J., 2005. Vertical structure of currents in the vicinity of the Iceland-Scotland ridge. Annales Geophysicae 23, 1963–1975
Chen, H., Zou, Q., 2019. Effects of following and opposing vertical current shear on nonlinear wave interactions. Applied Ocean Research 89, 23–35
Choi, W., 2003. Strongly nonlinear long gravity waves in uniform shear flows. Physical Review E 68, 026–305
Dalrymple RA (1975) Water waves on a bilinear shear current. In: Coastal Engineering 1974. American Society of Civil Engineers, Copenhagen, Denmark, pp 626–641
Duan, W.Y., Wang, Z., Zhao, B.B., Ertekin, R.C., Yang, W.Q., 2018. Steady solution of solitary wave and linear shear current interaction. Applied Mathematical Modelling 60, 354–369
Faraci C, Musumeci RE, Marino M, Ruggeri A, Carlo L, Jensen B, Foti E, Barbaro G, Elsaßer B (2021) Wave and current dominated combined orthogonal flows over fixed rough beds. Continental Shelf Research 220:104403
Faraci, C., Scandura, P., Musumeci, R., Foti, E., 2018. Waves plus currents crossing at a right angle: near-bed velocity statistics. Journal of Hydraulic Research 56, 464–481
Ferziger JH, Perić M, Street RL (2002) Computational methods for fluid dynamics, vol 3. Springer
Grue, J., 1992. Nonlinear water waves at a submerged obstacle or bottom topography. Journal of Fluid Mechanics 244, 455–476
Guyenne P (2017) A high-order spectral method for nonlinear water waves in the presence of a linear shear current. Computers & Fluids 154:224–235
Hayatdavoodi M, Ertekin RC, Valentine BD (2017) Solitary and Cnoidal wave scattering by a submerged horizontal plate in shallow water. AIP Advances 7:065212
Hayatdavoodi M, Seiffert B, Ertekin RC (2015) Experiments and calculations of Cnoidal wave loads on a flat plate in shallow-water. J Ocean Eng Marine Energy 1:77–99
Higuera P, Lara JL, Losada IJ (2013) Realistic wave generation and active wave absorption for Navier–Stokes models: application to OpenFOAM®. Coast Eng 71:102–118
Hirt, C.W., Nichols, B.D., 1981. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics 39, 201–225
Hirt CW, Nichols BD, Romero NC (1975) SOLA: A numerical solution algorithm for transient fluid flows
Hsu HC, Chen YY, Hsu JRC, Tseng WJ (2009) Nonlinear water waves on uniform current in lagrangian coordinates. Journal of Nonlinear Mathematical Physics 16:47–61
Jacobsen, N.G., Fuhrman, D.R., Fredsøe, J., 2012. A Wave Generation Toolbox for the Open-Source CFD Library: OpenFoam®. International Journal for Numerical Methods in Fluids 70, 1073–1088
Jeans, G., Grant, C., Feld, G., 2003. Improved current profile criteria for deep-water riser design. Journal of Offshore Mechanics and Arctic Engineering 125, 221–224
Jeans G, Prevosto M, Harrington-Missin L, Maisondieu C, Herry C, Lima JAM (2012) Deep-water current profile data sources for riser engineering offshore Brazil. In: International Conference on Offshore Mechanics and Arctic Engineering, American Society of Mechanical Engineers, Rio de Janeiro, Brazil. pp 155–168
Kemp, P.H., Simons, R.R., 1982. The interaction between waves and a turbulent current: waves propagating with the current. Journal of Fluid Mechanics 116, 227–250
Liang, B., Shao, Z., Wu, Y., Shi, H., Liu, Z., 2017. Numerical study to estimate the wave energy under wave-current interaction in the Qingdao coast, China. Renewable Energy 101, 845–855
Lim, K.Y., Madsen, O.S., 2016. An experimental study on near-orthogonal wave-current interaction over smooth and uniform fixed roughness beds. Coastal Engineering 116, 258–274
Markus D, Wüchner R, Bletzinger KU (2013) A numerical investigation of combined wave-current loads on tidal stream generators. Ocean Eng 72:416–428
Schmitt P, Windt C, Davidson J, Ringwood JV, Whittaker T (2020) Beyond VoF: alternative OpenFOAM solvers for numerical wave tanks. Journal of Ocean Engineering and Marine Energy 6:277–292
Sheikh R, Brown A (2010) Extreme vertical deepwater current profiles in the South China Sea, Offshore Borneo. In: International Conference on Offshore Mechanics and Arctic Engineering, Shanghai, China. pp 585–595
Swan C (1991) An experimental study of waves on a strongly sheared current profile. In: Coastal Engineering 1990. American Society of Civil Engineers, Delft, The Netherlands, pp 489–502
Swan, C., Cummins, I.P., James, R.L., 2001. An experimental study of two-dimensional surface water waves propagating on depth-varying currents. part 1. regular waves. Journal of Fluid Mechanics 428, 273–304
Thomas, G., 1981. Wave-current interactions: an experimental and numerical study. Part 1. Linear waves. Journal of Fluid Mechanics 110, 457–474
Thomas, G., 1990. Wave-current interactions: an experimental and numerical study. Part 2. Nonlinear waves. Journal of Fluid Mechanics 216, 505–536
Toffoli A, Waseda THTKD, Houtani H, Kinoshita T, Collins K, Proment D, Onorato M (2013) Excitation of rogue waves in a variable medium: An experimental study on the interaction of water waves and currents. Physical Review E 87:051201
Umeyama, M., 2005. Reynolds stresses and velocity distributions in a wave-current coexisting environment. Journal of Waterway, Port, Coastal, and Ocean Engineering 131, 203–212
Umeyama M (2009) Changes in turbulent flow structure under combined wave-current motions. J Waterw Port Coast Ocean Eng 135:213–227
Umeyama, M., 2011. Coupled PIV and PTV measurements of particle velocities and trajectories for surface waves following a steady current. Journal of Waterway, Port, Coastal, and Ocean Engineering 137, 85–94
Wang Z, Zhao BB, Duan WY, Ertekin RC, Hayatdavoodi M, Zhang TY (2020) On Solitary wave in nonuniform shear currents. J Hydrodyn 32:800–805
Windt C, Davidson J, Schmitt P, Ringwood JV (2019) On the assessment of numerical wave makers in CFD simulations. J Marine Sci Eng 7:47
Zhang J, Zhang Y, Jeng DS, Liu PLF, Zhang C (2014) Numerical simulation of wave-current interaction using a RANS solver. Ocean Eng 75:157–164
Acknowledgements
This work is partially based on funding from the Kaluosi-Qianghai New Energies Ltd. of China and Energy Technology Partnership (ETP) of Scotland. These fundings are gratefully acknowledged. Any findings and opinions contained in this present paper are those of the author and do not necessarily reflect the opinions of the funding agencies.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kumar, A., Hayatdavoodi, M. On wave–current interaction in deep and finite water depths. J. Ocean Eng. Mar. Energy 9, 455–475 (2023). https://doi.org/10.1007/s40722-023-00278-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40722-023-00278-x