1 Introduction

In the road to net-zero economies, renewable energy resources need to satisfy the continuous energy demand which requires a combination of technologies, such as wind, solar, wave, and tidal energy, among others. Offshore wind energy is becoming the most rapidly developed technology, especially in the United Kingdom with larger turbines being deployed which increases the capacity factor. Solar photovoltaic energy is being developed at a wider scale in countries at lower latitudes but its generation capabilities are bounded by sunlight hours. Thus, these energy resources are somewhat intermittent as they are driven by the variable weather, which requires a complementary energy resource to provide a more continuous energy generation unless the harnessed energy is somehow stored. To this end, tidal stream energy is driven by a predictable tidal resources in the short- and long term as it is governed by the periodic nature of tides (Lewis et al. 2019).

At present, most tidal stream energy projects consider the deployment of horizontal axis turbines (HATs) which have high power coefficients that enable to achieve a large energy yield in energetic sites, i.e. with flow velocities of over 2 m s\(^{-1}\). Such sites are mostly found in specific locations in the United Kingdom, Canada, South Korea, or France, which means that this technology is not suitable for most of the coastal regions in which velocities could be in the range of 1.0–1.5 m s\(^{-1}\). Lewis et al. (2021) performed a comprehensive global resource assessment and found that maximum flow velocities over 1 m s\(^{-1}\) are attained in less than 13% of the world’s coastline, whilst only 3.6% feature flow speeds over 1.5 m s\(^{-1}\). Neill et al. (2021) identified that developing technologies for currents of 1.5  m s\(^{-1}\) would increase by 16 times the number of sites suitable for harnessing tidal stream energy compared to the present HATs design targeting at 2.5 m s\(^{-1}\) currents. For these low-to-medium resource locations, vertical axis turbines (VATs) arise as a suitable technology capable of operating efficiently in low-to-medium velocities and at lower tip-speed ratios, beneficial to lower risk of collision of fish (Castro-Santos and Haro 2015). Tidal sites can be highly turbulent with bathymetry or waves adding further unsteadiness to that already present in the free-stream. As VATs operate independently to the flow direction, i.e. are omni-directional, they are more suitable to operate in such harsh turbulent environments compared to HATs (Han et al. 2013).

Tidal resources assessment of potential turbine arrays is commonly performed with depth-averaged shallow-water models which represent turbine as an added friction source (Lewis et al. 2015, 2021). These provide an upper bound estimate of the energy that can be harnessed but fail to capture wake effects, which are detrimental to the energy yield of secondary rows (Stansby and Ouro 2022). Both the spacing between turbines and their layout as an staggered or aligned array determines its efficiency with the latter providing an increase in turbine performance due to the high-momentum bypass flow developed between two turbines of the same row and which impinges the next turbine in the following row (Draper and Nishino 2014; Nishino and Willden 2013; Ouro and Nishino 2021).

At individual level, the hydrodynamic efficiency of VATs is lower than that of HATs as their blades rotate in a horizontal plane, with its axis normal to the flow direction, shedding vortical structures during the upstroke motion that interact with the blades during the downstroke rotation (Ouro and Stoesser 2017; Posa and Balaras 2018). Typical peak performance coefficients of VATs is approx. 0.25 but this can be influenced by the small scale of most devices tested as detrimental Reynolds numbers effects occur (Bachant and Wosnik 2016), whereas full-scale VATs can achieve efficiencies of 0.4 that is close to that of HATs (Barnes et al. 2021).

VAT rotors are rectangular with a given height-to-diameter aspect ratio that can be modified, unlike HAT rotors that are circular, to provide two positive effects: at devices scale, it decreases the negative impact in performance from supporting structural elements (Hunt et al. 2020); and, at array scale, the wake effects diminish as the kinetic energy removed in the horizontal plane reduces, increasing wake recovery (Boudreau and Dumas 2017; Ouro and Lazennec 2021). Furthermore, irrespective of the standalone turbine efficiency, the rectangular cross-section of VAT rotors allows to deploy two devices close to one another which induces a flow acceleration between them Posa (2019) that can increase the individual performance up to 5% (Hezaveh et al. 2018). Mueller et al. (2021) observed that the rotational direction of twin-VAT systems induces larger changes to the wake dynamics than the turbine spacing, with a counter-rotating forwards motion providing the fastest wake recovery. These synergistic effects means that in VAT arrays reduce detrimental wake effects to achieve large power densities, about 10–20 times larger than those achievable by HATs, meaning that a higher power capacity can be deployed per unit of planform area (Dabiri 2011).

The simulation of VAT hydrodynamics is challenging given the non-linear effects occurring during the rotation of the blades, e.g. dynamic stall, which notably change with parameters such as tip-speed ratio or rotor solidity (Parker and Leftwich 2016; Wei et al. 2021). To capture these transient flow phenomena in numerical simulations, the high-fidelity large-eddy simulation closure is required as it resolves the large-scale flow structures but it demands a high spatial resolution (Ouro and Stoesser 2017; Posa and Balaras 2018). A computationally efficient approach is to represent the moving blades as actuator lines (Shamsoddin and Porté-Age 2016) or surfaces (Massie et al. 2019; Kuppers and Reinicke 2021) which capture the far-wake structure well and thus allow to represent the flow in an array (Hezaveh et al. 2018; Arredondo-Galeana and Brennan 2021). However, the computational burden remains intractable to perform array design or optimisation even considering that tidal flows are mostly bi-directional which reduces the calculations (Stansby and Ouro 2022).

Analytical wake models based on the time-averaged velocity deficit field behind turbines have been shown to provide good estimates of the velocity field in HAT and VAT arrays at a reduced computational cost. These models can be used for the design of array layouts as an engineering-precision tool. Bastankhah and Porté-Agel (2014) developed a mass and momentum conserving wake model for horizontal axis turbines assuming a Gaussian distribution of the velocity deficit field that scales with the HAT’s diameter, following the classic far-wake behaviour (Tennekes and Lumley 1972), which agreed with experiments of horizontal axis tidal turbine wakes (Stallard et al. 2015; Stansby and Stallard 2016). As VATs feature a rectangular cross section, the velocity deficit field scales with both height and diameter developing a super-Gaussian distribution (Ouro and Lazennec 2021). These theoretical models are valid when turbine arrays are relatively small, e.g comprising three or four rows of turbines, as in deep arrays the vertical flux of kinetic energy is the main source of energy for secondary rows and cannot be easily captured with these models (Stevens et al. 2016; Zong and Porté-Agel 2020).

In this study, the efficiency of three-row tidal stream turbine arrays with aligned and staggered layouts and varying turbine spacing are investigated comparing results from HATs and VATs at three real sites, adopting analytical wake models to represent the velocity field.

2 Methodology

In this section, the geometry, operation and time-averaged wake characteristics of Horizontal Axis Turbines (HATs) and Vertical Axis Turbines (VATs) are discussed. In the following, variables denoted as \((\cdot )_H\) and \((\cdot )_V\) refer to horizontal and vertical axis turbines, respectively.

2.1 Rotor design and operation of HATs and VATs

The rotors of HATs typically comprise three blades that rotate in a plane normal to the oncoming flow direction. The swept area is circular, characterised by the turbine’s diameter D, which gives a cross-section area equal to \(A_H={\pi D^2}/{4}\). Conversely, VATs’ rotors feature a rectangular cross-section with a rotational axis normal to the flow direction, and characterised by its diameter D and height H, which can be chosen independently. The VAT rotor’s aspect ratio is a dimensionless number \(\xi = H/D\), i.e. the height-to-diameter ratio, such that the rotor area is \(A_V = HD = \xi D\)2.

To perform a similitude analysis between HATs and VATs with identical cross-sectional area A, a new characteristic geometric variable needs to be defined so both rotor designs are comparable, namely the normalised diameter is defined as \(D_0=\sqrt{A}\). Table  1 presents the dimensions of the HAT rotor and VAT rotors with an aspect ratio between 1 and 4 considered which have a constant cross-sectional area of A = 25 m2, i.e. with a normalised diameter \(D_0\) = 5 m. Whilst it is a relatively small turbine size, this is selected a realistic dimension that can be currently adopted by both HAT and VAT tidal developers (Lewis et al. 2021). For any given rotor area A, the actual HAT’s rotor diameter can be determined as \(D_H\) = 2\(\sqrt{A/\pi }\), whilst the VAT’s rotor diameter is computed based on its aspect ratio \(\xi \) as: \(D_V\) = \(\sqrt{A/~\xi }\), with the rotor height \(H_V\) = \(\sqrt{A~\xi }\). The hub height \(z_{h}\) is modified depending on the rotor’s characteristics but a constant clearance between the bottom bed and the lowest location of the turbine blades tips of 2.5 m is kept.

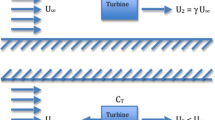
Table 1 Details of the geometry from the analysed turbines including height (H), diameter (D) and cross-sectional area (A), determined from a normalised diameter \(D_0\) equal to 5 m (A = 25 m\(^2\)), and turbine operating parameters
Full size table

The turbine power curve is defined according to a set of four parameters, namely (i) the cut-in (\(U_{in}\)) and cut-out (\(U_{out}\)) speeds that define the velocity range over which the turbine operates; (ii) the rated speed (\(U_{rated}\)) at which the turbine reaches its rated power (\(P_{rated}\)); and (iii) the thrust coefficient (\(C_T^{rated}\)) and power coefficient (\(C_P^{rated}\)) defined by the rated speed and power. The thrust and power coefficients obtained for any given velocity U are defined as:

$$\begin{aligned} C_T&= \frac{T}{\frac{1}{2}\rho A U^2}, \end{aligned}$$
(1)
$$\begin{aligned} C_P&= \frac{P}{\frac{1}{2}\rho A U^3}. \end{aligned}$$
(2)

Here, T is the thrust force exerted by the turbine, P is the output power, and \(\rho \) is the density of the fluid equal to 1025 kg m\(^{-3}\). Based on these parameters, the idealised curves of \(C_T\) and \(C_P\) for any given flow speed are shown in Fig. 1. These coefficients are constant and equal to their rated values in the velocity range of \([U_{in}{:}U_{rated}]\), and decrease beyond \(U_{rated}\) proportionally to \(C_T \propto (U_{rated}/U)^2\) and \(C_P \propto (U_{rated}/U)^3\), such that the power output remains constant until reaching the cut-out speed.

Fig. 1
figure 1

Turbine power curve of the reference VAT with rated power of 25 kW

Full size image

Table 1 shows the set of the operational parameters, namely thrust and power coefficient, cut-in, cut-out and rated speed, selected for each type of tidal turbines. For HATs, characteristic velocities are retrieved from full-scale devices used at the Meygen project (Atlantis 2016; Seagen 2018), with a peak \(C_{P_H}\) equal to 0.41 Meygen (2018) and a thrust coefficient equal to 0.80, which is a typical value adopted in the literature (Goss et al. 2021). Unfortunately, no full-scale VAT deployed to date has reported its operating data. In a comparison study between HAT and VAT wind turbines by Mendoza et al. (2019), VAT thrust and power coefficient are defined in accordance to these ratios: \(C_{P_V} = 0.6~C_{P_H} \) and \(C_{T_V} = 0.8~C_{T_H}\), which are herein considered.

2.2 Theoretical wake models

Analytical models for the wakes downstream of HATs and VATs are developed assuming that the devices are perfectly aligned with the flow direction, i.e. there is no yaw misalignment, as this can change the wake characteristics and performance (Bastankhah and Porté-Agel 2016). In the following, the Cartesian coordinates (x, y, z) are normalised and referred to the origin of coordinates (\(x_0,y_0,z_0\)) set at the centre of the rotor and at hub height, i.e. \({\tilde{x}} = ({x-x_0})/{D}\) and \({\tilde{y}} = ({y-y_0})/{D}\) for both HATs and VATs whilst in the vertical \({\tilde{z}} = ({z-z_0})/{D}\) for HATs and \({z} = ({z-z_0})/{H}\) for VATs. For simplicity, hereafter, these normalised coordinates \(\tilde{x_i}\) are written as \({x_i}\). The x-axis corresponds to the flow direction, y-axis denotes transverse direction, and the z-axis is the vertical direction.

The time-averaged normalised velocity deficit \(\Delta U (x)\) accounts for the loss in streamwise velocity in the wake region compared to that in the free-stream \(U_0\), and is defined as:

$$\begin{aligned} \Delta U (x)&= \frac{U_{0} - U (x)}{U_{0}}. \end{aligned}$$
(3)

The wake behind a single turbine can be considered to attain a quasi self-similar form after some distance downstream (Tennekes and Lumley 1972). This enables us to characterise the velocity deficit according to a velocity scale (C(x)) and a given spatial distribution in the plane normal to the flow (\(\textit{f}(y,z)\)), which evolve in the streamwise, i.e. \(\Delta U (x) = C(x) f(y,z)\). Whilst this wake description is applicable to both HATs and VATs, some modifications in the velocity and spatial distribution functions are required according to the rotor’s physical characteristics so that mass and momentum are conserved. Figure 2 presents the shape of the velocity deficit field downstream of a HAT (\(\Delta U_H (x)\)) and a VAT (\(\Delta U_V (x)\)). The HAT wake scales only with its rotor diameter D whilst both the rotor height H and diameter D are needed to define the length scales of VAT wakes (Bastankhah and Porté-Agel 2014; Ouro and Lazennec 2021).

Fig. 2
figure 2

Velocity deficit field distribution downstream of (a) a horizontal axis turbine and a vertical axis turbine over the (b) vertical (lateral view) and (c) horizontal (top view) planes. The wake expansion is represented by \(\sigma \) (x), hub height is \(z_h\) and the coordinate system is centre at the rotor

Full size image

In unbounded conditions, a HAT rotor has a circular wake shape and the velocity deficit is self-similar and two-dimensional (except for the very near wake) following a Gaussian shape, which has shown good agreement as validated in experiments and with LES data (Bastankhah and Porté-Agel 2014; Stallard et al. 2015; Stansby and Stallard 2016). However, in shallow conditions the wake recovery can be conditioned by the physical vertical constrain owed to the free-surface proximity, thus the mixing is predominantly over the transverse direction and limited in the vertical (Olczak et al. 2016; Ouro et al. 2021). Generally, the velocity deficit \(\Delta U_{H}(x_i)\) generated by a HAT is determined as:

$$\begin{aligned} \Delta U_{H}= & {} C_H(x)~f_H(y,z) \nonumber \\= & {} \left( 1- \sqrt{1-\frac{C_T}{8 {\tilde{\sigma }}_{H}^2}} \right) \exp { \left( - \frac{y^2+z^2}{2{\tilde{\sigma }}_{H}^2}\right) }. \end{aligned}$$
(4)

The wake expansion normal to the flow direction, i.e. in the yz-plane, is represented by \(\sigma _H\), which is a function of the wake expansion rate \(k^*_{H}\) = 0.35 \(I_u\), where \(I_u\) is the streamwise turbulence intensity (Fuertes et al. 2018), and reads:

$$\begin{aligned} {\tilde{\sigma }}_{H}({\tilde{x}}) = k^*_{H}~x + \varepsilon _H. \end{aligned}$$
(5)

The initial wake width is \({\tilde{\sigma }}_{H}({x}=0) = \varepsilon _H\) is \(0.2 \sqrt{\beta }\), with the parameter \(\beta \) defined as \(\frac{1}{2}({1 + \sqrt{1-C_T}})/{\sqrt{1 - C_T}}\), i.e. the wake width at its onset only depends on the thrust coefficient (Bastankhah and Porté-Agel 2014).

For a VAT, the self-similar velocity deficit field in the wake evolves unevenly in the horizontal and vertical direction, according to the rotor’s diameter and height, respectively (see Fig.  2). Ouro and Lazennec (2021) showed that theoretical Gaussian models fail at providing an accurate representation of the velocity deficit magnitude and shape for VAT wakes, and proposed a super-Gaussian model that improved the results for both near- and far-wake. This super-Gaussian model establishes that the velocity deficit \(\Delta U_{V}\) evolves according to a velocity scale \(C_V(x)\) and two super-Gaussian shape functions \(f_{V_y}(y)\) and \(f_{V_z}(z)\) that enable the transition from a nearly top-hat in the near-wake to a Gaussian shape far downstream in the streamwise direction (Fig. 2). This theoretical VAT wake model reads:

$$\begin{aligned} \Delta U_{V}&= C_{V} (x) ~\exp { \left( -\frac{y^{n_y}}{2{\sigma }_{V_y}^2}\right) } ~ \exp { \left( -\frac{z^{n_z}}{2{\sigma }_{V_z}^2}\right) } \end{aligned}$$
(6)
$$\begin{aligned}&= \left( 2^{\gamma -1} - \sqrt{ 2^{\gamma -2}-\frac{C_T}{8 ~{\sigma }_{V_y}^{2/n_y} ~{\sigma }_{V_z}^{2/n_z} ~\Gamma ({1}/{n_y})~\Gamma ({1}/{n_z})} } \right) \nonumber \\&\exp { \left( -\frac{y^{n_y}}{2{\sigma }_{V_y}^2} -\frac{z^{n_z}}{2{\sigma }_{V_z}^2}\right) }. \end{aligned}$$
(7)

Here, \(\gamma \) is equal to \(1/n_y + 1/n_z\) and the exponents that define the superimposed super-Gaussian distributions are \(n_y\) = 0.95 exp\({ \left( -0.35 x\right) }\) + 2.4 and \(n_z\) = 4.50 exp\({ \left( -0.70 x/ \xi \right) }\) + 2.4. Note that the asymptotic solution of the super-Gaussian function is for \(n_y\) = \(n_z\) = 2 so that the Gaussian shape is recovered, so that Eq.  7 is similar to Eq. 4 with distinct wake expansion rate. Equation 7 shows that VAT wakes are three-dimensional and vary depending on the VAT rotor’s aspect ratio (Ouro and Lazennec 2021). The wake width in the horizontal (\({\sigma }_{V_y}\)) and vertical (\({\sigma }_{V_z}\)) directions scale linearly proportional to the wake expansion rates \(k^*_{V_y}\) = \(k^*_{V_z}\) = 0.5\(I_u\), as:

$$\begin{aligned} {\tilde{\sigma }}_{V_y}&= k^*_{V_y} x + \varepsilon _{V_y}, \end{aligned}$$
(8)
$$\begin{aligned} {\tilde{\sigma }}_{V_z}&= k^*_{V_z} ~ x/\xi + \varepsilon _{V_z}. \end{aligned}$$
(9)

The initial wake width (at x = 0) is then:

$$\begin{aligned} \varepsilon _{V_y}&= \varepsilon _{V_z} = \left( \frac{C_T n_y n_z}{2^{\gamma +3} \Gamma (1/n_y)~\Gamma (1/n_z)}\right) ^{\gamma /2}. \end{aligned}$$
(10)

The required input parameters for both analytical wake models (Eqs.  4 and 7) are: the turbine’s rotor dimensions (diameter D and height H for VATs, and diameter D for HATs), thrust coefficient \(C_T\), incoming velocity distribution \(U_0=U(z)\), and turbulence intensity \(I_u\).

2.3 Wake superposition

In multi-row arrays, the turbines in the first row operate in undisturbed flow conditions, i.e. the approach velocity \(U_i\) is the incoming velocity \(U_0\) and thus the theoretical models Eqs.  4 and 7 can be directly applied. However, an \(i^{th}\)-device operating behind a number of n turbines can be affected by the impact of \(n^{i-1}\) upstream turbines whose low-velocity wakes overlap enhancing the velocity deficit. In a time-averaged sense, this wake interaction can be estimated using linear and quadratic wake superposition methods, as widely used in literature for both HATs (Stansby and Stallard 2016; Niayifar and Porté-Agel 2016; Lanzilao and Meyers 2021) and VATs (Mueller et al. 2021). Taking into account that each individual turbine generates a velocity deficit \(\Delta U^i\), this is adopted to calculate the local incident velocity for every turbine (\(U_0^i\)) in Eqs. 4 and 7 using a linear superposition of the velocity deficit field, as:

$$\begin{aligned} U^i_0&= U_0 - \sum \limits _{k=1}^{n^{i-1}} \Delta U^k. \end{aligned}$$
(11)

Although Stansby and Stallard (2016) used the linear superposition to predict the velocity deficit created by small HAT arrays with a good accuracy, in cases with more than three rows of turbines, the linear wake superposition may be insufficient to take into account complex intra-farm mechanics, e.g. vertical fluxes of kinetic energy. Thus, three rows are herein adopted to configure the layouts. In the wake of twin-VAT setups, the linear superposition provides less error compared to experimental data than the quadratic superposition in both fields of velocity deficit and turbulence intensity (Mueller et al. 2021).

3 Array layouts and performance

Perfectly aligned and staggered turbine array layouts are analysed as they are the two extreme scenarios when turbines operate fully in the wake of upstream devices or in the bypass flow going through the closest upstream pair of turbines (Stansby and Stallard 2016; Ouro and Nishino 2021). During a tidal cycle, if the direction of the incident flow is exactly reversed from ebb to flood any array operating as aligned or staggered configuration will still operate with such layout during the other half of the cycle. Conversely, if flow directions between ebb and flood tides are not parallel then the array can operate as aligned during part of the tidal cycle and as staggered during the other half, or vice versa. The two array design parameters are the downstream spacing between rows (\(S_x\)) and the lateral spacing (\(S_y\)) between turbines within a same row. To compare the performance between arrays of HAT and VATs of different aspect ratio, whose rotors have different dimensions, these spacing parameters are normalised by the turbine’s effective diameter \(D_0\), i.e. \({\tilde{S}}_x = S_x / D_0\) and \({\tilde{S}}_y = S_y / D_0\) as indicated in Fig. 3, which provides the dimensionless spacing parameter \({\tilde{S}}\), defined as:

$$\begin{aligned} {\tilde{S}} = \frac{\sqrt{S_x S_y}}{D_0}. \end{aligned}$$
(12)

This is similar to the normalised spacing in wind farms Stevens et al. (2016), but modified using \(D_0\) to enable a like-to-like comparison between HAT and VAT rotors.

The efficiency of renewable energy technologies can be represented by the ratio of energy generation capability per occupied land area (MacKay 2009; Dabiri 2011). However, the definition of the planform area occupied by tidal stream and wind turbines should not only consider the surface delimited by its perimeter, as shown in Fig. 3, as these devices generate wakes that reduce the energy resource in the adjacent downstream region, unlike other resources such as solar farms or biomass. Thus, the planform area occupied by a turbine array needs to be defined in terms of the whole influenced area equal to \({\mathcal {A}} = N_T {\tilde{S}}_x {\tilde{S}}_y\), i.e. the sum of the equivalent rectangular surface proportional to \({\tilde{S}}_x {\tilde{S}}_y\) per each of the \(N_T\) turbines in the array. This includes the wake region generated by the outermost turbines in which no additional turbines can be placed.

Table 2 Design characteristics of the five array layouts including normalised streamwise (\({\tilde{S}}_x\)) and spanwise (\({\tilde{S}}_y\)) turbine spacing
Full size table
Fig. 3
figure 3

Schematic of the array layout 3 with a staggered configuration including three rows of turbines comprising five, four and five turbines per row. Blue circles denote the location of the turbines, the dashed line indicates the planform area of the array based on the individual area assigned to each turbine measuring \(S_x / D_0 \cdot S_y / D_0\), and the dotted line corresponds to the array perimeter

Full size image

A total of 15 turbines distributed in three rows (five devices per row) are adopted in the aligned arrays whilst 14 devices are considered in staggered configurations with five, four and five turbines per row. Five different turbine spacing configurations are studied with the design parameters listed in Table  2. The efficiency of each array results from the sum of the individual power output \(P_i\) of each turbine calculated according to Eq. 13, with the maximum power output (\(P_i^{~max}\)) occurring when the turbine operates in undisturbed oncoming flow, i.e. \(U_i = U_{0}\).

$$\begin{aligned} P_i = \frac{1}{2}\rho ~C_p \int _{A} U_{i}^3 \,dA. \end{aligned}$$
(13)

The array efficiency (\(\eta \)) is defined as the ratio between the total power output from all turbines (\(P_{tot}\)) and the maximum power if they operated in undisturbed conditions (\({P_{tot}^{~max}}\)). The latter is computed with the rated \(C_P\) of each turbine so that the array efficiency includes both wake losses and capacity factor, and reads:

$$\begin{aligned} \eta = \frac{P_{tot}}{P_{tot}^{~max}} = \frac{\sum _{i=1}^{N_T} P_i}{{N_T} P_i^{~max} }. \end{aligned}$$
(14)

In a time-averaged sense, the array efficiency corresponds to the averaged Capacity Factor (CF) (Lewis et al. 2021). The array’s power density (PD) is then computed considering a non-uniform velocity at the inlet (\(U_{0}(y,z)\)) using Eq.  14 as:

$$\begin{aligned} PD= & {} \frac{P_{tot}}{{\mathcal {A}}}= \frac{ \eta \sum _{i=1}^{N_T} P_i^{~max}}{N_T S_x S_y} \nonumber \\= & {} \left( \frac{1}{S_x S_y} \frac{1}{2} \rho C_p \int _{A} \left[ U_{0}(y,z) \right] ^3 \,dA \right) \eta . \end{aligned}$$
(15)

Considering uniform incoming flow conditions, i.e. only vertical variation but homogeneous across the width of the inflow plane (\(U_{0}=U_0(z)\)), the power density can be re-written as:

$$\begin{aligned} PD&= \frac{1}{{S_x} S_y} \frac{1}{2} \rho A U_{0}^3 C_p \eta = \frac{P_0}{S_x S_y} ~ \eta . \end{aligned}$$
(16)

Alternatively, Dabiri (2011) proposed a similar form to calculate the power density but assigned a circular area to each VAT, which included a \(\pi \)/4 factor that is not in Eq. 16 as it assigns a rectangular area to each turbine irrespective of its rotational axis, as shown in Fig. 3. They included an aerodynamic loss factor to take into account wake effects and an explicit capacity factor that depends on the resource availability, which are analogous to \(\eta \) and accounted for in \(P_0\), respectively, in Eq. 16.

At every time instant (t) in which flow data are available, the \(N_t\) turbines comprising the array are rotated according to the incident flow direction (\(\theta \)) using its centre as pivot, as shown in Fig. 4. For this, they are ordered by their upmost location in the flow direction \((x_i)_{[1,N]}\)(t), so as to compute the velocity field at each turbine (i) including the wakes generated by the \(n^{i-1}\) upstream turbines. This alignment of the turbines with the flow incidence at \(\theta \) allows to compute the individual wakes in the downstream x-direction. No misalignment between flow direction and turbine orientation is included in the present models, i.e. devices are yawed according to the actual incident flow direction (\(\theta \)) at all times. This is irrelevant to VATs as they are omni-directional, i.e. neither their wake nor performance are affected by changes in flow direction. However, HATs operating in non-aligned flows with a yaw angle \(\theta \) experience a decrease in power proportional P(\(\theta \)) = P\(_0 \cdot \)cos\(^a\)(\(\theta \)) (with a theoretically equal to 3.0 (Zong and Porté-Agel 2021)) and their wake changes it shape to a non-Gaussian distribution and gets deflected laterally, consequently impacting the downstream recovery (Bastankhah and Porté-Agel 2016).

Fig. 4
figure 4

Layout of tidal turbines for the array 4 (only four turbines per row are shown) with aligned layout when (a) the flow direction is at \(0^{\circ }\), and (b) turbine layout rotated according to a non-zero incident flow angle (\(\theta \))

Full size image

4 Results

The energy yield of the tidal turbine arrays is assessed at three tidal sites, namely Ramsey Sound (Wales, UK), Ría de Vigo (Galicia, Spain) and Kobe Strait (Japan). These are selected as they represent scenarios in which there is a high to low tidal resource, thus providing a fair representation of potential deployment locations. Details of the flow conditions at these locations are summarised in Table 3 including peak velocity during spring tide (not necessarily included in the current simulations) and vertical distribution of velocities. No bathymetry is considered in the present calculations.

Table 3 Description of the location and flow characteristics at the three sites studied, including peak flow velocities during the simulated flood and ebb tides
Full size table

4.1 Site 1: Ramsey sound

The tidal site of Ramsey Sound is characterised by a high tidal energy potential, with peak velocities reaching \(U_0\) = 2.7 m s\(^{-1}\) during Spring tide (Harrold and Ouro 2019), in which the Deltastream turbine from Tidal Energy Ltd. was deployed (Evans et al. 2015; Harrold and Ouro 2019; Harrold et al. 2020). The time series of streamwise velocity and turbulence intensity during a tidal cycle over the water column are obtained from Harrold and Ouro (2019), which indicated that the vertical profile of velocities follows a logarithmic distribution, computed as:

$$\begin{aligned} U_{0}(z) = \frac{u_*}{\kappa }\left( \ln {\frac{z}{z_0}} + 2.2\right) , \end{aligned}$$
(17)

where \(u_*\) = 0.051 \(U_{0}^{h}\) is the friction velocity and \(U_{0}^{h}\) the flow velocity at hub height, \(\kappa = 0.41\) is the von-Karman constant, and \(z_0\) = 0.02 m is the estimated bed roughness. The log-law profile is developed until the boundary layer height after which a constant velocity distribution is observed with maximum value.

The simulated tidal cycle covers approx. 24 hours with velocities and turbulence intensity values presented in Fig.  5. The flow direction is considered perfectly bi-directional between both tidal cycles, i.e. flow direction is at 0\(^{\circ }\) and 180\(^{\circ }\) during flood and ebb tides respectively (Harrold and Ouro 2019), with magnitudes considerably larger during the former owed to the complex bathymetry at the site (Evans et al. 2015). The water depth is around 35 m so VATs with high aspect ratio (Table 1) are suitable for the deployment.

Fig. 5
figure 5

Details of the flow data from Ramsey Sound including velocity magnitude and turbulence intensity at hub height, and results of the instantaneous power generation for HATs and VATs with \(\xi \) = 1 and 4 for the staggered array 4 with \({\tilde{S}}\) = 2.12

Full size image

The time series of the power generated by the staggered array 4 (\({\tilde{S}}\) = 2.12) for HATs and VATs with \(\xi \) = 1 and 4 is presented in Fig. 5. During the low-velocity periods of the ebb tide, the power output is similar between HATs and VATs if these feature a \(\xi \) greater than 2, otherwise for \(\xi \) = 1 the power generation is about 30% lower. During flood tide the velocities at Ramsey Sound reach large values leading HATs to generate at peaks of about 500 kW. Conversely, the lower power coefficient and rated speed of VATs means that maxima of 290 kW and 320 kW are reached by rotors with \(\xi \) = 1 and 4, respectively, as seen in Fig. 5 at peak velocities. Considering the maximum rated power of these staggered VAT arrays with 15 turbines is 350 kW (Table 2), thus the wake losses at the period of highest flow speed account for 15%, 10%, 9.8%, and 7.7% for \(\xi \) = 1, 2, 3 and 4, respectively.

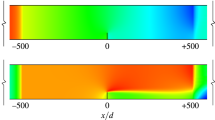
Contours of velocity deficit (\(\Delta U/U_{0}\)) over a horizontal plane at hub height for the array with \({\tilde{S}}\) = 2.4 comprising HATs and VATs with aspect ratio \(\xi = 1\), 2 and 3 are shown in Fig. 6 when the velocity reach \(U_{0}\) = 2 m s\(^{-1}\) at 7 h. The higher thrust exerted by HATs leads to pronounced wakes that feature a high velocity deficit, which notably reduces for VAT arrays. The latter develop low-velocity wakes whose lateral expansion reduces as the aspect ratio increases, because their diameter is effectively smaller. For \(\xi \) = 1, the VATs still experience wake effects whilst these mostly vanish for \(\xi \) = 3 and 4.

Fig. 6
figure 6

Contours of normalised velocity deficit (\(\Delta U / U_0\)) at hub height \(z=z_{hub}\) for the staggered array 3 (\({\tilde{S}}=2.45\)) computed after 3 hwith \(U_0 \approx \) 1.5 m s\(^{-1}\) and \(I_u=12\%\). *a HAT, and VATs with b \(\xi =1\), c \(\xi =2\), and d \(\xi =3\)

Full size image

Power density results obtained for the staggered and aligned arrays of VATs and HATs are presented in Fig. 7. For a large turbine spacing (\({\tilde{S}}\) = 4.90 and 3.46), VATs reach power densities of \(\approx \) 15 W m\(^{-2}\) independent of their aspect ratio and configuration, as the large streamwise spacing between turbine rows limit the impact of wake effects, and HATs notably increase the power density for this spacing with 25.6 W m\(^{-2}\) and 21.6 W m\(^{-2}\) for staggered and aligned layouts, respectively. Clustering the turbines closer leads to a noticeable increase in power density for all arrays, as the occupied area effectively decreases. HATs yield larger power density values than their vertical axis counterparts for all configurations due to the highly energetic nature of the tidal flow at Ramsey Sound, reaching maxima of 125.8 and 104.3 W m\(^{-2}\) for staggered and aligned arrays.

Figure 7 shows that in staggered configurations VATs benefit from having rotors with a larger aspect ratio when \({\tilde{S}} \le 2.5\) as wake losses reduce (see Fig.  6). A notable improvement is seen when comparing the efficiency obtained by arrays with VAT rotors with \(\xi \) = 2 with \(\xi \) = 1, e.g. for the layout with \({\tilde{S}}\) = 1.73 the former increases by 15% the power density of the latter. The modification of the VAT rotor with \(\xi \) = 3–4 provides a smaller improvement. In aligned configurations, such performance improvement from the rotor’s aspect ratio reduces.

Fig. 7
figure 7

Power density (top) and capacity factor (bottom) results obtained at Ramsey Sound with the (a) staggered and (b) aligned arrays

Full size image

The capacity factor (CF) from each of the arrays presented in Fig.  7 shows that for layouts with lowest wake effects, i.e. \({\tilde{S}}\) = 4.9, VATs reach a CF of up to 37% whilst this reduces to nearly 20% for HATs, which agrees with idealised predictions in Lewis et al. (2021). Wake effects in aligned configurations reduce the CF of the arrays, whereas staggered layouts in VATs with \(\xi \) larger than 2 experience a limited reduction in CF even for the layout with \({\tilde{S}}\) = 1.73.

4.2 Site 2: Ría de Vigo

Ría de Vigo is located in North-West Spain and is a tidal site with a lower resource potential than Ramsey Sound, but still reaches peak velocities of approx. 2.3 m s\(^{-1}\) during spring tide (Griño Colom 2015). The flow data were obtained from the tidal resource assessment presented in Griño Colom (2015) who used a shallow-water model. As only the depth-averaged speed was provided in this study, the flow direction is assumed to be perfectly bi-directional and the vertical profile of velocities was set to follow a \(1/7^{th}\) power law, as:

$$\begin{aligned} U_{0}(z) = \bar{U}\left( \frac{z}{\beta h} \right) ^{1/7}, \end{aligned}$$
(18)

where \(\beta \) = 0.3 is the dimensionless surface roughness coefficient and \(\bar{U}\) is the flow velocity averaged over the vertical direction (z) equal to the target velocity value (Lewis et al. 2017). The water depth h equal to 35 m is high enough to allow the deployment of VAT rotors investigated (Table  1), as in Ramsey Sound.

Figure 8 presents the time series of the velocities, turbulence intensity, and power generation during the two ebb-flood tide cycles simulated. Ría de Vigo is an estuary with particular geographic conditions in which ebb tides are characterised by low velocities reaching a maximum speed of 1.0 m s\(^{-1}\). The velocities during the flood tide increase and peak at values close to 2.0 m s\(^{-1}\). Similar turbulence intensity levels are observed during the flood and ebb tides. During flood tide, the higher velocities allow HATs to generate more power than VATs but similar values are obtained with VATs using \(\xi \) = 3 or 4. VAT rotors with \(\xi \) = 1 experience notable wake losses with an almost 40% lower peak power generation compared to HATs.

Fig. 8
figure 8

Details of the flow data from Ría de Vigo including velocity magnitude and turbulence intensity, and results of the instantaneous power generation (right) for HATs and VATs with \(\xi \) = 1 and 4 for the staggered array 2 (\({\tilde{S}}\) = 3.46)

Full size image

Power density results at Ría de Vigo for the proposed arrays are presented in Fig. 9. The lower available energy at this site compared to Ramsey Sound is reflected in lower power density values for the arrays with the largest \({\tilde{S}}\) attaining a power density \(\approx \) 5 W m\(^{-2}\) for both VATs and HATs, whilst at Ramsey Sound these reached 15 and 30 W m\(^{-2}\), respectively (Fig. 7). Our predictions for HATs based on analytical wake models yield a power density of 6.7  W m\(^{-2}\), similar to that obtained in Griño Colom (2015) with a depth-averaged shallow-water model for a two-row array with \({\tilde{S}}\) = 5.64 (\(\tilde{S_x}\) = 11.28 and \(\tilde{S_y}\) = 2.82).

Fig. 9
figure 9

Power density (top) and capacity factor (bottom) results obtained at Ría de Vigo with the (a) staggered and (b) aligned arrays

Full size image

With \({\tilde{S}}\) = 3.5, HATs and VATs feature a similar power density irrespective to their configuration. Further decreasing turbine spacing in staggered arrays, VATs constantly attain larger power density values when increasing \(\xi \). These results showcase that wake effects start to become critical and limit the efficiency of arrays with HATs and VATs with \(\xi \) = 1 to improve their power density. For the most packed staggered arrays with \({\tilde{S}}\) = 1.7, VATs reach power densities up to 35.2 W m\(^{-2}\) (\(\xi \) = 2) and nearly to 50.5 W m\(^{-2}\) (\(\xi \) = 4). Conversely, aligned VAT arrays offer a small gain in power density increase with changing the aspect ratio. For \({\tilde{S}}\) = 1.73, the maximum power density with \(\xi \) = 4 is 50% lower than that in its staggered counterpart, whilst for \(\xi \) = 1, this reduces by about 30%.

In this case with the flow being perfectly bi-directional, the power density obtained with a staggered configuration and \(\xi \) = 1 improves about 10–18% that of an aligned array with \(\xi \) = 4, except for \({\tilde{S}}\) = 3.46 in which the latter improves the former by 10%. Thus, the array performance is mostly driven by the incidence angle of the flow, i.e. its layout as staggered or aligned configuration, as the efficiency benefits arising from adopting high rotor aspect ratios are observed mostly in staggered configurations.

Figure 9 shows that the CF at this site again shows large differences between HATs and VATs, reaching capacity factors of 6.5% and 18%, respectively, for \({\tilde{S}}\) = 4.90. As seen at Ramsey Sound (Fig. 7), the CF is lower for aligned than staggered arrays due to wake effects, especially for small normalised turbine spacing in which VATs with high rotor aspect ratio maintain a nearly constant CF of approx. 15%, 14% and 14% for \(\xi \) = 4, 3 and 2, respectively.

4.3 Site 3: Kobe Strait

A third tidal site in Kobe Strait (Japan) is analysed using data from Garcia-Novo and Kyozuka (2017). Kobe Strait is one of the channels formed between islands in the Goto archipelago. The large amount of water moving from the Pacific Ocean to the Sea of Japan for flood tides and vice versa for ebb tides makes of these channels very promising areas for tidal stream energy exploitation. Two of these channels (Naru Strait and Tanoura Strait) have already been designated by the Japanese Government as test sites for MW-scale projects (Garcia-Novo et al. 2019). Kobe Strait, due to its morphological and resource characteristics, is more appropriate for the installation of smaller and low current speed converters. The site has a complex bathymetry that leads to highly unsteady conditions, i.e. large flow velocity and incident angle variations.

Data from a deployed ADCP covering a fully spring–neap cycle recorded from 27th February until 14th March 2015 is used to run this case with velocity magnitude and direction, and streamwise turbulence intensity, averaged over the first 5 minutes of each 20-min sample interval. The flow data at hub height is presented in Fig. 10 together with the incident flow direction. In the vertical direction, the velocity profile obtained from the ADCP follows a 1/7\(^{th}\) power law (Eq. 17) most of the time. This site is shallow with a water depth of 15 m that can restrain the size of the turbines to be deployed.

Fig. 10
figure 10

Time series of the velocity magnitude, turbulence intensity and directionality at Kobe Strait (Japan), together with the instantaneous power generation from HAT and VATs with \(\xi \) = 1 and 4 adopting a staggered configuration in array 2 (\({\tilde{S}}\) = 3.46)

Full size image

The power capacity and energy generation for the staggered array 2 (\({\tilde{S}}\) = 3.46) over the considered 360 h is presented in Fig.  11, which evidence the different operation characteristics between HATs and VATs with varying aspect ratio. During neap tides, there is a reduced operation of HATs whilst VATs harness kinetic energy from the flow during all tidal phases as velocities are over 0.5 m s\(^{-1}\) (except during slack tide), albeit this energy is relatively small. In spring tide, all turbine rotors produce energy with HATs featuring a higher power generation than that of VATs. Adopting the HAT array as reference, the cumulative energy generated by VATs increases 37%, 32%, 24% and 8% for \(\xi \) = 4, 3, 2 and 1, respectively.

Fig. 11
figure 11

Time series of the instantaneous power (top) and cumulative energy (bottom) generation from HAT and VATs with \(\xi \) = 1 and 4 adopting a staggered configuration in array 2 (\({\tilde{S}}\) = 3.46) at Kobe Strait (Japan)

Full size image

The comparison of the power density results for the tidal turbine arrays at Kobe Strait are presented in Fig. 12. For large turbine spacings, all configurations yield a power density of approx. 6 W m\(^{-2}\) which increases with decreasing \({\tilde{S}}\). For staggered and aligned arrays with a normalised turbine spacing lower or equal to 2.5, VATs outperform HATs except when adopting \(\xi \) = 1. A maximum power density of 32.4 W m\(^{-2}\) and 28.1 W m\(^{-2}\) is obtained for staggered and aligned configurations respectively, when the VATs have an aspect ratio of 4, as wake effects between turbines are almost negligible. VATs compensate their lower peak energy generation during spring tide with a less intermittent energy generation overall. This yields higher CFs compared to HATs as shown in Fig. 12. Note that no misalignment between flow direction and HATs’ orientation is considered which could further reduce their energy yield.

Fig. 12
figure 12

Power density (top) and capacity factor (bottom) results obtained at Kobe Strait with the (a) staggered and (b) aligned arrays

Full size image

The varying flow direction at this site reduces the sensitivity of the array to its initial configuration, as it does not operate as perfectly staggered or aligned array during flood and ebb tides. In the previous cases of Ramsey Sound and Ría de Vigo, the flow was deemed perfectly bi-directional making the array efficiency very sensitive to its configuration, with staggered ones notably outweighing the aligned ones. These results suggest that the role of the array layout is relevant if the flow direction is perfectly reversed during flood and ebb tides, e.g. at Ramsey Sound (UK) (Harrold and Ouro 2019), Anglesey (UK) (Piano et al. 2017) or Sound of Islay (UK) (Milne et al. 2013).

5 Discussion and conclusions

This paper studies the efficiency of perfectly aligned and staggered tidal stream turbine arrays that adopt different turbine rotor geometries, namely horizontal axis turbines (HATs) and vertical axis turbines (VATs) with different height-to-diameter aspect ratio (\(\xi \)) at three tidal sites (Ramsey Sound, Ría de Vigo and Kobe Strait) with increasing available resources. The velocity deficit field was represented using analytical wake models based on Gaussian and super-Gaussian distributions for HATs and VATs respectively, to account for wake effects that are detrimental to the energy yield.

Our results showed in terms of power density capacity, as this represents the power generation per planform area occupied by the array, indicate that HATs are the most suitable technology when the site has a high energy intensity resource, e.g. peak currents exceed 2.5 m s\(^{-1}\). For such scenario at Ramsey Sound, HATs attain minima of 21 W m\(^{-2}\) and 26 W m\(^{-2}\) when adopting aligned and staggered layouts with a non-dimensional spacing (\({\tilde{S}}\)) of 4.9, which increase up to 104 W m\(^{-2}\) and 126 W m\(^{-2}\) respectively, for \({\tilde{S}}\) = 1.73. VATs’ efficiency increases when using rotors with larger \(\xi \) as wake effects reduce, with values of power density of approx. 87 W m\(^{-2}\) and 115 W m\(^{-2}\) when adopting aligned and staggered layouts with \({\tilde{S}}\) = 1.7. In Ría de Vigo, flow speeds were up to 2.0 m s\(^{-1}\) and led VATs to reach higher power densities than HATs for packed arrays with \({\tilde{S}} \le \) 2.5, with larger differences for staggered arrays. Kobe Strait was characterised by lower velocities and changing flow directionality due to the complexity of the bathymetry. In this case, VATs yielded a higher power density compared to HATs for \({\tilde{S}} \le \) 3.6 in both aligned and staggered layouts.

The averaged Capacity Factor (CF) computed at the three sites show that VATs attain about 3 times larger CF than HATs for large turbine spacing, whilst this difference can increase further for packed arrays as former can reduce wake effects. At Ramsey Sound, HATs have a maximum CF of 19% which agrees with idealised predictions for turbines with rated speeds of 2.5 m s\(^{-1}\) computed using ocean models (Lewis et al. 2021). Conversely, VATs have a CF \(\approx \) 37% as their rated speed is lower. These CF values are lowered at Ría de Vigo and Kobe Strait as the tidal resource decreases but again with those from VATs exceeding those from HATs.

Overall, this study suggests that the rotor design that maximises the energy harnessing capabilities of a tidal stream turbine array depends on the available tidal resources. Lewis et al. (2021) showed maximum flow velocities over 1 m s\(^{-1}\) are found in less than 13% of the world’s coastline, whilst only 3.6% features flow speeds over 1.5 m s\(^{-1}\). HATs are the most suitable in highly energetic sites, while VATs reduce wake effects providing larger power densities at sites with medium-to-low resource. Optimisation of the cut-in and rated speeds in turbine design would allow to minimise wake interactions to maximise energy yield. The array layout as staggered or aligned is key when the flow is mostly bi-directional during flood and ebb tides, whilst for a velocity misalignment larger than 10\(^{\circ }\)–20\(^{\circ }\) (Lewis et al. 2015) this becomes less relevant as the array will not operate as perfectly staggered or aligned during the tidal cycle. Nonetheless, most resource assessment studies indicate the power density based on the available potential without taking into consideration how much energy can be harnessed by turbines and also lost due to wake effects and friction (Vennell et al. 2015; Stansby and Ouro 2022), which can be included in analytical wake models of arrays and thus enable to estimate the extractable power density (Adcock et al. 2013).

Our results suggest that tidal arrays and wind farms comprising VATs should consider rotors with a height-to-diameter aspect ratio of at least 3 to mitigate wake effects and thus improve the power density.

Averaging the power density obtained for each rotor design in all layouts considered at the three tidal sites, horizontal axis tidal turbines reach an averaged power density 49.3 W m\(^{-2}\) whilst that for vertical axis tidal turbines is 34.7 W m\(^{-2}\) for \(\xi \) = 1 and increases to 40.7 W m\(^{-2}\) for \(\xi \) = 4. These can be compared with the power density of other renewable energy technologies such as offshore wind 4.2 ± 1.7 W m\(^{-2}\) (Enevoldsen and Jacobson 2021), onshore wind 3.06 ± 0.7 W m\(^{-2}\)van Zalk and Behrens (2018), solar photovoltaic 7.5 ± 1.5 W m\(^{-2}\) (Enevoldsen and Jacobson 2021), solar CSP 9.7 ± 0.4 W m\(^{-2}\), or even vertical axis wind turbines 23.56 W m\(^{-2}\) (Dabiri 2011).

These results outline that tidal stream energy features one of the largest power density capacity among all renewable energy resources, with power densities at the sites analysed at least one order of magnitude higher than found for wind farms. Energetic tidal energy sites can provide more certainty about resource availability leading to a less intermittent energy generation which can play a key role in future net-zero energy grids (Coles et al. 2021). Further improvements could be obtained from the optimisation of the rated speed and operational curve for both HATs and VATs so as to maximise their power density and capacity factor at any given site. For such assessment, analytical wake models are invaluable tool to be used complementary to large-scale resource assessments with shallow water models providing the flow magnitude and direction at any location.

Future analyses should include: turbine blockage effects that represent local flow accelerations to account for beneficial effects in turbine performance and thus potentially increasing energy yield (Draper and Nishino 2014; Nishino and Willden 2013; Maskell 1965); combination of rotational directions in pairs of VATs could lead to further increase in efficiency but likely to affect the wake dynamics (Mueller et al. 2021); or, non-uniform flow direction due to coastal diversions such as headlands (Draper et al. 2013; Piano et al. 2017). Economic assessment of arrays with combination of rotor area and number of turbines could enable assessment of levelised cost of energy (LCOE) for tidal stream energy with HATs and VATs (Goss et al. 2021) so they can be compared to other technologies to motivate future governmental support (Coles et al. 2021). Similar discussions for offshore wind farms with different rotor designs would also be of interest to the renewable energy community.