1 Introduction

To alleviate the consequences of global warming, the world’s energy supply may have to utilize also renewable and sustainable energy resources. In the last decade, offshore wind turbines have become one of the fastest growing sources of electrical energy among renewable energy generators, among which the monopile foundation is by far the most widely used substructure due to its simplicity. The effects of operational wave-induced loads on offshore monopile wind turbines are reasonably well understood. For most existing and future sites, however, the water depth is such that steep, breaking or near-breaking waves will occur, causing high-frequency resonant responses and impulsive excitation of the foundation and, consequently, considerable stresses in and displacements of the foundation, the tower structure, and the turbine. It is well known that nonlinear high-frequency wave loads can lead to hydroelastic responses of resonant excitations, i.e., springing and ringing (Faltinsen 1993). Springing is characterized as a steady-state response caused by second-order wave effects at the sum frequencies, while ringing is characterized as a strong transient event, typically decaying to steady state at a logarithmic rate that depends upon its damping. Many laboratory studies have investigated the wave loads caused by various wave conditions, including strong nonlinear steep, near-breaking, and breaking waves. For instance, Stansberg et al. (1995) performed experimental study of nonlinear loads on vertical cylinders in steep random waves. They observed that the contributions of nonlinear high-frequency force components may be up 10–20% of the total external forces. Kyte and Tørum (1996) carried out an experimental investigation to assess wave forces from breaking regular and irregular waves acting on a vertical cylinder located on a shoal by comparing measured and calculated local and total forces. Huseby and Grue (2000) experimentally investigated the first- and higher harmonic wave loads on a vertical circular cylinder in a wave tank of small scale, and they found that for larger wave amplitudes, the adopted fully nonlinear potential-flow model gave conservative predictions. Wienke and Oumeraci (2005) theoretically and experimentally studied breaking waves acting on a slender cylindrical pile. Robertson et al. (2015) experimentally tested a fixed vertical truncated cylinder as well as an array of cylinders in irregular waves to determine the contribution of high-frequency force components generated in steep waves. To study the high-order nonlinear wave loading under extreme events, Chen et al. (2018) experimentally extracted the higher harmonics in wave–structure interactions using focused wave groups. Their results revealed that for certain wave conditions, the linear loading is less than 40% of the total wave loading and the high-order harmonics contribute more than 60% of the loading. When it comes to random waves, Riise et al. (2018) experimentally investigated the high-frequency resonant responses of a weakly damped monopile exposed to irregular deep water waves, where different wave load mechanisms, including wave-exciting inertia forces, wave slamming, the secondary load cycle, and possible drag forces, were discussed.

Aside from experimental studies, also numerical models and calculation methods have been developed to assess associated problems. Most methods to calculate wave loads on a structure aim for quick and trustworthy estimations. For instance, Morison equation (Morison et al. 1950) can be used to determine the linear part of wave-induced load, which consists of inertia and drag terms, and its coefficients need to be calibrated by experimental data or available guideline. While Morison equation was found to underpredict peak forces and moments on a fixed cylinder in strong nonlinear waves (Chaplin et al. 1997). To consider the wave-induced load in highly nonlinear situations, corrections to the inertia term of Morison formula (i.e., slender-body theory) were proposed in the works of Rainey (1989) and Rainey (1995), accounting for axial divergence, surface intersection, and surface distortion components. Higher order hydrodynamic loading models were also derived as perturbation theories, such as the M &M model (Malenica and Molin 1995) and the FNV theory (Faltinsen et al. 1995). A comparative study of Morison equation, slender-body theory, M &M model, and FNV theory was conducted using fully nonlinear wave kinematics (Bredmose et al. 2013). Recently, the FNV formulation was extended for finite water depth, where waves of intermediate steepness were studied (Kristiansen and Faltinsen 2017). Suja-Thauvin (2019) assessed different hydrodynamic load models, and quantified the response of monopile wind turbines to higher order wave loads. Another advanced technique is the Computational Fluid Dynamics (CFD) approach, which can account strong nonlinear free-surface flow, and reveal detailed information about various flow features. Christensen et al. (2005) computed the regular wave forces of a monopile on a sloping sea bed using a Navier–Stokes solver, and the breaking process was shown to have a major influence on the run-up and wave forces. Paulsen et al. (2014) investigated the forcing by steep regular water waves on a vertical circular cylinder at finite depth by coupling Navier–Stokes with a fully nonlinear potential-flow solver, where higher harmonic force components and the secondary load cycle were discussed. Burmester and Guérinel (2016) investigated wave-induced loads on a vertical cylinder by comparing solutions obtained from a potential- and a viscous-flow solver. In general, such a comparison yields small differences, with a slightly better agreement between the viscous-flow results and experiments, but with a significant increase of computational costs. In addition, the characteristics of higher harmonic breaking wave forces and secondary load cycles on a single vertical circular cylinder were studied for various Froude numbers (Liu et al. 2019a), and for different Keulegan–Carpenter (KC) numbers (Liu et al. 2019b). It is worth noting that a breaking wave load consists of two components, a quasi-static loading and an additional slamming force, which distinguishes from the impact of a non-breaking wave and the associated mechanisms. For detailed comparisons of breaking and non-breaking wave impact forces, see Mogridge and Jamieson (1978), Fullerton et al. (2009), Riise et al. (2018), and Zou et al. (2019). Breaking wave loads are outside the scope of the present study.

The review of research on wave-induced loads on vertical cylinders shows that the first-order loads can be well predicted using simple approaches based on potential-flow theory. While dealing with the subject of steep wave conditions, a potential-flow-based approach typically overpredicts the higher harmonic loads and the discrepancy in general increases monotonically with increasing wave steepness, as discussed by Kristiansen and Faltinsen (2017). In addition, it is unable to implicitly consider the viscous-flow effects, e.g., flow separations nor the associated secondary load cycles. Our purpose was to determine the capability of different modeling tools (i.e., a viscous-flow solver and a potential-flow solver) to accurately predict the hydrodynamic loads on a monopile foundation. We applied both methods to compute these loads for different wave conditions and validated our numerical predictions against model tests performed in a shallow water basin, performed within the scope of the Joint Industry Project WiFi (de Ridder et al. 2017). These tests were conducted to examine the effects of steep (and breaking) waves on the support structure of bottom-fixed offshore wind turbines by analyzing wave elevations, horizontal wave loads, and the corresponding overturning moments. We scrutinized the differences between a viscous-flow solver and a potential-flow solver in terms of accuracy and computational effort. This enabled us to better understand the applicability of these two methods. The adopted potential-flow solver relied on a weakly nonlinear time-domain solver (i.e., Green function). The viscous-flow solver used three solution schemes, namely, an Euler scheme that neglected the flow viscosity, a Laminar scheme that numerically integrated the full Navier–Stokes equations without a model accounting for the fluctuating portion of the velocity field, and a Reynolds-averaged Navier–Stokes (RANS) scheme that modeled turbulent flow via a two-equation eddy-viscosity model. In general, comparative results from the viscous-flow solver and the potential-flow solver revealed a better agreement between the viscous-flow results and the experiments, but with a significant increase of computational costs. The predictions of wave-induced loads were examined in terms of the adopted calculation schemes, higher harmonic forces and moments, wave steepness, and the secondary load cycles.

2 Numerical methods

This section describes the applied numerical methods, consisting of the viscous-flow solver and the potential-flow solver. Four numerical schemes were adopted to simulate the wave-induced loads under different flow regimes: (a) Reynolds-averaged Navier–Stokes equations with a two-equation eddy-viscosity model; (b) Navier–Stokes equations without turbulence model; (c) Euler equations by neglecting the flow viscosity; (d) inviscid and irrotational potential flow by solving Laplace equation, as depicted in Fig. 1. The adopted solvers are briefly introduced below, where the high-fidelity viscous-flow solver is the main focus of current work.

Fig. 1
figure 1

Hierarchy of simplifying assumptions of the adopted numerical approaches

Full size image

2.1 Viscous-flow solver

We used the open-source CFD library OpenFoam (Weller et al. 1998) to solve the free-surface flows. For the incompressible Newtonian fluids, the mass conservation equation is given as

$$\begin{aligned} \nabla \cdot \mathbf {v} = 0, \end{aligned}$$
(1)

where \(\mathbf {v}\) is the fluid velocity field vector in the global coordinate system. For computational gird with a relative motion velocity \(\mathbf {v}_m\), the conservation of momentum is governed by (Demirdžić and Perić 1988)

$$\begin{aligned} \frac{\partial \mathbf {v}}{\partial t} + \nabla \cdot \left[ \left( \mathbf {v}-\mathbf {v}_m\right) \mathbf {v}\right] = \nu _e\nabla ^2\mathbf {v}-\frac{1}{\rho _e}\nabla p_d, \end{aligned}$$
(2)

where \(\nu _e\) denotes the effective kinematic viscosity, and \(\rho _e\) is the effective density field. \(p_d\) presents the dynamic part of pressure p, given as

$$\begin{aligned} p_d = p-\rho _e \left( \mathbf {g}\cdot \mathbf {r}\right) , \end{aligned}$$
(3)

where \(\mathbf {g}\) is the gravity acceleration vector and \(\mathbf {r}\) is the position vector. For current hydrodynamic applications with free-surface flow, the effective density and kinematic viscosity can be derived in terms of water volume fraction \(\alpha \)

$$\begin{aligned} \rho _e=\alpha \rho _w+\rho _a(1-\alpha ) \end{aligned}$$
(4)
$$\begin{aligned} \nu _e=\alpha \nu _w+\nu _a(1-\alpha ), \end{aligned}$$
(5)

where subscripts a and w represent air and water, respectively. The volume fraction \(\alpha \) stands for a fraction of the volume occupied by water inside an arbitrary closed volume, namely Volume-Of-Fluid (VOF) approach (Hirt and Nichols 1981). Once the velocity is known, \(\alpha \) is advanced in time by the following conservation equation:

$$\begin{aligned} \frac{\partial \alpha }{\partial t} + \nabla \cdot \left( \mathbf {v}\alpha \right) + \nabla \cdot \left[ \mathbf {v}_r\alpha \left( 1-\alpha \right) \right] =0, \end{aligned}$$
(6)

where \(\mathbf {v}_r\) is a velocity field normal to the interface, denoting the artificial compression on the free surface and its magnitude is proportional to the instantaneous velocity. Equation (6) is an extended VOF formulation, which follows the work of Rusche (2003) and its boundedness is insured via the Multidimensional Universal Limiter with Explicit Solution (MULES) algorithm. Notice that despite the existence of this artificial compression term, the free surface can be smeared over a number of cells. The forces and moments acting on the body are given as follows:

$$\begin{aligned} \mathbf {F} = \mathbf {F}_p + \mathbf {F}_v = \int _S\mathbf {n} p~\mathrm{{d}}S + \int _{S}\rho _e \nu _{e} \mathbf {n} \cdot \varvec{\sigma }^*\mathrm{{d}}S \end{aligned}$$
(7)
$$\begin{aligned} \mathbf {M} = \mathbf {M}_p + \mathbf {M}_v= \int _{S}\mathbf {r}\times \left( \mathbf {n} p\right) ~\mathrm{{d}}S + \int _{S}\mathbf {r}\times \left( \rho _e\nu _{e} \mathbf {n} \cdot \varvec{\sigma }^*\right) \mathrm{{d}}S, \end{aligned}$$
(8)

where subscripts p and v denote the pressure and viscous component of the fluid-induced force and moment, which are obtained based on the pressure and velocity fields. p is the fluid pressure, \(\mathbf {n}\) stands for surface normal vector of the body surface. \(\varvec{\sigma }^*\) denotes the deviatoric component of stress tensor, and \(\mathbf {r}\) is the distance vector from current boundary surface to the mounted bottom of considered monopile.

Three numerical schemes were used in the viscous-flow solver, an Euler scheme that neglected the flow viscosity, a Laminar scheme that numerically integrated the full Navier–Stokes equations without a model accounting for the fluctuating portion of the velocity field, and a Reynolds-averaged Navier–Stokes scheme that modeled turbulent flow via a two-equation eddy-viscosity model. The Euler equations simplify the Navier–Stokes equations by considering the fluid to be inviscid. Except reducing the simulation time by disregarding the boundary layers effects, the inviscid fluid simplification does not make the Euler equations much easier to solve. Considering the effects of flow viscosity but ignoring the flow turbulent effects results in the Laminar scheme. Splitting the flow quantities into a time-average and fluctuating components leads to the RANS equations, where extra terms are closed via the k-\(\omega ~SST\) model (Menter 1994) in the present study. The solution domain is discretized into a finite number of control volume, which can be of arbitrary shape. The integrals are numerically approximated using the midpoint rule. The mass conservation is ensured using a pressure correction equation based on the hybrid PIMPLE approach (Patankar and Spalding 1983), which combines the Semi-Implicit Pressure Linked Equations (SIMPLE) algorithm with the Pressure Implicit with Splitting of Operators (PISO) algorithm. Temporal and spatial discretization schemes are of second order.

2.2 Potential-flow solver

We employed the potential-flow solver AQWA (ANSYS 2016), a weakly nonlinear hydrodynamic code widely used in the offshore industry. First-order hydrodynamics coefficients are calculated in the frequency domain based on a linear diffraction model. Applying radiation functions, these results are then used to perform weakly nonlinear time-domain simulations, where nonlinear Froude–Krylov and hydrostatic forces were estimated under instantaneous incident wave surface. The second-order wave loads are included, based on the full set of quadratic transfer functions (QTFs). For an incompressible, inviscid, and irrotational fluid flow, its velocity potential satisfies the Laplace equation everywhere in the fluid domain

$$\begin{aligned} \nabla ^2 \phi = \frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}+\frac{\partial ^{2}\phi }{\partial z^{2}}=0. \end{aligned}$$
(9)

The boundary condition on the seabed is given as

$$\begin{aligned} {\frac{\partial \phi }{\partial z}=0 \quad \text {for } z=-h }. \end{aligned}$$
(10)

At the instantaneous wetted body surface \(S_w\), the boundary condition is

$$\begin{aligned} { \frac{\partial \phi }{\partial n}=0 \quad \text {on } S_w}, \end{aligned}$$
(11)

where n denotes distance in the direction of the unit normal vector \(\mathbf {n}=(n_x,n_y,n_z)\) pointing outward from the fluid domain. At the free surface, the boundary condition must be satisfied

$$\begin{aligned} { \frac{\partial \phi }{\partial z} - \frac{\partial \eta }{\partial t} - \frac{\partial \phi }{\partial x} \frac{\partial \eta }{\partial x}- \frac{\partial \phi }{\partial y} \frac{\partial \eta }{\partial y}= 0 \quad \text {for } z=\eta }, \end{aligned}$$
(12)

where \(\eta \) denotes the free-surface elevation. The use of the conditions of irrotationality and the force potential enable one to reduce the Euler equations into the Bernoulli equation

$$\begin{aligned} \frac{1}{2} {\vert {\nabla \phi } \vert }^2 + \frac{\partial \phi }{\partial t} + \frac{p}{\rho } + gz = C\left( t\right) , \end{aligned}$$
(13)

where \(C\left( t\right) \) depends on the time, but not on position within the fluid (el Moctar et al. 2021a). Choosing the ratio of the wave amplitude to wave length as the smallness parameter \(\varepsilon \) , the perturbation approach is employed to describe the fluid potential and the fluid pressure, respectively

$$\begin{aligned} { \phi = \varepsilon \phi ^{(1)} + \varepsilon ^2 \phi ^{(2)} + O(\varepsilon ^3) } \end{aligned}$$
(14)
$$\begin{aligned} { p = p^{(0)} + \varepsilon p^{(1)} + \varepsilon ^2 p^{(2)} + O(\varepsilon ^3), } \end{aligned}$$
(15)

where the superscript (0) denotes the non-zero static value, and superscripts (1) and (2) indicate the first- and the second-order variations with respect to the perturbation parameter \(\varepsilon \). Based on Bernoulli’s equation in Eq. (13) and the fluid potential in Eq. (14), the hydrostatic pressure can be determined

$$\begin{aligned} { p^{(0)} = -\rho g z^{(0).} } \end{aligned}$$
(16)

The first-order pressure is given as

$$\begin{aligned} { p^{(1)} = - \rho g z^{(1)} - \rho \frac{\partial \phi ^{(1)}}{\partial t.} } \end{aligned}$$
(17)

Similarly, the second-order pressure is given as

$$\begin{aligned} { p^{(2)} = -\frac{1}{2}\rho {\vert {\nabla \phi ^{(1)}}\vert }^2 - \rho \left( \mathbf {r}^{(1)}\cdot \nabla \frac{\partial \phi ^{(1)}}{\partial t} \right) - \rho \frac{\partial ^2 \phi ^{(2)}}{\partial t^2.} } \end{aligned}$$
(18)

The total forces \(\mathbf {F}\) and moments \(\mathbf {M}\) follow from an integration of the pressure over the instantaneous wetted surface \(S_w\) of the body:

$$\begin{aligned} \mathbf {F}= \int _{{S_w}} p \mathbf {n}~ \mathrm{{d}}S \end{aligned}$$
(19a)
$$\begin{aligned} \mathbf {M} = \int _{{S_w}} \mathbf {r}\times \left( p \mathbf {n}\right) ~ \mathrm{{d}}S. \end{aligned}$$
(19b)

3 Test case description

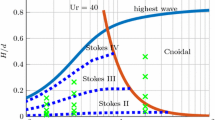
The adopted numerical solvers were examined for predicting wave-induced loads on an offshore monopile in an intermediate water depth, where highly nonlinear wave loads become pronounced. The model experiment tested at the shallow water basin of Maritime Research Institute Netherlands (MARIN) (de Ridder et al. 2017) is adopted for comparative purpose. Two steep waves were considered, and their properties are specified in Table 1, where H denotes the wave height; T, wave period; k, wave number; \(\zeta \), wave amplitude; \(k \zeta \), wave steepness. The set of two regular waves listed in Table 1 are intermediate waves and located on the Le Méhauté diagram in Fig. 2. We see from Fig. 2 that all of the presently considered non-breaking waves are within the Stokes 3rd-order wave theory regime. The same wave theory was used for numerically generating these waves. This section starts with the description of the experimental setup, followed by the details of numerical setup.

Table 1 Properties of the considered regular waves in full scale
Full size table
Fig. 2
figure 2

Locations of the considered regular waves in the Le Méhauté diagram (Le Méhauté 1976). H denotes the wave height; T, the wave period; g, the gravitational acceleration; and d, the water depth

Full size image
Fig. 3
figure 3

Overview of the experimental setup in the shallow water basin, together with the cross section of the model setup in a side view

Full size image

3.1 Experimental setup

Model tests were carried out in the shallow water basin of MARIN, which is 220 m long and 15.8 m wide, with a constant water depth of 0.884 m. This basin was equipped with a piston-type wave maker and a beach to absorb wave energy and to minimize wave reflections at its far end. The wave maker used a wave board to generate regular and irregular wave trains. During model tests, only a schematic representation of the bottom-fixed offshore wind turbine was modeled at a scale of 1:30.56, and its foundation was replicated up to the expected wave run-up. Froude scaling was applied to correctly generate gravity waves. Two physical models were tested during the experiments, namely a flexible model and a rigid model, respectively. Before moving on to the next phase that investigating the hydroelastic performance of the bottom-fixed offshore wind turbine in waves, the present study considers only the rigid model. The geometry of the still model is the same as the flexible one but extended only up to the expected maximum wave run-up, which was designed to be able to measure the hydrodynamic excitation with a non-responding model. One finds a more detailed description of the flexible model in Suja-Thauvin et al. (2017). The rigid model was placed next to a second flexible model. It was standing in a pit of 0.02 m depth below the tank floor. The bottom of the rigid model was mounted on a six-component measurement frame. Figure 3 shows an overview of the setup in the basin, and specifies the locations of the two wave probes. The tested model was situated a distance of 65.6 m from the wave generator. The fixed foundation was instrumented as follows: (a) an accelerometer was placed at the water level; (b) the six-component force frame measured forces and moments at the seabed (basin floor); (c) pressure sensors were situated at various heights along the model; (d) five relative wave probes were located at the front, at the back, and at the sides of the model. The model is composed of two cylindrical sections of diameters 0.229 m and 0.180 m, linked via a conical section (see Fig. 4). All signals were recorded at a rate of 200 Hz. Only the signals from the pressure transducers were recorded at a rate of 1000 Hz at model scale. Again, in the present study, we considered the rigid model in regular waves only.

Fig. 4
figure 4

The dimensions of the tested rigid model

Full size image

3.2 Numerical setup

A rectangular box defines the computational domain for the viscous-flow solver, as shown in Fig. 5. It consists of three layers, namely, a uniform high-resolution middle layer extending above and below the calm water level to enclose the minimum and maximum surface elevation, and two layers extending from the middle layer to the top and bottom of the domain. Although the wave absorption method (Higuera et al. 2013) was used at the outlet, cells become larger toward to the outlet, which dampened the waves and also significantly reduced computational resources. The water depth complies with the experiment. The inlet is situated more than one wavelength upstream and the outlet two wavelengths downstream of the monopile. The width of the numerical domain extends over 20 times the monopile’s diameter. Free slip boundary conditions were specified at tank walls and tank bottom. Figure 6 shows grid topologies surrounding the monopile. Grids were refined close to the monopile and near the free surface, but were kept constant in the vertical direction. The solution domain was discretized using a structured hexahedral mesh.

Fig. 5
figure 5

Computational domain of the monopile in waves for the viscous-flow solver

Full size image
Fig. 6
figure 6

Grid refinement at the free surface (left) and close to the monopile (right) for the viscous-flow solver

Full size image

In the potential-flow solver, the monopile was discretized using quadrangular panels, and an overview of the setup is visualized in Fig. 7. Contrary to the viscous-flow solver, the potential-flow solver is not sensitive to time-step size or grid size. Nevertheless, we carried out time-step and mesh sensitivity studies to check for convergence of our simulations. As expected no significant differences were observed, and we chose the moderate gird of 9247 panels with a time-step of 0.01 s for subsequent simulations in the potential-flow solver.

Fig. 7
figure 7

Schematic presentation of the numerical setup for the potential-flow solver

Full size image

4 Numerical error

As the predictions from the viscous-flow solver were sensitive to temporal and spatial discretizations, the corresponding numerical errors were quantified in this section. We neglected to determine the iterative errors, as a residual convergence criterion of \(10^{-4}\) was applied for the simulations, where a residual level of two orders of magnitude below the discretization error is expected (Eça and Hoekstra 2009). Consequently, we focused on the discretization error because of its influence on the wave elevation measured at the location of the monopile. We estimated the errors of our numerical simulations according to the approach of Oberhagemann (2016) and el Moctar et al. (2021b), where uniform refinement has to be done simultaneously in all spatial and temporal dimensions to keep a constant Courant–Friedrichs–Lewy (CFL) number

$$\begin{aligned} \mathrm {CFL} =u_i\frac{ \Delta t}{\Delta x_i} \end{aligned}$$
(20)

Here, the particle velocity in component notation is denoted by \(u_i\), the time-step by \(\Delta t\), and the grid spacing by \(\Delta x_i\). The associated discretization error, \(\delta _D\), was approximated as a function of the non-dimensional scalar grid refinement ratio, \(\Upsilon \)

$$\begin{aligned} \delta _D\left( \Upsilon \right) =\phi \left( \Upsilon \right) -\phi _\infty \end{aligned}$$
(21)
$$\begin{aligned} \ \phi (\Upsilon )=\phi _\infty +a_1\Upsilon +a_2\Upsilon ^2+\cdots , \end{aligned}$$
(22)

where \(\phi \left( \Upsilon \right) \) is a solution, \(\phi _\infty \) is the grid-independent solution, and \(a_i\) are the solution coefficients. For a second-order approximation, a minimum of three solutions (on three consecutively refined grids) are required to determine the solution \(\phi _\infty \) and the coefficients \(a_1\), \(\ a_2\). For a three-dimensional problem comprising coordinates x, y, and z, the non-dimensional scalar grid refinement ratio, \(\Upsilon \), is then determined as follows:

$$\begin{aligned} \Upsilon _i=\sqrt{\frac{1}{4}\left[ \left( \frac{\Delta t_i}{\Delta t_1}\right) ^2+\left( \frac{\Delta x_i}{ \Delta x_1}\right) ^2+\left( \frac{\Delta y_i}{\Delta y_1}\right) ^2+\left( \frac{\Delta z_i}{\Delta z_1}\right) ^2\right] }. \end{aligned}$$
(23)

Here, \(\Upsilon _\infty =0\) corresponds to a grid representing infinitely small grid spacing in all directions, which represents the grid-independent solution. We performed the sensitivity study for the regular wave of Case II only, because this case represented a relatively steeper wave. A refinement factor of \(c=\root 3 \of {2}\) was uniformly specified for all spatial directions. Ratios specifying the number of cells for the coarse grid (\(\mathrm {G_1}\)), the medium grid (\(\mathrm {G_2}\)), and the fine grid (\(\mathrm {G_3}\)) were well matched with this factor. Table 2 summarizes the grid spacings, the number of cells-per-wave-height (c.p.w.h.), and the total number of cells for each grid.

Table 2 Properties of grids \(\mathrm {G_1}\), \(\mathrm {G_2}\), and \(\mathrm {G_3}\)
Full size table
Fig. 8
figure 8

Wave elevations (left) and associated wave peaks (right) for the four different CFL numbers obtained on grid \(\mathrm {G_2}\)

Full size image
Fig. 9
figure 9

Wave elevations (left) and associated wave peaks (right) for the three different grids obtained on CFL number of 0.8

Full size image

We first investigated the effect of the CFL number on wave propagation, although this number was no longer critical to measure simulation stability, because the viscous-flow solver relies on implicit discretization schemes. Our simulations, performed with four different time-steps on grid \(\mathrm {G_2}\), resulted in the four different CFL numbers of \(\mathrm {CFL}_1 = 3.2\), \(\mathrm {CFL}_2 = 1.6\), \(\mathrm {CFL}_3 = 0.8\), and \(\mathrm {CFL}_4 = 0.4\). The left graph in Fig. 8 plots the associated normalized wave elevations over one wave period, where \(\eta \) is wave elevation, \(\zeta \) is wave amplitude, and t is time. The right graph in Fig. 8 plots the associated wave elevation peaks for the four different CFL numbers. As seen, even for \(\mathrm {CFL}= 1.6\), the deviation was small, demonstrating that decreasing the CFL number from 0.8 to 0.4 caused only a negligible amount of simulation inaccuracy, while substantially increasing the computational effort. Consequently, we performed the rest of simulations for a CFL number of 0.8.

To assess the sensitivity of the grid, we conducted simulations on three different grids, all for the selected CFL number of 0.8. Figure 9 plots the associated results. The left graph in Fig. 9 shows that significant differences of wave elevation peaks were obtained on the three grids \(\mathrm {G_1}\), \(\mathrm {G_2}\), and \(\mathrm {G_3}\). The right graph in Fig. 9 plots the associated normalized wave peaks obtained on the three grids, and we see that these peaks increased with grid fineness. Table 3 lists the resulting peaks, their time instances of occurrence, and their errors expressed as percentage deviations from the grid-independent solution, \(\phi _\infty \). The associated errors of peak heights and occurrence times from the coarse grid \(\mathrm {G_1}\) were higher than those from the medium grid \(\mathrm {G_2}\) and the fine grid \(\mathrm {G_3}\). The small discretization errors of 0.91% for wave peaks and 0.22% for occurrence times obtained on the medium grid were almost indistinguishable from those obtained on the fine grid. This demonstrated that the medium grid \(\mathrm {G_2}\) was fine enough to obtain reliable predictions.

Table 3 Normalized wave peaks, their times of occurrence, and their deviations from the grid-independent solution obtained on grids \(\mathrm {G_1}\), \(\mathrm {G_2}\), and \(\mathrm {G_3}\)
Full size table

5 Results and discussion

The wave-induced loads were numerically studied for the two wave conditions specified in Table 1. The experimentally measured wave elevations from wave probe 1 were used for comparison. No breaking waves occurred during the considered wave tests. Primarily, the numerical results are compared with experimental measurements in terms of wave elevations and associated wave-induced loads. Then, the differences between adopted four numerical schemes are addressed, including the rotational, viscous, and turbulent flow effects. In addition, the effects of wave steepness, higher harmonic forces/moments, and secondary load cycles are discussed.

5.1 Comparison with the experiment

Figure 10 shows the time-series of normalized wave elevation, \(\eta / \zeta \), extending over three wave periods. The solid line identifies results from the potential solver; symbol \(+\), results from the Euler scheme; symbol \(\circ \), results from the laminar scheme; symbol \(\times \), results from the RANS scheme; and symbol \(\square \), results from experimental measurements. This identification of results holds also for the other graphs. Some level of nonlinearity was noticed for the considered wave conditions, which is evident in the wave elevations with narrower, increased peaks and flatter, shallower troughs.

Fig. 10
figure 10

Time-series of distributed wave elevation around the monopile (wave probe 1)

Full size image

In general, all simulations of wave crests were nearly the same, and they were all in good agreement with the experimental measurements. Particularly, the computed wave elevations by solving Navier–Stokes or Euler equations agreed more favorably with the experimental measurements. The differences of the wave troughs were due to structure diffracted and higher order wave contents, which obviously could not be captured by the potential-flow solver. Increasing the wave steepness from wave I to wave II skewed the wave’s geometrical shapes. As a results, the increasing parts of the wave crests were steeper than the decreasing parts, whereas wave II indicated the opposite phenomenon.

Fig. 11
figure 11

Time-series of horizontal wave-induced forces for the considered regular waves

Full size image

Differences in wave shapes were associated with wave kinematics, which directly influenced the wave-induced loads. Figure 11 presents time-series of the normalized horizontal wave force, \({F_x}/{\rho gh \mathrm{{d}} \zeta }\), extending over three wave periods, where \(\rho \) is the water density; h, water depth; g, acceleration of gravity; d, monopile diameter at the free surface. Although all the simulated wave crests were almost identical to each other, the corresponding wave forces differed by small amounts. Aside from the differences in wave kinematics, the force calculation method also played a role. The potential-flow method computed the diffraction force, and the second-order wave loads were included based on the full set of QTFs. The viscous-flow solver obtained the horizontal wave forces directly by integrating the pressure field surrounding the monopile. The experimental measurement relied on force transducers to determine the wave-induced horizontal force. These differences caused discrepancies of wave force time-series shapes and the corresponding maximum and minimum values. As seen, the shape of the force cycles are asymmetric about a vertical nor a horizontal axis, and the decreasing parts of the forces crests were steeper than the increasing parts, resulting in skewed shapes. The most discrepancy occurred at the skewed crests for wave I, which might be assignable to the discrepancies of wave shapes during wave generation and propagation. It is worth mentioning that although the instantaneous incident wave surface was considered in the potential-flow approach, complex free-surface typologies interacting with the monopile, such as wave run-up, can only be considered by solving the Navier–Stokes or Euler equations. Overall, the nonlinearity in wave-induced force was not as pronounced as wave elevation. The nonlinear effects of scattered waves exhibited in the local wave elevations were integrated out when obtaining the associated forces. To demonstrate the force distributions along the monopile, Fig. 12 shows the corresponding bending moments at mudline. The mudline moments show the similar tendency as the wave-induced forces, but with stronger nonlinearities.

Fig. 12
figure 12

Time-series of wave-induced bending moments at the mudline for considered regular waves

Full size image
Fig. 13
figure 13

Harmonic components of wave-induced forces as function of time for an increasing number of harmonics over three wave periods

Full size image
Fig. 14
figure 14

Harmonic components of wave-induced moments at mudline as function of time for an increasing number of harmonics over three wave periods

Full size image

5.2 Higher order loads

To examine the capabilities of adopted different numerical approaches for predicting higher harmonic components of wave loads, the wave-induced forces and moments were split into results of integer multiples of the fundamental power frequency by taking the Fast Fourier Transform (Paulsen et al. 2014). We related the nth harmonic force components to the component of the force oscillating with the fundamental frequency instead of the wave elevations, since the force transducers were very accurate compared to the wave gauges. Figures 13 and  14 plot the harmonic components of the horizontal wave loading and the corresponding moments at mudline for regular wave I and regular wave II, respectively. The phase of the harmonic forces and moments were obtained relative to the phase of the incoming waves. It is worth mentioning that the adopted potential-flow solver is a second-order model, and only the first two harmonic components of forces and moments are presented. Different from the results of the potential-flow solver, excepting the first- and second-harmonics, there were also higher harmonic forces and moments in the results obtained from the viscous-flow solver and from the measurements, adding to the total loads. In the present study, we analyzed the first seven harmonic components of the calculated and measured horizontal forces and the corresponding bending moments.

We see that the total forces and moments are mainly contributed by their first harmonics. The numerical predictions of the first-harmonic force and moment compared to the associated experimental measurements with good agreements. However, the phases of the first-harmonic force were not well predicted by the computations for wave condition II. The higher harmonic forces and moments are significantly smaller than the first-harmonic force and moment for all considered wave conditions, where the second-, third-, and fourth-harmonic forces and moments become of comparable size. These findings are in agreement with the conclusions reported by Huseby and Grue (2000). When it comes to the fifth-, sixth-, and seventh-harmonic components, the experimentally measured forces are significantly smaller than the numerical predictions for wave I. While good agreements between measured and calculated the fifth-, sixth-, and seventh-harmonic forces are achieved for wave II. Due to the limitation of the adopted potential-flow solver, the comparison between the potential-flow solver and the viscous-flow solver are performed only for the first two harmonics. The results indicate that the selection of different flow regimes plays a part in accurately predicting the higher harmonic forces and moments, which is addressed in detail in Sect. 5.3. Apart from the assumption of different calculation schemes, the wave-induced force and moment on an offshore monopile depend also upon the wave steepness, which is covered in Sect. 5.4.

5.3 Calculation schemes

To clarify the influence of different calculation schemes, deviations of the numerical predicted forces and moments from the experimental measurements are listed in Table 4. We see that all schemes of the viscous-flow solvers were slightly better able to represent the measured load cycle than the potential-flow solver. Nevertheless, all the simulated forces reflected reasonably good agreements with experimental measurements for both considered wave conditions. Specifically, the reasonable prediction from the potential scheme indicated that the resultant force on a monopile was dominated by its inertia force. The associated viscous-flow effects could be ignorable for the considered wave conditions, which was also confirmed by the good agreements between the predictions from Euler scheme and experimental measurements. With regard to the bending moments, the similar circumstance was observed but with larger discrepancy errors to the experimental measurement. This is expected as the moment is known to be more nonlinear than the horizontal wave force (Feng et al. 2020). Also, the bending moment at mudline is challenging to be measured experimentally with good accuracy.

Table 4 Estimated solution discrepancies of wave-induced forces and moments from different calculation schemes, given in percentage of experimental measurements
Full size table
Fig. 15
figure 15

Time-series of the pressure forces and viscous forces for the considered steep waves. \(F_{px}\) denotes the pressure components; \(F_{vx}\), the viscous components. One finds that the viscous components are less than 0.5% of the pressure components

Full size image

The contribution of the viscous force was determined by comparing the results from Euler scheme to the results from Laminar and RANS schemes. From Table 4, we see that the predictions from Euler scheme were somewhat smaller than those obtained from Laminar and RANS schemes. To better demonstrate this, the pressure and viscous-force components were plotted separately in Fig. 15. We see that the contribution of viscous-force components was generally less than 0.5% of the pressure-force components. The pressure forces obtained from Euler, Laminar, and RANS schemes were almost identical to each other. The corresponding moments at mudline are plotted in Fig. 16. The results reveal that although the viscous moments are still very small compared to the pressure moments, their contributions to the total moments increase somehow compared to the contributions of viscous forces. The similar results obtained from Laminar and RANS calculations revealed that the adopted turbulence model has very limited effects, although the viscous force increased slightly due to the use of turbulence model. Comparing the results from the potential scheme to those from solving Navier–Stokes or Euler equations, we concluded that the effects of strong nonlinear motion of free surface (e.g., scattered waves and wave run-up) on the wave-induced horizontal forces were secondary. The contribution from the vortices around the monopile to the total impact force was not significant.

Fig. 16
figure 16

Time-series of the pressure moments and viscous moments for the considered waves. \(M_{px}\) denotes the pressure components; \(M_{vx}\), the viscous components. One finds that the viscous components are less than 0.5% of the pressure components

Full size image
Fig. 17
figure 17

Distributions of hydrodynamic pressures surrounding the monopile obtained from the laminar computation (left) and the turbulent calculation (right)

Full size image
Fig. 18
figure 18

Distributions of free-surface velocities surrounding the monopile obtained from the laminar computation (left) and the turbulent calculation (right)

Full size image

To better demonstrate the effects of turbulence model, Figs. 17 and 18 portray, respectively, the distributions of hydrodynamic pressures and free-surface velocities around the monopile in the regular wave II at time of \(t/T = 0.63\), i.e., when peak wave loads occurred. In these figures, the left graphs were obtained from computations based on the laminar scheme; the right graphs, from computations based on the turbulent scheme. Although these visualizations differed somewhat, pressures and velocities pointing in the direction of wave propagation were similar. In respect of the diffracted waves, the horizontal velocity field depicted in Fig. 18 shows that a relatively thicker boundary layer adjacent to the surface of monopile was acquired in the RANS calculation. The boundary-layer separation occurred earlier in the wake of RANS calculation. Although flow separation influenced the viscous-pressure loads, its effect was not noticeable for the considered cases. As shown in Figs. 15 and 16, the viscous components did not have important contributions to the total forces and moments on the monopile. In principle, the adopted k-\(\omega ~SST\) model usually overpredicts the turbulent viscosity on the air–water interface, arising excessive wave damping compared to laminar scheme. Consequently, a relatively finer grid or smaller time-step is required to obtain an identical wave height to the laminar calculation.

5.4 Wave steepness

To study the effects of wave steepness on wave-induced loads, Fig. 19 plots the computed mean peak values of total forces, together with their harmonic components over wave steepness \(k\zeta \). The wave height was kept unchanged for the consider waves, and the wave steepness altered due to the adjustment of wave periods. In general, the wave-induced total forces obtained from all numerical calculations increase with the increasing of wave steepness, which were consistent with the experimental measurement. With regard to the effects of wave steepness on the first-harmonic forces, we see that \(F_x^{(1)}\) obtained from the viscous-flow solver increased as \(k\zeta \) increase, which followed the same tendency of \(F_x^{total}\). However, an opposite tendency was observed for \(F_x^{(1)}\) obtained from the potential-flow solver and measurement. Generally, the first-harmonic components dominantly contributed to the total wave forces, which were around 75%.

Fig. 19
figure 19

Mean peak values of wave-induced horizontal force \(F_x^{total}\) over wave steepness, together with their harmonic components \(F_x^{(i)}\)

Full size image

In view of the higher harmonic components, we observe that they had much smaller magnitudes than the first-harmonic wave excitation forces. The amplitudes of the higher harmonic components \(F_x^{(2-7)}\) obtained from the viscous-flow solver decreased as the wave steepness increases. As the wave becomes steeper, stronger nonlinearities were introduced, whereas steeper and narrower wave crests led to the smaller inertial force relating to diffraction effect. On the other hand, the turbulence grew with the increase of wave steepness, giving rise to larger energy dissipation and viscous-pressure components, which also could be accountable for the mentioned reduction. These findings may vary as wave condition or the diameter of the monopile changes, since they are dependent on the wave steepness and its Keulegan–Carpenter number. Similar tendencies were also reported in the experimental work of Huseby and Grue (2000), and the numerical and experimental work of Stansberg and Kristiansen (2005). However, large discrepancies between calculations and measurements were found in terms of \(F_x^{(3)}\) and \(F_x^{(7)}\), where measured force components increased with the increase of \(k\zeta \).

Fig. 20
figure 20

Mean peak values of wave-induced bending moment at mudline \(M_y^{total}\) over wave steepness, together with their harmonic components \(M_y^{(i)}\)

Full size image

Correspondingly, the harmonic analysis of wave-induced moments at mudline is shown in Fig. 20. Compared to the force components, a very similar inclination was noticed for the moment components. Overall, the comparisons between numerical and measured total forces and moments show good agreements, respectively. Comparing the estimated harmonic components (\(F_x^{(1-7)}\) and \(M_y^{(1-7)}\)) with the corresponding measurements, with a few exceptions, fair agreements are obtained. Apart from the experimental errors in the measured force and moment, the typical error in the measured wave elevation introduced an additional error in the present non-dimensional analysis.

5.5 Secondary load cycle

Aside from the total and higher order forces, we took a closer look at the wave-induced forces to assess the secondary load cycle effects, albeit exemplarily only for the steeper wave train of case II. The secondary load cycle appears as a rapid and high-frequency variation in the excitation force. An exemplary time series of a secondary load cycle in regular wave II is plotted in Fig. 21, showing that such effects occurred when a wave crest passed the monopile.

Fig. 21
figure 21

Exemplary time-series of a secondary load cycle in regular wave II

Full size image

Figure 22 depicts four successive screenshots of free-surface elevation around the monopile, obtained at times t = \(t_1\), \(t_2\), \(t_3\), and \(t_4\), as illustrated in Fig. 21. This secondary load cycle started when the incident wave crest reached the front of the monopile and produced wave run-up, see figure of \(t=t_1\). The stagnation pressure caused a sheet of water to be accelerated upward. In particularly, there exists a remarkable accumulation of fluid mass upstream from the monopile, which was mainly irrotational. As the wave crest passed the monopile, its blockage created a cavity on its downstream side. This cavity was soon filled by the diffracted wave that propagated around the monopile, see figure of \(t=t_2\). When the front of the diffracted wave reached the downstream side of the monopile, the associated local pressure started to raise the water level, see figure of \(t=t_3\). At the end of this secondary load cycle, the incident wave crest passed the monopile and a steep local wave began to propagate upstream against the direction of wave propagation, see figure of \(t=t_4\). This flow was a consequence of the large wave run-up at the downstream side, which generated an force in the opposite direction, reducing the horizontal force. The viscous solvers captured this phenomenon, which was confirmed by the experimental measurements, as shown in Fig. 21.

Fig. 22
figure 22

Successive screenshots of free-surface elevation around the monopile in regular wave II at four different time instants

Full size image

Compared to the main impact peak force, the secondary load cycle was smaller in magnitude. However, it may cause the higher order excitations, which is associated with the occurrence of the ringing event (Grue and Huseby 2002). For considered wave conditions, the event of second load cycle was not evident, as pronounced secondary load cycles are dependent on the Froude number. Generally, in respect of the secondary load cycle, only the results from the viscous-flow solver correlated favorably with the experimental measurement.

6 Concluding remarks

To assess the capabilities of a viscous-flow solver and a potential-flow solver for predicting the wave-induced forces, we considered an offshore monopile in two regular wave trains by a systematic comparison of model test data to numerical simulations. Solving the Navier–Stokes or Euler equations, the viscous-flow method used three different solution schemes, here identified as the Euler, the Laminar, and the RANS approach. The Euler approach neglected viscosity, the Laminar approach directly solved the Navier–Stokes without accounting the fluctuating portion of the velocity field, and the RANS approach used a turbulence model that approximates turbulent flow. Two steep regular waves with the same wave height but different wave periods were considered, with reference to the associated wave elevations and wave-induced forces and moments. In particular, the effects of adopted calculation schemes, higher harmonic forces/moments, wave steepness, and the secondary load cycles were reviewed.

As our numerical predictions were sensitive to temporal and spatial discretizations, we quantified the numerical uncertainties of viscous-flow simulations. The temporal deviations of wave elevation peaks obtained for four different CFL numbers were small and, consequently, performing simulations for a CFL number of 0.8 sufficed. The spatial deviations obtained on three different grids revealed that the medium grid was fine enough to obtain nearly grid-independent predictions. The deviations of numerical predictions were given in percentage of the obtained grid-independent solutions.

In general, the main characteristics of wave-induced forces and moments were well predicted by both the potential- and the viscous-flow solvers. The relative difference between the numerically calculated and experimentally measured peak value of the horizontal wave force is about 2% for the two considered steep wave conditions. In terms of the discrepancy error in mudline moments, more than 10% is found for the two considered steep wave conditions. On one hand, the wave-induced moment is more nonlinear than the horizontal wave force in steep waves. On the other hand, the bending moment at mudline is hard to be accurately measured. Due to the limitations of the adopted potential-flow solver, higher harmonic forces included only the second-order load. The predictions from the viscous-flow solver compared more favorably to the experimental measurements, including the local free-surface elevations, higher harmonic forces and moments, and the secondary wave load cycles.

Inspecting the results from different calculation schemes, we observed that the contribution from the vortices around the monopile to the total impact force was not significant, which was revealed by the similar results obtained from the potential-flow solver and from the Euler scheme. Overall, the incident flow, being largely irrotational, dominated the wave-induced total force. However, the vortices attributed to the prediction of the secondary load cycle, as the violent motion of the free surface may introduce strongly nonlinear effects which were significant for the higher order loads. The good agreement between the values obtained from the Euler and the Navier–Stokes equations without and with a turbulence model (i.e., Laminar and RANS) indicated that the total wave-induced load was inertia dominated, and the contribution of viscous and turbulent effects was very limited. Nevertheless, the vicious and turbulent effects contributed to the wave scattering and higher order forces.

With regard to the effects of wave steepness, we found that the wave-induced total loads increased with the increase of wave steepness, which were well predicted by all the adopted numerical schemes. The first-harmonic load was rather well predicted by the potential-flow solver or alternatively the viscous-flow solver, and it was the supreme contribution to the total wave-induced load, around 75%. The effect of wave steepness on the wave-induced total force and moment was well predicted by all the adopted numerical schemes. That is, their values increased with the increase of the wave steepness. Nevertheless, the amplitude of the higher harmonic force components decreased with the increase of the wave steepness, which was well predicted via the adopted viscous-flow solver with a few exceptions. A closer look at the wave-induced loads revealed that only the viscous solver captured secondary load cycle, which were confirmed by the experimental measurements.

In terms of the computational efficiency, the time consumption of potential-flow solver is ignorable compared to the viscous-flow solver, which demanded 120 cores at the supercomputer magnitUDE about 12 h. Changing the computational scheme from Euler to Laminar or RANS increased the computational effort a little bit, but their differences are barely a few minutes. In principle, RANS calculation overpredicts the turbulent viscosity on the air–water interface, arising excessive wave damping compared to the laminar scheme. Consequently, a relatively finer grid or smaller time-step is required to obtain an identical wave height to the laminar calculation. For predicting the wave-induced loads in non-breaking steep waves, we recommend to use a viscous-flow solver without any turbulence models. The present study demonstrates the different capabilities of the adopted tools and how modeling choices affect the accuracy of their calculated hydrodynamic loads. For our next study, the hydroelastic performance of the offshore monopile in steep waves will be numerically simulated using the viscous-flow solver coupled with a structural solver.