Abstract
For tidal-stream energy to become a competitive renewable energy source, clustering multiple turbines into arrays is paramount. Array optimisation is thus critical for achieving maximum power performance and reducing cost of energy. However, ascertaining an optimal array layout is a complex problem, subject to specific site hydrodynamics and multiple inter-disciplinary constraints. In this work, we present a novel optimisation approach that combines an analytical-based wake model, FLORIS, with an ocean model, Thetis. The approach is demonstrated through applications of increasing complexity. By utilising the method of analytical wake superposition, the addition or alteration of turbine position does not require re-calculation of the entire flow field, thus allowing the use of simple heuristic techniques to perform optimisation at a fraction of the computational cost of more sophisticated methods. Using a custom condition-based placement algorithm, this methodology is applied to the Pentland Firth for arrays with turbines of \(3.05\,\hbox {m}/\hbox {s}\) rated speed, demonstrating practical implications whilst considering the temporal variability of the tide. For a 24-turbine array case, micro-siting using this technique delivered an array 15.8% more productive on average than a staggered layout, despite flow speeds regularly exceeding the rated value. Performance was evaluated through assessment of the optimised layout within the ocean model that treats turbines through a discrete turbine representation. Used iteratively, this methodology could deliver improved array configurations in a manner that accounts for local hydrodynamic effects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The levelised cost of energy (LCOE), defined as the average net present cost of electricity generation for a power plant over its lifetime, is often cited as a key metric for the competitiveness of an energy technology. Unless there is a rapid increase in installations, the LCOE for tidal-stream is set to remain at more than £150/MWh by 2025 (Smart and Noonan 2018; Topper et al. 2021), whilst the LCOE for solar and both onshore and offshore wind will fall to approximately £25–£32/MWh (U.S. Energy Information Administation 2020). Reducing LCOE is paramount if tidal-stream energy is to become a competitive, sustainable energy source (Coles et al. 2021). This could be achieved through several measures (Coles and Walsh 2019; Goss et al. 2020, 2021a, b): (i) physical infrastructure improvements, which could involve optimisation of the turbine design and operation, (ii) economies of scale in turbine design, (iii) economies of volume in manufacturing, operation and maintenance, (iv) technology innovation, (v) learning, and (vi) financing mechanisms. Turbines have now reached technology readiness levels of 7–8 (Chozas 2015; SIMEC Atlantis Energy 2020a) and need to be tested in large arrays for extended periods of time to reach full maturity and facilitate implementation of the aforementioned cost reduction mechanisms. In supporting this, strategies should be investigated and developed for the reliable assessment of the tidal resource (Neill et al. 2014, 2018; Robins et al. 2015; Mackie et al. 2021) to reduce investment uncertainty, as well as array design optimisation to maximise performance. Array optimisation has already shown potential to increase array power by up to 33% relative to a regular aligned layout, albeit with power capping removed (Funke et al. 2014). Hence, developing more robust, yet practical optimisation methods could be a key step to achieving further LCOE reductions (Coles et al. 2021).
Array power can be associated with up to eight controlling array effects, as outlined in Vennell et al. (2015). These include the reduction of free-stream velocity by the introduction of turbines and the relative size of the array in the channel. This leads to conflicting design performance interactions among turbines, particularly for large arrays that dominate channel dynamics. For example, minimising environmental impacts such as sediment transport may restrict array placement (Fairley et al. 2015; du Feu et al. 2019). Likewise, maintaining navigation routes through clearance constraints prevents exploitation of channel blockage, a beneficial phenomenon for larger arrays. As such, array optimisation is often posed as a multi-objective problem, adding additional complexity (Nash et al. 2014; Culley et al. 2016; du Feu et al. 2017, 2019; González-Gorbeña et al. 2018; Phoenix and Nash 2019).
Establishing the optimal array layout becomes computationally intensive when interlinked with the hydrodynamics as it presents a partial differential equation (PDE) constrained optimisation problem. Early work involved simplified hydrodynamic models, since ‘in-concert’ tuning of tidal turbines in an array would necessitate multiple runs which would require appreciable time in more detailed models (Vennell 2011, 2012). Investigations of channel-scale optimisation by large numbers of 2-D simulations for different array layouts and turbine tunings have been carried out, but are notably time and memory intensive (Divett et al. 2016). An alternative has been proposed using gradient-based optimisation that makes use of adjoint methods to efficiently calculate the objective function gradient, leading to immense reductions in the number of evaluations required (Funke et al. 2014, 2016). This enables optimisation with a capacity to account for impacts to the hydrodynamics, at a lower computational cost than techniques that estimate the gradient. The same approach has been adopted for wind farms to capture non-linear turbulent flow physics, as the adjoint method allows inclusion of higher fidelity 3-D computational fluid dynamics (CFD) (King et al. 2017). Nevertheless, adjoint optimisation remains fairly intensive as demonstrated by examples in the literature, which are largely constrained to idealised and semi-idealised cases (Funke et al. 2014; Barnett et al. 2014). Similarly, the integration of 3-D modelling with optimisation algorithms beyond idealised cases (as in King et al. (2017)) is scarce. Recent work on discrete turbine array optimisation has relied on 2-D coastal hydrodynamics models (Piggott et al. 2021), employing simplified turbine parameterisations whilst being constrained by either the attainable model structure or resolution, as in Phoenix and Nash (2019).
To circumvent intense computational effort, inspiration can be taken from wind energy research, where surrogate models are used to simplify the governing physics. These models may ignore important hydrodynamic effects such as blockage that can augment power production for tidal energy (Nishino and Willden 2012; Chen et al. 2019). For example, a “duct effect” may be exploited by placing turbines in a staggered arrangement, funnelling and accelerating the flow onto downstream turbines, as shown in Funke et al. (2014). Aside from certain examples restricted in idealised domains (Stansby and Stallard 2016), semi-analytical methods based on turbine wake superposition principles are often constrained to a structured turbine placement (Lo Brutto et al. 2016). Nevertheless, wake superposition methods have led to reasonable agreement against laboratory measurements for model tidal turbines and rapid optimisation within idealised low-blockage cases has predicted significant increases in array efficiency (Stansby and Stallard 2016).
In setting out this study, we outline our overarching goal: an array optimisation strategy that is computationally efficient and extensible to the multi-objective optimisation settings sought thereafter. Additionally, it must be reliable, accurate, and acknowledging important hydrodynamic factors and turbine characteristics that affect the optimal array design and performance. This paper aims to demonstrate a novel optimisation approach, retrofitting an analytical wake model designed for wind array optimisation (FLORIS from the US National Renewable Energy Laboratory) for use in conjunction with a coastal ocean model (Thetis). We provide details on an optimisation approach which includes the option of a custom greedy algorithm for micro-siting purposes. This is applied to a suite of representative idealised cases, progressing to a practical study of the Inner Sound of the Pentland Firth, UK.
2 Methodology
We combine a depth-averaged hydrodynamic model, ThetisFootnote 1, with an analytical wake model, FLORIS (FLOw Redirection and Induction in Steady-stateFootnote 2). FLORIS is used to perform array optimisation by importing ambient flow fields from Thetis, returning an optimised set of turbine coordinates. Sequentially, Thetis evaluates initial and optimised layouts, by representing the presence of turbines parameterised through momentum sink terms, quantifying impacts on flow field and overall array power. Both models rely on actuator disc theory to represent the tidal turbine rotor. However, differences between the two models necessitate the introduction of an intermediate calibration step. A schematic of the combined approach is shown in Fig. 1.
2.1 Shallow-water equation modelling with Thetis
Thetis is a 2-D/3-D model for coastal and estuarine flows based on the general-purpose finite-element partial differential equation (PDE) solver Firedrake (Rathgeber et al. 2016; Kärnä et al. 2018). It has been used for several studies on the feasibility and optimisation of tidal energy (Angeloudis et al. 2018; Baker et al. 2020; Zhang et al. 2022; Harcourt et al. 2019). We solve the non-conservative form of the non-linear shallow-water equations in 2-D
where \(\eta \) is the water elevation, \(H_d\) is the total water depth, \(\mathbf {u}\) is the depth-averaged velocity vector, and \(\nu \) is the kinematic viscosity of the fluid. The term \(f\mathbf {u}^{\perp }\) represents the Coriolis “force” included in non-idealised cases. In this term, \(\mathbf {u}^{\perp }\) is the velocity vector rotated counter-clockwise over \(90^\circ \), so that \(\mathbf {u}^\perp =(-v,u)\), where u, v are, respectively, the longitudinal and transverse components of \(\mathbf {u}\). In turn, \(f = 2 \Omega \text {sin}(\zeta )\) with \(\Omega \) the angular frequency of the Earth’s rotation and \(\zeta \) the latitude. In idealised cases, bed shear-stress (\(\varvec{\tau _b}\)) effects are represented through a quadratic drag formulation
For realistic cases the Manning’s \(n_M\) formulation is adopted, given as
and applied as in Mackie et al. (2021). When applicable, inter-tidal processes are treated using the wetting and drying formulation of Karna et al. (2011). The shallow-water equations are discretised using the discontinuous Galerkin finite-element method (DG-FEM) and the semi-implicit Crank–Nicolson scheme is selected for time-marching the solution. The resulting discrete system of equations is solved iteratively by Newton’s method as implemented in PETSc (Balay et al. 2016). Finally, \(c_\mathrm{t}\) is the parameterisation added to represent the turbines’ thrust as follows.
2.2 Discrete turbine representation in Thetis
Turbine rotors are represented in Thetis as areas of increased bed friction, adopting the linear momentum actuator disc theory (Kramer and Piggott 2016). In the 2-D depth-averaged form of the shallow-water equations, the force as a result of an array of turbines is
where \(c_\mathrm{t}(\mathbf {x})\) is a thrust coefficient function given as
where \(A_t\) is the turbine swept area, \(C_\mathrm{t}\) is the thrust coefficient as a function of the velocity \(\mathbf {u}(\mathbf {x})\), and \(d(\mathbf {x})\) is the local turbine density. The turbine density \(d(\mathbf {x})\) is constructed using a vector \(\mathbf {m}\) comprising the turbine coordinates of the array. This discrete turbine representation adopts the exponential bump function of Funke et al. (2014), which in 1-D takes the form
where r is the radius of the bump, set by default to D/2, where D is the diameter of the turbine. Equation (7) is employed in defining the turbine density \(d_i\) for a turbine i at a position \(m_i = (x_i,y_i)\) as the normalised product of 1-D bump functions
where \(\Xi = \int _{-1}^{1} \int _{-1}^{1} e^{\big (\frac{-1}{1-x^2}-\frac{1}{1-y^2}+2 \big )} \,\text {d}x \,\text {d}y \ \approx 1.45661\) is the integral of the bump function when \(r=1\). The aggregate of the individual turbine densities \(d_i\) provides the overall \(d(\mathbf {x})\) function
where N is the number of turbines deployed.
Following the notation in (5), the power extracted at any given moment by the array can be approximated as:
where \(c_\mathrm{p}(\mathbf {x})\) is a power coefficient function given as
where \(C_\mathrm{p}\) is a power coefficient which is related to the thrust coefficient through the formulation (Martin-Short et al. 2015b)
In Eqs. (5) and (10), it is assumed that the ambient velocity is the same as the velocity through the turbine, \(\mathbf {u}(\mathbf {x})\) (i.e., the velocity once the turbine is operating). This is a reasonable approximation for relatively coarse meshes with distributed rather than discrete turbine density fields (Schwedes et al. 2017). However, for micro-siting arrays where the thrust force is concentrated at the turbine location, this assumption becomes invalid. In addressing this, we adopt a correction relating free-stream and through-turbine velocities as derived in more detail by Kramer and Piggott (2016). In summary, denoting as \(U_{\infty }\) the magnitude of the approaching streamwise velocity the turbine experiences, it can be established using the continuity, momentum and Bernoulli’s principles that
where \(\hat{A_t} = H_d D\) is the numerical cross-section of the turbine. Equation (13) stems from the classical 1-D actuator disc theory, with the correction returning an approximation of the ambient velocity as per the relationship between \(U_\infty \) and \(\mathbf {u}\). It is noted that this process assumes that local blockage and shear effects are negligible (Garrett and Cummins 2007). The corrected velocity \(U_{\infty }\) from (13) is applied to correct the thrust (\(c_\mathrm{t}\)) and power (\(c_\mathrm{p}\)) coefficient values, compensating for the velocity drop by the introduction of the turbine momentum sink over the deployed area of the turbine.
2.3 Analytical wake modelling using FLORIS
FLORIS contains analytical models to predict the mean wake velocities and power output of turbine arrays (NREL 2020). In the present study, we apply FLORIS’s Gaussian model (Bastankhah and Porté-Agel 2014) which computes the normalised velocity deficit via the expression
where z is the wall-normal coordinate with \(z_h\) the turbine hub height, \(k^*\) is the growth rate of the wake (\(\partial \sigma / \partial x\)), and \(\epsilon \) is the normalised Gaussian velocity deficit at the rotor plane. For our calculations, the local wake growth rate \(k^*\) is estimated using the local streamwise turbulence intensity, \(\mathcal {I}\) (Niayifar and Porté-Agel 2016). We should note here that the Gaussian velocity model has been selected instead of the more traditionally used Jensen model (Jensen 1983) which is of similar computational cost, but is known to overestimate the velocity deficit in the outskirts of the wake (Chamorro and Porté-Agel 2009; Dufresne and Wosnik 2013). This is due to the Jensen model’s approach of setting a uniform velocity deficit across the wake width. In turn, turbine power output is calculated using a power thrust–velocity relationship specified for each individual turbine. This requires a combination model to account for the contributing wake velocity deficit from upstream and other neighbouring turbines. We use the free-stream linear superposition (FLS) method to account for the cumulative wake effects within the tidal array. Accordingly, the velocity deficit, \(\overline{\Delta \mathbf {u}}\left( x ,y\right) \), at a downstream location (x, y) is calculated as
where \(\overline{\Delta \mathbf {u}}_i |_{\left( x, y\right) }\) is the contribution of the wake of each turbine i at the downstream location (x, y) (Machefaux et al. 2015). Alternative superposition methods include summing the square of the velocity deficits (Katic et al. 1987) as well as the more recent work by Lanzilao and Meyers (2021) which takes into account the heterogeneity of the background velocity field.
2.4 Optimisation approach
We seek to maximise energy from our tidal-array system. In doing so, the existing layout optimisation procedure in FLORIS (Fleming et al. 2016) is repurposed to maximise the average power computed using several input flow fields, rather than the average annual energy production from a single wind rose. The latter is typical of wind farm optimisation and would not apply to tidal-array optimisation. To this end, we approach the tidal-array micro-siting problem by employing an initial Thetis simulation of the tidal channel and extract ambient velocity fields for a number of instances, or ‘frames’, over a tidal cycle. These ambient flow field data are then imported into FLORIS. If necessary, an initial (e.g., aligned/staggered) turbine layout is introduced to FLORIS and micro-siting is performed using an appropriate optimisation strategy subject to spatial constraints, and minimum turbine separation restrictions. As such, the objective function can be expressed as

where \(N_F\) is the number of flow field frames considered and \(\mathbf {m},\varvec{\tau }_i\) are vectors including turbine coordinates and optimisation constraints (e.g., minimum distance between turbines, array deployment area limits) respectively. \(\varvec{\tau }_l\), \(\varvec{\tau }_u\) correspond to the lower and upper limits for each of these constraints.
Upon optimisation in FLORIS, a derived turbine layout \(\mathbf {m}\) is evaluated in Thetis to assess its performance. A similar approach to optimisation has previously been undertaken to determine wind plant control strategy, with the objective of optimising yaw settings to minimise wake interaction and increase overall farm power (Gebraad et al. 2014). In a deviation from the study of Gebraad et al. (2014) which pioneered the blending of a CFD flow solver with FLORIS, we present herein a first attempt to combine FLORIS with a shallow-water solver for tidal applications.
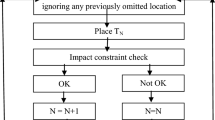
As we aim to demonstrate a proof-of-concept for the optimisation approach, investigations on specific optimisation algorithms are beyond the scope of this work. FLORIS’s default optimisation is initially performed using the SciPy minimise function for the idealised models (see Sect. 4), through the Sequential Least SQuares Programming (SLSQP) method (Kraft 1988). The number of iterations for each SLSQP minimisation problem was limited to the default value of 50. Altering 2N variables (i.e., x-, y-coordinates for N turbines) for each flow field over 50 iterations becomes highly time-consuming as the number of turbines N increases beyond a small array. An increased array size also entails a larger optimisation space, further stressing conventional optimisation, increasing the likelihood of converging to local maxima. To address the above, a heuristic-based greedy optimisation technique is tested which positions each turbine sequentially. This allows the imposition of constraints which form acceptance criteria, sequentially adding turbines until either desired capacity is installed or no feasible positions remain. This alternative approach allows for the rejection of proposed turbine placements based on aspects such as bathymetric gradient, forming a basis for non-trivial objective functions. The simplified sequence is described in Algorithm 1.

3 Turbine specifications and analytical wake calibration
Before considering the optimisation case studies, it is instructive to outline the turbine specifications and calibration process in configuring the analytical wake model parameters of FLORIS, so that shallow-water wakes are adequately represented. For the tidal turbines, consistent specifications summarised in Table 1 are applied across all case studies. Turbine dimensions, cut-in, and rated speeds (\(u_{\text {rated}}\)) are based on known parameters for the SIMEC Atlantis 2 MW AR2000 turbine (SIMEC Atlantis Energy 2016, 2020b). Combining Eqs. (10), (11), and (12) allows the determination of the thrust coefficient at \(u_{\text {rated}}\) (\(C_{t,\text {rated}}\)), considering the reported AR2000 turbine size (20 m) and its reported power output (2 MW). Given these specifications \(C_{t,\text {rated}} = 0.516\), noting that this is lower than the value of \(C_\mathrm{t} =\,\) 0.8 determined in lab-scale experiments (Bahaj et al. 2007; Stallard et al. 2015). Figure 2 shows the theoretical tailing of the thrust coefficient for higher velocities. This has been approximated by Cardano’s formula (Wituła and Słota 2010) to produce a simpler equation preventing the need for third-order polynomial inversion that is otherwise required to calculate \(C_\mathrm{p}\) throughout the hydrodynamic simulation. Below the cut-in speed, \(C_\mathrm{t}\) is ramped up exponentially to avoid discontinuities which may cause instabilities within the hydrodynamic model without affecting the total power produced. For consistency, \(C_\mathrm{t}\) and \(C_\mathrm{p}\) are applied uniformly for both FLORIS and Thetis, with the resultant power curve of Fig. 2.
3.1 FLORIS-specific inputs
As we apply FLORIS in the tidal-energy “domain”, FLORIS-specific parameters are altered to appropriate values for a tidal setting (Table 2). The flow shear power law exponent and veer which describe the change in vertical velocity and direction, respectively, are both set to 0, omitting vertical variability for consistency with Thetis. The turbulence model selected in FLORIS is documented by Crespo and Hernández (1996) and default coefficients in calculating the added streamwise turbulence intensity, \(\mathcal {I}_+\), are used. Accordingly, inputs for the axial induction factor exponent and the normalised downstream distance (x/d) exponent are set to the empirically determined values of 0.832 and \(-\,\)0.32, respectively. The initial turbulence intensity at the turbines, \(\mathcal {I}_0\), has been determined experimentally at smaller scales to be 12% at the rotor plane for three-blade model tidal turbines (Stallard et al. 2015). Hub height streamwise turbulence intensity has been determined from ADCP deployments upstream of the Meygen Phase 1A turbines to be approximately 10% and 12% for peak flood and ebb flows, respectively (Coles et al. 2018). Measured data in the Inner Sound of the Pentland Firth suggests the ambient turbulence intensities at peak flow speeds are 13% and 17% during flood and ebb tides, increasing linearly as the flow speed reduces (Hardwick et al. 2015). As the turbulence intensity is assumed uniform for simplicity, the initial ambient turbulence intensity is estimated to be 20%, as flow speeds (for optimisation purposes) will typically range from \(\approx \) 2 to 5.5 m/s.
3.2 Calibration of FLORIS wake effects
Wake-specific parameters are calibrated to replicate the depth-averaged velocity deficits exhibited by Thetis to render the evaluation of the 3-D FLORIS-based optimal array designs in Thetis meaningful. Through the representation of turbines by momentum sinks (Sect. 2.2), Thetis acknowledges essential hydrodynamic interactions in the assessment of tidal-stream arrays (e.g., turbine wake evolution, array blockage). Importantly, this is done within coastal ocean models that acknowledge complex morphologies as well as far-field forcings that drive the oscillatory flow over tidal-array development areas. As FLORIS does not consider flow interaction processes via the wake-superposition approach, its use to optimise arrays in Thetis can also be seen as a test for its potential application when linked with more computationally intensive models and real-world scenarios.
Parameters calibrated herein include \(k_a\) and \(k_b\), which specifically relate to turbulence intensity and wake width. These combine and determine the value of the wake growth rate, \(k^*\), which eventually enters the Gaussian velocity deficit Eq. (14) calculated as
Relative difference between Thetis and FLORIS flow fields with positive magnitude (red) representing a higher FLORIS estimation of velocity. The area indicated by a black square on the left shows Thetis area of increased friction, whilst the solid green line shows the FLORIS turbine representation. Black box on the right defines area over which r.m.s. error is calculated for calibration at \(u_{\text {rated}}\) alone; see Table 4
The second set of parameters \(\alpha \) and \(\beta \) are used for the quantity, \(x_0\), which defines the onset of the far wake
Calibration is performed using differential evolution [as implemented within SciPy’s optimisation library (Virtanen et al. 2020)] to optimise the wake parameters \(k_a\), \(k_b\), \(\alpha \) and \(\beta \), such that the r.m.s. error between wakes in Thetis and FLORIS is minimised. It should be noted that the velocity deficit magnitudes in FLORIS are averaged over regular depth increments to produce an equivalent depth-averaged FLORIS wake, used to optimise model parameters. Calibration is performed for \(u_{\text {rated}}\) only, and then compared to results from calibration exercises for speeds below and above \(u_{\text {rated}}\) to gauge the extent of deviations. An idealised model consisting of a single turbine in the channel described in Sect. 4.1 is used to create a velocity deficit to be investigated over 20 diameters downstream for this purpose.
Wake calibration results are shown in Table 3, with the r.m.s. error between Thetis and FLORIS fields below 0.6% in the area of interest from 1.5–20D downstream. The difference in turbine representation is presented in Fig. 3, clearly showing higher values of the FLORIS flow field velocity compared to Thetis as the velocity reduces over the bump function that represents the presence of the device. Immediately downstream of the FLORIS turbine, the velocity is lower than in Thetis due to the greater deficit imposed by FLORIS, which comes as a result of the discontinuous superposition of the analytical wake model at the turbine location. This discrepancy in turbine representation leads to the decision to calibrate based on the flow field from 1.5D downstream in a zone of width 3D to also capture the expansion width of the far wake. It should be noted that this is typically the region of highest error between not only differing turbine representation methods, but also to measured data; the existing research has already demonstrated that accurately capturing the wake dynamics may require investigation of several different approaches to turbine modelling (Sandoval et al. 2021). The central region of the wake is well calibrated, with increased r.m.s. error bands on the edges of the wake, though within margins of 1%. At \(u_{\text {rated}}\), this representation is considered acceptable, with a 1% velocity variation on the outer wake unlikely to impact optimisation, considering the assumptions within these parameterisations.
A comparative analysis of the wake parameters for \(u_{\text {rated}}\) against calibrations at varying flow speeds (Table 4) demonstrates that the overall r.m.s. error is still acceptable as the analytical wake model is applied within its expected range. With decreasing velocity, the wake width increases, and as the velocity approaches cut-in speed, the immediate wake width begins to exceed the turbine diameter, increasing the r.m.s. error, albeit within acceptable levels.
For completeness, we present results of a separate calibration performed between the analytical wake model and flume data (Stallard et al. 2013) capturing 3-D wake turbulence dynamics that are not present within 2-D depth-averaged models. A comparison between the different wake behaviour and the respective FLORIS calibrated solutions is shown in Fig. 4. Specifically, Fig. 4 shows
-
Thetis vs Thetis-calibrated FLORIS depth-averaged wake profiles;
-
Stallard et al. (2013) data vs the corresponding calibrated FLORIS prediction for an isolated turbine at hub-height \(z_{\text {hub}}\).
Froude-scaling has been applied for comparison against laboratory data (Stallard et al. 2013). Calibration to these data shows excellent agreement beyond \(\approx 3D\)–3.5D and, therefore, the potential to calibrate to 3-D data.
Even here however, the analytical representation of the near wake could be improved. This further highlights the challenge of calibration between Thetis and FLORIS as even on the depth-averaged profile, the immediate deficit downstream of the turbine is substantially greater relative to Thetis. Nevertheless, the Thetis calibrated wake has been well-calibrated beyond 1.5D; since turbines are unlikely to be placed in such close proximities in the streamwise direction, this is unlikely to impact optimisation. For real-world applications, the initial wake calibration step should be conducted against the best possible wake data available, from observations and/or high-resolution CFD.
Longitudinal profile for wake Froude number \(Fr=\frac{|\mathbf {u}|}{\sqrt{g H_d}}\), both depth-averaged for comparison between calibrated FLORIS vs Thetis and at hub height (\(z_{\text {hub}}\)) for comparison between calibrated FLORIS vs experimental data of Stallard et al. (2013)
4 Case studies
In demonstrating this tidal-array optimisation framework, we consider models of increasing complexity and denser turbine placement. First, we examine the micro-siting of aligned and staggered \(2\times 4\) turbine arrays of three rotor diameter (3D) spacing between rows and columns; the array itself is situated within an idealised channel with and without a headland. These exercises are then repeated with denser \(3\times 5\) turbine arrays of 2D lateral (between rows) spacing and 3D longitudinal (between columns) spacing. The idealised cases imitate two examples from Funke et al. (2014) and serve in validating the performance of the current approach prior to assessing a more realistic full-scale optimisation problem. For our realistic flow problem, we consider the Pentland Firth region with aligned and staggered array sizes of \(4\times 6\) turbines of 5D lateral and longitudinal spacing, followed by a staggered \(8\times 6\) case of 3D spacing.
The cases are illustrated in Figs. 5 and 6, respectively, including the computational meshes used by Thetis for the hydrodynamic simulations. In all cases, the mesh generation process employs the open-source code qmesh (Avdis et al. 2018), featuring a \(3\,\hbox {m}\) element resolution for the idealised cases, and \(5\,\hbox {m}\) for the Pentland Firth case within the allocated tidal array. This element size was selected using a mesh sensitivity study on the wake resolution confirming the mesh resolution independence of the results within the array.
The optimisation approach is informed by several spatial conditions/constraints. The “greedy” optimisation approach features an initial minimum of three diameters (3D) distance separating each turbine and a blocked radius of one diameter (1D) for each “failed iteration” (\({\varDelta }\) = 3D, E = 1D). Initially, the 3D separation constraint between turbines is applied for all optimisation techniques to prevent high-magnitude flow deficits impacting closely spaced turbines [the spacing is typically 1.5D–5D for tidal turbines (Stallard et al. 2013)]. However, towards making better use of the deployment area, the spatial constraint is then reduced to 1.5D to maximise the number of turbines within the domain. The conditions for 3D spacing are specified as a minimum 17.5% capacity factor per turbine, a 5% maximum reduction of power for individual turbines and a 9% maximum reduction in the cumulative power of the particular turbines subject to a power reduction (A = 17.5%, B = 5%, \({\varGamma }\) = 9%) as required. As turbine interactions are inevitable for 1.5D spacing, constraint limits need to be less stringent with A = 17.5%, B = 15%, \({\varGamma }\) = 25%. Specific details for each case study are expanded below.
4.1 Steady-state flow through an idealised channel
An idealised channel of dimension (640 m \(\times \) 320 m) featuring a (320 m \(\times \) 160 m) region where a tidal array is to be deployed provides sufficient space to tightly pack turbines across the width of the channel, but is short enough to prevent substantial wake recovery. The bathymetry is constant across the full domain at \(50\,\hbox {m}\) depth. Eddy viscosity is set to a constant value of \(1\,\hbox {m}^2 /\hbox {s}\) across the domain away from the boundaries as per previous studies (Vouriot et al. 2019). For simplicity, a quadratic drag coefficient \(C_D =\,0.0025\) (which represents a fairly smooth bed) is selected, following the previous investigations of the Pentland Firth, e.g. (Draper et al. 2014). For this steady case, the imposed flow is constant and can be represented by a single flow field, which was determined in Thetis with an inflow horizontal velocity, \(u =\, 3.175\hbox {m}/\hbox {s}\) (close to \(u_{\text {rated}}\)), and a constant elevation of 0 \(\hbox {m}\) at the outflow.
4.2 Transient flow around an idealised headland channel
Headlands and islands are key in providing highly energetic channels that make tidal streaming a feasible prospect. A simple headland model provides a location of concentrated higher energy density for turbines to be placed. In this case, the overall channel width and length are increased to \(480\,\hbox {m} \times 1280\,\hbox {m}\) for the headland (represented by a \(160\,\hbox {m}\) radius semi-circle) to be introduced (Fig. 5). Velocity becomes greater due to flow conservation at the constriction from 480 m to 320 m, which acts in a similar manner as a Venturi flume, accelerating the flow. A bathymetric gradient is applied radially, with the depth reduced gradually from 50 to 5 m along the headland, imitating a shore. A viscosity ‘sponge’ is introduced at the open boundaries of \(50\,\hbox {m}^2 /\hbox {s}\) linearly transitioning to \(1\,\hbox {m}^2 /\hbox {s}\) within a distance of 10% of the channel length. Simple harmonic signals are defined (Eqs. 19, 20) to drive the oscillatory flow to verify FLORIS’s capability to optimise for multiple fields of data. The following equations:
provide the assigned local elevation \(\eta _1, \eta _2\), at each of the boundaries and are signals of equal magnitude and opposite direction. Here, \(A_{\text {tide}}\) is the tidal amplitude, t is the simulation time and T is the tidal period. Values of \(T=\,1\,\hbox {h}\), and \(A_{\text {tide}}=\, 0.275\,\hbox {m}\), deliver a velocity profile with a peak magnitude close to \(u_{\text {rated}}\) (i.e. 2.5–3 m/s). Following a spin-up time of 1.5 h, fields exported for optimisation are between the cut-in and maximum speeds, over a single tidal cycle.
4.3 Application to the Pentland Firth, Scotland, UK
Computational domain for the Pentland Firth case study. a Domain extents and Marine Digimap bathymetry dataset (Edina Digimap Service 2020) interpolated to elements; b close-up to island scale; c) close-up to channel scale. The tide gauge and ADCP locations used to calibrate the model are also indicated, alongside the tidal-array deployment zone considered for array optimisation
The Orkney archipelagos in North Scotland, UK (Fig. 6) features sites characterised by high tidal-energy levels. This is especially pronounced in the area of Pentland Firth, a strait separating mainland Scotland from the Orkney Islands. There, flow speeds regularly exceed \(5\,\hbox {m} /\hbox {s}\) (Draper et al. 2014), and thus, the Inner Sound of the Pentland Firth is a prime site for tidal-array deployment as discussed by several studies investigating the energy resource (Adcock et al. 2013; Draper et al. 2014; O’Hara Murray and Gallego 2017), potential environmental impacts (Martin-Short et al. 2015a) as well as the micro-siting of turbines within arrays (Funke et al. 2014). At that location is the Meygen site, where a subset of a larger array has already been deployed.
The regional hydrodynamic model shown in Fig. 6a makes use of one arc-second resolution bathymetry, acquired from Edina Digimap Service (2020). Open boundaries are tidally forced using eight tidal constituents (Q1, O1, P1, K1, N2, M2, S2, K2) derived from TPXO (Egbert and Erofeeva 2002). The model, subjected to 2 days of spin-up time, hindcasts 32 days from 01/08/2017 to 01/09/2017. This timeframe is selected according to the availability of ADCP data (Coles et al. 2018), spanning sufficient duration to resolve the principal constituents driving the flow (i.e., M2 and S2). Over this period, predictions are simultaneously compared against UK Hydrographic Office data recorded at a tide gauge located at Wick (Table 5).
Left: correlation between observed and predicted u-velocity at Pentland Firth monitoring station (\(R^2 = 0.93\) and \(R^2=0.98\) for ADCP-1 and ADCP-2, respectively). Right: correlation between the observed and predicted v-velocity (\(R^2 = 0.95\) and \(R^2=0.84\) for ADCP-1 and ADCP-2, respectively). ADCP data provided by SIMEC Atlantis Energy with further details in Coles et al. (2018)
The Pentland Firth and Orkney Isles model for our optimisation study has an element size (\(\wedge h\)) ranging between 300 and 1500 m near-shore subject to proximity to the Meygen tidal site or certain island features. This resolution gradually increases to 20,000 m towards the open seaward boundaries. Increased refinement of a uniform element size \(\wedge h =\,5\,\hbox {m}\) has been imposed to resolve individual turbines within the Meygen tidal site. The simulation results are produced using a variable Manning’s \(n_M\) across the domain based on bed classification data provided by the British Geological Survey, as described by Mackie et al. (2021), and a timestep \(\Delta t = \,100\,\hbox {s}\).
Model calibration is more sensitive against measured velocity rather than elevation data. Velocity comparisons were established against observed data at the locations of ADCP-1 and ADCP-2 (Fig. 6). In Fig. 7, a misalignment can be observed in ADCP-1 during flood tide. This is attributed to several modelling decisions, such as the coarse model resolution surrounding the Meygen site and the rest of the computational domain. In addition, the relatively low resolution of the available bathymetric dataset used in the vicinity is influential. Nevertheless, the overall model accuracy is deemed appropriate for demonstrating the optimisation method within a practical scenario, acknowledging that these deviations between observational and model data would render further field observation and analysis essential to characterise the local dynamics more accurately. In terms of water elevation predictions, results agree well (Fig. 8) with observed values at Wick. There, correlation among observed and predicted water elevation data is approximately 0.982, whilst the root-mean-square (r.m.s.) error is equal to 0.11 \(\hbox {m}\).
5 Optimisation results
5.1 Steady-state flow through an idealised channel
The maximum power possible for setups of \(N_t=8\) and \(N_t=15\) turbines would be 16 MW and 30MW, respectively, given that the inflow (3.175 \(\hbox {m}/\hbox {s}\)) exceeds \(u_{\text {rated}}=\)3.05 m/s. Indicatively, an aligned turbine placement (Fig. 9a) yields power of \(>15\%\) below the maximum extractable power for both 8 and 15 turbine setups. Placing the turbines in the staggered arrangement of Fig. 9a leads to improved power output as anticipated, slightly below the maximum achievable.
Layout optimisation in FLORIS using SLSQP leads to a distribution of turbines across the channel width. This is shown in Fig. 9b for \(N_t=15\) setups (A.8-10), forming two rows of turbines separated by a sufficient longitudinal distance that allows velocity deficit recovery from upstream devices. Using the greedy approach provides a similar result in both cases, with turbines positioned to avoid wake interaction where possible. The SLSQP approach performed best in completing optimisation due to the simplicity of the input, whilst the greedy algorithm demonstrates sensitivity to the naive initial turbine placement. This is particularly notable on the \(N_t=15\) setup (A.9), whereby two columns of turbines are required, and therefore, poor initial placement could negatively impact array power to a much greater extent.
Array layouts (\(N_t\)=15) and Thetis-predicted velocity deficits (\(\overline{\Delta \mathbf {u}}\)) for rectangular steady-state idealised channel flow. a Standard (i.e., unoptimised) layouts (A.6–A.7, Table 6); b optimised layouts (A.8–A.10); c aligned layout (A.6) \(\overline{\Delta \mathbf {u}}\); d greedy optimisation layout (A.9) \(\overline{\Delta \mathbf {u}}\)
A Thetis adjoint-based tidal farm optimisation (Funke et al. 2014) (A.10) provides similar distributions of turbines across the channel as in Fig. 9, but with placement that appears to exploit the “duct effect”. Adjoint optimisation results in maximum power obtained across all approaches (as per Thetis simulations), since optimisation avoids inconsistencies in turbine representation, whilst also capitalising on beneficial hydrodynamic effects. The adjoint/gradient-based method was anticipated to be more effective in this case for the above reasons, particularly around (or below) \(u_{\text {rated}}\), whereby the velocity deficits can reduce the power produced. This is emphasised for the denser 15-turbine layout, where consideration of more devices places greater stress on the optimisation technique, whilst blockage and funnelling provide opportunities for greater power augmentation. Nevertheless, despite different layouts, the power performance is near identical among 8-turbine cases (A.3-5) and very similar between FLORIS’s SLSQP (A.8) and the adjoint (A.10) for the 15-turbine cases. This suggests that multiple solutions achieve the criterion of maximising power output, but with the adjoint taking significantly longer than either FLORIS approach.
5.2 Transient flow around an idealised headland
The idealised headland case considers oscillatory flow to demonstrate optimisation features over unsteady conditions. Three flow fields from each flood and ebb tide are exported to be used within FLORIS. For each of these sets, one is at peak velocity magnitude and two between cut-in and rated speeds. As flow direction and magnitude does not vary significantly, the total of six flow ‘frames’ performs sufficiently for optimisation in this case, with more frames delivering negligible benefit. Velocity contours for the peak flood flow without turbines are shown in Fig. 10 with layouts of different headland cases for the \(N_t=15\) configurations (B.5, B.6, and B.7) of Table 6 superimposed. As the flow develops around the headland, the combination of the vena contracta effect and the bathymetric gradient contributes to a velocity acceleration that diminishes away from the headland constriction. This provides radial bands of higher energy potential for turbine placement, with only the regions closest to the headland allowing maximum power production at peak flow speeds.
FLORIS’s SLSQP-based optimisation leads to placement of three turbines within these first two bands (i.e., in flow greater than 3 \(\hbox {m}/\hbox {s}\)) for the \(N_t=8\) setup (B.3), with the remainder of turbines spread across the width of the channel avoiding wake interaction in a similar manner to the steady-state idealised channel case. Meanwhile, greedy optimisation places the first turbine in the centre of the first band, subsequently leading to lower power production for the surrounding turbines, which can not be placed as closely within the first two bands due to the separation constraint. A similar trend is observed with 15 turbines and a reduced separation constraint of 1.5D; five turbines are placed within the first two bands by SLSQP and only two by the greedy algorithm (Fig. 10).
The average power produced by the greedy optimisation array after only 20 iterations (for the \(N_t=8\) setup of B.4) exceeds the staggered arrangement (B.2), which itself performs particularly well due to the flow direction. However, the greedy optimisation technique leads to 1.8% lower average power than SLSQP, although it does require almost 0.1% and 2% of the computational time for \(N_t=8\) and \(N_t=15\) turbine setups, respectively. Given the required time for a steady-state channel optimisation, the reduction in computational time becomes appreciable relative to adjoint optimisation, which has not been explored further in this work for unsteady cases.
5.3 Application to the Pentland Firth, Scotland, UK
Using three frames from each flood and ebb tide for spring, intermediate, and neap cycles, optimisation of \(N_t\)=24 turbines subject to a minimum spacing of 3D (C.4, Table 6) resulted to increased average P relative to an aligned case (C.1) by 12.4% over a month’s period. Optimisation made use of 18 flow frames, with additional frames delivering no substantial benefit to the overall performance. This is attributed to the generally consistent flow direction at peak magnitudes over flood and ebb tides (as illustrated by the flow fields in Fig. 11). The importance of using representative frames for a full tidal cycle (as well as a spring–neap cycle) is demonstrated by Fig. 12. Optimisation is less effective during flood flows, and even less so during spring tides. This is due to the deployment of turbines that experience flow velocities noticeably greater than \(u_{\text {rated}}\) for a large proportion of the velocity magnitudes expected within the allocated plot. As a result, these are predicted to deliver maximum power irrespective of compounded wakes. This would suggest that within this area, neglecting structural constraints and metrics such as the capacity factor, it may be worth using turbines of higher \(u_{\text {rated}}\) to fully exploit the potential energy available. Nevertheless, a positive increase in capacity factor from 42.6% to 47.9% is achieved for a minimum spacing of 3D; that could have a significant influence on the feasibility of such an installation.
Relative power increase (\(\Delta P /P\)) comparing greedy (C.4) to staggered (C.2) case of the Pentland Firth for 24 turbines. Shaded areas indicate periods used to extract ambient flow fields for optimisation. \(|P|_{T/4}\) corresponds to the average power in increments of T/4. Similar trends are observed comparing optimised layouts based on minimum 1.5D spacing (C.5 vs C.2, C.7 vs C.6)
Flood and ebb change in kinetic power density (KPD) for Pentland Firth case study at peak spring tide computed using the Thetis model with turbine drag simulated. a Staggered arrangement (C.2), ebb; b greedy optimised arrangement (C.5), ebb; c staggered arrangement (C.2), flood; d greedy optimised arrangement (C.5), flood; e staggered arrangement (C.6), ebb; f greedy optimised arrangement (C.6), ebb; g staggered arrangement (C.7), flood; h greedy optimised arrangement (C.7), flood
Greedy optimisation accomplished this improvement within 27 iterations, taking less than a minute. In loosening the minimum spacing constraint to 1.5D, a capacity factor increase to 49.4% is achieved, at the cost of additional iterations and computational time in the order of a few minutes. As Table 6 shows, in a practical case where velocities exceed \(u_{\text {rated}}\) and the flow field is more varied and complex largely due to the local bathymetric profile, a staggered arrangement (C.2) is less effective than in idealised geometries (e.g., A.2 and B.2). With more turbines within the staggered arrangement, the interaction of multiple wakes has a far more profound effect, as shown in Fig. 13a, c; the variation of flow velocities means that turbines perform better packed into regions of higher average kinetic power density (\(\overline{\text {KPD}}\), where KPD \(= \frac{1}{2}\rho |\mathbf {u}|^3\)). Again, this emphasises the optimisation’s sensitivity to turbine \(u_{\text {rated}}\); in regions where peak flow speeds regularly exceed \(u_{\text {rated}}\), turbines will operate at their maximum capacity, despite wake impingement. For an array of doubled size (\(N_t\) = 48), the relative increase in power becomes less significant for this reason. Although the initial staggered arrangement at 3D spacing (C.6) appears to allow for greater wake avoidance than the \(N_t\) = 24 array of 5D spacing (C.2) due to the localised flood direction, the increased density of turbines at the northern, more energy dense, section of the site in combination with low \(u_{\text {rated}}\) relative to the flow speed, corresponds to lesser noticeable gains. This issue leads to denser turbine arrangements, but is specific to layout optimisation seeking energy maximisation rather than mitigating hydrodynamic (wake) interactions. Figure 11d shows turbines positioned in areas of high KPD, whereby the southern parts of the site are avoided on the grounds of lower flow magnitudes. Notably, beyond the allocated area for turbine deployment, flow speed exceeds 5.5 \(\hbox {m}/\hbox {s}\) towards the island of Stroma (Fig. 6). Harnessing the kinetic energy there would be technically challenging due to the shallower bathymetry and sharper bed gradients. In the optimised configurations, a few turbines lie within the high velocity deficit region of upstream wakes due to conditions preventing the reduction of individual turbine power. This is particularly critical during neap tide when flow speeds are low enough to place emphasis onto wake interaction, hence the benefit of optimising for several varying tidal cycles.
A key consideration when examining practical cases is the impedance of the flow due to the presence of turbines (array blockage). The change in volumetric flow over a 1-day period is presented in Table 7 to quantify the impact of the turbine drag on the channel flux, as per Coles et al. (2017). Through the array width only, the reduction in volumetric flow remains around 4% for the 24 turbine cases, which is not particularly significant for a spring tide and results partially from the low global blockage of the array and the spaced out distribution of turbines to minimise velocity deficits. As the array size and its turbine density are relatively small when compared to the size of the channel, the influence on the Inner Sound is localised suggesting minimal diversion of flow on a regional scale. With increasing array size (Fig. 13e-h), the impact of global blockage effects will likely become more critical, particularly considering site-to-site interactions over the entire Pentland Firth and the Orkney Islands (De Dominicis et al. 2018). Although still sparse relative to the size of the Inner Sound, the reduction in volumetric flow through both the array width and the Inner Sound itself doubles when \(N_t = 48\) in case C.7, demonstrating a proportional increase in blockage effects. As FLORIS does not consider blockage effects, it becomes instructive to compare velocity changes, \(\overline{\Delta \mathbf {u}}\), relative to the equivalent Thetis setup, as in Fig. 14. Thetis predicts zones of velocity deficit and flow acceleration at the top and bottom of the array, respectively. These effects indicate the onset of notable array-scale impacts as turbines form a denser configuration, with wakes of turbines eventually merging to form wider \(\overline{\Delta \mathbf {u}}\) regions.
6 Discussion
6.1 On the turbine representation and the consideration of local and global blockage
The general array micro-siting pattern returned by the optimisation approaches (SLSQP and greedy alike) sees turbines positioned within high power density regions (Fig. 11) and otherwise spread to maintain separation whilst avoiding wake interaction. The latter agrees with results reported previously by Stansby and Stallard (2016) that emphasise wake avoidance within the optimisation process.
Under operational conditions below \(u_{\text {rated}}\), variation in wake representation can compromise optimisation, as key velocity deficit areas may not be captured accurately. If wake width is underestimated in the analytical model, some of the turbines may become partially immersed in upstream wakes when evaluated by the hydrodynamic model. This highlights the significance of calibrating the wake model parameters as per Sect. 3.2. Additional parameters can be considered to improve accuracy, such as varying the turbulent intensity, \(\mathcal {I}\), as a function of \(\mathbf {u}\), for better agreement against data when applied to non-idealised cases of complex bathymetry (as in Fig. 14). These parameters were assumed constant in this study for simplicity, but should be calibrated as they are subject to inflow conditions and varying turbulence levels. The inclusion of local blockage effects, which has been shown to be possible through ad-hoc corrections in analytical approaches such as FLORIS (Branlard and Meyer Forsting 2020), could also benefit optimisation in high-density, confined scenarios of rectilinear flow.
In the case study within the Pentland Firth, we consider a turbine array subject to a rating curve, varying flow directionality and practical clearance constraints. First, we note the necessity of the ambient flow model to correctly capture the flow magnitude and direction over the tidal-array deployment area as discussed in Sect. 4.3. Otherwise, even minor departures from the actual flow direction will lead to a sub-optimal array design (see Fig. 7). These deviations are typically attributed to under-resolved spatial features as discussed by Mackie et al. (2021). We observe that the varying flow direction over ebb and flood tides renders blockage challenging to exploit. Considering the flow velocity across the array, we also note the persistent exceedance of the rated velocity, \(u_{\text {rated}}\), across spatial and temporal scales. As velocities exceed \(u_{\text {rated}}\), wake effects become locally constrained. These conditions, compounded by non-rectilinear flow, make the “duct effect” difficult to exploit and thus less influential on power production. This is more noticeable during spring tides as \(|\mathbf {u}|> u_{\text {rated}}\) over a longer fraction of the tidal cycle, and optimal siting of turbines becomes less beneficial in terms of power output (Fig. 12). These observations are informed by current practices, where turbines are proposed to be deployed in channels where peak flow speeds comfortably exceed \(u_{\text {rated}}\). This is due to alternative objectives, such as maintaining a competitive capacity factor over the device lifetime.
Furthermore, minimum turbine spacing may be forced to exceed 3D (Ouro et al. 2019) in the in-stream direction (the value used in this study as a typical separation constraint). The minimum spacing of 1.5D that enables closer packing of turbines laterally, as in Ouro et al. (2019), can be challenging to accommodate due to O&M practicalities, complex terrain constraints, and non-rectilinear oscillatory flow. These considerations can restrict turbine placement and reduce to an extent the positive influence of local blockage. On that, Nishino and Willden (2013) analytically found that with increasing turbine density in a partial tidal fence, optimal local blockage will increase for both low and high global blockage cases. The benefit of exploiting blockage effects was demonstrated numerically in Funke et al. (2014) where an adjoint-optimisation approach promoted positioning of idealised turbines (i.e., not subject to a \(u_{\text {rated}}\)) to form highly dense fence-like structures. It must be remarked that in that case, the resistance introduced by individual turbines was exaggerated (as the focus was instead on demonstrating the adjoint-optimisation methodology), amplifying the benefits of local blockage. However, within the steady-state flow through an idealised channel, and whilst considering more practical representations of turbine resistance and turbine density (3D), the adjoint optimisation in Thetis delivers minimal gains over our greedy or FLORIS’s SLSQP-based approaches.
A feasible placement of turbines within a channel such as the Pentland Firth will be highly dependent on a number of factors including the bathymetry gradient, bedrock hardness, turbulence loading, and a variety of installation and maintenance challenges. The initial turbine density for the Pentland Firth case study was based on an initial separation of 5D. If the density is increased, so that maximum initial separation is reduced to 3D (whilst increasing the number of turbines in the initial array), local blockage effects become more prominent, as indicated by the increase in power density around devices in Fig. 13. Nevertheless, quantification of the blockage effects by monitoring fluxes and the power density changes over the array (Table 7) suggests that this remains a low-blockage case.
6.2 On the characterisation of array hydrodynamics
Our optimisation approach relies on the use of analytical wake models that typically assume steady-state conditions. The practice of wake superposition itself introduces a mass and momentum deficit that is not compensated without additional corrections (e.g., Branlard and Meyer Forsting (2020)); these necessitate the assessment of FLORIS derived layouts within hydrodynamics models (Fig. 14). On the other hand, the hydrodynamics model (in this case Thetis) does not capture horizontal flow structures below the mesh-size scale which means that many unsteady and quasi-steady flow phenomena are not considered in our analysis. In particular, turbulent mixing occurring at smaller scales is not modelled, which has been shown to influence wake evolution, as also recognised by the wind energy community (Singh et al. 2014). Overall, this represents an outstanding research area involving complex multi-scale flow modelling. Another phenomenon of relevance which is not captured in our simulations is dynamic wake meandering. As turbine wakes interact with the larger tidal-channel turbulent structures, such as near-wall high- and low-speed streaks, near-wake vortices start breaking down giving way to the generation of a cascade of turbulent scales. Additionally, the wake experiences lateral and vertical displacements caused by the larger scales leading to their significant lateral expansion. These effects are not encapsulated within hydrodynamic models unless the model spatial and temporal resolution is increased and/or combined with more robust turbulence models that capture these effects whilst avoiding excessive dissipation in the solution. Inherently, all 2-D models are limited in their ability to capture dispersion effects due to the assumed uniform vertical velocity. These considerations may have implications for the final prediction of the wake deficits and therefore also affect the optimal array layout solution. 3-D shallow-water models, on the other hand, can improve the representation of such scales as shown by Stansby (2003) through the addition of a horizontal mixing length scale which alters the velocity profile over the water column, resulting in greater vertical shear; however, further research is required to quantify their impact on wake dynamics.
Regarding the global array wake, experimental studies on turbulent wakes downstream of a two-dimensional porous obstruction (Zong and Nepf 2012) show that the steady wake region increases with increasing porosity, whereas the unsteady von Kármán vortex street may be delayed until well beyond the steady wake region. Given the low turbine density, as demonstrated by the global array volume flux (see Table 7), the array’s equivalent porosity is small; thus, we argue that no further quasi-steady effects are likely to be present in the array-scale wake region. Turbine-scale unsteadiness in the individual turbine’s near wake region may be accounted for by a locally modified eddy-viscosity.
An alternative approach for the local and global hydrodynamics may be undertaken using higher fidelity models such as those that utilise three-dimensional Reynolds-averaged Navier–Stokes (RANS) (Abolghasemi et al. 2016; Deskos et al. 2017) or large-eddy simulation (LES) methods (Churchfield et al. 2013; Ouro and Nishino 2021) which inherently allow for greater insight and accuracy in the near-wake region by allowing both horizontal and vertical wake dispersion through scale-resolving simulations. Such simulations emphasise how wake avoidance is not only critical for maximum exploitation of the channel potential, but also in reducing turbulence onto downstream turbines which may compromise the devices’ lifetime due to fatigue (Thiébaut et al. 2020). Nevertheless, 2-D models are currently the standard option for regional assessments (Coles et al. 2020) and help counteract the computational cost within an optimisation framework. As demonstrated in Sect. 3.2, and in particular Fig. 4, it would be entirely possible to apply the same methodology to a 3-D higher fidelity either coastal ocean or turbulence-resolving model to acquire greater consistency with measured data.
6.3 On the potential applications for large tidal-array optimisation
Whilst a number of optimisation approaches have been proposed for the micro-siting of tidal turbines, these have been limited to idealised setups, or limited control parameters in terms of turbine placement. Some of the more sophisticated methods (e.g., Funke et al. (2016); Culley et al. (2016)) that consider blockage effects remain computationally and memory intensive. Taking our practical example of the Pentland Firth, an earlier approach required 24–48 h on a 64-core supercomputer for a steady-state simulation (Funke et al. 2014). Though pioneering, practical constraints including rated turbines, transient tidal flows, and realistic bathymetry were not considered in early studies despite having an influence on the interactions between devices and the resource. Similarly, optimisation methods that estimate the objective function gradient iteratively (e.g., SLSQP) quickly become computationally demanding due to the quadratic complexity (\(\mathcal {O}(n^2)\)) of the optimisation algorithm. In the optimisation problem presented by the practical case (C.3), SLSQP becomes significantly more costly as the domain size and turbine number \(N_t\) increase. Given a tendency to converge to local minima, it becomes distinctively ineffective for complex domains in the absence of a reliable gradient calculation strategy. The customised greedy approach developed here overcomes these computational constraints and offers a route to also incorporate additional features. These may include cabling constraints (Culley et al. 2016), seabed gradient restrictions, several turbine options, and other factors such as wake steering which are considered in the optimisation of offshore wind farm operation (Deskos et al. 2020). However, greedy optimisation strategies possess shortcomings (Bang-Jensen et al. 2004), and whilst they can deliver a locally optimal solution in reasonable time, they must be applied and interpreted with their limitations in mind.
Adjoint-based and greedy methods could be combined in a cyclic manner for optimisation in larger domains whereby a greedy approach acts as a precursor that delivers an initial design to improve upon through adjoint optimisation. This will sequentially seek to exploit hydrodynamics effects by exploring the parameter space through localised turbine displacements starting from a decent design that should result in the requirement for less optimisation iterations than a pure adjoint-based approach. It may also mitigate the issue of getting stuck in a sub-optimal local optima. Alternatively, given the computational efficiency of the customised greedy optimisation, opportunities can be explored to optimise for \(N_s \subset N\) in fractions of the turbine deployment area at a time. Turbines introduced can then be included in forward hydrodynamics simulations to account for hydrodynamic impact and blockage effects when designing the rest of the array. This approach could avoid the sudden introduction of substantial array impacts (Fig. 14) by incremental addition of turbines in the array within an optimisation iteration. Extensions can also be made towards multi-objective optimisation that balances cost against environmental impacts (e.g., sediment transport or implications for benthic species habitats). This could follow recent work on environmentally constrained optimisation by du Feu et al. (2019).
7 Conclusions
A novel optimisation method was demonstrated by retrofitting an analytical wake-superposition model, in this case FLORIS, for use with a coastal hydrodynamics model, Thetis. The method is motivated upon reflection on the bottlenecks observed in the existing array optimisation approaches, which depending on acceptable computational costs may be constrained to (a) simplified flow geometries, (b) steady-state flow conditions, and (c) idealised turbine representations. The work is driven by the complexity of the array micro-siting problem, where an effective optimisation method should be able to deal with complex flows caused by local bathymetric features and regional coastline, the transient tidal flows over spring neap cycles, and the technical specifications and performance characteristics of the turbine technology that is to be deployed. Once a hydrodynamic model delivers the spatially and temporally varying flow information over a prospective development area, application of a custom greedy placement algorithm within an analytical wake-superposition model allows for rapid optimisation.
The methodology was applied to three cases of increasing complexity (in terms of geometry, oscillatory flow, and array turbine number), and was able to demonstrate its potential and highlight multiple considerations emerging as we progress from idealised to practical settings. For a simple steady-state rectangular channel, turbines were arranged in a longitudinally staggered fashion across the domain, utilising the full width of the domain whilst maintaining separation constraints, consistently with alternative optimisation strategies (e.g., SLSQP and adjoint-based optimisation). The headland case demonstrated the capacity to deal with more complicated flows and emphasised the trend of turbines being positioned in areas of higher power density, whilst avoiding wake effects from upstream turbines during ebb and flood flows. The optimisation scenario of 24 turbines in a confined region within the Pentland Firth demonstrated the ineffectiveness of staggered arrangements for non-rectilinear oscillatory flows, and the computationally efficient application of this methodology for complex geometries and flow dynamics. It was found that the resultant method yielded an overall improvement in power output in the order of 12% for 3D minimum spacing and up to almost 16% when reduced to 1.5D.
Finally, it was observed that flow asymmetry in conjunction with minimum distance requirements may render the exploitation of local blockage effects rather challenging. Case studies using 24 and then 48 turbines, respectively, within the Meygen site at the Pentland Firth indicated low levels of global blockage. However, as the number of turbines doubles to 48 in the latter case, blockage effects start to become more noticeable. Given the extensions expected as tidal arrays expand, it is proposed that the optimisation approach presented can be operated iteratively enabling the hydrodynamic model to account for array-scale blockage as the size of the array is extended.
Availability of data and materials
Data are available upon request.
References
Abolghasemi MA, Piggott MD, Spinneken J, Viré A, Cotter CJ, Crammond S (2016) Simulating tidal turbines with multi-scale mesh optimisation techniques. J Fluids Struct 66:69–90
Adcock TA, Draper S, Houlsby GT, Borthwick AG, Serhadlioǧu S (2013) The available power from tidal stream turbines in the Pentland Firth. Proc R Soc A Math Phys Eng Sci 469:20130072
Angeloudis A, Kramer SC, Avdis A, Piggott MD (2018) Optimising tidal range power plant operation. Appl Energy 212:680–690
Avdis A, Candy AS, Hill J, Kramer SC, Piggott MD (2018) Efficient unstructured mesh generation for marine renewable energy applications. Renew Energy 116:842–856
Bahaj AS, Molland AF, Chaplin JR, Batten WMJ (2007) Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew Energy 32:407–426
Baker AL, Craighead RM, Jarvis EJ, Stenton HC, Angeloudis A, Mackie L, Avdis A, Piggott MD, Hill J (2020) Modelling the impact of tidal range energy on species communities. Ocean Coast Manag 193:105221
Balay S, Abhyankar S, Adams MF, Brown J, Brune P, Buschelman K, Dalcin L, Eijkhout V, Gropp WD, Kaushik D, Knepley MG, McInnes LC, Rupp K, Smith BF, Zampini S, Zhang H, Zhang H (2016) PETSc users manual. Technical report ANL-95/11—revision 3.7, Argonne National Laboratory
Bang-Jensen J, Gutin G, Yeo A (2004) When the greedy algorithm fails. Discrete Optim 1(2):121–127
Barnett GL, Funke SW, Piggott MD (2014) Hybrid global-local optimisation algorithms for the layout design of tidal turbine arrays. arXiv:1410.2476
Bastankhah M, Porté-Agel F (2014) A new analytical model for wind-turbine wakes. Renew Energy 70:116–123
Branlard E, Meyer Forsting AR (2020) Assessing the blockage effect of wind turbines and wind farms using an analytical vortex model. Wind Energy 23(11):2068–2086
Chamorro LP, Porté-Agel F (2009) A wind-tunnel investigation of wind-turbine wakes: Boundary-Layer turbulence effects. Bound Layer Meteorol 132(1):129–149
Chen L, Bonar PA, Vogel CR, Adcock TA (2019) Local blockage effects for idealised turbines in tidal channels. In: Proceedings of the international conference on offshore mechanics and arctic engineering—OMAE 10, Glasgow, UK, pp 1–10
Chozas JF (2015) International levelised cost of energy for ocean energy technologies. Technical Report May, Ocean Energy Systems
Churchfield MJ, Li Y, Moriarty PJ (2013) A large-eddy simulation study of wake propagation and power production in an array of tidal-current turbines. Philos Trans R Soc Lond A Math Phys Eng Sci 371:20120421
Coles D, Angeloudis A, Greaves D, Hastie G, Lewis M, Mackie L, McNaughton J, Miles J, Neill S, Piggott M, Risch D, Scott B, Sparling C, Stallard T, Thies P, Walker S, White D, Willden R, Williamson B (2021) A review of the UK and British channel islands practical tidal stream energy resource. Proc R Soc A Math Phys Eng Sci 477(2255):20210469
Coles D, Blunden L, Bahaj A (2017) Assessment of the energy extraction potential at tidal sites around the channel islands. Energy 124:171–186
Coles D, Greenwood C, Vogler A, Walsh T, Taaffe D (2018) Assessment of the turbulent flow upstream of the Meygen phase 1A tidal stream turbines. In: 4th Asian wave and tidal energy conference, Taipei, Taiwan
Coles DS, Blunden LS, Bahaj AS (2020) The energy yield potential of a large tidal stream turbine array in the Alderney race. Philos Trans R Soc A Math Phys Eng Sci 378(2178):20190502
Coles DS, Walsh T (2019) Mechanisms for reducing the cost of tidal stream energy. In: 13th European wave and tidal energy conference, Naples, Italy
Crespo A, Hernández J (1996) Turbulence characteristics in wind-turbine wakes. J Wind Eng Ind Aerodyn 61(1):71–85
Culley DM, Funke SW, Kramer SC, Piggott MD (2016) Integration of cost modelling within the micro-siting design optimisation of tidal turbine arrays. Renew Energy 85:215–227
De Dominicis M, Wolf J, O’Hara Murray R (2018) Comparative effects of climate change and tidal stream energy extraction in a shelf sea. J Geophys Res Oceans 123(7):5041–5067
Deskos G, Abolghasemi MA, Piggott MD (2017) Wake predictions from two turbine models using mesh-optimisation techniques. In: Lewis A (ed) Proceedings of the twelfth European wave and tidal energy conference, University College Cork, Ireland. EWTEC. ISSN: 2309-1983
Deskos G, Laizet S, Palacios R (2020) Winc3d: a novel framework for turbulence-resolving simulations of wind farm wake interactions. Wind Energy 23(3):779–794
Divett T, Vennell R, Stevens C (2016) Channel-scale optimisation and tuning of large tidal turbine arrays using LES with adaptive mesh. Renew Energy 86:1394–1405
Draper S, Adcock TA, Borthwick AG, Houlsby GT (2014) Estimate of the tidal stream power resource of the Pentland Firth. Renew Energy 63:650–657
du Feu R, Funke S, Kramer S, Culley D, Hill J, Halpern B, Piggott M (2017) The trade-off between tidal-turbine array yield and impact on flow: a multi-objective optimisation problem. Renew Energy 114:1247–1257
du Feu RJ, Funke SW, Kramer SC, Hill J, Piggott J (2019) The trade-off between tidal-turbine array yield and environmental impact: a habitat suitability modelling approach. Renew Energy 143:390–403
Dufresne N, Wosnik M (2013) Velocity deficit and swirl in the turbulent wake of a wind turbine. Mar Technol Soc J 47(4):193–205
Edina Digimap Service (2020) Hydrospatial one, gridded bathymetry. http://digimap.edina.ac.uk/marine/. SeaZone Solutions Ltd. Accessed 2020
Egbert GD, Erofeeva SY (2002) Efficient inverse modeling of barotropic ocean tides. J Atmos Ocean Technol 19(2):183–204
Fairley I, Masters I, Karunarathna H (2015) The cumulative impact of tidal stream turbine arrays on sediment transport in the Pentland Firth. Renew Energy 80:755–769
Fleming PA, Ning A, Gebraad PM, Dykes K (2016) Wind plant system engineering through optimization of layout and yaw control. Wind Energy 19(2):329–344
Funke S, Farrell P, Piggott M (2014) Tidal turbine array optimisation using the adjoint approach. Renew Energy 63:658–673
Funke SW, Kramer SC, Piggott MD (2016) Design optimisation and resource assessment for tidal-stream renewable energy farms using a new continuous turbine approach. Renew Energy 99:1046–1061
Garrett C, Cummins P (2007) The efficiency of a turbine in a tidal channel. J Fluid Mech 588:243–251
Gebraad PMO, Teeuwiise FW, van Wingerden JW, Fleming PA, Ruben SD, Marden JR, Pao LY (2014) Wind plant power optimization through yaw control using a parametric model for wake effects-a CFD simulation study. Wind Energy 19(1):95–114
González-Gorbeña E, Qassim RY, Rosman PC (2018) Multi-dimensional optimisation of Tidal Energy Converters array layouts considering geometric, economic and environmental constraints. Renew Energy 116:647–658
Goss Z, Coles D, Piggott M (2021a) Economic analysis of tidal stream turbine arrays: a review
Goss ZL, Coles DS, Kramer SC, Piggott MD (2021) Efficient economic optimisation of large-scale tidal stream arrays. Appl Energy 295:116975
Goss ZL, Coles DS, Piggott MD (2020) Identifying economically viable tidal sites within the Alderney Race through optimization of levelized cost of energy: economic viability of the Alderney Race. Philos Trans R Soc A Math Phys Eng Sci 378(2178)
Harcourt F, Angeloudis A, Piggott MD (2019) Utilising the flexible generation potential of tidal range power plants to optimise economic value. Appl Energy 237:873–884
Hardwick J, Ashton I, Johanning L (2015) Field characterisation of currents and near surface eddies in the Pentland Firth. In: Proceedings of the 4th Oxford tidal energy workshop, March 2015, Oxford, UK, pp 34–35
Jensen NO (1983) A note on wind generator interaction. Technical report, Risø National Laboratory, Roskilde
Karna T, de Brye B, Gourgue O, Lambrechts J, Comblen R, Legat V, Deleersnijder E (2011) A fully implicit wetting–drying method for DG-FEM shallow water models, with an application to the Scheldt Estuary. Comput Methods Appl Mech Eng 200(5):509–524
Kärnä T, Kramer SC, Mitchell L, Ham DA, Piggott MD, Baptista AM (2018) Thetis coastal ocean model: discontinuous Galerkin discretization for the three-dimensional hydrostatic equations. Geosci Model Dev Discuss 2018:1–36
Katic I, Højstrup J, Jensen N (1987) A simple model for cluster efficiency publication. In: European wind energy association conference and exhibition, Rome, Italy
King RN, Dykes K, Graf P, Hamlington PE (2017) Optimization of wind plant layouts using an adjoint approach. Wind Energy Sci 2(1):115–131
Kraft D (1988) A software package for sequential quadratic programming. Technical report 28, Institut für Dynamik der Flugsysteme
Kramer SC, Piggott MD (2016) A correction to the enhanced bottom drag parameterisation of tidal turbines. Renew Energy 92:385–396
Lanzilao L, Meyers K (2021) A new wake-merging method for wind-farm power prediction in the presence of heterogeneous background velocity fields. Wind Energy 25(2):237–259
Lo Brutto OA, Thiébot J, Guillou SS, Gualous H (2016) A semi-analytic method to optimize tidal farm layouts—application to the Alderney Race (Raz Blanchard), France. Appl Energy 183:1168–1180
Machefaux E, Larsen GC, Leon JP (2015) Engineering models for merging wakes in wind farm optimization applications. J Phys Conf Ser 625(1):1–12
Mackie L, Evans PS, Harrold MJ, O’Doherty T, Piggott MD, Angeloudis A (2021) Modelling an energetic tidal strait: investigating implications of common numerical configuration choices. Appl Ocean Res 108(January):102494
Mackie L, Kramer SC, Piggott MD, Angeloudis A (2021) Assessing impacts of tidal power lagoons of a consistent design. Ocean Eng 240:109879
Martin-Short R, Hill J, Kramer S, Avdis A, Allison P, Piggott M (2015) Tidal resource extraction in the Pentland Firth, UK: potential impacts on flow regime and sediment transport in the inner sound of stroma. Renew Energy 76(Supplement C):596–607
Martin-Short R, Hill J, Kramer SC, Avdis A, Allison PA, Piggott MD (2015) Tidal resource extraction in the Pentland Firth, UK: potential impacts on flow regime and sediment transport in the Inner Sound of Stroma. Renew Energy 76:596–607
Nash S, O’Brien N, Olbert A, Hartnett M (2014) Modelling the far field hydro-environmental impacts of tidal farms—a focus on tidal regime, inter-tidal zones and flushing. Comput Geosci 71:20–27
Neill SP, Angeloudis A, Robins PE, Walkington I, Ward SL, Masters I, Lewis MJ, Piano M, Avdis A, Piggott MD et al (2018) Tidal range energy resource and optimization-past perspectives and future challenges. Renew energy 127:763–778
Neill SP, Hashemi MR, Lewis MJ (2014) Optimal phasing of the European tidal stream resource using the greedy algorithm with penalty function. Energy 73:997–1006
Niayifar A, Porté-Agel F (2016) Analytical modeling of wind farms: a new approach for power prediction. Energies 9(9):1–13
Nishino T, Willden RH (2012) Effects of 3-D channel blockage and turbulent wake mixing on the limit of power extraction by tidal turbines. Int J Heat Fluid Flow 37:123–135
Nishino T, Willden RH (2013) Two-scale dynamics of flow past a partial cross-stream array of tidal turbines. J Fluid Mech 730:220–244
NREL (2020) FLORIS. Version 2.2.0
O’Hara Murray R, Gallego A (2017) A modelling study of the tidal stream resource of the Pentland Firth, Scotland. Renew Energy 102:326–340
Ouro P, Nishino T (2021) Performance and wake characteristics of tidal turbines in an infinitely large array. J Fluid Mech 925:A30
Ouro P, Ramírez L, Harrold M (2019) Analysis of array spacing on tidal stream turbine farm performance using large-Eddy simulation. J Fluids Struct 91:102732
Phoenix A, Nash S (2019) Optimisation of tidal turbine array layouts whilst limiting their hydro-environmental impact. J Ocean Eng Mar Energy 5(3):251–266
Piggott MD, Kramer SC, Funke SW, Culley DM, Angeloudis A (2021) Optimization of marine renewable energy systems. In: Comprehensive renewable energy, 2nd edn. Elsevier
Rathgeber F, Ham DA, Mitchell L, Lange M, Luporini F, Mcrae ATT, Bercea G-T, Markall GR, Kelly PHJ (2016) Firedrake: automating the finite element method by composing abstractions. ACM Trans Math Softw 43(3):24:1-24:27
Robins PE, Neill SP, Lewis MJ, Ward SL (2015) Characterising the spatial and temporal variability of the tidal-stream energy resource over the northwest European shelf seas. Appl Energy 147:510–522
Sandoval J, Soto-Rivas K, Gotelli C, Escauriaza C (2021) Modeling the wake dynamics of a marine hydrokinetic turbine using different actuator representations. Ocean Eng 222(June 2020)
Schwedes T, Ham DA, Funke SW, Piggott MD (2017) An application: optimising the layout of tidal turbine arrays. In: Mesh dependence in PDE-constrained optimisation: an application in tidal turbine array layouts, chapter 3, 1st edn. Springer, Berlin, pp 79–107
SIMEC Atlantis Energy (2016) AR1500 tidal turbine brochure. https://www.atlantisresourcesltd.com/wp/wp-content/uploads/2016/08/AR1500-Brochure-Final-1.pdf. Accessed 16 Nov 2020
SIMEC Atlantis Energy (2020a) Meygen. https://simecatlantis.com/projects/meygen/. Accessed 16 Apr 2021
SIMEC Atlantis Energy (2020b) Tidal turbines. https://simecatlantis.com/services/turbines/. Accessed 18 Nov 2020
Singh A, Howard KB, Guala M (2014) On the homogenization of turbulent flow structures in the wake of a model wind turbine. Phys Fluids 26(2):025103
Smart G, Noonan M (2018) Tidal stream and wave energy cost reduction and industrial benefit: summary analysis. Technical report, ORE Catapult. https://ore.catapult.org.uk/app/uploads/2018/11/Tidal-Stream-and-Wave-Energy-Cost-Reduction-and-Industrial-Benefit.pdf. Accessed 14 Nov 2021
Stallard T, Collings R, Feng T, Whelan J (2013) Interactions between tidal turbine wakes: Experimental study of a group of three-bladed rotors. Philos Trans R Soc A Math Phys Eng Sci 371(1985)
Stallard T, Feng T, Stansby PK (2015) Experimental study of the mean wake of a tidal stream rotor in a shallow turbulent flow. J Fluids Struct 54:235–246
Stansby P, Stallard T (2016) Fast optimisation of tidal stream turbine positions for power generation in small arrays with low blockage based on superposition of self-similar far-wake velocity deficit profiles. Renew Energy 92:366–375
Stansby PK (2003) A mixing-length model for shallow turbulent wakes. J Fluid Mech 495:369–384
Thiébaut M, Filipot JF, Maisondieu C, Damblans G, Jochum C, Kilcher LF, Guillou S (2020) Characterization of the vertical evolution of the three-dimensional turbulence for fatigue design of tidal turbines: 3D turbulence for fatigue design of TEC. Philos Trans R Soc A Math Phys Eng Sci 378(2178)
Topper MB, Olson SS, Roberts JD (2021) On the benefits of negative hydrodynamic interactions in small tidal energy arrays. Appl Energy 297:117091
U.S. Energy Information Administration (2020) Levelized cost and levelized avoided cost of new generation resources in the annual energy outlook 2020. Technical report. U.S. Energy Information Administration
Vennell R (2011) Tuning tidal turbines in-concert to maximise farm efficiency. J Fluid Mech 671:587–604
Vennell R (2012) The energetics of large tidal turbine arrays. Renew Energy 48:210–219
Vennell R, Funke SW, Draper S, Stevens C, Divett T (2015) Designing large arrays of tidal turbines: a synthesis and review. Renew Sustain Energy Rev 41:454–472
Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, van der Walt SJ, Brett M, Wilson J, Millman KJ, Mayorov N, Nelson ARJ, Jones E, Kern R, Larson E, Carey CJ, Polat İ, Feng Y, Moore EW, VanderPlas J, Laxalde D, Perktold J, Cimrman R, Henriksen I, Quintero EA, Harris CR, Archibald AM, Ribeiro AH, Pedregosa F, van Mulbregt P, SciPy 1.0 Contributors, (2020) SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods 17:261–272
Vouriot CV, Angeloudis A, Kramer SC, Piggott MD (2019) Fate of large-scale vortices in idealized tidal lagoons. Environ Fluid Mech 19(2):329-348
Wituła R, Słota D (2010) Cardano’s formula, square roots, Chebyshev polynomials and radicals. J Math Anal Appl 363(2):639–647
Zhang J, Zhang C, Angeloudis A, Kramer SC, He R, Piggott MD (2022) Interactions between tidal stream turbine arrays and their hydrodynamic impact around Zhoushan island, China. Ocean Eng 246:110431
Zong L, Nepf H (2012) Vortex development behind a finite porous obstruction in a channel. J Fluid Mech 691:368–391
Acknowledgements
The provision of ADCP data by SIMEC Atlantis Energy is gratefully acknowledged. We would also like to acknowledge the rigorous comments of the reviewers that have helped improve the final manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
A. Angeloudis acknowledges the support of the NERC Industrial Innovation fellowship grant NE/R013209/2. D. Coles acknowledges the support of the Tidal Stream Industry Energiser project (TIGER), co-financed by the European Regional Development Fund through the INTERREG France (Channel) England Programme. M. Piggott acknowledges the support of EPSRC under Grants EP/M011054/1 and EP/R029423/1.
Author information
Authors and Affiliations
Contributions
CJ: methodology, formal analysis, investigation, writing—original draft, writing—review and editing, software, and visualisation. DD: methodology, formal analysis, software, and writing—review and editing. AF: validation, writing—review and editing. GD: conceptualisation, software, and writing—review and editing. DC: data curation, and writing—review and editing. MP: conceptualisation, methodology, writing—review and editing, supervision, and funding acquisition. AA: conceptualisation, methodology, software, investigation, resources, writing—review and editing, supervision, project administration, and funding acquisition.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no conflict of interests to declare.
Ethics approval
Not applicable.
Consent to participate
All authors have provided their consent to participate in this study.
Consent for publication
All authors provide consent for publication of the present work.
Code availability
The software used can be accessed in https://github.com/thetisproject/thetis and https://github.com/NREL/floris. Further information can be provided upon request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: one name in article note on page 1 was not correct.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jordan, C., Dundovic, D., Fragkou, A.K. et al. Combining shallow-water and analytical wake models for tidal array micro-siting. J. Ocean Eng. Mar. Energy 8, 193–215 (2022). https://doi.org/10.1007/s40722-022-00225-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40722-022-00225-2