MNLS simulations of surface wave groups with directional spreading in deep and finite depth waters

Abstract

We simulate focusing surface gravity wave groups with directional spreading using the modified nonlinear Schrödinger (MNLS) equation and compare the results with a fully-nonlinear potential flow code, OceanWave3D. We alter the direction and characteristic wavenumber of the MNLS carrier wave, to assess the impact on the simulation results. Both a truncated (fifth-order) and exact version of the linear dispersion operator are used for the MNLS equation. The wave groups are based on the theory of quasi-determinism and a narrow-banded Gaussian spectrum. We find that the truncated and exact dispersion operators both perform well if: (1) the direction of the carrier wave aligns with the direction of wave group propagation; (2) the characteristic wavenumber of the carrier wave coincides with the initial spectral peak. However, the MNLS simulations based on the exact linear dispersion operator perform significantly better if the direction of the carrier wave does not align with the wave group direction or if the characteristic wavenumber does not coincide with the initial spectral peak. We also perform finite-depth simulations with the MNLS equation for dimensionless depths ($k_{\text {p}}d$) between 1.36 and 5.59, incorporating depth into the boundary conditions as well as the dispersion operator, and compare the results with those of fully-nonlinear potential flow code to assess the finite-depth limitations of the MNLS.

1 Introduction

The modified nonlinear Schrödinger (MNLS) equation is frequently used in studies of “rogue” or “freak” ocean waves due to the low computational expense and high fidelity of the simulations. A comprehensive overview of rogue wave studies can be found in Kharif and Pelinovsky (2003), Kharif et al. (2008), Dysthe et al. (2008) and Adcock and Taylor (2014). Schrödinger equations are also frequently used to investigate optical rogue waves (Akhmediev et al. (2013), Onorato et al. (2013), Dudley et al. (2014)) including the dynamics of optical solitons (see, e.g., Pinar et al. (2020)). In this study, we use the MNLS equation for the first harmonic of the surface elevation as presented in Trulsen et al. (2000), based on the work of Trulsen and Dysthe (1996):

$$\begin{aligned}&\frac{\partial {B}}{\partial {t}}+{\mathfrak {L}}\,B+ \frac{1}{2}{i\omega _{0}k_{0}^{2}}{|B|}^{2}B+ \frac{3}{2}{\omega _{0}k_{0}}{|B|^{2}\frac{\partial {B}}{\partial {x}}}\nonumber \\&\quad +\frac{1}{4}{\omega _{0}k_{0}}B^{2}\frac{\partial {B^{*}}}{\partial {x}} +ik_0\frac{\partial {\overline{\phi }}}{\partial {x}}B=0, \end{aligned}$$

(1)

to simulate directionally-spread, steep groups of ocean waves formed by dispersive focusing. Here, B represents the complex wave envelope based on the first harmonic of the surface elevation and the characteristic wavenumber and angular frequency of the carrier wave are denoted by $k_0$ and $\omega _0$. Note that the velocity potential expression corresponding to (1) reverses the sign of the ${B^2}({\partial {B^*}/\partial {x}})$ term to be negative, as listed in Trulsen and Dysthe (1996). The dispersion operator $\mathfrak {L}$ in (1) may be based upon a truncated version of the linear dispersion relationship (see Trulsen and Dysthe (1996)) or an alternative pseudo-differential operator that preserves the exact linear dispersion relationship (see Trulsen et al. (2000)). We contrast the performance of the two dispersion operators and compare the results with a fully-nonlinear potential flow solver. We also consider the effect of selecting different characteristic wavenumbers and directions for the MNLS carrier wave. Finally, we perform finite-depth simulations with (1) using the arbitrary-depth linear dispersion relationship, $\omega =\sqrt{gk\tanh {(kd)}}$ to evaluate the exact version of $\mathfrak {L}B$ with finite-depth also incorporated into the boundary conditions to assess the finite-depth limitations of (1). We focus on the impact of four-wave, or “quartet”, interactions on the shape and spectral evolution of the focusing wave groups and assess the fidelity of the various MNLS formulations.

The MNLS formulation is based upon a carrier wave that requires a characteristic wavenumber and direction. In random seas, the selection of the characteristic wavenumber and direction is typically based on the background sea state. Examples of MNLS simulations of random seas include Dysthe et al. (2003), Socquet-Juglard et al. (2005), Gramstad and Trulsen (2007), Xiao et al. (2013) and Adcock et al. (2015). An appropriate value for the characteristic wavenumber may be clear if the wave spectrum is symmetric about a spectral peak. Similarly, a sea state featuring a concentration of wave components aligned to a particular direction provides a clear choice for the carrier wave direction. However, sea states without a clear spectral peak or dominant wave direction provide less clarity for the carrier wave parameters. For long simulations there may also be a change in the spectral peak due to non-linear physics and, if activated, energy input or damping. Furthermore, the characteristics of an individual steep wave event in a random sea may not be consistent with the background sea state. Individual wave events may form at an angle to the dominant wave direction and local spectral distortions may also arise in the vicinity of a steep wave event due to nonlinear wave–wave interactions. Thus, the selection of the characteristic direction and wavenumber for the MNLS carrier wave can present obstacles. We investigate the sensitivity of our results to the selection of the characteristic wavenumber and direction of the MNLS carrier wave. We deliberately test the MNLS equations beyond the parameter range expected in practice, to ascertain the limits of the various formulations.

Fig. 1

Surface elevation of wave groups at focus with a steepness ($Ak_p$) of 0.3, simulated with identical initial conditions using the fully-nonlinear potential flow solver OceanWave3D: a time marched with linear free surface boundary conditions; b time marched with nonlinear free surface boundary conditions. The formation of wing waves is indicated with $\mathcal {W}$

We simulate isolated wave groups formed by dispersive focusing rather than random seas. An isolated wave group, based on a coherent phase distribution, features the same nonlinear wave–wave interactions observed in random seas. However, the effect of the nonlinear interactions can be more easily identified and the computational expense is lower. Figure 1 shows focused wave groups simulated with a potential flow code. Identical initial conditions were used for the wave groups shown in Fig. 1a, b. However, Fig. 1a shows the focused wave event with linear free-surface boundary conditions and Fig. 1b shows the focused wave event with the fully-nonlinear free-surface boundary conditions. As can be seen, the shape of the focused wave event in Fig. 1b differs from Fig. 1a. The largest crest sits in the center of the wave group in Fig. 1a but has moved to the front of the wave group in Fig. 1b. Energy transfers to oblique components also results in the formation of “wing waves” in Fig. 1b, denoted with ${\mathcal {W}}$. Thus, nonlinear wave–wave interactions can significantly influence the formation of a steep wave event, and we investigate the fidelity of various MNLS formulations in resolving the nonlinear interactions. The wing-waves are themselves propagating at approximately 12$^{\circ }$ to the mean direction and are thus an example of the phenomena which may be poorly captured by an MNLS type model.

The MNLS equation accounts for linear dispersion of the wave components as well as nonlinear wave–wave interactions. The MNLS equation of Trulsen and Dysthe (1996) performs an expansion on the linear dispersion operator with truncation at the fifth order. In contrast, the MNLS equation of Trulsen et al. (2000) retains the exact linear dispersion relation by numerical evaluation of the linear dispersion operator. Use of the exact linear dispersion relation by Trulsen et al. (2000) is expected to increase the bandwidth limits of the MNLS equation while improving the resolution of four-wave “quartet” interactions and eliminating energy leakage. In this study, we contrast the results of the two dispersion operators. We note that the MNLS equations of Trulsen and Dysthe (1996) and Trulsen et al. (2000) are both fourth-order in steepness, shown by Stiassnie (1984) to only resolve quartet interactions. Thus, all the spectral changes observed in this study are attributed to quartet interactions.

The impact of finite depth on quartet interactions has been previously investigated. Benney and Roskes (1969) and McLean (1982) showed that the dominant directions of energy transfer for a degenerate quartet depend upon the dimensionless water depth. A variety of MNLS formulations have been proposed to account for the impact of depth on quartet interactions. Third-order “cubic” Nonlinear Schrödinger (NLS) equations for three-dimensional waves at finite depths have been presented by Benney and Roskes (1969) and Davey and Stewartson (1974). A fourth-order equation for water waves at finite depths has been presented by Brinch-Nielsen and Jonsson (1986). The classic MNLS equation of Trulsen and Dysthe (1996) does, however, incorporate finite-depth into the boundary conditions and the exact dispersion operator of Trulsen et al. (2000) allows depth effects to be included in the dispersion relationship with ease. Trulsen and Dysthe (1996) show that the classic MNLS formulation captures the bifurcation of the most unstable perturbation for a Stokes wave at finite depths, suggesting that the classic MNLS equation may be appropriate for some finite-depth simulations. Depth-sensitive coefficients for the nonlinear terms of the MNLS equation have also been proposed by Sedletsky (2003) and we use these coefficients together with the exact linear dispersion operator of Trulsen et al. (2000) as a potential finite-depth MNLS model. To assess the performance of our finite-depth MNLS simulations, we compare the results with those of a fully-nonlinear potential flow code.

2 Numerical methodology

We perform simulations with the MNLS equation as well as the fully-nonlinear potential flow code OceanWave3D based on wave groups formed by dispersive focusing. Our simulations follow a three-step process: (1) We use the theory of quasi-determinism to determine the shape of the wave group at focus; (2) Using the linear dispersion relation, we propagate the wave components for 15 characteristic wave periods backwards in time to calculate the initial conditions at $t/T_0=-15$; (3) We initialise the simulations at $t/T_0=-15$ and run the simulation forwards in time for 30 characteristic wave periods until $t/T_0=+15$. Steps 1 and 2 are identical for the OceanWave3D and MNLS simulations, i.e., we use identical initial conditions for the two types of simulations. Only step 3 differs, in terms of which code is used to do the forward propagation of the wave components in time.

2.1 Initial conditions

Implementation of the theory of quasi-determinism requires the underlying wave spectrum of the sea state. We define the variance density spectrum $F(k,\theta )$ as the product of a wavenumber magnitude spectrum S(k) and a spreading function $D(\theta )$. We use a Gaussian function as the wavenumber magnitude spectrum:

$$\begin{aligned} S(k)=S_0\exp {\bigg {(}\frac{-{(k-k_{\text {p}})}^{2}}{2{k_{\text {w}}}^{2}}\bigg {)}}, \end{aligned}$$

(2)

where k is the wavenumber, $k_{\text {p}}$ is the wavenumber corresponding to the initial spectral peak, and $k_{\text {w}}$ is the spectral width. A Gaussian distribution has also been used for the spreading function:

$$\begin{aligned} D(\theta )=\frac{1}{\varsigma _0\sqrt{2\pi }} \exp {\bigg {(}\frac{-(\theta -\chi )^2}{2{\varsigma _0^2}}\bigg {)}}, \end{aligned}$$

(3)

based on the initial spreading parameter ($\varsigma _0$) and the direction of the wave component ($\theta$). Here, $\chi$ represents the dominant angle of propagation for the wave components. The variance density spectrum $F(k,\theta )$ is thus defined as the product of two Gaussian functions, and Table 1 lists the values used in this study. All the simulations considered in this investigation are based upon a fixed steepness ($Ak_{\text {p}}$) with fixed spectral parameters ($k_{\text {p}}$, $k_{\text {w}}$, $\varsigma _0$). Only the parameters of the MNLS carrier wave and the dimensionless depth ($k_{\text {pd}}$) of the domain are varied. Barratt et al. (2021) showed that the absence of the spectral tail can result in augmented wave–wave interactions. Thus, the spectra used in this study represent a conservative test of the MNLS equation, since more realistic spectra are likely to result in weaker wave–wave interactions than those observed in this investigation. The initial spectrum used is reasonably narrow-banded and thus one would expect the MNLS model to perform well. However, the rapid weakly nonlinear wave–wave interactions will cause a broadening of the bandwidth in the mean wave direction (Gibbs and Taylor (2005); Adcock et al. (2012)) which potentially invalidates the narrow-banded assumption.

Table 1 Initial condition parameters

Quasi-determinism (QD) theory, based on Boccotti (2000) and Lindgren (1970), indicates that the average shape of an extreme event in a random, linear Gaussian field is the scaled auto-correlation function. The linear surface elevation of the wave group is, thus, given by:

$$\begin{aligned} \eta _{\text {L}}(x,y,t)={A_{\text {L}}}\frac{\sum _{i,j}{F(k_{i}, \theta _{j})\cos {(k_{i}\cos {\theta _{j}}\,x+k_{i} \sin {\theta _{j}}\,y-\omega _{i}{t}+\varphi _{0})}}}{\sum _{i,j}{F(k_{i},\theta _{j})}}. \end{aligned}$$

(4)

Here, $k_{i}$ is the magnitude of the wavenumber component, $\theta _{j}$ is the propagation direction and $A_{\text {L}}$ is the linear amplitude of the wave group at focus. A phase offset $\varphi _0$ is included in (6) to implement the “phase separation” method of removing bound harmonics (see Fitzgerald et al. (2014)). For the MNLS simulations, removal of the bound harmonics is not necessary and $\varphi _0$ is set to zero, causing linear focus to occur at ($x=0$, $y=0$, $t/T_{0}=0$). For the OceanWave3D simulations, each simulation is repeated with $\varphi _0$ values of $0^{\circ }$, $90^{\circ }$, $180^{\circ }$ and $270^{\circ }$ to remove the bound harmonics with four-phase separation, as used by Barratt et al. (2021). The angular frequency of each component ($\omega _{i}$) is calculated from the arbitrary-depth linear dispersion relationship, $\omega _{i}=\sqrt{gk_{i}\tanh {(k_{i}d)}}$, allowing the initial conditions to be calculated at $t/T_0=-15$. We calculate the corresponding velocity potential and apply exact second-order correction of the initial conditions using Dalzell (1999). The surface elevation and velocity potential are prescribed as initial conditions for the potential flow simulations.

For the MNLS simulations, we calculate the initial complex envelope $B(\varvec{x},t)$ using the linear surface elevation $\eta _{{\text {L}}}$ and the Hilbert transform of the linear surface elevation $\eta _{\text {L}}^{\text {H}}$ following Osborne (2010):

$$\begin{aligned} B(\varvec{x},t)=\{\eta _{\text {L}}+i\eta _{\text {L}}^{\text {H}}\}\exp {(-i[\varvec{k}_0 \cdot \varvec{x}-\omega _0\,{t}])}. \end{aligned}$$

(5)

Here, $\varvec{k}_0$ and $\omega _0$ are the properties of the carrier wave.

2.2 Potential flow simulations

OceanWave3D numerically solves the governing equations of potential flow for surface gravity waves (Currie 1993, pp. 201–204), including the fully-nonlinear free surface boundary conditions. Described in detail by Engsig-Karup et al. (2009), OceanWave3D is based on an Eulerian frame of reference and the three-dimensional spatial domain is discretized with Cartesian coordinates (x, y, z). Table 2 lists the horizontal grid resolution ($\Delta {x}$, $\Delta {y}$), which is uniform throughout the domain, together with the number of grid points ($N_x$, $N_y$) in the x and y-directions. We utilise a symmetry plane along the centreline of the wave group ($y=0$) for the potential flow simulations. Thus, the domain width based on Table 2 only represents half the effective domain width for the potential flow simulations. The vertical distribution of grid points follows the symmetric half of a Chebyshev–Gauss–Lobatto (CGL) distribution with the vertical number of grid points ($N_z$) listed in Table 2.

Table 2 Grid parameters for OW3D and MNLS simulations

We use eighth-order finite differencing of the spatial derivatives throughout the domain combined with fourth-order Runge–Kutta time marching and a Courant–Friedrichs–Lewy (CFL) condition of 0.5, based on the phase speed ($c_0$) associated with the wavenumber of the spectral peak ($k_{\text {p}}$) and the horizontal grid resolution in the x direction ($\Delta {x}$). Our selection of the simulation parameters is informed by the numerical error assessment of Barratt et al. (2020) based on similar simulations. The simulations of Barratt et al. (2020) were found to agree well with other potential flow codes with total energy conservation within 0.04% over 40 wave periods. For comparison against the MNLS simulations, we use the four-phase separation technique (Fitzgerald et al. (2014)), to remove the bound harmonics from the potential flow simulations and approximate the linear surface elevation ($\eta _{\text {L}}$). Using the Hilbert transform of the linear surface elevation ($\eta _{\text {L}}^{\text {H}}$), we calculate the absolute value of the complex wave envelope, |B|:

$$\begin{aligned} |B|=\sqrt{(\eta _{\text {L}})^{2}+(\eta _{\text {L}}^{\text {H}})^2}, \end{aligned}$$

(6)

to compare the envelope steepness between the potential flow and MNLS simulations. Note that the ability of the MNLS formulation to model bound harmonics has been considered by Adcock and Taylor (2016).

2.3 MNLS simulations

We perform simulations with the MNLS equations of Trulsen and Dysthe (1996) as well as Trulsen et al. (2000). We repeat the MNLS simulations based upon different characteristic wavenumbers for the carrier wave. We also alter the direction of the carrier wave relative to the direction of wave group propagation using the parameter $\chi$ as included in (3). The carrier wave is always aligned with the x-axis, corresponding to $\theta =0^{\circ }$, while the direction of wave group propagation is determined by $\chi$.

The MNLS formulation assumes that the surface elevation $\eta (\varvec{x},t)$ may be represented by modulation of a carrier wave with the characteristic wave vector $\varvec{k}_0=(k_0,0)$ based upon a characteristic wavenumber magnitude $k_0$. In this study, we normalise $k_0$ by the wavenumber of the initial spectral peak $k_{\text {p}}$ to define the ratio:

$$\begin{aligned} \beta =k_0/k_{\text {p}}. \end{aligned}$$

(7)

We perform simulations with $\beta$ values between 0.7 and 1.3 in increments of 0.1. We define the direction of the carrier wave relative to the direction of wave group propagation, following the coordinate system shown in Fig. 2. Our coordinate system aligns the carrier wave with the x-axis and the direction of wave group propagation aligns with the $x^{*}$-axis. The angle between the axes is denoted $\chi$ and we perform simulations with $\chi$ values between $0^{\circ }$ and $30^{\circ }$ in intervals of $5^{\circ }$. In the spectral domain, wavenumbers $k_x$ and $k_y$ correspond to the x and y-axes respectively while wavenumbers $k_x^*$ and $k_y^*$ correspond to the $x^*$ and $y^*$-axes, respectively. All spectral evolution plots are shown in terms of $k_x^*$ and $k_y^*$ based on the coordinate system of the wave group.

Fig. 2

Coordinate systems for MNLS simulations. Contour levels depict the surface elevation $\eta$ of the wave group, evenly distributed between 1 and 5 m in intervals of 1 m. The direction of the carrier wave coincides with the x-axis and the wave group propagates in the direction of the $x^{*}$-axis. The angle between the axes is denoted as $\chi$

The nonlinear evolution of the complex envelope is simulated with the MNLS equation, see (1), subject to the free surface and bottom boundary conditions, as well as continuity for the mean flow potential $\overline{\phi }$:

$$\begin{aligned} \frac{\partial {\overline{\phi }}}{\partial {z}}= & {} \frac{\omega _{0}}{2}\frac{\partial }{\partial {x}}|B|^{2}\text {at}z=0, \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial {\overline{\phi }}}{\partial {z}}= & {} 0\text {at}z=-d, \end{aligned}$$

(9)

$$\begin{aligned} \nabla ^{2}{\overline{\phi }}= & {} 0\text {for}{-\infty<z<0}. \end{aligned}$$

(10)

In (1), $\mathfrak {L}$ represents a dispersion operator, acting upon the complex envelope B, which can be expressed as:

$$\begin{aligned} \begin{aligned}&\mathfrak {L}\,B=\\&\frac{1}{4\pi ^{2}}\int _{-\infty }^{\infty }i[\omega (\varvec{k_{0}}+\varvec{\mu })-\omega _{0}]\exp {(i\varvec{\mu }\cdot (\varvec{x}-\varvec{y}))B(\varvec{y},t)\text {d}{\varvec{y}}\text {d}{\varvec{\mu }}}. \end{aligned} \end{aligned}$$

(11)

Here, $\varvec{u}=(\lambda ,\mu )$ is the modulation wavenumber and $\omega _0$ is the frequency corresponding to the characteristic wavenumber $k_0$ based on the linear dispersion relation. Expansion of $\omega (\varvec{k_{0}}+\varvec{\mu })$ in (11) utilising the linear dispersion relation, followed by truncation at the fifth order, yields the linear part of the Trulsen and Dysthe (1996) equation. Direct numerical evaluation of (11) avoids truncation, retaining the exact linear dispersion relation, as shown by Trulsen et al. (2000). Retention of exact linear dispersion in (11) increases the bandwidth limits of the MNLS equation and improves the resolution of four-wave interactions while eliminating energy leakage (see Martin and Yuen (1980) and Yuen and Lake (1980)), with almost no additional computational cost. We use both the truncated and exact versions of (11) in our simulations and compare the results to assess the impact of the truncated/exact linear dispersion operators. To perform our MNLS simulations, we incorporate the boundary conditions, (8) and (9), directly into the MNLS equation, (1), using the continuity condition for the mean flow, (10), as done with the fourth-order envelope equation of Janssen (1983). A single governing equation is, thus, obtained:

(12)

where $\mathcal {F}$ denotes a 2D Fourier transform in x and y and $\mathcal {F}^{\,-1}$ denotes the inverse operation. Note that (12) includes a depth-dependent return current term which results from the incorporation of finite depth into the bottom boundary condition in (9). For our simulations based on (12), we use the arbitrary-depth linear dispersion relation, $\omega =\sqrt{gk\tanh {(kd)}}$, to evaluate the dispersion operator $\mathfrak {L}\,B$ with the exact version of (11). We also perform MNLS simulations based on infinite depth (|k|d goes to $\infty$) with the corresponding expression:

(13)

For our simulations based on (13), we use the deep-water linear dispersion relation, $\omega =\sqrt{gk}$, to evaluate the dispersion operator $\mathfrak {L}\,B$. Our comparison of the truncated and exact versions of (11) is based upon (13). We directly discretize and numerically solve (12) and (13) using a split-step algorithm. We use spectral methods to evaluate both the exact and truncated versions of (11), using the Fourier transform to treat the spatial derivatives as multiplier operators for the linear dispersion terms presented in Trulsen and Dysthe (1996). We use fourth-order finite differencing with symmetric stencils for the spatial derivatives in the nonlinear terms. Time marching is performed with the classic fourth-order Runge–Kutta scheme. We perform simulations with Courant–Friedrichs–Lewy (CFL) conditions of 0.5 and 1.0 to assess the effect, based on the group speed ($c_{\text {g}}$) of the wave group ($k_{\text {p}}$) and the horizontal grid resolution in the x-direction ($\Delta {x}$). Note that the definition of the CFL differs between the potential flow and MNLS simulations since the group speed ($c_{\text {g}}$) is the characteristic velocity of the wave envelope in the MNLS simulations while the phase speed ($c_0$) is the characteristic velocity of the free surface in the potential flow simulations.

We also perform finite-depth MNLS simulations by combining the exact version of (11), based on the arbitrary-depth linear dispersion relation, with depth-sensitive coefficients for the nonlinear terms proposed by Sedletsky (2003):

(14)

denoted as $q_3$, $Q_{41}$ and $Q_{42}$ in (14) and plotted against dimensionless depth ($k_0{d}$) in Fig. 3. We note that the coefficients were first derived by Sedletsky (2003) and later confirmed by Slunyaev (2005). However, Slunyaev (2005) includes one additional term in the expansion of the mean flow and we use the versions of $q_3$, $Q_{41}$ and $Q_{42}$ listed in Gandzha and Sedletsky (2017), consistent with the results of Slunyaev (2005). An expansion of the induced mean flow allows the effect of the return current term to be encompassed within the coefficients $q_3$, $Q_{41}$ and $Q_{42}$. Thus, (14) does not contain a return current term. Finite-depth is known to suppress quartet interactions and Fig. 3 shows that the values of $q_3$, $Q_{41}$ and $Q_{42}$ decline as the dimensionless depth ($k_0{d}$) is reduced from 5.592 to 1.363. Notably, the value of $q_3$ goes to zero at $k_0{d}=1.363$, the critical depth of vanishing modulational instability for unidirectional waves, and $Q_{42}$ turns negative for $k_0{d}<1.731$. Thus, (14) may present a finite-depth MNLS model that captures the suppression of quartet interactions by finite-depth and we assess its performance.

Fig. 3

Coefficients $q_3$, $Q_{41}$ and $Q_{42}$ for dimensionless depths ($k_0{d}$) between 1.363 and 5.592 based on the expressions in Gandzha and Sedletsky (2017). The solid lines represent the coefficient values, used in (14), and the dotted lines represent the asymptotic infinite-depth limits, used in (12) and (13)

2.4 Grid resolution and CFL

We have analysed the discretization error for the MNLS simulations. The OceanWave3D simulations in this study are based on the same parameters as Barratt et al. (2020) and a detailed assessment of the discretization errors can be found therein. The MNLS simulations have been performed with two grid levels, termed “intermediate” and “fine”, with the parameters listed in Table 2. Note that a symmetry plane has not been used for the MNLS simulations. We have assessed the effect of the grid resolution and CFL with the results listed in Table 3. We consider the maximum steepness of the wave group ($Ak_{\text {p}}^{*}$), observed at any time in the simulation, as well as the corresponding time at which the maximum is reached ($t^{*}/T_0$). The Nonlinear Schrödinger (NLS) equation has an infinite number of conserved quantities (Zakharov and Shabat (1972)) and we consider the conserved quantity $I_2$.

Table 3 MNLS convergence study based on grid resolution/CFL

$$\begin{aligned} I_2=\sum _{i,j}|B(x_{i},y_{j})|^{2}, \end{aligned}$$

(15)

typically associated with energy conservation. We calculate $I_2$ at each time step and the maximum discrepancy in $I_2$ relative to the initial value (denoted as $\Delta {I_2^{*}}$), has been recorded and listed in Table 3 for the different grid resolutions and CFL conditions. Our assessment of grid resolution is based on dimensionless length scales for the wave envelope ($\Lambda _x$, $\Lambda _y$) in the x and y directions:

$$\begin{aligned} \Lambda _x=\frac{2\pi }{k_{\text {w}}},\Lambda _y=\frac{2\pi }{k_{\text {p}}\varsigma _0}, \end{aligned}$$

(16)

based on the spectral bandwidth ($k_{\text {w}}$), the initial peak wavenumber ($k_{\text {p}}$) and the initial spreading parameter ($\varsigma _0$) in radians. Dimensionless metrics for grid resolution, in the x and y-directions can, thus, be defined as:

$$\begin{aligned} n_x=\frac{\Lambda _x}{\Delta {x}},n_y=\frac{\Lambda _y}{\Delta {y}}, \end{aligned}$$

(17)

which approximately represent the number of grids spanning the wave envelope in the x and y-directions. Table 3 lists the values of $n_x$ and $n_y$ for the different MNLS grid resolutions.

Table 3 indicates that the maximum steepness of the wave group does not differ significantly between the different grid resolutions and CFL conditions for the MNLS simulations. An $Ak_{\text {p}}^{*}$ value of 0.304–0.305 occurs in all the cases. However, the time at which the max steepness occurs does show a dependency on the CFL condition. A combination of the intermediate grid resolution with a CFL value of 1.0 results in premature focusing of the wave group. Thus, we use the intermediate grid resolution with a CFL value of 0.5 which shows close agreement in focal time with the fine grid cases. We note that the $\Delta {I_2^{*}}$ value of 0.0106% indicates negligible changes to the conserved quantity $I_2$, associated with energy conservation. The maximum steepness $Ak_{\text {p}}^{*}$ and focal time $t^{*}/T_0$ of the MNLS simulations do differ from the potential flow results. We attribute the differences to an overestimation of nonlinear interactions by the MNLS equation, as discussed in the results section.

3 Results and discussion

We investigate focusing wave groups, in deep and finite depths, and compare the results of MNLS simulations, based on exact and truncated versions of the dispersion operator, with fully-nonlinear potential flow simulations performed with OceanWave3D. The impact of the carrier wavenumber for the MNLS simulations is assessed as well as the impact of the carrier wave direction, relative to the direction of wave group propagation. Our analysis considers the steepness of the wave envelope over the course of the simulations as well as the spectral evolution of the wave group.

Fig. 4

Envelope steepness over time for OceanWave3D (OW3D) and infinite-depth MNLS simulations, based on (13), performed with exact linear dispersion operator (‘MNLS00’) and truncated linear dispersion operator (‘MNLS96’). The amplitude A(t) is based on the maximum elevation of the wave envelope at time t

Fig. 5

Amplitude spectra of surface elevation for a OceanWave3D simulation with dimensionless depth of $k_{p}d=5.59$: a $t/T_{0}=-15$; b $t/T_{0}=0.0$; c $t/T_{0}=7.5$; d $t/T_{0}=15$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 6

Amplitude spectra of surface elevation for an infinite-depth MNLS simulation, based on (13), with exact linear dispersion operator: a $t/T_{0}=-15$; b $t/T_{0}=0.0$; c $t/T_{0}=7.5$; d $t/T_{0}=15$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 7

Amplitude spectra of surface elevation for an infinite-depth MNLS simulations, based on (13), with truncated linear dispersion operator: a $t/T_{0}=-15$; b $t/T_{0}=0.0$; c $t/T_{0}=7.5$; d $t/T_{0}=15$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 8

Envelope steepness over time for infinite-depth MNLS simulations, based on (13), with different characteristic wavenumbers ($\beta =k_0/k_p$), performed with: a exact linear dispersion operator; b truncated linear dispersion operator. The amplitude A(t) is based on the maximum elevation of the wave envelope at time t

3.1 Comparison of OceanWave3D and MNLS results

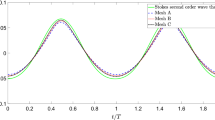
We compare the simulation results from OceanWave3D with infinite-depth MNLS simulations based on (13), both in terms of envelope steepness and spectral evolution. Figure 4 depicts envelope steepness $A(t)k_{\text {p}}$ over time for the OceanWave3D and MNLS simulations. The envelope amplitude A(t) is the maximum elevation of the envelope at time t. The general agreement between the potential flow and MNLS results is good, although the MNLS simulations tend to overpredict the steepness of the wave group at focus. The construction of the wave group implies that the steepness curve shown in Fig. 4 should be symmetric about the time of focus ($t=0$) if the evolution were linear. Thus, asymmetry in the steepness curve and a delay in focus beyond $t=0$ are the result of nonlinear wave–wave interactions. The competing effects of dispersion and nonlinear wave–wave interactions are captured by the Benjamin–Feir index, as discussed by Janssen (2003), impacting the lifespan of focused wave events. The potential flow results in Fig. 4 show evidence of suppressed dispersion causing the wave group to focus after $t=0$ and remain steep after focus, extending the lifespan of the focused wave event. Suppressed dispersion is also apparent for the MNLS simulations, but the effect is less noticeable than observed in the potential flow simulations, with only a small degree of asymmetry apparent for the steepness curve shown in Fig. 4. The MNLS results based on the exact and truncated dispersion operators also agree closely. The MNLS results based on the different dispersion operators are almost identical in the early stages of wave focusing but discrepancies arise during and after the nonlinear focused event.

The MNLS equation is limited in terms of bandwidth and steepness. Thus, the discrepancies may be caused by the increasing steepness of the wave group approaching focus and the oblique energy transfers which increase the spectral bandwidth. The exact dispersion operator is expected to have broader bandwidth limits and improved resolution of four-wave interactions. Thus, discrepancies between the exact and truncated dispersion operator may be expected for wave groups which are particularly steep or broad-banded, accounting for the difference observed during and after focus. Agreement between the MNLS simulations improves towards the end of the simulation, once the post focus wave group has dispersed and the steepness of the group is again reduced. Both of the MNLS results appear to overestimate nonlinearity, resulting in wave groups which are steeper at focus than the OceanWave3D result. However, the discrepancy in envelope amplitude at focus is less than 4%, indicating good agreement between the fully-nonlinear potential flow simulations and the approximate MNLS results.

We also compare the spectral evolution of the OceanWave3D and MNLS simulations to assess the resolution of four-wave interactions. Figure 5 shows the OceanWave3D result, depicting the amplitude spectrum of surface elevation for the initial condition ($t/T_0=-15$) in Fig. 5a and near the time of focus ($t/T_0=0$) in Fig. 5b. Post focus results are depicted at $t/T_0=7.5$ in Fig. 5c and $t/T_0=15$ in Fig. 5d. The initial condition shows a concentration of wave components around the spectral peak consistent with the wave spectrum defined by (2) and (3). Approaching nonlinear focus, the wave spectrum exhibits energy transfers to higher wavenumbers and oblique wave components, as can be seen in Fig. 5b. Post focus, the energy transfers to oblique components intensifies, as can be seen in Fig. 5c, d.

Fig. 9

Amplitude spectra of surface elevation for infinite-depth MNLS simulations, based on (13), performed with the exact linear dispersion operator. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different characteristic wavenumbers ($\beta =k_0/k_p$): a $\beta =0.7$; b $\beta =0.8$; c $\beta =1.0$; d $\beta =1.2$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 10

Amplitude spectra of surface elevation for infinite-depth MNLS simulations, based on (13), performed with the truncated linear dispersion operator. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different characteristic wavenumbers ($\beta =k_0/k_{\text {p}}$): a $\beta =0.7$; b $\beta =0.8$; c $\beta =1.0$; d $\beta =1.2$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Figures 6 and 7 show the corresponding results from the MNLS simulations. Figure 6 is based on the MNLS equation of Trulsen et al. (2000), using the exact version of (11). Figure 7 is based on the MNLS equation of Trulsen and Dysthe (1996), using the fifth order truncated version of (11). As can be seen, both versions of the MNLS equation capture the spectral evolution of the wave group. The energy transfers to oblique and high-wavenumber components are captured in the MNLS wave spectra, near the time of focus and post focus, in Figs. 6 and 7.

3.2 Wavenumber of MNLS carrier wave

The effect of the carrier wavenumber on the evolution of the wave envelope is shown in Fig. 8 for infinite-depth MNLS simulations based on (13). The results based on the exact dispersion operator are shown in Fig. 8a and the results based on the truncated dispersion operator are shown in 8b. Both figures depict the increasing envelope steepness during focusing followed by a post-focus decline in steepness as the wave group disperses. Figure 8a demonstrates that $\beta$ values less than unity do not significantly alter the evolution of the wave envelope if the exact dispersion operator is used. However, $\beta$ values greater than unity do alter the evolution of the envelope for the exact dispersion operator; a $\beta$ of 1.3 reduces the amplitude of the focused event by 4.0%. If the truncated dispersion operator is used, Fig. 8b reveals that $\beta$ values both great and less than unity can impact the evolution of the wave group, indicating a 9.6% reduction in amplitude at focus for a $\beta$ of 0.7. Thus, the truncated operator appears to be more sensitive than the exact operator to the selection of the $\beta$ value. Selecting a carrier wavenumber above/below the spectral peak effectively tests the bandwidth limits of the equation since the largest amplitude wave components exist around the spectral peak. Moving the carrier wavenumber away from the spectral peak, thus, shifts some large amplitude components away from the characteristic wavenumber. The superior performance of the exact dispersion operator, thus, demonstrates the improved bandwidth limits of the MNLS equation with exact dispersion, as indicated by Trulsen et al. (2000).

Fig. 11

Envelope steepness over time for infinite-depth MNLS simulations, based on (13), with different carrier wave directions ($\chi$), performed with: a exact linear dispersion operator; b truncated linear dispersion operator. The amplitude A(t) is based on the maximum elevation of the wave envelope at time t

The impact of the $\beta$ value on spectral evolution is demonstrated by Figs. 9 and 10 with the results for the exact dispersion operator shown in Fig. 9 and the results for the truncated dispersion operator shown in Fig. 10. The amplitude spectrum of surface elevation is shown at the end of the simulation for various $\beta$ values, including: $\beta =0.7$ in Figs. 9a and 10a; $\beta =0.8$ in Figs. 9b and 10b; $\beta =1.0$ in Figs. 9c and 10c; $\beta =1.2$ in Figs. 9d and 10d. Notably, both the exact and truncated dispersion operators appear to under predict oblique energy transfers for $\beta$ values less than unity and both appear to over predict oblique energy transfers for $\beta$ values greater than unity. As can be seen Figs. 9 and 10, the exact and truncated dispersion operators exhibit similar spectra for $\beta$ values of 1.0 and 1.2. However, for $\beta$ values less than unity, differences in the spectra arise between the exact and truncated dispersion operators. The truncated dispersion operator exhibits energy leakage to wavenumbers above the spectral peak forming a local peak at $k_x^*/k_{\text {p}}=1.67$ for $\beta =0.7$. However, no such energy leakage is apparent with the exact dispersion operator for $\beta$ values of 0.7 and 0.8. Energy leakage in the MNLS equation, reported by Martin and Yuen (1980), is a source of inaccuracy which can contaminate the solution, particularly in the context of long-term random sea simulation in which the effect accumulates over time. Trulsen et al. (2000) indicate that the exact dispersion operator eliminates energy leakage, and no significant evidence of energy leakage can be seen in Fig. 9 for all $\beta$ values.

3.3 Direction of MNLS carrier wave

The impact of the carrier wave direction on the evolution of the wave envelope is shown in Fig. 11 for infinite-depth MNLS simulations based on (13). The results for the exact dispersion operator are shown in Fig. 11a and the results for the truncated dispersion operator are shown in Fig. 11b. The steepness of the wave envelope over time is shown for relative angles ($\chi$) between $0^{\circ }$ and $30^{\circ }$ in intervals of $5^{\circ }$. The exact dispersion operator performs well even for a large relative angle between the carrier wave and direction of wave group propagation; an angle of $30^{\circ }$ results in a 3.1% reduction in amplitude at focus. The truncated dispersion operator performs well for small relative angles, an angle of $10^{\circ }$ results in a 4.5% reduction in amplitude at focus. However, the truncated dispersion operator performs less well for large relative angles; an angle of $30^{\circ }$ results in a 18.5% reduction in amplitude at focus. A relative angle between the carrier wave and the direction of propagation for the wave group is another means of testing the bandwidth limits of the MNLS equations. Introducing an angle between the carrier wave and the components which comprise the wave group effectively shifts the characteristic wavenumber in the azimuthal direction away from the spectral peak. Thus, the lower sensitivity of the exact dispersion operator to the relative angle demonstrates the superior bandwidth limits of the MNLS equation based on exact dispersion.

The spectral evolution of the wave group for various angles of the carrier wave ($\chi$) is shown in Figs. 12 and 13 for the exact dispersion operator and the truncated dispersion operator, respectively. The amplitude spectrum at the end of the simulation is shown for various angles of the carrier wave, including: $\chi =0^{\circ }$ in Figs. 12a and 13a; $\chi =10^{\circ }$ in Figs. 12b and 13b; $\chi =20^{\circ }$ in Fig. 12c and 13c as well as $\chi =30^{\circ }$ in Figs. 12d and 13d. The wave group is spatially symmetric about the $y^{*}$-axis, corresponding to spectral symmetry about the $k_y^{*}$-axis if all four-wave interactions are properly resolved. For the exact dispersion operator, Fig. 12 shows a low sensitivity to the angle of the carrier wave; an angle of $\chi =10^{\circ }$ introduces minor asymmetries into the spectral evolution but the result is highly consistent with the $\chi =0^{\circ }$ result. An angle of $\chi =30^{\circ }$ intensifies the asymmetries but the exact dispersion operator still facilitates the resolution of oblique energy transfers to positive and negative $k_y$ components. The truncated dispersion operator shows a higher sensitivity to the angle of the carrier wave, as depicted in Fig. 13. Oblique energy transfers to positive and negative $k_y$ components continue to be resolved for a relative angle of $\chi =10^{\circ }$. However, signs of energy leakage to oblique high-wavenumber components are apparent, resulting in significant asymmetry for $\chi =20^{\circ }$ and $\chi =30^{\circ }$. Thus, oblique energy transfers to positive $k_y$ components are not resolved for large angles of $\chi$ with the truncated dispersion operator. Thus, the results shown in Figs. 12 and 13 demonstrate the superior bandwidth limits of the exact dispersion operator as well as the improved resolution of four-wave interactions. The resonance conditions of Phillips (1960) are based upon the linear dispersion relation. Thus, accurate resolution of four-wave interactions is expected to depend on the dispersion operator. Trulsen et al. (2000) indicate that improved resolution of four-wave interactions is expected for the exact dispersion operator, and Fig. 12 demonstrates that high-angle oblique energy transfers continue to be resolved if the MNLS equation is combined with an exact linear dispersion operator.

Fig. 12

Amplitude spectra of surface elevation for infinite-depth MNLS simulations, based on (13), performed with exact linear dispersion operator. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different carrier wave directions: a $\chi =0^{\circ }$; b $\chi =10^{\circ }$; c $\chi =20^{\circ }$; d $\chi =30^{\circ }$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 13

Amplitude spectra of surface elevation for infinite-depth MNLS simulations, based on (13), performed with truncated linear dispersion operator. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different carrier wave directions: a $\chi =0^{\circ }$; b $\chi =10^{\circ }$; c $\chi =20^{\circ }$; d $\chi =30^{\circ }$. Contour levels are evenly distributed between 0.005 and 0.150 m in intervals of 0.005 m

Fig. 14

Amplitude spectra of surface elevation for OceanWave3D simulations. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different dimensionless depths: a $k_{\text {p}}{d}=5.59$; b $k_{\text {p}}{d}=3.14$; c $k_{\text {p}}{d}=2.60$; d $k_{\text {p}}{d}=2.00$; e $k_{\text {p}}{d}=1.60$; f $k_{\text {p}}{d}=1.36$. Contour levels are evenly distributed between 0.01 and 0.105 m in intervals of 0.005 m

3.4 Finite-depth MNLS simulations

We compare finite-depth MNLS simulations, based on (12) and (14), with the results of OceanWave3D for various dimensionless depths. Our comparison is based upon amplitude spectra of surface elevation at the end of simulation ($t/T_0=15$) for dimensionless depths ($k_{\text {p}}{d}$) of 5.59, 3.14, 2.60, 2.00, 1.60 and 1.36. The OceanWave3D results are shown in Fig. 14, demonstrating a weakening of wave–wave interactions with a reduction in depth as observed in previous studies. The spectra corresponding to $k_{\text {p}}d=5.59$ show energy transfers along the $k_x$-axis and towards oblique high-wavenumber components, as expected in deep water—McLean (1982) showed that deep-water waves of finite amplitude feature unidirectional as well as oblique instabilities. The unidirectional energy transfers are expected to be suppressed by depth due to an interplay between the modulation instability and the return current, as found by Benjamin (1967) and Whitham (1974) and discussed by Janssen and Onorato (2007). Furthermore, Benney and Roskes (1969) and McLean (1982) showed that the dominant/fastest component growth rates become oblique in waters of intermediate depth. In Fig. 14, the spectra all exhibit a significant reduction in energy transfers along the $k_x$-axis while the oblique energy transfers show less sensitivity to depth. Thus, the potential flow simulations exhibit an increasing dominance of oblique over unidirectional energy transfers as the water depth is reduced.

Fig. 15

Amplitude spectra of surface elevation for finite-depth MNLS simulations based on Trulsen et al. (2000) with a depth-sensitive return current term. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different dimensionless depths: a $k_{\text {p}}{d}=5.59$; b $k_{\text {p}}{d}=3.14$; c $k_{\text {p}}{d}=2.60$; d $k_{\text {p}}{d}=2.00$; e $k_{\text {p}}{d}=1.60$; f $k_{\text {p}}{d}=1.36$. Contour levels are evenly distributed between 0.01 and 0.105 m in intervals of 0.005 m

Fig. 16

Amplitude spectra of surface elevation for finite-depth MNLS simulations. The spectra correspond to the end of the simulations, $t/T_0=15$, performed with different dimensionless depths: a $k_{\text {p}}{d}=5.59$; b $k_{\text {p}}{d}=3.14$; c $k_{\text {p}}{d}=2.60$; d $k_{\text {p}}{d}=2.00$; e $k_{\text {p}}{d}=1.60$; f $k_{\text {p}}{d}=1.36$. Contour levels are evenly distributed between 0.01 and 0.105 m in intervals of 0.005 m

The corresponding MNLS results are shown in Figs. 15 and 16. Finite-depth MNLS simulations based on (12), the classic MNLS equation with arbitrary-depth linear dispersion and a depth-sensitive return current term, are shown in Fig. 15. Figure 16 shows the results based on (14), a combination of the exact version of (11), with arbitrary-depth linear dispersion, and the depth-dependent coefficients for the nonlinear terms proposed by Sedletsky (2003). Both finite-depth MNLS formulations exhibit weakening collinear energy transfers along the $k_x$-axis as depth is reduced from $k_{\text {p}}d=5.59$ to $k_{\text {p}}d=1.36$ accompanied by oblique energy transfers. Thus, both MNLS codes capture the shift of the dominant component growth rates away from the $k_x$-axis to oblique components as the dimensionless depth is reduced. However, the results based on the classic MNLS formulation in (12) show excellent agreement with OceanWave3D for the full range of depths, $1.36\le {k_{\text {p}}d}\le 5.59$. In contrast, the results based on (14) agree well with OceanWave3D for depths in the range $2.00\le {k_{\text {p}}d}\le 5.59$ but the agreement deteriorates for ${k_{\text {p}}d}<2.00$. Figure 16e, f depict a clear suppression of the oblique energy transfers for depths of $k_{\text {p}}d=1.60$ and $k_{\text {p}}d=1.36$ with negligible changes to the spectrum, throughout the entirety of the simulation, for the case of $k_{\text {p}}d=1.36$. Thus, the dimensionless depth $k_{\text {p}}d$ of 1.36 appears to be completely stable for the simulations based on (14), presumably since $q_3$ goes to zero and the two remaining nonlinear respectively diminish in amplitude or turn negative. In contrast, the potential flow simulations continue to feature oblique energy transfers for $k_{\text {p}}d=1.60$ and $k_{\text {p}}d=1.36$ and the case of $k_{\text {p}}d=1.36$ still results in oblique energy transfers and significant changes to the spectrum during the focused wave event. Thus, the formulation presented in (14) appears to under estimate the extent of the oblique energy transfers for $k_{\text {p}}d\,{\le }\,2.00$. The good agreement between Figs. 15 and 14 suggests that the coefficients of the nonlinear terms do not require modification for the range of finite-depths considered in this study. The scale of the return current beneath the wave group implies that the return current is especially sensitive to depth and the depth-sensitive return current term in (12) accounts for this effect. Combined with the arbitrary depth linear dispersion relation and the exact dispersion operator of Trulsen et al. (2000), the evidence suggests that (12) provides an excellent finite-depth MNLS model for narrow-banded wave groups with dimensionless depths between 5.59 and 1.36.

4 Conclusion

We have simulated directionally-spread surface gravity wave groups, formed by dispersive focusing, in deep and finite depths using the MNLS equation. We have compared the results with a fully nonlinear potential flow code and find that the fifth-order truncated dispersion operator of Trulsen and Dysthe (1996) and the exact linear dispersion operator of Trulsen et al. (2000) both perform well if the wavenumber of the carrier wave coincides with the spectral peak and the carrier wave direction is aligned with the direction of wave group propagation. The truncated dispersion operator shows marginally higher levels of diffusivity, impacting the steepness of the wave group after focus, but the spectral evolution agrees well between the truncated and exact dispersion operators. Selecting carrier wavenumbers above/below the spectral peak significantly impacts the results obtained with the truncated dispersion operator, reducing the steepness of the wave group at focus. Selecting a carrier wavenumber below the spectral peak can also aggravate energy leakage if the truncated dispersion operator is used. In contrast, the exact dispersion operator exhibits less sensitivity to the selection of the carrier wavenumber. Selecting a carrier wavenumber below the spectral peak does not significantly influence the steepness of the wave group at focus, if the exact dispersion operator is used, but carrier wavenumbers above the spectral peak can marginally reduce the steepness of the wave group at focus. Similarly, the truncated operator is more sensitive than the exact dispersion operator to misalignment between the carrier wave and the direction of wave group propagation. The steepness of the wave group at focus is significantly impacted by misalignment of $10^{\circ }$ or more, if the truncated operator is used. The exact dispersion operator demonstrates low sensitivity to misalignment, providing similar wave group steepnesses even for angles as large as $30^{\circ }$. The spectral evolution results show that misalignment aggravates energy leakage, if the truncated operator is used, reducing the resolution of oblique energy transfers. In contrast, the exact dispersion operator continues to resolve oblique energy transfers, even for the largest angles of misalignment, with no evidence of significant energy leakage. Thus, this study provides evidence that the exact dispersion operator of Trulsen et al. (2000) does extend the bandwidth limits of the MNLS equation for steep wave groups with directional spreading, while improving the resolution of four-wave interactions and suppressing energy leakage. We find that the MNLS equation of Trulsen et al. (2000) also works well at finite depths if the arbitrary depth linear dispersion relation is used to evaluate the dispersion operator and the bottom-boundary condition is imposed at finite depth. We observe good agreement with our fully-nonlinear potential flow code for narrow-banded wave groups with dimensionless depths between 5.59 and 1.36.