Reduction of wave-induced pitch motion of a semi-sub wind platform by balancing heave excitation with pumping between floats

Abstract

It is desirable to control pitch motion of semi-submersible wind platforms to reduce turbine hub acceleration and increase structural fatigue life. This is achieved by balancing the moment on the platform due to heave float excitation by generating a differential internal head of water between the floats though a pump. This is demonstrated with an experimentally validated linear diffraction-radiation-drag model of an idealised platform. Different scales of platform are considered corresponding to 5, 10 and 20 MW turbines. The pitch angles and hub accelerations generally reduce as scales increase. Pumping reduces hub accelerations by up to about 40% for larger sea states. The power required for pumping would be small with a hybrid pump also operating as a turbine to store energy for the pumping operation. Without storage the power requirement is still small relative to the turbine capacity except for very high wind speeds.

1 Introduction

Offshore wind energy is expected to become a major electricity provider. The semi-submersible floater is a popular support platform with relatively shallow draft and simple deployment compared with other concepts. Floating platforms have the advantage of accessing deep waters, typically greater than 30 m, but the disadvantage of additional wave-induced motions. The motions are: pitch and surge in line with the wave direction; yaw, sway and roll transverse to it; and heave vertically. The acceleration at the nacelle should be less than 0.3 g to avoid damage to the power electronics when operational (DNVGL 2019). This is partly caused by platform pitch which should also be minimised to improve the fatigue life, particularly of the turbine support column, and to reduce misalignment of the turbine axis with the wind direction to optimise power generation. Yaw also causes misalignment and roll due to multi-directional and cross waves may reduce fatigue life. In this paper we consider in line motion due to pitch and how this may be reduced by balancing the moment caused by heave excitation on the floats with an opposite moment generated by pumping water internally between floats, causing a differential head of water. The moment due to vertical hydrostatic forces due to water within the columns thus balances that due to vertical heave excitation within an enclosed U-tube type system. This technique is widely used on ships where water is pumped transversely between tanks to limit roll, e.g. Mazouk and Nayfeh (2009) and the historical review by Moaleji and Greig (2007), and has been considered for semi-sub wind platforms (Roddier et al. 2010; Roddier and Cermelli 2015), Fath et al. (2020). Mazouk and Nyfeh (2009) found that active anti-roll systems (using pumps) performed better than tuned passive systems which are roll frequency dependent. Fath et al. (2020) propose a tuned liquid multi-column damper controlled in semi-active mode.

The aim of this study is to determine to what degree pitch angle and hub acceleration may be reduced by balancing heave excitation for a range of wave heights, periods and wind speeds. For this purpose we use an idealised semi-sub platform which has been investigated experimentally and simulated with a linear diffraction-radiation-drag model allowing for drag on heave plates (Stansby et al. 2019). The model supports the NREL 5 MW turbine (Jonkman et al. 2009) at a scale of 1:50. The experiments were conducted without wind action and are used for hydrodynamic validation. With wind action the thrust is modified by the imposed oscillatory motion and it has been shown that highly efficient quasi-steady blade element momentum theory (BEMT) gives accurate unsteady thrust predictions (Apsley and Stansby 2020). This is imposed for a range of operational wind speeds with wave conditions for a fully arisen sea. This gives a representation of idealised coupled wind-wave interaction while in reality many combinations are possible due to varying weather systems. 5 MW wind turbines are now commonplace, 10 MW are being deployed and 20 MW designed. If we assume that the NREL 5 MW turbine may be simply scaled up relative to the laboratory the linear scales become 1:61 and 1:74 according to Froude scaling. These larger scales will also be run for the range of operational wind speeds.

This approach for pitch stabilisation based on balancing heave excitation requires instantaneous knowledge of the onset wave field or indirectly of some resulting characteristic such as acceleration through a real-time model. This has been achieved by auto-regression for wave energy systems giving forward predictions about two wave periods ahead (Liao et al. 2020). This study is concerned with motion in the wave (and wind) direction but it may readily be extended to account for roll in multi-directional and/or cross waves.

It is worth noting that hybrid floating platforms for combined wind and solar power generation are now being considered, with a large plan area suitable for supporting the solar panels. Pitch reduction is also desirable to reduce the motion of solar panels.

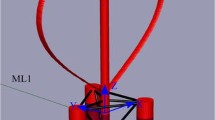
The physical model, shown in Fig. 1, represents the mass and inertia distribution of the NREL 5 MW turbine for hydrodynamic testing without wind effects. The damping plates shown on the base of each float require drag modelling. The mooring is by a hawser from single point mooring buoy attached to the buoy float.

Fig. 1

Diagram of the semi-sub platform with a plate at hub level representing the turbine mass

The structure of the paper is as follows. The next section describes the linear-diffraction-radiation-drag model. Comparison with experimental measurements follows and then the effect of pumping is presented. The following section shows results for operational wind speeds generating fully arisen seas with the effect of turbine scale. The results are then discussed and conclusions are drawn.

2 Linear diffraction-radiation-drag model

The computational model is modified from that presented in Stansby et al. (2019). The laboratory scale dimensions are shown in Fig. 2 with acceleration measuring points at the hub and close to the base of the turbine column.

Fig. 2

Dimensions of the platform at laboratory scale: a plan; b elevation

The motion is defined by the angular rotation $\theta$, clockwise positive, about the horizontal and the position of the reference point O, $x_{O} , z_{O}$, corresponding with an accelerometer position. For this study we only consider motion in a vertical plane. h is longitudinal horizontal distance from O positive in the stern direction, v is vertical distance from O positive below O. H and V are total hydrodynamic float forces in the.$x z$. directions, M is the individual pitch float moment .

There are N = 4 floats considered as a single body as shown in Fig. 1. Taking moments about O accounting for mooring force and all N_m masses (floats, ballast, beams, turbine),

$$\begin{aligned} - \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} v_{i} \ddot{x}_{i} - \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} h_{i} \ddot{z}_{i} + I\ddot{\theta } & = M_{w} + M_{p} + \mathop \sum \limits_{i = 1}^{N} M_{i} - \mathop \sum \limits_{i = 1}^{N} h_{i} V_{i} \\ & \quad - \mathop \sum \limits_{i = 1}^{N} v_{i} H_{i} + v_{M} H_{M} - h_{M} V_{M} , \\ \end{aligned}$$

(1)

I is moment of inertia about centre of mass, $M_{w}$ is the moment due to wind turbine thrust $H_{w}$ defined below, $M_{p}$ is the moment for pitch reduction due to pumping; $H_{M}$ and $V_{M}$ are horizontal and vertical mooring forces acting on the bow float; hydrodynamic forces, H and V, are assumed to act at the centre of buoyancy.

In the longitudinal horizontal direction

$$\mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} \ddot{x}_{i} = \mathop \sum \limits_{i = 1}^{N} H_{i} + H_{w} - H_{M} ,$$

(2)

and in the vertical direction

$$\mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} \ddot{z}_{i} = \mathop \sum \limits_{i = 1}^{N} V_{i} - V_{M} .$$

(3)

The positions of each component, $x_{i} , z_{i}$, linearised for small angles, are defined by:

$$x_{i} = x_{O} - v_{i} \theta ,$$

(4a)

$$z_{i} = z_{O} - h_{i} \theta .$$

(4b)

And for the wind turbine hub position, $x_{{{\text{hub}}}}$, at height $v_{{{\text{hub}}}}$ above O

$$x_{{{\text{hub}}}} = x_{O} - v_{{{\text{hub}}}} \theta .$$

(4c)

We have three equations for the three unknowns $x_{O}$, $z_{O} , \theta$, giving

$$\begin{aligned} \ddot{\theta }\left( {\mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} v_{i}^{2} + \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} h_{i}^{2} + I} \right) & = \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} v_{i} \ddot{x}_{O} + \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} h_{i} \ddot{z}_{O} + M_{w} + M_{p} \\ & \quad + \mathop \sum \limits_{i = 1}^{N} M_{i } - \mathop \sum \limits_{i = 1}^{N} h_{i} V_{i} - \mathop \sum \limits_{i = 1}^{N} v_{i} H_{i} + v_{M} H_{M} - h_{M} V_{M} . \\ \end{aligned}$$

(5)

In the horizontal longitudinal direction

$$\ddot{x}_{O} \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} = \mathop \sum \limits_{i = 1}^{N} H_{i} + H_{w} - H_{M} + \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} v_{i} \ddot{\theta }_{i} ,$$

(6)

and in the vertical direction

$$\ddot{z}_{O} \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} = \mathop \sum \limits_{i = 1}^{N} V_{i} - V_{M} + \mathop \sum \limits_{i = 1}^{{N_{m} }} m_{i} h_{i} \ddot{\theta }_{i} .$$

(7)

We thus have equations for $\ddot{\theta },\ddot{x}_{O} ,\ddot{z}_{O}$ which are further complicated by $H_{i} , V_{i} , M_{i}$ defined below also being a function of $\ddot{\theta },\ddot{x}_{O} ,\ddot{z}_{O}$. and hydrodynamic (WAMIT) coefficients (Lee and Newman 2013).

We are concerned with irregular waves which are specified by the standard JONSWAP spectrum S(f) defined by a significant wave height $H_{s}$ and a peak frequency $f_{p} = 1/T_{p}$ where $T_{p}$ is the peak period; a standard peak enhancement factor $\gamma$ is applied. Although the measured spectrum was always close to the target the measured spectrum was input to validate the model. The surface elevation $\eta$ at the bow float may be defined by linear superposition of the discretised wave amplitude components

$$\eta \left( t \right) = \mathop \sum \limits_{k = 1}^{K} a_{k} {\text{cos}}\left( { - k 2\pi \Delta f t + \varphi_{r,k} } \right),$$

(8)

where the upper limit on frequency was generally f_max = 4.0 Hz, between 3 and 8 times $f_{p}$, $\Delta f = f_{\max } /K$, $a_{k} = \sqrt {2 S\left( f \right)\Delta f}$, and $\varphi_{r}$ is phase from a uniform random distribution between 0 and $2\pi$. K is generally set to 200.

Hydrodynamic moments and forces are defined using WAMIT notation as shown in Table 1.

Table 1 WAMIT mode notation

Linear diffraction forces and moments for each float are defined by frequency-dependent coefficients for amplitude F and phase $\varphi$, or real and imaginary parts but the former is more convenient as there is already a random phase for each frequency component. For each float i = 1, N:

$${\text{Pitch moment}}\;\;M_{{D5 + 6\left( {i - 1} \right)}} = \mathop \sum \limits_{k = 1}^{K} a_{k} F_{{5 + 6\left( {i - 1} \right), k }} \cos \left( { - k 2\pi \Delta f t + \varphi_{{5 + 6\left( {i - 1} \right), k}} + \varphi_{r,k} } \right),$$

(9a)

$${\text{Vertical force}}\;\;V_{{D3 + 6\left( {i - 1} \right)}} = \mathop \sum \limits_{k = 1}^{K} a_{k} F_{{3 + 6\left( {i - 1} \right), k }} \cos \left( { - k 2\pi \Delta f t + \varphi_{{3 + 6\left( {i - 1} \right), k}} + \varphi_{r,k} } \right).$$

(9b)

Longitudinal horizontal force,

$$H_{{D1 + 6\left( {i - 1} \right)}} = \mathop \sum \limits_{k = 1}^{K} a_{k} F_{{1 + 6\left( {i - 1} \right), k }} \cos \left( { - k 2\pi \Delta f t + \varphi_{{1 + 6\left( {i - 1} \right), k}} + \varphi_{r,k} } \right).$$

(9c)

In addition there are second order forces associated with a stationary body due to the sum and difference frequencies in the spectrum which are small and the zero-difference frequencies generate a mean force. These forces may be defined by quadratic transfer functions (QTFs) obtained from WAMIT. There are additional horizontal mean forces due to the time-averaged power absorption by drag, and power required by the float motion to radiate waves (Stansby et al. 2019), also of second order. This power absorbed is balanced by a horizontal force multiplied by a representative wave speed (Mei 1999). The resulting mean force underestimates the measured mooring force by about 50% for the smaller wave heights investigated and also for larger wave heights. With the measured mean forces input into the model the peak forces underestimated the measured values by around 30%. This will be due to nonlinear effects not accounted for in the model. For the purposes of this analysis results with the measured mean mooring forces input into the model are presented. The influence of mean force on accelerations is however small. For example inputting the stationary body zero-difference mean force (10–30% of measured mean) gave rms and maximum accelerations generally within 5% of those shown.

For the time-domain model added mass and radiation damping forces and moments are defined by frequency-dependent coefficients A and B respectively using the Cummins method (Cummins 1962). With a single body and one degree of freedom x we have

$$m\mathop {x\left( t \right)}\limits = f\left( t \right) - A^{\infty } \ddot{x}\left( t \right) - \mathop \int \nolimits_{ - \infty }^{t} L\left( {t - \tau } \right)\dot{x}\left( \tau \right){\text{d}}\tau ,$$

(10)

where f includes forces due to excitation, restoring and drag in this case; $A^{\infty }$ is added mass for infinite frequency, $\tau$ is time and the impulse response function for radiation damping is given by B

$$L\left( t \right) = \frac{2}{\pi } \mathop \int \nolimits_{0}^{\infty } B\left( \omega \right)\cos \left( {\omega t} \right){\text{d}}\omega ,$$

(11)

In discrete form with time step $\Delta t$, time $t = n \Delta t$ and $\omega = 2 \pi f = k \Delta \omega$,

$$L^{m} = \frac{2}{\pi } \mathop \sum \limits_{k = 0}^{K} B_{k} \cos \left( {k \Delta \omega n\Delta t} \right) \Delta \omega ,$$

(12)

which is precomputed and in discrete form

$$\mathop \int \nolimits_{ - \infty }^{t} L\left( {t - \tau } \right) \dot{x}\left( \tau \right){\text{d}}\tau = \mathop \sum \limits_{{l = n - 2{\mathcal{M}}}}^{n} L^{n - l} \dot{x}^{l} \Delta \tau ,$$

(13)

where $\Delta \tau = \Delta t$ and ${\mathcal{M}} = T_{p} /\Delta t$. The lower limit $\left( {n - 2{\mathcal{M}}} \right)$ was generally used to represent − $\infty$ with almost identical results given by $\left( {n - 4{\mathcal{M}}} \right)$.

The right hand side (RHS) is generalised for each float with three modes.

For each float $i = 1, N$ moments are defined by:

$$\begin{aligned} M_{i} & = M_{{D5 + 6\left( {i - 1} \right)}} - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{5 + 6\left( {i - 1} \right),\;5 + 6\left( {j - 1} \right)}} \cdot \ddot{\theta }_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{5 + 6\left( {i - 1} \right),\;5 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{\theta }_{j} \left( \tau \right){\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{5 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right)}} \cdot \ddot{x}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{5 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right) \dot{x}_{j} \left( \tau \right) {\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{5 + 6\left( {i - 1} \right),\;3 + 6\left( {j - 1} \right)}} \cdot \ddot{z}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{5 + 6\left( {i - 1} \right),\;3 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right) \dot{z}_{j} {\text{d}}\tau \\ & \quad + M_{{{\text{rest}}\;i}} + M_{{{\text{drag}}\;i}} , \\ \end{aligned}$$

(14)

where the subscripts rest and drag indicate restoring and drag moments to be described below.

As an example the discrete form of the term is given by

$$- \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{5 + 6\left( {i - 1} \right),\;5 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{\theta }_{j} \left( j \right){\text{d}}\tau = - \mathop \sum \limits_{j = 1}^{N} \mathop \sum \limits_{{l = n - 2{\mathcal{M}}}}^{n} L_{{5 + 6\left( {i - 1} \right), \;5 + 6\left( {j - 1} \right)}}^{n - l} \dot{\theta }_{j}^{l} \Delta t,$$

but the integral form is used hereafter as it is more compact.

Vertical forces are defined by:

$$\begin{aligned} V_{i} & = V_{{D3 + 6\left( {i - 1} \right)}} - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{3 + 6\left( {i - 1} \right),\; 5 + 6\left( {j - 1} \right)}} \cdot \ddot{\theta }_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{3 + 6\left( {i - 1} \right),\; 5 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{\theta }_{j} \left( \tau \right){\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{3 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right)}} \cdot \ddot{x}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{3 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{x}_{j} \left( \tau \right){\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{3 + 6\left( {i - 1} \right), \;3 + 6\left( {j - 1} \right)}} \cdot \ddot{z}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{3 + 6\left( {i - 1} \right), \;3 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{z}_{j} \left( \tau \right){\text{d}}\tau \\ & \quad + V_{{{\text{rest}}\;i}} + V_{{{\text{drag}}\;i}} , \\ \end{aligned}$$

(15)

longitudinal horizontal forces are defined by:

$$\begin{aligned} H_{i} & = H_{{D1 + 6\left( {i - 1} \right)}} - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{1 + 6\left( {i - 1} \right),\;5 + 6\left( {j - 1} \right)}} \cdot \ddot{\theta }_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{1 + 6\left( {i - 1} \right),\;5 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{\theta }_{j} \left( \tau \right){\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{1 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right) }} \cdot \ddot{x}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{1 + 6\left( {i - 1} \right),\;1 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right) \dot{x}_{j} \left( \tau \right) {\text{d}}\tau \\ & \quad - \mathop \sum \limits_{j = 1}^{N} A^{\infty }_{{1 + 6\left( {i - 1} \right),\;3 + 6\left( {j - 1} \right) }} \cdot \ddot{z}_{j} - \mathop \sum \limits_{j = 1}^{N} \mathop \int \nolimits_{ - \infty }^{t} L_{{1 + 6\left( {i - 1} \right),\;3 + 6\left( {j - 1} \right)}} \left( {t - \tau } \right)\dot{z}_{j} \left( \tau \right){\text{d}}\tau \\ & \quad + H_{{{\text{drag}}\;i}} + H_{{{\text{mean}}\;i}} , \\ \end{aligned}$$

(16)

H_mean is due to the mooring force described above, assumed to be split equally between floats.

The restoring heave force for each float is given simply by $V_{{{\text{rest}}}} = - \rho g\pi r^{2} z$. For pitch the restoring moment about O, $M_{{{\text{rest}}}} = c \theta$, is due to the components of weight and buoyancy and the water plane restoring moment $- \rho g\pi \frac{{r^{4} }}{4}\theta$.. For the rigid float system the constant c is + 84.32 Nm/rad. However the heave restoring force dominates markedly. The drag forces are given by $H_{{{\text{drag}}\;i}} = - 0.5 \rho A_{i} C_{D } \left| {\dot{x}_{i} } \right| \dot{x}_{i}$, $V_{{{\text{drag}}\;i}} = - 0.5 \rho \pi r_{i}^{2} C_{D} \left| {\dot{z}_{1} } \right|\dot{z}_{1}$, and $M_{{{\text{drag}}\;i}} = - V_{{{\text{drag}}\;i}} h_{i} - H_{{{\text{drag}}\;i}} v_{i}$. $A_{i}$ is the vertical submerged frontal area for a float. Note float velocity relative to flow velocity is not considered and drag coefficient C_D is effectively a viscous tuning parameter which is large for damping plates.

Tao and Thiagarajan (2003) showed C_d > 4 for oscillating heave plates and C_d≈ 6 was a representative value although dependent on amplitude of motion to some degree. For heave C_d = 6 is assumed and C_d = 0 for surge since the horontal cross section of each float is circular and zero proved effective for WEC simulations with rounded base floats; CFD also showed drag coefficient was very small (Gu et al. 2018).

The wind thrust is given by

$$H_{w} = 0.5 \rho_{{\text{air }}} A_{{{\text{turb}}}} C_{T} \left( {U_{{{\text{hub}}}} - \dot{x}_{{{\text{hub}}}} } \right)^{2} ,$$

(17)

where $U_{{{\text{hub}}}}$ is wind speed at the hub, $x_{{{\text{hub}}}}$is hub velocity, $\rho_{{{\text{air}}}}$ is air density and $A_{{{\text{turb}}}}$ is the swept area for the rotor of radius $r_{{{\text{turb}}}}$ , $\pi r_{{{\text{turb}}}}^{2}$. The thrust coefficient $C_{T}$ is dependent on the wind speed and is determined from blade element momentum theory (BEMT) using the NREL 5 MW turbine characteristics (Jonkman et al. 2009). The force is assumed to be quasi steady and defined by the relative velocity $\left( {U_{{{\text{hub}}}} - \dot{x}_{{{\text{hub}}}} } \right)$. The quasi-steady behaviour has been shown to be a close approximation to CFD modelling using the actuator line model (Apsley and Stansby 2020). The $C_{T} v U_{{{\text{hub}}}}$ curve is shown in Fig. 3 for full scale with cut out of 25 m/s (at hub level). Above this value the turbine is parked.

Fig. 3

Variation of thrust coefficient $C_{T}$ with full scale wind speed at hub $U_{{{\text{hub}}}}$

For the purposes of this demonstration the wind velocity at the hub is assumed uniform across the swept area. The moment about O in Eqs. 1, 8 is $M_{w} = - v_{{{\text{hub}}}} H_{w}$.

The mooring comprises inelastic cables (Dyneema) attached to a spherical buoy, with one cable connecting the buoy to the bed and one connecting the bow float to the buoy. The mooring model accounting for buoyancy of the buoy is described in Stansby et al. (2019) and the mooring forces $H_{M}$ and $V_{M}$ act at the fairlead position on the bow float. With this arrangement the platform aligns naturally with the wave direction. Further effects of elastic mooring cables have been analysed in Stansby and Carpintero Moreno (2020) for a wave energy system showing elasticity causes marked reduction in snap loads.

The code for the model is written in Fortran and runs in less than one minute on a laptop.

3 Results for hydrodynamic only tests

Accelerations at hub and base level are compared with experiment for H_s ≈ 0.05–0.06 m in Figs. 4 and 5. The H_s values associated with each $T_{p}$ are given in Table 2.

Fig. 4

rms and maximum hub accelerations v. $T_{p}$ from experimental measurements and the linear model

Fig. 5

rms and maximum base accelerations v. $T_{p}$ from experimental measurements and the linear model

Table 2 Wave definition for H_s ≈ 0.05–0.06 m with JONSWAP spectra, $\gamma = 3.3$

The mass and inertia of the floats and components are given in Table 3.

Table 3 Mass of each platform component with centre of mass and inertia relative to O

At the hub the rms accelerations in Fig. 4 are in reasonable agreement and the maximum values are underestimated by up to about 25% for the larger wave periods of interest. The experimental runs were of 5 min duration. With repeated time series the maxima were remarkably similar, within 1%, but the durations are relatively short, corresponding to half an hour full scale. The model runs with the same spectra were of similar duration but the frequency components in the time series had random, not experimental, phases.

At the base the rms values in Fig. 5 are in close agreement but the maxima are again underestimated. The same effects are observed for large wave heights in Figs. 6 and 7 with rms accelerations remaining in approximate agreement, perhaps surprisingly with a linear model, and maxima are underestimated by similar amounts. Possible reasons for the underestimation in peak accelerations will be discussed. Note that with Froude scaling acceleration is unaffected by scale factor.

Fig. 6

rms and maximum hub accelerations v. significant wave height for $T_{p}$ = 1, 1.4 and 2 s from experimental measurements and the model

Fig. 7

rms and maximum base accelerations v. $H_{s}$ for $T_{p}$ = 1, 1.4 and 2 s from experimental measurements and the linear model

4 Results with heave excitation balanced by pumping between floats

Pumping internally between floats may control the differential water level between the floats with water also providing ballast. In the computational model we consider pumping between floats 1 (bow) and 3 (mid) which are of the same diameter. This provides vertical forces on the floats which may balance the heave excitation forces $V_{D}^{i}$ on floats i = 1, 4 in (15). Balancing each force individually would require pumping into and out of the float hull with associated leaking risks. Here we consider an enclosed water system so that the levels in floats 1 and 3 are equal and opposite (the volume in the floats and connecting pipe is constant). We do not consider any inertia effects which may be beneficial as tuned mass damping. The differential water levels generate a moment about O which is set to balance the moment due to heave excitation forces equal to

$$M_{H} = - h_{1} V_{D}^{1} - h_{2} V_{D}^{2} - h_{3} V_{D}^{3} - h_{4} V_{D}^{4} ,$$

(18)

where the superscript applies to float number (h is positive in stern direction). If the differential water level between floats 1 and 3 is $z_{p}$ a moment about O is given by

$$M_{p} = \rho gAh_{1} z_{p} /2 - \rho gAh_{3 } z_{p} /2,$$

(19)

where $A = \pi r^{2}$ and r is float radius. Putting $M_{p} = - M_{H}$ gives

$$z_{p} = 2 M_{H} /\rho gA \left( {h_{3} - h_{1} } \right).$$

(20)

The instantaneous pump power ignoring inertia,

$$P_{p} = \rho gA z_{p} \dot{z}_{p} .$$

(21)

In principle with no losses this gives an average power of zero if the pump also acts as a turbine, i.e. it generates and stores energy as a turbine as well as requiring power as a pump. On the other hand, if the pump freewheels when $P_{p} < 0$, energy is not stored. In addition there will always be losses to overcome in the pump and pipe system. Pump efficiencies are typically in the range 60–90% and with additional pipe and minor losses the average pump power required is assumed to be twice that calculated for $P_{p}$ when positive. This is somewhat arbitrary but is intended to give an indication of power requirement. In practice if the system were to be applied an axial flow pump/turbine suitable for high discharge against low heads should be developed to minimise power requirements.

Results are first shown for the experimental conditions without wind action for moderate H_s ≈ 0.05–0.06 m. Figure 8 shows that rms hub acceleration is reduced for T_p > 1 s by up to 40% and the maximum is similarly reduced. On the other hand base acceleration in Fig. 9 is hardly affected.

Fig. 8

rms and maximum hub acceleration variation with $T_{p}$ for experimental conditions with H_s ≈ 0.05–0.06 m with and without pumping

Fig. 9

rms and maximum base acceleration variation with $T_{p}$ for experimental conditions with H_s ≈ 0.05–0.06 m with and without pumping

The pitch angles in Fig. 10 are reduced corresponding with the reduction in hub acceleration. If power is only provided when $P_{p} > 0$ and total power is twice that without losses, the average and maximum power is shown in Fig. 11 as a proportion of the wind power capacity, 5.66 W at 1:50 scale. The average power required increases as $T_{p}$ increases and is greatest for $T_{p} = 2 s$ at 3% with a peak at 21% of wind capacity.

Fig. 10

rms and maximum pitch angle variation with $T_{p}$ for experimental conditions with H_s ≈ 0.05–0.06 m with and without pumping

Fig. 11

Average and maximum pump power, 2 $P_{p}$ for $P_{p} > 0$, variation with $T_{p}$ for H_s ≈ 0.05–0.06 m

For large waves, variations with $H_{s}$ are similar. Figure 12 shows pumping has little effect on hub acceleration for $T_{p}$ = 1 s and a significant effect for $T_{p}$ = 1.4 and 2 s, for both rms and peak values. For base accelerations shown in Fig. 13 pumping again has little effect. For pitch angle in Fig. 14 the reduction by pumping is similar to hub acceleration.

Fig. 12

rms and maximum hub acceleration v. $H_{s}$ for $T_{p}$ = 1, 1.4 and 2 s with and without pumping

Fig. 13

rms and maximum base acceleration v. $H_{s}$ for $T_{p}$ = 1, 1.4 and 2 s with and without pumping

Fig. 14

rms and maximum pitch angle v. $H_{s}$ for $T_{p}$ = 1, 1.4 and 2 s with and without pumping

The average pump power (defined as before) shown in Fig. 15 is now largest for $T_{p}$ = 2 s at about 10% of wind capacity with a peak value of about 58%.

Fig. 15

Variation of average and maximum pump power, 2 $P_{p}$ for $P_{p} > 0$, with $H_{s}$ for $T_{p}$ = 1,1.4 and 2 s

5 Effect of scale with wind effect

Results are now presented with wind action. The wind velocity determines the wave height and period depending on the weather patterns. To give some indication of combined wind wave action we consider the idealised fully arisen sea, where the wind blows in one direction for an infinite time over an infinite fetch. Formulae for wave height and period are given by $H_{s} = 0.0282 U_{10}^{2}$ and $T_{p} = 0.877 U_{10}$ where $U_{10}$ is velocity at 10 m above sea level (Shore Protection Manual 1973). The velocity U at hub height 90.2 m above sea level is given by the power law index of 0.11 such that $\frac{U}{{U_{10} }} = \left( \frac{z}{10} \right)^{0.11}$ (Hsu et al. 1994). Thus a velocity of 20 m/s at 10 m becomes 25 m/s at hub height which is the cut off limit. The wave spectrum is a Pierson–Moskowitz equivalent to JONSWAP with $\gamma = 1$. The values of $H_{s}$ and $T_{p}$ at full scale are shown in Table 4.

Table 4 Dependence of $H_{s}$ and $T_{p}$ on wind speed for fully arisen sea

Results are presented for 10 MW and 20 MW turbines as well as 5 MW for which the experiments were designed. The corresponding scales for 5, 10, 20 MW are 1:50, 61, 74 with Froude scaling. It is assumed that the thrust coefficient $C_{T}$ variation with wind speed is unchanged at the different scales. For these cases the mean platform force is set equal to the mean turbine thrust. Full scale results are presented for rms hub acceleration variation with wind speed in Fig. 16. This shows that accelerations decrease as turbine size increases. Results are only presented for $U_{10 } \le$ 16 m/s since $H_{s}$ = 7.21 m with $U_{10 }$ = 16 m/s at full scale, equivalent to 0.14 m at lab scale which is close to the largest value tested experimentally. The effect of pumping in reducing accelerations becomes significant for wind speeds greater than 8 m/s.

Fig. 16

Variation of rms hub acceleration with wind speed at 10 m for 5, 10, 20 MW turbines with and without pumping

A similar effect is seen for the maximum accelerations in Fig. 17. Base accelerations are not shown as pumping has negligible effect as seen for the experimental conditions.

Fig. 17

Variation of maximum hub acceleration with wind speed at 10 m for 5, 10, 20 MW turbines with and without pumping

Figure 18 shows the rms pitch angle reduced by pumping and the same occurs for the maximum pitch angles in Fig. 19.

Fig. 18

Variation of rms pitch angle with wind speed at 10 m for 5, 10, 20 MW turbines with and without pumping

Fig. 19

Variation of maximum pitch angle with wind speed at 10 m for 5, 10, 20 MW turbines with and without pumping

Results for pump power as a proportion of wind power are shown in Fig. 20, again assuming power is only required for $P_{p} > 0$ and twice $P_{p}$ is required to overcome losses. For the highest wind speed of 16 m/s (20 m/s at hub height) this ratio is about 17% for the 5, 10 and 20 MW turbines. The maximum instantaneous power would be about 95% of wind power for the 5 MW case, and slightly less for the 10 and 20 MW cases.

Fig. 20

Variation of average and maximum pump power, 2 $P_{p}$ for $P_{p} > 0$, with wind speed at 10 m for 5,10,20 MW turbines

6 Discussion

The platform was designed for simplicity and reasonably shallow draft, with a maximum of 8.9 m for the 1:50 scale. This proved quite stable in all wave conditions with pitch angles less than 4° in experimental conditions and less than 7° for the highest operational wind speed simulated. 10° is the maximum recommended for operational conditions (DNVGL 2019). The total model mass of 26 kg compares with 65 kg of Windfloat (Roddier and Cermelli 2015) and 108 kg of NREL’s OC4 (Robertson et al. 2014). The linear diffraction-radiation-drag model predicts rms accelerations approximately, underpredicting maximum accelerations by about 25% for the larger wave periods of main interest. The mean forces based on second-order effects were underpredicted due to nonlinear effects (Stansby et al. 2019) and the measured mean mooring forces were input in the model. Drag on the heave plates is significant and represented by a single drag coefficient of 6, which is consistent with previous studies, to give approximate agreement with experimental rms accelerations. Drag due to surge is assumed to be zero. There will be quite complex wake effects and drag coefficients in oscillatory flows are known to decrease as amplitude increases for plates (Graham 1980) and discs (Tao and Thiagarajan 2003). This could explain why maximum accelerations with relatively large amplitudes are underestimated. Note amplitude a in this context is defined by the non-dimensional Keulegan–Carpenter number ($2\pi a/D$ where is D is plate width).

Before we discuss stabilisation by pumping the effect of platform scale is interesting. While 5 MW turbines are common, 10 MW are now being deployed and 20 MW are planned. If the power coefficient v wind speed characteristic is unchanged, power scales as l^3.5 where l is length scale relative to the laboratory model scale and the corresponding scales are 50, 61, 74 respectively. The ratio of power to mass scales as l^0.5 and assuming cost is proportional to mass increasing size reduces cost of electricity. For 10 MW and 20 MW this ratio is 9.5% and 22% greater than for 5 MW respectively. The hub acceleration provides an important limit for turbine operation and rms and maximum values are shown in Fig. 21. Increasing size also generally reduces accelerations for a given wind speed.

Fig. 21

Variation of rms and maximum hub acceleration with wind speed for 5, 10, 20 MW turbines

Pumping between fore and aft floats is used to balance the moment due heave excitation on the floats. This is shown to be effective in reducing rms and maximum hub accelerations and pitch angle for experimental conditions in all cases. This is also the case for larger wind speeds generating a fully arisen sea. The base acceleration, just above deck level, is virtually unaffected by pump balancing as might be expected since this is determined by surge motion. Surge forces are relatively large and modelling has shown that balancing this motion by thrusters would require very large amounts of power which are not practical.

The conservative power calculation suggests that average power is less than 17% of wind power for wind speeds up to 16 m/s corresponding to $T_{p}$ of 14 s. The calculation assumes the pump freewheels when flow is driven by the differential head and power is only provided to act against a differential head; the average power required is assumed to be twice that calculated to account for losses. In practice an axial flow pump designed for high discharge with low head may also act as a turbine and power may be stored in batteries and/or supercapacitors for the pumping phase substantially reducing power requirements. Up to a wind speed of 16 m/s maximum hub accelerations appear always less than 2 m/s². The maximum suggested by DNVGL (2019) is 3 m/s². However it should be borne in mind that experimental measurements of acceleration indicate that the model underestimates by up to about 25%.

This pitch motion reduction is based on the physical idea of balancing heave excitation. To implement this the wave elevation should be known to define instantaneous heave excitation and hence pump discharge. Wave prediction, or wave force prediction, up to about two periods ahead has been successfully undertaken for the multi-float wave energy converter M4 using auto-regression (Liao et al. 2020). This should be simpler here as only instantaneous wave elevation, or a representative platform characteristic such as pitch angle or hub acceleration, is required to define differential head between floats determined by the pump discharge. The differential head variation will determine the instantaneous pump discharge. However optimal control to minimise hub acceleration could also be applied and this provides an alternative approach. Various levels of control have been applied in a wave energy context, from linear optimal non-causal (Liao et al. 2020), to model predictive and sliding mode control (Zhang et al. 2020) with the latter accounting for uncertainties in model predictions.

Pumping between floats requires a connecting pipe housing the turbine. This is not shown here and may be above or below water level. If below there will be additional small hydrodynamic forcing to be taken into account with advantageous damping; this will also improve overall structural strength. If above water level maintenance would be simpler.

7 Conclusions

Reducing wave-induced pitch motion is desirable for semi-sub platforms supporting wind turbines. Pumping water internally between floats to generate a differential head to balance the moment induced by heave excitation forces achieves this, demonstrated through an experimentally validated linear diffraction-radiation-drag model. The reduction in hub acceleration and pitch angle is up to 40% for a larger wave conditions and corresponding wind speeds. The average power required would be small for a pump operating in hybrid pump-turbine mode. If freewheeling when the head differential drives the flow the average power is small relative to turbine capacity except for very high wind speeds with corresponding large peak wave periods. It is further shown that hub accelerations and pitch angles generally reduce as the system size increases; 5, 10 and 20 MW turbines are considered. Pump control requires instantaneous prediction of wave elevation or an excited characteristic such as hub acceleration, which could be provided by auto regression.