Abstract
CFD modelling of tidal turbines in arrays is described and assessed against experimental studies of turbines operating either at constant speed or constant torque. Rotor blades are represented by rotating actuator lines, whilst supports are represented by partially-blocked-out cells. For a single turbine the model successfully reproduces towing-tank measurements of thrust and power coefficients across a range of tip-speed ratios. For two turbines staggered streamwise, it is demonstrated that loads may be reduced or augmented, according as the downstream turbine is in the wake or bypass flow of the upstream turbine. When the downstream turbine is partially in the wake, individual blades are subject to large cyclic load fluctuations. Array performance is evaluated by comparison with experimental data, modelling up to 12 turbines in up to three staggered rows. The speed of each turbine is continuously adjusted in response to flow-induced torque. Distribution of thrust coefficients within the array is well reproduced, but there is greater discrepancy in angular speed. With actuator representation of blades, the choice of turbulence model has little effect on load coefficients for an isolated turbine or row of turbines, but a significant effect on the wake, and hence on downstream turbines in an array.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tidal energy represents a promising, yet largely under-exploited, source of renewable energy, offering high energy density and predictable generating periods. Public opposition to the expense and unknown environmental consequences of large barrages have led to consideration of tidal-stream devices—predominantly axial-flow turbines—which aim to extract the kinetic energy of a tidal current rather than the potential energy built up by impounding water. In numerous sites around the world, narrow straits lead to tidal currents in excess of 2.5 m s−1, where tidal-stream energy is expected to become commercially viable (Black and Veatch 2005). A large number of demonstration devices have been tested at the EMEC site in the Orkney Isles and the FORCE site in Nova Scotia’s Bay of Fundy, whilst grid-connected arrays are under construction in the Pentland Firth off Scotland (MeyGen) and Raz Blanchard off Normandy (Alstom/GDF Suez and OpenHydro/EDF).
Unsurprisingly, given the cost of designing and testing radically new devices, tidal-stream technology is strongly influenced by the more mature technology of wind power. Most devices are of the three-bladed, horizontal-axis type. Marine turbines, however, face many additional challenges not relevant to wind power; for example: the need for much more substantial blades, nacelle and support; ability to deploy in a short time window; difficulty of access for maintenance; bio-fouling; marine debris; cavitation; fluctuating loads due to site-specific turbulence; velocity shear and waves.
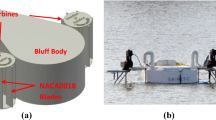
Small-scale laboratory studies have been conducted in towing tanks and flumes (Bahaj et al. 2007; Stallard et al. 2013; Olczak et al. 2016), but these can cover only a limited range of operating conditions and are subject to scale effects. Theoretical studies include the wind-turbine-derived blade-element-momentum theory (BEMT) and, increasingly, computational fluid dynamics (CFD). CFD has been used to undertake geometry-resolved simulations of real devices in both low-turbulent flow (McNaughton et al. 2014) and realistic site turbulence and velocity shear (Afgan et al. 2013; Ahmed et al. 2017). However, it is computationally impractical to represent accurately both near-blade and wake fields for multiple devices simultaneously and for a representative set of operating conditions including turbulence and waves. Instead, to model interactions between multiple turbines (and also between turbines and waves) we have turned to the practice used in the wind-energy industry (Sørensen and Shen 2002; Sarlak et al. 2016) of replacing a geometry-resolved turbine (Fig. 1a) by an “actuator” model—essentially a body-force distribution that provides as closely as possible the same reactive forces as a real turbine. This may be done at a coarse axially symmetric level with an actuator disk (Fig. 1b), where momentum (and, sometimes, angular momentum) body-force density is distributed over a swept volume (either uniformly, or as a function of radius) to match total thrust and torque (Schluntz and Willden 2015a; Olczak et al. 2016), or, with extra computational expense but better near-wake agreement, resolution of fluctuating loads and no a priori assumption about total loads, by representing the blades as rotating actuator lines, or, more strictly, lines of discrete points (Fig. 1c) (Sørensen and Shen 2002; Schluntz and Willden 2015b; Porté-Agel et al. 2011; Baba-Ahmadi and Dong 2017).
Advantages of the rotating-actuator-line approach include a substantial reduction in computer resources (because it is not necessary to fit a finely resolved and rotating mesh region around each rotor), ease of changing rotor design or blade pitch (as there is no need to re-mesh), adding other turbines, and decoupling of the turbine motion from the background grid (so allowing, for example, the calculation of wave motion—Apsley et al. (2016)—or flows in regions with complex bathymetry). Disadvantages include the range of validity of reaction forces based upon 2-d flow around aerofoil sections (particularly, near blade tips), absence of finer-scale turbulence generated by boundary layers or flow separation on the blades, and the relatively low resolution of the nacelle and support tower (which are far more substantial for marine than for wind turbines). Also, in contrast to momentum sources spread over an actuator disk, rotating actuator lines require a time-dependent calculation.
The remainder of this paper is as follows. Section 2 describes the computational model, whilst Sect. 3 validates it for a single rotor. Section 4 examines the simple but informative case of two interacting turbines, investigating the opposing effects of reduced onset flow inside, and increased bypass flow outside, the wake of the upstream turbine, as well as temporal fluctuations in load on individual blades. Section 5 compares simulations with experimental data for arrays of up to 12 rotors in up to 3 rows; in this section, rotor speeds are allowed to vary in response to flow-induced torque. Section 6 concludes with key findings, areas where models need improvement and suggestions for future research.
2 Numerical modelling
2.1 The CFD code (STREAM)
The code used for all calculations presented here is STREAM, an in-house finite-volume solver. The code uses the SIMPLE pressure-correction algorithm to solve the Reynolds-averaged Navier–Stokes (RANS) equations on multi-block, structured, curvilinear meshes. The code contains an extensive range of advanced RANS turbulence models (Apsley and Leschziner 2000); several of these were tested during this work. The code employs cell-centred storage, with the standard Rhie–Chow pressure-smoothing algorithm for mass fluxes. For all calculations presented here, the third-order flux-limited UMIST scheme (Lien and Leschziner 1994) was used for advective fluxes and the second-order Crank–Nicolson scheme for time stepping. Although not used for the array calculations presented here, STREAM has the capacity (Apsley and Hu 2003) to use a moving-mesh, surface-fitting approach at the free surface rather than the volume-of-fluid (VOF) method which is prevalent in general-purpose commercial codes; the free-surface capability is currently being used to investigate turbine performance in waves (Apsley et al. 2016).
MPI parallelisation is by blockwise domain decomposition. All calculations presented here were run with up to eight cores, either on a desktop PC or the Computational Shared Facility (CSF) at the University of Manchester.
2.2 Rotor representation
Drawing on the actuator-line model of Sørensen and Shen (2002), with more recent guidance on parameters by Sarlak et al. (2016), the turbine rotor is replaced by rotating lines of actuator points (Fig. 1c). The body forces associated with these are derived from 2-d aerofoil theory, selected for the predefined blade geometry (shape, chord and blade angle) at each radial distance and the local approach-flow velocity.
At the start of each time step, the lines of points representing each blade are rotated to a new angle using the current angular velocity. For computational efficiency, the cell index of each actuator point within the computational mesh is identified and stored in memory at this instant, as are the set of non-zero transfer weighting functions between actuator point and the relatively small number of local cells affected by it—see Eq. (2). (The cell-search process would have to be repeated if the background mesh changed within a time step, for example if stretching due to wave motion was extended through the whole water column.)
At each inner iteration (cycle of the SIMPLE algorithm) the local approach-flow velocity Ua at an actuator point is combined with the instantaneous blade velocity (Ωr tangentially) and projected onto the plane perpendicular to the blade to determine the relative velocity Urel. For predefined twist angle β(r), this determines angle of attack α and, thence, using chord c(r) and prescribed blade section lift and drag coefficients CL(α,r) and CD(α,r), an actuator force for radial length Δr of
where \({{\hat{\bf e}}}_{{\text{D}}} \) and \({{\hat{\bf e}}}_{{\text{L}}}\) are unit vectors along and normal to the local relative velocity Urel in this blade section (Fig. 2).
“Approach-flow velocity” Ua is not straightforward to establish, since taking the fluid-velocity part by interpolation to the actuator point in the CFD simulation involves using a value that is itself within the volume affected by the actuator body forces. Physically, the flow is distorted by local circulation associated with blade lift and to loss of momentum flux by drag. An attempt to incorporate the local circulation was made by Schluntz and Willden (2015b), who sampled a triplet of surrounding points on the assumption that the flow is adequately described by approach flow plus circular vortex; however, their modification has not been made here. Note, however, that for large TSR, the approach velocity to the blade element in its own reference frame is dominated by the motion of the blade itself, which does not rely on interpolation within the flow field.
Each isolated point force Fp is distributed over a wider volume of scale σ as a force density:
where x is cell centre and xp an actuator point. This is multiplied by cell volume to produce the body force for that cell. As weighting factors are evaluated at the cell centre, a small amount of rescaling is needed to ensure that these sum to 1.0. f falls to 1% of its maximum at 2.1σ; in this work, the search for influence is cut off at 2.5σ. Sarlak et al. (2016) provide guidance on σ. Here, a value of roughly two times the local cell size (V1/3, where V is cell volume) was used. Numerical experiment showed that 30 equally spaced actuator points along each blade was sufficient to obtain number-independent results.
Lookup tables are created to interpolate for chord c(r), blade angle β(r) and lift and drag coefficients CL(α,r) and CD(α,r). Manufacturers’ data prescribe the first two. Where experimentally derived aerofoil data are not available, we have used data from XFoil simulations to determine force coefficients. In principle, particularly at laboratory scale, CL and CD have a weak dependence on Reynolds number, which changes with local flow speed, but this has not been considered here and the lookup tables use values based on a typical chord-based Reynolds number for each case.
At blade ends, flow leaks around the tips from the high-pressure side to the suction side, reducing pressure difference and loads, as well as creating tip vortices. Because they have no direct means of reacting to this pressure difference, BEMT calculations often use tip-correction factors to reduce drag and lift forces. However, in common with blade-resolving CFD, actuator-line approaches do see the pressure changes in response to the reaction forces and any radial component of velocity is removed by projection when evaluating actuator forces. We believe that this makes explicit tip corrections unnecessary; they have not been used in the simulations presented here and the agreement with experiment for a single rotor (Sect. 3) is better without them.
Time-step-dependence tests for a single rotor yielded a (conservative) Δt = Trot/250, where Trot is the turbine rotation period, which varies with tip-speed ratio (TSR). With this value of Δt, the distance swept by a rotor tip in one time step (ΩRΔt) was the same or smaller than the grid spacing in the vicinity of the rotor.
2.3 Nacelle and support-structure representation
The nacelle and support structure for tidal-stream turbines are far more substantial than their wind-turbine counterparts. Ignoring a nacelle would fail to incorporate its blocking effect and provide a low-resistance route for streamlines to bypass the actuators representing the blades. Ignoring the support mast eliminates the fluctuating load on individual blades as they pass in front of it. However, creating a grid that completely resolves and aligns with the non-rotor structures runs counter to the desire to decouple the turbine from a simple background grid.
In these simulations, we have adopted a technique akin to the early CFD approach of simulating bluff bodies by “blocking-out” cells, except that here we allow for cells to be partially blocked, according to the fraction f of them covered by a nacelle or other blockage (Fig. 3). Insofar as we use a volume fraction of the cell occupied by fluid or solid, there are some similarities to the VOF method used by many codes to accommodate free surfaces, as well as “cut-cell” techniques. Here, however, there is no question of solving an equation for f, and the method simply modifies the blocking-out approach. In this work, a nacelle is approximated by a cylindrical tube of appropriate position, diameter and streamwise length. The overlapping fraction in any cross-stream plane is approximated by that for a polygon (Fig. 3). Where considered, a support mast is very roughly represented by a rectangular-section blockage of the correct projected width and length. The representation is by partial blocking-out of cells, not a drag-related body-force distribution as was used, for example, by Porté-Agel et al. (2011).
Cell blocking is accomplished by modifying the source term in the finite-volume equations for the momentum components. The discretised equation for the velocity u in the pth cell is
where the LHS results from discretising advection and diffusion and the RHS is the linearised source term. The final, implicit, negative-coefficient part is transferred to the LHS to augment the diagonal factor in the matrix equations (\( a_{\text{p}} \to a_{\text{p}} - s_{\text{p}} \)). In the classic blocking-out technique, up is effectively forced to be zero by taking sp = –(large number). This “large number” is usually taken as something numerically large (say, 1030), but it does not actually have to be as large … and it ought to have dimensions. Since the LHS of Eq. (3) is of order (mass × acceleration) or
where V is the volume of the cell, we can outweigh the LHS term with an expression of the correct physical dimensions by taking
where u* is a velocity scale significantly larger than the onset flow (say, 10 times inflow velocity) and L is a typical cell scale (e.g. \( V^{1/3} \)). Simulations showed that, for a bluff body, this approach generated a velocity and pressure field (including recirculating flow) very similar to those on a geometry-resolving multiblock mesh.
2.4 Turbulence modelling
High-Reynolds-number versions of turbulence models were used throughout, as turbulent boundary layers were not resolved on the blades. Where necessary, standard wall functions were used for the bed boundary condition in deep boundary-layer approach flow (Sect. 5), but these played no role in the rotor dynamics.
As will be shown in the subsequent sections, choice of turbulence model made little difference to loads on an isolated rotor, but produced significant differences in wake velocity distributions (Sect. 5), and thus can be expected to influence predictions of multiple turbines in an array. The turbulence models investigated in this paper were:
-
the “standard” k-ε model of Launder and Spalding (1974);
-
the realisable (linear) k-ε model of Shih et al. (1995);
-
the SST k-ω model of Menter (1994);
-
the Reynolds-stress-transport model of Gibson and Launder (1978).
For the full forms of the turbulence models, one is referred to the original references, or the summary in Apsley and Leschziner (2000). However, we draw attention here to two particular models. The literature shows that the SST k-ω model is an extremely popular turbulence closure for external flows in general and aerofoils in particular. This model is a hybrid of k-ω (near-wall) and k-ε (free-stream) closures expressed in k-ω form, with additional shear-stress limiting near solid boundaries. However, in our actuator model there are no solid boundaries associated with the blades, so that this model would simply revert to a k-ε-type model and the shear-stress limiting (which depends on wall distance) does not occur. Differences from the standard k-ε model here are thus solely due to the coefficients in the length-scale-determining equation. There are also significant differences between the standard k-ε model and the realisable model of Shih et al. (1995). These stem from the strain sensitivity built into the latter’s eddy-viscosity formulation and length-scale-determining (ε) equation. It is the strain dependence of these terms which suppresses the excessive production of turbulence that is found with the standard k-ε model in highly straining flows.
The standard k-ε model is found to be excessively diffusive in the highly strained flow near the turbine disk, leading to more rapid breakdown of flow structures in the near wake. However, the decay rate further downstream was more accurately predicted by the standard k-ε model (see Sect. 5.2) so that, as a significant emphasis was to be placed on array simulations, this is, except where specified, the model employed in calculations in this paper.
3 Validation for a single rotor
Bahaj et al. (2007) published measurements with a three-bladed axial-flow turbine in a towing tank and a cavitation flume. Here, we attempt to simulate the former, equivalent to a low-turbulence uniform onset flow in a fixed domain. For the CFD simulation, cross-stream dimensions were the same as the towing tank, thus accurately reproducing the blockage ratio. The upper surface was treated as a stress-free rigid lid (effectively, a symmetry plane) since, at low Froude numbers, the surface displacement due to the presence of the turbine is small.
Blade twist β(r) and chord c(r) distributions were as specified in Bahaj et al. (2007), whilst aerofoil section coefficients CD(α,r) and CL(α,r) were generated by XFoil. Bahaj et al. reported results for two blade pitches, but only the 20° pitch angle at blade root (“design case”) has been simulated here. Simulations were undertaken with a nacelle of the same diameter and length as the experiments, but the support strut was deemed sufficiently far downstream to be neglected in the CFD simulations, as only time-averaged loading and power, not wake velocities, were to be compared.
In design conditions, nominally TSR = 6, where
is tip-speed ratio, numerical tests with successively finer grids demonstrated that satisfactory grid independence for load coefficients was obtained with a mesh extending 3D upstream and 7D downstream of the rotor (where D = 2R is the rotor diameter), with a background mesh of 690,000 cells, clustered at the centre of the rotor and allowed to expand uniformly in all directions. With a low-turbulence, uniform approach flow, the total number of cells was found to be less important than the size of cells in the vicinity of the rotor (here, 0.01D at rotor centre, but expanding outward). For parallelisation on a multi-core desktop PC the domain was divided into eight streamwise blocks. Calculation times were of the order of a few hours, with final loads being obtained rapidly, but wake velocity evolving for longer.
Figure 4 illustrates wake and vortex structures at TSR = 6. Streamwise velocity is shaded on a central plane and an isosurface of the non-dimensional vorticity indicator Q, where
Sij and Ωij are mean strain and vorticity tensors. In this unsheared, low-turbulence onset flow, wake recovery is slow and the well-defined tip vortices are very persistent. Also evident is an accelerated bypass flow, due to the relatively high blockage (7.5%).
Figure 5 compares the main turbine load characteristics, i.e. thrust and power coefficients:
Thrust and power coefficients as a function of TSR, compared with the data of Bahaj et al. (2007)
across a range of TSR with the measurements of Bahaj et al. (2007). Thrust and torque are directly related to momentum deficit and angular momentum in the near wake. In Fig. 5 (but not our subsequent sections), corrections for blockage have been performed in the same way as in Bahaj et al.’s paper, because the original uncorrected load coefficients were not provided in that paper. Computed thrust is slightly low, but power is well predicted across the whole range tested, and particularly so near design conditions (TSR = 6). Actuator-line computations demonstrate the significant fall-off in power at off-design TSR that simple BEMT models (e.g. Batten et al. 2008) are not able to replicate.
Figure 5 also shows that, for a single turbine and an actuator representation of blades, choice of turbulence model makes little difference to predicted loads on an isolated turbine. By contrast, Sect. 5 will show that it can make a significant difference to velocities in the wake.
4 Two interacting turbines
An actuator approach makes it particularly straightforward to accommodate additional turbines and/or change their relative positions. Only minor changes are necessary to refine the background non-uniform, but still Cartesian, grid in the vicinity of rotors. In this section, to illustrate the effects associated with multiple rotors in a narrow channel we consider a (hypothetical) interaction between two rotors with the same geometry and channel dimensions as Sect. 3, with the rotors running at fixed angular speed. In Sect. 5 we compare with experimental data from more extensive arrays, with rotors able to establish their own speed according to the hydrodynamic torque.
Figure 6 shows predicted wake velocity distributions for two turbines separated streamwise by 5D and laterally by 0, ½ and 1D (between centrelines). The computational domain is similar to that in Sect. 3, but has been extended downstream. In this Section, a fixed rotation speed (TSR = 6, based on onset flow far upstream) is used for both turbines, although the downstream device will experience a different onset velocity, dependent on its position; for this turbine “tip-speed ratio” is nominal. In the low-turbulence flow here, wakes develop slowly, so that turbine interactions are exaggerated; in real marine flows, turbulence and velocity shear promote more rapid wake recovery. Figure 7 shows the resulting power and thrust coefficients.
In all cases, the upstream turbine experiences essentially the same loading as the individual turbine of Sect. 3. (Blockage corrections have not been applied here, resulting in small changes of load-coefficient values from the previous section.) However, the lateral position of the second turbine leads to large differences in load. This has significant implications for the layout of real turbine arrays, where onset flow direction may change over the tidal cycle.
In Fig. 6a, the second turbine is directly downstream of the first turbine. Unsurprisingly, its load coefficients are substantially reduced, but the reduction is exaggerated here, as, for more realistic turbulence levels, wakes would spread and recover more rapidly.
In Fig. 6b, the downstream turbine is “half-shaded” by the upstream turbine (i.e. lateral separation between centrelines is ½D). The whole-rotor power coefficients in Fig. 7 show the expected reduction in thrust and mean power. However, Fig. 8, which plots power coefficients for the whole rotor and for an individual blade on each turbine (scaled by the blade count of 3), indicates how individual blades on the downstream turbine experience huge cyclical changes in loading as they rotate in and out of the upstream turbine’s wake, with implications for fatigue damage. By contrast, blades on the upstream turbine suffer only small fluctuations, solely as a result of their changing position relative to the surface or bed.
For the case shown in Fig. 6c, with lateral spacing 1D, Fig. 7 shows that the downstream turbine can actually experience greater thrust and torque than the upstream turbine. In this instance, the downstream turbine is effectively in the bypass flow of the upstream turbine. Because of the relatively large channel blockage ratio (BR = 0.075 for each device) and low wake-spreading rate in the low-turbulence onset flow, this results in a higher onset velocity to the downstream turbine. If the wake region flow was to be completely ignored, then the power, scaling as velocity cubed, would become
or an increase in power coefficient from 0.49 to 0.62. An increase of this size is not observed as the flow is not completely excluded from the wake region. However, it does illustrate the possibility of enhancing power production in a narrow channel by judicious use of blockage effects, as analysed by Nishino and Willden (2012) and by Garrett and Cummins (2007). A consequence of the additional speed in the bypass flow around each individual turbine is that it is theoretically possible to exceed the Betz limit for power of an isolated rotor.
5 Multi-turbine arrays
Simulations in this section were undertaken to compare with an extensive experimental study of tidal-turbine wakes and their interactions carried out in the 12 m × 5 m wave and current flume at the University of Manchester. The characteristics of the onset flow, turbine geometry and behaviour of an individual turbine wake are described in Stallard et al. (2015), whilst measurements of array interactions are given in Stallard et al. (2013) and Olczak et al. (2016). The latter paper also includes simulations with the commercial code StarCCM+ using a BEMT–CFD hybrid.
5.1 Flow, geometry and array configurations
The flume width is 5 m. Experiments were conducted with depth-averaged velocity 0.463 m s−1 in water of depth 0.45 m. In contrast to the low-turbulence flows of the previous two sections, a screen at inflow was used to produce a deep turbulent boundary layer with (streamwise) turbulence intensity of about 10%. To prevent undesirable profile development upstream of the turbine in the CFD simulations, fully developed inflow profiles of all transport variables were supplied by a precursor 1-d boundary-layer simulation with the given bulk velocity and water depth, for the same vertical mesh distribution and turbulence model. The resulting non-dimensional mean-velocity profile (for the standard k-ε model) is shown in Fig. 9 and compared to the experimental data (actually, the smooth-wall log-law fit, with friction velocity uτ = 0.0187 m s−1, cited by Olczak et al. (2016), as individual data points were unavailable). A fully developed mean-velocity profile matches the experimental data reasonably well, but the simulated turbulence intensities are about half those in the experiments, irrespective of turbulence model. Increasing turbulence levels to match these would have led to significant evolution of the mean velocity profile upstream of the turbine.
Identical turbine rotors were deployed, with diameter 0.27 m, a Göttingen 804 blade section and radially varying pitch and chord as given in Stallard et al. (2015). The particular blade was chosen so that the variation of thrust coefficient with tip-speed ratio was similar to that for a realistic full-scale turbine, despite the much lower Reynolds number inherent in experimental measurements at this scale. At this Reynolds number, the maximum power coefficient is about 0.3, occurring around TSR = 4.5. Blade-sectional drag and lift coefficients, CL- and CD, were also given in Stallard et al. (2015), based on an earlier report. However, for simulations with torque-driven variations in speed, the CFD simulations showed a propensity to stall in downstream rows of turbines; this was found to be due to the resulting torque coefficient falling off too fast at low-to-moderate TSR. New coefficients were therefore generated with XFoil which, although showing little difference in a BEMT model near design TSR, maintained sufficient torque at lower speeds. Turbines were centred at mid-depth. Cross-sectional channel blockage per turbine is 2.5%.
Each experimental rotor had a gearbox and mast supporting it from an overhead gantry. Due to their potential effect on turbine wakes, simple blocked-cell representations of these (with the same maximum streamwise, spanwise and vertical dimensions) were included in the CFD simulations, in accordance with Sect. 2.3. These additional components had a minor impact on loads, affecting the fluctuating rather than mean load coefficients, but the vertical support had more effect on wake velocities, where it served to disrupt tip vortices.
Results are reported here for a single turbine (as reference, and to investigate the effect of turbulence model), one row of five turbines, and two or three staggered rows of turbines (in arrays of up to 12 devices). In all cases considered computationally, lateral separation between turbine centres was 1.5D and streamwise separation between rows was 4D, although many more array configurations with larger lateral and streamwise separations were examined experimentally (Olczak et al. 2016). The array configurations simulated are described in Sect. 5.3, where we discuss loading.
Unlike the cases covered by previous sections, rotor speed is not fixed for the multi-turbine simulations in this section. Whilst full-scale turbines may employ a number of techniques to control speed, including pitch control and stall control, in the flume experiments a retarding torque was applied to each rotor with a torque-speed characteristic such that an isolated rotor would operate at a TSR of 4.5. To attempt to mimic this in the CFD simulation, for the multi-rotor arrays each rotor speed Ω is updated every time step in accordance with the angular momentum equation:
where I is the moment of inertia, T the hydrodynamic torque (derived from the actuator force distribution) and Tretard the applied retarding torque. In this instance, we used (Fig. 10):
where T0 is the hydrodynamic torque operating on a single, isolated rotor turning at angular velocity Ω0 corresponding to TSR = 4.5. Moment of inertia I is not known in this case, but it affects only relaxation time and fluctuations about steady state, not the mean rotation speed. As only average rotation rates were available from the experiments, it was sufficient here simply to set I large enough to suppress large fluctuations in speed.
5.2 Simulation results for a single rotor
A single rotor, operating near maximum power and a fixed speed, with TSR = 4.5 was studied as a precursor to the full-wake simulations in Sect. 5.3. Both TSR and the thrust and power coefficients, CT and CP, use the rotor-disk-averaged onset velocity for non-dimensionalisation. The predicted mean thrust coefficient is 0.767, in reasonably good agreement with the experiment (~ 0.81). The power coefficient was not measured directly in the experiments, but the predicted mean value of 0.291 is in good agreement with a BEMT model. There are additional cyclic fluctuations of a few per cent in both thrust and power coefficients due to tower crossing and velocity shear in the approach flow.
Wake development was reported in Stallard et al. (2013). Figure 11 shows time-averaged mean-velocity deficit (normalised by disk-average onset velocity) on the hub axis as a function of streamwise distance, with the turbulence models described in Sect. 2.4.
A significant finding of this particular set of flume measurements was the substantial centreline velocity deficit reported from the flume measurements (corresponding to a near-zero absolute velocity) extending several diameters downstream of the rotor plane. Indeed, there is experimental evidence (both here, and in other turbine studies) of a short region where the centreline mean velocity deficit actually increases slightly with downstream distance in the near wake, possibly a consequence of fluid being drawn away from the axis towards the very-low-pressure core of the encircling tip vortices, in contrast with a non-rotating wake typified by a monotonic velocity recovery. Beyond the vortical near-wake region, the centreline velocity is, by continuity, a fairly good indicator of wake spreading rate.
In contrast to load and approach-flow predictions, simulations of the centreline velocity deficit varied substantially between different turbulence closures downstream of the rotor disk. In general, the standard k-ε model predicted greater turbulence levels and diffusive wake recovery, with much greater velocities (smaller velocity deficit) in the region from 1 to 4 diameters downstream. The realisable k-ε model of Shih et al. (1995) has a shear-dependent eddy-viscosity coefficient Cμ which acts to suppress production of turbulence in strongly straining flows, thus reducing diffusion. This gave better agreement in the near wake, but insufficient wake recovery further downstream. Reynolds-stress transport models (and we tried others besides the Gibson and Launder (1978) model reported here) showed a short region of increasing velocity deficit on the centreline, which was hinted at in the experimental measurements. However, again the wake further downstream decayed more slowly in simulations than experiments; this may be a consequence of the lower free-stream turbulence in the former. Second-moment-closure models do not fit comfortably with the actuator-line representation of blades because they depend too strongly on blade-generated turbulence and turbulence anisotropy which is not supplied in this approach. Since the main objective of this study was to examine the interactions of turbines in arrays, and because predicted loads were largely insensitive to turbulence modelling (within the actuator-line approach), the decision was taken to use the standard k-ε model for array calculations, as it produced the most realistic wake recovery at downstream distances of 4D and beyond.
Figure 12 shows the spanwise distribution (at hub height) of time-averaged mean-velocity deficit (with the standard k-ε turbulence model). Experimental data is only available for comparison at x/D = 2 and 4. Simulations (with all turbulence models) significantly underpredict the velocity deficit at the first of these, but are more acceptable at x/D = 4. The apparent “negative deficit” outside the wake results from the increased bypass flow due to blockage and is evident in both CFD and experimental measurements. The velocity wake spreads only slowly, being bounded by strong and persistent tip vortices.
5.3 Simulations of multi-rotor arrays
A major objective of this work was to conduct simulations of multiple turbines in arrays. This section concludes with a selected sample of simulations for arrays of 5–12 turbines, in 1–3 staggered rows, comparing with the experimental results reported in Olczak et al. (2016). Note that, in contrast to previous sections, rotor speed is not fixed and individual speeds within the array become a quantitative measure for comparison. All turbines rotate in the same direction (right-hand rotation about the x axis in the present notation).
Figure 13 indicates the typical interaction of wakes in the most complicated array simulated. Downstream of the first row, distinct wakes are evident. Due to the lateral staggering and close proximity of rotors, distinct wakes are lost downstream of the second and third rows. The graphic, which comprises transverse and horizontal planes and isosurfaces of the Q vorticity indicator (Eq. 7), coloured by mean-velocity magnitude, illustrates vortices shed from blade tips and the downstream influence of the support masts. Note that each turbine in a row presents a blockage ratio of about 2.5%; in the final row the cumulative blockage ratio of 12.5%, together with persistent wakes from the upstream turbines, leads to a significant increase in the bypass velocity on either side of the array. Although not clear from this figure, the common direction of rotation, combined with vertical velocity shear and the different bed (non-slip) and free-surface (stress-free) boundary conditions, leads to a small amount of lateral asymmetry, particularly for the outermost turbines of the array.
For a single row of turbines, the number and spanwise spacing of rotors are important variables, as well as the overall blockage of the channel. Figure 14 shows the wake development downstream of a single row of five turbines. The signature of five individual rotor wakes is clear in both simulations and experiments at x/D = 4; at this distance CFD underpredicts the wake deficit (but successfully predicts the speedup in the bypass flow). Similar discrepancies in the near wake were observed by Olczak et al. (2016) using the commercial code StarCCM+ and a BEM/CFD hybrid. In the CFD simulations distinct wakes are detectable at least as far as x/D = 12, but, as Fig. 14 shows, experiments suggest almost complete merging by x/D = 8. This is probably a consequence of the greater approach-flow turbulence intensity in the flume experiments.
Figure 13 illustrates the general wake features of a three-row array of 12 turbines, with 3, 4, 5 turbines, respectively in upstream, middle and downstream rows. Streamwise spacing is 4D and the lateral spacing between turbines within a row is 1.5D. The middle row is staggered with respect to upstream and downstream rows.
Figure 15 shows within-array distribution of rotor thrust. Since predictions for an isolated turbine gave a thrust coefficient 0.767 compared with an experimental value of about 0.81, a meaningful evaluation of the relative sheltering effect at different positions within the array is only possible if thrusts are normalised by the comparable figures for an isolated rotor.
For the first two rows at least, agreement between CFD and experiment for the relative change in thrust is good. In the front row, blockage effects (increasing the bypass velocity) increase the thrust relative to an isolated rotor. Turbines are sufficiently closely packed that there are successive reductions in wake velocity, and hence turbine thrust, in the middle and downstream rows. The outermost turbines in the downstream row experience opposing effects of part sheltering from upstream turbines but increased bypass flow around the whole array (Sect. 4). The CFD simulations accordingly demonstrate higher thrust on the two outermost turbines, although by less than that found experimentally.
Moment or power coefficients were not reported for the experiments. However, simulations suggest that relative changes in power coefficient across the array follow closely the relative changes in CT. From this distribution, therefore, it would be possible to estimate the likely output from marine turbines at prescribed positions in the array.
Thrust coefficients for a five-turbine single row and for two staggered rows of three and four turbines are shown in Fig. 16. Comments are similar to those for the three-row array. For the single-row array a greater predicted increase in thrust is due to greater channel blockage.
Figure 17 shows the predicted and measured turbine speeds (presented non-dimensionally as tip-speed ratio, based on undisturbed-flow, disk-averaged velocity) within the 3-row, 12-turbine array. In the experiments each rotor was supplied with a constant retarding torque equal to that which would maintain a TSR of 4.5 for that turbine in isolation. In the upstream row, as with the blockage-induced increase in thrust, there are predicted and measured increases in turbine speed, the CFD agreeing with measurements for two out of three turbines. In subsequent rows, CFD predicts qualitatively correct behaviour: a row-on-row diminution in turbine speed with reduced hydrodynamic torque. However, speed reduction is significantly greater in the CFD predictions. Investigation with a BEMT model showed that for this particular rotor geometry, there was a significant drop-off in torque at low speeds, and that at the low Reynolds numbers here, this was very sensitive to the prescribed blade segment coefficients. Indeed, these were reanalysed with XFoil due to a tendency of the coefficients provided in previous publications to cause turbines in the furthest downstream row to stall.
6 Conclusions
Rotating actuator lines are a computationally efficient means of combining real tidal-turbine geometries for one or more devices with complex fluid flows. Applications include optimising the layout of multiple turbines, predicting the impact of complex flows (bathymetry, turbulence, velocity shear or waves) and devising turbine speed-control strategies. The relatively short computation times (compared with blade geometry-resolved calculations), ease of changing blade properties and decoupling from the background grid make this level of sophistication practical for design.
The robust nacelle and support structures required by tidal-stream devices can be flexibly and adequately represented outside their immediate vicinity by a simple “blocked-cell” approach.
Single-turbine characteristics have been successfully computed and validated against experimental data across a range of TSR.
Two-turbine calculations have shown both positive and negative effects due to interactions between turbines. These demonstrate in particular that, depending on relative arrangement, channel blockage can be either detrimental or advantageous in extracting power, whilst fatigue-inducing fluctuations in loading on individual blades can occur in the presence of wakes generated by upstream devices, even where the whole-rotor power formed by summation over three blades is relatively constant.
With an actuator-line representation of rotating blades, predicted loads for an isolated turbine (or even a single row of turbines) are relatively insensitive to choice of turbulence model. By contrast, the highly strained flow, particularly in the region affected by tip vortices, leads to substantial differences in the wake behaviour of different turbulence models and thus the results from dense, multi-row arrays. The standard k-ε turbulence model is more diffusive in the near wake than other popular eddy-viscosity and Reynolds-stress-transport models, but the computations here suggest that this simple model predicts the wake spreading rate downstream more accurately than these more advanced models. CFD indicates a substantial velocity deficit up to four diameters downstream, with rotation effects and the presence of persistent tip vortices creating a velocity distribution very different from that downstream of a stationary plane disk.
Whole-array calculations have been undertaken and compared with experimental data for arrays of up to 12 turbines in up to three staggered rows. The effect of position in an array on the turbine thrust coefficient is well predicted, but individual turbine speeds varying in response to hydrodynamic torque are less so, with implications for simultaneous modelling of hydrodynamics and power take-off.
Inevitably, given the modelling approximations involved, some aspects are not resolved well by this approach. Here, we list phenomena which we believe would benefit from further improvement. These include: a better means of establishing “approach-flow velocity” for individual blade elements; examination of the influence of radial flow and transient behaviour on the blades; influence of high turbulence intensity on sectional lift and drag coefficients; inclusion of turbulence sources to represent generation in blade boundary layers.
Future work will include integration with a realistic drive-train model and speed-control strategy, and the modelling of turbine interaction with waves.
In summary, the main advances expressed in this paper are: the application of, and validation of, actuator-line methods to arrays; the use of torque-controlled, variable-speed rotors; the inclusion of bulk effects of support tower and nacelle.
References
Afgan I, McNaughton J, Apsley DD, Rolfo S, Stallard T, Stansby PK (2013) Turbulent flow and loading on a tidal stream turbine by LES and RANS. Int J Heat Fluid Flow 43:96–108
Ahmed U, Apsley DD, Afgan I, Stallard T, Stansby PK (2017) Fluctuating loads on a tidal turbine due to velocity shear and turbulence: comparison of CFD with field data. Renew Energy 112:235–246
Apsley DD, Hu W (2003) CFD simulation of two- and three-dimensional free-surface flow. Int J Numer Methods Fluids 42:465–491
Apsley DD, Leschziner MA (2000) Advanced turbulence modelling of separated flow in a diffuser, Flow. Turbul Combust 63:81–112
Apsley DD, Stallard T, Stansby PK (2016) Actuator-line CFD modelling of tidal-stream turbines. In: 2nd international conference on marine renewable energy (CORE2016), Glasgow
Baba-Ahmadi MH, Dong P (2017) Numerical simulations of wake characteristics of a horizontal axis tidal stream turbine using actuator line model. Renew Energy 113:669–678
Bahaj AS, Molland AF, Chaplin JR, Batten WMJ (2007) Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew Energy 32:407–426
Batten WMJ, Bahaj AS, Molland AF, Chaplin JR (2008) The prediction of the hydrodynamic performance of marine current turbines. Renew Energy 33:1085–1096
Black and Veatch (2005) Phase II UK tidal stream energy resource assessment. Rep. 107799/D/2200/03 for carbon trust
Garrett C, Cummins P (2007) The efficiency of a turbine in a tidal channel. J Fluid Mech 588:243–251
Gibson MM, Launder BE (1978) Ground effects on pressure fluctuations in the atmospheric boundary layer. J Fluid Mech 86:491–511
Launder BE, Spalding DB (1974) The numerical computation of turbulent flows. Comput Method Appl Mech Eng 3:269–289
Lien FS, Leschziner MA (1994) A general non-orthogonal collocated finite volume algorithm for turbulent flow at all speeds incorporating second-moment turbulence-transport closure, Part 1: computational implementation. Comp Methods Appl Mech Eng 114:123–148
McNaughton J, Afgan I, Apsley DD, Rolfo S, Stallard T, Stansby PK (2014) A simple sliding-mesh interface procedure and its application to the CFD simulation of a tidal-stream turbine. Int J Numer Methods Fluids 74:250–269
Menter FR (1994) Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J 32:1598–1605
Nishino T, Willden RHJ (2012) Effects of 3-D channel blockage and turbulent wake mixing on the limit of power extraction by tidal turbines. Int J Heat Fluid Flow 37:123–135
Olczak A, Stallard T, Feng T, Stansby PK (2016) Comparison of a RANS blade element model for tidal turbine arrays with laboratory scale measurements of wake velocity and rotor thrust. J Fluids Struct 64:87–106
Porté-Agel F, Wu Y-T, Lu H, Conzemius RJ (2011) Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J Wind Eng Ind Aerodyn 99:154–168
Sarlak H, Nishino T, Martìnez-Tossas LA, Meneveau C, Sørensen JN (2016) Assessment of blockage effects on the wake characteristics and power of wind turbines. Renew Energy 93:340–352
Schluntz J, Willden RHJ (2015a) The effect of blockage on tidal turbine rotor design and performance. Renew Energy 81:432–441
Schluntz J, Willden RHJ (2015b) An actuator line method with novel blade flow field coupling based on potential flow equivalence. Wind Energy 18:1469–1485
Shih T-H, Liou WW, Shammir A, Yang Z, Zhu J (1995) A new k-ε eddy-viscosity model for high Reynolds number turbulent flows. Comput Fluids 24:227–238
Sørensen JN, Shen WZ (2002) Numerical modelling of wind turbine wakes. J Fluids Eng 124:393–399
Stallard T, Collings R, Feng T, Whelan J (2013) Interactions between tidal turbine wakes: experimental study of a group of 3-bladed rotors. Phil Trans R Soc A Math Phys Eng Sci 871:20120159
Stallard T, Feng T, Stansby PK (2015) Experimental study of the mean wake of a tidal stream rotor in a shallow turbulent flow. J Fluids Struct 54:235–246
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Apsley, D.D., Stallard, T. & Stansby, P.K. Actuator-line CFD modelling of tidal-stream turbines in arrays. J. Ocean Eng. Mar. Energy 4, 259–271 (2018). https://doi.org/10.1007/s40722-018-0120-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40722-018-0120-3