Abstract
Oscillating surge wave energy converters (OSWECs) offer the possibility to convert ocean wave energy in the near shore region into electricity. One of the unique challenges they present is that the forces experienced in each direction differ. The curved geometry of the CCell device exaggerates this difference. Presented in this paper is a novel method of dealing with this difference which does not rely on high buoyancy within the paddle but, instead, variations in the control signals. This reduces the likelihood and severity of end stop collisions , resulting in improved survivability and reduced lifetime costs without increasing the volume and cost of the device. The algorithm presented may further be used to compensate for individual manufacturing tolerances or deterioration to OSWECs whilst in operation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
CCell is an oscillating surge wave energy converter (OSWEC) which is unique in its curved geometry Fig. 1. This geometry has structural benefits and is believed to provide significant power capture benefits. The device has been extensively studied both numerically and in laboratory wave tank tests at various scales (Chandel et al. 2016; Hillis et al. 2017; Zyba Ltd 2017). A scale prototype is currently under development for sea deployment in 2017.
Floating CCell device. Image courtesy of Zyba Ltd (2017)
Numerous strategies have been proposed for the control of wave energy converters (WEC) the majority of which seek to keep the movement of the primary converter in phase with wave excitation.
In complex-conjugate control, data about future waves and a hydrodynamic model are used to construct a control signal. The requirement for data on future waves makes practical implementation difficult. Further, it can result in forces or motions that exceed the device’s physical constraints (Nebel 1992; Bjarte-Larsson and Falnes 2005; Falnes 2007).
Model predictive control (MPC) can counter this problem to provide an optimal control signal using a detailed model of the entire WEC system into which physical constraints can be included. This is very computationally expensive which makes real-time implementation difficult, particularly in scaled devices which operate in higher frequency waves and therefore require higher sample times (Hals et al. 2010; Richter et al. 2013; O’Sullivan and Lightbody 2017).
Sub-optimal controllers include discrete control where the WEC movement is either stopped entirely (latching) or unrestricted (declutching) for some portion of the wave cycle. As a result, peak loads are normally greater than in continuous cases (Babarit and Clément 2006; Folley and Whittaker 2009; Babarit et al. 2009; Clément and Babarit 2012). Also included are controllers such as the ’Simple and Effective Controller’ Fusco and Ringwood (2013) which use similar approaches to MPC or complex-conjugate control but make assumptions or simplifications in order to implement them in real time.
With the exception of Nebel (1992) all the strategies discussed above were developed for point absorbers and, in most cases, demonstrated using a single degree-of-freedom linear model. OSWEC’s are flap type devices which are constrained such that they oscillate with the surge (horizontal) motion of sea waves. It is beneficial for them to be placed near-shore where this surge motion is exaggerated. As such their operation is quite different from point absorber type devices which interact with the heave (vertical) motion of sea waves and therefore generally operate in deep water. Because of this difference not all results or findings can be directly related to CCell. Indeed, one study of a surface piercing OSWEC found that at ‘optimal’ damping the phase angle between wave and paddle position had not, as linear theory would suggest it should, reached zero (Schmitt et al. 2016). Further more, as a result of focussing on point absorbers, little attention has been given to the difference in wave excitation torque experienced by opposing sides of an OSWEC, something which is magnified by the curved geometry of CCell.
This paper will consider the fundamental theory for the asymmetry in wave forces before proceeding to develop a hydrodynamic model of the CCell device which includes these asymmetric forces but ignores mean drift force (another form of asymmetric loading). However, it is believed that the controller discussed would work in a similar manner with this asymmetry. A supervisory controller, which could be used in conjunction with the controllers discussed above, which seeks to overcome some issues these forces can pose will then be shown working with a simple power maximising algorithm both in simulation and experimentally.
2 Asymmetry of wave excitation force
The difference between the wave excitation force experienced by an OSWEC in the seaward and shoreward directions necessitates an opposing force with equal magnitude to maintain a neutral operating position. There are two possible sources of this force. The first is buoyancy. If the buoyancy of the paddle is sufficiently large then it will limit the displacement of the paddle before the end stops on the hydraulic piston or other control member are reached (Evans 1981). The second option is to supply this force from the PTO system, either in the form of a spring or by varying the damping rate in each direction.
Existing OSWEC designs are believed to overcome this issue with high buoyancy. A survey of the published findings from other OSWEC projects revealed that asymmetric forces were not discussed elsewhere (Gomes et al. 2012; Tom et al. 2016; Crooks et al. 2016). The problem with high buoyancy is that it is analogous to having a large spring attached to the paddle which reduces paddle motion and can adversely effect power capture whilst also increasing the paddle size.
3 Dynamic modelling
In order to develop a suitable controller to mitigate the asymmetric forces on the paddle it was first necessary to create and validate a dynamic model of CCell. Whilst CFD has been successful in modelling surface piercing OSWEC’s (Schmitt and Elsaesser 2015) the computational overhead involved make such models unsuitable for control design purposes. Semi-analytical models of the form used in Crooks et al. (2016) are significantly more computationally efficient.
If standard linear wave theory assumptions of incompressible and irrotational flow are made then CCell’s motion may be expressed by:
where I is the moment of inertia about the paddles hinge, \(\theta \) is the angular displacement of the paddle, \(m_\mathrm{E}\) is the moment due to wave excitation and the subscripts H, R, P and V similarly denote hydrostatic buoyancy, radiation damping, PTO damping and viscous drag. Both \(m_\mathrm{E}(t)\) and \(m_P(t)\) are considered exogenous forcing terms.
The frequency-domain excitation moment is given by:
where \(H(\omega )\) is the Fourier Transform of \(\eta (t)\), the instantaneous wave elevation relative to the mean free surface and \(\varGamma (\omega )\) is the frequency-dependant excitation coefficient. As mentioned above this moment is asymmetric and thus is modified to include the influence of wave direction, therefore departing from linear theory:
where \(\kappa \) is a piecewise linear function with two breakpoints.
The hydrostatic restoring moment, \(m_H(t)\) is represented by:
this can be simplified for small displacements by replacing the non-linear \(\sin \theta (t)\) term with \(\theta (t)\). For the purpose of tuning the controller gains this was done. It is further simplified in this case as the centre of gravity and buoyancy are assumed coincident.
Where \(V_\mathrm{p}\) is the paddle volume, \(\rho _w\) and \(\rho _\mathrm{p}\) are the density of the water and paddle respectively, \(c_b\) and \(c_g\) are the distances from the paddle hinge to centre of buoyancy and gravity respectively, h is the height of the paddle and d is the vertical distance from the mean free surface.
The radiation moment represents the resistance to the paddle’s motion through the water. This is frequency dependant and can be modelled as:
where \(A(\omega )\) and \(B(\omega )\) are added moment of inertia and wave radiation damping coefficients respectively. The hydrodynamic coefficients \(\varGamma (\omega )\), \(A(\omega )\) and \(B(\omega )\) can be determined using a number of methods; experimental testing (Crooks et al. 2016), in a similar manner using the outputs of CFD and panel method codes such as WAMIT, AQWA or NEMOH. Figure 2 shows the added moment of inertia and radiation damping calculated using the Nemoh code and a 3D model of the CCell paddle.
As stated earlier panel methods assume inviscid flow and therefore ignore the viscous drag on the paddle. To compensate for this it is normal to apply a quadratic damping term Babarit et al. (2012) like that in Eq. 6.
where \(C_d\) is the damping coefficient and the challenge is to select an appropriate value for this coefficient. This can be found from Computational Fluid Dynamics (CFD) which does model viscosity, inferring from experimental results or taken from the range of published values for a number of different shapes. This latter approach is the most convenient and a value of \(1.8 \cdot c_g\) was selected based on the work in Bhinder et al. (2012). The original coefficient is multiplied by the distance to centre of gravity to allow for the linear motion in the original paper. The WEC used in Bhinder et al. (2012) had a flat face and had a different aspect ratio to the CCell device so this is unlikely to be truly representative, therefore work is underway to improve this assumption through the use of CFD simulations.
Panel method codes produce linear excitation force coefficients and therefore do no account for the asymmetry in wave forces. Therefore \(\varGamma (\omega )\) was found using empirical data gathered from testing in the Kelvin Hydrodynamics Laboratory at the University of Strathclyde (Zyba Ltd 2017) with an identical set-up to Sect. 5. The excitation force for a series of irregular wave tests was back calculated using the measured PTO force and the model given above. This was then used along with recorded wave elevations at the paddle to identify a model of the form in Eq. 3. Matlab’s non-linear Hammerstein–Wiener function (NLHW) was used to conduct the model identification (MATLAB 2015). Figure 3 shows the piecewise function \(\kappa (t)\) and Fig. 4 a Bode plot of \(\varGamma (\omega )\) for the fifteenth scale model:
It can be seen that the degree of asymmetry changes with wave height; larger waves producing greater asymmetry. Positive wave heights drive the paddle towards to shore, whilst negative ones return in seaward. It is this behaviour that means a static control correction cannot be made for the asymmetry.
The PTO developed for use in scale testing of CCell is capable of providing complex and non-linear torques \(m_P(t)\), to enable it to mimic realistic systems. A fuller description can be found in Sect. 5. For the purpose of investigating asymmetric wave forces, however, it was controlled to behave as a linear damper, the damping coefficient of which is dependent on the direction of angular velocity. It can therefore be modelled as a piecewise linear system:
where p is the distance from the hinge to the PTO attachment point (0.17 m) and c is a bilinear damping coefficient given by:
Table 1 displays the system parameters used for simulation:
When compared with measured data the model above gives a good fit. Figure 5 shows the simulated and measured results with a JONSWAP spectral wave input with significant wave height (\(H_\mathrm{s}\)) of 0.117 m and significant period (\(T_\mathrm{s}\)) of 2.71 s. The PTO was modelled as in Eq. 8 with \(c^+=2\times 10^{4}Ns/m\) and \(c^-=1\times 10^{4}\) Ns/m where velocity is defined as positive paddle motion towards the shore.
Figure 6 shows a section of the time response of the model against measured data.
This inaccuracy is believed to arise mainly from two simplifications. Firstly static friction within the PTO and bearings has been neglected. Secondly it was assumed that the paddle was mounted in a fixed location, in reality the paddle is floating and attached to the tank floor by legs and so is able to move within the water column.
4 Self zeroing controller
Active control was chosen to enforce operation around the piston’s mid point. This allowed the piston stroke to be smaller than would be expected in a buoyancy dependant device and also allowed the operating point to be moved away from the neutrally buoyant position if desired.
The first challenge in actively controlling the paddle’s operating point is to accurately characterise it. A simple low pass filter of the paddle’s angle (or position) with a time constant of several wave lengths could provide a useful measurement but the phase lag introduced would cause problems for online control given the pistons stroke is only twice the expected motion. Instead the peaks of each motion were found and the operating point calculated as being at their centre. Figure 7 shows, schematically, how this was achieved. This measurement naturally updated each half wave cycle and Fig. 8 shows this measurement against measured angle.
As mentioned previously, the correlation between asymmetry and wave height means that a static correction cannot be applied. Instead, a Proportional plus Integral (PI) controller was used to generate a correction signal. This signal was then added to the shoreward control member’s signal and subtracted from the seaward’s signal to create an offset. The gains of this controller were tuned empirically using the model given above.
Figure 9 shows the self zeroing controller working in regular seas with \(H = 0.083\) m and \(T = 1.93\) s. At 60 and 120 s the target damping was changed by a simple stepping controller in an attempt to increase power capture, Fig. 10 shows how this controller operates all steps are of equal size.
It can be seen that the self-zeroing controller rapidly acts to balance out the asymmetry in the wave excitation force and continues to adjust as the target damping is changed. In irregular seas such neat convergence is not achievable as the asymmetry will change from wave to wave. Figure 11 shows the paddle angle and damping in an irregular sea with \(H_\mathrm{s}=0.083\,\hbox {m}\) and \(T_\mathrm{s}=1.98\,\hbox {s}\).
Whilst the neat convergence seen in regular waves is absent, the actions of the self-zeroing controller can be seen from the offset in the two signals. The gradual trend towards higher damping is a result of the stepping controller.
4.1 Increasing buoyancy
As mentioned previously a significant increase in the paddle’s buoyancy could also be used to mitigate the effect of asymmetric wave forces.
To investigate the difference on power generation, paddle loads and movement the self-zeroing controller was turned off and buoyancy increased until the paddle operated around 5°in large seas (\({H}=0.234\,\hbox {m}\) and \({T}=3.44\,\hbox {s}\)) with extreme damping 1MNs/m. This corresponded to an increase in buoyancy of 6.5 times. Naturally to increase the buoyancy to this extent the shape of the device would need to be modified. For the purpose of this investigation it is assumed that \(\varGamma (\omega ), A(\omega )\) and \(B(\omega )\) remain unchanged however.
Whilst not realistically achievable the result is still of interest. Increasing paddle size whilst maintain performance results in a degrading of most metrics for WECs. Therefore, demonstration of a smaller device and superior performance even if only in simulation is worthwhile.
Figure 12 shows the energy capture in an irregular sea with \(H_\mathrm{s}=0.083\,\hbox {m}\) and \(T_\mathrm{s}=1.98\,\hbox {s}\) with the self-zeroing controller and normal buoyancy against no self-zeroing controller and increased buoyancy.
In both cases the damping was optimised to give maximum power capture without end stop collisions. A lower damping was used with the self-zeroing controller due to its ability to keep the paddle operating around the centre of its travel. This power increase is believed to be a result of two things, firstly the ability to select a lower damping rate. Secondly that the increase in buoyancy effectively introduces a large spring force which is constant through all sea-states. In many waves this spring force will be far from optimal resulting in increased phase shift between the device and the waves.
5 Experimental methodology
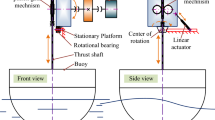
A 1/15th scale model of the CCell device was tested in the 76 m \(\times \) 4.6 m wave tank at the Kelvin Hydrodynamics Laboratory, at a water depth of 2 m. Figure 13 shows the positioning of the model and wave gauges within the tank, more information on the testing can be found in Zyba Ltd (2017).
It is envisioned that the full-scale PTO for CCell will be a purely dissipative design meaning energy cannot be returned to the paddle from the PTO. The PTO is expected to utilise hydraulics and an asynchronous generator, meaning the controller would therefore vary the generator field excitation based on the sign of piston velocity. It is important to consider the form of the final PTO when controlling devices during scale testing to ensure the methods are applicable. Figure 14 shows a functional circuit diagram of the anticipated design with component descriptions provided in Table 2.
It is not possible to directly scale each of the components in the design in order to develop a PTO for scale testing. Start torque on hydraulic motors in particular doesn’t scale linearly and can cause problems at the scale used for this testing. Instead a system that can deliver the same controllability was designed. Figure 15 shows the circuit diagram of the scale PTO and Table 3 contains information on the components.
Comparison of energy capture between self-zeroing control and increased buoyancy in sea with \(H_\mathrm{s}=0.117\,\hbox {m}\) and \(T_\mathrm{s}=2.71\,\hbox {s}\). Image courtesy of Zyba Ltd (2017)
A pair of controllable solenoid valves control flow out of the equal area cylinder with a check valve supplying flow to the opposite side of the cylinder. An accumulator is used to avoid cavitation and a small needle valve to ensure a small flow in the cylinder in case of loss of power to the solenoid valves. Figure 16 shows the PTO assembled to the device.
The control valves are used to provide resistance instead of a hydraulic motor as they provide greater control resolution than a motor at this scale and can be made to mimic the behaviour of a range of PTO configurations. One was used for each cylinder chamber instead of rectifying the flow, as in Fig. 14, as this reduced the required control bandwidth of the valve in-line with off-shelf-components. There is no energy storage within the system as this reduces control bandwidth and the hoses connecting the cylinder to the valves provided sufficient smoothing for this application. During the testing covered in this document the PTO was constrained to act as a piecewise linear damper as in Sect. 3. The valve control voltages were created by combining the offset generated by the self-zeroing controller with a fixed damping command as in simulation. However, both signals were normalised such that 1 was minimum damping and 0 was maximum damping. These were then passed through a pair of pre-calibrated maps to create valve voltage demand signals. These maps were created from bench testing of the PTO to provide a more linear characteristic to the controller and also mitigate any discrepancy in the two valves’ behaviour. Figure 17 shows the maps.
Visible in Fig. 16 is a small load cell (Richmond Industries 200 series) connecting the cylinder to the paddle and also a pair of pressure sensors (Parker PTDVB060) on the cylinder outlets. These were supplemented by an angle sensor (Novotechnik RFD4000) on the hinge of the paddle. These sensors were logged using a National Instruments PCI-6229 DAQ card and a Simulink Real-Time model running with a sample time of 7 ms. The same system provided control voltages to the solenoid valves.
PTO assembled to fifteenth scale model. Image courtesy of Zyba Ltd (2017)
6 Experimental results
To emphasise the need for a self-zeroing controller in OSWECs with low buoyancy Fig. 18 shows the paddle angle with symmetrical damping in regular seas with \(H=0.083\) m and \(Tp = 1.93\) s.
At time zero the self-zeroing controller is turned off such that a symmetrical damping is applied by the PTO. At 30 s the self-zeroing controller was re-engaged to prevent collision with an end-stop. Figure 19 shows the velocity and control force (measured using the pressure sensors) for the same time period, demonstrating this symmetry.
In Fig. 18 a high damping was commanded. At lower damping settings it is expected that the paddle would reach its end-stop significantly quicker. Both static friction and hysteresis can be seen in the PTO’s response, Fig. 19. These were not modelled in the PTO used for simulation and so will contribute to the misalignment between simulated and measured results.
Figure 20 shows the paddle’s angle in the same wave conditions but with the self-zeroing controller enabled.
The paddle was started near one of the end-stops and can be seen converging on its intended operating point, in the opposite direction from that in Fig. 18. Once this position was reached the specified damping was varied multiple times. After each change it can be seen that the operating point changes briefly before the force asymmetry is balanced again. Figure 21 shows the damping characteristic between 270 and 300 s (the lowest damping setting).
As with simulation in regular waves there is a steady convergence towards the operating point. Figure 22 shows the offset for the rest of the test along with the normalised command which was combined with the offset from the self-zeroing controller to produce the control voltage.
Each time there is a step change in the command the self-zeroing controller changes the offset between the valves.
Figure 23 shows the paddle angle in a section of irregular seas with a \(H_\mathrm{s} = 0.117\) m and \(Tp = 2.71\) and self-zeroing engaged.
The asymmetry in the damping force used to achieve these results is quite pronounced as shown in Fig. 24.
Figure 25 shows the measured offset for the rest of the test and the valve commands (between 0 and 1).
Although the offset is constantly being updated there is a clear trend in the command data over this period suggesting that a fixed offset may be suitable within each seastate. The offset is, as expected, less stable than in regular seas. In the large seas shown above there is more variation in offset than was seen in small seas. It is suggested that replacing the simple PI controller with a gain scheduling controller may counter this. It would enable a larger contribution from the self-zeroing controller when large forces are measured in the PTO.
7 Conclusion
It has been shown that it is possible to change the operating position of an OSWEC using a passive PTO by varying the damping in either direction. This has been used to offset the asymmetry of wave forces acting on the CCell paddle. This allows less buoyancy to be used in the creation of the paddle or for the paddle to continue to operate if some buoyancy was lost due to damage or wear. As a result device size and therefore cost can be reduced without suffering from increased and significant end-stop collisions.
A similar technique could be used to help account for difference in buoyancy distribution between paddles due to manufacturing tolerances or to manoeuvre the paddle in place to be locked down for maintenance or safety reasons. It is not intended as an alternative to other control methods that seek to maximise power generation but may instead be used in a supervisory manner to ensure operation around a desired point.
References
Babarit A, Clément A (2006) Optimal latching control of a wave energy device in regular and irregular waves. Appl Ocean Res 28(2):77–91
Babarit A, Guglielmi M, Clément AH (2009) Declutching control of a wave energy converter. Ocean Eng 36(12):1015–1024
Babarit A, Hals J, Muliawan M, Kurniawan A, Moan T, Krokstad J (2012) Numerical benchmarking study of a selection of wave energy converters. Renew Energy 41:44–63
Bhinder MA, Babarit A, Gentaz L, Ferrant P (2012) Effect of viscous forces on the performance of a surging wave energy converter. In: The Twenty-second International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, Rhodes, pp 545–549
Bjarte-Larsson T, Falnes J (2005) Investigation of phase-controlled wave-power buoy. In: Proceedings of 6th European Wave and Tidal Energy Conference. Glasgow, U.K., pp 47–50
Chandel DRS, Sell NP, Plummer AR, Hillis AJ (2016) Discrete control of an Oscillating Wave Surge Converter. Control 2016–11th International Conference on Control. U.K. Auto. Contr. Council. Belfast, U.K
Clément A, Babarit A (2012) Discrete control of resonant wave energy devices. Philos Trans R Soc Lond A Math Phys Eng Sci 370(1959):288–314
Crooks D, vant Hoff, J, Folley M, Elsaesser B (2016) Oscillating wave surge converter forced oscillation tests. ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering. The American Society of Mechanical Engineers, Busan, South Korea
Evans D (1981) Maximum wave-power absorption under motion constraints. Appl Ocean Res 3(4):200–203
Falnes J (2007) A review of wave-energy extraction. Mar Struct 20(4):185–201
Folley M, Whittaker T (2009) The control of wave energy converters using active bipolar damping. Proc Inst Mech Eng Part M J Eng Marit Environ 223(4):479–487
Fusco F, Ringwood JV (2013) A simple and effective real-time controller for wave energy converters. IEEE Trans Sustain Energy 4(1):21–30
Gomes R, Henriques J, Gato L, Falcão AO (2012) Hydrodynamic optimization of an axisymmetric floating oscillating water column for wave energy conversion. Renew Energy 44:328–339
Hals J, Falnes J, Moan T (2010) Constrained optimal control of a heaving buoy wave-energy converter. J Offshore Mech Arctic Eng 133(1)
Hillis AJ, Sell NP, Chandel DRS, Plummer AR (2017) Control of the CCell Oscillating Surge Wave Energy Converter. 20th World Congress of the International Federation of Automatic Control, Toulouse, France, pp 14686–14691
MATLAB (2015) version 8.6.0 (R2015b). The MathWorks Inc., Natick, Massachusetts
Nebel P (1992) Maximizing the efficiency of wave-energy plant using complex-conjugate control. Proc Inst Mech Eng Part I J Syst Control Eng 206(4):225–236
O’Sullivan A, Lightbody G (2017) Co-design of a wave energy converter using constrained predictive control. Renew Energy 102(Part A): 142–156
Richter M, Magana M, Sawodny O, Brekken T (2013) Nonlinear model predictive control of a point absorber wave energy converter. IEEE Trans Sustain Energy 4(1):118–126
Schmitt P, Elsaesser B (2015) On the use of openfoam to model oscillating wave surge converters. Ocean Eng 108:98–104
Schmitt P, Asmuth H, Elser B (2016) Optimising power take-off of an oscillating wave surge converter using high fidelity numerical simulations. Int J Mar Energy 16:196–208
Tom N, Lawson M, Yu YH, Wright A (2016) Development of a nearshore oscillating surge wave energy converter with variable geometry. Renew Energy 96:410–424
Zyba Ltd (2017) NWEC stage 1 - public report. Tech. rep., Wave Energy Scotland
Acknowledgements
The authors would like to thank Zyba Ltd. for their collaboration in this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors are grateful for financial support from EPSRC/ Innovate UK under Grant EP/N508445/1 and the Wave Energy Scotland Novel WEC competition.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sell, N.P., Plummer, A.R. & Hillis, A.J. A Self-zeroing position controller for oscillating surge wave energy converters with strong asymmetry. J. Ocean Eng. Mar. Energy 4, 137–151 (2018). https://doi.org/10.1007/s40722-018-0113-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40722-018-0113-2