Linear diffraction analysis of the three-float multi-mode wave energy converter M4 for power capture and structural analysis in irregular waves with experimental validation

Abstract

A frequency domain dynamic model based on the DIFFRACT code has previously been applied to the moored, three-float, multi-mode wave energy converter M4 in regular waves, modelled as a two-body problem, showing good agreement of relative rotation and power capture with experiments for small wave height (Sun et al., 2016 J Ocean Eng Mar Energy 2(4):429–438). The machine has both a broad-banded and relatively high capture width for the range of wave periods typical of offshore sites. The float sizes increase from bow to stern facilitating alignment with the local wave direction; the bow and mid float are rigidly connected by a beam and the stern float is connected by a beam to a hinge above the mid float where the relative rotation is damped to absorb power. The floats are approximately half a representative wavelength apart so the float forces and motion in anti-phase generate relative rotation. The mid and stern floats have hemispherical and rounded bases giving negligible drag losses. Here the multi-body model is generalised to enable bending moment prediction in the beams and by including excitation by irregular wave fields with and without directional spreading. Responses are compared with experiments with input wave spectra of JONSWAP type. In uni-directional waves, the measured spectra were a close approximation to the target JONSWAP spectra and were input into the model giving excellent predictions of relative rotation and bending moment in all cases and slight overprediction of power. Predictions of bending moment in regular waves were surprisingly somewhat less accurate. With multi-directional waves the measured wave spectra did not match the target JONSWAP spectra as well, particularly for smaller periods, and the directional spreading was not measured. However with the target spreading function and the measured spectra input to the model the predictions were again excellent. Since the model is validated for uni-directional waves it seems likely that it will also be valid in multi-directional waves and the accurate predictions thus suggest that the actual spreading was indeed close to the target. The model indicates that realistic directional spreading can reduce power capture by up to about 30%. However, optimising the damping coefficient in the linear damper can increase power capture by a similar amount, and optimising the vertical hinge position can increase this further although this cannot be varied in situ. Power optimisation is inevitably less marked than with regular waves. Good agreement with experiment is thus achieved for small to moderate wave heights (about twice average) at typical full scales, indicating that this efficient frequency domain method is valuable for fatigue analysis and energy yield assessment. Accurate prediction based on linear diffraction theory in steep or extreme waves is however not expected.

1 Introduction

Many devices have been considered for the conversion of ocean wave motion into electricity; for a comprehensive review see Falcão (2010). The wave resource is greatest offshore in deeper water and we consider here the moored, three-float, multi-mode line absorber (or attenuator) M4, shown to have high crest capture widths across a broad band of wave frequencies as described in Stansby et al. (2015a, b). The float sizes increase from bow to stern; this facilitates self-rectifying alignment with the local wave direction. The bow and mid float are rigidly connected by a beam and the stern float is connected by a beam to a hinge above the mid float where the relative rotation is damped to absorb power; the power take off (PTO) is thus above deck with easy access. The floats are approximately half a representative wavelength apart so the float forces and motion in anti-phase generate relative rotation. The mid and stern floats have hemispherical and rounded bases giving negligible drag losses. This has been modelled effectively for operational conditions using linear diffraction theory in the time domain (Stansby et al. 2015a, 2016) and the frequency domain (Eatock Taylor et al. 2015; Sun et al. 2016). Eatock Taylor et al. provided a general structural model based on dynamic substructuring and hydrodynamic finite element analysis assuming that the floats act in isolation giving good predictions of experimental results for response and power for longer wave periods, accounting for drag effects with flat-based floats. An eigen analysis provided the four mode shapes and natural periods. Sun et al. (2016) provided a two-body analysis with full hydrodynamic interaction using the DIFFRACT code giving response and power capture predictions in regular waves, giving good experimental prediction for smaller wave heights, with optimisation of damping coefficient and vertical hinge position for power capture. A photograph from the laboratory test is shown in Fig. 1. They also investigated interaction due to small rows of devices, up to five. A more general structural-hydrodynamic model is however necessary for fatigue analysis and in this paper we generalise the multi-body approach of Sun et al. (2016) to allow rigid connections and hinges between bodies which now comprise three floats and two beams, following (Sun et al. 2011, 2012). In this way, a complete structural definition is provided, though without internal dynamic behaviour arising from structural flexibility, with full hydrodynamic interaction between floats using DIFFRACT; regular, irregular and directional waves are input. The model is validated against experimental measurements of relative rotation, power capture and beam-bending moment. The paper is structured with the theoretical background of the numerical method in Sect. 2. The experimental setup is described in Sect. 3. In Sect. 4, numerical results are validated by comparing with measurements in uni-and multi-directional irregular waves. The damping coefficient and vertical hinge position are optimised to maximise absorbed power for different random sea states in Sect. 5. Effects of directional spreading on the performance are analysed in Sect. 6. Some discussion is given in Sect. 7 and conclusions are presented in Sect. 8.

Fig. 1

Photograph of M4 in the wave basin. Note the PTO on a prototype would be hinged at deck level

Fig. 2

Five-body dynamic model in numeral analysis (unit m)

2 Numerical model

2.1 Linear multi-body dynamic model

Under the potential flow assumption, the motion equations for multiple floating bodies without mechanical connections can be written in the frequency domain (Sun et al. 2011, 2012)

$$\begin{aligned} \left[ {-{\omega ^{2}} \left( {\mathbf {M}+{} \mathbf{A}_{H} } \right) -\hbox {i}\omega \left( {\mathbf{B}+{} \mathbf{B}_{H} } \right) +\left( {\mathbf{C}+{} \mathbf{C}_{H} } \right) } \right] \left\{ \xi \right\} =\left\{ {f_{ex} } \right\} \nonumber \\ \end{aligned}$$

(1)

in which, complex vector {$f_{ex}$} on the right hand side represents the linear wave excitation forces/moments for the geometries of floating bodies and the incident waves (considering water depth d, wave height H, wave period T and wave incident angle $\beta$). The unknowns {$\xi$} in Eq. (1) denote complex frequency-dependent 6 degree-of-freedom motions of each floating body. The matrix M is the mass matrix for the N bodies, while B and C are the external linear damping and the mooring restoring force matrices, respectively. Matrix C $_{\varvec{H}}$ represents the hydrostatic restoring force coefficients. Matrices A $_{\varvec{H}}$ and B $_{\varvec{H}}$ are the added mass and radiation-damping matrices that are related to the radiation forces due to the body motions. Eq. (1) can be simplified as

$$\begin{aligned} {\hbox {K}} \left\{ \xi \right\} =\left\{ {f_{ex} } \right\} \end{aligned}$$

(2)

For a system consisting of N bodies, {$\xi$} and {$f_{ex}$} include 6N components. The matrix K is $6N\times 6N$.

To consider the physical constraints (e.g. rigid connections and hinges) between modules, the technique of Lagrange multipliers {$\lambda$} is introduced to define the reaction forces/moments at the connections and the motion equations become (Sun et al. 2011, 2012)

$$\begin{aligned} \left[ {{\begin{array}{ll} {\mathbf{K}}&{} {\mathbf{D}^{T}} \\ {\mathbf{D}}&{} 0 \\ \end{array} }} \right] \left\{ {{\begin{array}{ll} \xi \\ \lambda \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ll} {f_{ex} } \\ 0 \\ \end{array} }} \right\} \end{aligned}$$

(3)

where D is a constraint matrix, which defines the kinematic connectivity between the modules (e.g. floats and beams).

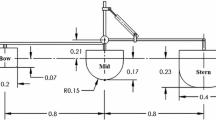
As shown in Fig. 2, the left float and middle float of M4 are rigidly connected by a beam, the right float connected by a beam to a hinge above the middle float where the rotational relative motion is damped to absorb power. The wave energy converter M4 can be modelled as a 5-body dynamic system consisting 3 floats (referred as “Float 1”, “Float 2” and “Float 3”) and 2 beams (referred as “Beam 1” and “Beam 2”) as shown in Fig. 2. “Float 1” and “Beam 1” have a rigid connection at “C1”, “Beam 1” and “Float 2” have a rigid connection at “C2”. “Float 2” and “Beam 2” have a hinge connection at “hinge O”, “Beam 2” and “Float 3” have a rigid connection at “C3”.

There are a total of 30 degrees of freedom for the present 5-body dynamic system before considering the physical connections, and indices for the degrees of freedom for each body can be found in Table 1. The constraints between floats and beams can be categorised into two types: rigid connections (at “C1”, “C2” and “C3”) and a hinge (at “hinge O”). For rigid connections, the form of the constraint matrix D can be found in Sun et al. (2011) and the corresponding constraint matrix for the hinge connection can be found in Sun et al. (2016).

Table 1 Index of degree of freedom

When the PTO at “hinge O” in Fig. 2 is simplified as a linear rotational damper with damping coefficient $B_{d}$, the moments introduced by the PTO can be calculated as $f_{PTO} (\omega )=-B_{d} \dot{{\theta }}_{r} =i\omega B_{d} \theta _{r}$, where $\dot{{\theta }}_{r}$ and $\theta _{r}$ are complex relative angular velocity and relative rotations at “hinge O”, respectively. Here, $\dot{{\theta }}_{r} =-\hbox {i}\omega \theta _{r}$ as relative rotations in time domain can be written in the form of $\mathrm{Re}\{\theta _{r} e^{-\mathrm{i}\omega t}\}$, where $\mathrm{Re}\{\}$ denotes the real part of a complex variable. The relative pitch motion at the “hinge O” can be calculated as $\theta _{r} =$ $\xi _{29}$ – $\xi _{11}$, where $\xi _{11}$ is the pitch motion of “Float 2” and $\xi _{29}$ is the pitch motion of “Beam 2”. The corresponding coefficients of relative rotations $\theta _{r}$ can be absorbed into the matrix K in Eq. (3) by putting the coefficients i$\omega \,B_{d}$ and -i$\omega \,B_{d}$ at corresponding locations (Eatock Taylor et al. 2016). The equations of motion for the multiple float system containing the PTO become

$$\begin{aligned} \left[ {{\begin{array}{ll} {\mathbf{K}_{2} }&{} {\mathbf{D}^{T}} \\ {\mathbf{D}}&{} 0 \\ \end{array} }} \right] \left\{ {{\begin{array}{ll} \xi \\ \lambda \\ \end{array} }} \right\} =\left\{ {{\begin{array}{ll} {f_{ex} } \\ 0 \\ \end{array} }} \right\} \end{aligned}$$

(4)

The mass and inertia of the floats, damping moments of PTO, hydrostatic and radiation forces have been included in matrix K $_{\mathrm {\mathbf {2}}}$. There is no external mechanical damping and the effect of mooring forces is assumed to be small ($\mathbf{B}=0$ and $\mathbf{C}=~0$ in Eq. (1)). For “Beam 1” and “Beam 2” which are above the still water level (SWL) as shown in Fig. 2, A $_{\varvec{H}}=$ 0, B $_{\varvec{H}}=$ 0 and C $_{\varvec{H}}=$ 0 in Eq. (1).

After solving Eq. (4), both the motions of each body {$\xi$} and connection reaction forces/moments {$\lambda$} can be obtained. The mean power absorbed in regular waves at every frequency $\omega$ can be written as, e.g. Mei et al. (2005),

$$\begin{aligned} P_{c}^\mathrm{REG} =\frac{1}{2}\omega ^{2} B_{d} |\theta _{r} |^{2} \end{aligned}$$

(5)

From Eq. (5), it can be seen that mean absorbed power at each wave frequency is proportional to the relative pitch rotation ${\vert }\theta _{r}{\vert }^{\mathrm {2}}$ (and so it is also proportional to the square of the amplitude of incident wave $A_{i})$. The relative pitch rotation $\theta _{r}$ becomes the response amplitude operator of relative pitch rotation $\theta _{r}^\mathrm{RAO}$ when the wave amplitude $A_{i}=$ 1.0 m. Corresponding bending moments (constraint moments) are expressed using $\lambda _{b}^\mathrm{RAO}$, the response amplitude operator of bending moments. The corresponding mean absorbed power is expressed as $P_{c}^\mathrm{QTF}$, the quadratic transfer function (QTF) of absorbed power or power capture per unit amplitude input wave.

2.2 Root mean square of relative pitch rotation, bending moments and capture width ratio of WECs in irregular waves

Relative pitch rotations at “Hinge O” and bending moments on “Beam 1” were measured in experiments (as shown “C2$^{{*}}$” in Fig. 2) and root mean square of relative rotations were calculated. In the present frequency domain analysis, the root mean square of relative pitch rotation can be obtained through the following equation (Bhattacharyya 1978)

$$\begin{aligned} \theta _{r}^\mathrm{RMS} =\sqrt{\int _0^\infty {S_{\eta } (\omega )\left| {\theta _{r}^\mathrm{RAO} (\omega )} \right| ^{2}\mathrm{d}\omega } }, \end{aligned}$$

(6)

where $S_{\eta }(\omega )$ is the energy spectrum of the incident waves. Similarly, the root mean square of bending moments at beams can be defined as

$$\begin{aligned} \lambda _{b}^\mathrm{RMS} =\sqrt{\int _0^\infty {S_{\eta } (\omega )\left| {\lambda _{b}^\mathrm{RAO} (\omega )} \right| ^{2}\mathrm{d}\omega } }, \end{aligned}$$

(7)

where $\lambda _{b}^\mathrm{RAO}$ is the response amplitude operator of bending moment, giving the response when the wave amplitude $A_{i}=$ 1.0 m.

The mean power absorbed in uni-directional irregular waves defined by an energy spectrum can be written as (Newman 1979; Babarit 2010)

$$\begin{aligned} P_{c}^\mathrm{IRR} =\int _0^\infty {2S_{\eta } (\omega ) P_{c}^\mathrm{QTF} (\omega )\mathrm{d}\omega } \end{aligned}$$

(8)

The corresponding mean power absorbed in multi-directional irregular waves with any energy spectrum and directional spreadings can be calculated by

$$\begin{aligned} P_{c}^\mathrm{IRR} =\int _0^\infty {\int {2S_{\eta } (\omega ) \;D(\theta _{m} )\; P_{c}^\mathrm{QTF} (\omega ,\hbox { }\theta _{m} )\mathrm{d}\theta _{m} \mathrm{d}\omega } }, \end{aligned}$$

(9)

where $P_{c}^\mathrm{QTF}$($\omega$, $\theta _{m})$ is the quadratic transfer function of absorbed power for directional components $\theta _{m}$ at frequency $\omega$. The directional spreading function D($\theta _{m})$ can have a variety of different expressions (Det Norske Veritas 2014) depending on the complexity of the chosen representation.

Fig. 3

Side view of the experimental setup with the lab-scale M4 model (not to scale)

For irregular waves with significant wave height $H_{s}$, the mean incident power per unit width is

$$\begin{aligned} P_{i}^\mathrm{IRR} =\frac{1}{16}\rho gH_{s}^{2} c_{ge}, \end{aligned}$$

(10)

where $c_{ge}$ is the group velocity corresponding to the energy period $T_{e}$ and $c_{ge}=$ g$T_{e}/4\pi$ in deep water. As described by Stansby et al. (2015a), $T_{e}=$ 0.78$T_{p}$ (for $\gamma =$ 1.0) and $T_{e}=$ 0.84$T_{p}$ (for $\gamma =$ 3.3) where $\gamma$ is the spectral peakedness factor in the JONSWAP spectrum, though these values are slightly dependent on the selected upper frequency cut-off of the spectrum.

To indicate the power absorption capability of any wave energy converter, the capture width (Falnes 2002) can be defined as

$$\begin{aligned} \mathrm{CW}=\frac{P_{c}^\mathrm{IRR} }{P_{i}^\mathrm{IRR} }. \end{aligned}$$

(11)

In the present analysis, the capture width ratio (CWR) is defined as

$$\begin{aligned} \mathrm{CWR}=\frac{\mathrm{CW}}{L_{e}}, \end{aligned}$$

(12)

where $L_{e}$ is the wavelength corresponding to the energy period $T_{e}$ and $L_{e}=$ g$T_{e}^{2}$/2$\pi$ in deep water. This form of CWR enables the comparison with theoretical maxima for an individual float in resonance in regular waves of wavelength L, e.g. $L/2\pi$ for heave $L/\pi$ in surge and pitch, and $3L/2\pi$ for any combination involving heave (Falnes 2002). A further useful reference is that of a slender two-raft wave energy converter with a PTO at the connecting hinge analysed by Newman (1979). With rafts of equal length, a maximum CWR of 4/3 $\pi$ was determined in the zero wave number limit.

3 Setup of experiments and data analysis

The experiments were undertaken in the COAST wave basin at Plymouth University: 35 m long, 15.5 m wide with a depth of 1.0 m for these tests (as shown in Fig. 3). Waves were generated by 24 hinged flap paddles at one end and there was an absorbing beach at the other giving a reflection coefficient of around 5% in regular waves. The device was moored from a small buoy (approximately 10 cm in diameter) connected by a light cord to the tank bed. Independent tests in the smaller 5 m wide flume in Manchester showed that the motions were almost unchanged when using a light horizontal tether. Two wave probes were placed in line with the device (in the centre of the wave basin) at 3.0 and 2.15 m from the centre of “Float 1” in Fig. 3. Strain gauges were placed on the two parallel front beams (shown as “Beam 1” in Fig. 2) between the bow float and middle float, at about 16 cm from the centre of the middle float; each beam was bolted on to the lid at two positions and becomes unrestrained at 5.7 cm from the middle float centre: C2$^{{*}}$ in Fig. 2. The strain gauges were calibrated and give the measured bending moments at point C2$^{{*}}$.

As shown in Fig. 2, the vertical position of the “hinge O” is $Z_{h}=$ 0.21 m from the still water level (SWL). As discussed in Sect. 2, the wave energy converter M4 can be simplified as a 5-body dynamic system in the present analysis. Mass and inertia properties of the physical model (about CoG) and the position of the centre of gravity, measured with respect to the point where the vertical axis of float 2 crosses through the undisturbed water surface, have been listed in Table 2.

Table 2 Mass and inertia of physical model (about CoG)

3.1 Model tests in regular and irregular waves

For the physical model shown in Fig. 1, the standard pneumatic actuator or damper (Norgren Type RM/8016/M/100) used was almost linear, although the damping factor varied from one wave case to another. The force in the actuator shown in Fig. 1 was measured with a load cell (Omega LCMFD-10N) and converted to a moment about hinge O (shown in Fig. 2) by multiplying by the lever arm. The relative angle between column and beam $\theta _{r}$ was measured using an incremental shaft encoder (Wachendorrf 10000 PPR TTL). The damping factor was determined by postprocessing the damping moment assumed to be of the form

$$\begin{aligned} M_\mathrm{{fit}} =B_{0} +B_{d} \dot{{\theta }}_{r} +B_{a} \ddot{{\theta }}_{r} \end{aligned}$$

(13)

The least squares goodness-of-fit R$^{\mathrm {2}}$ was always greater than 0.9 and generally around 0.95. An example of the time variation of moment at the power take-off hinge $M_{h}$ is shown in Fig. 4. The inertial component with $B_{a}$ in Eq. (13) was very small in relation to that due to body masses and the small mean $B_{0}$ does not contribute to damping; both are ignored in the numerical model where Eq. (13) is simplified as $M_{h} \approx B_{d} \dot{{\theta }}_{r}$.

Fig. 4

Time history of hinge moment $M_{h}$ at point O for M4 in irregular waves ($H_{s}\approx$ 0.06 m, $T_{p}=$ 0.8 s, $\gamma =$ 1). The full line is from the measured force and dashed line is fit by Eq. (13) (R$^{2}=$ 0.96)

Table 3 Wave height H and $B_{d}$ in regular waves

Table 4 $H_{s}$ and $B_{d}$ in uni-directional irregular waves

The model tests in regular waves have been divided into 2 groups according to target wave height ($H\approx$ 0.03 m and $H\approx$ 0.05 m) as shown in Table 3. Exact values of wave height H and mechanical damping of PTO $B_{d}$ were different for wave periods of $T=0.6$–1.6 s ($\Delta T=$ 0.1 s). Similarly, there were 4 groups of the incident uni-directional irregular waves generated by different input signals to the wavemaker (defined by significant wave height $H_{s}$ and $\gamma$ in the JONSWAP spectra) which are shown in Table 4. Two spreading factors ($s=$ 30 and $s=$ 5 for a spreading function of cosine shape, cos$^{2s}$($\theta _{m}$/2)) were used for $H_{s}\approx$ 0.06 m and $\gamma =$ 1.0 for JONSWAP spectra in multi-directional waves. Corresponding information is shown in Table 5. Both significant wave height $H_{s}$ and mechanical damping of PTO $B_{d}$ in tests also varied for $T_{p}=$ 0.6–1.6 s.

3.2 Analysis of measurements at Probe 1 in irregular waves

As mentioned in Sect. 3.1, JONSWAP spectra were used to generate the irregular waves and two spectral peakedness factors were selected ($\gamma =$ 3.3 and $\gamma =$ 1.0) for uni-directional waves. Examples of standard JONSWAP spectra with $H_{s}\approx$ 0.04 m ($\gamma =$ 3.3 in Table 4) have been compared with the spectra of the measured data at Probe 1 in Fig. 5. Although there is an experimental frequency cut off at 2 Hz, the level of agreement is quite close and the measured spectra are used for our subsequent dynamic analysis.

Table 5 $H_{s}$ and $B_{d}$ in multi-directional irregular waves

Fig. 5

Spectra of surface elevations in uni-directional irregular waves ($H_{s}\approx$ 0.04 m and $\gamma =$ 3.3)

For multi-directional irregular waves, examples of standard JONSWAP spectra with $H_{s}\approx$ 0.06 m ($\gamma =$ 1.0 and $s=$ 5.0 in Table 5) have been compared with the spectra of measured data at Probe 1 in Fig. 6. The agreement between target input spectra and that measured is now much less close particularly for the smaller periods. The wave directionality was not measured and given the difference between input and measured spectra there must also be uncertainty about the actual directionality. The choice here is to input the measured spectra for dynamic analysis and assume the input directionality is valid, to compare with experiment.

4 Validation of numerical model

4.1 Numerical results of M4 in regular waves

As mentioned in Sect. 3, bending moments at point “C2$^{{*}}$” were measured in the experiments. Corresponding results have been obtained by the present dynamic model and compared with experimental measurements in regular waves in Fig. 7. There is generally reasonable agreement, though not as good as relative rotation (Sun et al. 2016).

4.2 Numerical results of M4 in irregular waves

As mentioned in Sect. 2.2, the numerical predictions of M4 in irregular waves need both information on incident wave spectra (as shown in Figs. 5 and 6) and the corresponding transfer function ($\theta _{r}^\mathrm{RAO}$, $\lambda _{b}^\mathrm{RAO}$ and $P_{c}^\mathrm{QTF})$. Measured spectra at Probe 1 have been used in the following analysis. As shown in Figs. 5 and 6, there is almost no contribution below $f=$ 0.2 Hz and above $f=$ 2.4 Hz. Indeed, the wavemakers have an upper frequency limit of 2.0 Hz. To get accurate results, 441 frequencies have been calculated in the range of $f =$ 0.2$\sim$2.4 Hz and $\Delta f =$ 0.005 Hz. From Tables 4 and 5, it can be seen that $B_{d}$ varies in the range of 3.58Nms to 9.34Nms. Three values of $B_{d}=$ 4 Nms, 6 Nms and 8 Nms are selected to show the effects of $B_{d}$ on $\theta _{r}^\mathrm{RAO}$, $P_{c}^\mathrm{QTF}$and $\lambda _{b}^\mathrm{RAO}$, which are shown in Figs. 8, 9 and 10. It can be seen that damping coefficients $B_{d}$ show little effect on the values of the peak frequencies but do have a significant effect on the peak values of $\theta _{r}^\mathrm{RAO}$ (in Fig. 8) and $P_{c}^\mathrm{QTF}$ (in Fig. 9).

Fig. 6

Spectra of surface elevations in multi-directional irregular waves ($H_{s}\approx$ 0.06 m, $\gamma =$ 1.0 and $s=$ 5)

Fig. 7

Bending moments at point C2$^{{*}}$ in regular waves. Note that H and $B_{d}$ are different for each point as defined in Table 3

To compare with the measured bending moments, the response amplitude operator of bending moments at point “C2$^{{*}}$” as shown in Fig. 2 under different $B_{d}$ have been shown in Fig. 10a. Reaction moments at three other locations (“C1”, “C2” and “C3” in Fig. 2) have also been shown in Fig. 10b, c and d, respectively. It can be seen that damping coefficient $B_{d}$ has a significant effect on $\lambda _{b}^\mathrm{RAO}$ except for $f>$1.4 H$_{\mathrm {z}}$. Comparing the peak values of bending moments at four locations in Fig. 10, it can be seen that the smallest reaction moments are obtained at “C1” above the small float 1 and the largest reaction moments are found at “C3” above the largest and stern float.

The root mean square (RMS) of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio (CWR) in irregular waves (as listed in Tables 4 and 5) have been calculated as described in Sect. 2 using transfer functions which are functions of both frequency and wave approach angle for the spread sea cases. The corresponding results have been compared with those from measurements as shown in Figs. 11, 12, 13, 14, 15, 16. Generally, the agreements are very close (in contrast to those for regular waves). Power is slightly overestimated for the smaller periods.

Figures 15 and 16 show results with input $s=$ 30 and 5, respectively. The prediction of relative rotation and bending moment remains very close while the power capture is again slightly overpredicted; the CWR shows greater difference at lower periods. This agreement occurs although there is possible uncertainty in directional spreading which will be discussed. The machine was observed to be always closely aligned with the principal wave direction. Model results with regular waves indicate that misalignment up to 10$^{\mathrm {o}}$ has negligible influence on the capture width ratio (Sun et al. 2016) and observed misalignment here was within these limits.

5 Optimisation of damping and hinge height for power capture in uni-directional irregular waves

As described in Sect. 2 and shown in Figs. 8, 9, 10, the damping factor $B_{d}$ will affect the responses, structural loads on the beams and absorbed power. Another parameter which is likely to influence the performance is the vertical position of the “hinge O” $Z_{h}$ (distance to the still water level) which was set to 0.21 m in experiments, following some initial testing at maximum power capture.

The capture width ratio in uni-directional irregular waves (JONSWAP spectra with $H_{s}=0.04$ m and $\gamma =$ 3.3 which have been shown in Fig. 17) has been calculated using different combinations of $B_{d}$ and $Z_{h}$. Values of $B_{d}$ are considered between 0.0 Nms and 14.0 Nms ($\Delta B_{d}=$ 0.1 Nms). At the same time, the heights of “hinge O” $Z_{h}$ have been varied in the range of 0.05 m–0.35 m (at intervals $\Delta Z_{h} =$ 0.01 m). Example of results at $T_{p} =$ 0.8, 1.0, 1.2 and 1.4 s can be found in the contour plots of Fig. 18, which have been normalised by dividing by the maximum absorbed power in each sea state. It can be seen that the areas with magnitude greater than 0.95 are relatively large, which implies that the performance of M4 is not very sensitive to the PTO configuration (combination of $B_{d}$ and $Z_{h})$.

Fig. 8

Response amplitude operator of relative rotation at “hinge O” ($Z_{h}=$ 0.21 m)

Fig. 9

Quadratic transfer function of absorbed power ($Z_{h}=$ 0.21 m)

Fig. 10

Response amplitude operator of bending/reaction moments at different locations ($Z_{h}=$ 0.21 m)

Fig. 11

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in uni-directional irregular waves ($H_{s}\approx$  0.04 m and $\gamma =$ 3.3). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 4

Fig. 12

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in uni-directional irregular waves ($H_{s}\approx$ 0.04 m and $\gamma =$ 1.0). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 4

Fig. 13

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in uni-directional irregular waves ($H_{s}\approx$ 0.06 m and $\gamma =$ 3.3). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 4

Fig. 14

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in uni-directional irregular waves ($H_{s}\approx$ 0.06 m and $\gamma =$ 1.0). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 4

Fig. 15

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in multi-directional irregular waves ($H_{s}\approx$ 0.06 m, $\gamma =$ 1.0 and $s=$ 30). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 5

Fig. 16

RMS of relative rotation, RMS of bending moments at “C2$^{{*}}$”, absorbed power and capture width ratio in multi-directional irregular waves ($H_{s}\approx$ 0.06 m, $\gamma =$ 1.0 and $s=$ 5). Note that $H_{s}$ and $B_{d}$ are different for each point as defined in Table 5

Optimum combinations of $Z_{h}$ and $B_{d}$ in uni-directional irregular waves ($H_{s}=$ 0.04 m and $\gamma =$ 3.3) for $T_{p}=$ 0.8–1.4 s are given in Table 6. To obtain maximum power capture, the vertical positions of hinge should be higher as $T_{p }$ increases. It can be seen that optimum values of $B_{d}$ decrease with $T_{p}$. The corresponding optimum CWR have been listed in Table 6 and improvement to the experimental values of CWR in Fig. 11d have been given alongside the absolute values. Worthwhile improvements have been achieved which are at the range of 17–36%.

To give a better understanding of the performance of M4 with ideal optimised combinations of $Z_{h}$ and $B_{d}$, response amplitude operator of relative rotation $\theta _{r}^\mathrm{RAO}$, absorbed power $P_{c}^\mathrm{QTF}$ and reaction moments $\lambda _{b}^\mathrm{RAO}$ (at locations of “C1”, “C2” and “C3”) for $T_{p}=$ 0.8, 1.0, 1.2 and 1.4 s are shown in Figs. 19, 20 and 21. It can be seen that the heights of “hinge O” $Z_{h}$ have significant effect on the peak frequencies and the shapes of transfer functions ($\theta _{r}^\mathrm{RAO}$, $P_{c}^\mathrm{QTF}$ and $\lambda _{b}^\mathrm{RAO})$. With the increase of $Z_{h}$, frequencies for the peak power decrease and the response functions of $\theta _{r}^\mathrm{RAO}$, $P_{c}^\mathrm{QTF}$ become narrow. The largest value of the response functions $\lambda _{b}^\mathrm{RAO}$ is found for location “C2” when $T_{p}=$ 1.4s.

The effect of $Z_{h}$ and $B_{d}$ on RMS of relative rotations are shown in Fig. 22. It can be seen that larger $\theta _{r}^\mathrm{RMS}$ are obtained with optimised $Z_{h}$ and $B_{d}$. Improvements have been shown in Table 6 and Fig. 23. Another concern from the viewpoint of design is the reaction moment at connecting points (“C1”, “C2” and “C3”) which have been shown in Fig. 24. It can be seen that larger reaction moments are caused with optimised $Z_{h}$ and $B_{d}$ particularly at larger periods, which increase the requirements of structural strength.

6 Effect of directional spreading in irregular waves

The directional spreading of irregular waves may affect the response, structural loads and power capture. M4 was tested in multi-directional irregular waves with an input spreading function of cosine shape cos$^{2s}$($\theta _{m}$/2). The target spectra were not reproduced well particularly at smaller periods and the actual spreading was not measured which is a cause of uncertainty. With unidirectional waves there was no such uncertainty and predictions were quite accurate indicating that the linear model assumptions are valid. This is likely to remain the case with directional spreading and the accurate predictions with the target directional spreading input to the model suggest that this assumption is justified, or possibly that results are relatively insensitive to directional spreading.

The model is thus expected to be valid for multi-directional waves and optimisation is undertaken. Both $s=$ 30 and $s=$ 5 were used experimentally which can represent swell and wind sea, respectively (Det Norske Veritas 2014). To show the gradual changes from long-crested waves ($s=\infty )$ to short-crested waves ($s=$ 5), $s=$ 15 is added to the model results in Figs. 25, 26, 27. It can be seen that directional spreading has significant effects on the relative rotation, capture width ratio and reaction moments. Marked reductions can be seen in short-crested waves with $s=$ 5. In Fig. 25, reduction of relative rotation at “hinge O” is up to 21.4% when $T_{p}=$ 1.4s. In Fig. 26, reduction of CWR is up to 37.8% when $T_{p}=$ 1.4s. In Fig. 27, reduction of bending moments is up to 21.1% at “C2” when $T_{p}=$ 1.4 s. With directional spreading some roll motion is predicted (and observed experimentally) but at least in the model suppressing this has no effect on power capture.

Fig. 17

JONSWAP spectrum with $H_{s}=$ 0.04 m and $\gamma =$ 3.3

Fig. 18

Effects of $B_{d}$ and $Z_{h}$ on the normalised mean power

Table 6 Optimum combinations of $Z_{h}$ and $B_{d}$ in uni-directional irregular waves ($H_{s}=$ 0.04 m and $\gamma =$ 3.3)

7 Discussion

The two-body linear diffraction model of Sun et al. (2016) gave good predictions of relative rotation and power capture in regular waves with smaller wave heights ($H\approx$ 0.03 m in experiments) and were less accurate with larger waves ($H\approx$ 0.05 m). In this paper, the model has been developed as a five-body model (3 floats and 2 beams) to enable full structural analysis (without internal dynamic behaviour arising from structural flexibility) with irregular waves including directional spreading. The five-body model was tested first with regular waves and the beam bending moment was predicted approximately at both wave heights. JONSWAP spectra were used for irregular waves and in the experiments the measured spectra were a close approximation to the input when uni-directional. With multi-directional waves, however, there were substantial differences particularly for smaller periods; directional spreading was not measured and is therefore uncertain.

In all cases, the measured spectra were used as input to the numerical model and for multi-directional waves the target spreading function was used. The predictions of relative rotation and beam bending moment were now quite accurate for all cases ($H_{s} \approx$ 0.04 m and 0.06 m) and power capture was generally slightly overpredicted. It is perhaps surprising that more complex wave states produce better predictions than simple regular waves. This may be because reflection effects are likely to be more prominent with regular waves although it may be noted that the wave basin is quite large in relation to the experimental model.

Linear diffraction modelling with accurate body specification and input wave conditions thus gives very accurate predictions in known uni-directional irregular waves when the effect of reflections are expected to be minimal due to frequency averaging. This does suggest that the linear model will also be valid with directional spreading and the correspondingly accurate predictions with the target spreading function input to the model suggests that actual spreading is close to the target. Full confirmation, however, does require directional spreading to be measured directly.

Fig. 19

Response amplitude operator of relative rotation (with optimised $Z_{h}$ and $B_{d}$ in Table 6)

Fig. 20

Quadratic transfer function of absorbed power (with optimised $Z_{h}$ and $B_{d}$ in Table 6)

The poor experimental reproduction of multi-directional waves but not uni-directional waves may be because the individual paddle width within the composite wave maker is not small in relation to wavelength, an effect which gets worse as wave period decreases. For $T=$ 0.6 s the wavelength is about 0.6 m which is similar to the paddle width.

In relation to full scale conditions where typical peak wave periods are in the range 7–9 s, a laboratory period of about 1.1 s for peak power implies a length scale of about 1:50. Laboratory wave heights of 0.04 m and 0.06 m would thus be 2 and 3 m at full scale. These may be considered average to moderate wave heights for many sites. This highly efficient frequency domain modelling may thus be considered valuable for fatigue analysis and energy capture prediction. For the latter, defining performance in terms of capture width ratio versus peak period is a convenient general way of converting scatter diagram information into annual energy capture. This has been undertaken for sites in the NE Atlantic over many decades showing how actual annual energy generation shows much less decadal variation than the resource variation which occurs due to the North Atlantic Oscillation (Santo et al. 2016). The capture width ratio (normalised by wavelength) has a theoretical upper limit of 3/2$\pi \approx$ 0.48 for point absorbers in regular waves acting in a combination of heave and other modes in resonance. Another useful idealisation is that of two equal slender rafts connected by a hinge which gives a slightly lower maximum capture width ratio of 4/3$\pi \approx$ 0.42 and the present system may be considered as a hybrid. Here, the maximum value in irregular waves with optimisation was about 0.35 and in regular waves was 0.45 (Sun et al. 2016). The regular wave value is just less than the theoretical point absorber limit and just above the two-raft limit, while the irregular wave value was 78% of the regular wave value. Some recent developments have shown that increasing the length of the front beam by about 50% can improve the capture width ratio in irregular waves further (Stansby et al. 2016). The aim of this paper however is to demonstrate the prediction capability of multi-body structural modelling in irregular waves and generalise to directional spreading in small to moderate wave heights. Parallel work on extreme wave conditions will be reported separately.

To generalise response and power capture prediction for steep waves, computational fluid dynamics (CFD) may be applied incorporating all important physical characteristics. For the present device in waves where drag effects are negligible, nonlinear time-domain potential flow modelling would, however, be suitable although much more computationally demanding than the linear diffraction modelling presented here. Incorporation of viscous effects for such a problem would be yet more demanding, typically involving parallel processing with many cores. As a compromise, nonlinear effects in excitation and buoyancy forces may be added in the present model if the free surface around the floats is known. Such partial improvements however require validation and direct calibration of linear modelling against experiment may also be considered.

Fig. 21

Response amplitude operator of reaction moments (with optimised $Z_{h}$ and $B_{d}$ in Table 6)

Fig. 22

Effect of $Z_{h}$ and $B_{d}$ on RMS of relative rotations

Fig. 23

Effect of $Z_{h}$ and $B_{d}$ on capture width ratio (CWR)

Fig. 24

Effect of $Z_{h}$ and $B_{d}$ on reaction moments at connecting points

Fig. 25

Effects directional spreading on the relative rotations at “hinge O”

Fig. 26

Effects directional spreading on the capture width ratio (CWR)

8 Conclusions

A general multi-body linear-diffraction model has been developed to enable structural analysis of the M4 wave energy converter in irregular waves including directional spreading. Validation against experiment has shown excellent predictions of relative rotation and beam bending moment and slight overprediction of power capture in uni-directional waves which can be considered small to moderate. This is achieved with measured spectra input to the model. Drag effects are negligible. Although the target spectra are close to the measured for uni-directional waves, there can be substantial differences with directional spreading which deteriorates as wave period decreases, probably because the individual paddle width is not small in relation to wavelength. The actual directional spreading was not measured and is thus unknown. However, with the target directional spreading input to the model predictions remained quite accurate and since the linear model gave accurate predictions in uni-directional waves where input conditions were known precisely the model may also be expected to be valid with directional spreading. The accurate predictions for these cases suggest that the actual spreading was close to the target but this will be validated in future experimental work.

The model shows how increasing wave directional spreading reduces power capture, by about 1/3 with spreading factor $s=$ 5 (short-crested seas). The variation of capture width ratio, normalised by wavelength, with wave period provides a general characteristic for device performance convenient for determining annual energy capture from a scatter diagram and this may be optimised by varying damping coefficient and vertical hinge position. Increases in power capture of about 30% may be achieved in irregular waves. Whilst it might be possible to alter the damping coefficient in the PTO on a sea-state basis, it wouldn’t be reasonable to attempt to change the basic machine geometry.

Fig. 27

Effects directional spreading on the reaction moments at connecting points

The value of such an efficient structural-hydrodynamic model for load and energy prediction has thus been demonstrated through careful validation. An unexpected result is that the accuracy of prediction generally increases as the complexity of the wave field increases; this is possibly because any effect of reflections in a confined (albeit large) wave basin will be minimal when frequency averaged.