A numerical investigation of second-order difference-frequency forces and motions of a moored ship in shallow water

Abstract

A 3D time-domain Rankine source method is developed to study the hydrodynamic loads and motions of a moored ship in shallow water waves in head sea conditions. Both the wave steepness and ship motions relative to the ship’s draft are assumed small and the exact free-surface and body-boundary conditions are expanded about the mean surface by a Taylor series. A formulation correctly to second order in the wave steepness is adopted. A fourth-order Runge–Kutta method is used to time integrate the boundary conditions and the six degree of freedom motion equations. It is found that the water depth has significant effects on the hydrodynamic coefficients, especially on the vertical modes of motions. The linear horizontal motions of a moored ship have distinct increment in shallower water depth in the low-frequency domain. Further, the horizontal slow-drift excitation forces increase significantly with decreasing water depth and the second-order velocity potential gives dominant contribution in a frequency range of importance for moored ships in shallow water. Lastly, the slowly varying motions of an LNGC is simulated and the satisfactory agreements with experiments demonstrate that the present method can predict the slowly varying motions of a moored ship in finite-amplitude shallow water waves with acceptable results.

1 Introduction

It is well known that slow-drift excitation forces can induce lateral resonance oscillations of a moored ship. In the last 30 years, the difference-frequency problem has been studied mainly in deep water. To avoid the calculation of the second-order velocity potential, which is computationally difficult to obtain especially for three-dimensional bodies, Newman (1974) proposed an approximation of the slow-drift excitation forces. This approximation assumes that a natural frequency associated with slow-drift motions is sufficiently small so that the exact quadratic transfer function (QTF) for difference-frequency forces can be approximated by the mean drift force value which is a second-order effect depending only on the first-order velocity potential and motions. For many applications, the validity of Newman’s approximation is appropriate. Afterward, Faltinsen and Løken (1978, 1979) solved consistently to second order the difference-frequency forces on an infinitely long horizontal cylinder in beam sea and irregular waves in deep water. They concluded that the contribution from the second-order velocity potential to the slow-drift excitation forces was small and that Newman’s approximation was a practical way to calculate the horizontal slow-drift excitation force on a ship in irregular beam sea waves. Pinkster (1980) made an extensive investigation of slow-drift forces on three-dimensional bodies. However, the effect of the second-order velocity potential was incorporated by an approximated method. He found that the approximation was good when the difference frequency was small and that the approximation gave higher values than the exact solution for large difference frequencies. Generally, Pinkster’s approximation gives the right order of magnitude to the slow-drift excitation forces due to the contribution of the second-order velocity potential. Further, Chen and Duan (2007) proposed a novel $O(\Delta \omega )$ approximation for the difference-frequency QTF, in which the double sum of the wave components is reduced to one sum. They divided the total QTF into two parts, one depending on the quadratic products of the first-order wave fields and the other depending on the second-order velocity potential. The first part is calculated by the ‘middle field’ method by Chen (2006a, b), in which the integration over the body surface is transformed to integration over control surfaces at a distance from the body. The calculation of the second-order velocity potential contributions is performed by an ‘indirect method’ proposed by Molin (1979), in which Green’s second identity is used to evaluate the second-order velocity potential contributions without solving the second-order boundary value problem (BVP). Recently, Shao and Faltinsen (2011) proposed an alternative formulation of the BVP for added resistance analysis based on a body-fixed coordinate system, which was first used in the wave-body problem by Shao and Faltinsen (2010). Good agreement with experimental results was obtained for several types of ships which include a modified Wigley I hull, a Series 60 ship and S175 container ship at moderate forward speeds.

In addition to predicting the slow-drift excitation forces, accurate calculation of the wave-drift damping is necessary for estimating the amplitude of the slowly varying drift motion correctly as illustrated by Faltinsen (1990). In the simplest damping model, the value is just set as a fraction of critical damping empirically. A more rational way is to include wave-drift damping by the added resistance gradient (ARG) method. Since the wave-drift damping coefficient is related to the low-frequency velocity-dependent part of the wave-drift force, the surge damping coefficient without the presence of current can be approximated by the derivative of mean longitudinal wave-drift force with respect to the forward velocity at zero forward speed. Wichers (1988) measured for a VLCC model the mean longitudinal drift force for small forward speed and derived derivative values. The good agreement with wave-drift damping coefficients from experimental extinction tests demonstrated the correctness of the ARG method. The accuracy of the ARG method was further demonstrated by Hearn and Tong (1986), Hearn et al. (1987a, b). They used a strip theory including an enhanced forward speed-dependent diffraction analysis and their calculated wave-drift damping was compared with experimental data. The agreement was good for a moored VLCC, a moored barge and a semisubmersible. Zhao et al. (1988) developed a theory for first order in wave amplitude and current velocity and proposed a corresponding numerical procedure which made the direct calculation of wave-drift damping in three-dimensional problems possible. Grue and Palm (1993) and Hermans (1998) also developed 3D numerical models and applied it to wave-drift damping of ships. In practice, a formula based on the asymptotic theory proposed by Faltinsen et al. (1980) gives good estimation of wave-drift damping for small wavelengths in head sea.

In addition to studying wave-drift damping, Zhao and Faltinsen (1988) showed that eddy-making damping and slowly varying wave-drift damping may also give important contributions to slow-drift motions of a moored structure in irregular waves. Their considered problem was two dimensional. They found that the slowly varying wave-drift damping had little influence on the standard deviation of the motions, while it had significant effects on the extreme values. Moreover, they showed that for a sufficiently small natural frequency that the standard deviation could be estimated in the frequency domain by Newman’s approximation for the slow-drift excitation force and by neglecting the slowly varying wave-drift damping. However, mean wave-drift damping has to be included. Drag damping can be included by equivalent linearization.

All the works mentioned above were conducted in deep water. However, with the increase of LNG terminals designed to operate in offshore areas next to harbors, where the water depth is finite or shallow, the accurate prediction of the hydrodynamic loads and motions of a ship in shallow water becomes important for the design of the mooring system. Compared with the works in deep water, less research exists on wave-induced hydrodynamic loads and motions of ships in shallow water. Oortmerssen (1976) studied the motions of a VLCC in shallow water, both theoretically and experimentally. A linear frequency-domain BEM code was used and the numerical results of the first-order excitation forces and ship motions agreed well with the experimental data. More recently, Li et al. (2003) presented experimental results of motions of a large FPSO in extremely shallow water with irregular waves. They found that the wave frequency motions of the FPSO decrease with the decrease of the water depth. There is less published research for the slow-drift excitation forces acting on a ship in shallow water. Pinkster and Huijsmans (1992) reported both experimental and numerical results for a VLCC in shallow water in both regular and irregular waves. A dynamic system of restraint was used in the experiments to restrict the ship model from slow-drift motions and avoid corresponding dynamic magnification effects due to resonance oscillations. Both the computational and experimental results showed that decreasing water depth led to increasing wave-drift forces. Pinkster’s approximation provides reasonably good results for slow-drift excitation forces, although it is an incomplete theory. Recently, Chen and Rezende (2008) applied the $O(\Delta \omega )$ approximation to calculate the difference-frequency QTF for an LNG in shallow water and found that it provided good results in the small difference-frequency domain compared with the complete QTF.

In the present paper, a 3D time-domain Rankine source method based on a complete second-order theory is developed to study the hydrodynamic loads and motions of a moored ship in shallow water waves. Firstly, the hydrodynamic coefficients and linear motions of a VLCC in shallow water are calculated and compared with available experimental and numerical results. The influence of water depth on the hydrodynamic coefficients and linear motions are discussed. Then, the wave-drift forces and the difference-frequency QTF are calculated and compared with Pinkster’s experimental data and calculations. The results by the present method agree better with experimental data than that given by Pinkster’s approximation, especially when the difference frequency is relatively large. Different components that contribute to the wave-drift forces are analyzed and the contribution from the second-order velocity potential is found to be dominant in the difference-frequency range that is important for moored ships. This is different from the situation in deep water, where the second-order velocity potential’s contribution is negligible. At last, the wave-drift damping of a LNGC in shallow water is calculated by the ARG method with a wave–current–body interaction model. The slowly varying motions of the vessel is then simulated and compared with the experimental data by Kristiansen (2010). The agreement is, in general, satisfactory and the error sources are discussed.

2 Mathematical formulation

2.1 Coordinate systems

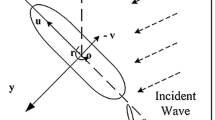
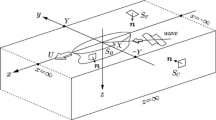
Two Cartesian coordinates systems are defined as shown in Fig. 1, i.e. $OXYZ$ and $Gxyz.OXYZ$ is Earth fixed with the $OXY$ plane on the calm water surface and with the $OZ$-axis positive upward. $Gxyz$ is a body-fixed system with origin at the centre of gravity of the body and therefore moves with the unsteady motions of the body.

Fig. 1

Sketch of the coordinate systems

2.2 Boundary value problem

Potential flow of incompressible water without surface tension is assumed. The velocity potential $\phi (X,Y,Z,t)$ satisfies the Laplace equation in the water domain, i.e.

$$\begin{aligned} \nabla ^2\phi =0 \end{aligned}$$

(1)

The water domain is bounded by a horizontal bottom, a free surface, a body surface and vertical boundaries far from the ship. On the free surface, the fully non-linear kinematic and dynamic boundary conditions are:

$$\begin{aligned} \zeta _t =\phi _Z -\phi _X \zeta _X -\phi _Y \zeta _Y,\quad Z=\zeta (X,Y,t), \end{aligned}$$

(2)

$$\begin{aligned} \phi _t =-g\zeta -\frac{1}{2}\nabla \phi \cdot \nabla \phi ,\quad Z=\zeta (X,Y,t). \end{aligned}$$

(3)

Here, the subscripts indicate partial differentiations, $\zeta (X,Y,t)$ denotes the free-surface elevation and $g$ is the acceleration of gravity. The atmospheric pressure is taken to be constant and can thus be omitted in the dynamic free-surface boundary condition.

On the body surface, the impermeable condition is used to ensure that water particles cannot penetrate it.

$$\begin{aligned} \phi _n =(\ddot{\varvec{\xi }}+\dot{\varvec{\alpha }} \times \mathbf{r }_b) \cdot {\mathbf{n }},\quad S_b. \end{aligned}$$

(4)

Here, the operator ‘$\cdot$’ means the first-order time derivative at a fixed point. The vector ${\varvec{\xi }} = (\xi _1, \xi _2, \xi _3)$ describes the translatory displacements due to surge, sway and heave, while the vector ${\varvec{\alpha }}=(\xi _4, \xi _5, \xi _6)$ represents roll, pitch and yaw angles. $\mathbf{r }_{b}$ means the position vector of a point on the body surface relative to the gravitational centre. The effect of finite rotation angles is neglected. Further, $\mathbf{n }$ is the normal unit vector pointing positively out of the water domain.

On the bottom and the vertical side wall, the impermeable condition is used, i.e. the velocity component in the normal direction is zero.

$$\begin{aligned} \phi _n =0 \end{aligned}$$

(5)

A numerical wave beach is introduced by means of a free-surface damping layer.

2.3 Perturbation method

The amplitudes of the incident waves and the oscillatory body motions are assumed small compared to the characteristic body dimensions. We do not introduce the ratio between water depth and the incident wave length as a small parameter. Therefore, the velocity potential, wave elevation and body motions can be written as series expansions.

$$\begin{aligned} \begin{array}{l} \phi =\varepsilon ^1\phi ^{(1)}+\varepsilon ^2\phi ^{(2)}+\cdots \\ \zeta =\varepsilon ^1\zeta ^{(1)}+\varepsilon ^2\zeta ^{(2)}+\cdots \\ {\varvec{\xi }}=\varepsilon ^1{\varvec{\xi }}^{(1)}+\varepsilon ^2{\varvec{\xi }}^{(2)}+\cdots \\ {\varvec{\alpha }}=\varepsilon ^1{\varvec{\alpha }}^{(1)}+\varepsilon ^2{\varvec{\alpha }}^{(2)}+\cdots \\ \end{array} \end{aligned}$$

(6)

Here, $\varepsilon$ is a perturbation parameter with respect to the wave steepness and the superscripts denote the order of the expansions. Introducing the series expansions (6) into the free-surface boundary conditions (2) and (3), then Taylor expanding about $Z=0,$ the following free-surface boundary conditions can be obtained:

$$\begin{aligned}&\!\!\!\zeta _{t}^{(m)} - \phi _z^{(m)} =F_1^{(m)}\end{aligned}$$

(7)

$$\begin{aligned}&\!\!\!\phi _{t}^{(m)} + g\zeta ^{(m)} =F_2^{(m)}. \end{aligned}$$

(8)

The terms $F_1^{(m)}, F_2^{(m)} (m=1,2)$ are given as:

$$\begin{aligned} \begin{array}{l} F_1^{^{(1)}} =0 \\ F_2^{^{(1)}} =0 \\ F_1^{^{(2)}} =-\bar{\nabla }\phi ^{^{(1)}}\cdot \bar{\nabla }\zeta ^{^{(1)}}+\zeta ^{^{(1)}}\frac{\partial ^2\phi ^{^{(1)}}}{\partial Z^2}\\ F_2^{^{(2)}} =-\frac{1}{2}\nabla \phi ^{^{(1)}}\cdot \nabla \phi ^{^{(1)}}-\zeta ^{^{(1)}}\frac{\partial ^2\phi ^{^{(1)}}}{\partial Z\partial t} \\ \end{array} \end{aligned}$$

(9)

The vector operators $\nabla$ and $\bar{\nabla }$ are defined as:

$$\begin{aligned} \begin{array}{l} \nabla ={\mathbf {i}}\frac{\partial }{\partial X}+{\mathbf {j}}\frac{\partial }{\partial Y}+{\mathbf {k}}\frac{\partial }{\partial Z} \\ \bar{\nabla }={\mathbf {i}}\frac{\partial }{\partial X}+{\mathbf {j}}\frac{\partial }{\partial Y} \\ \end{array} \end{aligned}$$

(10)

Here, i, j and k denote unit vectors along the $X$-, $Y$- and $Z$-axes, respectively.

The wave field is separated into an incoming part and a scattered part which is generated due to the presence and motions of the body. The description of the irregular incoming waves consistent with second order can be found in Dalzell (1999). Chen (2006a, b) found an extra set-down term that has to be added in bichromatic waves of two wave frequencies up to second order. Otherwise, a discontinuity should appear on either side of the diagonal of the QTF for second-order vertical forces. We can write

$$\begin{aligned} \begin{array}{l} \zeta ^{(m)}=\zeta _s^{(m)} +\zeta _w^{(m)}\\ \phi ^{(m)}=\phi _s^{(m)} +\phi _w^{(m)}\\ \end{array} \end{aligned}$$

(11)

Here, the subscripts ‘$w$’ and ‘$s$’ denote the wave elevation due to incoming and scattered waves, respectively.

Then the free-surface boundary condition can be rearranged as:

$$\begin{aligned} \frac{\partial \zeta _s^{(m)}}{\partial t}=\frac{\partial \phi _s^{(m)}}{\partial Z}+\left[ \frac{\partial \phi _w^{(m)} }{\partial Z}-\frac{\partial \zeta _w^{(m)} }{\partial t}\right] +F_1^{(m)}, \quad Z=0,\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} \frac{\partial \phi _s^{(m)} }{\partial t}=-g\zeta _s^{(m)}-\left[ \frac{\partial \phi _w^{(m)} }{\partial t}+g\zeta _w^{(m)} \right] +F_2^{(m)},\quad Z=0.\nonumber \\ \end{aligned}$$

(13)

Similarly, the body-boundary condition (4) can be expanded as:

$$\begin{aligned} \frac{\partial \phi _s^{(m)} }{\partial n}=B^{(m)},\quad S_{b0} \end{aligned}$$

(14)

with

$$\begin{aligned} B^{(1)}&={\mathbf {n}}^{(0)}\cdot \left[ {\dot{\mathbf {\xi }}}^{(1)}+{\dot{\mathbf {\alpha }}}^{(1)}\times {\mathbf {r}}_b -\nabla \phi _w^{(1)}\right] \nonumber \\ B^{(2)}&={\mathbf {n}}^{(0)}\cdot \left[ {\dot{\mathbf {\xi }}}^{(2)}+{\dot{\mathbf {\alpha }}}^{(2)}\times {\mathbf {r}}_b -\nabla \phi _w^{(2)}\right. \nonumber \\&\left. \quad -\{({\mathbf {\xi }}^{(1)}+{\mathbf {\alpha }}^{(1)}\times {\mathbf {r}}_b)\cdot \nabla \}\nabla \phi ^{(1)}\right] \nonumber \\&\quad +{\mathbf {n}}^{(1)}\cdot \left[ {\dot{\mathbf {\xi }}}^{(1)}+{\dot{\mathbf {\alpha }}}^{(1)}\times {\mathbf {r}}_b -\nabla \phi ^{(1)}\right] , \end{aligned}$$

(15)

where ${\mathbf {n}}^{(0)}$ denote the normal vector positive out of the body when the body is at rest ${\mathbf {n}}^{(1)}={\mathbf {\alpha }}^{(1)}\times {\mathbf {n}}^{(0)}$.

2.4 Hydrodynamic forces and moments

The hydrodynamic forces and moments are calculated by pressure integration. The pressure on the body surface is given by the Bernoulli’s equation:

$$\begin{aligned} p=-\rho \left( \phi _t +\frac{1}{2}\nabla \phi \cdot \nabla \phi +gZ\right) . \end{aligned}$$

(16)

The pressure on the instantaneous body surface can be approximated by Taylor expansion about the wetted mean body surface. Keeping to second order, the pressure is separated into three parts:

$$\begin{aligned} p=p^{(0)}+p^{(1)}+p^{(2)}, \end{aligned}$$

(17)

where $p^{(0)},\,p^{(1)}$ and $p^{(2)}$ denote the ‘hydrostatic’, first-order and second-order pressure, respectively. They are defined as follows:

$$\begin{aligned} p^{(0)}&=-\rho gZ\nonumber \\ p^{(1)}&=-\rho \left[ \phi _t^{(1)} +g\left( \xi _3^{(1)} +y\xi _4^{(1)} -x\xi _5^{(1)}\right) \right] \nonumber \\ p^{(2)}&=-\rho \left[ \phi _t^{(2)} +\frac{1}{2}\nabla \phi ^{(1)}\cdot \nabla \phi ^{(1)}+\left\{ \left( {\mathbf {\xi }}^{(1)}+{\mathbf {\alpha }}^{(1)}\times {\mathbf {r}}_b \right) \right. \right. \nonumber \\&\left. \left. \quad \cdot \nabla \right\} \phi _t^{(1)}+g\left( \xi _3^{(2)} +y\xi _4^{(2)} -x\xi _5^{(2)}\right) \right] . \end{aligned}$$

(18)

The hydrodynamic forces and moments can be expressed as:

$$\begin{aligned} \begin{array}{l} {\mathbf {F}}=\iint _{s_b } {p{\mathbf {n}}\mathrm{d}s} \\ {\mathbf {M}}=\iint _{s_b } {p({\mathbf {r}}_b \times {\mathbf {n}})\mathrm{d}s}\\ \end{array} \end{aligned}$$

(19)

Introducing (19) into (20), the following approximation can be obtained:

$$\begin{aligned} \begin{array}{l} {\mathbf {F}}={\mathbf {F}}^{(0)}+{\mathbf {F}}^{(1)}+{\mathbf {F}}^{(2)}\\ {\mathbf {M}}={\mathbf {M}}^{(0)}+{\mathbf {M}}^{(1)}+{\mathbf {M}}^{(2)}\\ \end{array} \end{aligned}$$

(20)

with

$$\begin{aligned} {\mathbf {F}}^{(0)}&=\iint _{s_{b_0}}{p^{(0)}{\mathbf {n}}^{(0)}\mathrm{d}s} \nonumber \\ {\mathbf {F}}^{(1)}&=\iint _{s_{b_0}}{\left( p^{(1)}{\mathbf {n}}^{(0)}+p^{(0)}{\mathbf {n}}^{(1)}\right) \mathrm{d}s} \nonumber \\ {\mathbf {F}}^{(2)}&=\iint _{s_{b_0}}{\left( p^{(2)}{\mathbf {n}}^{(0)}+p^{(1)}{\mathbf {n}}^{(1)}+p^{(0)}{\mathbf {n}}^{(2)}\right) \mathrm{d}s}\nonumber \\&\quad +\int _{cw_0 } {\frac{1}{2}} \rho g\left[ \zeta ^{(1)}-\left( \xi _3^{(1)}\right. \right. \nonumber \\&\left. \left. \quad +y\xi _4^{(1)} -x\xi _5^{(1)}\right) \right] ^2{\mathbf {n}}^{(0)}{/}\sqrt{1-\left( {\mathbf {n}}_3^{(0)} \right) ^2} \mathrm{d}l \nonumber \\ {\mathbf {M}}^{(0)}&=\iint _{s_{b_0}}{p^{(0)}\left( {\mathbf {r}}_b\times {\mathbf {n}}^{(0)}\right) \mathrm{d}s} \nonumber \\ {\mathbf {M}}^{(1)}&=\iint _{s_{b_0}}{\left[ p^{(1)}\left( {\mathbf {r}}_b\times {\mathbf {n}}^{(0)}\right) +p^{(0)}\left( {\mathbf {r}}_b \times {\mathbf {n}}^{(1)}\right) \right] \mathrm{d}s} \nonumber \\ {\mathbf {M}}^{(2)}&=\iint _{s_{b_0}}\left[ p^{(2)}\left( {\mathbf {r}}_b\times {\mathbf {n}}^{(0)}\right) +p^{(1)}\left( {\mathbf {r}}_b \times {\mathbf {n}}^{(1)}\right) \right. \nonumber \\&\left. \quad +p^{(0)}\left( {\mathbf {r}}_b \times {\mathbf {n}}^{(2)}\right) \right] \mathrm{d}s\nonumber \\&\quad +\int _{cw_0}{\frac{1}{2}}\rho g\left[ \zeta ^{(1)}-\left( \xi _3^{(1)}\right. \right. \nonumber \\&\left. \left. \quad +y\xi _4^{(1)} -x\xi _5^{(1)}\right) \right] ^2({\mathbf {r}}_b \times {\mathbf {n}}^{(0)}){/}\sqrt{1-\left( {\mathbf {n}}_3^{(0)} \right) ^2} \mathrm{d}l. \end{aligned}$$

(21)

Here, $s_{b_0}$ and $cw_0$ denote mean wetted body surface and mean waterline, respectively ${\mathbf {n}}^{(k)}={\mathbf {\alpha }}^{(k)}\times {\mathbf {n}}^{(0)},\,\,\,(k=1,2)$.

2.5 Rigid-body motion equations

The generalized rigid-body motion equations can be written as:

$$\begin{aligned} \sum \limits _{j=1}^6 {m_{i,j} } \ddot{\xi }_j^{(m)} +k_{i,j} \xi _j^{(m)}=F_i^{(m)}. \end{aligned}$$

(22)

Here, the operator ‘$^{..}$’ means the second-order time derivative. $m_{i,j}$ represents the element of the $6\times 6$ generalized mass matrix and $\xi _j$ is the body displacement in the $j$ th generalized direction. $k_{i,j}$ denotes an element of the $6\times 6$ restoring force matrix due to the mooring system and $F_i^{(m)}$ represents the generalized hydrodynamic forces and moments about the centre of gravity of the body in the $i$-th generalized direction. Infinite-frequency added mass terms were added on both sides of the equations to stabilize the time integration which will be described in the following section.

3 Numerical implementation

3.1 Boundary element method (BEM)

Applying the Green’s second identity, a boundary integral equation using a Rankine source as the Green function $G(p,q)$ can be expressed as:

$$\begin{aligned} C(p)\phi (p)=\iint \limits _S \left[ (G(p,q)\frac{\partial \phi (q)}{\partial n} -\phi (q)\frac{\partial G(p,q)}{\partial n}\right] \mathrm{d}S\nonumber \\ \end{aligned}$$

(23)

Here, $p(X,Y,Z)$ and $q(\xi , \eta , \zeta )$ are the field point and source point, respectively. $C(p)$ is the solid angle at the field point, which equals to $2\pi$ when $p(X,Y,Z)$ is on a smooth surface and $4\pi$ when $p(X,Y,Z)$ is in the solution domain. $S$ denotes the boundaries of the water domain which include the free surface, the body surface and the bottom and the side walls. When the solution domain is symmetric about the $OXZ$ plane, and the bottom is horizontal, the Rankine source and its image with respect to the symmetry plane and the bottom are used as a Green function to reduce the computational boundaries and time. In the numerical method, the computational boundaries are discretized by bilinear plane elements. Four nodes are placed on each plane element. After introducing shape functions $N_j(\xi ,\eta )$ for each surface element, variables like displacement, velocity potential and its derivatives can be written in the following forms:

$$\begin{aligned} \left\{ {\begin{array}{l} {\mathbf {X}}(\xi , \eta )=\sum \limits _{j=1}^K {N_j (\xi , \eta )} {\mathbf {X}}_j \\ \phi (\xi , \eta )=\sum \limits _{j=1}^K {N_j (\xi , \eta )} \phi _j \\ \frac{\partial \phi (\xi , \eta )}{\partial n}=\sum \limits _{j=1}^K {N_j(\xi , \eta )} \frac{\partial \phi _j }{\partial n} \\ \end{array}} \right. \end{aligned}$$

(24)

Here, $K$ is the number of nodes in the element, ${\mathbf {X}}_j$ and $\phi _j$ express the position and potential, respectively, and $(\xi , \eta )$ are local intrinsic coordinates. Then, the boundary integral equation can be expressed as:

$$\begin{aligned}&C(p)\phi (p)\nonumber \\&\quad = \sum \limits _{n=1}^N\sum \limits _{m=1}^M \left\{ G(q_m,p)\left[ \sum \limits _{j=1}^K N_j (\xi ,\eta ) \left( \frac{\partial \phi }{\partial n}\right) _{j}\right] \right. \nonumber \\&\quad \left. -\frac{\partial G(q_m, p)}{\partial n} \!\left[ \sum \limits _{j=1}^K {N_j (\xi ,\eta )\phi _j}\!\right] \!\right\} \! w_m \!\left| {J_m (\xi ,\eta )}\right| \end{aligned}$$

(25)

Here, $M$ is the number of sampling points used in the standard Gauss–Legendre integration method, $w_m$ is the integral weight at the $m$-th sampling point, $J_m (\xi , \eta )$ is the Jacobian transformation from the global coordinate to the local one and $N$ is the number of elements. When the field point is located in a particular element, the corresponding singularity is evaluated by using the triangular polar coordinate transformation by Li (1985). The solid angle $C(p)$ is calculated from the influence coefficient matrix as Wu and Eatock Taylor (1989) did.

3.2 Numerical wave beach

A numerical wave beach as proposed by Ferrant (1993) is used. This means damping terms are introduced in the free-surface conditions in the ‘wave beach’ region. The modified free-surface conditions are:

$$\begin{aligned} \begin{array}{l} \zeta _t^{(m)} =\phi _z^{(m)} +F_1^{(m)} -\upsilon (r)\zeta _s^{(m)} \\ \phi _t^{(m)} =-g\zeta ^{(m)} +F_2^{(m)} -\upsilon (r)\phi _s^{(m)}\\ \end{array} \end{aligned}$$

(26)

Here, $r$ denotes the horizontal distance from one point on the free surface to the gravitational centre of the body. The damping coefficient $\upsilon$ is defined as:

$$\begin{aligned} \upsilon (x)=\left\{ \begin{array}{ll} \alpha \omega (\frac{r-r_0 }{\beta \lambda })^2 &{}\quad r\ge r_0 \\ 0 &{}\quad r<r_0 \\ \end{array} \right. \end{aligned}$$

(27)

Here, $r_0$ denotes a reference value specifying the horizontal distance to the gravitational centre of the body, and $\lambda$ and $\omega$ are the wavelength and wave frequency, respectively. In bichromatic wave conditions, the mean wavelength and mean wave frequency of the two primary waves are used. Further, $\alpha$ and $\beta$ control the strength and length of the damping zone, respectively.

3.3 Time-integration scheme

An explicit fourth-order Runge–Kutta method (RK4) is used to time integrate the boundary conditions and the six degree of freedom motion equations. Actually, the equations of motion (22) take the following form, since the hydrodynamic forces depend on the acceleration of the body:

$$\begin{aligned} {\dot{\mathbf {y}}}=f({\dot{\mathbf {y}}},{\mathbf {y}},t). \end{aligned}$$

(28)

Here, vector ${\mathbf {y}}$ denotes the variable of interest and $f({\dot{\mathbf {y}}},{\mathbf {y}},t)$ represents a function of both space and time. This form may lead to instabilities due to the impulsive term in the hydrodynamic forces proportional to the acceleration, especially when the added mass is much larger than body mass (this happens in the vertical modes of motions of a ship in shallow water according to our numerical study). Kvålsvold (1994) obtained a stable form of the equation of motions by merely adding an infinite-frequency added mass term on both sides of the equation. Then the equation of motion takes the form:

$$\begin{aligned} {\dot{\mathbf {y}}}=f({\mathbf {y}},t) \end{aligned}$$

(29)

which is similar with the free-surface boundary conditions. The solution for the above first-order ordinary equation by RK4 is expressed as follows:

$$\begin{aligned} {\mathbf {y}}(t+\Delta t)={\mathbf {y}}(t)+\frac{1}{6}(k_1 +2k_2 +2k_3 +k_4), \end{aligned}$$

(30)

where

$$\begin{aligned} \begin{array}{l} k_1 =\Delta t\cdot f(t,{\mathbf {y}}) \\ k_2 =\Delta t\cdot f(t+\frac{\Delta t}{2},{\mathbf {y}}+\frac{k_1 }{2}) \\ k_3 =\Delta t\cdot f(t+\frac{\Delta t}{2},{\mathbf {y}}+\frac{k_2 }{2}) \\ k_4 =\Delta t\cdot f(t+\Delta t,{\mathbf {y}}+k_3 ) \\ \end{array} \end{aligned}$$

4 Numerical studies

Two small parameters are introduced in this section. One is the ratio between the water depth and the ship draft $\delta =h{/}d$ and the other is the water depth-to-wave length ratio $\Lambda =h{/}\lambda _m.$ Here, $\lambda _m$ is the wave length corresponding to the mean wave frequency $\upsilon$ of the two primary waves in the bichromatic waves.

4.1 Hydrodynamic coefficients and RAOs of a VLCC

To investigate the influence of the water depth on hydrodynamic coefficients of a moored VLCC, numerical forced motion tests are performed based on linear theory and the calculated hydrodynamic coefficients are compared with experimental data by Oortmerssen (1976). Three water-depth values are chosen corresponding to water depth-to-draft ratios $\delta =1.1,\,\delta =1.2$ and $\delta =2.0,$ respectively. The main particulars of the VLCC are listed in Table 1. As shown in Figs. 2 and 3, the added mass and damping coefficients predicted by the present code agree well with the experimental data in general. The ship length $L$ used in non-dimensionalizing results is the length between perpendiculars. The added mass in sway increases with decreasing water depth in the low-frequency domain, while the opposite is the tendency in the high-frequency domain. The maximum slope of the curve increases considerably with decreasing water depth, which means a significant increase of sway-added mass in the low-frequency domain in shallow water. The damping in sway also increases with decreasing water depth, but the difference is smaller at higher frequencies. Moreover, both the added mass and damping in heave increase with decreasing water depth. This is in accordance with the results presented by Kim (1968). The same trends also occur in the other horizontal and vertical modes of motions due to our numerical tests. However, they are not shown due to the lack of experimental data to compare with. Therefore, the influence of the water depth on the added mass and damping can be significant.

Table 1 Main particulars of the ships

Fig. 2

Experimental and numerical non-dimensional added mass and damping in sway for a fully loaded VLCC with parameters $\delta =1.1, \delta =1.2$ and $\delta =2.0$ presented as a function of non-dimensional frequency

Fig. 3

Experimental and numerical non-dimensional added mass and damping in heave for a fully loaded VLCC with parameters $\delta =1.1, \delta =1.2$ and $\delta =2.0$ presented as a function of non-dimensional frequency

The strip theory may lead to wrong results in shallow water due to strong three-dimensional effects at the ship ends, especially in the lateral modes of motions. We consider as an example the sway-added mass of the middle cross section of the VLCC. The non-dimensional value at zero frequency for a rectangular profile with breadth-to-draft ratio $B/d=2.5$ is $A_{22}{/}(\rho Bd)\approx 11.0$ at a water depth-to-draft ratio $\delta =1.2$ according to Flagg and Newman (1971). However, the non-dimensional 3D added mass in sway at zero frequency is $A_{22} /(\rho \nabla )\approx 3.0$ according to the experimental and present numerical results. Kim (1968) reported results of ship motions in restricted water depth by strip theory. He concluded that strip theory can be used to predict vertical motions, but cannot be used for lateral motions.

The linear motions of freely floating VLCC in regular head waves are calculated by the present linear code. Figures 4, 5, 6 shows RAOs of the VLCC in surge, heave and pitch for different water depths in regular head sea waves. When the wave frequency $\omega$ is small, the corresponding wavelength is large relative to the ship length and the ship tends to behave as a fluid particle. The oscillating particle motions in linear incident waves in the $X$- and $Z$-directions can be described as

$$\begin{aligned} \left\{ {\begin{array}{l} \xi _1 =-A\frac{\cosh k(z+h)}{\sinh kh}\sin (\omega t-kx) \\ \xi _3 =A\frac{\sinh k(z+h)}{\sinh kh}\sin (\omega t-kx) \\ \end{array}} \right. \end{aligned}$$

(31)

which means that the fluid particle has an elliptical path. Here, $A,\,k$ and $\omega$ represent the incident wave amplitude, wave number and wave frequency, respectively. $\xi _1$ and $\xi _3$ denote the horizontal and vertical fluid particle motion, respectively. The ratio between the maximum horizontal motion and maximum vertical motion is $\coth k(z+h).$ The consequence is the well-known fact that maximum horizontal motion for a given water depth is always larger than the maximum vertical motion. Further, we note that the maximum vertical motion occurs for $\omega =0$ and is equal to $A.$ The pitch motions amplitude $\xi _{5a}$ approaches $kA$ when the wave frequency $\omega$ becomes very small. On the other extreme case when $\omega$ becomes large, the corresponding wavelength becomes small and hence the linear wave excitation forces decrease with the consequence that the ship motions go to small values. We will somewhat arbitrarily use as a criterion for the ship to behave as fluid particle that $\lambda \ge 3L,$ where $L$ denotes the ship length between perpendiculars. For the small water depth case with $\delta =1.2,$ when the non-dimensional wave frequency $\omega \sqrt{L/g} \le 0.56,$ the corresponding wavelength $\lambda \ge 3L.$ The ship then tends to behave as a fluid particle. On the other hand, when $\omega \sqrt{L/g} \ge 6.55,$ the water depth $h\ge \frac{\lambda }{2}$ and the ship behaves as though it is in deep water. When it comes to the larger water depth case, the wavelength $\lambda \ge 3L$ corresponds to $\omega \sqrt{L/g} \le 1.03$ and the water depth $h\ge \frac{\lambda }{2}$ corresponds to $\omega \sqrt{L/g} \ge 3.42.$ As shown in Fig. 4, the surge motion amplitude increases dramatically in the low-frequency domain and our numerical results agree well with the fluid particle motions. For the heave motion amplitudes present in Fig. 5, all the numerical values for small non-dimensional frequencies tend to 1.0 and this is consistent with the fluid particle motions. However, for the pitch motion amplitudes shown in Fig. 6 there are big discrepancies between our numerical results and Oortmerssen (1976) calculations in the low-frequency domain. Our results for $\xi _{5a} /kA$ tend to 1.0 when $\omega \rightarrow 0,$ while the results by Oortmerssen go to unreasonably large values. For the larger water depth case, both our numerical results and Pinkster (1980) calculation of $\xi _{5a} /kA$ have the same tendency and approach 1.0 for very small frequency values. When the non-dimensional frequency becomes large, all the considered motion amplitudes for different water depths go to zero as a consequence of small wave excitation load.

Fig. 4

Experimental and numerical RAOs in surge of a fully loaded VLCC with parameters $\delta =1.2$ and $\delta =4.4$ presented as a function of non-dimensional frequency. $A$ is the amplitude of incoming waves

Fig. 5

Experimental and numerical RAOs in heave of a fully loaded VLCC with parameters $\delta =1.2$ and $\delta =4.4$ presented as a function of non-dimensional frequency. $A$ is the amplitude of incoming waves

Fig. 6

Experimental and numerical RAOs in pitch of a fully loaded VLCC with parameters $\delta =1.2$ and $\delta =4.4$ presented as a function of non-dimensional frequency. $A$ is the amplitude of incoming waves

4.2 Slow-drift excitation forces on a VLCC

The second-order wave-drift forces acting on a VLCC is calculated and compared with Pinkster’s experimental and numerical results. The model tests were carried out with a 1:82.5 scale model of the VLCC in fully loaded conditions and in head sea. Two sets of restraint systems were used in the model tests. One was a simple soft-spring system which was used in regular waves. The other was a dynamic positioning system used in irregular waves. The purpose of it was to allow the vessel to move freely at wave frequency while restraining the motions at the difference frequency. The consequence is that the slow-drift excitation forces can be determined. The model tests were carried out in two different water depths corresponding to water depth-to-draft ratios $\delta =1.6$ and $\delta =1.2,$ respectively. The irregular waves with two sets of parameters were used in the two different water depths. All model tests in irregular waves were carried out for a duration of 6 h in full scale to generate long-time records of the measured forces. To extract the slow-drift excitation forces accurately, a cross-bispectral technique (CBS) was used to analyse the measured force records in irregular waves and form the QTFs for slow-drift excitation surge force. More details about the setup of the model test and the analysis of the experimental data can be found in Pinkster and Huijsmans (1992). According to Faltinsen (1990), the generalized slow-drift excitation surge force $F_1^{sv}$ can be represented as

$$\begin{aligned} F_1^{sv}&= \sum \limits _{j=1}^N \sum \limits _{i=1}^M A_i A_j\left\{ T_{ji}^{ic}\cos [(\omega _i-\omega _j)t+(\beta _i-\beta _j)]\right. \nonumber \\&\left. \quad +T_{ji}^{is}(\omega _i,\omega _j)\sin [(\omega _i -\omega _j)t+(\beta _i-\beta _j)]\right\} . \end{aligned}$$

(32)

Here, $A_i$ and $A_j$ denote the amplitudes of the linear incident waves with frequency $\omega _i$ and $\omega _j ,$ respectively. $T_{ji}^{ic}$ and $T_{ji}^{is}$ denote the QTF for the slow-drift excitation forces in phase and out of phase with the difference-frequency incident waves, respectively. $\beta _i$ and $\beta _j$ denote the random phase angles of the incident waves with frequency $\omega _i$ and $\omega _j ,$ respectively. According to the definition of Newman (1974), we have $T_{ji}^{ic} =T_{ij}^{ic}$ and $T_{ji}^{is} =-T_{ij}^{is}.$ Further, the amplitude of the QTF for the second-order difference-frequency force $\left| {T_{ji} } \right| =\sqrt{(T_{ji}^{ic} )^2+(T_{ji}^{is} )^2}.$

To obtain the QTFs and compare with the experimental data, we study the slow-drift excitation surge force on the moored VLCC in bichromatic waves. Since the QTFs are independent of the incoming wave amplitude, the linear wave amplitudes of the two components in bichromatic waves are set to be unity. Moreover, the phase angles of the incoming waves are set to be zero in the simulations. The ship is restrained from the low-frequency motions but free to wave-frequency motions like the conditions in the model tests. Fourier analysis is used to analyze the time history of the second-order forces and extract the amplitudes of the difference-frequency components. In case the frequencies of the two primary waves are different, the amplitude of the difference-frequency force has to be divided by a factor 2 to get the correct QTFs. When the frequencies of the two primary waves are identical, only sum frequency and a mean part exist in the second-order force time history. At this time, the total slow-drift excitation force equals four times the mean drift force in regular wave, which is the same with one component in the bichromatic waves. This is not difficult to explain. When the two waves are identical in the bichromatic waves, it is identical with a regular wave with the same frequency and amplitude doubled. The slow-drift excitation force is proportional to the square of the amplitude of the incoming wave. Therefore, the slow-drift excitation force has to be divided by a factor 4 to get the correct QTFs at this time.

The QTFs for different mean frequencies $\upsilon$ of the bichromatic waves and water depth-to-wave length ratios $\Lambda =h/\lambda _m$ are plotted in Figs. 7, 8, 9, 10. It can be seen that the smallest value of $\Lambda$ is still larger than 0.1, which is the shallow water waves’ limit. However, please note that $\lambda _m$ is not the same as the longer wave length $\lambda _2$ in the bichromatic waves. If we consider the case with parameters $\upsilon =0.43\, \text{ rad/s },\,\mu =0.24\, \text{ rad/s }$ and $\Lambda =0.11,$ for instance, the water depth-to-wave length ratio for the longer wave in the bichromatic waves $\Lambda _2 =h/\lambda _2 =0.078,$ which satisfies shallow water wave condition. Moreover, the difference-frequency waves satisfy shallow water condition in all the considered cases. Therefore, the characteristics of shallow water waves are included in the following case studies. As shown in Figs. 7, 8, 9, 10, both Pinkster’s approximation and the present complete second-order theory give the QTFs with the same magnitude as the experimental data, except in the high mean wave frequency range $\upsilon \ge 0.76\, \text{ rad/s }$ and when the difference frequency $\mu \ge 0.1\, \text{ rad/s }.$ In this case, the wave lengths of the two primary waves are approximately $\frac{1}{4}$ and $\frac{1}{3}$ of the ship length, respectively. It becomes difficult for a traditional BEM method to calculate wave-drift forces for so short wave lengths. It is noted that the QTFs with a difference frequency close to 0.05 rad/s, which is important for a moored ship with natural period near 125 s, is considerably higher than that for zero difference frequency. That means Newman’s approximation underestimates the values of QTFs significantly in this difference-frequency range. Compared with experimental data and our complete second-order results, Pinkster’s approximation overpredicted the QTFs in the small wave frequency range and especially when the difference frequency $\mu \ge 0.05\,\text{ rad/s }.$ This is because Pinkster’s approximation only considers the contributions of the second-order undisturbed incoming waves to the second-order potential, while neglecting the interactions of the first-order diffraction and radiation effects, which are not small when the wave frequency is close to 0.45 rad/s due to large vertical modes of motions.

Fig. 7

QTF of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.6$, $\upsilon =$ 0.43–0.59 rad/s and $\Lambda =$ 0.13–0.20)

Fig. 8

QTF of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.6$, $\upsilon =$ 0.65–0.81 rad/s and $\Lambda =$ 0.23–0.33)

Fig. 9

QTF of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.2$, $\upsilon =$ 0.43–0.59 rad/s and $\Lambda =$ 0.11–0.17)

Fig. 10

QTF of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.2$, $\upsilon =$ 0.65–0.81 rad/s and $\Lambda =$ 0.19–0.26)

With the purpose of investigating the proportion of different components in the slow-drift excitation force, we first separate the total second-order force into several parts following Pinkster (1980).

$$\begin{aligned} F^{(2)}=F_1 +F_2 +F_3 +F_4 +F_5 \end{aligned}$$

(33)

with

$$\begin{aligned} \begin{array}{l} \displaystyle F_1 =\frac{1}{2}\rho g\int _{cw_0 } \left[ \zeta ^{(1)}-\left( \xi _3^{(1)} +y\xi _4^{(1)} -x\xi _5^{(1)}\right) \right] ^2\\ \displaystyle \qquad \quad {\mathbf {n}}^{(0)}\Big /\sqrt{1-\left( {\mathbf {n}}_3^{(0)} \right) ^2} \mathrm{d}l \\ \displaystyle F_2 =-\iint _{s_{b_0 } } {\frac{1}{2}\rho \nabla \phi ^{(1)}\cdot } \nabla \phi ^{(1)}{\mathbf {n}}^{(0)}\mathrm{d}s \\ \displaystyle F_3 =-\iint _{s_{b_0 } } {\rho [({\mathbf {\xi }}^{(1)}+{\mathbf {\alpha }}^{(1)}\times {\mathbf {r}}_b )\cdot } \nabla \phi _t^{(1)} ]{\mathbf {n}}^{(0)}\mathrm{d}s \\ \displaystyle F_4 ={\mathbf {\alpha }}^{(1)}\times m{\varvec{\ddot{\xi }}}^{(1)} \\ \displaystyle F_5 =-\iint _{s_{b_0 } } \rho \phi _t^{(2)} {\mathbf {n}}^{(0)}\mathrm{d}s\\ \end{array} \end{aligned}$$

Here, we select the case with mean wave frequency $\nu =0.49\, \text{ rad/s }$ as an example to illustrate the different components in the slow-drift excitation forces. Both the amplitudes and phase angles of the different components of the slow-drift excitation forces with parameters $\delta =1.6,\,\Lambda =0.16$ and $\delta =1.2,\,\Lambda =0.13$ are plotted in Figs. 11 and 12. $F_1$ dominates in most of the difference-frequency domain, while $F_5$ takes a larger part when the difference frequency $\mu$ is close to 0.1 rad/s at water depth $\delta =1.6.$ However, in the case of $\delta =1.2,\,F_5$ dominates when the difference frequency $\mu \ge 0.03\, \text{ rad/s }.$ The relative magnitude of $F_1 \sim F_4$ is in agreement with Pinkster (1980) results for mean drift forces of the same VLCC in regular waves.

Fig. 11

Amplitudes and phase angles of different components of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.6$, $\Lambda =0.16$ and $\nu =0.49\, {\text{ rad/s }})$

Fig. 12

Amplitudes and phase angles of different components of the surge drift force in head waves for a fully loaded VLCC ($\delta =1.2$, $\Lambda =0.13$ and $\nu =0.49\,\text{ rad/s })$

According to Pinkster (1975), the spectral density $S_F$ of the slow-drift excitation forces can be calculated once the QTFs are obtained. The formula is

$$\begin{aligned} S_F (\mu )=8\int _0^\infty {\left| {T(\omega , \omega +\mu )}\right| ^2S(\omega )S(\omega +\mu )\mathrm{d}\omega }. \end{aligned}$$

(34)

Here, $S(\omega )$ represents the wave spectrum. In deep water, the QTFs can be calculated as follows by the mean forces according to Newman’s approximation:

$$\begin{aligned} T(\omega ,\omega +\mu )&=\frac{1}{2}[T(\omega , \omega )+T(\omega +\mu , \omega +\mu )]\nonumber \\&=\frac{1}{2}\left[ \frac{F_m^{(2)} (\omega )}{A^2}+\frac{F_m^{(2)} (\omega +\mu )}{A^2}\right] . \end{aligned}$$

(35)

Here, $F_m^{(2)} (\omega )$ and $F_m^{(2)} (\omega +\mu )$ denote the mean drift force in regular waves with frequencies $\omega$ and $\omega +\mu ,$ respectively. $A$ represents the incident wave amplitude. By choosing the modified Pierson–Moskowitz spectrum with mean wave period $T_m =9.74\, \text{ s }$ and significant wave height $Hs=2.76\, \text{ m },$ we plot the corresponding slow-drift excitation force spectrum in Fig. 13 with QTFs given by Newman’s approximation, Pinkster’s approximation, the present complete theory and experimental data. Compared with the experimental results, Newman’s approximation underpredicts the slow-drift excitation force spectrum significantly, while Pinkster’s approximation overpredicts the values. The present complete theory provides results with the same magnitude as the experimental results. This confirms the necessity of including the contribution of the second-order potential properly in estimating slow-drift excitation forces in shallow water. However, for the larger water depth case, our numerical results have large discrepancies with the experimental results in the small difference-frequency domain. This is due to the big discrepancies between the experimental and numerical QTFs in the low difference-frequency range as shown in Figs. 7 and 8. The values of the experimental QTF are basically smaller than our numerical results in the low difference-frequency range. It even approaches zero near zero difference frequency in the case with $\nu =0.49\,\text{ rad/s },\,\Lambda =0.16$ and $\delta =1.6,$ which means the mean drift force is zero in this case. This is unphysical and one possible reason is the statistical uncertainty in the CBS analysis of the measured forces by Pinkster (personal communication 2012). The CBS technique is expecting oscillatory quantities and the QTF for the mean forces is a result of oscillation frequencies approaching zero. There is a large statistical uncertainty in the CBS analysis, especially for the QTF values close to zero difference frequency. To reduce the uncertainty, one should conduct many long-duration tests in irregular waves so that the statistical averages become relatively stationary.

Fig. 13

Spectrum of the surge drift forces in head waves for a fully loaded VLCC at different water depths ($\delta =1.6$ and $\delta =1.2)$

4.3 Slowly varying motions of a moored LNGC

We have also studied the slowly varying surge of an LNGC model in bichromatic waves and head sea and compared the numerical results with experimental data from Marintek by Kristiansen (2010). The main particulars of the LNGC are listed in Table 1 and the wave parameters of the tests, which are in full scale, are given in Table 2. The water depth-to-wave length ratio $\Lambda =h/\lambda _m$ is much larger than the shallow water wave limit 0.1 for the primary waves in the bichromatic waves. Therefore, it is finite water depth condition in the tests. However, for the difference-frequency waves, shallow water condition is satisfied in the considered cases. The model tests were done with a 1:40 scale model and in an ocean basin with length and width 80 m $\times$ 50 m and water depth 0.715 m. The corresponding water depth-to-draft ratio $\delta =2.4.$ The bichromatic waves were generated by a multi-flap wavemaker located at one end of the basin and propagating over a ramp at a distance of 7.7 m from the wavemaker in the longitudinal direction. A 20 m-long beach was located in the other end of the basin to absorb propagating waves. The LNGC model was located in the middle of the basin and at a distance of 35.6 m from the wavemaker in the longitudinal direction. A soft spring system was used and its stiffness in surge $k_x =420\,\text{ N }/\text{ m }.$

Table 2 Parameters of the bichromatic waves in full scale

Since the analytical second-order Stokes waves in finite water depth are used as incoming waves in the present method, the elevations without the ship model are first compared with the experimental results. Four tests are selected and the results in full scale are plotted in Fig. 14. The satisfactory agreement shows that the incoming wave fields can be described well by the analytical Stokes waves.

Fig. 14

Time histories of analytical and experimental wave elevations at the position $(0,0,0)$ in the body-fixed coordinate system with parameters $\delta =2.4$ and $\Lambda =0.22,0.15,0.20,0.25$, respectively

The wave-drift damping is calculated by the ARG method as previously described. Mean drift forces in surge for different small forward speeds in regular waves are obtained by a 3D wave–current–body model which keeps correctly first-order terms in the forward speed. More details about the theory and formulas can be found in Zhao et al. (1988). The mean drift forces in surge are plotted in Fig. 15 as a function of incoming wave frequencies. Then a line-fitting technique is used to calculate the gradient of mean drift force with respect to the forward speed for each wave frequency. The resulting wave-drift damping is plotted as a function of incoming wave frequencies in Fig. 16. Wave-drift damping in bichromatic waves are approximated by the sum of the two values in regular waves, which can be obtained from the curve in Fig. 16.

Fig. 15

Mean drift forces of an LNGC at different forward speeds as a function of non-dimensional incoming wave frequencies. $L$ and $B$ denote the ship length between perpendiculars breadth, respectively. $A$ is the incident wave amplitude

Fig. 16

Wave-drift damping of an LNGC as a function of non-dimensional incoming wave frequencies. $L$ and $B$ denote the ship length between perpendicular breadth, respectively. $A$ is the incident wave amplitude

The viscous damping in surge is approximated by the equation of shear force in non-separated laminar flow condition, which can be found in Faltinsen (1990).

$$\begin{aligned} B_{11}^v =\rho \sqrt{\omega _n \tau } S \end{aligned}$$

(36)

Here, $B_{11}^v$ denotes viscous damping in surge and $\omega _n$ is the surge natural frequency of the moored ship. Further, $S$ is the wetted area of the ship surface and $\tau =10^{-6}\,\text{ m }^{2}\text{/s }.$ The ratios between the wave-drift damping $B_{11}^{wd}$ and the critical damping in surge $B_{11}^{crit}$ of the moored ship are 0.45, 0.45, 0.48, 0.39 %, corresponding to the four tests in Table 2, in which the wave parameters are listed. The wave-drift damping is basically small in the considered cases due to the small wave amplitudes. The ratio between the viscous damping $B_{11}^v$ and the critical damping in surge $B_{11}^{crit}$ is 0.39 %. Moreover, in the experiments, the mooring springs were located in the air and therefore we do not consider its damping.

After the first- and second-order forces and wave-drift damping are obtained at each time step, the motion equations are solved and the corresponding acceleration, velocity and motions of the ship become known. We focus on the surge motions of the LNGC model in bichromatic head waves, whose parameters are given in Table 2. The ratios between the difference frequency of the incident waves $\mu$ and the natural frequency of the moored ship $\omega _n$ for different tests are also listed in Table 2. The ratio is closest to 1.0 in test 5230 and the surge damping values have significant influence on the surge motions. For example, there is a 23 % decrease in the slowly varying surge motion amplitude if the surge damping is two times the real value according to our numerical simulations. However, in the other tests, where the ratios are far away from 1.0, the effects of damping on surge motions are negligibly small. The simulations and the experimental results of the surge motions are plotted in Figs. 17, 18, 19, 20. The upper figures present the total motions, while the lower figures show the difference-frequency motions obtained by a low-pass filtering technique. It can be seen that the simulated difference-frequency motions agree well, in general, with the experiment results. However, there are clear discrepancies in the total motions between the simulated results and experimental data. There are several possible error sources. Firstly, parasitic low-frequency free waves were created when the bichromatic waves propagated over the bottom ramp near the wavemaker. Although a correction signal was added to the wavemaker, it was difficult to eliminate them completely. The influence of parasitic low-frequency free waves is obvious in test 5210 and test 5280, which are shown in Figs. 18 and 19. There are significant low-frequency components in the surge motions whose frequencies are different from the difference frequency of the bichromatic incident waves. One main reason of the unintentional low-frequency waves was the influence of the ramp near the wavemaker, which does not exist in the numerical model. Further, the amplitudes of the first harmonic components in the incident waves vary along the longitudinal direction of the basin in the bichromatic wave experiments without a moored ship, which may due to refraction and viscous effects. Therefore, the first-order incident wave amplitudes vary over a distance of $2\xi _{1a} ,$ where $\xi _{1a}$ denotes the surge motion amplitude, due to the surge motion of the ship and this cannot be simulated in the numerical model. In the worst case, the amplitude of the first harmonic of the incident waves varied approximately 5 % over a distance of 0.40 m in model scale.

Fig. 17

Time histories of experimental (test 5200) and numerical surge motions of an LNGC in head bichromatic waves with parameters $\delta =2.4$ and $\Lambda =0.22$ (the top figure shows the total motions and the lower figure the difference-frequency motions)

Fig. 18

Time histories of experimental (test 5210) and numerical surge motions of an LNGC in head bichromatic waves with parameters $\delta =2.4$ and $\Lambda =0.15$ (the top figure shows the total motions, and the lower figure the difference-frequency motions)

Fig. 19

Time histories of experimental (test 5280) and numerical surge motions of an LNGC in head bichromatic waves with parameters $\delta =2.4$ and $\Lambda =0.20$ (the top figure shows the total motions, and the lower figure the difference-frequency motions)

Fig. 20

Time histories of experimental (test 5230) and numerical surge motions of an LNGC in head bichromatic waves with parameters $\delta =2.4$ and $\Lambda =0.25$ (the top figure shows the total motions, and the lower the difference-frequency motions)

4.4 Convergence tests

Convergence tests have been done by varying the mesh size on the body surface and the free surface, as well as the time increment. Since it is easy to obtain convergent results for the linear excitation and motions, the convergence tests for the second-order forces are only shown here. Our numerical studies found that the results are not sensitive to the size of the damping zone when the length of it is larger than $2\lambda _2.$ Here, $\lambda _2$ represents the wavelength of the longer primary wave. Therefore, the length of the damping zone is chosen to be $2.5\lambda _2$ in the present studies. Further, the results are not sensitive to the distance between the ship and the beginning part of the damping zone as long as the control parameter of the damping zone satisfies $\alpha \le 2.$ Actually, the results are identical if this distance is larger than the ship length in our numerical studies. So we chose this distance to be two ship lengths $2L$ with control parameter $\alpha =1.$

Here, the parameters $\upsilon =0.49\,\text{ rad/s },\,\Lambda =0.13\,$ and $\mu =0.16\,\text{ rad/s }$ are chosen for the convergence studies of the VLCC and the parameters in test 5280 are used for the convergence studies of the LNGC. First of all, the discretization of the body surface and free surface should be sufficiently large to guarantee a sufficient panel number within one wavelength. According to our numerical tests, at least 11 bilinear panels should be used for one wavelength to calculate the first-order forces and motions accurately and this number increases to 18 for accurate prediction of the second-order mean and difference-frequency forces. A circular free surface is chosen in the present study and the mesh size increases with the increase in the distance to the ship. It is reasonable to have meshes that have exponentially increasing size in the vertical direction due to the exponential characteristic of the velocity potential. However, in the present numerical studies, the results are not sensitive to the vertical mesh size when the panel number is larger than 6 on the body surface and along the ship draft direction. Therefore, we just use 11 constant vertical-size panels along the vertical direction on the ship surface. Further, the number of panels on the body surface should be sufficiently large to guarantee the difference between the volumes of the generated panel model and the designed hull shape is acceptable for hydrodynamic analysis. Most industry and ship classification societies suggest that this difference $\gamma =100(\nabla _N -\nabla _D )/\nabla _D$ should be less than 1.0 for seakeeping analysis. However, for the investigation of global loads acting on ships, no exact guideline has been found. Here, we use four kinds of mesh schemes to descretize the ship surface and use $\gamma =1$ as a reference. Figure 21 shows the relations between panel numbers and $\gamma .$ We chose the largest and second largest panel numbers on the body surface as ‘Mesh1’ and ‘Mesh2’ for convergence tests for both the VLCC and LNGC models. Figures 22 and 24 shows the generated panel models for the VLCC and LNGC by the two selected mesh schemes, while Figs. 23 and 25 give the free-surface panel plot.

Fig. 21

The difference between the volumes of the generated panel model and the designed hull shape as a function of different body surface panel numbers divided by one

Fig. 22

Two mesh schemes (Mesh1 and Mesh2) for a fully loaded VLCC

Fig. 23

Free-surface mesh in the two mesh schemes (Mesh1 and Mesh2) for a fully loaded VLCC

Fig. 24

Two mesh schemes (Mesh1 and Mesh2) for an LNGC

Fig. 25

Free-surface mesh in the two mesh schemes (Mesh1 and Mesh2) for an LNGC

Figure 26 shows the second-order difference-frequency force on the ship with two different mesh schemes. For the VLCC, there are 880 panels on the body surface and 4,400 panels on the free surface for ‘Mesh1’, and 1,760 panels on the ship surface and 8,800 panels on the free surface for ‘Mesh2’. For the LNGC, there are 1,120 panels on the ship surface and 5,200 panels on the free surface for ‘Mesh1’, ans 2,240 panels on the ship surface and 10,400 panels on the free surface for ‘Mesh2’. The results for the different mesh arrangements have 0.26 % difference for the VLCC and 1.12 % difference for the LNGC, which is small from a practical point of view. This is because the second-order difference-frequency force mainly depends on the long wave component in the incoming waves which is not sensitive to the mesh size. In the present numerical studies, ‘Mesh2’ is adopted to keep the accuracy. Figure 27 shows the convergence test results for different time increments. It is noted that 75 time steps per period can provide satisfactory accurate results. However, 100 time steps per period are used in all the presented numerical studies.

Fig. 26

Time histories of the surge difference-frequency force $F_1^{(2)}$- on a fully loaded VLCC (the left-hand figure) and an LNGC (the right-hand figure) for different mesh schemes ($\Delta t=T_1/100)$

Fig. 27

Time histories of the surge difference-frequency force $F_1^{(2)}$- on a fully loaded VLCC (the left-hand figure) and a LNGC (the right-hand figure) for different time increments (Mesh 2)

5 Conclusions and future works

Investigations on wave-induced loads and motions of a moored ship in shallow water are performed by a second-order perturbation method with the incident wave slope as a small parameter. Two types of realistic ships are chosen which are a VLCC and an LNGC. It is demonstrated numerically that the added mass and damping coefficients increase with decreasing water depth in general, except for the added mass in longitudinal modes of motions in the high wave frequency domain. The linear surge motion amplitude has distinct increment in shallower water depth in the low-frequency domain, which is consistent with fluid particle motions. However, the influences of water depth on the surge motion amplitude are not significant in the wave-frequency domain, while the heave and pitch motion amplitudes tend to be smaller with reducing water depth. Further, according to our numerical results, the longitudinal slow-drift excitation forces on the moored VLCC increase with decreasing water depth and the second-order velocity potential dominantly contributes in a frequency range which is important for moored ships in shallow water. Therefore, as expected, Newman’s approximation in which the second-order velocity potential is neglected significantly underpredicts the slow-drift excitation loads in shallow water. Moreover, the results tend to be overpredicted by Pinkster’s approximation, which only considers the second-order components in the incident waves, although the orders of magnitudes are still the same with experimental and our complete second-order numerical results. Lastly, the slowly varying motions of an LNGC in head waves are simulated and compared with available experimental data. Both the numerical and experimental results show that the low-frequency components dominate in the surge motions of the moored ship, while the magnitudes of the wave-frequency motions are relatively small. The influences of the wave-drift damping on the ship surge motions are significant when the difference frequency is close to the natural frequency of the moored ship. The satisfactory agreements demonstrate that the present method can provide acceptable results for slowly varying motions of a moored ship in shallow water waves.

The present model can be used for simulating moored ship motions in six degrees of freedom. However, only three degrees of freedom are considered in the present paper due to the head sea conditions in the experiments. The lateral hydrodynamic loads and motions of a moored ship in oblique waves in shallow water will be considered in the future. Further, the influence of a weak current on slow-drift excitation forces on a moored ship in shallow water will be investigated in future studies.