1 Introduction

Floods are a critical phenomenon, given the alarming magnitude of fatalities and the extensive damage they inflict. The overwhelming power and destructive force of floods are awe-inspiring, as illustrated by the staggering loss of lives and the immense devastation they leave behind. According to statistics, between 1998 and 2017, climate-related and geophysical disasters claimed the lives of 1.3 million individuals and left an additional 4.4 billion people injured, homeless, displaced, or in dire need of emergency assistance (Wallemacq et al. 2018). Among these calamities, floods stand out as the most prevalent, comprising 43% of all recorded events and affecting over two billion individuals-the highest number among natural disasters (Wallemacq et al. 2018).

The recent surge in the frequency of flooding events attributed to climate change (Yannopoulos et al. 2015), along with the resulting devastating consequences, underscores the need to address and mitigate flood risks. Experts further predict that the risk of floods will escalate in the future, driven by the continued presence of climate change (Al-Aizari et al. 2022; Balasbaneh et al. 2019; Bouwer et al. 2010). It is of paramount importance, therefore, to proactively address the risks associated with floods and implement measures aimed at preventing or mitigating their devastating impact.

In response to these challenges, there has been a significant rise in academic research focused on enhancing the evaluation of flood hazard, vulnerability and risk for communities worldwide. By deepening our knowledge and understanding of flood risks, we can develop effective strategies to minimize their impact. Accurate identification of flood-prone areas holds particular importance for policymakers as it enables the design and implementation of comprehensive planning and management interventions.

Giannakidou et al. (2020) assert that the extent of flood risk hinges upon the diverse levels of vulnerability and hazards linked to a specific situation or location. These factors collectively shape and define the potential risks faced by individuals and communities, necessitating proactive measures to mitigate and manage them effectively.

Hazard (H) is defined as a source of potential harm, a situation with the potential to cause damage or a threat/condition with the potential to create loss of lives or to initiate a failure to the natural, modified or human systems (Tsakiris 2007). Simultaneously, vulnerability (V) to a natural hazard refers to the extent to which an element or a system is prone to damage from that hazard. The risk associated with an element is ultimately determined by the sum of expected losses and damage of any kind due to a particular natural phenomenon, as function of the natural hazard and the vulnerability of the element at risk (UNDRO 1991). This relationship is expressed as the product of the hazard and vulnerability components (UNDRO 1991), as follows:

$$R=H \cdot V$$
(1)

Flood risk is also often defined as a function of hazard (typically expressed as the probability of a flood event), exposure, and vulnerability. In this context, vulnerability is described as the societal capacity to cope with the event (IPCC 2012; Kron 2005). However, other scholars adopt a different perspective, asserting that risk comprises both hazard and vulnerability. According to Chan et al. (2022), the concept of vulnerability encompasses various factors, including exposure and sensitivity, and is multidimensional. Consequently, the distinction between vulnerability and exposure is not always clear, with exposure often being considered part of the broader vulnerability concept. Authors frequently segment vulnerability into distinct criteria, further breaking them down into indicators or subcriteria. While some investigations accord equal significance to these criteria, as demonstrated by Van et al. (2019), others, such as Chan et al. (2022), opt for a classification based on social, physical, and environmental dimensions. This article employs a causal diagram to assess the weights of vulnerability factors. The use of a causality diagram is particularly advantageous when dealing with a significant number of factors, providing a more comfortable framework for experts (Bakas et al. 2023).

Flood risk mapping proves to be invaluable for identifying areas at risk of flooding. Numerous studies have been conducted globally, regionally, and nationally proposing various approaches that integrate data and tools through geospatial methods, such as remote sensing (RS) and geographic information systems (GIS), to explore various aspects of flood risk assessment (Ekmekcioğlu et al. 2022; Gupta and Dixit 2022; Malekian and Azarnivand 2016).

GIS has gained popularity in recent years as an invaluable tool for decision-making purposes, owing to its advanced database and analytical capabilities. This system, which is defined as a comprehensive framework for efficiently capturing, storing, manipulating, analyzing, and displaying spatial information, has revolutionized the way spatial data is handled and utilized (Tsihrintzis et al. 1996). According to Danso et al. (2020), GIS can help identify vulnerable areas and act as an early warning system, allowing for better preparedness and planning during emergencies. For instance, GIS technologies have been applied for: inundation modeling (Chen et al. 2009); finding an ideal location for flood shelter (Sanyal and Lu 2009); public engagement in flood risk management through participatory GIS (White et al. 2010); flood delineation techniques (Strobl et al. 2012); extracting texture analysis of flood risk areas (Pradhan et al. 2014); and optimizing urban flood solutions cost-effectively (Singh et al. 2020).

In recent studies, flood mapping techniques have been explored extensively across various methodologies in the literature. These include: hydrological and hydrodynamic models (Abdelkarim et al. 2020; Patel et al. 2020; Singh et al. 2020; Yin et al. 2016); statistical models (SM) such as frequency ratio (FR) (Samanta et al. 2018); logistic regression (LR) (Shafapour Tehrany et al. 2019); weights of evidence (Ding et al. 2017) and genetic algorithms (Hong et al. 2018); and the machine learning methods (ML) (Costache et al. 2021; Luu et al. 2021; Towfiqul et al. 2021) such as adaptive neuro-fuzzy inference system (ANFIS), decision tree (DT) (Yariyan et al. 2020), artificial neural network (ANN) (Kia et al. 2012; Ngo et al. 2018), support vector machine (SVM) (Choubin et al. 2019), and random forest (RF) (Gudiyangada Nachappa et al. 2020).

The previously mentioned methods explore flooding from a quantitative perspective and have demonstrated effectiveness in flood assessment and mapping but each of them comes with its own set of limitations. Hydrological and hydrodynamic models necessitate detailed mapping of topographic features (Cai et al. 2007; Jha and Afreen 2020) and extensive hydro-meteorological data for the study area (Cabrera and Lee 2019), making their application challenging due to data scarcity. On the other hand, statistical models utilize deterministic models and probabilistic approaches, establishing mathematical relationships between various flood-triggering factors and the spatial distribution of recorded flood events in the study area. The objective is to calculate the probability of flood occurrence, requiring a comprehensive flood inventory database (Samanta et al. 2018), which is a major constraint for their application. Moreover, these methods are time-consuming and require precise scaling for accurate identification of flood-prone areas (Asare-Kyei et al. 2015). Lastly, machine learning techniques are commonly employed in flood assessment (Mojaddadi et al. 2017). However, they are time-consuming and demand high-performance computing systems, and require specific software and rigorous input parameters, limiting their usability, especially in cases where the spatial database of historical flood events is unavailable (Shafapour Tehrany et al. 2019). Unfortunately, there are several areas without a systematic measurement of discharges, and hence, the analysis must be exploited both quantitative and qualitative information.

In contrast with the concept of hazard, the vulnerability concept is a multidimensional ill constructed concept. An interesting point is that multi-criteria decision making (MCDM) tools consider both quantitative and qualitative aspects in their approach to flood mapping. Even though the MCDM methods exploit qualitative information, they can lead to crisp results (Bakas et al. 2023). MCDM encompasses a variety of methods that can be used to structure and assess alternatives based on multiple criteria and objectives. These methods are beneficial in making specific decisions because they can manage the inherent complexity and uncertainty of such issues and incorporate the knowledge of numerous stakeholders.

Apart from the lumped models, MCDM could be applied to integrate geographical, spatial, environmental and socio-economic objectives offering valuable solutions to complex decision problems (Ghanbarpour et al. 2013). There are different MCDM tools and many researchers have applied them in flood mapping. Most researchers employed AHP or fuzzy AHP methods to produce flood hazard maps of various watersheds, municipalities, or cities (Das 2020; Dung et al. 2022; Hategekimana et al. 2018; Papaioannou et al. 2015; Vojtek and Vojteková 2019). The significance of flood hazard assessment has brought to light the critical need to understand the vulnerability associated with floods. Vulnerability has received relatively limited attention from researchers concerning flood vulnerability evaluations in various regions (De Brito et al. 2018). However, in recent years, this aspect has gained traction and is now becoming more prevalent in disaster studies (Chan et al. 2022). Most of these flood vulnerability studies have adopted a traditional indexing approach to quantifying flood risk by assigning weights based on existing literature and criteria designed by modelers (Ekmekcioğlu et al. 2022; Hamidi et al. 2020; Pham et al. 2021; Salazar-Briones et al. 2020).

Several studies have used different methods to assess flood risks. For example, Zou et al. (2012) graded towns in Jingjiang district, China, based on hazard and vulnerability, ranging from low to high risk. Chen et al. (2015) developed a framework for flood risk assessment in mining sites in Bowen Basin, Australia, considering six criteria, i.e., five for hazard (rainfall, evapotranspiration, topography, drainage network, and flow measurements) and one for vulnerability (land cover). Ekmekcioğlu et al. (2022) employed a fuzzy AHP-TOPSIS model to analyze stakeholder perspectives in flood risk management. Their research identified specific criteria related to hazard and vulnerability clusters, revealing that the return period of a storm event held the utmost importance, followed closely by imperviousness and the stormwater pipe network. Tang et al. (2021) conducted a spatial multi-criteria analysis utilizing the AHP method to assess coastal watersheds in southeastern China. They examined flood risk across three dimensions: hazard, exposure, and vulnerability. Their findings highlighted peak discharge, maximum daily rainfall, age of people, proportion of wetland, and reservoir storage capacity as the five key indicators crucial for understanding the spatiotemporal patterns of flood risk. Feng et al. (2023) conducted a study on hurricane-induced flooding in urban areas, using Hurricane Harvey in Houston, USA, as a case study. They introduced a social-ecological systems (SES) flood risk assessment framework, addressing the oversight of urban ecosystem elements in existing assessments. The study compared flood risks in different parts of Houston during Hurricane Harvey, employing the AHP and equal weighting methods for indicator weighting. Results indicated higher flood risks in the western part of the city. These studies utilized various Multi-Criteria Decision-Making (MCDM) methods, each with unique advantages. Despite this, there is a lack of comprehensive research exploring these methods in flood risk mapping. Additionally, interrelationships among criteria, crucial for methods like the Decision-Making Trial and Evaluation Laboratory (DEMATEL), which has limited implementations in the flood risk mapping literature, have been neglected in the existing literature. Addressing these gaps could significantly enhance future flood risk assessment research.

In light of the inherent limitations of individual methods and the absence of comprehensive flood inventories in our study area, adopting an integrated approach that combines qualitative and quantitative methods becomes crucial for the assessment of flood-areas where there is a luck of data as in the case of Kosynthos River catchment on a regional scale. The distinguishing feature of this study lies in its innovative integration of the DEMATEL technique into flood risk management, providing a robust methodological framework. This integration addresses challenges posed by missing, invalid, or corrupted data, offering decision-makers effective strategies to manage flooding in areas where conventional numerical modeling is unfeasible.

The proposed framework not only bridges data gaps but also empowers decision-makers with tools to formulate and implement sustainable flood risk management strategies. A key contribution of the article is the provision of two new causality diagrams for assessing both hazard and vulnerability in treating flood phenomena. The first diagram is critical for assessing the flood hazard because of the absence of data. The second causality diagram offers a multidimensional analysis where the interactions among the criteria are taken into account. Especially the causality diagram which refers to flood vulnerability can be adaptive to local (or national) conditions. The DEMATEL method is employed for the exploitation of these diagrams, emphasizing its preference over the AHP, as it takes into account the interdependency among various factors, making it a more attractive method according to previous studies (Hosseini et al. 2021). By creating a comprehensive flood risk map that incorporates various parameters, this study not only fills knowledge gaps but also provides insights for practitioners, enabling the development of more effective and resilient approaches to mitigate the impact of floods on communities and infrastructure.

2 Study Area Description

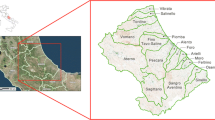
In this study, the Kosynthos River Basin located in the Thrace, Greece was used as study area (Fig. 1). It comprises an area about 530 km2. The river originates from the tops of Koula Mountain in central Rhodope, flows through Pomakochoria, and passes by the city of Xanthi before discharging into the northwest part of Vistonis Lagoon. The hydrological network being examined is 94 km in total length. The average land slope is 23.82%, and the elevation about 1830 m with a mean of 479 m. The basin is characterized by diverse land use activities, including residential, urban, agricultural, and extensive forest areas. The primary rock types in the region are alluvium, igneous, and metamorphic.

Fig. 1
figure 1

Map of the study area

Full size image

Xanthi is a multicultural city rich in history, traditions, and customs. It is built amphitheatrically at the foot of the Rhodope Mountain. It is divided into two parts by the Kosynthos River, with the old and modern town located in the west and the east part of the area’s rich natural environment. The mountainous village of Myki suffered significant damage, as massive volumes of moving by the river materials destroyed or covered houses, cars, and animals, causing loss of life. In the city of Xanthi, the damage was primarily limited in the old town and the low-lying areas where the bazaar is held. The streets transformed into rushing torrents that swept away cars, flooded basements and ground floors, and threatened human lives. Additionally, a section of the national road and the railway line near Kimmeria were destroyed. These events highlight the importance of understanding and managing the risk of flooding in the region to minimize the damage caused by future natural disasters.

3 Materials and Methods

This study aimed to assess the flood risk in districts within the Kosynthos River Basin through the utilization of an innovative methodology that integrated a Multi-Criteria Decision-Making (MCDM) approach with Geographic Information System (GIS) techniques. To accomplish this objective, a multi-step methodology was implemented, as depicted in Fig. 2. The initial step involved conducting a comprehensive literature review to identify 19 indicators related to hazard and vulnerability, encompassing 7 flood hazards and 12 vulnerability indicators. The interrelationships among the hazard indicators were determined based on a modified casual graph developed by Kourgialas and Karatzas (2011), as supported by prior research conducted by Efraimidou et al. (2022). For assessing flood vulnerability, a questionnaire was devised to gather individual judgments from participants. The causal graphs for both vulnerability and hazard were then employed to construct the respective square matrices known as the direct-influence matrices. These matrices were subsequently utilized in DEMATEL analysis to estimate the weights of the vulnerability indicators. Using GIS, the corresponding maps were generated for each indicator, resulting in the creation of flood hazard and flood vulnerability maps, ultimately culminating in the estimation of the flood risk map.

Fig. 2
figure 2

Flowchart of the proposed methodology

Full size image

3.1 Data Collection and Preparation

In the analysis of flood risk, the establishment of a robust spatial database plays a crucial role, demanding a deliberate selection of relevant indicators. This process entails a thorough examination of existing literature to identify and incorporate flood hazard and flood vulnerability indicators. By drawing upon the extensive body of literature, these indicators are thoughtfully chosen, ensuring a comprehensive and informed approach to evaluating and understanding flood risk dynamics. The assessment of flood hazard involved a detailed analysis of factors such as land use, flow accumulation, elevation, slope, geology, rainfall intensity, and distance to the river, collectively providing a comprehensive understanding of potential flood risks in the study area. Simultaneously, the vulnerability evaluation integrated a system of risk factors, considering potential catastrophic impacts on human life, property, social systems, and economic resources. This comprehensive Vulnerability index incorporated indicators like population density, land use, proximity to critical facilities, economic deprivation, distance to industrial zones, effectiveness of early warning systems, proximity to residential and cultivated areas, sanitation infrastructure, natural areas, cultural heritage monuments, and distance from roads. The selection of these indicators ensures a holistic assessment of vulnerabilities, capturing the intricate interplay between socio-economic and environmental factors crucial for understanding flood risk dynamics.

The primary sources for the creation of spatial layers in GIS are displayed in Table 1, representing key references utilized in this process.

Table 1 Details of sources of the dataset used in the study
Full size table

3.1.1 Flood Hazards Indicators

Land Use

The relationship between hydrological parameters such as runoff, infiltration, and rainfall abstraction are governed by land use (Toosi et al. 2019). The efficiency of rainfall interception and flood prevention vary greatly depending on the type of land use, including natural vegetation cover such as forests and grasslands, as well as developed areas. Soil moisture conditions relate directly to land use as the vegetation cover controls both the amount and the time of precipitation reaching the soil surface.

Flow Accumulation

Flow accumulation refers to the total amount of water flowing towards a specific point within the catchment from upstream areas. As such, higher flow accumulation is directly linked to flood hazard. This accumulation tends to be lower upstream, but increases downstream as tributaries join the main channel further downstream.

Elevation and Slope

The movement of water is dictated by the natural flow from higher to lower elevations, meaning that the slope of an area has a significant impact on the amount of surface runoff and infiltration (Kazakis et al. 2015). The slope of the topography is a key indicator that can limit water velocity and help to control flooding. Additionally, the topographic gradient can significantly impact the rate of infiltration (Das 2019). This means that in low-lying areas with flat topography and low geographic slopes, a large volume of water can become sluggish, resulting in a higher hazard to flooding.

Geology

The porosity and permeability of rocks can be influenced by geologic conditions, which can in turn amplify or mitigate the impact of flood events. Permeable formations are conducive to water infiltration, throughflow, and groundwater flow, while impermeable rocks like crystalline rocks tend to favor surface runoff. The influence of Geology extends to soil infiltration, interacting with soil characteristics. Ren et al. (2020) further emphasize that a higher infiltration rate and capacity within a given environment contribute to a notable reduction in surface runoff.

Rainfall Intensity

The likelihood of flooding is heavily influenced by the intensity and duration of rainfall, as heavier rainfall leads to an increased flood hazard. Heavy rainfall can cause the underground hydrostatic level and water pressure to rise, further contributing to the risk of flooding. Moreover, when there is a significant amount of rainfall in a short period of time from an upstream point, the potential for maximum flood events is higher (Cao et al. 2016).

Distance from the River

During river overflow, water volume surpasses its drainage capacity, leading to a significant increase in water depth in areas near the riverbed. The consequences of the flood inundation are not limited to the immediate vicinity of the river; waterlogging and the hazard of flooding can extend to the surrounding regions.

Thematic maps of elevation, slope and flow accumulation were generated by the digital elevation model (DEM). Additionally, geological data provided details about geological units, while land use data contributed to the creation of relevant thematic maps. Buffer zones around drainage network data were employed to determine distances from river. Finally, rainfall intensity was calculated by using an equation provided by the Geological and Mineral Research Institute of Greece. This Eq. (2) represents the change in precipitation per unit of altitude in the study area.

$$P=0.529\ z+515.1$$
(2)

where P represents the rainfall depth (mm) at altitude z above sea level (m asl).

3.1.2 Flood Vulnerability Indicators

Population Density

Higher population density is directly associated with greater vulnerability because a larger number of people are likely to be exposed to hazardous events in areas with high population density (Chakraborty and Mukhopadhyay 2019). Studies have consistently shown that regions with high population density face a higher risk of casualties and collateral damage during natural hazards (Das 2020; Kandilioti and Makropoulos 2012). The flood risk vulnerability is anticipated to be higher in areas characterized by inadequate living conditions, such as overcrowding.

Land Use

The land use of a region reflects how humans and natural factors have utilized the topography (Ajin et al. 2013). Anthropogenic activities such as deforestation and urbanization directly contribute to environmental disasters, and regions with large settlements are particularly vulnerable to flooding, making land use an important indicator in flood vulnerability mapping (Komolafe et al. 2018).

Distance to Critical Facilities

Floods can cause significant damage to infrastructure, making it challenging for people to access essential services during and after a flood event. These facilities include hospitals, police stations, and fire stations. The availability and accessibility to them can have a substantial impact on the ability of the affected population to cope with the flood event and to recover from its aftermath.

Deprived Area

Deprived areas are at a higher risk of suffering from flood-related losses. This is because they often lack the necessary resources and infrastructure for flood preparation and response, such as adequate housing, healthcare, and disaster preparedness resources. Due to their lower socioeconomic status, deprived areas are more vulnerable to the impacts of floods, which can lead to greater losses and slower recovery times.

Distance to Industrial Areas

Industries often store hazardous materials, which can pose a significant threat to public health and safety during a flood. Floodwaters can damage storage facilities, leading to the release of toxic chemicals, which can cause environmental contamination and pose health hazards to nearby communities. Furthermore, industrial areas may have a higher vulnerability to flooding due to their proximity to water bodies or their location in flood-prone areas. This can result in significant damage to infrastructure, leading to disruption of essential services and economic activity.

Early Warning System

Early warning systems provide advance notice of an impending flood event, allowing for early preparation and response. By detecting changes in water levels or weather patterns, an early warning system can alert authorities and the public to the potential for flooding, enabling them to take measures to protect themselves, their homes, and their communities. This can include evacuation orders, setting up emergency shelters, and moving important equipment and resources out of harm’s way. By providing advance warning, an early warning system can help reduce the impact of floods, save lives, and minimize damage to infrastructure and property.

Distance to Residential Areas

The proximity of housing to flood-prone areas can significantly impact the safety and well-being of the population. Residential areas located in flood-prone regions are more vulnerable to flooding, and the distance to these areas can influence the severity of the impact. Additionally, the distance to residential areas can also impact the effectiveness of evacuation plans and emergency response efforts, as it can affect the accessibility of these areas and the ability of individuals to quickly evacuate to safe locations.

Distance to Cultivated Areas

Floods can cause significant damage to crops and agricultural land. Cultivated areas are an essential part of the economy, and the destruction of crops can have negative effects on the local economy, food security, and livelihoods. In addition, the loss of fertile soil due to floods can have long-term impacts on agricultural productivity and sustainability.

Sanitation

Floods can contaminate water sources and damage sanitation systems, leading to the spread of water-borne diseases. Poor sanitation practices can exacerbate these problems, increasing the risk of illness and death. In addition, areas with inadequate sanitation infrastructure may have limited access to clean water and sanitation facilities during and after a flood event, making it more difficult for people to maintain their health and hygiene.

Natura Areas and Cultural Heritage Monuments

Natura areas and Cultural heritage monuments represent valuable resources for local communities and the entire nation. Floods can cause significant damage to these areas, leading to irreversible loss of cultural and ecological heritage. The loss of natural habitats can affect the biodiversity of the area, which can have significant ecological and economic consequences. Furthermore, the irreplaceable nature of cultural heritage monuments and artifacts underscores the high risk associated with floods, as these unique elements of heritage may be lost in the event of a flood, leading to a profound and irreparable loss for the community and the nation.

Distance from Foads

Heavy rains can cause flooding in highways, leading to significant problems with connectivity and accessibility (Das 2020). In times of flooding, the availability of major roads is crucial, especially for providing relief work, as rescue and assistance efforts often rely on national and state highways (Ghosh and Kar 2018).

Using GIS (ArcMap 10.8.1), the flood hazard and flood vulnerability indicators were converted into a grid database that possess a uniform spatial resolution of 30 × 30 m in order to minimize the error. To enhance objectivity, the value range of each indicator was classified into 5 classes. Each class was assigned a corresponding numerical value to represent its level of significance. While the specific values may be somewhat arbitrary, their selection is intended to represent a logical and meaningful progression from very low to very high levels of significance. Specifically, a scale of 2, 4, 6, 8, and 10 was employed to denote the very low, low, medium, high, and very high levels, respectively, similarly to a previous study by Kazakis et al. (2015). Other studies have similarly employed the practice of assigning numerical values to signify the level of significance, as exemplified by the work of Huan et al. (2012) and Vojtek and Vojteková (2019). By assigning specific values to each class, the classification system provided a clear and intuitive framework for understanding the relative importance and impact of the indicators. For quantitative indicators characterized by continuous scales or numeric values, namely flow accumulation, rainfall intensity, elevation, slope, and population density, four distinct classification techniques, i.e., Equal Interval (EI), Geometrical Interval (GI), Quantile and Jenks’ Natural Break, were implemented to examine the sensitivity of the final flood risk map to the classification technique. Historical flood data were utilized to identify the most suitable classification technique. However, for all the other qualitative indicators, such as land use and geology, the classification was based on previous studies with some adjustments to account for site-specific characteristics. The maps, generated using the classification method of Jenks’ Natural Break for all selected indicators, are visually depicted in Figs. 3 and 4. Meanwhile, the classification values for each indicator of flood hazard and flood vulnerability are detailed in Table 2. By using the overlay method through Raster Calculator of the Map Algebra tool in the Spatial Analyst module, it was possible to create a single grid database for hazard and vulnerability index through a linear combination by incorporating the weights of the evaluation maps of the DEMATEL analysis. The overlay technique enables the merging of evaluation maps in a linear manner to create a single grid database. This linear methodology ensures that operations maintain the proportional relationships between input and output values, thereby upholding a steadfast level of consistency.

Fig. 3
figure 3

Classified indicators of flood hazard

Full size image
Fig. 4
figure 4figure 4

Classified indicators of flood vulnerability

Full size image
Table 2 Indicator classes and corresponding ratings
Full size table

3.2 Identification of Interrelationships Among Indicators by Causal Diagrams

The process of identifying and characterizing the interrelationships among hazard indicators was originally based on a study conducted by Kourgialas and Karatzas (2011) by using the concept of causality. In their research, six factors, namely flow accumulation, slope, elevation, land use, rainfall intensity and geology were examined, and weights were assigned on them based on an empirical method which considers the effect on each factor on all other factors (Shaban et al. 2001). The causality among the factors were specified based on a schematic depiction where arrow lines indicated the major or minor effect. Then, the rates of each factor were computed as the summation of the corresponding to the effects emanating from the factor. Subsequently, the rates and weights were combined by multiplying the proposed weights by the rate of effect, which yields the total weight of each factor.

In this study, a new causal graph was constructed depicted in Fig. 5, by adding one more significant indicator, the distance from the river, as suggested by Kazakis et al. (2015). As Kourgialas and Karatzas (2011)proposed in the case of main effect, a change of the first factor has a direct effect on the other factor, whilst in the case of the minor factor, a change of the first factor has an indirect effect on the other. In the diagram (Fig. 5), a solid line connecting two indicators signifies a clear causal relationship, indicating that one indicator directly influences the other, as denoted by the arrow (Major effect). On the other hand, a dashed line connecting two factors implies that one factor has a less prominent impact on the other, as pointed out by the arrow. In other words, any change in the first factor results in an indirect effect on the other factor (Minor effect).

Fig. 5
figure 5

Casual graph of hazard indicators

Full size image

To evaluate the interrelationships between indicators of flood vulnerability, a meticulously crafted questionnaire was developed with the aim of collecting individual judgments and perspectives from the participants. They were asked to draw a line with an arrow indicating the effect one indicator has on another, illustrating the directional relationship. For this study, six esteemed experts specializing in the hydraulic sector of the Civil Engineering Department of Democritus University of Thrace were purposively selected to complete the questionaries. The decision to involve only six experts was guided by the specialized nature of our investigation, aiming to tap into the specific knowledge and extensive experience of individuals in this domain. Their valuable insights and expertise were sought to enrich the study and provide a comprehensive understanding of the flood vulnerability for the study area. This approach ensured that the study benefited from the diverse viewpoints of individuals well-versed in the intricacies of the hydraulic sector. The causal graphs generated from the questionnaires are shown in Fig. 6.

Fig. 6
figure 6

Outcomes of the questionnaires: Causal graph of vulnerability indicators

Full size image

3.3 Determination of Weights Using DEMATEL

The weighting of flood hazard and vulnerability indicators is determined through the application of the Decision-Making Trial and Evaluation Laboratory (DEMATEL) method, which is a Multi-Criteria Decision Analysis (MCDA) technique based on causal diagrams.

In decision-making problems with multiple dimensions, indicators are interrelated either directly or indirectly, as stated by Büyüközkan and Güleryüz (2016). The DEMATEL method was originally created in the 1970s to address the challenge of identifying cause-and-effect relationships in complex problems (Gabus and Fontela 1972; Fontela and Gabus 1974). Since then, the method has been extensively modified and applied to multi-criteria decision-making. The main benefit of the DEMATEL method, as per Dou et al. (2014) and Lee et al. (2013), is its capacity to construct intricate causal relationships by means of a direct relation matrix.

The direct-influence matrix A is constructed based on the direct-influence graph. It is a square matrix whose dimensions match the number of objects analyzed. The matrix rows correspond to the first objects in the comparison, with zeros appearing on the main diagonal. The non-zero elements Aij (i ≠ j) indicate the influence of the i-th object on the j-th object. Zero values can appear also outside of the main diagonal in the direct-influence matrix if the relevant indicator does not exert a significant influence on one another.

Matrix A is normalized by dividing each element by the maximum value of the row sum or by the maximum value of the column sum:

$$\widehat{\varvec{A}}=\frac{1}{\underset{i}{\text{max}}\left(\sum\nolimits_{j=1}^{n}{b}_{i,j} \right)}\varvec{A}$$
(3)
$$\widehat{\varvec{A}}=\frac{1}{\underset{j}{\text{max}}\left(\sum\nolimits_{j=1}^{n}{b}_{i,j} \right)}\varvec{A}$$
(4)

From the normalized direct-influence matrix \(\widehat{\varvec{A}}\), the total influence matrix (T) was calculated, which covers direct and indirect influences \(\varDelta \widehat{\varvec{A}}\):

$$\varvec{T}= \widehat{\varvec{A}}+\varDelta \widehat{\varvec{A}}$$
(5)

The total-influence matrix is described by Eq. 6:

$${\varvec{T}}=\widehat{\varvec{A}}{(\varvec{{\rm I}}-\widehat{\varvec{A}})}^{-1}$$
(6)

where I is the n × n unit matrix.

The matrix T provides a way to describe the relationship between the objects under consideration, encompassing both direct and indirect effects. To achieve this, specific measures are utilized known as the importance indicator (t+) and the relation indicator (t−). These measures are calculated based on the row and column sums of matrix T corresponding to the i-th object, employing addition and subtraction operations:

$${t}_{i}^{+}=\sum\limits_{j=1}^{n}{t}_{i,j}+\sum\limits_{j=1}^{n}{t}_{j,i}$$
(7)
$${t}_{i}^{-}=\sum\limits_{j=1}^{n}{t}_{i,j}-\sum\limits_{j=1}^{n}{t}_{j,i}$$
(8)

The term \({t}_{i}^{+ }\)stands for the degree of central role that the factor plays in the system and it is named as “prominence”. The term \({t}_{i}^{-}\) “Relation” shows the net effect that the factor contributes to the system, and it is named as “relation (Si et al. 2018).

A positive relationship indicator value of relation affirms that the criterion is the cause, whereas a negative value demonstrates the criterion’s effect nature. The absolute value of the indicator measures the strength of the criterion’s effect nature.

There are multiple approaches available for estimating the weights. In this study the weights were calculated using the following dependencies (Si et al. 2018, Dalalah et al. 2011):

$${w}_{i}^{}=\frac{{t}_{i}^{-}}{\sum\nolimits_{i=1}^{n}{t}_{i}^{-}}, \ \text{where} \ {t}_{i}^{-}=\left|\sum\nolimits_{j=1}^{n}{t}_{i,j}-\sum\nolimits_{j=1}^{n}{t}_{j,i}\right|$$
(9)
$$w_i^{}=\frac{t_i^+}{\sum_{i=1}^nt_i^+},\;\text{where}\;t_i^+=\sum\nolimits_{j=1}^nt_{i,j}+\sum\nolimits_{j=1}^nt_{j,i}$$
(10)
$${w}_{i}= \frac{{\omega }_{i}}{\sum\nolimits_{i=1}^{n}{\omega }_{i}}, \ \text{where} \ {\omega }_{i}=({({{t}_{i}^{+})}^{2}+{{(t}_{i}^{-})}^{2})}^{1/2}$$
(11)

When Eq. (9) is applied, the emphasis is given to the prominence, that is, in the connectivity. In the case when Eq. (10) is used, the emphasis is given to the relation, that is on causality. In the case when Eq. (11) is used, a more balanced aggregation between prominence and relation is achieved. More specifically, Εq. (11) shows the length of the vector starting from the origin to each criterion (Dalalah et al. 2011).

The causal graph of Fig. 5 illustrates the causal interactions among flood hazard indicators, generating a matrix detailed in Table 3. In this table, values of 0, 0.5, and 1 signify “No effect,” “Minor effect,” and “Major effect,” respectively. Additionally, the direct influence graphs derived from the questionnaires, depicted by the causal graph of Fig. 6 for flood vulnerability indicators, incorporate participant-noted effects as outlined in Table 4. Here, values of 1, 2, 3, and 4 correspond to the number of participants mentioning the respective effect.

Table 3 The direct-influence matrix for flood hazard
Full size table
Table 4 The direct-influence matrix for flood vulnerability
Full size table

The weights for the flood hazard indicators were determined using Eq. (10) since they better described the ‘causality relation”, where the distinction between cause and effects is more reliable. In many environmental problems it is customary to use qualitative variables and modern techniques to deal with such as the graph theory, fuzzy sets etc., instead of ordinary mathematics. The distinction between cause and effect is more difficult in the case of complex problems as the vulnerability assessment. Therefore, Eq. (11) is preferred due to its incorporation of both prominence and dominance concepts, in contrast to an exclusive emphasis on causality. Tables 5 and 6 include the normalized values of the criteria of Tables 3 and 4, and eventually the corresponding weights w produced by the equation of each indicator. In the current research, the DEMATEL method was run in the MATLAB R2020b.

Table 5 Normalized criteria for flood hazard
Full size table
Table 6 Normalized criteria for flood vulnerability
Full size table

3.4 Mapping of FHI, FVI and FRI

The numerical expression of risk is given in terms of its inherent elements of hazard and vulnerability. Therefore, it is evident that formulation of the risk map is the end product preceded by the determinations of the hazard and vulnerability maps. These maps are, in fact, generated based on the indicator’s weight obtained through DEMATEL and produced using ArcMap, utilizing the raster calculator and the corresponding index. In this context, the Flood Hazard Index is defined as:

$$\begin{array}{l}Flood \ Hazard \ Index\, \left(FHI\right)=0.243 \ EL+0.231 \ FA+0.182 \ LU+0.128 \ DFTR+0.087 \ SL+0.077 \ G+ \\ 0.052 \ RI\end{array}$$
(12)

where EL, FA, LU, DFTR, SL, G, RI indicate elevation, flow accumulation, land use, distance from the river, slope, geology and rainfall intensity.

The Flood Vulnerability Index is calculated by:

$$\begin{array}{l}Flood \ Vulnerability \ Index\, \left(FVI\right)=0.155 \ PD+0.120 \ LU+0.103 \ DA+0.098 \ EWS+ \\ 0.097 \ DTCF+0.096 \ DTIA+0.090 \ DTRA+0.064 \ DTCA+0.053 \ NA+0.048 \ S+0.044 \ CHM+ \\ 0.315 \ DFR\end{array}$$
(13)

where PD, LU, DA, EWS, DTCF, DTIA, DTRA, DTCA, NA, S, CHM, DFR refer to population density, land use, deprived area, early warning system, distance to critical facilitates, distance to industrial areas, distance to cultivated areas, natura area, sanitation, cultural heritage monuments, distance from roads.

Eventually, flood hazard and flood vulnerability maps are created, defining fives classes from very low to very high. This classification is achieved through application of Equal Interval (EI), Geometrical Interval (GI), Quantile, and Jenks’ Natural Break methodologies.

Upon the completion of the flood hazard and vulnerability mapping, the subsequent and final stage entails the production of the Flood Risk Maps. This involves the utilization of Eq. (14) (Chakraborty and Mukhopadhyay 2019; Danumah et al. 2016; Das 2020; Ghosh and Kar 2018). The Flood Risk Index is computed based on the spatial interaction between hazard and vulnerability, leading to the creation of corresponding maps:

$$Flood \ Risk \ Index\, \left(FHI\right)=FHI \times FVI$$
(14)

These resultant Flood Risk Maps intricately categorize the risk into five classes—very low, low, medium, high, and very high—employing the same classification methods utilized in the initial hazard and vulnerability mapping phase: Equal Interval (EI), Geometrical Interval (GI), Quantile, and Jenks’ Natural Break.

4 Results

In this study, we integrated GIS with graph theory, employing DEMATEL technique. The comprehensive flood risk assessment conducted for the Kosynthos River Basin has yielded outcomes in the form of flood hazard maps, flood vulnerability maps and flood risk maps, as illustrated in Figs. 7, 8, and 9, respectively. These maps utilize a grid raster format, classifying flood intensity into five distinct levels, ranging from very low to very high. Four classification techniques namely Equal Interval (EI), Geometrical Interval (GI), Quantile, and Jenks’ Natural Break were employed in order to reclass the final result.

Fig. 7
figure 7

Flood Hazard maps: FHI index using (a) Equal Interval (EI), (b) Geometrical Interval (GI), (c) Quantile, and (d) Jenks’ Natural Break classification techniques

Full size image
Fig. 8
figure 8

Flood Vulnerability maps: FVI index using (a) Equal Interval (EI), (b) Geometrical Interval (GI), (c) Quantile, and (d) Jenks’ Natural Break classification techniques

Full size image
Fig. 9
figure 9

Flood Risk maps: FRI index using (a) Equal Interval (EI), (b) Geometrical Interval (GI), (c) Quantile, and (d) Jenks’ Natural Break classification techniques

Full size image

The FHI considered multiple indicators, with the most significant influences being elevation (weight = 0.2430), flow accumulation (weight = 0.2312), and land use (weight = 0.1820). Meanwhile, the FVI prioritized key indicators such as population density (weight = 0.1518), land use (weight = 0.1182), and distance to critical facilities (weight = 0.1023) when assessing vulnerability to flood impacts.

The hazard level of disaster-causing indicators in the research area exhibits a decreasing distribution pattern from south to north, with high-risk areas primarily concentrated near the river and in lowland regions. The vulnerability level of disaster-prone areas is generally low, while very high-vulnerability zones are concentrated in the municipal district of Xanthi and in mountain villages. These vulnerable zones coincide with densely populated regions and residential land use. The areas with high and medium vulnerability are characterized by sparse populations with cultivations.

By incorporating the Flood Hazard Index (FHI) and the Flood Vulnerability Index (FVI), the Flood Risk Maps in Fig. 9 provide a detailed representation of flood risk across the entire basin based on the used classification techniques. The amalgamation of the selected indicators within the grid raster framework offers a comprehensive understanding of flood risk in the Kosynthos River Basin, empowering decision-makers with valuable insights to devise effective flood management strategies and enhance the basin’s resilience against future flood events.

5 Validation

5.1 Historical Flooded Data

The primary objective of flood risk assessment studies is to gather information about areas or locations which are at risk to future flooding. It is crucial to evaluate the accuracy and reliability of the models used in such studies, particularly when dealing with unknown future flood events (Rahmati et al. 2016). However, the assessment process presented substantial challenges in regions with insufficient data, as evident in the current scenario. The lack of detailed flood depth and impact data at the micro level posed difficulties in making precise numerical judgments. To address this issue, we bolstered the credibility of our study results by validating them using a database compiled based on data from the Ministry of Environment, Energy, and Climate Change of Greece (“Ministry of Environment and Energy (n.d.)”), which documented reported flood-prone areas. In this specific case, the ministry identified eight flood locations, which were then transformed into georectified points and analyzed within the ArcGIS environment.

Significantly, these flood locations included instances of damages for which compensation was provided by the state. It is crucial to note that these eight flood events are widely scattered on the map, with two situated in the mountainous part of the watershed near the village of Myki and the remainder located in the plain part, spanning the city of Xanthi, the area of Kimmeria, and near the village of Amaxades. This additional information underscores the gravity of these locations, as these flood points constitute hazards with serious implications affecting the local population, infrastructure, and the economic activities of the region.

The dispersed nature of these events amplifies their significance, making them particularly suitable for assessment due to the associated risks of flooding. This approach serves a dual purpose; aiding not only in the overall risk assessment but also in identifying the most suitable classification technique for our study. The profound impact of these flood points on the vulnerability of the area emphasizes their relevance and suitability for validation with flood risk maps, providing valuable insights into the potential consequences on both the community and the local environment.

It is evident that the classification methods yield varying distributions of vulnerability, hazard, and overall risk across different categories. The Equal Interval method tends to categorize a significant portion of areas into the “Very low” and “Low” vulnerability, hazard, and risk classifications. This tendency raises concerns about its effectiveness in capturing subtle distinctions in flood risk. Notably, when considering the number of floods alongside the risk areas, the method identifies only one point in the high-risk zone, whereas most actual flood events (5 out of 8) occurred in the low-risk zone. This discrepancy underscores the importance of critically evaluating the Equal Interval method’s reliability in accurately reflecting historical flood occurrences.

Conversely, the Jenks’ Natural Break method exhibits a more equitable distribution across vulnerability, hazard, and risk categories, adeptly capturing distinctions in risk levels. Remarkably, the method accurately identified all eight flood spots within the very high-risk zone. A similar outcome was observed with the Geometrical Interval technique; however, the high-risk category encompasses 16.13%, nearly twice that of the Jenks’ Natural Break method, which stands at 8.96%. This marked difference in the efficiency of risk allocation underscores the effectiveness of the Jenks’ Natural Break method in discerning and categorizing flood risk levels more accurately. Notably, the method’s reliability is underscored by its utilization in past research, including studies by Kazakis et al. (2015), Huan et al. (2012), as well as Vojtek and Vojteková (2019), emphasizing its established track record in flood risk analysis. Additionally, regarding the Quantile method, it is notable that its risk categories display a distinct pattern, with a notable concentration of flood events in the “High” and “Very high” categories. This distribution suggests the potential of the Quantile method to capture specific risk extremes, warranting further exploration of its utility in risk assessment.

5.2 Sensitivity Analysis

The integration of the Flood Hazard Index (FHI) and Flood Vulnerability (FV) into a sensitivity analysis process within this study assesses the impact of each criterion on the methodology, enhancing our understanding of the individual roles of parameters in flood risk assessment. The application of sensitivity analysis serves to unveil the subjective significance of diverse indicators, shedding light on the intricate interplay between weighting values assigned to each criterion. This process also sets the stage for an evaluation of the Jenks’ Natural Break method in the following.

Originating from the work of Napolitano and Fabbri (1996), the single-parameter analysis technique has found widespread utility, extending beyond its initial application in estimating aquifers’ vulnerability to pollution. Notably, this methodology has been employed in various studies, including those conducted by Pacheco et al. (2015) and Kazakis et al. (2015) underscoring its relevance in the context of the present investigation. A parallel single-parameter sensitivity analysis, mirroring the approach outlined by Napolitano and Fabbri (1996), has been incorporated to assess aquifer vulnerability to pollution within the framework of this study.

In the sensitivity analysis process, the conventional, arbitrary values of the indices employed by DEMATEL undergo substitution with derivative indices known as “effective weights.” These weights are derived through Eq. (15), as extensively discussed by Napolitano and Fabbri (1996), and are employed to calculate the revised Flood Hazard Index and Flood Vulnerability Index during the Sensitivity analysis (FHIS and FVIS, respectively). These effective weights, along with their corresponding values, are depicted in Tables 7 and 8 for reference and clarity.

$$W=\frac{{P}_{r}\times {P}_{w}}{V}\cdot 100$$
(15)

where W, Pr, Pw and V refer to the effective weight of each indicator, the indicator’s rating, the indicator’s weight, and the aggregated value of the applied index.

Table 7 Statistics of the effective weights-sensitivity analysis for flood hazard
Full size table
Table 8 Statistics of the effective weights-sensitivity analysis for flood vulnerability
Full size table

The FHIS and FVIS indices, while evaluating the same indicators and class ratings as the FHI and FVI indices, employ different weights. Specifically, they utilize the average effective weight obtained from the sensitivity analysis, transformed to a scale of 10. Across a spectrum of indicator values, FHIS and FVIS are systematically estimated, and their comparison with the FHI and FVI underscores the dependence (sensitivity) of Flood Risk (FRIS) on various indicators within the proposed methodology.

The FHIS index map, FVIS index map, and FRIS index map, depicted in Fig. 10, respectively, undergo a visual examination in conjunction with Fig. 9 FRI index using Jenks Natural Break classification technique. This visual comparison reveals a notable alignment, suggesting that the sensitivity analysis broadly corresponds with the outcomes of the Flood Hazard Index (FHI), Flood Vulnerability Index (FVI), and Flood Risk Index (FRI). Further insights are provided in Table 9, where comparisons between FHI-FHIS, FVI-FVIS, and FRI-FRIS are illustrated. The results indicate a general underestimation of very high flood hazard, vulnerability, and risk areas by FHI, FVI, and FRI. This is also supported by the recurrence of flood events in the very high-risk area.

Fig. 10
figure 10

Flood Hazard map: (a) FHIS Index, (b) Flood Vulnerability map: FVIS Index, and (c) Flood Risk map: FRIS Index

Full size image
Table 9 Classes of flood hazard, flood vulnerability and flood hazard
Full size table

Following the sensitivity analysis, a notable revelation emerges: the proportion of areas classified as having a very high flood hazard has surged to 22.03%, surpassing the initial coverage of 13.48% of the total area. Conversely, the areas designated as high flood hazard have experienced a decline to 21.68%, deviating from the initial percentage of 30.32%. This substantial shift underscores the dynamic nature of hazard distribution and underscores the role of sensitivity analysis in refining the precision of hazard assessments.

Giving attention to the areas categorized as very low, low, and medium, the present percentages of 14.36%, 21.8%, and 20.04%, respectively, exhibit marginal differences from the initial percentages of 13.13%, 18.75%, and 24.41%. The minimal variance in these categories suggests a stability in the risk assessment for regions with lower to medium flood hazards. This consistency in the less vulnerable areas, combined with the notable adjustments in high-risk zones, emphasizes the efficacy of the sensitivity analysis in discerning and accurately portraying the evolving landscape of flood risk.

In conclusion, validating the weights for the Flood Hazard Index (FHI) and Flood Vulnerability Index (FVI) has enhanced the reliability of the flood risk assessment method. This validation leads to recommending the adoption of the FHIS index and the FVIS index, calculated from Eqs. (16) and (17), respectively, for assessing flood risk areas. These refined indices, backed by validated weights, provide a more accurate understanding of flood risk, contributing to improved strategies for managing flood risks.

$$FHIS =0.35 \ EL+0.10 \ FA+0.15 \ LU+0.11 \ DFTR+0.12 \ SL+0.11 \ G+0.06 \ RI$$
(16)
$$\begin{array}{l}FVIS=0.19 \ PD+0.16 \ LU+0.05 \ DA+0.24 \ EWS+0.05 \ DTCF+0.05 \ DTIA+0.06 \ DTRA+0.07 \ DTCA+ \\ 0.03 \ NA+0.03 \ S+0.02 \ CHM+0.05 \ DFR\end{array}$$
(17)

5.3 Comparison with Other Methodologies

In addition, to enrich the depth of our research, we conducted a comparative analysis with established methodologies in the field, notably drawing upon the works of Kazakis et al. (2015) and Kourgialas and Karatzas (2011). While both studies focused on flood hazard assessment and employed similar hydrogeological and geomorphological variables consistent with our research framework, it is noteworthy that Kourgialas and Karatzas (2011) differentiated their approach by utilizing one parameter less, specifically the drainage distance, in the Koiliaris River basin, Greece. Kazakis et al. (2015), on the other hand, employed the Analytical Hierarchical Process (AHP) to develop a Flood Hazard Index (FHI) and flood maps in a flood-prone area in north-eastern Greece. Additionally, our study area shares similar hydrogeological conditions with these comparative studies, providing a valuable basis for meaningful comparisons. By critically assessing and comparing our methodology with these studies, we aimed to enhance the rigor and relevance of our research, thereby contributing insights to the field of flood hazard assessment.

In the context of hazard assessment, integration of weights from the methodologies of Kazakis et al. (2015) and Kourgialas and Karatzas (2011), as detailed in Table 10, served to highlight their findings and refine the overall approach. Notably, elevation, distance from the river, and slope were identified by Kazakis et al. (2015) as primary influencing parameters in their studied region—a conclusion also supported by Kourgialas and Karatzas (2011), who specifically highlighted elevation as the most significant parameter. The approach employed affirmed elevation as the paramount factor, reinforcing its role in hazard assessment. This consistent trend underscores the robustness of the findings and emphasizes the enduring importance of elevation in comprehending and mitigating hazards in similar contexts. The utilization of these weights led to refinement in the methodology for generating hazard maps and, subsequently, risk maps, which were validated against historical flood point locations. These maps are depicted in Fig. 11.

Table 10 Weights of flood hazard indicators
Full size table
Fig. 11
figure 11

Flood Risk Maps: FRI Index produced using weights by (a) Kazakis et al. (2015), and (b) Kourgialas and Karatzas (2011)

Full size image

The flood risk map generated using Kazakis et al. (2015) weighted bases pinpointed six flood points in the area categorized in the very high risk and two in the high risk zone. Similarly, the corresponding map from Kourgialas and Karatzas (2011) identified seven and six flood points in these respective risk areas. In contrast to the map if Fig. 11A, where 13.75% of the area was classified as very high risk, both alternative methodologies provide lower estimates, with Kazakis et al. (2015) at 8.96% and Kourgialas and Karatzas (2011) at 3.99%. It is worth noting that in our study, all identified flood locations were categorized as very high risk. Notably, neither Kazakis et al. (2015) nor Kourgialas and Karatzas (2011) methods classified the one flood event in the upland area of the catchment as of very high risk; instead, both categorized them as high risk. These findings emphasize the potential applicability of these methodologies in areas with similar hydro-morphological characteristics, underscoring the significance of contextual considerations in flood risk assessments.

6 Conclusions

The scientific community widely agrees that it is impossible to entirely prevent highly destructive natural disasters such as floods. Nevertheless, the implementation of effective flood risk modeling plays a crucial role in mitigating a significant portion of the human casualties and socio-economic consequences experienced in present times (Khosravi et al. 2019). Consequently, flood risk modeling serves as a proactive measure for managing flood risks (Ali et al. 2019).

The proposed framework serves a dual purpose by not only addressing data gaps but also equipping decision-makers with tools to design and implement sustainable flood risk management strategies. This research has twofold objectives. First, it demonstrates the utility of the DEMATEL technique in assessing flood risk in basins by exploiting the two proposed causality diagrams. The first causal diagram is critical for assessing the flood hazard because of the absence of data. The second causality diagram offers a multidimensional consideration where the interactions among the criteria are taken into account. Especially the causality diagram which refers to flood vulnerability can be adaptive to local (or national) conditions, keeping in mind that the vulnerability is an ill-defined concept. In addition, the causality diagram is user-friendly regarding the participation of either the experts or the stakeholders during this process.

Leveraging the DEMATEL method for the interpretation of these diagrams, this study emphasizes its superiority over the AHP, given its ability to account for the interdependency among indicators, as highlighted in previous studies. Integrating hazard and vulnerability indicators into GIS software, the study validates these against historical flood events, culminating in the development of a comprehensive flood risk map. In addition, the use of GIS enables us to exploit quantitative data, and furthermore, to provide the location of the areas with significant risk.

The proposed methodology is characterized by its adaptability, understandable either to stakeholders or experts and rapidity in generating flood risk maps for areas where quantitative methods based on numerical modeling are unfeasible due to missing, invalid, or corrupted data. Nevertheless, if reliable data is available, it is ideal to compare the flood risk map with the recorded information.

To enhance the validation and effectiveness of this approach, future research should focus on testing it in basins where sufficient discharge measurements are available and where the development of a hydrodynamic simulation is possible.