Abstract
This paper describes the relation of noble gas temperature (NGT) and mean annual air (MAAT) and soil (MAST) temperature through studying water samples and meteorological data from six Hungarian regions. Alluvial plains, hilly and mountainous regions were studied to investigate the effects of geomorphological, hydrogeological and micro-climatic conditions. Water samples were collected from springs and wells fed from different aquifers. Comparing NGTs derived from these water samples with the MAAT and MAST values of the given region, we identified differences between the sampled areas. In case of the Geresd Hills, Mezőföld, Danube-Tisza Interfluves and Nyírség, the NGTs (13.0 ± 0.9 °C, 12.1 ± 1.1 °C, 12.1 ± 0.6 °C and 12.7 ± 1.6 °C, respectively) generally reflect MAST, however in karstic Bükk Mts. (6.8 ± 0.6 °C) and Mecsek Mts. (10.7 ± 1.9 °C) they are closer to MAAT. Consequently, it can be concluded that the direct relationship between noble gas temperature and mean annual air temperature is not always as well-defined as it is often assumed. It is shown that MAAT and MAST should be distinguished, especially when using NGT as a paleoclimate proxy.
Highlights
• In case of the studied regions NGT does not always reflect MAAT of a given area.
• Differences in the relation of NGT and MAAT or MAST are due to geology and climate.
• During climatic reconstruction using NGT, MAAT and MAST should be distinguished.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As a result of research developments over the past three decades, the measurement of concentrations of noble gases from a groundwater sample can provide a realistic insight into the predominant paleoclimatic conditions when the water infiltrated the subsurface (e.g., Heaton and Vogel 1981; Stute and Schlosser 1993; Ballentine and Hall 1999; Aeschbach-Hertig et al. 1999; Varsányi et al. 2011; Saadi et al. 2017; Túri et al. 2020).
The theory of using dissolved noble gases in groundwater as proxies for paleotemperature is based on the temperature dependence of gas solubility in water and the chemical inertness of noble gases (Stute and Schlosser 1993). According to Henry’s Law, the solubility decreases with increasing temperature (Kipfer et al. 2002). On entering the aqueous phase, an equilibration process occurs within the vadose zone between the percolating water and the local soil atmosphere (Klump et al. 2007).
Despite the importance and advantages of the method, there are several influencing factors that cannot be excluded in order to understand recharge conditions and/or the interpretation of noble gas recharge temperatures. This approach is based on the original observations of Mazor (1972), who showed that evaluation of noble gas temperature (NGT) could only be reliable if the concentrations of noble gases remained unchanged in the system. He proved that as the ambient temperature changes, re-equilibration of the water with gases could occur resulting in changes in concentration of dissolved noble gases. The concept was further investigated by Stute and Schlosser (1993), who explored the principles of the theory by studying influencing factors like ground temperature, depth of the water table, composition of ground air, amount of entrapped air bubbles in the groundwater, seasonal variations of the recharge on the dissolution mechanism of noble gases and also the change in dissolved gas concentrations due to transient flow in the aquifer from recharge to the zone of discharge. They found that dispersion processes (within an aquifer or between aquifers), the presence of excess air (discussed later) and also partial degassing can limit the reliability of the method.
Factors influencing noble gas temperature are still the subject of many studies. According to Hall et al. (2012) on a daily, weekly, monthly scale sudden meteorological events (e.g., sudden snowmelt) can have significant effects on NGT, and they suggest averaging conditions over longer periods, possibly several years. However, it is very common to use NGT for estimating mean annual air temperature (MAAT) on a one-year-scale (e.g., Hall et al. 2005; Castro et al. 2007; Mann et al. 2009).
The concept that mean annual air temperature can be derived from the interpretation of noble gas concentrations is derived from the assumption that the mean annual soil temperature (MAST) should be equal to the MAAT. Below 10 m, soil temperature has a negligible oscillation with seasonality of less than 0.2 °C. Stute and Schlosser (1993) simulated the depth dependency of the annual variation of monthly averaged ground temperature profile for a typical soil, assuming 10 °C for average surface ground temperature and also amplitude of the annual temperature in the surface. They concluded that as depth increases, the amount of oscillation decreases and is less affected by the variation of air temperature. Consequently, calculated noble gas concentration values can provide information about the MAAT as climatic factor at the time of recharge (Stute and Schlosser 1993). However, according to Cey (2009), the reliability of the applied method can be questioned in those cases when there are differences between the value of the MAST and MAAT. This measurement bias may be caused by factors influencing heat transport in the ground, such as changes in water table depth, recharge, precipitation and the thickness of snow deposited on the surface or vegetation cover. Cey (2009) conducted numerical modelling for the case of sand and loam as representative of typical soil materials, to investigate to what extent certain factors may influence the ground temperature. While increased precipitation resulted in cooling of soil due to induced evaporation, in contrast, a deeper water table could be responsible for warmer water table temperature that are higher than the mean annual air temperature. As Cey (2009) found a change in air temperature has a greater influence on the difference between air and water table temperature, as mean annual air temperature increased, the difference decreased, while in the opposite case, as air temperature decreased, a higher difference between the two values could be measured due to the accumulation of snow pack on the surface. The insulating effect of snow cover was also emphasized by Mann et al. (2009) who found significant differences in annual ground surface and surface air temperature by studying long-term Holocene climate trends in the Northern Hemisphere.
According to Beyerle et al. (2003), NGTs of young samples (<1 kyr BP) rather reflect soil temperature and both are higher than MAAT. Based on previous studies (Smith et al. 1964; Stute and Sonntag 1992; Stute and Schlosser 1993), the role of vegetation and humidity is emphasized in evaluating the relationship of NGT and soil/air temperatures. NGT tends to be about 1 °C higher than MAAT in temperate climate, whereas in arid regions this difference can be larger due to the lack of rich vegetation (Smith et al. 1964). Differences can be observed even within a temperate zone where NGTs of groundwater sampled from a forest was 2 °C cooler than the ones from fields (Stute and Sonntag 1992). Findings of Beyerle et al. (2003) and Cey et al. (2009) suggest the possibility that the relationship of NGT and MAAT may have changed in the past as climate (and thus soil cover) changed. Aeschbach-Hertig and Solomon (2013) thoroughly sum up recent knowledge about the relationship of NGT with soil and air temperature stating similar correspondences and highlighting the importance of appropriate noble gas model.
Also, Klump et al. (2006) stated that NGT and MAAT (or MAST) do not need to be equal. They emphasized the role of seasonal variation of the excess air component and the thickness of the unsaturated zone. In their research, NGTs were similar to the in situ soil temperatures at the date of sampling. The soil temperature, however, showed a seasonal variation, therefore, NGT values significantly differed from MAAT and MAST. Regarding the thickness of unsaturated zone, if it exceeds several meters, the seasonal variation of soil temperature at the water table is less, while in case of a shallow unsaturated zone, the difference can amount to several degrees.
The presence of excess air can be a limiting factor for determining NGT. Entrapped air was discovered when the amount of concentration values of noble gases exceeded expected values due to equilibration of infiltrating water with atmospheric air. This excess amount of gas in groundwater is known as excess air (Herzberg and Mazor 1979; Andrews and Lee 1979; Heaton and Vogel 1981). Its origin and composition are subjects of much study since it may supply information about the conditions of infiltration. Some have suggested that this excess air may itself be a valuable paleoclimate proxy (Aeschbach-Hertig et al. 2002; Castro et al. 2007). This topic is of special interest since the presence of excess air may result in an inadequate interpretation of physical parameters.
Up to now, several models have been developed to define the phenomenon of excess air and to help quantify its amount in the water and the partitioning of soil gases in the unsaturated zone (see a review by Aeschbach-Hertig and Solomon 2013). The first model for fractionated excess air was the partial re-equilibration (PR) model by Stute et al. (1995) presuming partial loss of excess air through diffusion-controlled gas exchange. The model assumes that in case of water level rise, the entrapped soil air bubbles are completely dissolved (without any fractionation), and then, the dissolved gases are partially diffusing out from the water. Contrary to this diffusion driven fractionation effect, Aeschbach-Hertig et al. (2000) proposed the “closed-system equilibration” (CE) model for the formation of excess air. The CE-model suggests that the entrapped air is not completely dissolved, resulting in fractionation of excess air. The basic assumption of this model is that solubility equilibrium is attained in a closed system of initially air-saturated water and entrapped air under a constant hydrostatic pressure.
Systematic discrepancy between NGTs and air as well as soil temperatures found in southern Michigan by Ma et al. (2004) motivated Hall et al. (2005) to suggest an explanation for the bias. They proposed the “oxygen depletion” (OD) model arguing that biological processes depleting O2 without an equivalent production or preferential removal by dissolution of CO2 may lead to a pressure deficit that is compensated by rising the partial pressure of the remaining gases, including noble gases. This results in apparently lower NGTs. Several studies investigated the reliability of the different models (Sun at al. 2010; Hall et al. 2000; Cey et al. 2009; Aeschbach-Hertig et al. 2012) and all of them agree that consideration of benefits and disadvantages of noble gas models is crucial before applying them.
In our case dissolved oxygen concentrations were 2 to 8 mg L−1 in each water sample independently of the study area, which indicates that the oxygen mixing ratio in the soil gas is close to atmospheric. Freundt et al. (2013) investigated the conditions under which the oxygen depletion mechanism occurs and whether it has significant effect on the noble gas composition of soil air. They found that soil respiration indeed has a significant influence on the noble gas composition. However, they noted that the observed maximum in noble gas enrichments were not sufficiently high to support such strong effects of oxygen depletion, suggesting that previous studies may have overestimated its magnitude. In this study, we assumed that oxygen depletion does not play a significant role, thus only the CE-model was applied to the calculation and interpretation of noble gas concentration data.
Due to the biases found between mean annual air and ground temperatures, which decreases the accuracy of the results of temperatures obtained from noble gas studies, the aim of this study is to compare the temperatures calculated from the measured noble gas concentrations to actual mean annual air and soil temperatures at the selected sampling sites.
2 Materials and Methods
2.1 Description of the Sampling Areas
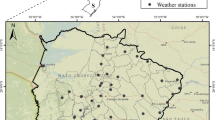
Water samples have been collected from six micro-regions of Hungary representing different hydrogeological and climatic conditions, in order to study the influence of these factors on the relation of NGT and mean annual temperature values. Hungary has a quite uniform continental climate, however, meso-scale climatic heterogeneity can be observed. To describe the sampling areas, we refer to the climate classification system of Feddema adapted by Ács et al. (2015). Describing the climate of an area the method of Köppen (1918) is worldwide accepted and applied. However, it cannot reflect the climatic heterogeneity at a meso-scale, e.g., in case of the regions of Hungary sampled in our study. Feddema’s classification (Feddema 2005) uses four factors to give information about thermal and moisture conditions and seasonal variability. These are potential evapotranspiration, moisture index, climatic variable possessing seasonality and magnitude of seasonality. Thus, a more detailed system of 16 classes was generated that can represent meso-climatic differences. For more details see Ács et al. (2015).
Samples have been collected from shallow groundwater wells located in the Great Hungarian Plain (Mezőföld, Danube-Tisza Interfluves, Nyírség) and from springs of the Hungarian mountain range and hilly regions (Geresd Hills, Bükk Mountains, Mecsek Mountains). The location of the sampled areas can be seen in Fig. 1, while coordinates of sampling sites are summarized in Supplementary Material (SM), Table SM1.
2.1.1 Mecsek Mountains
The Mecsek Mountains are in an area where karstic features formed in the limestone are represented by caves and dolines in the karst plateaus. Karstic built-up can make infiltration of precipitation relatively fast but it can be reduced in case of covered karst such as Mecsek Mts. Its climate is moderately cool and moist with relatively high temperature seasonality. Samples were collected from the northern part of the mountains where mean annual temperature is 10-11 °C and annual precipitation is over 700 mm.
Samples were collected from different recharge elevations in the Mecsek mountains. The elevations of the infiltrating precipitation water discharging in the sampled springs used for the calculation are estimated for 420 and 430 m aBSl (above Baltic Sea level) in case of the Csurgó Spring, 480 and 500 m aBSl in case of Anyák- and Melegmányi Spring, Mariska- and Kánya Spring and probably, Pásztor Spring has the highest recharge elevation with 550 m aBSl. The sampled springs are fed by karst aquifers with varying discharge rates. For instance, while Kánya Spring produces a significant amount of water, between 20 and 500 L/min, in contrast, the discharge rate of the Melegmányi Spring is quite low and changes between 1 and 6 L/min.
No information from the isotopic composition of the spring waters regarding seasonality was obtained because waters seep through several flow paths toward the karst aquifer, resulting in different recharge times and averaging of seasonal characteristics. The ages of these waters were estimated to be 0-4 years using the 3 H/3He dating method.
2.1.2 Geresd Hills
The core of the hills is built up from crystalline rocks but due to intensive erosional processes only some remnant outcrops can be observed on the surface surrounded by clastic deposits. Loess sediments were deposited in thick layers between the valleys during glacial periods creating wide interfluves separating them and determining infiltrating processes.
The climate of Geresd Hills is moderately cool and moderately moist with close to extreme temperature seasonality. The mean annual temperature of the area is 10-11 °C while the annual precipitation varies from 650 to 700 mm. A significant amount of this precipitation infiltrates through the mentioned loose loessial sedimentary cover supplying groundwater aquifers.
The elevations of the infiltrating rain water discharging in the sampled springs used for the calculation (Anyák, Anikó, Henrik, Véménd) are estimated between 240 and 270 m aBSl. These sampled springs are fed from confined aquifers, which gives higher recharge times than in the case of a karst aquifer and can vary between 5 and 30 years.
2.1.3 Mezőföld
Mezőföld lies on the alluvial plain of the Danube with elevation above Baltic Sea level varies between 100 and 213 m. The region is considered to be a sedimentary basin that is composed of sedimentary rocks settled in various periods. In the Pleistocene, accumulation of loess and wind-blown sand formations took place on the surface above the alluvial sediments.
The area where the sampled shallow groundwater wells have been installed is covered by humic sandy soils and alluvial meadow soils generated on the fluvial sediments, which enable good infiltrating conditions and good storage capacity for the water. The wells have been installed near Paks city in the micro-region of Southern Mezőföld at depth of 16.0-20.6 m with elevation of 95.3 and 97.0 m aBSl. Ages of the water were estimated to 0-30 years.
Moderately cool, dry climate with close to extreme temperature seasonality dominates the region. Mean annual average temperature of the southern part of the region (where the sampling wells were installed) is around 11-12 °C and the annual precipitation is 560-580 mm.
2.1.4 Danube-Tisza Interfluves
The area is part of the Great Hungarian Plain, considered an alluvial plain, which is covered by thick blown sand deposits originating from the sediments of Danube carried and deposited by the wind and periglacial loess formations in thick layers (30-120 m). The area is a flatland with sand dunes at elevation of 100-130 m aBSl. Sandy deposits result in a porous medium with ideal conditions for infiltration of precipitation. Blown sand deposits with significant permeability property also cover the area where the sampled shallow groundwater wells have been installed, thus there are very good infiltrating conditions.
The climate of the region is moderately cool, dry with extreme temperature seasonality, which is confirmed by the mean annual air temperature values of 11-12 °C and the mean annual precipitation of 520-570 mm.
Well nests have been installed on two sites with four wells on both sites. Sampling depths have been 7.93-23.14 m in Méntelek and 7.30-22.71 m in Fischerbócsa.
2.1.5 Bükk Mountains
Limestone formations of the Bükk Mts. are greatly affected by karstification, with well-developed karst aquifers, huge cave systems and springs with considerable yield. Infiltration is intense, in large joints flow velocity of greater extent while in less porous matrix slow diffuse flow dominates.
The climate of the region is cool, moderately dry with very high temperature seasonality. The mean annual air temperature varies between 6.5 and 7 °C and the mean annual precipitation can reach up to 800 mm in the highlands. The air temperature values increase toward the southernmost parts of the region, up to 9 °C, and the precipitation values drop to 600 mm. The sampled spring is situated in the southern part of the mountains where the average annual temperature is around 8-9 °C.
Elevation of the sampled part of the middle mountain range of the Bükk Mountains varies between 185 and 703 m aBSl. Recharge area of Ódor spring is very narrow and situated at the elevation of 600 m.
2.1.6 Nyírség
Similarly to the Danube-Tisza Ridge, this is an alluvial plain with thick blown sand coverage characterized by various features of sand dunes and deflation pits due to wind. The blown sand with glacial origin deposited in between 1 and 25 m thickness near the surface, while alluvial sand was deposited in thickness of 1-5 m during interglacial periods in the Holocene.
Insignificant amounts of shallow groundwater can be found usually in 2-4 m depth below surface, while groundwater bodies stored in confined aquifers in depth slightly under 100 m are abundant in the region. Recharge of the sampled shallow groundwater wells is rapid due to the blown sand deposits also covering the study area providing very good infiltration conditions.
The climate of the region is cool, moderately dry with close to extreme temperature seasonality, and the mean annual temperature is about 11-12 °C. This is reflected in the water regime with sparse runoffs having low or no discharge in the driest period, causing a negative water balance. Mean annual precipitation is 550-590 mm, with higher values on the eastern and the lowest values in northwestern part of the region.
Sampled wells near Nyíradony are shallow groundwater wells at an elevation of 151.5 m aBSl with sampling depth of 7.70-14.50 m.
2.2 Sampling and Measurement
Water samples for noble gas analysis were collected in copper tubes clamped at both ends and analyzed for Ne, Ar, Kr and Xe isotopes. Helium concentration and 3He/4He isotope ratios were also determined to calculate 3 H/3He ages. These ages confirm the low residence times of the water. Some of the results have already been published (Szűcs et al. 2015; Palcsu et al. 2017). Processing of samples were carried out by noble gas mass spectrometry at the Isotope Climatology and Environmental Research (ICER) Centre, Institute for Nuclear Research, Hungarian Academy of Sciences, Debrecen, Hungary. Samples were undertaken to an extraction method using a sample preparation system to prepare the gases for the concentration measurement carried out by VG 5400 noble gas mass-spectrometer (neon to xenon) (Papp et al. 2012) and a Helix SFT (helium isotopes).
For the calculation of NGT only Ne, Ar, Kr, Xe have been used. He has been excluded from calculations since the concentrations have been slightly elevated due to some terrigenic component. In most cases, the solubility of equilibrium has been achieved confirmed by 20Ne/22Ne ratios of 9.78 ± 0.02.
There are different pieces of software or codes available to calculate NGTs using inverse modelling: Noble 90 (a MATLAB code) (Peeters et al. 2002), Noblebook (an Excel workbook) (Aeschbach-Hertig et al. 2008), and PANGA (an open-source software written in C++) (Jung and Aeschbach, 2018). Estimated recharge temperatures of the investigated wells and springs were calculated with the Noble90 and the Noblebook. Both programs provide the same values but Noble90 gives the uncertainties of the NGTs. Input data for Noblebook and results of modelling are summarized in Table SM3.
Meteorological data (Table SM2) evaluated over a one-year interval (2016) with spatial resolution of 0.125 × 0.125 grad and temporal resolution of monthly average were gained from ECMWF ERA Interim (2019).
3 Results
3.1 Mean Annual Air and Soil Temperatures
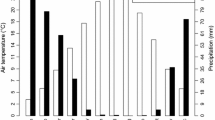
The mean monthly air and soil temperatures obviously differ from each other (Fig. 2), and in all sampled regions similar trends of about a two-month-lag between air and soil temperature values can be observed. In particular, mean monthly soil temperatures show uniformity in case of all but one (Bükk Mts.) sampled areas. Despite this similarity, there are some minor differences between the regions in the temperature curves and the mean annual temperature values due to meso- and/or micro-climatic effects.
The most remarkable phenomenon can be seen in case of Bükk Mts., where mean monthly temperatures were consistently lower in each and every month than that of any other sampled region (MAAT is 10.7 °C and MAST is 11.1 °C). The other karst mountains, Mecsek Mts. gave higher MAAT (11.8 °C) and MAST (12.2 °C) values deriving from their warmer climate and covered karst nature. Mean monthly temperatures varied from -0.3 °C (December) to 23 °C (July) in case of air and from 5.5 °C (February) to 19.7 °C (September) in case of soil. Considering the difference between MAAT and MAST (0.6 °C), Geresd Hills as a hilly region showed a transitional value between mountains and alluvial plains. For air, the coldest month was December (-0.4 °C) and the warmest one was July (23 °C), while in case of soil, these were February (5.6 °C) and September (20 °C), respectively.
On alluvial plains, ΔT (= MAST-MAAT) was 0.3-0.4 °C higher than in mountainous regions. Maximum and minimum temperature values of Mezőföld were 22.8 °C in July, -0.5 °C in December in case of air, and 19.9 °C in September and 5.5 °C in February in case of soil. Danube-Tisza Interfluves showed the highest ΔT value and the coldest month was January with a temperature of -0.7 °C. The highest mean monthly air temperature (22.9 °C) was observed in July, while in case of soil the minimum and maximum values were 5.5 and 20.0 °C in February and September, respectively. In case of Nyírség, the air temperature curve is not so pointed as the ones of other regions indicating steadily high temperature during summer months. Its maximum mean monthly air temperature was 22.1 °C in July, the minimum was -1.7 °C in December, and Nyírség proved to be the second coolest sampled region after the Bükk Mts. Regarding soil temperature data, Nyírség was comparable to the other sampled areas (19.4 °C in September and 5.4 °C in February).
3.2 Noble Gas Temperature
The distribution of derived noble gas temperatures is summarized in a boxplot (Fig. 3). The distinctness of the sampled mountainous regions and alluvial plains can be observed. It can also be seen that a dominant mass of the data defines an average noble gas temperature of 11.2 ± 2.3 °C for all regions. Bükk Mts. differs from it at a greater extent. We expected that Bükk Mts. would present the lowest derived temperature but the calculated mean value of 6.8 ± 0.6 °C was less than the average multi-annual temperature of the sampled part of the region (8-9 °C) irrespective of the date of sampling. Mean NGT value of summer sampling was 7.24 ± 0.5 °C, while that of winter sampling was 6.28 ± 0.1 °C.
In the Mecsek Mts., water samples from six springs with slightly different recharge elevations were investigated during a 4-year-long sampling period. These springs are fed from a karst aquifer just as the springs of Bükk Mts. Our tritium measurements and 3 H/3He apparent ages confirm what was demonstrated, that mean residence time is only up to a few years. Despite of the similarities owing to the different climatic circumstances, temperatures in Mecsek Mts. are a few degrees higher than in the northern mountainous region of the country. The derived mean noble gas temperature (10.7 ± 1.9 °C) reflects the average value of the region (10-11 °C).
The mean calculated noble gas temperature of Geresd Hills (13.0 ± 0.9 °C) was 2-3 °C higher than the known average mean annual temperature (10-11 °C) of the region. The coldest water was produced by Henrik-spring with a mean value of 11.6 °C, while all the rest gave NGT values over 12 °C. The mean result of Nyírség (12.7 ± 1.6 °C) shows similarity with the one of Geresd Hills and these values are above the average mean annual temperature of 9.7 °C. Samples from Mezőföld have similar NGT values yielding a mean of 12.1 ± 1.1 °C over a three-year-long period. Danube-Tisza Interfluves also gave very similar results with its mean NGT of 12.1 ± 0.6 °C.
3.3 Comparison of NGT with MAAT and MAST Values
To get an insight into the connection of air and soil temperature values and derived noble gas temperature, Table 1 presents the calculated mean values for all sampled regions.
The data resemble the early findings of Smith et al. (1964) regarding the relationship of MAAT and MAST that is soil temperature tends to be slightly higher than annual mean air temperature (in temperate climate).
Taking into consideration the NGT values of Mecsek Mts. and comparing them to the calculated MAST and MAAT (Table 1), it seems that calculated noble gas temperature (10.7 ± 1.9 °C) is closer to the values of MAAT (11.8 °C). According to Stute and Schlosser (1993), in karstic areas the recharging water does not have enough time for equilibration with the ground air which results in lower recharge temperature. However, the Mecsek Mts. is a covered karst where, comparing to an open karst, a soil layer can slow down infiltration processes.
The Bükk Mts., the other sampled karst mountains presented the lowest temperature values in every sense. It has been already discussed that it is considered the coldest mountainous part of Hungary, and taking into account this fact, MAAT (10.7 °C) and MAST (11.1 °C) data were not very different, but the calculated NGT was even lower (6.8 ± 0.6 °C). It can be assumed that the infiltrating groundwater does not follow the warming of the soil due to the unique properties of recharge in karstic area, since the soil cover above the karst aquifer can be thin enough or the infiltration can occur rapidly enough through dolines and sinkholes to make heat and also the gas exchange between the soil and infiltrating water more difficult. Comparing the two studied karstic areas, it can be concluded that on those areas, where the infiltration rates are very high or the recharge does not have sufficient time for equilibration with the ground air, NGT can have a bias from MAAT, and in certain cases this bias can be very significant as it can be seen in case of Bükk Mts.
We have to mention other possible explanations for the discrepancy between NGTs and air as well as soil temperatures found in Mecsek and Bükk Mts. According to Warrier et al. (2012), owing to the presence of preferential flow paths in fractured systems leading to rapid infiltration, recharge water may reflect rather the ground surface temperature at the time of infiltration than mean annual air temperature. Lower NGTs may be explained also by the above discussed oxygen depletion (Hall et al. 2005). However, well aerated conditions of karsts does not confirm this assumption, and we cannot reject it. This is confirmed by the dissolved oxygen concentrations of samples from karstic areas varying from 3.2 to 6.4 mg L−1.
In Geresd Hills, the calculated noble gas temperature (13.0 ± 0.9 °C) rather reflects MAST (12.4 °C) in this region, and despite of the similarity with Mecsek Mts. regarding MAAT and MAST, NGT is significantly higher in Geresd Hills. This can be explained by the different recharge rate originating in different geological and soil conditions, as already discussed.
Mezőföld, Danube-Tisza Interfluves and Nyírség seem to be quite similar considering all of the given temperature values (Table 1). Each of them are alluvial plains, parts of the Great Hungarian Plain, and they have some similarities in their geological characteristics, since the dominating sediment is sand. At all three sites, shallow groundwater wells were installed at similar depth and elevations that could result in similar temperatures. Temperature values of these regions (Mezőföld: NGT=12.1 ± 1.1 °C, MAAT=11.6 °C, MAST=12.3 °C; Danube-Tisza Interfluves: NGT=12.1 ± 0.6 °C, MAAT=11.6 °C, MAST=12.4 °C; Nyírség: NGT=12.7 ± 1.6 °C, MAAT=11.4 °C, MAST=12.1 °C) show that the noble gas temperatures rather reflect the values of MAST instead of MAAT.
Examining the relation of NGT to MAAT or MAST, it was confirmed that acceptance of NGT as an indicator of past mean air temperature can sometimes be misleading. If someone wishes to use NGT as a paleoclimate proxy, more detailed studies regarding MAAT, MAST and their relation with NGT need to be carried out.
4 Conclusions
In this study, evaluation of the relationship of noble gas temperature and mean annual air and soil temperatures has been carried out by comparing noble gas temperatures of the sampled regions to recent MAAT and MAST at the same location. Differences and similar patterns are observed in case of plains and hilly or mountainous regions. Calculated noble gas temperatures rather reflect mean annual soil temperature values in sampling sites located in the Great Hungarian Plains, exceeding the values of air temperatures. In contrast, in the mountainous regions where the sampled springs are fed by karst aquifers, the calculated recharge temperatures reflect mean annual air temperatures that are significantly lower than the registered soil temperature values. Therefore, it can be confirmed that differing equilibration mechanisms between air and water must be taking place in aquifers due to recharging from rapid infiltration processes.
The conclusion of this study is that noble gas paleothermometry can be a reliable tool for paleoclimate studies; however, differences in recharge conditions should carefully consider whether the mean annual air or soil temperatures can be derived from calculated noble gas temperature values given the local conditions.
Data Availability
The data that supports the findings of this study are available in the supplementary material of this article.
References
Ács F, Breuer H, Skarbit N (2015) Climate of Hungary in the twentieth century according to Feddema. Theor Appl Climatol 119:161–169. https://doi.org/10.1007/s00704-014-1103-5
Aeschbach-Hertig W, El-Gamal H, Wieser M, Palcsu L (2008) Modeling excess air and degassing in groundwater by equilibrium partitioning with a gas phase. Water Resour Res 44:1–12. https://doi.org/10.1029/2007WR006454
Aeschbach-Hertig W, Peeters F, Beyerle U, Kipfer R (1999) Interpretation of dissolved atmospheric noble gases in natural waters. Water Resour Res 35(9):2779–2792
Aeschbach-Hertig W, Peeters F, Beyerle U, Kipfer R (2000) Paleotemperature reconstruction from noble gases in groundwater accounting for equilibration with entrapped air. Nature 405:1040–1044
Aeschbach-Hertig W, Solomon DK (2013) Noble gas thermometry in groundwater hydrology. In: Burnard P (ed) The Noble Gases as Geochemical Tracers. Springer, Berlin, pp 81–122
Aeschbach-Hertig W, Stute M, Clark JF, Reuter R, Schlosser P (2002) A paleotemperature record derived from dissolved noble gases in groundwater of the Aquia aquifer (Maryland, USA). Geochim Cosmochim Acta 66(5):797–817
Andrews JN, Lee DJ (1979) Inert gases in groundwater from the Bunter Sandstone of England as indicators of age and palaeoclimatic trends. J Hydrol 41:233–252
Ballentine CJ, Hall CM (1999) Determining paleotemperature and other variables by using an error-weighted, nonlinear inversion of noble gas concentrations in water. Geochim Cosmochim Acta 63(16):2315–2336
Beyerle U, Rueedi J, Leuenberger M, Aeschbach-Hertig W, Peeters F, Kipfer R, Dodo A (2003) Evidence for periods of wetter and cooler climate in the Sahel between 6 and 40 kyr BP derived from groundwater. Geophys Res Lett 30(4):1173. https://doi.org/10.1029/2002GL016310,2003
Castro MC, Hall CM, Patriarche D, Goblet P, Ellis BR (2007) A new noble gas paleoclimate record in Texas—basic assumptions revisited. Earth Planet Sci Lett 257:170–187
Cey BD (2009) On the accuracy of noble gas recharge temperatures as a paleoclimate proxy. J Geophys Res Atmos 114:1–9
Cey BD, Hudson GB, Moran JE, Scanlon BR (2009) Evaluation of noble gas recharge temperatures in a shallow unconfined aquifer. Ground Water 47:646–659
ECMWF ERA Interim (2019) https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc/. Accessed 18 January 2019
Feddema JJ (2005) A revised Thornthwaite-type global climate classification. Phys Geogr 26:442–466
Freundt F, Schneider T, Aeschbach-Hertig W (2013) Response of noble gas partial pressures in soil air to oxygen depletion. Chem Geol 339:283–290
Hall CM, Castro MC, Lohmann KC, Ma L (2005) Noble gases and stable isotopes in a shallow aquifer in southern Michigan: Implications for noble gas paleotemperature reconstructions for cool climates. Geophys Res Lett 32:1–4
Hall CM, Castro MC, Lohmann KC, Sun T (2012) Testing the noble gas paleothermometer with a yearlong study of groundwater noble gases in an instrumented monitoring well. Water Resour Res 48:1–18
Heaton THE, Vogel JC (1981) Excess air in ground water. J Hydrol 50:201–216
Herzberg O, Mazor E (1979) Hydrological applications of noble gases and temperature measurements in underground water systems: examples from Israel. J Hydrol 41:217–231
Jung M, Aeschbach W (2018) A new software tool for the analysis of noble gas data sets from (ground)water. Environ Modell Softw 103:120–130
Kipfer R, Aeschbach-Hertig W, Peeters F, Stute M (2002) Noble gases in lakes and ground waters. In: Porcelli D, Ballentine C, Wieler R (eds) Noble Gases in Geochemistry and Cosmochemistry.: Rev. Mineral. Geochem., vol 47. Mineralogical Society of America, Geochemical Society, Washington DC, 615–700
Klump S, Brennwald MS, Kipfer R (2006) Comment on "Noble gases and stable isotopes in a shallow aquifer in southern Michigan: Implications for noble gas paleotemperature reconstructions for cool climates" by Chris M. Hall et al. Geophys Res Lett 33:L24403. https://doi.org/10.1029/2006GL027496.
Klump S, Tomonaga Y, Kienzler P, Kinzelbach W, Baumann T, Imboden D, Kipfer R (2007) Field experiments yield new insights into gas exchange and excess air formation in natural porous media. Geochim Cosmochim Acta 71:1385–1397
Köppen W (1918) Klassifikation der Klimate nach Temperatur, Niederschlag und Jahresablauf. Petermanns Geogr Mitt 64:193–203
Mann ME, Schmidt GA, Miller SK, Le Grande AN (2009) Potential biases in inferring Holocene temperature trends from long-term borehole information. Geophys Res Lett 36:1–5. https://doi.org/10.1029/2008GL036354
Ma L, Castro MC, Hall CM (2004) A late Pleistocene–Holocene noble gas paleotemperature record in southern Michigan. Geophys Res Lett 31:L23204. doi:https://doi.org/10.1029/2004GL021766
Mazor E (1972) Paleotemperatures and other hydrological parameters deduced from noble gases dissolved in groundwaters; Jordan Rift Valley, Israel. Geochim Cosmochim Acta 36:1321–1336. https://doi.org/10.1016/0016-7037(72)90065-8
Palcsu L, Kompár L, Deák J, Szűcs P, Papp L (2017) Estimation of the natural groundwater recharge using tritium-peak and tritium/helium-3 dating techniques in Hungary. Geochem J 51:439–448. https://doi.org/10.2343/geochemj.2.0488
Papp L, Palcsu L, Major Z, Rinyu L, Tóth I (2012) A mass spectrometric line for tritium analysis of water and noble gas measurements from different water amounts in the range of microlitres and millilitres. Isotopes Environ Health Stud 48:494–511. https://doi.org/10.1080/10256016.2012.679935
Peeters F, Beyerle U, Aeschbach-Hertig W, Holocher J, Brennwald MS, Kipfer R (2002) Improving noble gas based paleoclimate reconstruction and groundwater dating using 20Ne/22Ne ratios. Geochim Cosmochim Acta 67:587–600
Saadi R, Túri M, Palcsu L, Marah H, Oum K, Hakam, Rinyu L, Molnár M, Futó I (2017) A potential groundwater aquifer for palaeoclimate reconstruction: Turonian aquifer, Tadla basin, Morocco. J Afr Earth Sci 132:64–71
Smith GD, Newhall F, Robinson LH, Swanson D (1964) Soil temperature regimes: their characteristics and predictability USDA. Soil Conservation Service Report SCS-TP-144
Stute M, Schlosser P (1993) Principles and applications of the noble gas paleothermometer. In: Climate Change in Continental Isotopic Records. Geophys Monogr Ser (ed. Swart PK) 78:99.89 – 100 (AGU: Washigton D. C)
Stute M, Sonntag C (1992) Palaeotemperatures derived from noble gases dissolved in groundwater and in relation to soil temperature, in Isotopes of Noble Gases as Tracers in Environmental Studies. IAEA Rep STI/PUB/859. Int At Energy Agency, Vienna, pp 111–122
Stute M, Clark J, Schlosser P, Broecker W (1995) A 30,000 yr continental paleotemperature record derived from noble gases dissolved in groundwater from the San Juan Basin, New Mexico. Quat Res 43:209–220
Sun T, Hall CM, Castro MC (2010) Statistical properties of groundwater noble gas paleoclimate models: Are they robust and unbiased estimators? Geochem Geophys Geosyst 11:Q02002. https://doi.org/10.1029/2009GC002717
Szűcs P, Kompár L, Palcsu L, Deák J (2015) Estimation of the groundwater replenishment change at a Hungarian recharge area. Carpathian J Earth Environ Sci 10:227–236
Túri M, Saadi R, Marah H, Temovski M, Molnár M, Palcsu L (2020) Paleotemperature reconstructions using environmental isotopes and noble gases in groundwaters in Morocco. Hydrogeol J. https://doi.org/10.1007/s10040-020-02121-1
Varsányi I, Palcsu L, Kovács L (2011) Groundwater flow system as an archive of palaeotemperature: Noble gas, radiocarbon, stable isotope and geochemical study in the Pannonian Basin, Hungary. Appl Geochem 26:91–104. https://doi.org/10.1016/j.apgeochem.2010.11.006
Warrier RB, Castro MC, Hall CM (2012) Recharge and source-water insights from the Galapagos Islands using noble gases and stable isotopes. Water Resour Res 48:W03508. https://doi.org/10.1029/2011WR010954
Funding
Open access funding provided by ELKH Institute for Nuclear Research. The research was supported by the European Union and the State of Hungary, co-financed by the European Regional Development Fund in the project of GINOP-2.3.2-15-2016-00009 ‘ICER’.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Carmen Szenász-Fekete, László Kompár, Andor Hajnal, Elemér László, Anita Puskás-Preszner and László Palcsu. The first draft of the manuscript was written by Anita Puskás-Preszner and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing Interests/Conflict of Interest
The Authors declare that there is no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Puskás-Preszner, A., Szenász-Fekete, C., László, E. et al. Comparison of Noble Gas Temperature with Recent Mean Annual Air and Soil Temperature in different regions of Hungary. Environ. Process. 9, 4 (2022). https://doi.org/10.1007/s40710-021-00557-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40710-021-00557-5