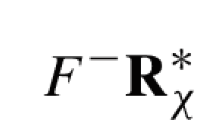On Ribet’s lemma for GL$_2$ modulo prime powers

Abstract

Let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be a continuous representation of a compact group G over a complete discretely valued field K with ring of integers $\mathcal {O}$ and uniformiser $\pi$. We prove that ${{\,\textrm{tr}\,}}\rho$ is reducible modulo $\pi ^n$ if and only if $\rho$ is reducible modulo $\pi ^n$. More precisely, there exist characters $\chi _1,\chi _2 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ such that $\det (t - \rho (g))\equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n}$ for all $g\in G$, if and only if there exists a G-stable lattice $\Lambda \subseteq K^2$ such that $\Lambda /\pi ^n\Lambda$ contains a G-invariant, free, rank one $\mathcal {O}/\pi ^n\mathcal {O}$-submodule. Our result applies in the case that $\rho$ is not residually multiplicity-free, in which case it answers a question of Bellaïche and Chenevier (J Algebra 410:501–525, 2014, pp. 524). As an application, we prove an optimal version of Ribet’s lemma, which gives a condition for the existence of a G-stable lattice $\Lambda$ that realises a non-split extension of $\chi _2$ by $\chi _1$.

1 Introduction

Let $\mathcal {O}$ be a complete discrete valuation ring with fraction field K, uniformiser $\pi$, discrete valuation $v_\pi$ normalised such that $v_\pi (\pi )=1$ and residue field $\textbf{F}$. Let G be a compact group, and let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be a continuous representation. Suppose that there exists an integer n and continuous characters $\chi _1, \chi _2 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ such that, for all $g\in G$, we have

$$\begin{aligned} P_{\rho (g)}(t):=\det (t - \rho (g)) \equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n}, \end{aligned}$$

(1.1)

where $P_{\rho (g)}(t)$ is the characteristic polynomial of $\rho (g)$. The goal of this paper is to answer the following questions, the first of which is equivalent to [4, Question, pp. 524]:

Question 1

Is $\rho$ reducible modulo $\pi ^n$, i.e. does there exist a G-stable lattice $\Lambda \subseteq K^2$ such that $\Lambda /\pi ^n\Lambda$ contains a G-invariant, free, rank one $\mathcal {O}/\pi ^n\mathcal {O}$-submodule V?

Equivalently, does there exist a basis for $K^2$ with respect to which the image of $\rho$ is a subgroup of

$$\begin{aligned} \Gamma _0(\pi ^n):= \left\{ \begin{pmatrix}a&{}\quad b\\ c&{}\quad d\end{pmatrix}\in {{\,\textrm{GL}\,}}_2(\mathcal {O}): c\equiv 0\pmod {\pi ^n}\right\} ? \end{aligned}$$

Question 2

Can we choose $\Lambda$ so that the free rank one submodule V is isomorphic to $\chi _1$? Moreover, if $\rho$ is irreducible, can we choose $\Lambda$ so that $\Lambda /\pi ^n\Lambda$ is a non-split extension of $\chi _2$ by $\chi _1$?

Question 1 has previously been studied by Katz [11] in the context of Galois representations attached to elliptic curves and answered in the case that K is a finite extension of $\textbf{Q}_p$ and $\chi _1$ is the trivial character [11, Thm. 1], though his proof can be generalised to any $\chi _1,\chi _2$. Our proof is completely different and works in the more general case of discretely valued fields. Moreover, our argument only requires G to be a semigroup.

1.1 The Bruhat–Tits tree of ${{\,\textrm{PGL}\,}}_2(K)$

In order to answer these questions, we rephrase them in the language of Bruhat–Tits trees.

By a lattice in $K^2$, we mean a rank two $\mathcal {O}$-module $\Lambda \subseteq K^2$ that spans $K^2$ as a vector space. We say that two lattices $\Lambda _1, \Lambda _2$ are homothetic if there is an element $a\in K$ such that $\Lambda _1 = a\Lambda _2$.

Definition 1.1

The Bruhat–Tits tree $\mathcal {X}$ of is the graph whose vertices are the homothety classes of lattices in . Two vertices $x, y\in \mathcal {X}$ are joined by an edge if we can choose representatives $\Lambda _x,\Lambda _y$ of x, y such that

$$\begin{aligned} \pi \Lambda _x\subsetneq \Lambda _y\subsetneq \Lambda _x. \end{aligned}$$

Equivalently, $x, y\in \mathcal {X}$ are neighbours if there exists a basis $(v_1, v_2)$ of $\Lambda _x$ such that the homothety class of the lattice with basis $(v_1, \pi v_2)$ is y. After fixing such a basis, the other neighbours of $\Lambda _x$ are the lattices with bases $(\pi v_1, v_2 + i v_1)$ where $i\in \mathcal {O}$ runs over a set of representatives for the congruence classes of $\mathcal {O}$ modulo $\pi$. Thus, if q denotes the (possibly infinite) cardinality of $\textbf{F}$, then $\mathcal {X}$ is a $(q+1)$-regular tree.

By extension, suppose that $x, y\in \mathcal {X}$ are two vertices of $\mathcal {X}$ of distance $d = d(x, y)$ from each other, where d(x, y) is the number of edges in the path connecting x to y. Then, d is the smallest integer for which we can choose representatives $\Lambda _x,\Lambda _y$ such that

$$\begin{aligned} \pi ^d\Lambda _x\subsetneq \Lambda _y\subsetneq \Lambda _x. \end{aligned}$$

Equivalently, d is the unique integer for which there exists a basis $(v_1, v_2)$ of $\Lambda _x$ such that $(v_1, \pi ^d v_2)$ is a basis of $\Lambda _y$.

The representation $\rho$ induces an action of G on the vertices of $\mathcal {X}$. Let $\mathcal {X}(\rho )$ be the subgraph of $\mathcal {X}$ whose vertices are homothety classes of G-stable lattices. Then, for each $x\in \mathcal {X}(\rho )$ with representative $\Lambda _x$, there is a bijection between vertices $y\in \mathcal {X}(\rho )$ with $d(x, y) = n$ and free rank one G-invariant $\mathcal {O}/\pi ^n\mathcal {O}$-submodules of $\Lambda _x/\pi ^n\Lambda _x$ (Lemma 2.3). Thus, an affirmative answer to Question 1 follows from the following theorem, which is our main result:

Theorem 1.2

The following are equivalent:

• (i) There exist two vertices $x,y\in \mathcal {X}(\rho )$ with $d(x,y)=n$.

• (ii) There exists a pair of characters $\chi _1, \chi _2 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ such that, for all $g\in G$, $P_{\rho (g)}(t)\equiv (t- \chi _1(g))(t- \chi _2(g))\pmod {\pi ^n}$.

Questions 1 and 2 have been answered in far greater generality in the case that $\rho$ is residually multiplicity-free, i.e. if $\chi _1\not \equiv \chi _2\pmod \pi$ [2, 5, 6, 8]. In the residually multiplicity-free case, the graph $\mathcal {X}(\rho )$ is just a finite line segment, and the theory is simplified considerably by the fact that the characters $\chi _1, \chi _2$, if they exist, are unique.

However, the non-residually multiplicity-free case is far more mysterious. This case has been studied by Bellaïche–Chenevier [4], who classify the types of graphs $\mathcal {X}(\rho )$ can be, prove that (i) implies (ii) in Theorem 1.2 and give a partial result in the opposite direction [4, Thm. 45]. They pose as a question whether (i) and (ii) are equivalent [4, Question, pp. 524]. As well as answering this question, we complete Bellaïche–Chenevier’s description of the shape of $\mathcal {X}(\rho )$: we describe the shape of $\mathcal {X}(\rho )$ in terms of certain pseudocharacter invariants of $\rho$ (Theorem 5.1). Conversely, we also show how to compute these invariants from the shape of $\mathcal {X}(\rho )$ (Theorem 5.3).

1.2 Ribet’s lemma

In his celebrated 1976 paper [13], Ribet pioneered a technique to construct non-split extensions of Galois representations using congruences between modular forms. Suppose that $\rho :{{\,\textrm{Gal}\,}}(\overline{\textbf{Q}}/{\textbf{Q}})\rightarrow {{\,\textrm{GL}\,}}_2(K)$ is an irreducible Galois representation that is residually reducible: there exist characters $\chi _1, \chi _2 :{{\,\textrm{Gal}\,}}(\overline{\textbf{Q}}/{\textbf{Q}})\rightarrow \textbf{F}^\times$ such that $P_{\rho (g)}(t)\equiv (t- \chi _1(g))(t- \chi _2(g))\pmod {\pi }$. Ribet showed that there exists a ${{\,\textrm{Gal}\,}}(\overline{\textbf{Q}}/{\textbf{Q}})$-stable lattice $\Lambda$ such that $\Lambda /\pi \Lambda$ is a non-split extension of $\chi _2$ by $\chi _1$.

Ribet’s Lemma has been generalised to higher-dimensional representations, to mod $\pi ^n$ congruences, and to representations over more general rings [2, 5,6,7, 18]. These generalisations are crucial components of proofs of Iwasawa main conjectures and cases of the Bloch–Kato conjecture [2, 15, 17, 20]. However, these generalisations all assume that $\rho$ is residually multiplicity-free.

The non-residually multiplicity-free case is, again, more mysterious. Indeed, the naïve generalisation of Ribet’s lemma is false: in Sect. 4.2, we give examples of representations $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ with $P_{\rho (g)}(t)\equiv (t- \chi _1(g))(t- \chi _2(g))\pmod {\pi ^n}$, but such that there is no G-stable lattice $\Lambda \subseteq K^2$ for which either of $\chi _1, \chi _2$ is a submodule of $\Lambda /\pi ^n\Lambda$. Note that, if $\rho$ is irreducible, then Theorem 1.2 shows that there do exist pairs of characters $\eta _1, \eta _2$ and G-stable lattices $\Lambda$ such that $\Lambda /\pi ^n\Lambda$ is a non-split extension of $\eta _2$ by $\eta _1$. The problem is that, unlike in the multiplicity-free case, the decomposition of $P_{\rho (g)}\pmod {\pi ^n}$ as a product of characteristic polynomials of characters is not unique, and only some of the decompositions can actually be realised by lattices.

Our first application of Theorem 1.2 is the following generalisation of Ribet’s Lemma, which is optimal, in the sense that the integer s is as large as possible in general:

Theorem 1.3

Let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be an irreducible representation, and let $\chi _1,\chi _2 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ be characters such that, for all $g\in G$, the characteristic polynomial $P_{\rho (g)}(t)$ of $\rho (g)$ factors as $(t- \chi _1(g))(t- \chi _2(g))\pmod {\pi ^n}$. Let $m=m(\chi _1, \chi _2)$ be the largest integer such that $\chi _1\equiv \chi _2\pmod {\pi ^m}$. Define

$$\begin{aligned} s = s(\chi _1, \chi _2) = {\left\{ \begin{array}{ll}n-m(\chi _1, \chi _2) &{}\quad {\textrm{if}}\; m(\chi _1,\chi _2)<\frac{n}{2}\\ \left\lceil \frac{n}{2}\right\rceil &{}\quad {\textrm{if}}\; m(\chi _1,\chi _2)\geqslant \frac{n}{2}.\end{array}\right. } \end{aligned}$$

Then there exists a G-stable lattice $\Lambda$ such that $\Lambda /\pi ^s\Lambda$ is a residually non-split extension of $\chi _1\pmod {\pi ^s}$ by $\chi _2\pmod {\pi ^s}$.

Here, by a residually non-split extension, we mean that $\Lambda /\pi \Lambda$ is indecomposable. We note in Corollary 2.14 that the integer s depends only on $\rho$ and n and not on the choice of characters $\chi _1, \chi _2$.

1.3 Isogenies of elliptic curves

Let F be a number field and let E/F be an elliptic curve. If $\mathfrak p$ is a prime of good reduction for E and if the absolute ramification index $e_{\mathfrak p}$ of $\mathfrak p$ satisfies $e_\mathfrak p<p-1$, then there is an injective map $E(F)_{\textrm{tors}}\hookrightarrow E(\textbf{F}_{\mathfrak p})$ from the torsion subgroup of E(F) to the points of E over the residue field $\textbf{F}_{\mathfrak p}$. In particular, if $\ell$ is a prime, $n\geqslant 1$ and $\ell ^n\mid \#E(F)_{\textrm{tors}}$, then $\ell ^n\mid \#E(\textbf{F}_{\mathfrak p})$ for all primes $\mathfrak p$ of good reduction.

In [11], Katz studied Question 1 in order to prove a converse to this statement. Let

$$\begin{aligned} \rho _{\ell } :{{\,\textrm{Gal}\,}}(\overline{F}/{F})\rightarrow {{\,\textrm{GL}\,}}_2(\textbf{Q}_\ell ) \end{aligned}$$

be the $\ell$-adic Galois representation attached to (the isogeny class of) E. Then lattices inside $\rho _\ell$ are in bijective correspondence with elliptic curves $E'$ that are $\ell$-power isogenous to E, and the $\ell$-isogeny graph of E is exactly the invariant subtree $\mathcal {X}(\rho _\ell )$. By the Chebotarev density theorem and the definition of $\rho _\ell$, the condition that $\ell ^n\mid \#E(\textbf{F}_{\mathfrak p})$ for all primes $\mathfrak p$ of good reduction is equivalent to $\rho _\ell$ satisfying

$$\begin{aligned} \det (1 - \rho _\ell (g))\equiv 0\pmod {\ell ^n} \end{aligned}$$

for all $g\in {{\,\textrm{Gal}\,}}(\overline{F}/{F})$, which is equivalent to (1.1) with $\chi _1= 1$ and $\chi _2$ the mod $\ell ^n$ cyclotomic character. By answering Question 1 with $K = \textbf{Q}_p$ and $\chi _1 = 1$, Katz showed that if $\ell ^n\mid \#E(\textbf{F}_{\mathfrak p})$ for all primes $\mathfrak p$ of good reduction, then there is an elliptic curve $E'$, isogenous to E over F, such that $\ell ^n\mid \#E'(F)_{\textrm{tors}}$.

Similarly, if E admits a cyclic $\ell ^n$-isogeny over F, then there is a character $\chi :{{\,\textrm{Gal}\,}}(\overline{F}/{F})\rightarrow (\textbf{Z}/\ell ^n\textbf{Z})^\times$ such that $\chi (g)$ is a root of the characteristic polynomial $P_{\rho (g)}(t)$ modulo $\ell ^n$, for all $g\in {{\,\textrm{Gal}\,}}(\overline{F}/{F})$. Moreover, if E has good reduction at a prime $\mathfrak p\not \mid \ell$, then $\chi$ is unramified at $\mathfrak p$. On the other hand, E is isogenous over F to an elliptic curve $E'$ that admits a cyclic $\ell ^n$-isogeny if and only if there is a line of distance n in its $\ell$-isogeny graph, which is exactly $\mathcal {X}(\rho _\ell )$. Hence, as an immediate consequence of Theorem 1.2, we deduce the following corollary:

Corollary 1.4

Let E be an elliptic curve over a number field F, and let S be the set of primes of bad reduction for E and the primes above a rational prime $\ell$. Let $\rho _\ell :{{\,\textrm{Gal}\,}}(\overline{F}/{F})\rightarrow {{\,\textrm{GL}\,}}_2(\textbf{Q}_\ell )$ be the $\ell$-adic Galois representation attached to E. The following are equivalent:

• (i) E is isogenous over F to an elliptic curve $E'$ that admits a cyclic $\ell ^n$-isogeny.

• (ii) There exists a character $\chi : {{\,\textrm{Gal}\,}}(\overline{F}/{F})\rightarrow (\textbf{Z}/\ell ^n\textbf{Z})^\times$, unramified outside S, such that $\chi ({{\,\textrm{Frob}\,}}_{\mathfrak p})$ is a root of the characteristic polynomial $P_{\rho _\ell ({{\,\textrm{Frob}\,}}_{\mathfrak p})}(t)$ modulo $\ell ^n$, for set of primes $\mathfrak p$ of F of Dirichlet density 1.

Note that, if in part (ii), we instead just assume that the characteristic polynomial of $\rho _\ell ({{\,\textrm{Frob}\,}}_\mathfrak p)$ is reducible modulo $\ell ^n$ for each $\mathfrak p$, then the equivalence is false. Indeed, this latter condition is equivalent to E being isogenous to an elliptic curve $E'$ that admits a cyclic $\ell ^n$-isogeny everywhere locally. However, there exist elliptic curves with no global isogenies that have isogenies everywhere locally [1, 3, 16, 19]. We note that, since $\det \rho _\ell$ is the $\ell$-adic cyclotomic character, the assumption $\sqrt{\left( \frac{-1}{\ell }\right) \ell }\notin F$ imposed in [1, 16] forces $\rho _\ell$ to be residually multiplicity-free.

2 Preliminaries

In this section, we recall key properties of the Bruhat–Tits tree $\mathcal {X}$ of ${{\,\textrm{PGL}\,}}_2(K)$ and, for a representation $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$, we define the $\rho (G)$-invariant subtree $\mathcal {X}(\rho )$ and discuss its shape. We then discuss the decompositions of $\rho$ modulo $\pi ^n$ and define the index of irreducibility $n(\rho )$ and the index of irreducibility with multiplicity $m(\rho )$. Our key reference is [4, §2] (see also [14]).

2.1 The $\rho (G)$-invariant subtree

Let be a representation of a group G and assume that there exists a $\rho (G)$-stable lattice . In particular, for every $g\in G$ the characteristic polynomial $P_{\rho (g)}(t)$ of g is an element of $\mathcal {O}[t]$. This condition is automatically satisfied for most representations of interest, for example, if G is compact and $\rho$ is continuous.

Choosing a basis for $\Lambda$, we obtain a representation $\rho _\Lambda :G\rightarrow {{\,\textrm{GL}\,}}_2(\mathcal {O})\subseteq {{\,\textrm{GL}\,}}_2(K)$ that is isomorphic to $\rho$. Hence, we can define the residual representation $\overline{\rho }_\Lambda :G\rightarrow {{\,\textrm{GL}\,}}_2(\textbf{F})$ as well as the mod $\pi ^n$ representations $\rho _\Lambda \pmod {\pi ^n}$. In general, the isomorphism class of the representation $\overline{\rho }_\Lambda$ depends on the homothety class of $\Lambda$.

Definition 2.1

Let $A\subseteq {{\,\textrm{M}\,}}_2(K)$ be a set of matrices. We denote by $\mathcal {X}(A)$ the induced subtree of $\mathcal {X}$ of all A-stable vertices, i.e. vertices $x\in \mathcal {X}$ for which $a\Lambda _x\subseteq \Lambda _x$ for all $a\in A$ and for some (and hence any) representative $\Lambda _x$. We define $\mathcal {X}(\rho )$ to be $\mathcal {X}(\rho (G))$.

Remarks 2.2

• (i) If $A\subseteq A'$, then $\mathcal {X}(A)\supseteq \mathcal {X}(A')$.

• (ii) If $a,b\in {{\,\textrm{M}\,}}_2(K)$ and $\lambda , \mu \in \mathcal {O}$, then $\mathcal {X}(\{a,b\}) = \mathcal {X}(\{a,b,ab\}) = \mathcal {X}(\{a,b, \lambda a + \mu b\})$. Hence, if $A\subseteq {{\,\textrm{M}\,}}_2(K)$ is a finitely generated $\mathcal {O}$-algebra, then we can compute $\mathcal {X}(A)$ by computing $\mathcal {X}(\{a_1, \ldots , a_n\})$ for an explicit set of generators.

• (ii) Similarly, if $R :\mathcal {O}[G]\rightarrow {{\,\textrm{M}\,}}_2(K)$ is the algebra homomorphism corresponding to $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$, then $\mathcal {X}(\rho ) = \mathcal {X}(R(\mathcal {O}[G]))$.

The following lemma shows the relationship between the structure of the graph $\mathcal {X}(\rho )$ and subrepresentations of $\rho _\Lambda \pmod {\pi ^n}$:

Lemma 2.3

[4, Prop. 11] Let $x\in \mathcal {X}(A)$ and fix a representative $\Lambda _x$ of x. There is a bijection between

• Points $y\in \mathcal {X}(A)$ with $d(x, y) = n$;

• free rank one $\mathcal {O}/\pi ^n\mathcal {O}$-submodules of $\Lambda _x/\pi ^n\Lambda _x$ that are A-stable.

Given a point $y\in \mathcal {X}(A)$ with $d(x,y)=n$, the corresponding submodule of $\Lambda _x/\pi ^n\Lambda _x$ is given by $\Lambda _y/\pi ^n\Lambda _x$, where $\Lambda _y$ is chosen so that $\pi ^n\Lambda _x\subsetneq \Lambda _y\subsetneq \Lambda _x$.

Remark 2.4

Note that Lemma 2.3 immediately shows that Theorem 1.2 is equivalent to Question 1. Moreover, we see that:

• (i) The tree $\mathcal {X}(\rho )$ is bounded if and only if $\rho$ is an irreducible representation [4, Lem. 10].

• (ii) $\mathcal {X}(\rho )$ consists of a single point x if and only if $\overline{\rho }_{\Lambda _x}$ is irreducible.

• (iii) A vertex $x\in \mathcal {X}(\rho )$ is a leaf, i.e. a vertex with exactly one neighbour, if and only if $\Lambda _x/\pi \Lambda _x$ is indecomposable.

2.2 The shape of $\mathcal {X}(\rho )$

In [4], Bellaïche–Chenevier classify the possible shapes of $\mathcal {X}(\rho )$. To describe this classification, we recall their terminology (see Figs. 1, 2 and 3 for examples).

Definition 2.5

Let S be a line segment in $\mathcal {X}$, and let r be a positive integer. The band B(S, r) with nerve S and radius r is the subtree of $\mathcal {X}$ consisting of all vertices x with $d(x, S)\leqslant r$.

We distinguish two particular types of bands:

• If $S=\{x\}$ is a single vertex, $B(x,r):= B(\{x\}, r)$ is the ball of radius r and centre x.

• If $S=\{x,y\}$ consists of two adjacent vertices, we call B(S, r) a generalised ball. One can think of B(S, r) as a ball of radius $r+\frac{1}{2}$ around the middle of the segment [x, y].

Fig. 1

A ball of radius 3 in the Bruhat–Tits tree for $\textbf{Q}_3$

Fig. 2

A generalised ball of radius 3 in the Bruhat–Tits tree for $\textbf{Q}_3$

Bellaïche–Chenevier have shown that if $\rho$ is irreducible, then $\mathcal {X}(\rho )$ is a band with finite diameter and radius [4, Thm. 21, Prop. 24].

Definition 2.6

Suppose that $\rho$ is irreducible, so that $\mathcal {X}(\rho )$ is a band. Define $d(\rho )$ to be the diameter of $\mathcal {X}(\rho )$ and $r(\rho )$ to be its radius.

By definition, the diameter of a tree is the length of a maximal path. The diameter of the band B(S, r) is therefore $\ell (S) + 2r$, where $\ell (S)$ is the length of the nerve S.

Fig. 3

A band in the Bruhat–Tits tree for $\textbf{Q}_3$, with diameter 7 and radius 2. The solid points form the nerve S

To further illustrate the connection between the shape of $\mathcal {X}(\rho )$ and the representation theory of $\rho$, we record the following useful lemma:

Lemma 2.7

Fix $A\subseteq {{\,\textrm{M}\,}}_2(K)$ and let H be the semigroup generated by A. Fix $x\in \mathcal {X}(A)$ and $r\geqslant 1$. Then H acts by a one-dimensional character on $\Lambda _x/\pi ^r\Lambda _x$ if and only if $B(x, r)\subseteq \mathcal {X}(A)$.

Proof

Note that H acts as a one-dimensional character on $\Lambda _x/\pi ^r\Lambda _x$ if and only if every free rank one $\mathcal {O}/\pi ^r\mathcal {O}$-submodule of $\Lambda _x/\pi ^r\Lambda _x$ is stable under the action of H. By Lemma 2.3, this latter condition is equivalent to $B(x, r)\subseteq \mathcal {X}(H)$. By Remark 2.4, $\mathcal {X}(A) = \mathcal {X}(H)$. $\square$

2.3 Conjugate characters modulo $\pi ^n$

Let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be a representation.

Definition 2.8

(c.f. [4, Def. 29]) Let $\chi _1,\chi _2 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ be a pair of characters modulo $\pi ^n$ for some positive integer n. We call $(\chi _1, \chi _2)$ a pair of conjugate characters for $\rho$ modulo $\pi ^n$ if the characteristic polynomial $P_{\rho (g)}(t)$ of $\rho (g)$ factors as

$$\begin{aligned} P_{\rho (g)}(t):=\det (t - \rho (g)) \equiv (t-\chi _1(g))(t-\chi _2(g)) \pmod {\pi ^n} \end{aligned}$$

for all $g\in G$.

Remark 2.9

When the residue characteristic of K is not 2, by the identity ${{\,\textrm{tr}\,}}(A)^2-{{\,\textrm{tr}\,}}(A^2)=2\det (A)$ for all $A\in {{\,\textrm{M}\,}}_2(K)$, the above condition is equivalent to

$$\begin{aligned} {{\,\textrm{tr}\,}}\rho (g) \equiv \chi _1(g) + \chi _2(g)\pmod {\pi ^n} \end{aligned}$$

for all $g\in G$.

Remark 2.10

If G is compact, K is a p-adic local field, $\rho$ is continuous and $\chi :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ is a character that factors through the image of $\rho$, then $\chi$ is automatically continuous. Indeed, any finite index subgroup of the closed subgroup $\rho (G)\subseteq {{\,\textrm{GL}\,}}_2(\mathcal {O})$ is open in $\rho (G)$ [12, Thm. A].

Definition 2.11

(c.f. [4, Def. 30]) If $(\chi _1,\chi _2)$ is a pair of characters modulo $\pi ^n$, let $m(\chi _1, \chi _2)$ denote the largest integer $m\leqslant n$ such that

$$\begin{aligned} \chi _1(g) \equiv \chi _2(g)\pmod {\pi ^m} \end{aligned}$$

for all $g\in G$.

In particular, $m(\chi _1, \chi _2) = 0$ if $\chi _1\not \equiv \chi _2\pmod {\pi }$.

If $\rho$ is not residually multiplicity-free, then, in general, there exist multiple distinct pairs of conjugate characters modulo $\pi ^n$ for every $n\geqslant 2$. The following lemma shows that any two pairs of conjugate characters agree modulo $\pi ^s$, where s is as in Theorem 1.3.

Lemma 2.12

Let $(\chi _1,\chi _2)$ and $(\eta _1,\eta _2)$ be two pairs of conjugate characters modulo $\pi ^n$, for some n. Let

$$\begin{aligned} s = s(\chi _1, \chi _2) ={\left\{ \begin{array}{ll}n-m(\chi _1, \chi _2) &{}\quad {\textrm{if}}\; m(\chi _1,\chi _2)<\frac{n}{2}\\ \left\lceil \frac{n}{2}\right\rceil &{}\quad {\textrm{if}}\; m(\chi _1,\chi _2)\geqslant \frac{n}{2}.\end{array}\right. } \end{aligned}$$

Then, up to reordering, we have

$$\begin{aligned} \chi _1\equiv \eta _1\pmod {\pi ^s}\quad \text {and}\quad \chi _2\equiv \eta _2\pmod {\pi ^s}. \end{aligned}$$

Proof

First suppose that $m(\chi _1, \chi _2) \geqslant \frac{n}{2}$. Let $i = 1$ or 2. Then, for each $g\in G$,

$$\begin{aligned} v_\pi (\chi _1(g) - \chi _2(g))\geqslant \frac{n}{2}. \end{aligned}$$

It follows that $v_\pi (\eta _i(g) - \chi _1(g)) \geqslant \frac{n}{2}$ if and only if $v_\pi (\eta _i(g) - \chi _2(g)) \geqslant \frac{n}{2}$.

Now, $\eta _i(g)$ is a root of $P_{\rho (g)}(t)\pmod {\pi ^n}$, i.e.

$$\begin{aligned} (\eta _i(g)-\chi _1(g))(\eta _i(g)-\chi _2(g))\equiv 0\pmod {\pi ^n}. \end{aligned}$$

It follows that $\eta _i\equiv \chi _1\equiv \chi _2\pmod {\pi ^{\lceil \frac{n}{2}\rceil }}$.

Now suppose that $m(\chi _1, \chi _2) < \frac{n}{2}$. Choose $g\in G$ for which $v_\pi (\chi _1(g) - \chi _2(g)) = m(\chi _1, \chi _2)$. As before, we have

$$\begin{aligned} (\eta _1(g)-\chi _1(g))(\eta _1(g)-\chi _2(g))\equiv 0\pmod {\pi ^n}. \end{aligned}$$

Hence, at least one of the two factors must have valuation greater than or equal to $\frac{n}{2}$. Since ${m(\chi _1, \chi _2) <\frac{n}{2}}$ and since

$$\begin{aligned} v_\pi \big ((\eta _1(g)-\chi _2(g)) - (\eta _1(g)-\chi _1(g))\big ) = v_\pi (\chi _1(g) - \chi _2(g)) = m(\chi _1, \chi _2), \end{aligned}$$

we see that one of the factors must have valuation exactly $m(\chi _1, \chi _2)$. Up to reordering $\chi _1$ and $\chi _2$, we may therefore assume that

$$\begin{aligned} v_\pi (\eta _1(g) - \chi _1(g)) \geqslant n - m(\chi _1, \chi _2)\quad \text {and}\quad v_\pi (\eta _1(g)-\chi _2(g)) = m(\chi _1, \chi _2). \end{aligned}$$

Let $h\in G$ and consider the two identities

$$\begin{aligned} \eta _1(h)-\chi _1(h)&=(\eta _1(g)-\chi _1(g))\eta _1(g^{-1}h)+\chi _1(g)(\eta _1(g^{-1}h)-\chi _1(g^{-1}h)),\\ \eta _1(h)-\chi _2(h)&=(\eta _1(g)-\chi _2(g))\eta _1(g^{-1}h)+\chi _2(g)(\eta _1(g^{-1}h)-\chi _2(g^{-1}h)). \end{aligned}$$

If $v_\pi (\eta _1(g^{-1}h)-\chi _1(g^{-1}h)) \geqslant n-m(\chi _1, \chi _2)$, it follows from the first identity that $\eta _1(h)\equiv \chi _1(h)\pmod {\pi ^{n-m(\chi _1, \chi _2)}}$. Assume that $v_\pi (\eta _1(g^{-1}h)-\chi _1(g^{-1}h)) < n-m(\chi _1, \chi _2)$. Since $\eta _1(g^{-1}h)$ is a solution of the characteristic polynomial of $\rho (g^{-1}h)$, we have

$$\begin{aligned} (\eta _1(g^{-1}h) - \chi _1(g^{-1}h))(\eta _1(g^{-1}h) - \chi _2(g^{-1}h)) \equiv 0\pmod {\pi ^n}. \end{aligned}$$

Hence, $v_\pi (\eta _1(g^{-1}h) - \chi _2(g^{-1}h)) > m(\chi _1, \chi _2)$. Since $v_\pi (\eta _1(g) - \chi _2(g)) = m(\chi _1, \chi _2)$, it follows from the second identity that

$$\begin{aligned} v_\pi (\eta _1(h) -\chi _2(h)) = m(\chi _1, \chi _2). \end{aligned}$$

Since $(\eta _1(h)-\chi _1(h))(\eta _1(h)-\chi _2(h))\equiv 0\pmod {\pi ^n}$, we have $\eta _1(h) \equiv \chi _1(h) \pmod {\pi ^{n-m(\chi _1, \chi _2))}}$ in this case as well.

Repeating the above argument with $\eta _1$ replaced by $\eta _2$, we see that either $\chi _2\equiv \eta _1\pmod {\pi ^{n-m(\chi _1,\chi _2)}}$, or $\chi _2\equiv \eta _2\pmod {\pi ^{n-m(\chi _1,\chi _2)}}$. The first would imply that $\chi _1\equiv \chi _2\pmod {\pi ^{n-m(\chi _1,\chi _2)}}$, contradicting the assumption that $m(\chi _1,\chi _2)<n/2$. Therefore, $\chi _2\equiv \eta _2\pmod {\pi ^{n-m(\chi _1,\chi _2)}}$. $\square$

Remark 2.13

In fact, the proof of Lemma 2.12 shows that, if $m(\chi _1, \chi _2) \geqslant \frac{n}{2}$, then $\chi _1\equiv \chi _2\equiv \eta _1\equiv \eta _2\pmod {\pi ^s}$.

Corollary 2.14

Let $(\chi _1,\chi _2)$ and $(\eta _1,\eta _2)$ be two pairs of conjugate characters modulo $\pi ^n$, for some n.

• (i) If $m(\chi _1,\chi _2)\geqslant n/2$, then $m(\eta _1,\eta _2)\geqslant n/2$.

• (ii) If $m(\chi _1,\chi _2)<n/2$, then $m(\eta _1,\eta _2)=m(\chi _1,\chi _2)$.

Proof

If $m(\chi _1,\chi _2)\geqslant n/2$, then by Lemma 2.12, $\chi _i \equiv \eta _i\pmod {\pi ^{\lceil \frac{n}{2}\rceil }}$ for each i. Hence,

$$\begin{aligned} \eta _1 \equiv \chi _1\equiv \chi _2\equiv \eta _2\pmod {\pi ^{\lceil \frac{n}{2}\rceil }}, \end{aligned}$$

so $m(\eta _1, \eta _2)\geqslant n/2$.

If $m(\chi _1, \chi _2) < n/2$, then by Lemma 2.12,

$$\begin{aligned} \eta _i \equiv \chi _i\; \left( \!\!\!\!\!\!\mod \!\! {\,\,\pi ^{n-m(\chi _1, \chi _2)}}\right) \end{aligned}$$

for each i. Since $n-m(\chi _1, \chi _2) > m(\chi _1, \chi _2)$, it follows that $m(\chi _1, \chi _2) = m(\eta _1, \eta _2)$. $\square$

Remark 2.15

In particular, the integer s in the statement of Theorem 1.3 depends only on $\rho$ and n, and is independent of the choice of characters $\chi _1, \chi _2$.

2.4 The invariants $n(\rho )$ and $m(\rho )$

We recall the invariants $n(\rho )$ and $m(\rho )$ defined in [4, §4.2].

Definition 2.16

Let $n(\rho )=\sup \{n: \text {there exists a pair of conjugate characters modulo } \pi ^n\}$.

Definition 2.17

If $n(\rho )$ is finite, then we define $m(\rho )=\max m(\chi _1,\chi _2)$, where the maximum runs over all pairs of conjugate characters modulo $\pi ^{n(\rho )}$.

We think of $n(\rho )$ as the index of reducibility of $\rho$ and of $m(\rho )$ as the index of reducibility with multiplicity.

An immediate consequence of Lemma 2.3 is that $d(\rho )\leqslant n(\rho )$. The main result of [4] is that $d(\rho ) \geqslant \max (n(\rho )/2, n(\rho ) - m(\rho ))$. Using Lemma 2.3, an immediate corollary of Theorem 1.2 is that $d(\rho ) = n(\rho )$.

Remark 2.18

Define $n(\rho (G))$ to be the largest integer n for which there exists a pair of conjugate characters $(\chi _1, \chi _2)$ modulo $\pi ^{n}$, such that $\chi _1, \chi _2$ factor through $\rho (G)$. Then it is clear that $n(\rho (G))\leqslant n(\rho )$. However, in general there do exist pairs of conjugate characters that do not factor through the image of $\rho$, so a priori, it is not clear that these invariants should be equal. However, it follows from Theorem 1.2 that indeed $n(\rho (G)) = n(\rho ) = d(\rho )$. Note that in [4], the authors only consider $n(\rho (G))$.

2.5 Boundary points

Definition 2.19

Let $U\subseteq \mathcal {X}$ be a subset of the tree $\mathcal {X}$. We say that a vertex $x\in U$ is an interior point of U if $B(x, 1)\subseteq U$. Otherwise, we say that x is a boundary point of U.

Example

Suppose that $U=B(S,r)$ is a band with nerve S and radius r. If $r=0$, then U is a line segment and any vertex $x\in U$ is a boundary point. If $r>0$, the boundary points of U are exactly its leaves.

The following lemma is a slight generalisation of [4, Lem. 36]:

Lemma 2.20

Let $g\in {{\,\textrm{M}\,}}_{2}(\mathcal {O})$ and let x be a boundary point of $\mathcal {X}(\{g\})$. Assume that the characteristic polynomial $P_g(t)$ of g factors as

$$\begin{aligned} P_g(t)\equiv (t-\alpha ) (t-\beta )\pmod {\pi ^n}, \end{aligned}$$

for some $\alpha ,\beta \in \mathcal {O}/\pi ^n\mathcal {O}$. Then there exists a basis $(v_1,v_2)$ of $\Lambda _x/\pi ^n\Lambda _x$ with respect to which $g\pmod {\pi ^n}$ is represented by the matrix

$$\begin{aligned} \begin{pmatrix}\alpha &{} \quad 1 \\ 0 &{} \quad \beta \end{pmatrix}. \end{aligned}$$

Proof

Recall that, by Definition 2.1, $\mathcal {X}(\{g\})$ is the subtree of $\mathcal {X}$ consisting of homothety classes x of lattices $\Lambda _x$ such that $g\Lambda _x\subseteq \Lambda _x$. Note that, by Lemma 2.7, x is an interior point of $\mathcal {X}(\{g\})$ if and only if g acts by a scalar on $\Lambda _x/\pi \Lambda _x$

Suppose that x is a boundary point. Since g does not act by a scalar on $\Lambda _x/\pi \Lambda _x$, there exists an element $\overline{v}\in \Lambda _x/\pi \Lambda _x$ such that $(\overline{v},g \overline{v})$ is a basis of $\Lambda _x/\pi \Lambda _x$. By Nakayama’s lemma (for the ring $\mathcal {O}$), if $v\in \Lambda _x/\pi ^{n}\Lambda _x$ lies above $\overline{v}$, then (v, gv) is basis of $\Lambda _x/\pi ^n\Lambda _x$. Denote $w_2=v$ and let $w_1\in \Lambda _x/\pi ^n\Lambda _x$ be the vector

$$\begin{aligned} w_1=(g-\beta )\cdot w_2. \end{aligned}$$

Clearly, $(w_1,w_2)$ is a basis of $\Lambda _x/\pi ^n\Lambda _x$. In this basis, g is represented by the matrix

$$\begin{aligned} \begin{pmatrix}\alpha &{} \quad 1 \\ 0 &{} \quad \beta \end{pmatrix}. \end{aligned}$$

Indeed,

$$\begin{aligned} g\cdot w_2 = (g-\beta )\cdot w_2+\beta w_2 = w_1+\beta w_2 \end{aligned}$$

and, by the Cayley–Hamilton theorem,

$$\begin{aligned} g\cdot w_1 = (g^2 - \beta g)\cdot w_2 = \alpha (g-\beta )\cdot w_2 = \alpha w_1. \end{aligned}$$

$\square$

Corollary 2.21

Let $g\in {{\,\textrm{M}\,}}_2(\mathcal {O})$, and let x be a boundary point of $\mathcal {X}(\{g\})$. Let n be a positive integer. The following are equivalent:

• (i) The characteristic polynomial $P_g(t)$ is reducible modulo $\pi ^n$.

• (ii) There exists a point $y\in \mathcal {X}(\{g\})$ with $d(x,y)=n$.

Proof

Assume (i). Let $(v_1,v_2)$ be a basis of $\Lambda _x/\pi ^n\Lambda _x$ as in Lemma 2.20. Then, $v_1$ spans a g-invariant free rank one submodule of $\Lambda _x/\pi ^n\Lambda _x$, which by Lemma 2.3 corresponds to a point $y\in \mathcal {X}(\{g\})$ at distance n from x.

Assume (ii). Choose $\Lambda _y$ such that $\pi ^n\Lambda _x\subsetneq \Lambda _y\subsetneq \Lambda _x$. The image of $\Lambda _y$ in $\Lambda _x/\pi ^n\Lambda _x$ is a free rank one submodule, stable under the action of g. Thus, there exists a basis $(v_1,v_2)$ of $\Lambda _x/\pi ^n\Lambda _x$ with respect to which g is upper triangular. Hence, $P_g(t)$ is reducible modulo $\pi ^n$. $\square$

3 Proof of Theorem 1.2

Recall that is a representation, with G a compact group. Let $(\chi _1,\chi _2)$ be a pair of conjugate characters modulo $\pi ^n$. By definition, the characteristic polynomial $P_{\rho (g)}(t)$ of $\rho (g)$ factors as

$$\begin{aligned} P_{\rho (g)}(t)\equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n}, \end{aligned}$$

for all $g\in G$.

To prove Theorem 1.2, instead of working with the group representation $\rho$, we work with the corresponding algebra homomorphism $R :\mathcal {O}[G]\rightarrow {{\,\textrm{M}\,}}_2(K)$. Write $\mathcal {O}[\rho (G)] \subseteq {{\,\textrm{M}\,}}_2(K)$ for the image of R. Then, $\mathcal {O}[\rho (G)]$ is the $\mathcal {O}$-algebra spanned by the image of G in ${{\,\textrm{GL}\,}}_2(K)\subseteq {{\,\textrm{M}\,}}_2(K)$.

Lemma 3.1

Let $g,h\in G$, let $a,b\in \mathcal {O}$ and let $f=a \rho (g)+b \rho (h)\in {{\,\textrm{M}\,}}_2(K)$. Then, modulo $\pi ^n$, the characteristic polynomial $P_f(t)$ of f factors as

$$\begin{aligned} P_f(t)\equiv \big (t-\left( a \chi _1(g)+b\chi _1(h) \right) \big ) \big (t-\left( a \chi _2(g)+b\chi _2(h) \right) \big )\pmod {\pi ^n}. \end{aligned}$$

Proof

We need to show that

$$\begin{aligned} {{\,\textrm{tr}\,}}(f)\equiv \left( a \chi _1(g)+b\chi _1(h) \right) +\left( a \chi _2(g)+b\chi _2(h) \right) \pmod {\pi ^n} \end{aligned}$$

(3.1)

and

$$\begin{aligned} \det (f)\equiv \left( a \chi _1(g)+b\chi _1(h) \right) \left( a \chi _2(g)+b\chi _2(h) \right) \pmod {\pi ^n}. \end{aligned}$$

(3.2)

Identity (3.1) follows from the linearity of the trace and the fact that ${{\,\textrm{tr}\,}}(\rho (g)) \equiv \chi _1(g)+\chi _2(g)\pmod {\pi ^n}$. Identity (3.2) follows from the identity

$$\begin{aligned} \det (A+B)-\det (A)-\det (B)={{\,\textrm{tr}\,}}(A)\cdot {{\,\textrm{tr}\,}}(B)-{{\,\textrm{tr}\,}}(A B), \end{aligned}$$

(3.3)

where $A,B\in {{\,\textrm{M}\,}}_2(K)$, by taking $A=a\rho (g)$ and $B=b\rho (h)$. Indeed, we have

$$\begin{aligned} \det (f)&=\det (a\rho (g)+b\rho (h))\\&=\det (a\rho (g))+\det (b\rho (h))+{{\,\textrm{tr}\,}}(a\rho (g))\cdot {{\,\textrm{tr}\,}}(b\rho (h))-{{\,\textrm{tr}\,}}((a\rho (g))\cdot (b\rho (h)))\\&=a^2\det (\rho (g))+b^2\det (\rho (h))+ab {{\,\textrm{tr}\,}}(\rho (g)) {{\,\textrm{tr}\,}}(\rho (h))-ab{{\,\textrm{tr}\,}}(\rho (g)\rho (h))\\&\equiv a^2\chi _1(g)\chi _2(g)+b^2\chi _1(h)\chi _2(h)\\&\quad +ab\big ((\chi _1(g)+\chi _2(g))(\chi _1(h)+\chi _2(h))-(\chi _1(gh)+\chi _2(gh))\big )\pmod {\pi ^n}\\&\equiv a^2 \chi _1(g)\chi _2(g)+b^2\chi _1(h)\chi _2(h)+ab\big (\chi _1(g)\chi _2(h)+\chi _1(h)\chi _2(g)\big )\pmod {\pi ^n}\\&\equiv \left( a\chi _1(g)+b\chi _1(h) \right) \left( a\chi _2(g)+b\chi _2(h) \right) \pmod {\pi ^n}. \end{aligned}$$

$\square$

Remark 3.2

The identity (3.3) is a polarisation identity. Indeed, consider the symmetric bilinear form $\langle A,B\rangle ={{\,\textrm{tr}\,}}(A)\cdot {{\,\textrm{tr}\,}}(B)-{{\,\textrm{tr}\,}}(AB)$ on . The associated quadratic form $q(A)=\langle A,A\rangle$ is equal to $2\det (A)$. As usual, one recovers a symmetric bilinear from its associated quadratic form by $\langle A,B\rangle =\frac{1}{2}(q(A+B)-q(A)-q(B))$, which is exactly identity (3.3).

Using the same calculation and induction, we deduce the following corollary:

Corollary 3.3

Let $R :\mathcal {O}[G]\rightarrow {{\,\textrm{M}\,}}_2(K)$ be the algebra homomorphism corresponding to $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$. Suppose that there is an integer $n\geqslant 1$ and $\mathcal {O}$-algebra homomorphisms $\chi _1, \chi _2 :\mathcal {O}[G]\rightarrow \mathcal {O}/\pi ^n\mathcal {O}$ such that the characteristic polynomial $P_{\rho (g)}(t)$ of $\rho (g)$ factors as

$$\begin{aligned} P_{\rho (g)}(t) \equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n} \end{aligned}$$

for all $g\in G$. Then

$$\begin{aligned} P_{R(g)}(t) \equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n} \end{aligned}$$

for all $g\in \mathcal {O}[G]$.

We can now prove Theorem 1.2:

Proof of Theorem 1.2

If $\mathcal {X}(\rho ) = \mathcal {X}$, then $\rho (G)$ contains only scalar matrices and the claim is easy. Hence, we may assume that $\mathcal {X}(\rho )$ has boundary points in the sense of Definition 2.19.

The fact that (i) implies (ii) follows immediately from Lemma 2.3. Indeed, if $x,y\in \mathcal {X}(\rho )$ are two points with $d(x,y)=n$, then there is a lattice $\Lambda _x$ such that $\Lambda _x/\pi ^n\Lambda _x$ contains a free rank one G-stable $\mathcal {O}/\pi ^n\mathcal {O}$-submodule. Let $\chi _1 :G\rightarrow (\mathcal {O}/\pi ^n\mathcal {O})^\times$ be the associated representation, and let $\chi _2$ be the quotient of $\rho _{\Lambda _x}\pmod {\pi ^n}$ by $\chi _1$. Then $(\chi _1,\chi _2)$ is a pair of conjugate characters modulo $\pi ^n$.

Assume (ii). Let $(\chi _1,\chi _2)$ be a pair of conjugate characters modulo $\pi ^n$. Let $g_0\in G$ be an element for which $v_\pi (\chi _2(g_0)-\chi _1(g_0))$ is minimal. Here, $v_\pi$ is the truncated valuation on $\mathcal {O}/\pi ^n\mathcal {O}$, taking values $0,1,\ldots ,n$.

We proceed differently in two cases according to whether $\mathcal {X}(\{\rho (g_0)\})=\mathcal {X}(\rho )$ or not. If $\mathcal {X}(\{\rho (g_0)\})=\mathcal {X}(\rho )$, then, by Corollary 2.21 there exist $x,y\in \mathcal {X}(\{\rho (g_0)\})=\mathcal {X}(\rho )$ with $d(x,y)=n$, and we are done.

Assume that $\mathcal {X}(\{\rho (g_0)\})\supsetneq \mathcal {X}(\rho )$. Then there exist two neighbours $x,y\in \mathcal {X}$ such that $x\in \mathcal {X}(\rho )$ and $y\in \mathcal {X}(\{\rho (g_0)\}) \setminus \mathcal {X}(\rho )$. In particular, there exists an element $g_1\in G$ such that $y\notin \mathcal {X}(\{\rho (g_1)\})$. By the choice of $g_0$, there exists an element $a\in \mathcal {O}$ such that

$$\begin{aligned} \chi _2(g_1)-\chi _1(g_1)=a\left( \chi _2(g_0)-\chi _1(g_0) \right) . \end{aligned}$$

Then,

$$\begin{aligned} \chi _2(g_1)-a\cdot \chi _2 (g_0)=\chi _1(g_1)-a\cdot \chi _1(g_0). \end{aligned}$$

Let $f=\rho (g_1)-a\cdot \rho (g_0)$, which is an element of $\mathcal {O}[\rho (G)]$, and let $\delta =\chi _1(g_1)-a\cdot \chi _1(g_0)$. Then, by Lemma 3.1,

$$\begin{aligned} P_f(t)\equiv (t-\delta )^2\pmod {\pi ^n}. \end{aligned}$$

By construction, the point x is a boundary point of $\mathcal {X}(\{f\})$. Hence, by Lemma 2.20, there exists a basis $(v_1,v_2)$ of $\Lambda _x/\pi ^n\Lambda _x$ with respect to which f is represented by the matrix

$$\begin{aligned} \begin{pmatrix}\delta &{} \quad 1 \\ 0 &{} \quad \delta \end{pmatrix}. \end{aligned}$$

Now, let $g\in G$ be any element and let

$$\begin{aligned} \begin{pmatrix}a_g &{} \quad b_g \\ c_g &{} \quad d_g \end{pmatrix}\in {{\,\textrm{GL}\,}}_2(\mathcal {O}/\pi ^n\mathcal {O}) \end{aligned}$$

be the matrix that represents $\rho (g)$ with respect to the basis $(v_1,v_2)$. We will show that $c_g=0$ by computing ${{\,\textrm{tr}\,}}(\,f\cdot \rho (g))\pmod {\pi ^n}$ in two different ways. On the one hand,

$$\begin{aligned} {{\,\textrm{tr}\,}}(\,f\cdot \rho (g)) \equiv {{\,\textrm{tr}\,}}\left( \begin{pmatrix}\delta &{} \quad 1 \\ 0 &{} \quad \delta \end{pmatrix}\cdot \begin{pmatrix}a_g &{} \quad b_g \\ c_g &{} \quad d_g \end{pmatrix} \right) \equiv c_g+\delta \cdot {{\,\textrm{tr}\,}}(\rho (g))\pmod {\pi ^n}. \end{aligned}$$

On the other hand,

$$\begin{aligned} {{\,\textrm{tr}\,}}(\,f\cdot \rho (g))&={{\,\textrm{tr}\,}}((\rho (g_1)-a\cdot \rho (g_0))\cdot \rho (g))\\&={{\,\textrm{tr}\,}}(\rho (g_1g))-a{{\,\textrm{tr}\,}}(\rho (g_0g))\\&\equiv \chi _1(g_1g)+\chi _2(g_1g)-a\cdot (\chi _1(g_0g)+\chi _2(g_0g))\pmod {\pi ^n}\\&\equiv \left( \chi _1(g_1)-a\cdot \chi _1(g_0) \right) \cdot \chi _1(g)+\left( \chi _2(g_1)-a\cdot \chi _2(g_0) \right) \cdot \chi _2(g)\pmod {\pi ^n}\\&\equiv \delta \cdot \chi _1(g)+\delta \cdot \chi _2(g)\pmod {\pi ^n}\\&\equiv \delta \cdot {{\,\textrm{tr}\,}}(\rho (g))\pmod {\pi ^n}. \end{aligned}$$

Combining the two computations, we see that $c_g\equiv 0\pmod {\pi ^n}$ for all $g\in G$. Thus, the element $v_1$ generates a free $\rho (G)$-stable $\mathcal {O}/\pi ^n\mathcal {O}$-submodule of $\Lambda _x/\pi ^n\Lambda _x$. Hence, by Lemma 2.3, there exists a point $z\in \mathcal {X}(\rho )$ with $d(x, z) = n$. $\square$

Remark 3.4

In Theorem 1.2, we can replace the assumption that G is a group with the assumption that G is a set with multiplication, and $\rho :G\rightarrow {{\,\textrm{M}\,}}_{2}(K)$ is a multiplicative map. Indeed, the notion of conjugate characters and the definition of $\mathcal {X}(\rho )$ apply as they are to the more general case, and the proof of Theorem 1.2 only uses the fact that G is closed under multiplication.

The same arguments as above prove the following slightly more general statement in terms of $\mathcal {O}$-algebras:

Theorem 3.5

Let A be an $\mathcal {O}$-algebra and let $R :A\rightarrow {{\,\textrm{M}\,}}_2(K)$ be an $\mathcal {O}$-algebra homomorphism. Assume that A stabilises at least one lattice $\Lambda \subseteq K^2$. Suppose that there is an integer $n\geqslant 1$ and $\mathcal {O}$-algebra homomorphisms $\chi _1, \chi _2 :A\rightarrow \mathcal {O}/\pi ^n\mathcal {O}$ such that the characteristic polynomial $P_{R(g)}(t)$ of R(g) factors as

$$\begin{aligned} P_{R(g)}(t) \equiv (t-\chi _1(g))(t-\chi _2(g))\pmod {\pi ^n} \end{aligned}$$

for all $g\in A$. Then there exist A-stable lattices $\Lambda ' \subseteq \Lambda \subseteq K^2$ such that $\Lambda '/\pi ^n\Lambda \subseteq \Lambda /\pi ^n\Lambda$ is a free $\mathcal {O}/\pi ^n\mathcal {O}$-module of free rank one

4 A generalisation of Ribet’s lemma

4.1 Proof of Theorem 1.3

Proof of Theorem 1.3

Let $s=s(\chi _1,\chi _2)$. Since $\rho$ is irreducible, by Remark 2.4, the diameter $d(\rho )$ of $\mathcal {X}(\rho )$ is finite, and by Theorem 1.2 and Lemma 2.3, $d(\rho ) = n(\rho )$. Let $x,y\in \mathcal {X}(\rho )$ be two vertices with $d(x, y) = n(\rho )$. Then, both x and y are leaves of $\mathcal {X}(\rho )$. Choose lattices $\Lambda _x,\Lambda _y$ representing x, y such that

$$\begin{aligned} \pi ^{n(\rho )}\Lambda _x\subsetneq \Lambda _y\subsetneq \Lambda _x. \end{aligned}$$

By Lemma 2.3, $\Lambda _y/\pi ^{n(\rho )}\Lambda _x$ is a free rank one G-stable submodule of $\Lambda _x/\pi ^{n(\rho )}\Lambda _x$, so G acts on it by a character $\eta _1$. Similarly, $\pi ^{n(\rho )}\Lambda _x/\pi ^{n(\rho )}\Lambda _y$ is a G-stable, free rank one submodule of $\Lambda _y/\pi ^{n(\rho )}\Lambda _y$, so G acts on it by a character $\eta _2$. We see that $\Lambda _x/\pi ^{n(\rho )}\Lambda _x$ is an extension of $\eta _2$ by $\eta _1$, and $\Lambda _y/\pi ^{n(\rho )}\Lambda _y$ is an extension of $\eta _1$ by $\eta _2$. Both extensions are residually non-split because $\Lambda _x/\pi \Lambda _x$ and $\Lambda _y/\pi \Lambda _y$ are indecomposable, by Lemma 2.3.

Denote by $\overline{\eta }_1$ and $\overline{\eta }_2$ the reductions of $\eta _1$ and $\eta _2$ modulo $\pi ^s$. Then $\Lambda _x/\pi ^{s}\Lambda _x$ is a residually non-split extension of $\overline{\eta }_2$ by $\overline{\eta }_1$ and $\Lambda _y/\pi ^{s}\Lambda _y$ is a residually non-split extension of $\overline{\eta }_1$ by $\overline{\eta }_2$. By Lemma 2.12 we can reorder $\eta _1,\eta _2$ so that $\chi _i\pmod {\pi ^s}=\overline{\eta }_i$. $\square$

4.2 Linearly extendable characters and a counterexample

The version of Ribet’s Lemma we give in Theorem 1.3 is optimal: if $(\chi _1, \chi _2)$ is a pair of conjugate characters modulo $\pi ^n$, then it is not true in general that there exists a homothety class $x\in \mathcal {X}(\rho )$ such that $\Lambda _x/\pi ^t\Lambda _x$ is a non-split extension of $\chi _1$ by $\chi _2$ when $t>s$. When $K = \textbf{Q}_2$, one can already find counterexamples arising from elliptic curves over $\textbf{Q}$.

Example

Consider the elliptic curve $E=X_0(24) : y^2 = x^3 -x^2 -4x + 4$, with LMFDB label 24.a4. Then $E[2](\textbf{Q}) = \textbf{Z}/4\textbf{Z}\times \textbf{Z}/2\textbf{Z}$. If $\rho :{{\,\textrm{Gal}\,}}(\overline{\textbf{Q}}/{\textbf{Q}})\rightarrow {{\,\textrm{GL}\,}}_2(\textbf{Q}_2)$ is the 2-adic Galois representation attached to E, then for all $g\in {{\,\textrm{Gal}\,}}(\overline{\textbf{Q}}/{\textbf{Q}})$, we have $P_{\rho (g)}(t)\equiv (t- 1)(t-\chi _{cyc}(g))\pmod {8}$, where $\chi _{cyc}$ is the mod 8 cyclotomic character. In this example, we have $n(\rho ) = 3$, $m(\rho ) = 1$, and $s(1, \chi _{cyc}) = 2$.

By Theorem 1.3, there is a lattice for $\rho$ such that $\Lambda /4\Lambda$ is a non-split extension of $\chi _{cyc}$ by 1 modulo 4. Now, $\mathcal {X}(\rho )$ is exactly the 2-power isogeny graph of E. The lattice $\Lambda$ should correspond to an isogenous elliptic curve $E'$ such that $E'[2](\textbf{Q}) = \textbf{Z}/4\textbf{Z}$. One such choice is $E' :y^2 = x^3- x^2 + x$, with LMFDB label 24.a5.

Since E is not $\textbf{Q}$-isogenous to any elliptic curve with an 8-torsion point, there is no stable lattice $\Lambda$ for $\rho$ such that $\Lambda /8\Lambda$ contains the trivial representation. Hence, Theorem 1.3 is optimal in this example. See [9, Table 2] for further counterexamples arising from elliptic curves over $\textbf{Q}$.

More generally, when K is an arbitrary complete valued field, there are two evident obstructions. First, if such an $x\in \mathcal {X}(\rho )$ exists, then $\chi _1$ and $\chi _2$ must factor through the image of $\rho$. Second, the characters $\chi _1,\chi _2$ must extend $\mathcal {O}$-linearly to $\mathcal {O}[\rho (G)]$. Indeed, if there is a lattice $\Lambda _x$ such that $\Lambda _x/\pi ^t\Lambda _x$ is a non-split extension of $\chi _1$ by $\chi _2$, then we can choose a basis $(v_1,v_2)$ of $\Lambda _x$ such that any $g\in G$ is represented by a matrix

$$\begin{aligned} \begin{pmatrix}\widetilde{\chi }_1(g) &{} \quad b_g \\ \pi ^tc_g &{} \quad \widetilde{\chi }_2(g) \end{pmatrix}, \end{aligned}$$

where $\widetilde{\chi }_1(g),\widetilde{\chi }_2(g)$ are some lifts of $\chi _1(g),\chi _2(g)$ to $\mathcal {O}$. Then, with respect to this basis, any element of $\mathcal {O}[\rho (G)]$ is represented by a matrix in

$$\begin{aligned} {{\,\textrm{M}\,}}_0(\pi ^t):=\left\{ \begin{pmatrix}a &{} \quad b \\ c &{} \quad d \end{pmatrix}: a,b,c,d\in \mathcal {O},\ \pi ^t\mid c\right\} . \end{aligned}$$

Since the maps ${{\,\textrm{M}\,}}_0(\pi ^t)\rightarrow \mathcal {O}\pmod {\pi ^t}$ given by $\left( {\begin{matrix}a &{} b\\ c\pi ^t&{}d\end{matrix}}\right) \mapsto a, d\pmod {\pi ^t}$ are algebra homomorphisms, we see that $\chi _1, \chi _2$ extend $\mathcal {O}$-linearly to $\mathcal {O}[\rho (G)]$.

Definition 4.1

Let $\chi$ be a character modulo $\pi ^n$ of G. We say that $\chi$ is linearly extendable with respect to $\rho$, or simply linearly extendable, if $\chi$ factors through the image of $\rho$ and extends linearly to a map on $\mathcal {O}[\rho (G)]$.

The character $\chi$ is linearly extendable if and only if for each $g_1,\ldots ,g_k\in G$ and $a_1,\ldots ,a_k\in \mathcal {O}$ such that

$$\begin{aligned} \sum _{i=1}^ka_i\rho (g_i)=0, \end{aligned}$$

we have

$$\begin{aligned} \sum _{i=1}^ka_i\chi (g_i)=0. \end{aligned}$$

Using these obstructions, we prove that Theorem 1.3 is best possible:

Proposition 4.2

Fix integers n, s such that $n\geqslant 1$ and $\frac{n}{2}\leqslant s \leqslant n$. Then there exists a group G, a representation $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(\mathcal {O})$ with $n(\rho ) = n$ and a pair of conjugate characters $(\chi _1,\chi _2)$ modulo $\pi ^n$ with $s(\chi _1,\chi _2) = s$ such that for all $t>s(\chi _1,\chi _2)$, there does not exist a vertex $x\in \mathcal {X}(\rho )$ such that $\Lambda _x/\pi ^t\Lambda _x$ is a non-split extension of $\chi _1$ by $\chi _2$ or of $\chi _2$ by $\chi _1$.

Proof

Let

$$\begin{aligned}m = {\left\{ \begin{array}{ll} n &{}\quad s = \lceil \frac{n}{2} \rceil \\ n-s &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

and let G be the group

$$\begin{aligned} G=\left\rbrace \begin{pmatrix}a &{} \quad b \\ \pi ^nc &{} \quad d \end{pmatrix}\in {{\,\textrm{GL}\,}}_2(\mathcal {O})\ \big |\ a,b,c,d\in \mathcal {O},\ a\equiv d\equiv 1\pmod {\pi ^m}\right\lbrace \end{aligned}$$

and let $\rho :G\hookrightarrow {{\,\textrm{GL}\,}}_2(\mathcal {O})$. By [12], any closed subgroup of ${{\,\textrm{GL}\,}}_2(\mathcal {O})$ is topologically finitely generated, so G is topologically finitely generated. By the classification of topologically finitely generated abelian profinite groups, the abelianisation $G^{ab}$ of G is isomorphic to $\textbf{Z}_p^r\times T$ where T is a finite group.

We make the assumption that $r\geqslant 5$, which can always be achieved by choosing appropriately. For example, for any prime p, we can take K to be any degree 5 extension of $\textbf{Q}_p$. Indeed, $G\supset \mathcal {O}^\times$, embedded as the diagonal matrices, and $\mathcal {O}^\times$ contains a finite index subgroup isomorphic to $\mathcal {O}^+\cong \textbf{Z}_p^5$ as a $\textbf{Z}_p$-module.

Let $\chi _1,\chi _2$ be the characters

$$\begin{aligned} \chi _1\left( \begin{pmatrix}a &{} \quad b \\ \pi ^nc &{} \quad d \end{pmatrix} \right) =a\pmod {\pi ^n},\ \ \ \chi _2\left( \begin{pmatrix}a &{} \quad b \\ \pi ^nc &{} \quad d \end{pmatrix} \right) =d\pmod {\pi ^n}. \end{aligned}$$

Then $(\chi _1,\chi _2)$ is a pair of conjugate characters of G modulo $\pi ^n$. We have $n(\rho )=n$. Certainly $m(\chi _1,\chi _2)=m$, so $s(\chi _1, \chi _2) = s$ by definition. The characters $\chi _1,\chi _2$ are evidently linearly extendable. We will construct another pair $(\eta _1,\eta _2)$ of conjugate characters of G modulo $\pi ^n$ such that $\eta _1\pmod {\pi ^t}$ is linearly extendable only when $t\leqslant s(\eta _1, \eta _2)$. Note that, by Remark 2.15, $s(\eta _1, \eta _2) = s$.

Let $g_1, \ldots , g_r, \ldots g_k\in G$ be the pre-images of a minimal set of topological generators for the abelianisation $G^{ab}\simeq \textbf{Z}_p^r\times T$, such that the images of $g_1, \ldots , g_r$ generate $\textbf{Z}_p^r$. By assumption, $r\geqslant 5$, and has dimension 4. Therefore, there exist elements $a_1, \ldots , a_r\in K$, not all zero, such that $\sum _{i = 1}^ra_ig_i = 0$ in , and, up to scaling and reordering, we may assume that $a_i\in \mathcal {O}$ for all i and that $a_1 = 1$.

Let $R_n$ denote the additive group of $\mathcal {O}/\pi ^n\mathcal {O}$. Let $\gamma \in \pi ^sR_n{\setminus }\pi ^{s+1}R_n$. Let $\epsilon :G\rightarrow R_n$ be the unique group homomorphism that satisfies

$$\begin{aligned} \epsilon (g_1)=\chi _1(g_1)^{-1}\gamma ,\ \ \ \epsilon (g_i)=0 \text { for }i =2, \ldots , k. \end{aligned}$$

The image of $\epsilon$ also lies in $\pi ^sR_n$, but not in $\pi ^{s+1}R_n$.

Define $\eta _1(g)=\chi _1(g)(1+\epsilon (g))$ and $\eta _2(g)=\chi _2(g)(1-\epsilon (g))$. A simple computation, based on the fact that $\epsilon (g)\epsilon (h)=0$, shows that $\eta _1$ and $\eta _2$ are characters.

Next, since $\chi _1\epsilon =\chi _2\epsilon$ (recall that $2s\geqslant n$), it is easy to check that $\eta _1+\eta _2=\chi _1+\chi _2$, and since $\epsilon ^2 =0$, we have $\eta _1\eta _2 = \chi _1\chi _2$ Therefore, $\eta _1,\eta _2$ are conjugate characters modulo $\pi ^n$.

Finally, we show that $\eta _1\pmod {\pi ^t}$ is linearly extendable only if $t\leqslant s$. Recall that $\sum _{i=1}^ra_ig_i=0$ where $a_1,\ldots ,a_r\in \mathcal {O}$ and $a_1=1$. Using the fact that $\chi _1$ is linearly extendable, we see that, if $\eta _1\pmod {\pi ^t}$ is linearly extendable, then

$$\begin{aligned} 0\equiv \sum _{i=1}^ra_i\eta _1(g_i) \equiv \sum _{i=1}^ra_i\left( \eta _1(g_i)-\chi _1(g_i) \right) \equiv \chi _1(g_1)\epsilon (g_1) \equiv \gamma \pmod {\pi ^t}. \end{aligned}$$

Since $\gamma \in \pi ^sR_n\setminus \pi ^{s+1}R_n$, we see that $\eta _1\pmod {\pi ^t}$ is linearly extendable only if $t\leqslant s$. $\square$

5 The shape of $\mathcal {X}(\rho )$

In this section, we give a complete classification of the shape of $\mathcal {X}(\rho )$ in terms of the invariants $n(\rho )$ and $m(\rho )$. Conversely, given the shape of $\mathcal {X}(\rho )$ and one additional piece of data, we show how to compute $n(\rho )$ and $m(\rho )$. Given reasonable access to the representation $\rho$ (e.g. a finite list of topological generators of $\rho (G)$), it is easy to compute $\mathcal {X}(\rho )$, but comparatively difficult to compute $m(\rho )$ and $n(\rho )$. Throughout this section, we assume that the characteristic of the residue field of K is not 2.

After [4, Prop. 24], we may assume, without loss of generality, that $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ is irreducible. In this case, $\mathcal {X}(\rho )$ is a band whose shape is determined by its radius $r(\rho )$ and its diameter $d(\rho )$ [4, Thm. 21].

The following theorem, whose proof will occupy the rest of the paper, completes the classification of [4, Thm. 45]:

Theorem 5.1

Suppose that the residue characteristic of K is not 2. Let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be an irreducible representation. Then $\mathcal {X}(\rho )$ is a band of diameter $d(\rho ) = n(\rho )$ and radius

$$\begin{aligned}r(\rho )= {\left\{ \begin{array}{ll} m(\rho ) &{}\quad {\textrm{if}}\; m(\rho )\ne n(\rho )\\ \lfloor \frac{m(\rho )}{2}\rfloor &{}\quad {\textrm{if}}\; m(\rho ) = n(\rho ). \end{array}\right. } \end{aligned}$$

Given $m(\rho )$ and $n(\rho )$, Theorem 5.1 gives the exact shape of $\mathcal {X}(\rho )$. On the other hand, just knowing $d(\rho )$ and $r(\rho )$ is not enough to recover $n(\rho )$ and $m(\rho )$. By definition, if $x,y\in \mathcal {X}$ are neighbours, then the generalised ball $B(\{x,y\}, r)$ of radius r is also a band of diameter $2r +1$ and radius r and, in this case, two representations $\rho , \rho '$ with $n(\rho ) = n(\rho ')$ and $m(\rho ) \ne m(\rho ')$ can have $\mathcal {X}(\rho ) = \mathcal {X}(\rho ') = B(\{x,y\}, r)$. We can tell these cases apart by using thin elements.

Definition 5.2

Let $g\in G$. We say that g is a thin element for $\rho$ if $\mathcal {X}(\{\rho (g)\})$ is an infinite band of radius $r(\rho )$. Equivalently, g is a thin element for $\rho$ if there exists a basis of with respect to which $\rho (g)$ is represented by the matrix

$$\begin{aligned} \begin{pmatrix}\alpha &{} \quad 0 \\ 0 &{} \quad \beta \end{pmatrix}, \end{aligned}$$

where $\alpha ,\beta \in \mathcal {O}$ and $v_\pi (\beta -\alpha )=r(\rho )$.

Theorem 5.3

Suppose that the residue characteristic of K is not 2. Let $\rho :G\rightarrow {{\,\textrm{GL}\,}}_2(K)$ be an irreducible representation, and suppose that $\mathcal {X}(\rho )$ is a finite band of diameter $d(\rho )$ and radius $r(\rho )$. Then, $n(\rho ) = d(\rho )$ and

$$\begin{aligned}m(\rho ) = {\left\{ \begin{array}{ll} d(\rho ) &{}\quad {\textrm{if}}\; d(\rho ) = 2r(\rho )\\ d(\rho ) &{}\quad {\textrm{if}}\; d(\rho ) = 2r(\rho )+1\; {\textrm{and}}\; {\textrm{if}}\; G\; {\textrm{does}}\; {\textrm{not}}\; {\textrm{contain}}\; {\textrm{a}}\; {\textrm{thin}}\; {\mathrm{element.}}\\ r(\rho ) &{}\quad {\textrm{otherwise}}. \end{array}\right. } \end{aligned}$$

Remark 5.4

Suppose that $d(\rho ) = 2r(\rho )+1$, i.e. that $\mathcal {X}(\rho )$ is a generalised ball. Then we can determine whether or not G contains a thin element by looking at any list of topological generators of $\rho (G)$, since, in this case, if $g,h\in G$ and gh is a thin element, then g or h must be a thin element.

Indeed, let $(\chi _1,\chi _2)$ be a pair of conjugate characters modulo $\pi ^{d(\rho )}$ of G. First, since $d(\rho )>2r(\rho )$, by a version of Hensel’s lemma (Lemma 5.10), if $v_\pi (\chi _2(g)-\chi _1(g))\leqslant r(\rho )$, for an element $g\in G$, then g is a thin element. Thus, if h and g are not thin elements

$$\begin{aligned} v_\pi (\chi _2(g)-\chi _1(g))>r(\rho ),\ \ \ \text {and}\ \ \ v_\pi (\chi _2(h)-\chi _1(h))>r(\rho ). \end{aligned}$$

By writing

$$\begin{aligned} \chi _2(gh)-\chi _1(gh) =\chi _2(g)(\chi _2(h)-\chi _1(h))+\chi _1(h)(\chi _2(g)-\chi _1(g)), \end{aligned}$$

we see that

$$\begin{aligned} v_\pi \left( \chi _2(gh)-\chi _1(gh) \right) >r(\rho ). \end{aligned}$$

Thus, gh is not a thin element of G.

Therefore, if $d(\rho ) = 2r(\rho )+1$, then G contains a thin element if and only if one the generators of $\rho (G)$ is a thin element.

5.1 The invariant $k(\rho )$

Definition 5.5

We denote by $k(\rho )$ the largest integer k for which the map

$$\begin{aligned} g\mapsto \frac{{{\,\textrm{tr}\,}}\rho (g)}{2}\pmod {\pi ^k} \end{aligned}$$

is multiplicative.

Let $\chi$ denote the character $g\mapsto \frac{{{\,\textrm{tr}\,}}\rho (g)}{2}\pmod {\pi ^k}$. Then, by definition, ${{\,\textrm{tr}\,}}(\rho ) = \chi +\chi \pmod {\pi ^k}$, and since $p\ne 2$, $(\chi ,\chi )$ is a pair of conjugate characters modulo $\pi ^{k(\rho )}$. In particular,

$$\begin{aligned} P_{\rho (g)}(t)\equiv \left( t-\frac{{{\,\textrm{tr}\,}}\rho (g)}{2} \right) ^2\pmod {\pi ^{k(\rho )}} \end{aligned}$$

for all $g\in G$. Note that $m(\rho )\leqslant k(\rho ) \leqslant n(\rho )$.

Remark 5.6

Recall that the invariant $m(\rho )$ is the largest integer m for which there exists a pair of conjugate characters $(\chi _1, \chi _2)$ modulo $\pi ^{n(\rho )}$ such that $\chi _1\equiv \chi _2\pmod {\pi ^m}$. In particular, $m(\rho )$ is the largest integer m for which there exists a character $\chi$ modulo $\pi ^m$ with ${{\,\textrm{tr}\,}}\rho (g) = 2\chi \pmod {\pi ^m}$ such that $\chi$ lifts to a character modulo $\pi ^{n(\rho )}$. By contrast, $k(\rho )$ is the largest integer k for which there exists a character $\chi$ modulo $\pi ^k$ such that ${{\,\textrm{tr}\,}}\rho = 2\chi \pmod {\pi ^k}$, but $\chi$ need not lift to a character modulo $\pi ^{n(\rho )}$.

Remark 5.7

There appears to be a gap in the proof of [4, Thm. 45]: in [4, Prop. 32], the authors claim that $r(\rho ) \leqslant m(\rho )$. However, their proof only shows that $r(\rho ) \leqslant k(\rho )$. Indeed, their proof shows that there is a lattice $\Lambda$ such that the action of G on $\Lambda /\pi ^{r(\rho )}\Lambda$ is by a character; however, it is not clear why this character should extend to a character on $\Lambda /\pi ^{n(\rho )}\Lambda$. The fact that $r(\rho ) \leqslant m(\rho )$ is a consequence of the next three lemmas.

Lemma 5.8

(c.f. [4, Prop. 31])

• (i) Either $m(\rho )=n(\rho )$ or $2m(\rho )<n(\rho )$.

• (ii) We have

  $$\begin{aligned} k(\rho ) = {\left\{ \begin{array}{ll}2m(\rho ) &{}\quad {\textrm{if}}\; m(\rho )\ne n(\rho )\\ m(\rho ) &{}\quad {\textrm{if}}\; m(\rho ) = n(\rho ).\end{array}\right. } \end{aligned}$$

Proof

Part (i) is [4, Prop. 31].

For part (ii), if $m(\rho ) = n(\rho )$, the result follows immediately from the inequality $m(\rho )\leqslant k(\rho )\leqslant n(\rho )$. So assume that $m(\rho ) \ne n(\rho )$, and let $(\chi _1, \chi _2)$ be a pair of conjugate characters modulo $\pi ^{n(\rho )}$ such that $\chi _1\equiv \chi _2\pmod {\pi ^{m(\rho )}}$. Since $\chi _1(g)\equiv \chi _2(g)\pmod {\pi ^{m(\rho )}}$, it is easy to verify that the map

$$\begin{aligned} g\mapsto \frac{\chi _1(g)+\chi _2(g)}{2}=\frac{{{\,\textrm{tr}\,}}\rho (g)}{2}\pmod {\pi ^{2m(\rho )}} \end{aligned}$$

is multiplicative. Hence, $2m(\rho ) \leqslant k(\rho )$.

For $i=1,2$, we have

$$\begin{aligned} \left( \chi _i(g)-\frac{{{\,\textrm{tr}\,}}(\rho (g))}{2} \right) ^2\equiv 0 \pmod {\pi ^{k(\rho )}}, \end{aligned}$$

for all $g\in G$. Therefore, $\chi _1(g)\equiv \frac{{{\,\textrm{tr}\,}}(\rho (g))}{2}\equiv \chi _2(g)\pmod {\pi ^{\lceil k(\rho )/2\rceil }}$, for all $g\in G$. It follows that $2m(\rho )\geqslant k(\rho )$. Hence, $2m(\rho ) = k(\rho )$. $\square$

Lemma 5.9

We have $k(\rho )\geqslant 2r(\rho )$. If, in addition, G contains a thin element then $k(\rho )=2r(\rho )$.

Proof

Let x be a point on the nerve of $\mathcal {X}(\rho )$, and let $\ell _1,\ell _2$ be two leaves of $\mathcal {X}(\rho )$, both at distance $r(\rho )$ from x and at distance $2r(\rho )$ from one another. Then, there exists a basis $(v_1,v_2)$ of $\Lambda _{\ell _1}$ such that $(v_1,\pi ^{r(\rho )}v_2)$ is a basis of $\Lambda _x$ and $(v_1,\pi ^{2r(\rho )}v_2)$ is a basis of $\Lambda _{\ell _2}$.

For all $g\in G$, let

$$\begin{aligned} \begin{pmatrix}a_g &{} \quad b_g \\ \pi ^{2r(\rho )}c_g &{} \quad d_g \end{pmatrix} \end{aligned}$$

be the matrix representing the action of g with respect to the basis $(v_1,v_2)$. Then the action of g, with respect to the basis $(v_1,\pi ^{r(\rho )}v_2)$, is

$$\begin{aligned} \begin{pmatrix}a_g &{} \quad \pi ^{r(\rho )}b_g \\ \pi ^{r(\rho )}c_g &{} \quad d_g \end{pmatrix}. \end{aligned}$$

From the first presentation, we see that the maps $g\mapsto a_g\pmod {\pi ^{2r(\rho )}}$ and $g\mapsto d_g\pmod {\pi ^{2r(\rho )}}$ are characters of G. Moreover, since x is in the nerve of $\mathcal {X}(\rho )$, by definition, $B(x, r(\rho ))\subseteq \mathcal {X}(\rho )$. Hence, by Lemma 2.7, G acts on $\Lambda _x/\pi ^{r(\rho )}\Lambda _x$ by a character. Therefore, $a_g\equiv d_g\pmod {\pi ^{r(\rho )}}$. It follows that the function $G\rightarrow (\mathcal {O}/\pi ^{2r(\rho )}\mathcal {O})^\times$ given by

$$\begin{aligned} g\mapsto \frac{1}{2}(a_g+d_g)\equiv \frac{{{\,\textrm{tr}\,}}(g)}{2}\left( \textrm{mod}\,\, {\pi ^{2r(\rho )}}\right) \end{aligned}$$

is a multiplicative character, and hence, $k(\rho )\geqslant 2r(\rho )$.

Assume that G contains a thin element $h\in G$. It remains to show that $k(\rho )\leqslant 2r(\rho )$. The characteristic polynomial of h factors as

$$\begin{aligned} P_h(t)=(t-\alpha )(t-\beta ), \end{aligned}$$

for some $\alpha ,\beta \in \mathcal {O}$ with $v_\pi (\beta -\alpha )=r(\rho )$. Modulo $\pi ^{k(\rho )}$ we have

$$\begin{aligned} P_h(t)\equiv (t-\alpha )(t-\beta )\equiv (t-\gamma )^2\pmod {\pi ^{k(\rho )}}, \end{aligned}$$

where $\gamma =\frac{1}{2}{{\,\textrm{tr}\,}}(h) = \frac{\alpha +\beta }{2}$. It follows that

$$\begin{aligned} \left( \frac{\alpha +\beta }{2}\right) ^2 \equiv \alpha \beta \pmod {\pi ^{k(\rho )}} \end{aligned}$$

and hence that $(\alpha -\beta )^2 \equiv 0\pmod {\pi ^{k(\rho )}}$. Hence, $k(\rho )\leqslant 2r(\rho )$. $\square$

5.2 Proof of Theorems 5.1 and 5.3

Recall the following version of Hensel’s Lemma [10, Thm. 7.3]:

Lemma 5.10

Let $P(t)\in \mathcal {O}[t]$ be a monic quadratic polynomial and let n be a positive integer. Suppose that

$$\begin{aligned} P(t)\equiv (t-\alpha )(t-\beta )\pmod {\pi ^n}, \end{aligned}$$

for some $\alpha ,\beta \in \mathcal {O}$ with $v_\pi (\alpha -\beta )<\frac{n}{2}$. Then there exist $\alpha ',\beta '\in \mathcal {O}$ such that

$$\begin{aligned} P(t)=(t-\alpha ')(t-\beta '). \end{aligned}$$

Moreover, $v_\pi (\alpha -\beta )=v_\pi (\alpha '-\beta ')$.

Lemma 5.11

If $d(\rho ) > 2r(\rho )+1$, then G contains a thin element.

Proof

Fix $x,y\in \mathcal {X}(\rho )$ with $d(x,y)=d(\rho )$. Then there exists a basis $(v_1,v_2)$ of $\Lambda _x$ such that $(v_1,\pi ^{d(\rho )}v_2)$ is a basis of $\Lambda _y$. With respect to this basis, the action of any $g\in G$ is represented by a matrix of the form

$$\begin{aligned} \begin{pmatrix}a_g &{} \quad b_g \\ \pi ^{d(\rho )}c_g &{} \quad d_g \end{pmatrix}. \end{aligned}$$

Now let $z\in \mathcal {X}(\rho )$ be a vertex in the centre of the nerve of $\mathcal {X}(\rho )$ (if the nerve has even cardinality, let z be the central point closest to x). Let $\ell \in \mathcal {X}(\rho )$ be a boundary point with $d(\ell ,z)=r(\rho )$. If $\mathcal {X}(\rho )=B(S,r(\rho ))$ and S is a line segment of length a, then $d(\rho )=a+2r(\rho )$ and $d(x,z)=r+\lfloor a/2\rfloor$. Note that if $r(\rho )=0$, then $\ell =z$.

We can choose an element $h\in G$ such that both x and $\ell$ are boundary points of $\mathcal {X}(\{h\})$. Indeed, let $g_1\in G$ be such that x is a boundary point of $\mathcal {X}(\{\rho (g_1)\})$ and let $g_2\in G$ be such that $\ell$ is a boundary point of $\mathcal {X}(\{\rho (g_2)\})$. Then, either $\ell$ is also a boundary point of $\mathcal {X}(\{\rho (g_1)\})$, x is a boundary point of $\mathcal {X}(\{\rho (g_2)\})$ or both x and $\ell$ are boundary points of $\mathcal {X}(\{\rho (g_1g_2)\})$. Indeed, if x is not a boundary point of $\mathcal {X}(\{\rho (g_2)\})$, then, by Definition 2.19, all its neighbours are fixed by $\rho (g_2)$. Since x is a boundary point of $\mathcal {X}(\{\rho (g_1)\})$ by definition, there exists a neighbour $x'$ of x such that $\rho (g_1)\Lambda _{x'} \ne \Lambda _{x'}$, where $\Lambda _{x'}$ is any representative of $x'$. But then $\rho (g_1g_2)\Lambda _{x'} = \rho (g_1)\Lambda _{x'} \ne \Lambda _{x'}$, so x is not a boundary point of $\mathcal {X}(\{\rho (g_1g_2)\})$. The argument for $\ell$ is similar.

The vectors $(v_1,\pi ^{d(x,z)}v_2)$ form a basis of $\Lambda _z$, with respect to which, the action of h is represented by the matrix

$$\begin{aligned} \begin{pmatrix}a_h &{} \quad \pi ^{d(x,z)}b_h \\ \pi ^{d(\rho )-d(x,z)}c_h &{} \quad d_h \end{pmatrix}. \end{aligned}$$

Note that, by the definition of z, $r(\rho )< \frac{d(\rho )-1}{2}\leqslant d(x,z)$ and that $r(\rho )<d(\rho )-d(x,z)$. Therefore, modulo $\pi ^{r(\rho )+1}$, h is represented by the matrix

$$\begin{aligned} \begin{pmatrix}a_h &{} \quad 0 \\ 0 &{} \quad d_h \end{pmatrix}\pmod {\pi ^{r(\rho )+1}}. \end{aligned}$$

Now, $\mathcal {X}(\rho )$ contains the ball of radius $r(\rho )$ around z, so $v_\pi (d_h - a_h) \geqslant r(\rho )$. On the other hand, by the way we chose h, $B(z,r(\rho )+1)\not \subseteq \mathcal {X}(\{h\})$, so, by Lemma 2.7, h does not act as a scalar on $\Lambda _z/\pi ^{r(\rho ) + 1}\Lambda _z$. Hence, $v_\pi (d_h - a_h) = r(\rho )$. By Lemma 5.10, we see that h is a thin element for $\rho$. $\square$

Proof of Theorems 5.1 and 5.3

By Theorem 1.2, we always have $d(\rho ) = n(\rho )$. Note that Theorem 5.3 implies Theorem 5.1, so we only need to prove the former theorem.

If $d(\rho ) = 2r(\rho )$, then, by Lemma 5.9

$$\begin{aligned} n(\rho ) = d(\rho ) = 2r(\rho ) \leqslant k(\rho ) \leqslant n(\rho ) \end{aligned}$$

so $k(\rho ) = n(\rho )$. Hence, by Lemma 5.8, $m(\rho ) = n(\rho )$.

If $d(\rho )>2r(\rho ) + 1$, then, by Lemma 5.11, G contains a thin element, so by Lemma 5.9,

$$\begin{aligned} k(\rho ) = 2r(\rho ) < d(\rho ) = n(\rho ), \end{aligned}$$

so $k(\rho ) \ne n(\rho )$. Hence, by Lemma 5.8, $k(\rho ) = 2m(\rho )$. So $m(\rho ) = r(\rho )$.

Finally, suppose that $d(\rho )=2r(\rho ) + 1$. If G contains a thin element, then, by Lemma 5.9, $k(\rho ) = 2r(\rho ) = d(\rho ) -1 < n(\rho )$. Thus, by Lemma 5.8, $k(\rho ) = 2\,m(\rho )$, so $m(\rho ) = r(\rho )$.

Now suppose that G does not contain a thin element. Suppose for contradiction that $m(\rho ) \ne n(\rho )$. Then, by Lemma 5.8, $2m(\rho )<n(\rho )$. Thus, there exists an element $g\in G$ such that the characteristic polynomial of $\rho (g)$ factors as

$$\begin{aligned} P_{\rho (g)}(t)\equiv (t-\alpha ) (t-\beta )\pmod {\pi ^{n(\rho )}}, \end{aligned}$$

with $\alpha ,\beta \in \mathcal {O}/\pi ^{n(\rho )}\mathcal {O}$ satisfying $v_\pi (\beta -\alpha )=m(\rho )<n(\rho )/2$. Thus, by Lemma 5.10, g is a thin element in G, a contradiction. $\square$